Int. J. Communications, Network and System Sciences, 2012, 5, 520-533
http://dx.doi.org/10.4236/ijcns.2012.59063 Published Online September 2012 (http://www.SciRP.org/journal/ijcns)
Classification of Multi-User Chirp Modulation Signals
Using Wavelet Higher-Order-Statistics Features and
Artificial Intelligence Techniques
Said E. El-Khamy, Hend A. Elsayed
Department of Electrical Engineering, Faculty of Engineering, Alexandria University, Alexandria, Egypt
Received July 2, 2012; revised July 30, 2012; accepted August 13, 2012
ABSTRACT
Higher order statistical features have been recently proved to be very efficient in the classification of wideband com-
munications and radar signals with great accuracy. On the other hand, the denoising properties of the wavelet transform
make WT an efficient signal processing tool in noisy environments. A novel technique for the classification of
multi-user chirp modulation signals is presented in this paper. A combination of the higher order moments and cumu-
lants of the wavelet coefficients as well as the peaks of the bispectrum and its bi-frequencies are proposed as effective
features. Different types of artificial intelligence based classifiers and clustering techniques are used to identify the
chirp signals of the different users. In particular, neural networks (NN), maximum likelihood (ML), k-nearest neighbor
(KNN) and support vector machine (SVMs) classifiers as well as fuzzy c-means (FCM) and fuzzy k-means (FKM)
clustering techniques are tested. The Simulation results show that the proposed technique is able to efficiently classify
the different chirp signals in additive white Gaussian noise (AWGN) channels with high accuracy. It is shown that the
NN classifier outperforms other classifiers. Also, the simulations prove that the classification based on features ex-
tracted from wavelet transform results in more accurate results than that using features directly extracted from the chirp
signals, especially at low values of signal-to-noise ratios.
Keywords: Artificial Intelligence Techniques; Classification; Discrete Wavelet Transform; Higher Order Statistics;
Multi-User Chirp Modulation Signals
1. Introduction
Automatic signal classification plays an important role in
various applications. For example, in military applications,
it can be employed for electronic surveillance and moni-
toring. In civil applications, it can be used for spectrum
management, network traffic administration, signal con-
firmation, cognitive radio, software radios, and intelli-
gent modems [1]. The early researches were concentrated
on analog signals in [2] and have been recently extended
to digital types of signals used in modern communication
systems [3-5]. In this paper, we present an automatic
digital signal type classifier for multi-user chirp signals
in additive white Gaussian noise channels. Chirp modu-
lation has been considered for many applications as bea-
cons, aircraft ground data links via satellite repeaters,
low rate data transmission in the high frequency (HF)
band. It is commonly used in sonar and radar, but it has
other applications. For example, it can be used in multi-
user spread spectrum and UWB communications.
Higher order statistical (HOS) features have been
recently proved to be very efficient in the classification
of wideband communications, radar and biomedical
signals with great accuracy [6-9]. For example, an auto-
matic classifier of different digital modulation signals, in
additive white Gaussian noise channels, was suggested
using a combination of the higher order moments and
higher order cumulants up to order eighth as features and
using multilayer preceptor neural network (NN) in [3],
and using a Hierarchical support vector machine (SVM)
based Classifier in [4] and [5]. The bispectrum features
were used as to classify mental tasks from EEG signals in
[6] and to classify heart rate signals in [7]. Classification of
arrhythmias has been made using K-means clustering in
[8]. Classifying emotions using fuzzy C-means (FCM)
and fuzzy K-means (FKM) were introduced in [9]. Using
combination of fuzzy clustering and hierarchical clustering
for symbol based modulation classification was described
in [10]. FCM algorithm was suggested for texture based
segmentation in [11]. The Mary Shift Keying Modulation
Scheme Identification Algorithm using Wavelet Transform
and Higher Order Statistical Moment is made in [12] and
the automatic modulation recognition in wireless systems
C
opyright © 2012 SciRes. IJCNS

S. E. EL-KHAMY, H. A. ELSAYED 521
using cepestral analysis and neural networks with fea-
tures that are extracted from discrete transforms has been
considered [13].
A preliminary investigation on the classification of
multi-user chirp modulation signals using higher order
moments and cumulants with four artificial intelligence
classification types along with FCM and FKM clustering
has been considered by the authors in [14] and [15].
Bispectrum features were also considered by the authors
in [16]. In this paper, we also consider using wavelet
transform (WT) for efficient features extraction. Wavelet
transform has a variable time-frequency resolution, which
leads to locality in both the time and frequency domains
[17]. The locality of the transform of a signal is impor-
tant in two ways for pattern recognition. Firstly, different
parts of the signal may convey different amounts of
information. Secondly, when the signal is corrupted by
local noise in time and/or frequency domain, the noise
affects only a few coefficients if the coefficients represent
local information in the time and frequency domains. In
fact, the wavelet transform is used to divide a given
modulated signal into different subbands of different
scales to study each scale, separately. The idea of the
discrete wavelet transform (DWT) is to represent a signal
as a series of approximation (low pass version) and
details (high pass version) at different resolutions. The
signal is low pass filtered to give half of its length called
an approximation signal and high pass filtered to give
another half of its length called details signal. Both of
them can be used to model the signal. The simplest type
of wavelets is Haar wavelet. Haar wavelets are related to a
mathematical operation called the Haar transform in the
discrete form. All other wavelet transforms used the Haar
transform as a prototype.
In general, automatic digital signal classification is
divided into two main steps which are the feature extraction
and classification. In this classifier, the additive white
Gaussian noise (AWGN) corrupted input signals are nor-
malized to have zero mean and unit variance and the
normalized signals are passed to the feature extraction
step. In this paper, features are extracted by using three
methods. The first one is the selected combination of the
higher order moments and higher order cumulants up to
order eighth from the signal itself. The second method is
the selected combination of the higher order moments
and higher order cumulants up to order eighth from the
DWT of the signal. The third feature extraction method
is the selected peaks of the bispectrum of the signal itself
and its bi-frequencies. Different types of classification
techniques are utilized to use these features to classify
the input signals and get the signal type. Different types
of classifiers were used such as maximum likelihood
classifier, k-nearest neighbor classifier, support vector
machine classifier, and neural network classifier as well
as FKM and FCM clustering.
This paper is organized as follows. Section 2 describes
higher order statistics, and Section 3 describes multi-user
chirp modulation signals. Section 4 describes features
extraction and Section 5 describes classification tech-
niques. Section 6 shows simulation results and finally,
Section 7 concludes the paper.
2. Higher Order Statistics
The auto-moment of the random variable may be defined
as follows [18] and [19]:
The pth order moments of a discrete signal s is defined as

*q pq
pq
MEss







 (1a)
For example,


344
41

M
Eajb ajbEa b

 

(1b)
Assuming a zero-mean discrete based-band signal se-
quence of the form s = a + jb, the pth order cumulant is
defined as:
 
**
terms terms
Cum,, ,,,
pq
pq q
Csss

s












j
(2)
where,
 
1
1
1
Cum,,11 !
q
nj
vjv jvq
s
sqEsE


 
 
 

 


s
(3)
and the summation is being performed an all partitions v
= (v1, ···, vq) for the set of indices (1, ···, n).
The higher order statistics have the ability to suppress
additive colored Gaussian noise of unknown power spec-
trum, identify non minimum phase system or reconstruct
non minimum phase signal and extract information due
to deviation from Gaussianity. A non Gaussian signal can
be decomposed into its higher order cumulant functions
where each one of them may contain different informa-
tion about the signals. This can be very useful in signal
classification problems where distinct classification fea-
tures can be extracted from higher order spectrum domain.
3. Multi-User Chirp Modulation Signals
Chirp modulation has been considered for many applica-
tions as beacons, aircraft ground data links via satellite
repeaters, low rate data transmission in the high fre-
quency (HF) band, in the market; from imaging radars,
test signals, optical imaging to instrumentation and sili-
con yield enhancement. It is commonly used in sonar and
radar, but has other applications, such as in spread
spectrum communications. In spread spectrum usage,
surface acoustic wave (SAW) devices are often used to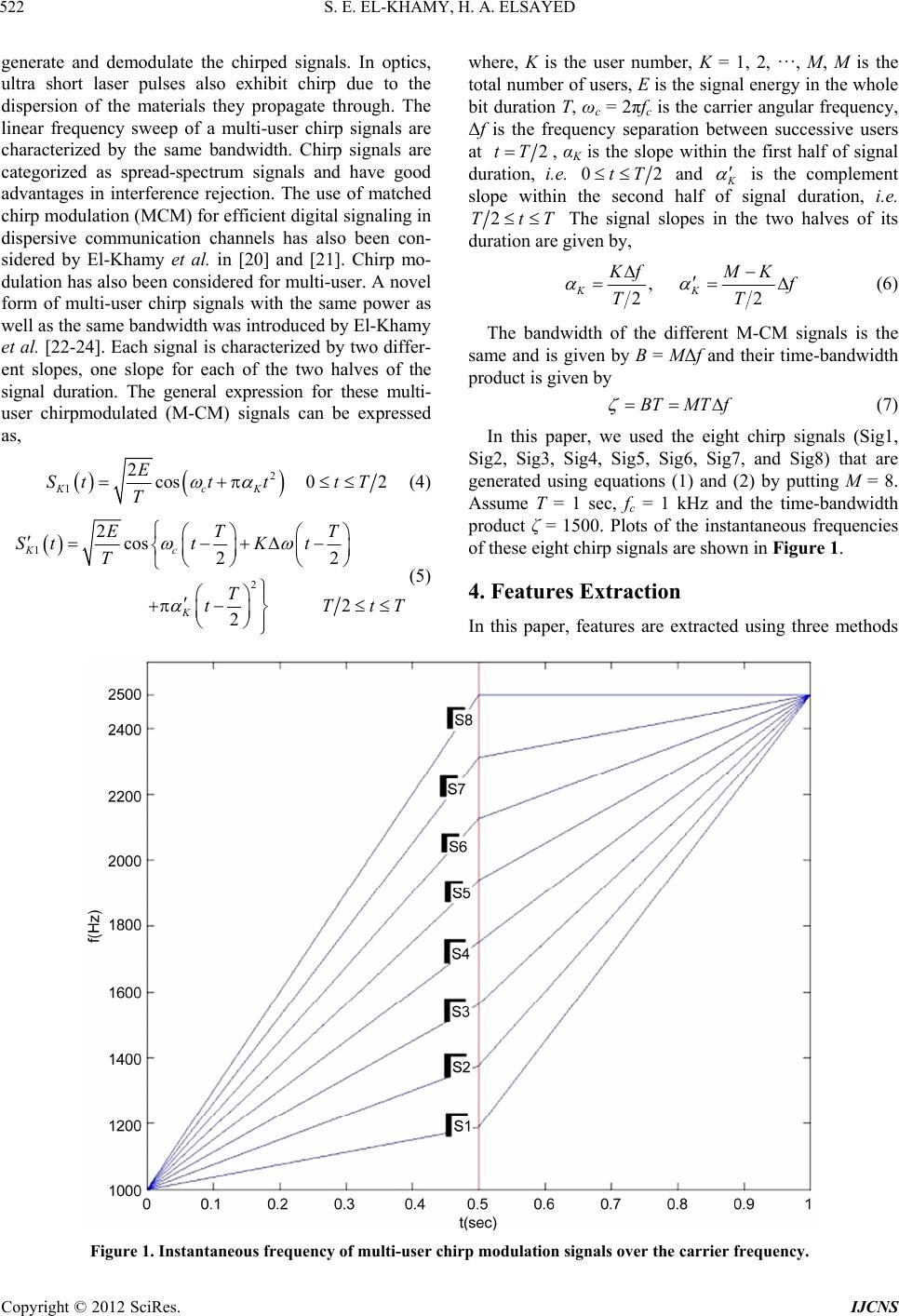

S. E. EL-KHAMY, H. A. ELSAYED
522
generate and demodulate the chirped signals. In optics,
ultra short laser pulses also exhibit chirp due to the
dispersion of the materials they propagate through. The
linear frequency sweep of a multi-user chirp signals are
characterized by the same bandwidth. Chirp signals are
categorized as spread-spectrum signals and have good
advantages in interference rejection. The use of matched
chirp modulation (MCM) for efficient digital signaling in
dispersive communication channels has also been con-
sidered by El-Khamy et al. in [20] and [21]. Chirp mo-
dulation has also been considered for multi-user. A novel
form of multi-user chirp signals with the same power as
well as the same bandwidth was introduced by El-Khamy
et al. [22-24]. Each signal is characterized by two differ-
ent slopes, one slope for each of the two halves of the
signal duration. The general expression for these multi-
user chirpmodulated (M-CM) signals can be expressed
as,
where, K is the user number, K = 1, 2, ···, M, M is the
total number of users, E is the signal energy in the whole
bit duration T, ωc = 2πfc is the carrier angular frequency,
Δf is the frequency separation between successive users
at 2tT

, αK is the slope within the first half of signal
duration, i.e. 02tT

 and
K

 is the complement
slope within the second half of signal duration, i.e.
2TtT

 The signal slopes in the two halves of its
duration are given by,
,
22
KK
KfM K
f
TT




 (6)
The bandwidth of the different M-CM signals is the
same and is given by B = MΔf and their time-bandwidth
product is given by
BTMTf


 (7)
In this paper, we used the eight chirp signals (Sig1,
Sig2, Sig3, Sig4, Sig5, Sig6, Sig7, and Sig8) that are
generated using equations (1) and (2) by putting M = 8.
Assume T = 1 sec, fc = 1 kHz and the time-bandwidth
product ζ = 1500. Plots of the instantaneous frequencies
of these eight chirp signals are shown in Figure 1.


2
1
2cos0 2
KcK
E
Stt ttT
T
  (4)

1
2
2cos 22
2
2
Kc
K
ET T
SttK t
T
T
tT


 

 
 




  





tT
(5) 4. Features Extraction
In this paper, features are extracted using three methods
Figure 1. Instantaneous frequency of multi-user chirp modulation signals over the carrier frequency.

S. E. EL-KHAMY, H. A. ELSAYED 523
the first one is a combination of higher order moments
and cumulants from the signal used, the second one is the
higher order moments and cumulants from the discrete
wavelet transform coefficients of the signal, and the third
one is the peaks of the bispectrum of the signal used it-
self and its bi-frequencies.
4.1. Higher Order Moments and Cumulants
We used six features for classification; these features are
the even higher order moments and cumulants up to eight.
Even order moments and cumulants expressions up to
eighth order are found in [18] and compare its perform-
ance with the cases of only using two features that is the
fourth order moments and cumulants, the two only fea-
tures that have the highest standard deviation (STD) of
each feature for these signals, and the only four sixth and
eighth order features are used. The selected features are
those which show significant differences between the
different chirp signals.
4.2. Features from Discrete Wavelet Transform
The features are extracted using higher the even higher
order moments and cumulants up to eight from wavelet
transform coefficients and approximation coefficients
and details coefficients of the eight chirp signals we used
six features for classification and compare its performance
with using the features from the signal itself.
4.3. Bispectrum Features
The third order cumulants generating function is called the
tricorrelation and is shown in Equation (8). The Fourier
transform of the tricorrelation is a function of
two frequencies and called the bispectrum or the third
order polyspectrum in Equation (8) [25] and [26].

3,
x
Ckm

 


3,
x
CkmE xnxnmxnk 

 

(8)
 
12
22
312 3
,,
j
fkjf m xx
km
SffCkme e
  
 
 (9)
The bispectrum or the third order poly-spectrum is the
easiest to compute and hence the most popular and falls
in the category of the Higher Order Spectral Analysis
Matlab Toolbox (HOSA) [26]. The features are the high-
est peaks of the bispectrum and the corresponding two
frequency components. The selected features are those
which show significant differences between the different
chirp signals.
5. Classification Techniques
5.1. Maximum Likelihood Classifier
In the maximum likelihood (ML) approach, the classifi-
cation is viewed as a multiple hypothesis testing problem,
where a hypothesis, Hi, is arbitrarily assigned to the ith
modulation type of m possible types. The ML classifica-
tion is based on the conditional probability density func-
tion [27].
5.2. K-Nearest Neighbor Classifier
K-Nearest Neighbor algorithm (KNN) is one of the sim-
plest but widely using machine learning algorithms. An
object is classified by the “distance” from its neighbors,
with the object being assigned to the class most common
among its k distance-nearest neighbors. If k = 1, the al-
gorithm simply becomes nearest neighbor algorithm and
the object is classified to the class of its nearest neighbor
[28].
5.3. Support Vector Machine Classifier
SVMs were introduced on the foundation of statistical
learning theory. The basic SVM deals with two-class
problems; however, with some methods it can be devel-
oped for multiclass classification [29]. Binary-SVM per-
forms classification tasks by constructing the optimal
separating hyper-plane (OSH). OSH maximizes the mar-
gin between the two nearest data points belonging to the
two separate classes. The performance of SVM depends
on penalty parameter (C) and the kernel parameter, which
are called hyper-parameters. In this paper we have used
the GRBF, because it shows better performance than
other kernels. Thus hyper-parameters (σ and C) are se-
lected to have the values one and 10 respectively for all
SVMs. There are three widely used methods to extend
binary SVMs to multi-class problems. One of them is
called the one-against-all (OAA) method. Suppose we
have a P-class pattern recognition problem. P independent
SVMs are constructed and each of them is trained to
separate one class of samples from all others. When test-
ing the system after all the SVMs is trained, a sample is
input to all the SVMs. Suppose this sample belongs to
class P1. Ideally, only the SVM trained to separate class
P1 from the others can have a positive response. Another
method is called the one-against-one (OAO) method. For
a P-class problem,


1
2
pp
SVMs are constructed and each of them is trained to
separate one class from another class. Again, the decision
of a testing sample is based on the voting result of these
SVMs. The third method is called a hierarchical method.
In this method the received signal is fed to the first SVM
(SVM1). SVM1 determines to which group the received
signal belongs. This process will be continued in the
same manner until the signal types are identified by the
last SVMs. One of the advantages of this structure is that

S. E. EL-KHAMY, H. A. ELSAYED
524
the number of SVMs is less than in cases of OAO and
OAA.
5.4. Neural Network Classifier
We have used a MLP neural network with back-propagation
(BP) learning algorithm as the classifier. A MLP feed
forward neural network consists of an input layer of source
nodes, one hidden layer of computation nodes (neurons)
and an output layer. The number of nodes in the input
and the output layers depend on the number of input and
output variables, respectively and the number of nodes in
the hidden layer is 17 neurons. And the classifier is al-
lowed to run up to 5000 training and with MSE is taken
to be 10-6, the activation functions used for hidden layer
and for output layer respectively are Hyperbolic tangent
sigmoid and Linear transfer function [3].
5.5. Fuzzy K-Means Clustering
The main idea behind fuzzy k-means is the minimization
of an objective function, which is normally chosen to be
the total distance between all patterns from their respec-
tive cluster centers. Its solution relies on an iterative
scheme, which starts with arbitrarily chosen initial clus-
ter memberships or centers. The distribution of objects
among clusters and the updating of cluster centers are the
two main steps of the c-means algorithm. The algorithm
alternates between these two steps until the value of the
objective function cannot be reduced anymore [2].
5.6. Fuzzy C-Means Clustering
The c-means algorithm allows for fuzzy partition, rather
than hard partition, by using the objective function. Fuzzy
c-means clustering is a data clustering algorithm in
which each data point belongs to a cluster to a degree
specified by a membership grade. This algorithm is pro-
posed as an improvement to fuzzy k-means clustering
technique. FCM partitions a collection of n vector into c
fuzzy groups, and finds a cluster center in each group
such that a cost function of dissimilarity measure is
minimized. The steps of FCM algorithm are therefore
first described in brief [2].
6. Simulation Results
In this section, we evaluate the performance of automatic
signal classification of the eight considered multi-user
chirp modulation signals (Sig1, Sig2, Sig3, Sig4, Sig5,
Sig6, Sig7, and Sig8) shown in Figure 1. We choose 100
realizations as training data and 50 realizations as testing
data sets from each signal type so we used 150 realiza-
tions and each signal has 4096 samples length (1 second).
The features are extracted using three methods after
passing these signals to white Gaussian noise channel.
6.1. Higher Order Moments and Cumulants
The features are extracted using even order moments and
cumulants up to eight using equations in [18]. Table 1
shows the features for the eight chirp signals. These val-
ues are computed under the constraints of zero mean,
unit variance and noise free. From the results, we show
that the second order moments and cumulants for all
signals are the same, for this reason, we don’t use it as
features. We use the higher order moments and cumu-
lants as features for classification. The fourth order mo-
ments are the same for each signal so we use one of them
for each signal. Also for the fourth order cumulants, the
sixth and eight order moments and cumulants, we used
one for each, i.e. M40 = M41 = M42 = M4, C40 = C41 =
C42 = C4, M60 = M61 = M62 = M63 = M6, C60 = C61
= C62 = C63 = C6, M80 = M81 = M82 = M83 = M84 =
M8 and C80 = C81 = C82 = C83 = C84 = C8. Thus, only
six features are used for classification. These six features
are F4 (M4, C4, M6, C6, M8 and C8) are shown in Ta-
ble 1.
The above method is compared with a one using the
features F3 (M6, C6, M8 and C8) and the features F1
(M4 and C4) as in [30]. The standard deviation (STD) of
each feature for these signals is arranged and the two
highest values which are (C8 and C6) used as features F2
for classification. The performance of the mutli-user chirp
modulation signals using multilayer perceptron neural
network and features F1, F2, F3, and F4 are shown in
Figure 2. Figure 3 shows the performance of the multi-
user chirp modulation signals using different Classifiers
Table 1. Features for eight multi-user chirp modulation signals using moments and cumulants.
Sig1 Sig2 Sig3 Sig4 Sig5 Sig6 Sig7 Sig8 STD
M4 1.5 1.48 1.51 1.47 1.48 1.48 1.49 1.49 0.01
M6 2.5 2.43 2.56 2.42 2.46 2.44 2.49 2.46 0.04
M8 4.36 4.21 4.56 4.16 4.29 4.21 4.363 4.26 0.11
C4 –1.49 –1.51 –1.48 –1.52 –1.51 –1.51 –1.5 –1.5 0.01
C6 9.95 10.23 9.79 10.24 10.11 10.18 10.02 10.1 0.14
C8 –73.29 –80.81 –68.42 –81.25 –77.64 –79.63 –75.11 –77.36 4.03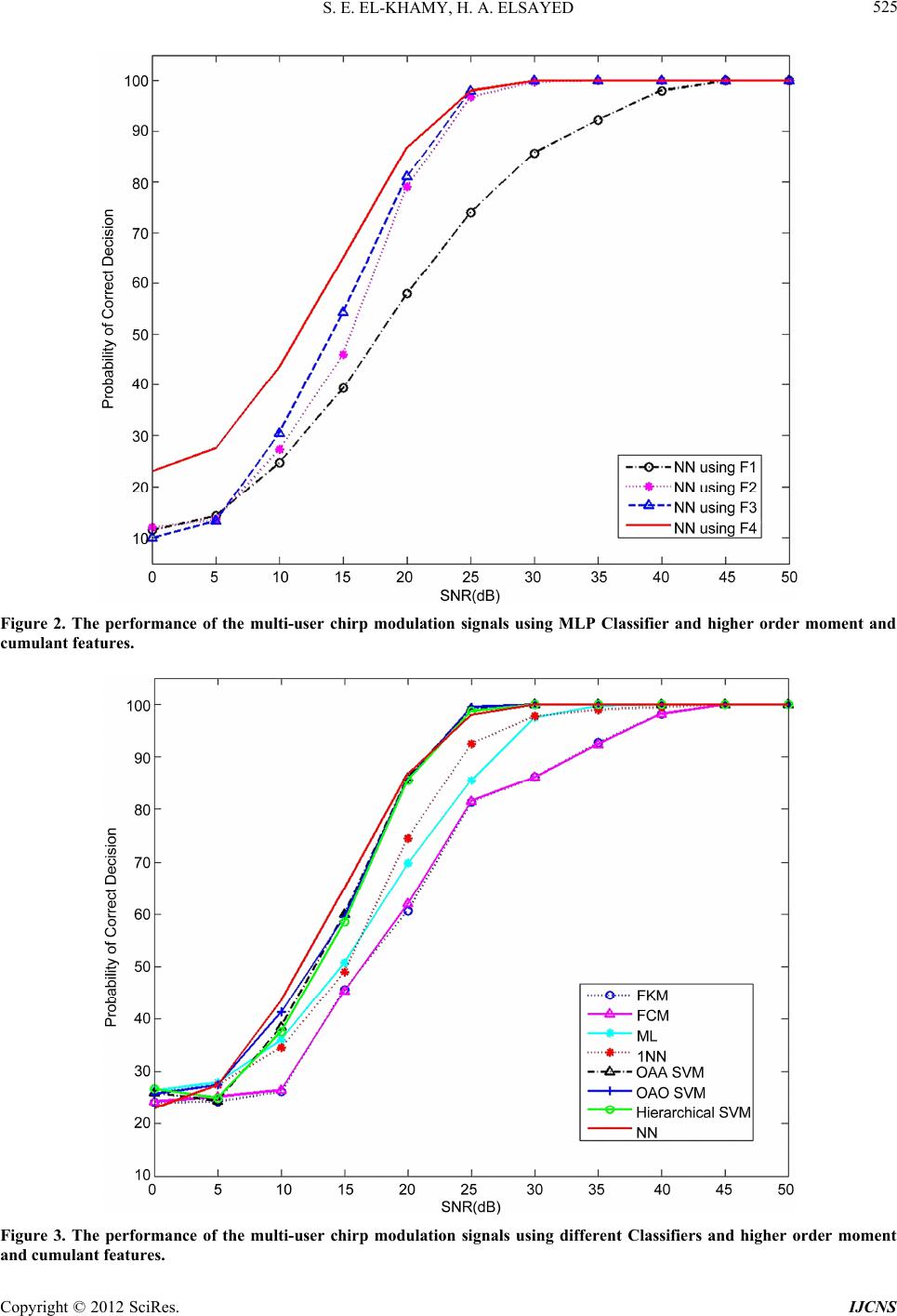

S. E. EL-KHAMY, H. A. ELSAYED 525
Figure 2. The performance of the multi-user chirp modulation signals using MLP Classifier and higher order moment and
cumulant features.
Figure 3. The performance of the multi-user chirp modulation signals using different Classifiers and higher order moment
and cumulant features.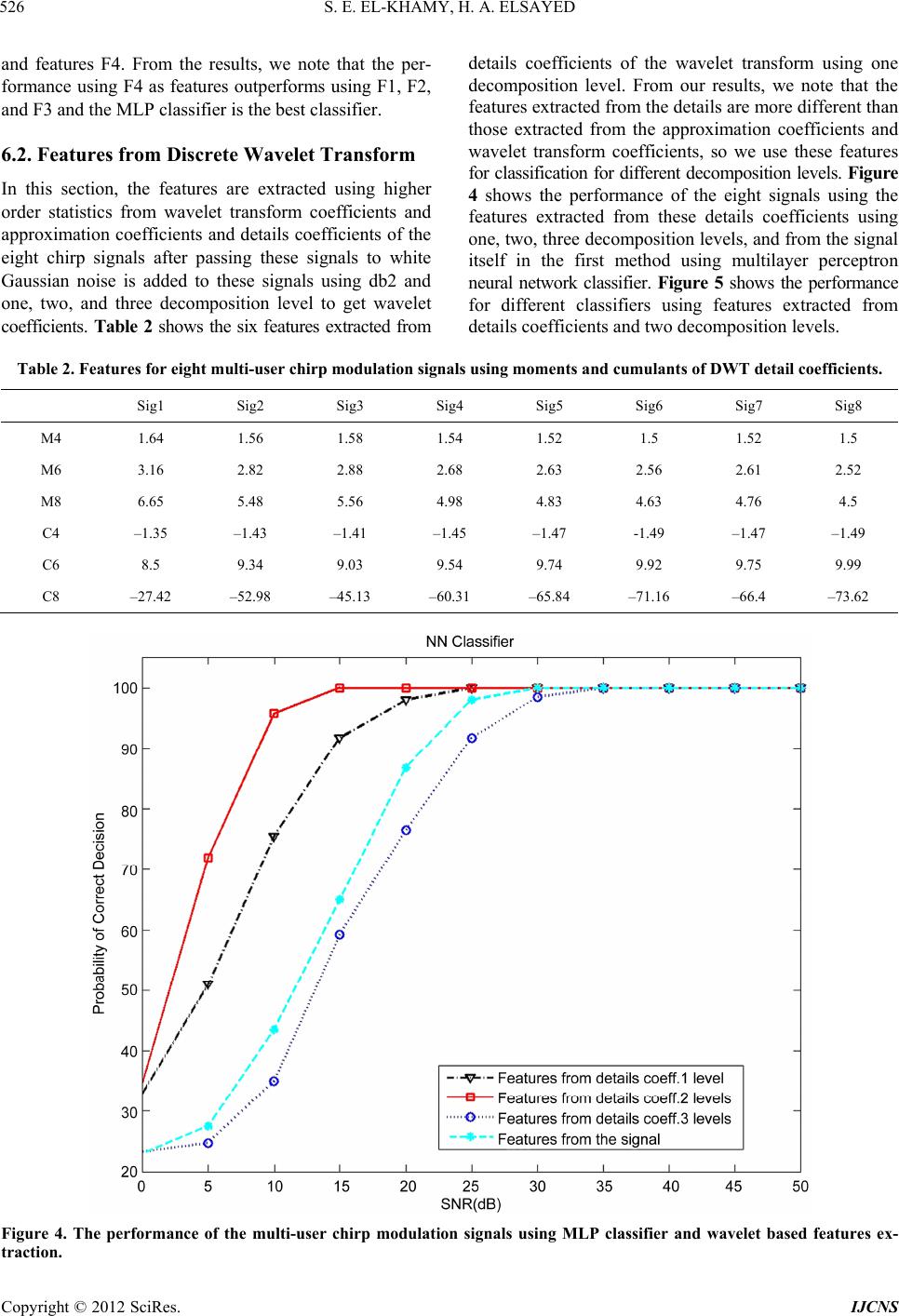

S. E. EL-KHAMY, H. A. ELSAYED
526
details coefficients of the wavelet transform using one
decomposition level. From our results, we note that the
features extracted from the details are more different than
those extracted from the approximation coefficients and
wavelet transform coefficients, so we use these features
for classification for different decomposition levels. Figure
4 shows the performance of the eight signals using the
features extracted from these details coefficients using
one, two, three decomposition levels, and from the signal
itself in the first method using multilayer perceptron
neural network classifier. Figure 5 shows the performance
for different classifiers using features extracted from
details coefficients and two decomposition levels.
and features F4. From the results, we note that the per-
formance using F4 as features outperforms using F1, F2,
and F3 and the MLP classifier is the best classifier.
6.2. Features from Discrete Wavelet Transform
In this section, the features are extracted using higher
order statistics from wavelet transform coefficients and
approximation coefficients and details coefficients of the
eight chirp signals after passing these signals to white
Gaussian noise is added to these signals using db2 and
one, two, and three decomposition level to get wavelet
coefficients. Table 2 shows the six features extracted from
Table 2. Features for eight multi-user chirp modulation signals using moments and cumulants of DWT detail coefficients.
Sig1 Sig2 Sig3 Sig4 Sig5 Sig6 Sig7 Sig8
M4 1.64 1.56 1.58 1.54 1.52 1.5 1.52 1.5
M6 3.16 2.82 2.88 2.68 2.63 2.56 2.61 2.52
M8 6.65 5.48 5.56 4.98 4.83 4.63 4.76 4.5
C4 –1.35 –1.43 –1.41 –1.45 –1.47 -1.49 –1.47 –1.49
C6 8.5 9.34 9.03 9.54 9.74 9.92 9.75 9.99
C8 –27.42 –52.98 –45.13 –60.31 –65.84 –71.16 –66.4 –73.62
Figure 4. The performance of the multi-user chirp modulation signals using MLP classifier and wavelet based features ex-
traction.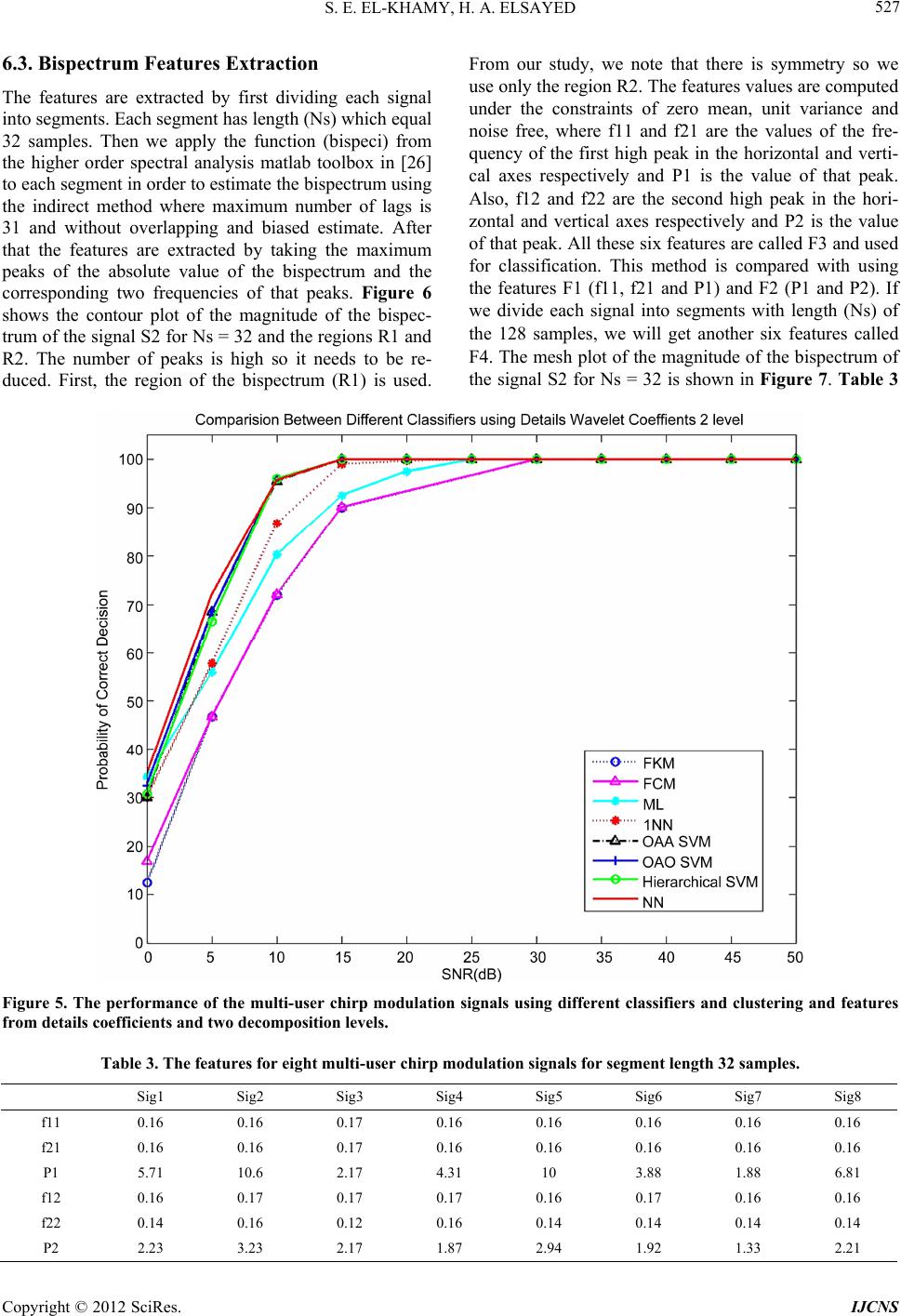

S. E. EL-KHAMY, H. A. ELSAYED 527
6.3. Bispectrum Features Extraction
The features are extracted by first dividing each signal
into segments. Each segment has length (Ns) which equal
32 samples. Then we apply the function (bispeci) from
the higher order spectral analysis matlab toolbox in [26]
to each segment in order to estimate the bispectrum using
the indirect method where maximum number of lags is
31 and without overlapping and biased estimate. After
that the features are extracted by taking the maximum
peaks of the absolute value of the bispectrum and the
corresponding two frequencies of that peaks. Figure 6
shows the contour plot of the magnitude of the bispec-
trum of the signal S2 for Ns = 32 and the regions R1 and
R2. The number of peaks is high so it needs to be re-
duced. First, the region of the bispectrum (R1) is used.
From our study, we note that there is symmetry so we
use only the region R2. The features values are computed
under the constraints of zero mean, unit variance and
noise free, where f11 and f21 are the values of the fre-
quency of the first high peak in the horizontal and verti-
cal axes respectively and P1 is the value of that peak.
Also, f12 and f22 are the second high peak in the hori-
zontal and vertical axes respectively and P2 is the value
of that peak. All these six features are called F3 and used
for classification. This method is compared with using
the features F1 (f11, f21 and P1) and F2 (P1 and P2). If
we divide each signal into segments with length (Ns) of
the 128 samples, we will get another six features called
F4. The mesh plot of the magnitude of the bispectrum of
the signal S2 for Ns = 32 is shown in Figure 7. Ta ble 3
Figure 5. The performance of the multi-user chirp modulation signals using different classifiers and clustering and features
from details coefficients and two decomposition levels.
Table 3. The features for eight multi-user chirp modulation signals for segment length 32 samples.
Sig1 Sig2 Sig3 Sig4 Sig5 Sig6 Sig7 Sig8
f11 0.16 0.16 0.17 0.16 0.16 0.16 0.16 0.16
f21 0.16 0.16 0.17 0.16 0.16 0.16 0.16 0.16
P1 5.71 10.6 2.17 4.31 10 3.88 1.88 6.81
f12 0.16 0.17 0.17 0.17 0.16 0.17 0.16 0.16
f22 0.14 0.16 0.12 0.16 0.14 0.14 0.14 0.14
P2 2.23 3.23 2.17 1.87 2.94 1.92 1.33 2.21

S. E. EL-KHAMY, H. A. ELSAYED
528
Figure 6. Contour plot of the magnitude of the bispectrum of the signal S2 for Ns = 32 on the bi-frequencies (f1, f2) and the
regions R1 and R2.
Figure 7. Mesh plot of the magnitude of the bispectrum of the signal S2, Ns = 32.

S. E. EL-KHAMY, H. A. ELSAYED
529
neural network outperforms other classifiers such as
maximum likelihood classifier, support vector machine
classifier, k nearest neighbor classifiers, fuzzy c-means
clustering, and fuzzy k-means clustering because it take
long time for training. In addition, the performance of the
fuzzy c-means clustering is better than the fuzzy k-means
clustering for most the SNR in case of using higher order
moments and cumulants as features. Also, using features
extracted from WT get better performance than without
WT because the WT have denoising properties which remove
the noise, features extracted form details coefficients is
better than using features extracted from the approxima-
tion and wavelet coefficients and using two decomposi-
tion is better than one and three and bispectrum features
is better than higher order moment and cumulant features
and features extracted from the details discrete wavelet
transform coefficients using two decomposition levels.
We also note that, in the support vector machine classifiers,
the performance of the one-against-all classifier is better
than one-against-one and hierarchical support vector machine.
Finally, we note that, the performance of non clustering
techniques is better than clustering techniques but
clustering don’t need to train the classifier and it is easy
to implement and faster than non clustering techniques.
shows the features for the eight chirp signals when Ns is
32 samples. Figure 8 shows the contour plot of the eight
signals where Ns = 32 samples is used and the region R2 is
shown. The performance of the mutli-user chirp modula-
tion signals using multilayer perceptron neural network
and features F1, F2, F3, and F4 is shown in Figure 9.
Figure 10 shows the performance of the multi-user chirp
modulation signals using different classifiers and features
F4 is used. From these results, we note that using F4 as
features outperforms using F1, F2, and F3. Figure 11
shows the comparison between the performances of the
multi-user chirp modulation signals using multilayer per-
ceptron neural network classifier and the three different
features extraction methods using higher order moment
and cumulant (F4), using features extracted from the de-
tails discrete wavelet transform coefficients using two
decomposition levels, and bispectrum features (F4). From
this figure, we note that using bispectrum features is bet-
ter than using features extraction from higher order mo-
ment and cumulant (F4) and using features extracted
from the details discrete wavelet transform coefficients
using two decomposition levels at low signal to noise
ratio and the low signal power
From these results, we note that the performance using
Figure 8. Contour plot of the magnitude of the bispectrum of the eight signals on the bi-frequencies (f1, f2) and the region R2.

S. E. EL-KHAMY, H. A. ELSAYED
530
Figure 9. The performance of the multi-user chirp modulation signals using MLP classifier and bispectrum features.
Figure 10. The performance of the multi-user chirp modulation signals using different classifie r s and Bispectrum features F4.

S. E. EL-KHAMY, H. A. ELSAYED
531
Figure 11. Comparison between the performances of the multi-user chirp modulation signals using MLP classifier and dif-
ferent features ex traction methods.
7. Conclusions the classifier and it is easy to implement and faster than
non clustering techniques. Also, using features extracted
from WT get better performance than without WT be-
cause the WT have denoising properties which remove
the noise, features extracted form details coefficients is
better than using features extracted from the approxima-
tion and wavelet coefficients and using two decomposi-
tion is better than one and three and bispectrum features
is better than higher order moment and cumulant features
and features extracted from the details discrete wavelet
transform coefficients using two decomposition levels.
So this signal is type of UWB because it needs low signal
to noise ratio and then it is low signal power and also, we
deals with low power level spectrum signal, so this chirp
signal is type of spread spectrum signals.
In this paper, we presented classification of multi-user
chirp modulation signals using wavelet higher order sta-
tistics features and artificial intelligence techniques. In
this method, different types of classifiers are used and
different features extraction methods are used. We note
the dependence of the classifier performance on the clas-
sifier type, the classifier parameters, the features used,
the discrete wavelet coefficients, number of decomposi-
tion levels, the method of features extraction, and the
length of each segment.
Simulation results show that the performance of the
multilayer perceptron neural network classifier is better
than other classifiers such as maximum likelihood classi-
fier, support vector machine classifier, k nearest neighbor
classifiers, fuzzy c-means clustering, and fuzzy k-means
clustering because it take long time for training. In addi-
tion, the performance of the fuzzy c-means clustering is
better than the fuzzy k-means clustering for most the
SNR in case of using higher order moments and cumu-
lants as features. We also note that, in the support vector
machine classifiers, the performance of the one-against-
all classifier is better than one-against-one and hierarchi-
cal support vector machine. Finally, we note that, the
performance of non clustering techniques is better than
clustering techniques but clustering don’t need to train
REFERENCES
[1] C. R. C. M. da Silva, W. C. Headley, J. D. Reed and Y.
Zhao, “The Applications of Distributed Spectrum Sensing
and Available Resources Maps to Cognitive Radio Sys-
tems,” Proceedings of Information Theory and Applica-
tion Workshop, San Diegoq, 27 January-1 February 2008,
pp. 53-57.
[2] H. Guldemır and A. Sengur, “Comparison of Clustering
Algorithms for Analog Modulation Classification,” Ex-
pert Systems with Applications, An International Journal,

S. E. EL-KHAMY, H. A. ELSAYED
532
Vol. 30, No. 4, 2006, pp. 642-649.
[3] A. Ebrahimzadeh and M. Ebrahimzadeh, “An Expert Sys-
tem for Digital Signal Type Classification,” Journal of
Electrical Engineering, Vol. 58, No. 6, 2007, pp. 334-341.
[4] X. Zhou, Y. Wu and B. Yang, “Signal Classification Meth-
od Based on Support Vector Machine and High-Order
Cumulants,” Wireless Sensor Network, Vol. 2, No. 1, 2010,
pp. 48-52. doi:10.4236/wsn.2010.21007
[5] A. Ebrhimzadeh, H. Azimi and H. M. Naeemi, “Classifi-
cation of Communication Signals Using an Optimized
Classifier and Efficient Features,” The Arabian Journal
for Science and Engineering, Vol. 35, No. 1B, 2010, pp.
225-235.
[6] S. M. Zhou, J. Q. Gan and F. Sepulveda, “Classifying
Mental Tasks Based on Features of Higher-Order Statis-
tics from EEG Signals in Brain-Computer Interface,” In-
formation Sciences, Vol. 178, No. 6, 2008, pp. 1629-1640.
doi:10.1016/j.ins.2007.11.012
[7] C. K. Chua, V. Chandran, R. U. Acharya and L. C. Min,
“Cardiac Health Diagnosis Using Higher Order Spectra
and Support Vector Machine,” The Open Medical Infor-
matics Journal, Vol. 3, 2009, pp. 1-8.
doi:10.2174/1874431100903010001
[8] M. Kaur and A. S. Arora, “Unsupervised Analysis of Arr-
hythmias Using K-Means Clustering,” International Jour-
nal of Computer Science and Information Technologies,
Vol. 1, No. 5, 2010, pp. 417-419.
[9] M. Murugappan, M. Rizon, R. Nagarajan, S. Yaacob, I.
Zunaidi and D. Hazry, “EEG Feature Extraction for Clas-
sifying Emotions Using FCM and FKM,” Internat- ional
Journal of Computers and Communications, Vol. 1, 2007,
pp. 21-25.
[10] N. Ahmadi and R. Berangi, “Symbol Based Modulation
Classification Using Combination of Fuzzy Clustering
and Hierarchical Clustering,” Signal Processing: An In-
ternational Journal, Vol. 4, No. 2, 2010, pp. 123-137.
[11] M. Sayadi, L. Tlig and F. Fnaiech, “A New Texture Seg-
mentation Method Based on the Fuzzy C-Mean Algorithm
and Statistical Features,” Applied Mathematical Sciences,
Vol. 1, No. 60, 2007, pp. 2999-3007.
[12] P. Prakasam and M. Madheswaran, “Mary Shift Keying
Modulation Scheme Identification Algorithm Using Wave-
let Transform and Higher Order Statistical Moment,” Jour-
nal of Applied Science, Vol. 8, No. 1, 2008, pp. 112-119.
doi:10.3923/jas.2008.112.119
[13] R. M. Al-Makhlasawy, W. Hamouda, M. M. Abd Elnaby,
H. A. El-Khobby and F. E. Abd El-Samie, “Automatic
Modulation Recognition Using Cepestral Analysis and
Neural Networks in Wireless Systems,” 29th National
Radio Science Conference, Cairo, 10-12 April 2012.
[14] S. E. El-Khamy H. A. Elsayed and M. M. Rizk, “Classi-
fication of Multi-User Chirp Modulation Signals Using
Higher Order Cumulant Features and Four Types of Clas-
sifiers,” 28th National Radio Science Conference, Cairo,
Egypt, 26-28 April 2011.
[15] H. A. Elsayed, S. E. El-Khamy and M. R. Rizk, “Higher
Order Statistics Classification of Multi-User Chirp Modu-
lation Signals Using Clustering Techniques,” URSI GASS
2011, Istanbul, 13-20 August 2011.
[16] S. E. El-Khamy, H. A. Elsayed and M. R. Rizk, “Bispec-
trum Classification of Multi-User Chirp Modulation Sig-
nals Using Artificial Intelligent Techniques,” WorldComp
2011, Las Vegas, 18-21 July 2011.
[17] S. E. El-Khamy and M. B. Al-Ghoniemy, “The Wavelet
Transform: A Review and Application to Enhanced Data
Storage Reduction in Mismatched Filter Receivers,” Pro-
ceedings of the Thirteenth National Radio Science Con-
ference, Cairo, 19-21 March 1996.
[18] M. P. Fargues and G. Hatzichristos, “A Hierarchical Ap-
proach to the Classification of Digital Modulation Types
In Multipath Environments,” Conference Record of the
Thirty-Fifth Asilomar Conference on Signals, Systems and
Computers, Pacific Grove, 4-7 November 2001.
[19] C. L. Nikias and J. M. Mendel, “Signal Processing with
Higher Order Spectra,” IEEE Signal Processing Maga-
zine, Vol. 10, No. 3, 1993, pp. 10-37.
doi:10.1109/79.221324
[20] S. E. El-Khamy, “Matched Swept-Frequency Digital Mo-
dulation for Binary Signaling in Inhomogeneous Disper-
sive Media,” IEEE Transactions on Antennas and Pro-
pagation, Vol. 28, No. 1, 1980, pp. 29-35.
doi:10.1109/TAP.1980.1142283
[21] S. E. El-Khamy and S. E. Shaaban, “Matched Chirp Mo-
dulation: Detection and Performance in Dispersive Com-
munication Channels,” IEEE Transactions on Communi-
cations, Vol. 36, No. 4, 1988, pp. 506-509.
doi:10.1109/26.2777
[22] S. E. El-Khamy, S. E. Shaaban and E. A. Thabet, “Multi-
User Chirp Modulation Signals (M-CM) for Efficient
Multiple Access Communication Systems,” Proceedings
of the Thirteenth National Radio Science Conference,
Cairo, 19-21 March 1996.
[23] S. E. El-Khamy, S. E. Shaaban and E. A. Thabet, “Effic-
ient Multiple-Access Communications Using Multi-User
Chirp Modulation Signals,” IEEE 4th International Sym-
posium on Spread Spectrum Techniques and Applications
Proceedings, Mainz, 22-25 September 1996, pp. 1209-1213.
[24] S. E. El-Khamy, S. E. Shaaban and E. A. Thabet, “Fre-
quency Hopped-Chirp Modulation (FH-CM) for Multi-
User Signaling in Multipath Dispersive Media,” IEEE
Antennas and Propagation Society International Sympo-
sium, Orlando, 11-16 July 1999, pp. 396-399.
[25] C. L. Nikias and A. P. Petropulu, “Higher-Order Spectra
Analysis: A Nonlinear Signal Processing Framework,”
PTR Prentice-Hall, Englewood Cliffs, 1993.
[26] High Order Spectral Analysis Matlab Toolbox (9 February
2011).
http://www.mathworks.com/matlabcentral/fileexchange/3
013
[27] A. V. Rosti, “Statistical Methods in Modulation Classifi-
cation,” Master’s Thesis, Tampere University of Technol-
ogy, Tampere, 1999.
[28] H. Yoshioka, “A Fast Modulation Recognition Technique
Using Nearest Neighbor Rules with Optimized Threshold
for Modulation Classification in Rayleigh Fading Chan-
nels,” Proceedings of WPMC, Honolulu, 27-30 October

S. E. EL-KHAMY, H. A. ELSAYED
533
2002, pp. 1049-1052.
[29] C. Burges, “A Tutorial on Support Vector Machines for
Pattern Recognition,” Data Mining and Knowledge Dis-
covery, Vol. 2, No. 2, 1998, pp. 121-167.
doi:10.1023/A:1009715923555
[30] A. Swami and B. M. Sadler, “Hierarchical Digital Modu-
lation Classification Using Cumulants,” IEEE Transac-
tions on Communications, Vol. 48, No. 3, 2000, pp. 416-429.
doi:10.1109/26.837045