Paper Menu >>
Journal Menu >>
 J. Software Engineering & Applications, 2010, 3, 683-695 doi:10.4236/jsea.2010.37078 Published Online July 2010 (http://www.SciRP.org/journal/jsea) Copyright © 2010 SciRes. JSEA 683 Melody Generator: A Device for Algorithmic Music Construction Dirk-Jan Povel Centre for Cognition, Donders Institute for Brain, Cognition and Behaviour, Radboud University Nijmegen, Nijmegen, The Netherlands. Email: povel@NICI.ru.nl Received April 15th, 2010; revised May 25th, 2010; accepted May 27th, 2010. ABSTRACT This article describes the development of an application for generating tonal melodies. The goal of the project is to as- certain our current understanding of tonal music by means of algorithmic music generation. The method followed con- sists of four stages: 1) selection of music-theoretical insights, 2) translation of these insights into a set of principles, 3) conversion of the principles into a computational model having the form of an algorithm for music generation, 4) test- ing the “music” generated by the algorithm to evaluate the adequacy of the model. As an example, the method is im- plemented in Melody Generator, an algorithm for generating tonal melodies. The program has a structure suited for generating, displaying, playing and storing melodies, functions which are all accessible via a dedicated interface. The actual generation of melodies, is based in part on constraints imposed by the tonal context, i.e. by meter and key, the settings of which are controlled by means of parameters on the interface. For another part, it is based upon a set of construction principles including the notion of a hierarchical organization, and the idea that melodies consist of a ske- leton that may be elaborated in various ways. After these aspects were implemented as specific sub-algorithms, the de- vice produces simple but well-structured tonal melodies. Keywords: Principles of Tonal Music Construction, Algorithmic Composition, Synthetic Musicology, Computational Model, Realbasic, OOP, Melody, Meter, Key 1. Introduction Research on music has yielded a huge amount of con- cepts, notions, insights, and theories regarding the struc- ture, organization and functioning of music. But only since the beginning of the 20th century has music be- come a topic of rigorous scientific research in the sense that aspects of the theory were formally described and subjected to experimental research [1]. Starting with the cognitive revolution of the 1960s [2] a significant in- crease in the scientific study of music was seen with the emergence of the disciplines of cognitive psychology and artificial intelligence. This gave rise to numerous ex- perimental studies investigating aspects of music percep- tion and music production, for overviews see [3,4], and to the development of formal and computational models describing and simulating various aspects of the process of music perception, e.g., meter and key induction, har- mony induction, segmentation, coding, and music repre- sentation [5-13]. Remembering Richard Feynman’s adage “What I can’t create, I don’t understand”, this article is based on the belief that the best estimate of our understanding of mu- sic will be obtained from attempts to actually create mu- sic. For that purpose we need a computer algorithm that generates music. 1.1 Algorithmic Music Construction The rationale behind the method is simple and straight- forward: if we have a theory about the mechanism un- derlying some phenomenon, the best way to establish the validity of that theory is to show that we can reproduce the phenomenon from scratch. Applied to music: if we have a valid theory of the structure of music, then we should be able to construct music from its basic elements (sounds differing in frequency and duration), at least in some elementary fashion. The core of the method there- fore consists in the generation of music on the basis of insights accumulated in theoretical and experimental music research. In essence, the method includes four stages 1) specifi- cation of the theoretical basis; 2) translation of the theory into a set of principles; 3) implementation of the princi- ples as a generative computer algorithm; 4) test of the output. This article only describes the three former stages:  Melody Generator: A Device for Algorithmic Music Construction Copyright © 2010 SciRes. JSEA 684 the theoretical background and the actual development of the algorithmic music construction device. The testing of the device which calls for a separate dedicated study will be reported in a separate article. Compared to the experimental method, the algorithmic construction method has two advantages: first, it studies all structural aspects of music in a comprehensive way (because all aspects have to be taken into account if one wants to generate music) thus exhibiting the “big pic- ture”: the working and interaction of all variables; second, it requires utmost precision, enforced by the fact that the model is implemented as a computer algorithm. Experi- mental research in music, because of inherent limitations of the method, typically focuses on a restricted domain within the field of music, taking into account just one or two variables. As a result of this, the interpretation of the experimental results and their significance for the under- standing of music as a whole, is often open to discussion. 1.2 Related Work The possibility to create music by means of computer algorithms, so-called algorithmic composition, has at- tracted a lot of interest in the last few decades [14-16]. Algorithmic composition employs various methods [17]: Markov chains [18,19]; Knowledge-based systems [20]; Grammars [14,21-24]; Evolutionary methods divided into genetic algorithms, [25] and interactive genetic al- gorithms [26]; and learning systems [27,28]. Because the method presented here generates music it could be seen as an instance of algorithmic composition. But, since its purpose is to serve as a means to test music theory, it does not merely rely on classical AI methods but capitalizes on music theoretical insights to guide the implementation of the music generating device. As such it resembles the approaches taken by [9,29-31]. 1.3 Organization of the Paper The present article is organized as follows. In Section 2 the theoretical foundation of the method is described: the theoretical starting point, the basic assumptions, the in- sights regarding the configuration of the time dimension and the ensuing constraints, the configuration of the pitch dimension and ensuing constraints, and the basic con- struction rules for generating melodies. In Section 3, the implementation of the algorithm is discussed: the various functions of the program, its underlying structure, its user interface, and the implementation of the tonal context and the construction principles. 2. Theoretical Foundation Before describing the theoretical basis of the project, I should point out that what is being presented here is a particular set of theoretical notions based on a specific interpretation of the findings in the literature. Thus, I do not claim that this is the only possible theoretical basis, and certainly not that it is complete. The main purpose of this paper is to study the adequacy of a melody generat- ing device based on specific theoretical ideas about the construction of tonal music. Starting point of the project is the conception of music as a psychological phenomenon, i.e., as the result of a unique perceptual process carried out on sequences of pitches. In the case of tonal music this process has two distinct aspects: 1) Discovering the context in which the music was conceived (meter, key, and harmony) and representing the input within that context. By this repre- sentation the input, consisting of sounds varying in pitch, is transformed into tones and chords having specific mu- sical meanings; 2) Discovering the structural regularities in the input (e.g., repetition, alternation, reversal) and using these to form a mental representation [5,7]. These processes evolve largely unconsciously: What the lis- tener experiences are the effects of these processes, spe- cifically the experiences that accompany the expectations arising while the music develops and the ways in which these expectations are subsequently resolved. Sometimes these experiences are described by the terms tension and relaxation, but these hardly seem to cover the subtle and varied ways humans may respond to music. This basic conception of the process of music percep- tion has guided the choice of assumptions, and the de- velopment of the models of music construction described below, as well as the shaping of the interface of the computer algorithm. 2.1 Basic Assumptions The model is based on the following assumptions: 1) Tonal music is conceived within the context of time and pitch, where time is configured by meter (imposing con- straints as to when notes may occur), and pitch by key and harmony (imposing constraints as to what notes may occur). 2) Within that context tone sequences are gener- ated using construction rules specifying the (hierarchical) organization of tones into parts, and of parts into larger parts etc., relating to concepts such as motives, phrases, repetition and variation, skeleton, structural and orna- mental tones, etc. In line with these assumptions two components may be discerned in the program: one component that man- ages the context, and another that handles the construc- tion rules. Below, we discuss the configuration of the time di- mension, the configuration of the pitch dimension, the interaction between these dimensions, the basic princi- ples of music construction, and the resulting constraints and rules. 2.2 The Time Dimension of Tonal Music The time dimension in tonal music is configured by me- ter. Meter is a temporal framework in which a rhythm is  Melody Generator: A Device for Algorithmic Music Construction Copyright © 2010 SciRes. JSEA 685 cast. It divides the continuum of time into discrete peri- ods. Note onsets in a piece of tonal music coincide with the beginning of one of those periods. Meter divides time in a hierarchical and recurrent way: time is divided into time periods called measures that are repeated in a cyclical fashion. A measure in turn is sub- divided in a number of smaller periods of equal length, called beats, which are further hierarchically subdivided (mostly into 2 or 3 equal parts) into smaller and smaller time periods. A meter is specified by means of a fraction, e.g., 4/4, 3/4, 6/8, in which the numerator indicates the number of beats per measure and the divisor the duration of the beat in terms of note length (1/4, 1/8 etc.), which is a relative duration. The various positions defined by a meter (the begin- nings of the periods) differ in metrical weight: the higher the position in the hierarchy (i.e. the longer the delimited period), the larger the metrical weight. Figure 1 displays two common meters in a tree-like representation indicat- ing the metrical weight of the different positions (the weights are defined on an ordinal scale). As shown, the first beat in a measure (called the down beat) has the highest weight. Phenomenally, metrical weight is associ- ated with perceptual markedness or accentuation: the higher the weight, the more accented it will be. Although tonal music is commonly notated within a meter, it is important to realize that meter is not a physi- cal characteristic, but a perceptual attribute conceived of by a listener while processing a piece of tonal music. It is a mental temporal framework that allows the accurate representation of the temporal structure of a rhythm (a sequence of sound events with some temporal structure). Meter is obtained from a rhythm in a process called met- rical induction [32,33]. The main factor in the induction of meter is the distribution of accents in the rhythm: the more this distribution conforms to the pattern of metrical weights of some meter, the stronger that meter will be induced. The degree of accentuation of a note in a rhythm is determined by its position in the temporal structure and by its relative intensity, pitch height, dura- tion, and spectral composition, the temporal structure Figure 1. Tree-representations of one measure of 3/4 and 6/8 meter with the metrical weights of the different levels. For each meter a typical rhythm is shown being the most powerful [34]. The most important deter- miners of accentuation are 1) Tone length as measured by the inter-onset-interval (IOI); 2) Grouping: the last tone of a group of 2 tones and the first and last tone of groups of three or more tones are perceived as accentu- ated [33,35]. 2.2.1 Metrical Stability The term metrical stability denotes how strongly a rhythm evokes a meter. We have seen that the degree of stability is a function of how well the pattern of accents in a rhythm matches the pattern of weights of a meter. This relation may be quantified by means of the coeffi- cient of correlation. If the metrical stability of a rhythm (for some meter) falls below a critical level, by the oc- currence of what could be called “anti-metric” accents, the meter will no longer be induced, leading to a loss of the temporal framework and, as a consequence, of the understanding of the temporal structure. 2.2.2 Basic Constraints Regarding the Generation of Tonal Rhythm Meter imposes a number of constraints on the use of the time dimension when generating tonal music: 1) it de- termines the moments in time, the locations, at which a note may begin; 2) it requires that the notes are posi- tioned such that the metrical stability is high enough to induce the intended meter. 2.3 The Pitch Dimension of Tonal Music The pitch dimension of tonal music is organized on three levels: key, harmony, and tones. These constituents maintain intricate mutual relationships represented in what is called the tonal system. This system describes how the different constituents relate and how they func- tion: e.g., how close one key is to another, which are the harmonic and pitch elements of a key, how they are re- lated, how they function musically, etcetera. For a review of the main empirical facts see [4]. It should be noted that these relations between the elements of the tonal system do not exist in the physical world of sounds (al- though they are directly associated with it), but refer to knowledge in the listener’s long-term memory acquired by listening to music. Key is the highest level of the system and changes at the slowest rate: in shorter tonal pieces like hymns, folk- songs, and popular songs there is often only one key which does not change during the whole piece. A key is comprised of a set of 7 tones, the diatonic scale. The tones in a scale differ in stability and the de- gree in which they attract or are attracted [36]. For in- stance, the first tone of the scale, the tonic, is the most stable and attracts the other tones of the scale, directly or indirectly, to different degrees. The last tone of the scale, the leading tone, is the least stable and is strongly at-  Melody Generator: A Device for Algorithmic Music Construction Copyright © 2010 SciRes. JSEA 686 tracted by the tonic. Phenomenally, attractions are ex- perienced by a listener as expectations. A key also contains a set of harmonies, basically in- stantiated by triads built on the 7 degrees of the scale. The triads on the 1st, 4th, and 5th degree are the primary ones. Like the tones, the harmonies, depending on their stability, may either attract or be attracted by other har- monies [37-39]. We start from the assumption that tonal melodies are built upon an underlying harmonic progres- sion [40]. These musical functions only become available after a listener has recognized the key of the piece in a process analogous to finding the meter, called key induction. For an overview see [13]. 2.3.1 Basic Constraints Associated with Key and Harmony Once a selection for a particular key has been made, the tones of the diatonic scale are the primary candidates for the construction of a melody. The non-key or chromatic tones play a secondary role and can only be used under strict conditions and mainly as local ornaments. The se- lection of a specific harmonic progression reduces the selection of tones even more since the tones within some harmony must, in principle, be in accordance with that harmony: only the tones that are part of the harmony can be sounded together with it. These tones are called har- monic tones or chord tones. There are melodies only consisting of chord tones (e.g., Mozart, Eine kleine Nachtmusik), but most melodies also contain non-chord tones (e.g., suspensions, appoggiatura’s, passing tones, neighbor tones etc.) (Figure 2). As non-chord tones form dissonances with the har- mony their use is restricted: they must be “anchored” by (resolved to) a succeeding chord tone close in pitch [41, 42]. Most often a non-chord tone is anchored immedi- ately, i.e., by the next succeeding tone, but it can also be anchored with some delay, as in the case of F A G, in which G is a chord tone and F and A are non-chord tones. Figure 2. Three melodic fragments with different distribu- tions of chord tones and non-chord tones (indicated +). (a) only chord tones; (b) non-chord tones on weak metrical positions; (c) non-chord tones on strong metrical positions 2.4 Relations between Meter and Key Above it was mentioned that the notes within a key differ in stability. In general, the more stable a note, the more structurally important it will be in the melody. From this it follows that stable notes, in order to enforce their prominent role, tend to appear at metrically strong posi- tions. This, however, is not always the case: sometimes a non-chord tone is placed on a beat (a strong position) and resolved by a chord tone on a weaker metrical position (appoggiatura). See note example c in Figure 2. These different uses of non-chord tones is style dependent, see [43]. 2.5 Principles of Melody Construction So far I have described the major characteristics of the context within which tonal music is constructed: Meter which defines the positions at which notes may begin and the perceptual salience of these positions. Key defining the basic units of a tonal piece: tones and chords, their relation and their musical function. And lastly the har- monic progression underlying a melody that defines the chord tones and non-chord tones. Now the question must be answered how a melody is generated within this con- text. We start with the following basic principles: 1) A me- lody consists of parts that may consist of subparts, which in turn may contain subparts, etc., thus forming a hierar- chical organization; 2) Parts are often created from other parts by means of variation; 3) A part consists of a ske- leton of structural tones, which may be elaborated (or- namented) to different extents. The hierarchical organization of tonal music has been described by many authors. Bamberger [44] describes the hierarchical organization of tunes in terms of trees con- sisting of motives, phrases, and sections connected by means of 3 organizing principles: repetition, sequential relations, and antecedent-consequent relations. Lerdahl & Jackendoff [7] conceive of the organization of tonal pieces in terms of hierarchical trees, resulting from a time-span reduction (based on the rhythmical structure) and a prolongational reduction expressing harmonic and melodic patterns of tension and relaxation. Schoenberg [45] describes the hierarchical organization of classical music on several levels: large forms (e.g., sonata form), small forms (e.g., minuet), themes (e.g., the period and the sentence consisting of phrases and motives). The idea that the surface structure of a melody can be reduced by a stepwise removal of less important tones thereby revealing the underlying framework or skeleton has a long history in music theory. Schenker [46] laid the theoretical foundation for the notion which was formal- ized in [7]. Similar ideas are found in [9,29,31,43,47]. Baroni et al. [30] proposed a set of transformations by  Melody Generator: A Device for Algorithmic Music Construction Copyright © 2010 SciRes. JSEA 687 which a melodic skeleton can be elaborated into a full- fledged melody (see Subsection 2.5.2). Marsden [31] proposed a framework for representing melodic patterns yielding a set of elaborations to produce notes between two parent notes. In view of the foregoing, we must first decide how to form a skeleton and next how to elaborate it. In line with the two major units of tonal music, the (broken) chord and the scale, and based upon analyses of large samples of tonal melodies, two models emerged: the “Chord- based model” and the “Scale-based model”. The Chord- based model builds a melodic skeleton from chord tones, whereas the skeleton in the Scale-based model consist of a scale fragment. The application described below con- tains a third model, called Basic, which is useful to com- pare tone sequences that are created either within or without a tonal context. The latter model will not further be discussed here. 2.5.1 The Chord-Based Model This model is based on the following assumptions: 1) A melody is superimposed upon an underlying harmonic progression; 2) A melody consists of structural tones (a skeleton) and ornamental tones; 3) The skeleton is as- sembled from chord tones; 4) Skeleton tones are primar- ily located at metrically strong positions. To actually generate a skeleton melody within this model, apart from the parameters related to the rhythm and the harmonic progression, a few additional parameters are needed to further shape the skeleton, namely: Range (determining the highest and lowest note), Contour (the up-down movement of the melody), Location (on beats or down-beats), and Interval (the size of the steps between the successive notes of the skeleton). After generation of the skeleton it may be elaborated or ornamented to dif- ferent degrees by means of an algorithm that interpolates notes between the notes of the skeleton. More informa- tion will follow in Section 3. 2.5.2 The Scale-Based Model The Scale-based model is largely based on the same as- sumptions as the Chord-based model, with one essential difference: the skeleton is not formed of a series of chord tones, but consists of a scale fragment. The idea that the skeleton of tonal melodies consist of scale fragments has been proposed, among others, by [30,48]. The latter au- thors studied melodies from a period of almost 10 centu- ries and concluded that “...every melodic phrase can be reduced, at its deep level, to a kernel which not only pro- gresses by conjunct step, but which is also monodirec- tional”. This rule applies to the “body” of the phrase, not to a possible anacrusis, or “feminine ending”. The vari- ability on the surface is seen as the result of the applica- tion of two types of transformations to the kernel: linear transformations (repetition, neighbor, (filled) skip), and a harmonic transformation. The latter transformation, called “chord transposition”, substitutes a note for an other note of the underlying harmony. The relative fre- quency of harmonic transformations increases over time (Händel, Mozart, Liszt). Figure 3 presents the reverse Figure 3. The reduction of two melodies to their kernel. The kernel of melody a consists of an ascending scale fragment fol- lowed by a descending fragment. In the descending fragment the D is not realized in the surface. The highest level of melody b. consists of the scale fragment F Gb Ab (bars 1, 6, 9 respectively), of which each tone is augmented with a descending scale fragment. In bar 4 the Ab is replaced by F and in bar 11 there is an downward octave jump 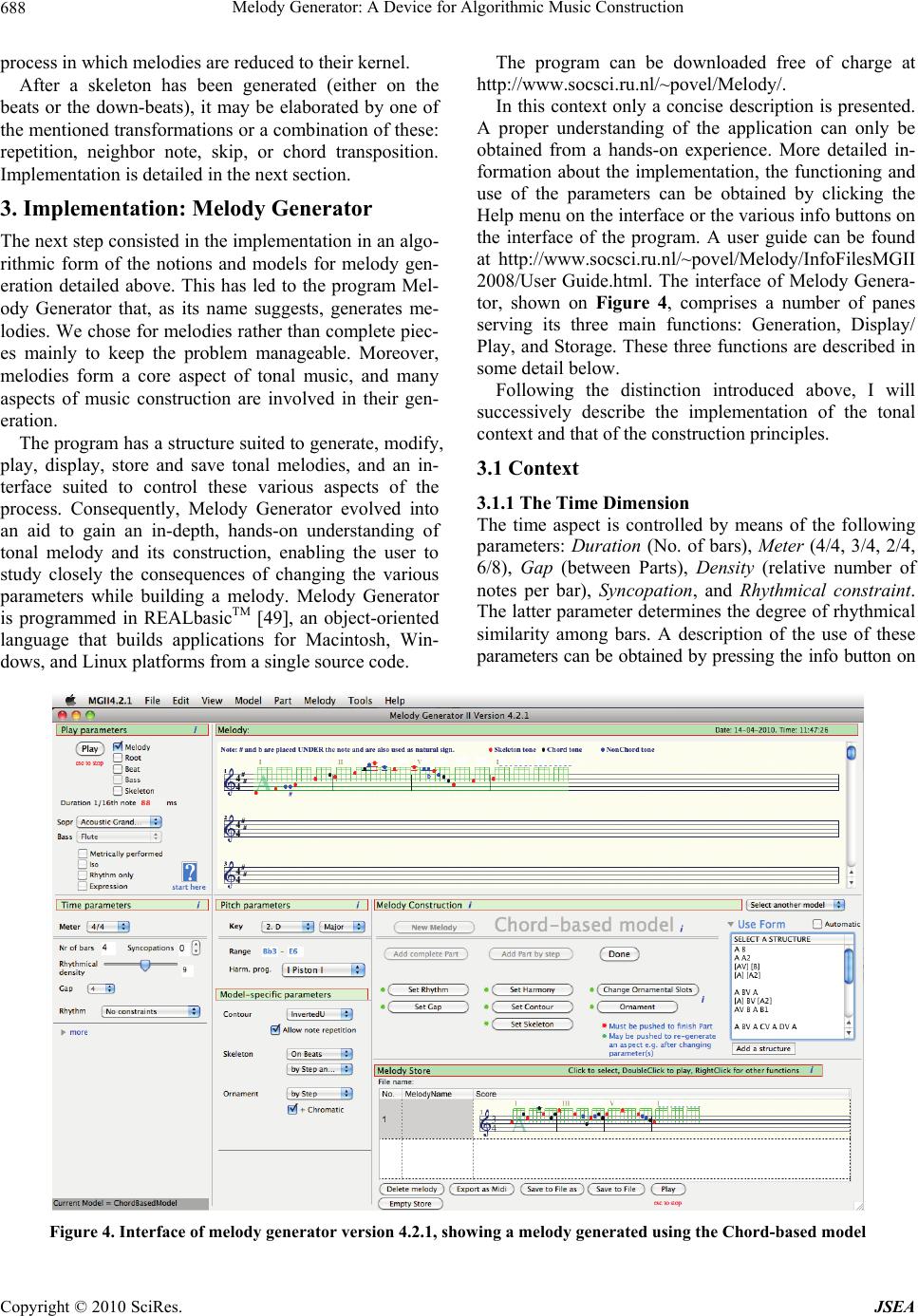 Melody Generator: A Device for Algorithmic Music Construction Copyright © 2010 SciRes. JSEA 688 process in which melodies are reduced to their kernel. After a skeleton has been generated (either on the beats or the down-beats), it may be elaborated by one of the mentioned transformations or a combination of these: repetition, neighbor note, skip, or chord transposition. Implementation is detailed in the next section. 3. Implementation: Melody Generator The next step consisted in the implementation in an algo- rithmic form of the notions and models for melody gen- eration detailed above. This has led to the program Mel- ody Generator that, as its name suggests, generates me- lodies. We chose for melodies rather than complete piec- es mainly to keep the problem manageable. Moreover, melodies form a core aspect of tonal music, and many aspects of music construction are involved in their gen- eration. The program has a structure suited to generate, modify, play, display, store and save tonal melodies, and an in- terface suited to control these various aspects of the process. Consequently, Melody Generator evolved into an aid to gain an in-depth, hands-on understanding of tonal melody and its construction, enabling the user to study closely the consequences of changing the various parameters while building a melody. Melody Generator is programmed in REALbasicTM [49], an object-oriented language that builds applications for Macintosh, Win- dows, and Linux platforms from a single source code. The program can be downloaded free of charge at http://www.socsci.ru.nl/~povel/Melody/. In this context only a concise description is presented. A proper understanding of the application can only be obtained from a hands-on experience. More detailed in- formation about the implementation, the functioning and use of the parameters can be obtained by clicking the Help menu on the interface or the various info buttons on the interface of the program. A user guide can be found at http://www.socsci.ru.nl/~povel/Melody/InfoFilesMGII 2008/User Guide.html. The interface of Melody Genera- tor, shown on Figure 4, comprises a number of panes serving its three main functions: Generation, Display/ Play, and Storage. These three functions are described in some detail below. Following the distinction introduced above, I will successively describe the implementation of the tonal context and that of the construction principles. 3.1 Context 3.1.1 The Time Dimension The time aspect is controlled by means of the following parameters: Duration (No. of bars), Meter (4/4, 3/4, 2/4, 6/8), Gap (between Parts), Density (relative number of notes per bar), Syncopation, and Rhythmical constraint. The latter parameter determines the degree of rhythmical similarity among bars. A description of the use of these parameters can be obtained by pressing the info button on Figure 4. Interface of melody generator version 4.2.1, showing a melody generated using the Chord-based model  Melody Generator: A Device for Algorithmic Music Construction Copyright © 2010 SciRes. JSEA 689 the pane “Time Parameters” of the program. A detailed description of the algorithm to generate rhythms, varying in density and metrical stability, is also presented there. 3.1.2 The Pitch Dimension: Key and Harmony Melody Generator has parameters for selecting a key (and mode) and for selecting a harmonic progression. Various template progressions are provided, partly based upon Schenker’s notion that tonal music is constructed by applying transformations on a “Background” consist- ing of a I-V-I harmonic progression (Ursatz), [50-52]. Basic harmonic templates typically begin with I and end with V-I (full cadence) or V (half cadence). The interme- diate harmonies are derived from Piston’s “Table of usual root progressions” [53]. This table, shown here as Table 1, lists the transition probabilities between harmonies in tonal music. These probabilities are loosely defined by the terms “usually”, “sometimes” and “less often”. Since the choice of a chord is only determined by the immediately preceding chord, it only provides a first-order approximation of harmonic progressions in tonal music. Also needed is a structure representing the various elements of the selected key and their mutual relations (mentioned above in Subsection 2.3). This includes in- formation concerning the specification of the scale de- grees, their stability and their spelling, the various chords on these degrees, etc. This information is accumulated in the object KeySpace. Figure 5 displays one octave of the KeySpace of C-major. 3.2 Construction To effectively construct melodies we need a structure allowing the flexible generation and modification of a hierarchically organized temporal sequence consisting of parts and subparts, divided into bars, in turn divided into beats and “slots” (locations where notes may be put). For this purpose an object called Melody, was designed com- prising one or more instances of the objects Piece, Part, Bar, Beat, Slot, and Note. See Figure 6. Since any part may contain a subpart, the hierarchy of a piece can be extended indefinitely. The generation of a melody progresses according to the following stages: Construction, Editing, (Re)arrange- ment, and Transformation. 3.2.1 Part Construction Construction is performed in the “Melody Construction” pane: after setting the Meter and Key parameters and pushing the “New Melody” button, the first Part of a melody may be generated either stepwise or at once. In the stepwise mode, the various aspects of a melody: its Rhythm, Gap, Harmony, Contour, Skeleton, and Orna- mentation are generated in separate steps. Prior to each Table 1. The table of usual root progressions for the Major mode from Piston & DeVoto. Given a chord in the first column, the table shows the chords that succeed that chord, usually (1st column), sometimes (2nd column), or less often (3rd column) Chord Usually followed by Sometimes by Less often by I IV or V VI II or III II V IV or VI I or III III VI IV I, II or V IV V I or II III or IV V I VI or IV III or II VI II or V III or IV I VII III I - Figure 5. Part of the object KeySpace used in the construction of melodies  Melody Generator: A Device for Algorithmic Music Construction Copyright © 2010 SciRes. JSEA 690 Figure 6. The object melody step the relevant parameters (indicated by highlighting) may be set. Each aspect can at each time be generated anew, for instance with a different parameter setting to study its effect on the resulting melody. The order in which the aspects can be constructed is controlled by enabling and disabling the construction buttons and by means of little “lights” located left of the buttons (see Figure 4). By pushing the “Done” button the generation of a Part is terminated. 3.2.2 Structure-Based Construction In the chord-based model it is possible to construct a melody with a pre-defined structure of parts. Examples of such structures are: A B A, A A1 A2 B, Ant Cons, [A VBV] [Dev AI BI], in which the capital letters A-G are used to identify parts, a digit following a letter to indicate a variation, and the Roman numerals I, II ... VII to iden- tify the initial or final harmony of a part; Ant and Cons are used in the Antecedent-Consequent formula. Other reserved words are Dev for Development, and Coda in- dicating a part at the end of a structure. The user can add custom structures using the above coding. The default way of constructing is part by part in which the user separately sets the parameters for each part. However, it is also possible to construct a structured melody automatically in which case the different parts are all constructed consecutively using randomly selected Time and Pitch parameters and default variations (if ap- plicable). A detailed description is provided on the inter- face. An example of a structure based melody is shown be- low. 3.2.3 Editing By right-clicking in the melody a drop-down menu ap- pears that enables to add a note or to change the pitch of an existing note (Figure 7). A melody can also be transposed or elaborated. The degree of elaboration is determined by the setting of the density parameter in the “Time parameters” pane. Elabo- rations may again be removed. 3.2.4 (Re)arrangement After one or more Parts have been generated, Parts can be removed, moved and duplicated using the drop-down menu shown in Figure 7. 3.2.5 Transformation After a Part has been finished (the Done button having been pushed) the user may apply one or more transfor- mations. Such transformations are most useful to create variations of a Part. The Transformation panel is opened either by right clicking on the Part and selecting “Trans- form Part”, or by left-clicking and pushing the appearing “Transform?” button. Next, the Transform pane will be shown and the Part being transformed will be highlighted in red. At present the following transformations can be applied to a Part: Increase elaboration, Decrease elabo- ration, Transpose 1 (applies a transposition of 1, 2, or 3 steps within the current harmony), Transpose 2 (applies a transposition of 1-7 degree steps up or down, thereby adjusting the harmony), Change Pitch (changes the pitches of the Part keeping rhythm and harmony intact), Change Rhythm (changes (only) the rhythm of the Part). More options will be added in the future. Applied trans- formations can be undone by clicking Edit: Undo Editing 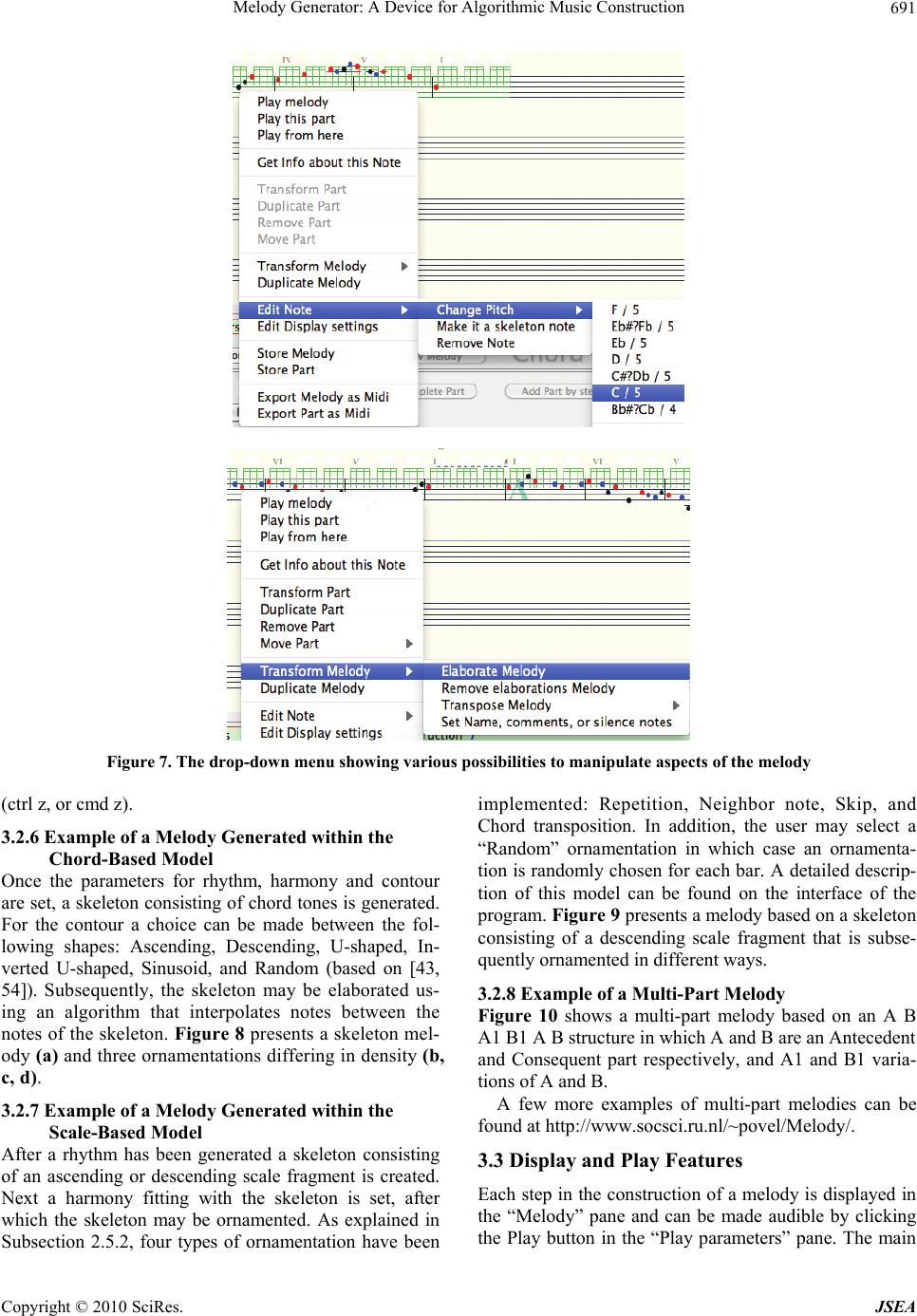 Melody Generator: A Device for Algorithmic Music Construction Copyright © 2010 SciRes. JSEA 691 Figure 7. The drop-down menu showing various possibilities to manipulate aspects of the melody (ctrl z, or cmd z). 3.2.6 Example of a Melody Generated within the Chord-Based Model Once the parameters for rhythm, harmony and contour are set, a skeleton consisting of chord tones is generated. For the contour a choice can be made between the fol- lowing shapes: Ascending, Descending, U-shaped, In- verted U-shaped, Sinusoid, and Random (based on [43, 54]). Subsequently, the skeleton may be elaborated us- ing an algorithm that interpolates notes between the notes of the skeleton. Figure 8 presents a skeleton mel- ody (a) and three ornamentations differing in density (b, c, d). 3.2.7 Example of a Melody Generated within the Scale-Based Model After a rhythm has been generated a skeleton consisting of an ascending or descending scale fragment is created. Next a harmony fitting with the skeleton is set, after which the skeleton may be ornamented. As explained in Subsection 2.5.2, four types of ornamentation have been implemented: Repetition, Neighbor note, Skip, and Chord transposition. In addition, the user may select a “Random” ornamentation in which case an ornamenta- tion is randomly chosen for each bar. A detailed descrip- tion of this model can be found on the interface of the program. Figure 9 presents a melody based on a skeleton consisting of a descending scale fragment that is subse- quently ornamented in different ways. 3.2.8 Example of a Multi-Part Melody Figure 10 shows a multi-part melody based on an A B A1 B1 A B structure in which A and B are an Antecedent and Consequent part respectively, and A1 and B1 varia- tions of A and B. A few more examples of multi-part melodies can be found at http://www.socsci.ru.nl/~povel/Melody/. 3.3 Display and Play Features Each step in the construction of a melody is displayed in the “Melody” pane and can be made audible by clicking the Play button in the “Play parameters” pane. The main 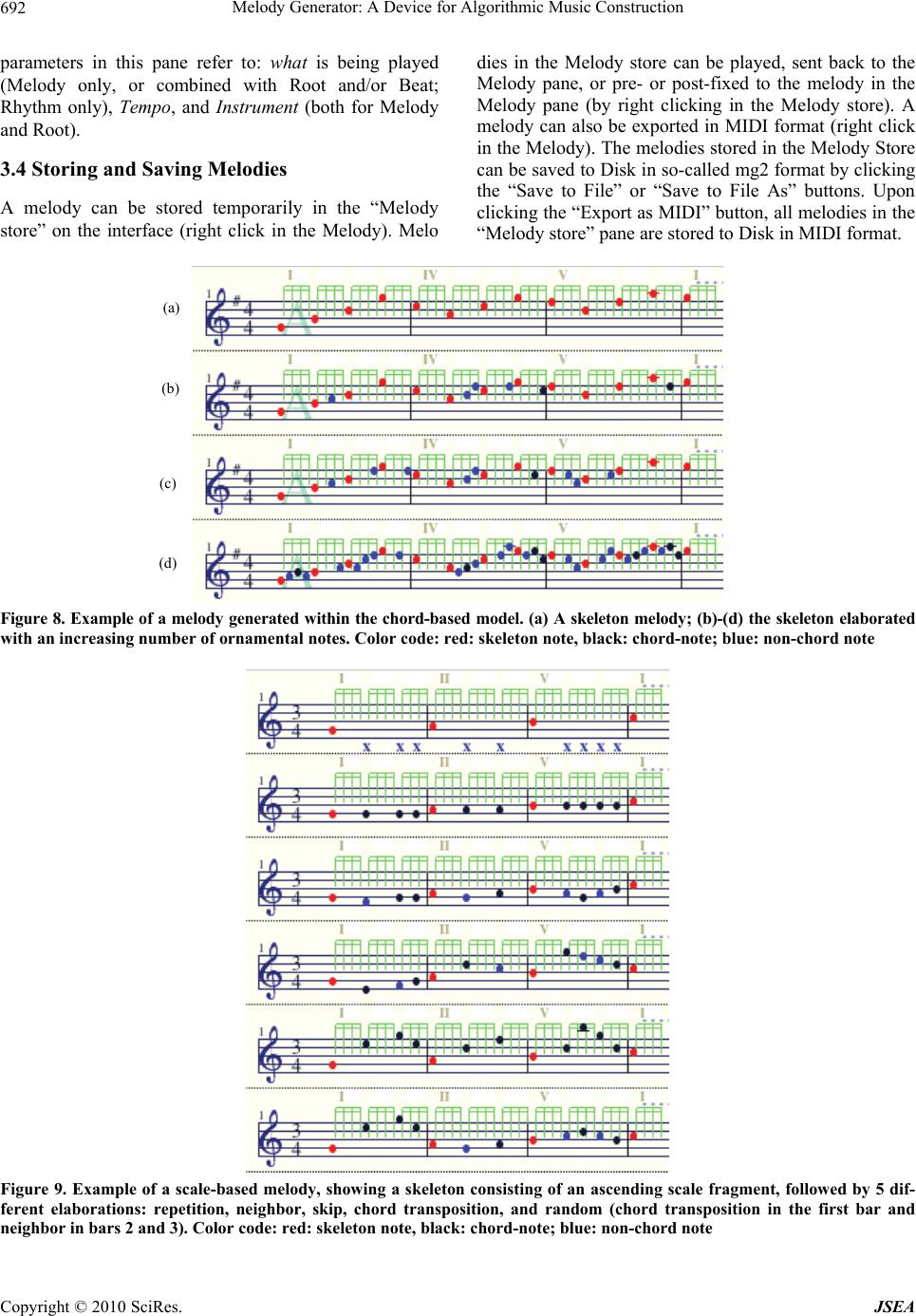 Melody Generator: A Device for Algorithmic Music Construction Copyright © 2010 SciRes. JSEA 692 parameters in this pane refer to: what is being played (Melody only, or combined with Root and/or Beat; Rhythm only), Tempo, and Instrument (both for Melody and Root). 3.4 Storing and Saving Melodies A melody can be stored temporarily in the “Melody store” on the interface (right click in the Melody). Melo dies in the Melody store can be played, sent back to the Melody pane, or pre- or post-fixed to the melody in the Melody pane (by right clicking in the Melody store). A melody can also be exported in MIDI format (right click in the Melody). The melodies stored in the Melody Store can be saved to Disk in so-called mg2 format by clicking the “Save to File” or “Save to File As” buttons. Upon clicking the “Export as MIDI” button, all melodies in the “Melody store” pane are stored to Disk in MIDI format. Figure 8. Example of a melody generated within the chord-based model. (a) A skeleton melody; (b)-(d) the skeleton elaborated with an increasing number of ornamental notes. Color code: red: skeleton note, black: chord-note; blue: non-chord note Figure 9. Example of a scale-based melody, showing a skeleton consisting of an ascending scale fragment, followed by 5 dif- ferent elaborations: repetition, neighbor, skip, chord transposition, and random (chord transposition in the first bar and neighbor in bars 2 and 3). Color code: red: skeleton note, black: chord-note; blue: non-chord note (a) (b) (c) (d)  Melody Generator: A Device for Algorithmic Music Construction Copyright © 2010 SciRes. JSEA 693 Figure 10. Example of a multipart melody built on the structure Ant, Cons, Ant1, Cons2, Ant, Cons, i.e. an Antecedent- Consequent formula repeated twice in which the first repetition is slightly varied (ornamented) 3.5 Additional Functions Apart from the functions that may be invoked from the main interface, a few additional functions are available through the Menu, such as displaying the current KeyS- pace, displaying properties of the notes in the melody, changing the display parameters, displaying information about the operation of the program, etc. 4. Conclusions This article describes a device for the algorithmic con- struction of tonal melodies, named Melody Generator. Starting from a few basic assumptions, a set of notions were formulated concerning the context of tonal music and the construction principles used in its generation. These notions served as the starting points for the devel- opment of a computer program that generates tonal me- lodies the characteristics of which are controlled by means of adjustable parameters. The architecture and implementation of the program, including its multipur- pose interface, are discussed in some details. Presently, we are working on a formal and systematic validation of the melodies produced by the device in or- der to obtain a reliable estimation of the positive and negative qualities of its various aspects. This evaluation will provide the necessary feedback to further develop and refine the algorithm and its underlying theoretical notions. Results of this evaluation will be reported in a forthcoming publication. 5. Acknowledgements My former students Hans Okkerman, Peter Essens, René van Egmond, Erik Jansen, Jackie Scharroo, Reinoud Roding, Jan Willem de Graaf, Albert van Drongelen, Thomas Koelewijn, and Daphne Albeda, all played an indispensable role in the development of the ideas un- derlying the project described in this paper. I am most grateful to David Temperley for his support over the years, to Hubert Voogd for his help in tracing and crushing numerous tenacious bugs, and Herman Kolk and Ar Thomassen for suggestions to improve the text. REFERENCES [1] W. V. D. Bingham, “Studies in Melody,” Psychological Review, Monograph Supplements, Vol. 12, Whole No. 50, 1910. [2] H. Gardner, “The Mind’s New Science: A History of the Cognitive Revolution,” Basic Books, 1984. [3] D. Deutsch, (Ed.) “The Psychology of Music,” Academic Press, 1999.  Melody Generator: A Device for Algorithmic Music Construction Copyright © 2010 SciRes. JSEA 694 [4] C. L. Krumhansl, “Cognitive Foundations of Musical Pitch,” Oxford University Press, 1990. [5] D. Deutsch and J. Feroe, “The Internal Representation of Pitch Sequences,” Psychological Review, Vol. 88, No. 6, 1981, pp. 503-522. [6] K. Hirata and T. Aoyagi, “Computational Music Repre- sentation Based on the Generative Theory of Tonal Music and the Deductive Object-Oriented Database,” Computer Music Journal, Vol. 27, No. 3, 2003, pp. 73-89. [7] F. Lerdahl and R. Jackendoff, “A Generative Theory of Tonal Music,” MIT Press, Cambridge, 1983. [8] H. C. Longuet-Higgins and M. J. Steedman, “On Interpret- ing Bach,” In: B. Meltzer and D. Michie, Eds., Machine Intelligence, University Press, 1971. [9] A. Marsden, “Generative Structural Representation of Tonal Music,” Journal of New Music Research, Vol. 34, No. 4, 2005, pp. 409-428. [10] D. J. Povel, “Internal Representation of Simple Temporal Patterns,” Journal of Experimental Psychology: Human Perception and Performance, Vol. 7, No. 1, 1981, pp. 3- 18. [11] D. J. Povel, “A Model for the Perception of Tonal Music,” In: C. Anagnostopoulou, M. Ferrand and A. Smaill, Eds., Music and Artificial Intelligence, Springer Verlag, 2002, pp. 144-154. [12] D. Temperley, “An Algorithm for Harmonic Analysis,” Music Perception, Vol. 15, No. 1, 1997, pp. 31-68. [13] D. Temperley, “Music and Probability,” MIT Press, Cambridge, 2007. [14] D. Cope, “Experiments in Music Intelligence,” MIT Press, 1996. [15] E. Miranda, “Composing Music with Computers,” Focal Press, 2001. [16] R. Rowe, “Machine Musicianship,” MIT Press, 2004. [17] G. Papadopoulos and G. Wiggins, “AI Methods for Algo- rithmic Composition: A Survey, a Critical View and Future Prospects,” Proceedings of the AISB’99 Sympo- sium on Musical Creativity, Edinburgh, Scotland, 6-9 April 1999. [18] C. Ames, “The Markov Process as a Compositional Model: A Survey and Tutorial,” Leonardo, Vol. 22, No. 2, 1989, pp. 175-187. [19] E. Cambouropoulos, “Markov Chains as an Aid to Computer Assisted Composition,” Musical Praxis, Vol. 1, No. 1, 1994, pp. 41-52. [20] K. Ebcioglu, “An Expert System for Harmonizing Four Part Chorales,” Computer Music Journal, Vol. 12, No. 3, 1988, pp. 43-51. [21] M. Baroni, R. Dalmonte and C. Jacoboni, “Theory and Analysis of European Melody,” In: A. Marsden and A. Pople, Eds., Computer Representations and Models in Music, Academic Press, London, 1992. [22] D. Cope, “Computer Models of Musical Creativity,” A-R Editions, 2005. [23] M. Steedman, “A Generative Grammar for Jazz Chord Sequences,” Music Perception, Vol. 2, No. 1, 1984, pp. 52-77. [24] J. Sundberg and B. Lindblom, “Generative Theories in Language and Music Descriptions,” Cognition, Vol. 4, No. 1, 1976, pp. 99-122. [25] G. Wiggins, G. Papadopoulos, S. Phon-Amnuaisuk and A. Tuson, “Evolutionary Methods for Musical Composi- tion,” Partial Proceedings of the 2nd International Con- ference CASYS’98 on Computing Anticipatory Systems, Liège, Belgium, 10-14 August 1998. [26] J. A. Biles, “Genjam: A Genetic Algorithm for Generat- ing Jazz Solos,” 1994. http://www.it.rit.edu/~jab/ [27] P. Todd, “A Connectionist Approach to Algorithmic Composition,” Computer Music Journal, Vol. 13, No. 4, 1989, pp. 27-43. [28] P. Toiviainen, “Modeling the Target-Note Technique of Bebop-Style Jazz Improvisation: An Artificial Neural Network Approach,” Music Perception, Vol. 12, No. 4, 1995, pp. 399-413. [29] M. Baroni, S. Maguire and W. Drabkin, “The Concept of a Musical Grammar,” Musical Analysis, Vol. 2, No. 2, 1983, pp. 175-208. [30] M. Baroni, R., Dalmonte and C. Jacoboni, “A Computer- Aided Inquiry on Music Communication: The Rules of Music,” Edwin Mellen Press, 2003. [31] A. Marsden, “Representing Melodic Patterns as Networks of Elaborations,” Computers and the Humanities, Vol. 35, No. 1, 2001, pp. 37-54. [32] H. C. Longuet-Higgins and C. S. Lee, “The Perception of Musical Rhythms,” Perception, Vol. 11, No. 2, 1982, pp. 115-128. [33] D. J. Povel and P. J. Essens, “Perception of Temporal Patterns,” Music Perception, Vol. 2, No. 4, 1985, pp. 411-440. [34] F. Gouyon, G. Widmer, X. Serra and A. Flexer, “Acoustic Cues to Beat Induction: A Machine Learning Approach,” Music Perception, Vol. 24, No. 2, 2006, pp. 177-188. [35] D. J. Povel and H. Okkerman, “Accents in Equitone Sequences,” Perception and Psychophysics, Vol. 30, No. 6, 1981, pp. 565-572. [36] D. J. Povel, “Exploring the Elementary Harmonic Forces in the Tonal System,” Psychological Research, Vol. 58, No. 4, 1996, pp. 274-283. [37] F. Lerdahl, “Tonal Pitch Space,” Music Perception, Vol. 5, No. 3, 1989, pp. 315-350. [38] F. Lerdahl, “Tonal Pitch Space,” Oxford University Press, Oxford, 2001. [39] E. H. Margulis, “A Model of Melodic Expectation,” Music Perception, Vol. 22, No. 4, 2005, pp. 663-714. [40] D. J. Povel and E. Jansen, “Harmonic Factors in the Perception of Tonal Melodies,” Music Perception, Vol. 20, No. 1, 2002, pp. 51-85. [41] J. J. Bharucha, “Anchoring Effects in Music: The Resolution of Dissonance,” Cognitive Psychology, Vol. 16, No. 4, 1984, pp. 485-518.  Melody Generator: A Device for Algorithmic Music Construction Copyright © 2010 SciRes. JSEA 695 [42] D. J. Povel and E. Jansen, “Perceptual Mechanisms in Music Processing,” Music Perception, Vol. 19, No. 2, 2001, pp. 169-198. [43] E. Toch, “The Shaping Forces in Music: An Inquiry into the Nature of Harmony, Melody, Counterpoint, Form,” Dover Publications, NY, 1977. [44] J. Bamberger, “Developing Musical Intuitions,” Oxford University Press, Oxford, 2000. [45] Schoenberg, “Fundamentals of Musical Composition,” Faber and Faber, 1967. [46] H. Schenker, “Harmony,” Chicago University Press, Chicago, 1954. [47] V. Zuckerkandl, “Sound and Symbol,” Princeton Univer- sity Press, Princeton, 1956. [48] H. Schenker, “Free Composition (Der freie Satz),” E. Oster, Translated and Edited, Longman, New York, 1979. [49] M. Neuburg, “REALbasic. The Definitive Guide,” O’Reilly, 1999. [50] M. G. Brown, “A Rational Reconstruction of Schenkerian Theory,” Thesis Cornell University, 1989. [51] M. G. Brown, “Explaining Tonality,” Rochester Univer- sity Press, Rochester, 2005. [52] Jonas, “Das Wesen des musikalischen Kunstwerks : eine Einführung in die Lehre Heinrich Schenkers,” Saturn, 1934. [53] W. Piston and M. Devoto, “Harmony,” Victor Gollancz, 1989. [54] D. Huron, “The Melodic Arch in Western Folksongs,” Computing in Musicology, Vol. 10, 1989, pp. 3-23. |

