Journal of Modern Physics
Vol.06 No.13(2015), Article ID:60760,6 pages
10.4236/jmp.2015.613199
Scattering of Conduction Electrons on the Static Deformation Raised by Irradiation in n-GaP Crystals
Norik Е. Grigoryan1, Hrant N. Yeritsyan1*, Vachagan V. Harutyunyan1, Narek A. Hakobyan1, Eduard A. Aleksanyan1, Vahan A. Sahakyan2
1A. Alikhanian National Science Laboratory, Yerevan Physics Institute, Yerevan, Armenia
2National Institute of Metrology, Yerevan, Armenia
Email: *grant@mail.yerphi.am
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 September 2015; accepted 26 October 2015; published 29 October 2015
ABSTRACT
Study of spectral dependences of absorption coefficient at the region of absorption by free carriers shows that the introduction of radiation defects in n-GaP crystals leads to the appearance of additional scattering besides of traditional ones. A new scattering mechanism on “frozen” phonons (deformation localized near the radiation defects) is suggested and its behavior in experimental and theoretical aspects taking into account Х1с-Х3с transitions at the scattering process has been studied. It was shown that the increase of “frozen” phonons’ concentration results to the growth of this mechanism contribution in the whole scattering and the absorption coefficient by free carriers is described approximately by low a ~ w-r, where −1/2 ≤ r ≤ 7/2. Suggested scattering mechanism allows explaining qualitatively the decrease of r. It was established that the dis- ordered by irradiation region effectively decreases the concentration of free carriers, but being a region of increased resistivity, it influences the scattering slightly even at the actual quantum region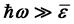
Keywords:
Free Carriers, Absorption, Irradiation, Scattering Mechanism, Deformation Potential, Phonon, Gallium Phosphide

1. Introduction
The basic information about the scattering mechanisms has been obtained from the temperature and field dependences of kinetic coefficients. In respect of electron-phonon scattering mechanisms, the problem primarily consists in finding the electron-phonon coupling constants in the expression for kinetic coefficients as parameters to be determined experimentally. However, the temperature dependences of kinetic coefficients alone are often insufficient to fully define all of above constants. As shown in [1] , even for well-known material such as silicon, it is impossible to consider the scattering mechanisms as finally established. In this regard, the study of frequency dependences of the coefficient of light absorption by free carriers in the quantum frequency range ( , where is the mean kinetic energy of carriers) opens up new possibilities for scientific and applied developments.
, where is the mean kinetic energy of carriers) opens up new possibilities for scientific and applied developments.
Quantum theory of the absorption by free carriers predicts power degree dependences of absorption coefficient:
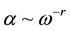 , (1)
, (1)
where r is determined by the scattering mechanisms [2] . Therefore, it can be assumed that different frequency characteristics a are related to different relative contributions of scattering mechanisms. Chemical bond in GaP crystals is of mixed type, so along with the ionized impurities (r ≈ 3 - 35) both acoustic (r 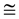 1.5) and optical phonons (r
1.5) and optical phonons (r 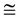 2.5) contribute to the scattering of conduction electrons, and, according to the results of [2] , experimentally observed values of degree r should be within the following limits: 3/2 ≤ r ≤ 7/2.
2.5) contribute to the scattering of conduction electrons, and, according to the results of [2] , experimentally observed values of degree r should be within the following limits: 3/2 ≤ r ≤ 7/2.
For n-GaP usually r  1.8 but, as shown in [1] [3] , none of the scattering mechanisms, including acoustic-phonon scattering, does not describe absorption of light by free carriers in this crystal. Papers [1] [4] justified the existence of once more type of scattering in n-GaP related to the features of its band structure (so-called i-scattering). However, even though explaining small r for n-GaP, the proposed mechanism does not explain the observed decrease of r with deterioration of the crystal structure perfection, e.g., with increasing compensation ratio [5] [6] .
1.8 but, as shown in [1] [3] , none of the scattering mechanisms, including acoustic-phonon scattering, does not describe absorption of light by free carriers in this crystal. Papers [1] [4] justified the existence of once more type of scattering in n-GaP related to the features of its band structure (so-called i-scattering). However, even though explaining small r for n-GaP, the proposed mechanism does not explain the observed decrease of r with deterioration of the crystal structure perfection, e.g., with increasing compensation ratio [5] [6] .
This paper presents the results of study the light absorption by free carriers in n-GaP crystals irradiated by high energy (50 MeV) electrons, i.e., a defects concentration and compensation ratio of free carriers in crystals was carried out by introducing radiation defects. Both experimental and theoretical investigations were applied in the course of electron irradiation at various doses and proposed theory explained the experimental data sufficiently.
2. Experimental Results
The measurements of free carrier absorption in n-GaP crystals doped with tellurium (free carrier concentration n = (1.5 - 2) × 1017 cm−3) in infrared region (l = 2 - 15 μm) were carried out using UR-20 spectrophotometer at room temperature. The concentration of charge carriers was determined from the intensity of 3 μm absorption band based on the value of the absorption cross-section for X1c-X3c transitions, s = 9 × 10−17 cm2 [7] . Irradiation by 50 MeV electrons at current density of 1 μA/cm2∙s at room temperature was carried out using a linear accelerator of Yerevan Physics Institute.
Figure 1 shows the spectral dependence in infrared region of the absorption coefficient of n-GaP crystals irradiated by 50 MeV electrons with various integral fluxes. Absorption in this field is mainly due to: 1) transfer of electrons from the absolute minimum of conduction band X1с to the minimum X3с located higher by 0.4 eV; 2) absorption by free carriers.
The curves reveal an absorption band at l = 3 μm (type (1) transition) on the background of uniformly increased with absorption wavelength described by function like (1) due to type (2) transitions. Table 1 shows the concentration of free electrons, NA/ND compensation ratio (NA-acceptors concentration, Nd-donors concentration), a/n ratio at l = 6.25 μm in the initial crystal and after electron irradiation. Also, some data from [5] are presented for identical sample compensated by chemical impurity.
It is seen that as a result of irradiation, the concentration of free electrons decreases and the compensation ratio increases. At the same time, a decrease of degree r in the spectral dependence of the absorption coefficient down to 1.13 takes place. Here, a/n ratio after irradiation increases. When irradiating with 50 MeV electrons, point radiation defects and more thermo-stable disordered regions are simultaneously formed in GaP crystals [8] [9] . Figure 2 shows the absorption spectra of the crystals: the non-irradiated, irradiated (50 MeV electrons at a dose of 1017 el/cm2) and after heat treatment at 525˚C. For the crystals irradiated with so high integral electron fluxes, the free carriers density decreases sharply, in consequence of which no absorption by free carriers is observed. It was shown in [9] that the point radiation defects in GaP crystals annealed at 525˚C, so the differences
Figure 1. Spectral dependence of the absorption coefficient a for n-GaP sample NO 1 irradiated by 50 MeV electrons with doses: 1-D = 0; 2-D = 4.3 × 1015 el/cm2; 3-D = 7 × 1015 el/cm2; 4-D = 8.6 × 1015 el /cm2.
Figure 2. Spectral dependence of the absorption coefficient a for n-GaP sample NO 2: 1-initial; 2-after irradiation (D = 1 × 1017 el/cm2) and annealing at 525˚C during 20 min.
between curves 1 and 2 (see Figure 2) are due to disordered regions.
It is obvious that whereas only 25% of free electron concentration was recovered after the annealing, the r value in (1) was recovered completely, the a/n ratio also was recovered.
Table 1. The concentration of free electrons.
*After irradiation, the sample was annealed at 525˚C during 20 min.
3. Theory
The coefficient of absorption by free carriers was calculated by the second order of the perturbation theory [1] :
 (2)
(2)
where i, m, f represent the initial, intermediate and final electron state, respectively,  is the matrix element of electron interaction with any crystal imperfection (cr.i),
is the matrix element of electron interaction with any crystal imperfection (cr.i), 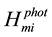 is the matrix element of the electron-photon interaction, factor
is the matrix element of the electron-photon interaction, factor 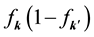 indicates the presence of electrons in the initial and final states. Here, a(w) rela-
indicates the presence of electrons in the initial and final states. Here, a(w) rela-
tionship is determined by the dependence of matrix elements on k, k' vectors. The expressions ,
, 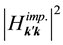 ,
,
 describe conduction electron interaction with crystal imperfections [1] . It is shown that
describe conduction electron interaction with crystal imperfections [1] . It is shown that 





to the (2) defines a(w) relationship.
In accordance with [1] , the frequency dependence of a(w) for n-GaP taking into account all traditional scattering mechanisms: on acoustic (ac.) and optical (opt.) phonons, on ionized impurities (imp.), inter-valley (in.v.) scattering; and different types of intermediate states (both intra-band X1c and for overlying X3c zone)-can be represented in the following form:

where 


where N is the carrier concentration, n is the refractive index. The second term in (3) corresponds to the inclusion of intermediate states in the next conduction band (X1c-X3c virtual transitions), which formally looks like the presence of one more scattering mechanism, called i-scattering [1] [4] .
The above mentioned experimental results show that the degree r in (1) decreases with increasing NA/ND in the case of both doping [5] and irradiation. In both cases the total number of static imperfections increases and around these lattice defects static deformation fields may arise [6] . The additional deformation potential associated with them does not differ, in principle, from the deformation potential caused, for example, by acoustic phonons. The phonons, which correspond to static deformation fields, will be conditionally called “frozen.”
The basic idea of the deformation potential approximation is that the operator of interaction with phonons should be replaced by a quantity characterizing the crystal deformation. It is supposed that the deformation caused by static field arising in the presence of radiation defects, is responsible for local changes in the size and shape of the crystal unit cell much as in the case of the deformation due to lattice vibrations. If the phonons are the sum of normal vibrations, then the static field near the radiation defects can be considered as the sum of a large number of Fourier components corresponding to the “frozen” lattice vibrations. Obviously, their number is proportional to the density of radiation defects.
Scattering on the “frozen” phonons can be taken into account, on the whole, within the framework of the theory of deformation potential. It is known that in this approximation, when describing the electron interaction with one phonon with wave vector

where Dq, wfroz., nfroz. are the interaction constants, frequency and distribution function of such “frozen” phonons, respectively. For small q 

and similar to the interaction with the photons, if (Dq)q=0 ≠ 0, the transition is “permitted”, and if (Dq)q=0 = 0, the electron-phonon transition is “forbidden”.
For the “frozen” phonons, wfroz. and nfroz. weakly depend on q, therefore for the permitted transitions
does not depend on q, afroz.(w) is the same as for the acoustic phonons, so these data cannot explain our experimental results.
However, for the “forbidden” transitions

where
For the “forbidden” transitions (Dq)q=0 = 0, and the electron-phonon interaction will be of the first order in q. Note that for all types of phonons apart from acoustic ones, such scattering does not practically contribute to the kinetic phenomena due small q. However, in the case of the absorption of free carriers, where the scattering is no
longer elastic due to presence of high-energy photons 

should be also considered.
Assuming that the interaction with the “frozen” phonons is described by the first order terms in q, with the growth of the number of such phonons the scattering on them can be an essential mechanism competing with the scattering on acoustic phonons.
Below, calculation of a(w) for this mechanism is presented similar to the method from [1] for all conventional scattering mechanisms.
Substituting 


which can easily be represented in the following form:

where 



It follows from the form of afroz. that afroz. ~w−1/2 (i.e. l1/2), and it is related to the fact that
Therefore, the frequency dependence of the total coefficient of absorption by free carriers, taking into account
the scattering on the “frozen” phonons, should approximately be described by (1) with
be noted, making allowance for all known scattering mechanisms, that naturally, from a large number of terms not all of them make equal contributions to the final result. In addition, i-scattering should be sufficiently intensive as X1c-X3c transition in n-GaP is dipole-allowed. Consideration of all these features allows explaining anomalously low values of r in the frequency dependence of a(w) and the tendency for a decrease in r with increasing the concentration of radiation-induced defects.
4. Discussion and Conclusions
The increase in a/n ratio after irradiation shows that the introduced radiation defects in n-GaP crystals lead to the emergence of an additional scattering mechanism. The change in the scattering mechanism is also indicated by a decrease of r in (1) after irradiation.
The comparison of changes in the power degree r as a result of introduction of radiation-induced defects with the impact of introduction of compensating impurity atoms on r (see Table 1) shows that the radiation-induced defects change the scattering mechanism much more efficiently than impurities.
It is known that in AIIIBY semiconductor compounds, the radiation defects reveal a significant specific deformation per one point defect which is much more than the specific deformation for a substitution impurity atom. Therefore, the above proposed theoretical conclusion that the scattering on the “frozen” phonons can play a significant role in the absorption by free carriers is explained by additional scattering on local deformations.
In this connection it is interesting to note a much greater influence on the basic absorption edge in GaP, exerted by radiation defects in comparison with impurity centers, which is also explained by deformation effects [8] [9] .
The results shown in Figure 1 reveal a cumulative effect of point radiation defects and disordered regions on the absorption by free carriers in n-GaP.
The relationships shown in Figure 2 enable to separate the effect of disordered regions on the absorption by free carriers. It follows from Figure 2 and Table 1 that the disordered regions both decrease effectively the free carriers concentration and influence on the spectral dependence of the coefficient of absorption by free carriers and on the ratio a/n, and hence influence on the scattering mechanism.
Revealing high potential barrier [9] , the disordered regions in n-GaP are non-permeable for majority carriers. Therefore, scattering can only be carried either in peripheral parts of disordered regions, or outside them.
Cite this paper
Norik Е.Grigoryan,Hrant N.Yeritsyan,Vachagan V.Harutyunyan,Narek A.Hakobyan,Eduard A.Aleksanyan,Vahan A.Sahakyan, (2015) Scattering of Conduction Electrons on the Static Deformation Raised by Irradiation in n-GaP Crystals. Journal of Modern Physics,06,1935-1941. doi: 10.4236/jmp.2015.613199
References
- 1. Demidenko, Z.A. and Tomchuk, P.M. (1981) Physics and Technique of Semiconductors, No. 8, 1589-1595. (In Russian)
- 2. Giehler, M., Kostial, H., Hey, R. and Grahn, H.T. (2004) Journal of Applied Physics, 96, 4755-4761.
http://dx.doi.org/10.1063/1.1803635 - 3. Demidenko, Z.A., Brailovskii, E.Yu., Grigoryan, N.E. and Yeritsyan, H.N. (1983) Izvestia Academy of Sciences of Republic of Armenia, Physics, 18, 19-25. (In Russian).
- 4. Beliaev, A.E., Gorodnichii, O.P., Demidenko, Z.A. and Tomchuk, P.M. (1982) Ukrainian Physical Journal, 27, 666-671. (In Russian)
- 5. Remeniuk, A.D., Zabelina, L.G., et al. (1968) Physics and Technique of Semiconductors, No. 5, 666-670. (In Russian)
- 6. Slupinski, T., Molas, M. and Papierska, J. (2009) Acta Physica Polonika, 116, 979-982.
- 7. Abagyan, S.A., Ivanov, G.A., et al. (1978) Physics and Technique of Semiconductors, No. 7, 1397-1403. (In Russian)
- 8. Yeritsyan, H., Grigoryan, N., Harutyunyan, V., Hakhverdyan, E. and Baghdasaryan, V. (2014) Journal of Modern Physics, 5, 51-54.
http://dx.doi.org/10.4236/jmp.2014.51008 - 9. Brailovskii, E.Yu., Grigoryan, N.E. and Eritsyan, G.N. (1980) Physica Status Solidi (A), 62, 649-655.
http://dx.doi.org/10.1002/pssa.2210620237
NOTES
*Corresponding author.








