Journal of Modern Physics
Vol.05 No.16(2014), Article ID:51085,9 pages
10.4236/jmp.2014.516177
Influence of the Delay and Dispersion in Mechanics
Evelina V. Prozorova
Mathematics & Mechanics Faculty, St. Peterburg State University, St. Peterburg, Russia
Email: e.prozorova@spbu.ru
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 August 2014; revised 25 September 2014; accepted 21 October 2014
ABSTRACT
The aim of this work is to clarify the new mathematical model describing the mechanics of continuous media and rarefied gas. The present study is associated with the formulation of conservation laws as conditions of equilibrium of angular momentums, while usually formulated in terms of balance of force. The equations for gas are found from the modified Boltzmann equation and the phenomenological theory. For a rigid body, the equations used the phenomenological theory, but changed their interpretation. We elucidate the contribution of cross-effects in the conservation laws of continuum mechanics, including the self-diffusion, thermal diffusion, etc., which indicated S. Wallander. The paradox of Hilbert in the solution of the Boltzmann equation by the Chapman-Enskog method was resolved. Refined model of the boundary conditions for rarefied gas flows and transient flow were near the moving surfaces. We establish conditions for the existence of the A. N. Kolmogorov inertial range on the basis of the proposed theory. Based on the theory, derivation of the Prandtl formula for boundary layer was received. Delay in mechanics plays an important role on commensurability of relaxation times and lateness. New accounting delay option is proposed to consider the difference between the time derivative as a limit and end values of the mean free path in a rarefied gas. The role of individual time delay for each particle velocity and the average time is debated. The Boltzmann equation is written with an additional term. This situation is typical for discrete medium. The transition from discrete to continuous environment is a key issue mechanics. Summary records of all effects lead to a cumbersome system of equations and therefore require the selection of main effects in a particular situation. The role of the time has similar problems in quantum mechanics. Some examples are suggested.
Keywords:
Angular Momentum Conservation Laws, Unbalanced Stress Tensor, The Boltzmann Equation, Chapman-Enskog Method

1. Introduction
The proposed work involves new mathematical modeling of processes in the mechanics of fluids, gases and solids in classical and quantum cases. I agree with Stanislaw Jerzy Lec: I think that the amount of zeros is a formidable figure. It seems that continuum mechanics evolving for centuries by many luminaries of science has acquired a finished look in the formulation of its basic laws, but it is not. To date, we have complete mathematical description of certain physical phenomena insufficiently. Some of the issues will be discussed in this paper. The main question is the ratio of discrete and continuous descriptions. One of these effects will be discussed in this work. Previous studies have examined the effects of the angular momentum influence and the associated with its rotation of the elementary volume on writing of the conservation laws of continuum mechanics and kinetic theory. [1] repeated the analysis of previous work. Since gas often significantly alters the properties on small distance, the equations of the state are not sufficiently accurate to describe the structure of flow and solids. Dissipative effects occur at the borders, including on the contact surfaces through the formation and growth of the boundary layers and form turbulence. A large number of experiments tell us about the bad turbulence theories, bad equations of state of water and other liquids, poor boundary conditions in the case of transient flow and poor models of formation of various structures in the solid if gradients and large cracks tell us about the importance of gradients of physical quantities (density, momentum, energy, angular momentum). Our classical models work well when the gradients of physical values are small. We modified the Liuville equation and Bogolubov equation. L. D. Landau, C de Groot, P. Mazur, I. Deyrmati, I. Prigogine, L. I. Sedov, A. A. Ishlinskii, D. D. Ivlev et al. point at the role of angular momentum. It is the most developed area in the momentum theory of elasticity (R. D. Mindlin, V. A. Palmov, A. G. Gorshkov, E. I. Starovoitov, A. V. Yarovoy, V. Levin, S. E. Kanaun, E. L. Aero, etc.). Any movement of an elementary volume of liquid at the moment can be considered as a result of the following motion: quasisolid motion that is translated with selecting pole, rotating motion around this pole and deformation motion. This theorem was proved by H. Gelmholtz. L. Prandtl formulated conception of hardplastic body as the theory of ideal plasticity. Usually, we do not take into account twist velocity. The angular momentum is responsible for the twist velocity. Thus, in the classical Newton mechanics we have four conservation laws: masses, liner momentum, energy and angular momentum. In continuous mechanics, we use only three first laws. However, the law of conservation of angular momentum requires a particular frame of reference and a particular radius vector from the origin to the elementary volume. In the classical approach, the law of conservation of angular momentum does not fit. For these formulations, actually, they postulated symmetry of the material frame of reference and, as a consequence, the symmetry of the stress tensor and the violation of the “continuity” of the environment. Mathematically, this fact follows from the choice of the conditions of equilibrium of forces as a condition of equilibrium. Selection of the conditions of equilibrium of momentum of forces leads to new formulations of equations. The kinetic theory does not save the situation. The law of angular momentum is not implemented in the Boltzmann equation. Classical theory, the second viscosity, is predicted. But usually, we suppose that it is in need to take into consideration for molecules with inner of degree of freedom or for dense gas. The modified kinetic theory gives the second viscosity for molecules without structure. As a result, asymmetric stress tensor is obtained and sets the method of accounting of the asymmetric tensor. It is found that the stress tensor is asymmetric for particles without structure as for kinetic as for phrnomenological theories. It was suggested the kinetic theory with the angular momentum is as an additional variable, using a more accurate asymptotic approximation for macro parameters with a resolution of Hilbert’s paradox. We believed that elementary volume can be rotated around the axis of inertia or to be involved in the rotational movement. In both
cases, the density of the flow is across the border changes as 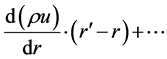 by the rotation of the ele-
by the rotation of the ele-
mentary volume. The contribution of other components is small, taking into account the smallness of the volume and the absence of rotation on axis. Additional issues arise when writing communications stress tensors with tensors of strain rate. Thus, we propose valuing the order of the dependence of the classical relations in this paper. The order equations were increased, requiring additional boundary conditions. If we are dealing with a continuous medium, the boundary condition at the outer edge of the boundary layer can be defined by the value of the vortex or the value of the vertical velocity on the surface you want to set the friction. The turbulent layer usually gives friction. A rarefied gas flow must be set apart beside the usual boundary conditions. In general, the formulation of the boundary conditions requires a further study. Adhesion conditions hold true on a large scale for the flow of Newtonian type. In addition to the angular momentum, the impact of large gradients in the collision integral is essential. Field description (continuum mechanics) implies a transition from a discrete to a continuous medium with aspiration of the distances between atoms (molecules) to zero. In rarefied gas, unusual situation arises when we use the ratio of the increment limit function to the increment of the argument to describe derivatives. It turns out that for recording the time derivative we can consider only the high-speed components as slow collisions do not have time to occur at finite mean free path (rarefied gas). One model was suggested by B. V. Aleekseev [2] . Therefore, there is a need to add the second derivative of the Taylor series for inclusion in the work of the other more slowly components or use the average value of the derivative. For a finite-length path of the molecules when the Knudsen number of order unity, in the collision integral must also be taken into account “delay.” Additional term can be computed. Given the orders of magnitude, the additional integral can be used locally equilibrium distribution function. This means that you can find the new core of the Navier-Stokes equations. In all cases, the classical theory is considered a limiting case when the volume-to-point, but the material point (particle)-simple physical models in mechanics—the ideal body size, and rotation may be neglected. We can also assume infinitely small body size compared with other dimensions or distances within the assumptions of the problem considered. As it was said derivation of conservation laws in classical mechanics is based on the integral conservation laws, shrinking to a point. In the second transition to the classical theory of conservation laws is accomplished by using the density sum of delta functions on the difference 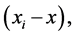 similar to line up for the conservation laws of momentum and energy. Thus, the transition from a discrete medium and back is carried out without taking into account the spatial distribution of physical quantities, static points. A similar situation is observed in quantum mechanics. Some of the questions for the probability density function associated with the transition from quantum to classical mechanics are discussed. Perhaps the best option theory of continuous medium is discrete approach in the integral form for elementary volume, which requires further study. Some examples are suggested. The part of examples one can find in [3] -[5] .
similar to line up for the conservation laws of momentum and energy. Thus, the transition from a discrete medium and back is carried out without taking into account the spatial distribution of physical quantities, static points. A similar situation is observed in quantum mechanics. Some of the questions for the probability density function associated with the transition from quantum to classical mechanics are discussed. Perhaps the best option theory of continuous medium is discrete approach in the integral form for elementary volume, which requires further study. Some examples are suggested. The part of examples one can find in [3] -[5] .
2. Some Singularities of the Boltzmann Equation
We try to receive the modified Navie-Stokes equations from kinetic theory with angular momentum. Common essential in the Bogolubov theory assumptions are: infinite volume is considered; potential forces of the interaction of two particles rapidly abate with increasing of distance between two particles; the appearance of a finite volume’s effect is investigated when the influence of the boundary is unessential, gas is rarefied but has a finite average density. The description of movement of the particles is based on neglect of the variation angular momentum for particles in an elementary volume (in a small neighborhood of the considered one). This is correct for relaxation process for which theory was developed. Essential that the fourth term in formula (1) for nonhomogenеous gas and for nonequilibrium gas does not vanish, when  [6] -[10] .
[6] -[10] .
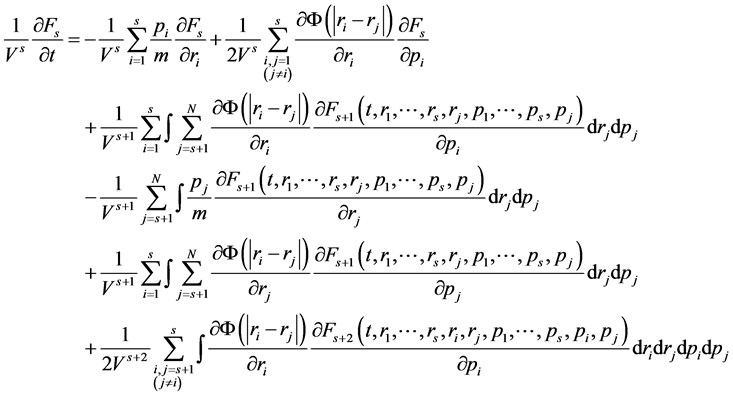 (1)
(1)
Usually we suggest that for 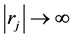
 ,
,
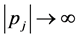 .
.
There are: t—time, r—coordinate, p—momentum, r—density, Ф—potential of molecules interaction. The last three terms are equal to zero at indicated conditions. For nonequilibrium case spatial derivatives do not equal to null. It does not equal to null in case, as example for interaction blowing gas from the surface with nonequilibrium gas of flow near the body. For the enumerated cases particles are not pairwise permutable and we does not have sum. Besides the flows of molecules have to include as the boundary conditions.
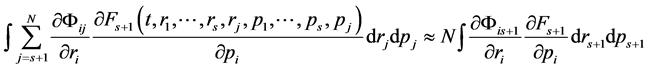
Essentially, we cannot receive equation for Ѕ-particle distribution function under great gradients of physical values by using ordinary approximations. Hence it is not possible to construct the Boltzman equation from the Hamilton formalism but we can use only the laws of conservation for mass, momentum and energy and angular momentum. We now construct of equation for N-particle distribution function for nonequilibrium case taking into account the great gradient of the physical values by using the ordinary notations, i.e.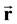 —radius-vector;
—radius-vector;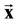 — coordinate of the point and according to definition function fN in element of physical volume
— coordinate of the point and according to definition function fN in element of physical volume 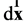 near the point
near the point  in moment t probable number of molecules with velocity in element
in moment t probable number of molecules with velocity in element  near the
near the 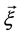 are equal to
are equal to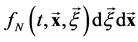 . Let us calculate the change of the angular momentum near the point
. Let us calculate the change of the angular momentum near the point


It is necessary do because flow tube of an elementary volume must be order of free path and need to contain many molecules for ensuring of statistical property. Finally, we obtain the variation of angular momentum in any volume and this result is
Hence, it follows that
The convective operator is modified as

Further we used this operator.
3. Equation
Presented in previous our papers the equations of motion, energy and angular momentum were obtained. In classical case we do not written the angular momentum equation. The modified equations are received by usually kinetic theory methods:
There are t—time, x, y, z—coordinate,
Figure 1 shows that the linear velocity 

The degree of asymmetric stress tensor we can received from momentum equation (in projections) (σ = τ). The non-symmetric tensor τ is indicated.

Another problem for the solving of the Boltzmann equation is the asymptotical methods. It is essential that selecting the local equilibrium distribution function f0 as the basis in solution of the Boltzmann equation by the Chapman-Enskog method exploits macroscopic parameters in f0 from the Euler equations [10] . Macroscopic parameters are determined by the Chapman-Enskog. Distribution function leads to the Euler equations parameters and tensor P is symmetric. Formally in that way we have values (density, linear moment, energy) with mistake of the first order. This fact was noted by Hilbert without further use and correction.
there β-macroscopic parameters.
So for the equilibrium in collision integral
Figure 1. Change in density during the rotation of the elementary volume.
and for nonequilibrium distribution function
we have the same macroparameters in f0. The nonequilibrium distribution function is such that integral of it contains only the integral of equilibrium function f0 and gives containing in f0 macroscopic parameters. The remaining term gives null. Besides it is essentially for the value of viscosity. So it is necessary to do iteration all values (density, linear momentum, energy). It is possible for equation with angular momentum. In classic theory thus tensor P is entering as the value P in the Euler equations and as symmetric tensor in the Navier-Stokes equations. Consequently the theory value P for the Navie-Stokes equations is not equal to value P for the macroscopic Euler equations.
Also the angular momentum is very important characteristic for large gradients and the associated effects in the presence of charged particles. Now the angular momentum does not take consideration to calculate potential [11] . In the presence of interactions (that is to say, between different types of physical fields) quanta lost independence. Quantum theory of these fields does not sufficiently develop. Conserved angular momentum of a closed system and central forces, but in general, the law must be built. However, for the problem of decay of particles with mass defect after the collapse, we consider only the law of conservation of energy and momentum. In quantum mechanics separately makrozakon conservation of angular momentum is not issued. It is obtained by multiplying the vector equation for the amount of traffic on the vector r.

Partially account the angular momentum occurs in solving the molecular dynamics method. Causality principle and the principle of the finite velocity of propagation of interactions require that the differential equations describing the fundamental fields belong to hyperbolic type. Despite the apparent first-order equations for the wave function and the equations of motion (for speed) together, we actually have a second-order equation and formally we can determine the velocity and momentum [12] [13] .



In continuum mechanics equations, were derived previously given angular momentum [1] . From this consideration, we need to consider angular momentum in quantum mechanics, i.e. taking as independent variables except the coordinate and momentum angular momentum. It will be a small correction, but for some options that have many interacting components, it can play a big role.
4. Boundary Layer
The Blasius problem was considered in [1] by numerical and analytical. New equations of uniform translational movement of cylinder are

Boundary conditions are

Here x, y are the coordinates, u, ν are the velocities, 


We have stretch team inside boundary layer. Result of numerical solution is on Figure 2.
Some results for infinite plate will be formulated here. The equation for this case is (the new term is selected)
Boundary conditions are
Integrating gives
The Prandtl formula is received from this equation. From this equation we can receive the results of A. N. Kolmogorov.
We investigated the effect of the asymmetry of the distribution function for the equilibrium case, As since in directional velocity at the outer edge of a thin layer appears as a slow component, and high-energy. Therefore there is a walk along the surface of the particles to the slow component and the introduction of particles into the crystal for the fast component. It should be noted the possibility of a theoretical calculation of fatigue effects ideal surface in normal conditions. To do this, we need to calculate using the equilibrium distribution function of the value of the gas molecules with high energy for a given temperature, with a preliminary study, a similar representation.
The results we can see in [6] . One of results is on Figure 3.
Figure 2. Stream function is inside the boundary layer at the vortex perturbation at the upper limit.
Figure 3. Reacting the directed gas stream with the equilibrium surface.
5. Delay
In the kinetic theory, the role of delay in the considering should be to deal with the question of what values measure in the experiment: the instantaneous or averaged. If the experiment has to do with the average at the agreed time, in this case consider the delay is not necessary, except in cases of commensurability of relaxation times and the delay in otherwise, it is necessary to bear in mind the following: all interactions occur at a finite rate. Consider the action finite values of the propagation velocity of the interacting particles in the kinetic theory.
With that said, the Boltzmann equation can be written as

Similarly, calculated values with a stroke since the molecule must fly during the free path, the mean free path of the molecules and the travel time to and after the collision can be different (may be different values of the incident and impinging molecules (with index one).
However, structural gas, for example, at altitudes above 120 km the mean free time at three Mach numbers, i.e. lag time 10−8 c and more that can be comparable with the relaxation time. In fact, the expression can be simplified by considering the order of magnitude. Then

Then the integrals are computed and we obtain the corresponding kernel of the Navier-Stokes equations. For small and medium gradients mean free time one and one mean free path. But significant differences are in the interaction of gases with different properties.
6. Conclusions
The effect of the delay in a discrete medium under the transition to a continuous (field) description is investigated. A modification of the equations of a rarefied gas is done. Besides, we investigate the influence of angular momentum in the volume element. The influence of these effects in continuum mechanics and kinetic theory is showed. Some numerical results are demonstrated. Conditions of their application are studied and concrete situation are discussed.
Addition. All continuum mechanics have the same laws. So the theory elasticity needs to include the law of angular momentum. We suggest some examples.
Examples. If we shall consider protozoa task about beam and shall take into attention angular momentum, we shall receive the classical result. Consequently, we can choose the beam of variable cross-section. For beam on elastic foundation results distinguishes. In another case of transmission pressure at beam by intermediate designs of external force P (Figure 4) passes through hard lever of length l that can twist around hinge we show below.

At the end of elastic beam transfers force is


So we have at end of length


Now
If we write equations in classical case for stress values of elasticity theory, we have six unknown quantities and three equations. In our case, we add the equation for angular momentum but we have nine unknown quantities. As a result, we have old situation. For our case, we suppose that one possible solution we can receive is using the classical supposition. Consequently, we need to add equations for geometrical and physical properties. Now we consider four educational problems for long beam. The first one is the beam under longitudinal force. Suggested that
Here are the problems where three angular momentums are equal to zero. A new way to decide problem does not give new result. The second case is the clean torsion.
Let us consider the problem where two angular momentums are equal to zero. Consequently, the laws of equilibrium forces are fulfilling. In this case, all three laws of force’s balance must be equal to zero. For problem for transverse beam gives same results same for the second case. But for problem about twisting of the beam, we receive another solution
We consider the Lame and Kirsha problems. In the first problem, loading on the sides is homogeneous. So momentum can be only in corner. For the same loading on all sides, angular momentum does not work. But for different loading, momentum works and added strength will be activity. The result is raising or going down. For the second problem besides the corner’s effects, we have momentum near the axis z. So at cross of the circle and
Figure 4. Transmission pressure at beam by intermediate designs of external force P.


Figure 5. Illustrate for the problems of Lama and Kirsch.
axis y, we have added forces that have the direction of the stress on side. So the new way to decide a problem does not give new results. The second problem is the clean torsion.
Angular momentums are equal to zero. Consequently, the laws of forces are fulfilled. In this case all, three laws of force’s balance must be equal to zero. For problem about transverse beam gives same results as for the second case. But for problem about twisting of the beam, we have another solution 

References
- Prozorova, E.V. (2013) International Scientific IFNA-ANS Journal Problems of Nonlinear Analysis in Engineering Systems, 19, 45-57.
- Alexeev (2004) Generalized Boltzmann Physical Kinetics. Elsevier, Amsterdam.
- Prozorova, E.V. (2012) Electronic Journal Physico-Chemical Kinetics in Gas Dynamics, 13. http://www.chemphys.edu.ru/pdf/2012-10-30-001.pdf (in Russian)
- Prozorova E.V. and Shadrin, A. (2013) Influence Dispersion in Gas and Solid for Moving Body. 5th European Conference for Aeronautics and Space Sciences, Munich, 1-5 July 2013/Holiday Inn Munich City Centre, Munich.
- Prozorova, E.V. (2013) Influence of the Dispersion in Model of Continuous Mechanics. VVM Publishing Ltd., St.- Peterburg. (in Russian)
- Bogolubov, N.N. (1946) Problems of Dynamic Theory in Statistical Physics. Gostexizdat, M-L. (in Russian)
- Cercignani, C. (1969) Mathematical Methods in Kinetic Theory. Macmillan.
- Ferziger, J.H. and Kaper, H.G. (1972) Mathematical Theory of Transport Processes in Gases. Amsterdam-London.
- Hirschfelder, J.O., Curtiss, C.F. and Bird, R.B. (1954) The Molecular Theory of Gases and Liquids. New York.
- Kogan, M.N. (1967) The Dynamics of the Rarefied Gases. Nauka, M. (in Russian)
- Lazić, I. (2009) Atomic Scale Simulation of Oxide and Metal Film Growth. Chapter 3. General Performance Testing, Chapter 4. An Improved Molecular Dynamics Potential for Studying Aluminum Oxidation. Part1-Parameter Optimization for the Electrostatic Part of the Potential. College Voor Promoties.
- Zubarev, D.N. (1971) Nonequilibrium Statistical Thermodynamics. Nauka, Moscow, 414 p.
- Fermi, E. (1968) Quantum Mechanics. Wiley, New York.
- Eugene, P. (1970) Wigner Symmetries and Reflections. Bloomigston-London.



































