Journal of Modern Physics
Vol.4 No.8A(2013), Article ID:36688,17 pages DOI:10.4236/jmp.2013.48A022
The Mathematical Foundations of General Relativity Revisited
CERMICS, Ecole des Ponts ParisTech, Marne-la-Vall_ee Cedex 02, France
Email: jean-francois.pommaret@wanadoo.fr, pommaret@cermics.enpc.fr
Copyright © 2013 Jean-Francois Pommaret. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 13, 2013; revised June 19, 2013; accepted July 29, 2013
Keywords: General Relativity; Riemann Tensor; Weyl Tensor; Ricci Tensor; Einstein Equations; Lie Groups; Lie Pseudogroups; Differential Sequence; Spencer Operator; Janet Sequence; Spencer Sequence; Differential Module; Homological Algebra; Extension Modules; Split Exact Sequence
ABSTRACT
The purpose of this paper is to present for the first time an elementary summary of a few recent results obtained through the application of the formal theory of partial differential equations and Lie pseudogroups in order to revisit the mathematical foundations of general relativity. Other engineering examples (control theory, elasticity theory, electromagnetism) will also be considered in order to illustrate the three fundamental results that we shall provide successively. 1) VESSIOT VERSUS CARTAN: The quadratic terms appearing in the “Riemann tensor” according to the “Vessiot structure equations” must not be identified with the quadratic terms appearing in the well known “Cartan structure equations” for Lie groups. In particular, “curvature + torsion” (Cartan) must not be considered as a generalization of “curvature alone” (Vessiot). 2) JANET VERSUS SPENCER: The “Ricci tensor” only depends on the nonlinear transformations (called “elations” by Cartan in 1922) that describe the “difference” existing between the Weyl group (10 parameters of the Poincaré subgroup + 1 dilatation) and the conformal group of space-time (15 parameters). It can be defined without using the indices leading to the standard contraction or trace of the Riemann tensor. Meanwhile, we shall obtain the number of components of the Riemann and Weyl tensors without any combinatoric argument on the exchange of indices. Accordingly and contrary to the “Janet sequence”, the “Spencer sequence” for the conformal Killing system and its formal adjoint fully describe the Cosserat equations, Maxwell equations and Weyl equations but General Relativity is not coherent with this result. 3) ALGEBRA VERSUS GEOMETRY: Using the powerful methods of “Algebraic Analysis”, that is a mixture of homological agebra and differential geometry, we shall prove that, contrary to other equations of physics (Cauchy equations, Cosserat equations, Maxwell equations), the Einstein equations cannot be “parametrized”, that is the generic solution cannot be expressed by means of the derivatives of a certain number of arbitrary potential-like functions, solving therefore negatively a 1000 $ challenge proposed by J. Wheeler in 1970. Accordingly, the mathematical foundations of electromagnetism and gravitation must be revisited within this formal framework, though striking it may look like. We insist on the fact that the arguments presented are of a purely mathematical nature and are thus unavoidable.
1. Introduction
The purpose of this paper is to present an elementary summary of a few recent results obtained through the application of the formal theory of systems of ordinary differential (OD) or partial differential (PD) equations and Lie pseudogroups in order to revisit the mathematical foundations of general relativity (GR). More elementary engineering examples (elasticity theory, electromagnetism (EM)) will also be considered in order to illustrate the quoted three fundamental results that we shall provide. The paper, based on the material of two lectures given at the department of mathematics of the university of Montpellier 2, France, in may 2013 and Firenze, Italy, in june 2013, is divided into three parts corresponding to the different formal methods used.
PART 1: In 1880 S. Lie (1842-1899) studied the groups of transformations depending on a finite number of parameters and now called Lie groups of transformations. Ten years later he discovered that these groups are only examples of groups of transformations solutions of linear or nonlinear systems of ordinary differential (OD) or partial differential (PD) equations which may even be of high order and are now called Lie pseudogroups of transformations. During the next fifty years the latter groups have only been studied by two frenchmen, namely Elie Cartan (1869-1951) who is quite famous today, and Ernest Vessiot (1865-1952) who is almost ignored today. We have proved in many books and papers that the Cartan structure equations have nothing to do with the Vessiot structure equations still not known today. Accordingly, the quadratic terms appearing in the Riemann tensor must not be identified with the quadratic terms appearing in the well known Maurer-Cartan equations for Lie groups. In particular, curvature + torsion (Cartan) must not be considered as a generalization of curvature alone (Vessiot).
PART 2: Though we consider that the first formal work on systems of PD equations is dating back to Maurice Janet (1888-1983) who introduced as early as in 1920 a differential sequence now called Janet sequence, it is only around 1970 that Donald Spencer (1912-2001) developped, in a quite independent way, the formal theory of systems of PD equations in order to study Lie pseudogroups, exactly like E. Cartan did with exterior systems. However, all the physicists who tried to understand the only book “Lie equations” that he published in 1972 with A. Kumpera, have been stopped by the fact that the examples of the Introduction (Janet sequence) have nothing to do with the core of the book (Spencer sequence). We may say that the work of Cartan is superseded by the use of the canonical Spencer sequence while the work of Vessiot is superseded by the use of the canonical Janet sequence but the link between these two sequences and thus these two works is not known today. Accordingly, the Spencer sequence for the conformal Killing system and its formal adjoint fully describe the Cosserat equations, Maxwell equations and Weyl equations but general relativity (GR) is not coherent with this result because we shall prove that the Ricci tensor only depends on the nonlinear transformations (called elations by Cartan in 1922) that describe the “difference” existing between the Weyl group (10 parameters of the Poincaré subgroup + 1 dilatation) and the conformal group of space-time (15 parameters).
PART 3: At the same time, mixing differential geometry and homological algebra but always supposing that the reader knows a lot about the work of Spencer, V.P. Palamodov (constant coefficients) and M. Kashiwara (variable coefficients) developped “algebraic analysis” in order to study the formal properties of finitely generated differential modules that do not depend on their presentation or even on a corresponding differential resolution, namely the algebraic analogue of a differential sequence. Using double duality theory, we prove that, contrary to other equations of physics (Cauchy equations, Cosserat equations, Maxwell equations), the Einstein equations cannot be “parametrized”, that is the generic solution cannot be expressed by means of the derivatives of a certain number of arbitrary potential-like functions, solving therefore negatively a 1000 $ challenge proposed by J. Wheeler in 1970.
The new methods involve tools from differential geometry (jet theory, Spencer operator, ![]() -cohomology) and homological algebra (diagram chasing, snake theorem, extension modules, double duality). The reader may just have a look to the book [1] (review in Zbl 1079. 93001) in order to understand the amount of mathematics needed from many domains.
-cohomology) and homological algebra (diagram chasing, snake theorem, extension modules, double duality). The reader may just have a look to the book [1] (review in Zbl 1079. 93001) in order to understand the amount of mathematics needed from many domains.
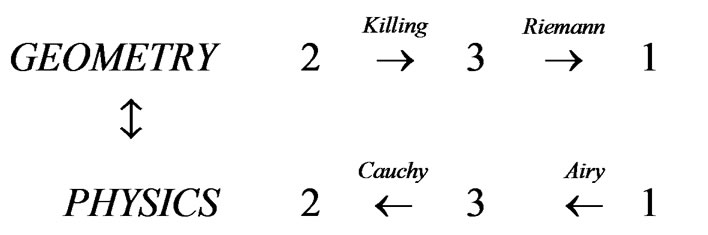
The following diagram summarizes at the same time the historical background and the difficulties presented in the introduction:
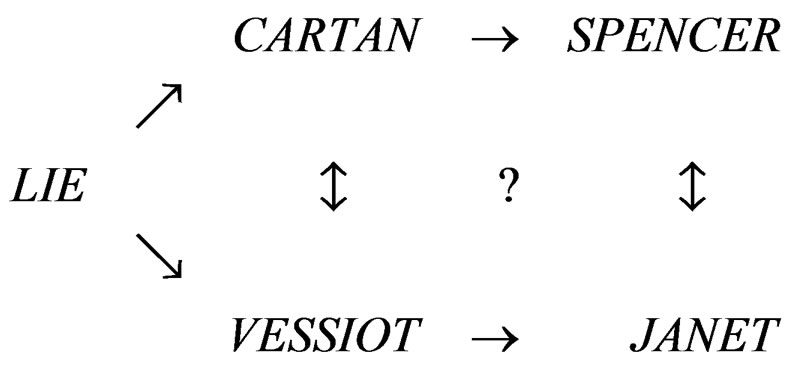
Roughly, Cartan and followers have not been able to “quotient down to the base manifold” [2,3], a result only obtained by Spencer in 1970 through the nonlinear Spencer sequence [4-7] but in a way quite different from the one followed by Vessiot in 1903 for the same purpose [8,9]. Accordingly, the mathematical foundations of mathematical physics must be revisited within this formal framework, though striking it may look like for certain apparently well established theories such as EM (J. C. Maxwell, 1864) and GR (A. Einstein, 1915).
2. First Part: From Lie Groups to Lie Pseudogroups
If 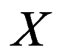 is a manifold with local coordinates
is a manifold with local coordinates ![]() for
for
 , let
, let ![]() be a fibered manifold over
be a fibered manifold over
 , that is a manifold with local coordinates
, that is a manifold with local coordinates 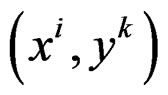 for
for 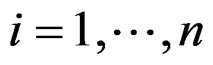 and
and 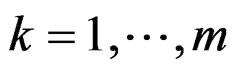 simply denoted by
simply denoted by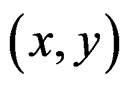 , projection
, projection
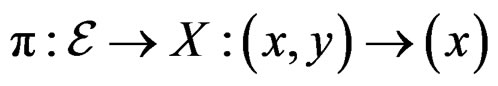
and changes of local coordinates
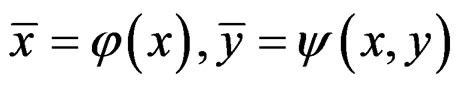 .
.
If ![]() and
and  are two fibered manifolds over
are two fibered manifolds over  with respective local coordinates
with respective local coordinates 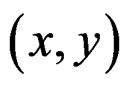 and
and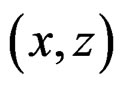 , we denote by
, we denote by 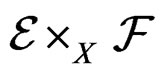 the fibered product of
the fibered product of ![]() and
and 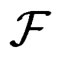 over
over 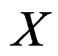 as the new fibered manifold over
as the new fibered manifold over 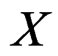 with local coordinates
with local coordinates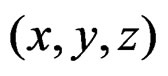 . We denote by
. We denote by
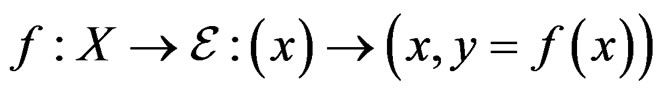
a global section of![]() , that is a map such that
, that is a map such that 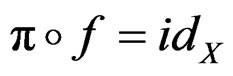 but local sections over an open set
but local sections over an open set 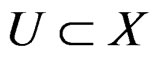 may also be considered when needed. We shall use for simplicity the same notation for a fibered manifold and its set of sections while setting
may also be considered when needed. We shall use for simplicity the same notation for a fibered manifold and its set of sections while setting . Under a change of coordinates, a section transforms like
. Under a change of coordinates, a section transforms like
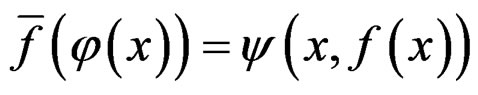
and the derivatives transform like:
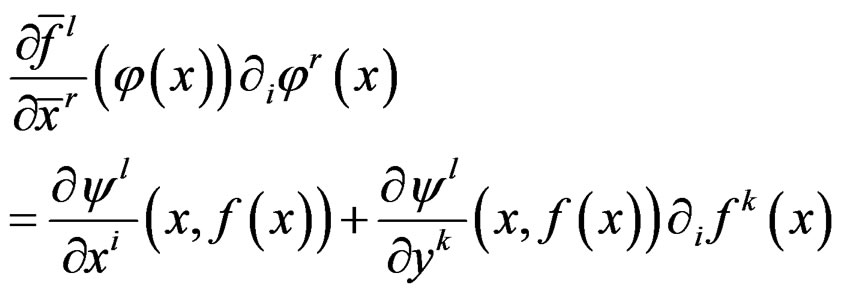 .
.
We may introduce new coordinates 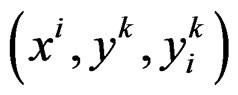 transforming like:
transforming like:
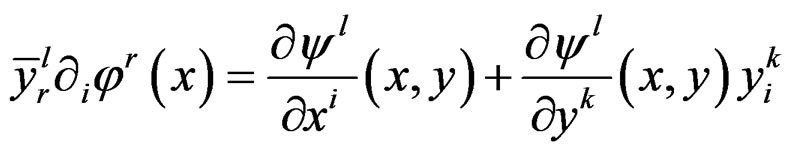 .
.
We shall denote by 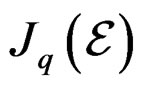 the q-jet bundle of
the q-jet bundle of ![]()
with local coordinates
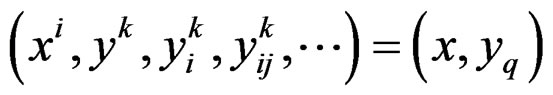
called jet coordinates and sections
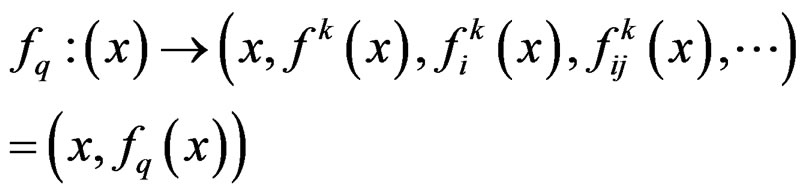
transforming like the sections
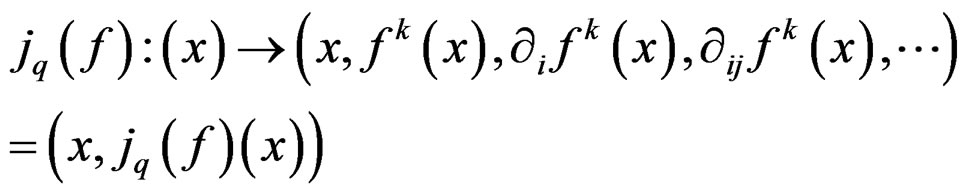
where both  and
and 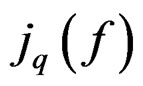 are over the section
are over the section 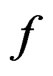 of
of
![]() . Of course
. Of course 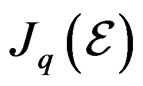 is a fibered manifold over
is a fibered manifold over 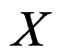
with projection 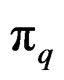 while
while 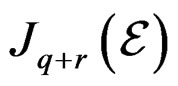 is a fibered manifold over
is a fibered manifold over 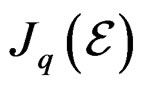 with projection
with projection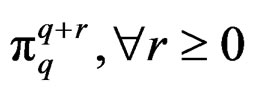 .
.
DEFINITION 1.1: A (nonlinear) system of order 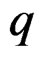 on
on ![]() is a fibered submanifold
is a fibered submanifold 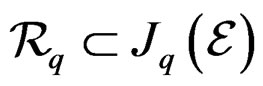 and a solution of
and a solution of 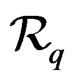 is a section
is a section 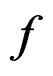 of
of ![]() such that
such that 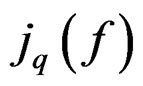 is a section of
is a section of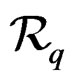 .
.
DEFINITION 1.2: When the changes of coordinates have the linear form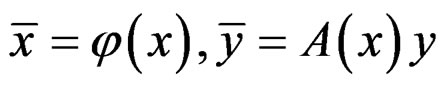 , we say that
, we say that ![]() is a vector bundle over
is a vector bundle over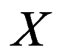 . Vector bundles will be denoted by capital letters
. Vector bundles will be denoted by capital letters 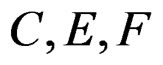 and will have sections denoted by
and will have sections denoted by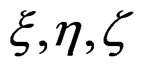 . In particular, we shall denote as usual by
. In particular, we shall denote as usual by 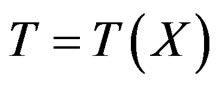 the tangent bundle of
the tangent bundle of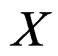 , by
, by
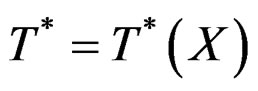 the cotangent bundle, by
the cotangent bundle, by 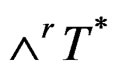 the bundle of r-forms and by
the bundle of r-forms and by 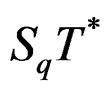 the bundle of qsymmetric covariant tensors. When the changes of coordinates have the form
the bundle of qsymmetric covariant tensors. When the changes of coordinates have the form
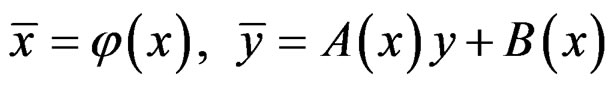
we say that ![]() is an affine bundle over
is an affine bundle over 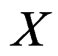 and we define the associated vector bundle
and we define the associated vector bundle 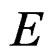 over
over 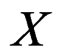 by the local coordinates
by the local coordinates 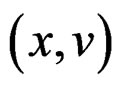 changing like
changing like 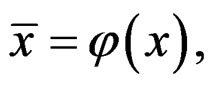
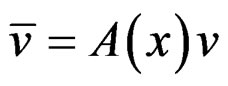 . Finally, If
. Finally, If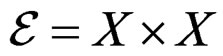 , we shall denote by
, we shall denote by
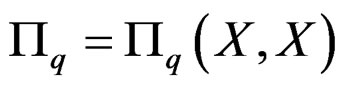 the open subfibered manifold of
the open subfibered manifold of
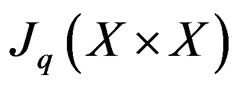 defined independently of the coordinate system by
defined independently of the coordinate system by 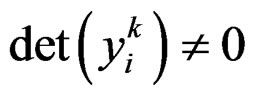 with source projection
with source projection
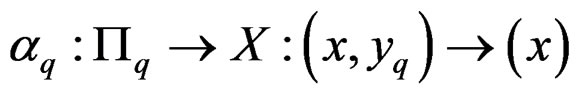
and target projection
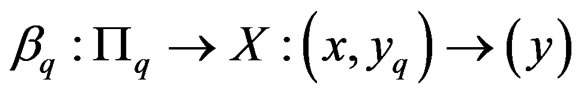 .
.
DEFINITION 1.3: If the tangent bundle 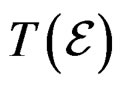 has local coordinates
has local coordinates 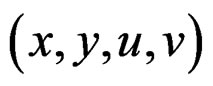 changing like
changing like
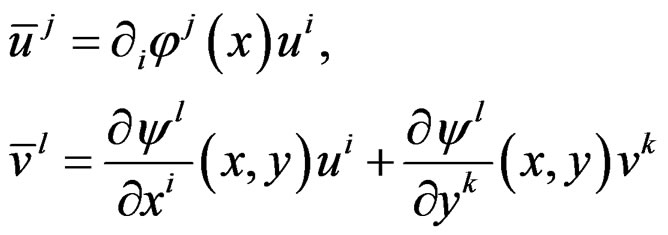 we may introduce the vertical bundle
we may introduce the vertical bundle 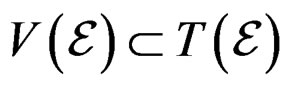 as a vector bundle over
as a vector bundle over ![]() with local coordinates
with local coordinates 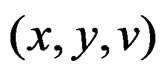 obtained by setting
obtained by setting 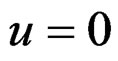 and changes
and changes
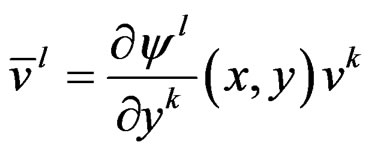 .
.
Of course, when ![]() is an affine bundle over
is an affine bundle over 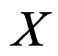 with associated vector bundle
with associated vector bundle 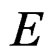 over
over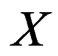 , we have
, we have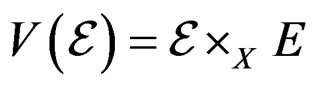 .
.
For a later use, if ![]() is a fibered manifold over
is a fibered manifold over 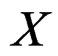 and
and 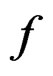 is a section of
is a section of![]() , we denote by
, we denote by 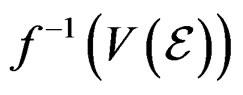 the reciprocal image of
the reciprocal image of 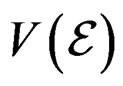 by
by 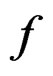 as the vector bundle over
as the vector bundle over 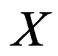 obtained when replacing
obtained when replacing 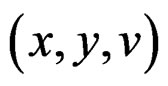 by
by 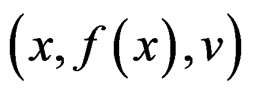 in each chart. A similar construction may also be done for any affine bundle over
in each chart. A similar construction may also be done for any affine bundle over![]() .
.
We now recall a few basic geometric concepts that will be constantly used through this paper. First of all, if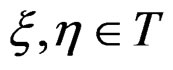 , we define their bracket
, we define their bracket 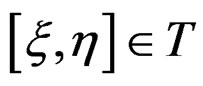 by the local formula
by the local formula
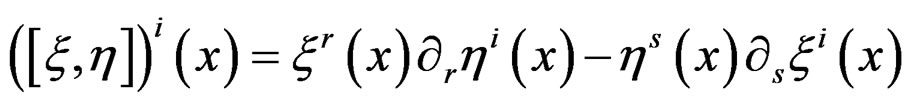
leading to the Jacobi identity
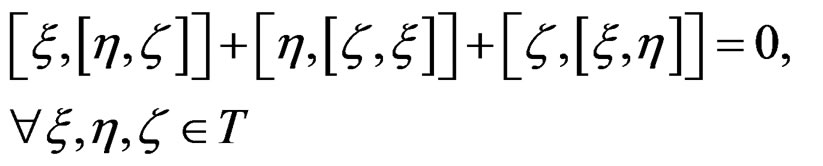
allowing to define a Lie algebra and to the useful formula
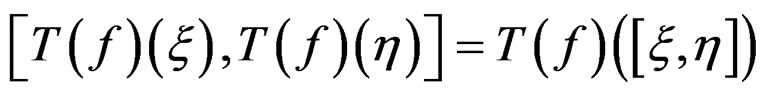
where 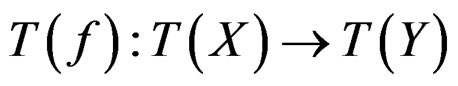 is the tangent mapping of a map
is the tangent mapping of a map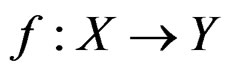 .
.
When 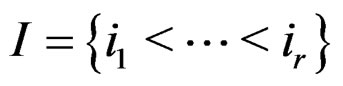 is a multi-index, we may set
is a multi-index, we may set
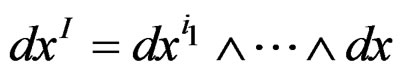
for describing 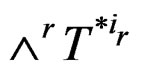 by means of a basis and introduce the exterior derivative
by means of a basis and introduce the exterior derivative
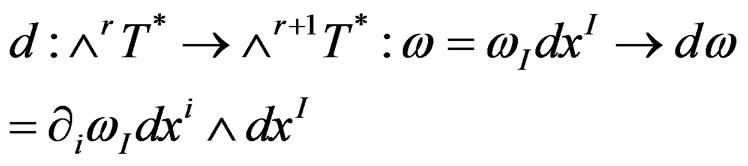
with 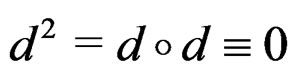 in the Poincaré sequence:
in the Poincaré sequence:
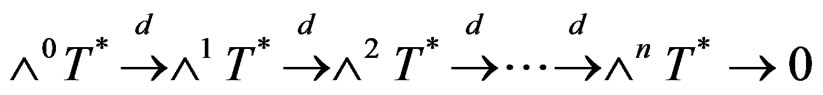 .
.
The Lie derivative of an 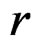 -form with respect to a vector field
-form with respect to a vector field 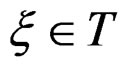 is the linear first order operator
is the linear first order operator 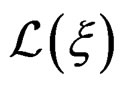 linearly depending on
linearly depending on 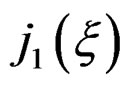 and uniquely defined by the following three properties:
and uniquely defined by the following three properties:
1)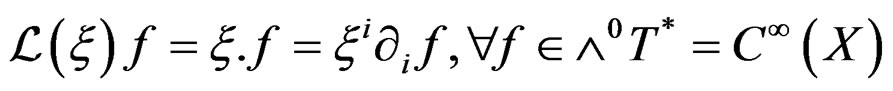 .
.
2)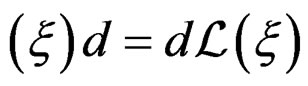 .
.
3) 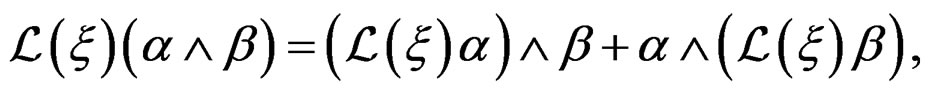
 .
.
It can be proved that
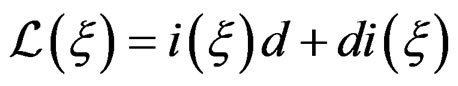
where 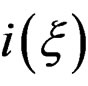 is the interior multiplication
is the interior multiplication
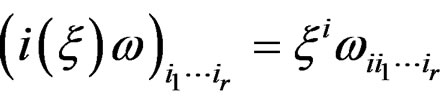
and that
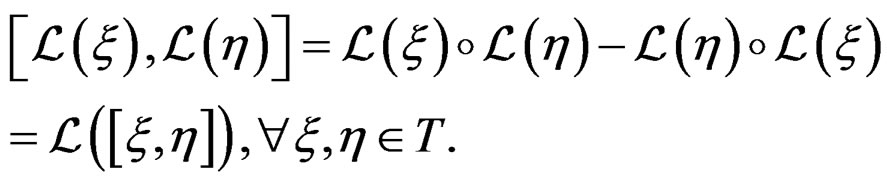
We now turn to group theory and start with two basic definitions:
Let 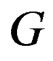 be a Lie group, that is a manifold with local coordinates
be a Lie group, that is a manifold with local coordinates 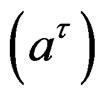 for
for 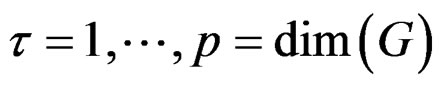 called parameters, a composition
called parameters, a composition
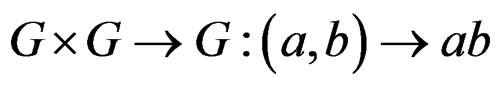 an inverse
an inverse 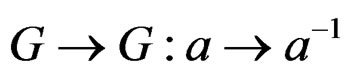 and an identity
and an identity 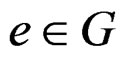 satisfying:
satisfying:
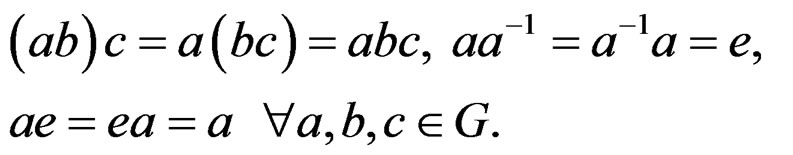
DEFINITION 1.4:  is said to act on
is said to act on 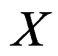 if there is a map
if there is a map 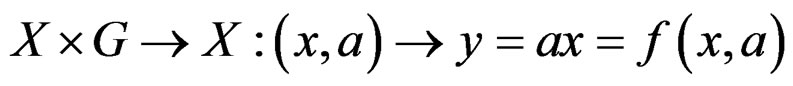 such that
such that 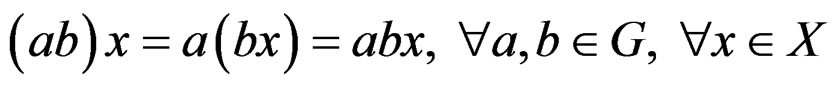 and we shall say that we have a Lie group of transformations of
and we shall say that we have a Lie group of transformations of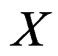 . In order to simplify the notations, we shall use global notations even if only local actions are existing. It is well known that the action of
. In order to simplify the notations, we shall use global notations even if only local actions are existing. It is well known that the action of 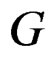 onto itself allows to introduce a purely algebraic bracket on its Lie algebra
onto itself allows to introduce a purely algebraic bracket on its Lie algebra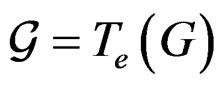 .
.
DEFINITION 1.5: A Lie pseudogroup of transformations 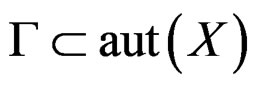 is a group of transformations solutions of a system of OD or PD equations such that, if
is a group of transformations solutions of a system of OD or PD equations such that, if  and
and 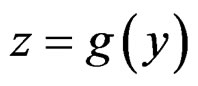 are two solutions, called finite transformations, that can be composed, then
are two solutions, called finite transformations, that can be composed, then
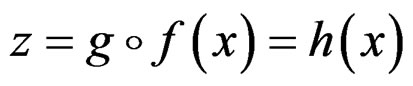
and
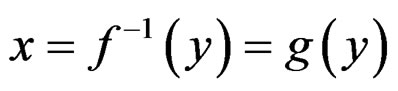
are also solutions while  is the identity solution denoted by
is the identity solution denoted by 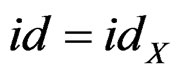 and we shall set
and we shall set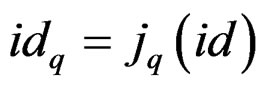 . In all the sequel we shall suppose that
. In all the sequel we shall suppose that ![]() is transitive that is
is transitive that is
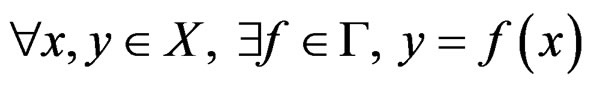 .
.
It becomes clear that Lie groups of transformations are particular cases of Lie pseudogroups of transformations as the system defining the finite transformations can be obtained by eliminating the parameters among the equations
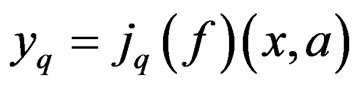
when 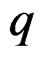 is large enough. The underlying system may be nonlinear and of high order. Looking for transformations “close” to the identity, that is setting
is large enough. The underlying system may be nonlinear and of high order. Looking for transformations “close” to the identity, that is setting 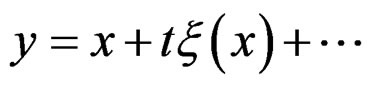 when
when  is a small constant parameter and passing to the limit
is a small constant parameter and passing to the limit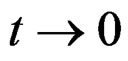 , we may linearize the above nonlinear system of finite Lie equations in order to obtain a linear system of infinitesimal Lie equations of the same order for vector fields. Such a system has the property that, if
, we may linearize the above nonlinear system of finite Lie equations in order to obtain a linear system of infinitesimal Lie equations of the same order for vector fields. Such a system has the property that, if 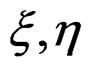 are two solutions, then
are two solutions, then 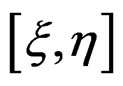 is also a solution. Accordingly, the set
is also a solution. Accordingly, the set 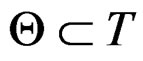 of solutions of this new system satisfies
of solutions of this new system satisfies 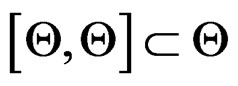 and can therefore be considered as the Lie algebra of
and can therefore be considered as the Lie algebra of![]() .
.
EXAMPLE 1.6: While the affine transformations 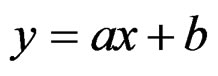 are solutions of the second order linear system
are solutions of the second order linear system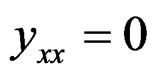 , the projective transformations
, the projective transformations
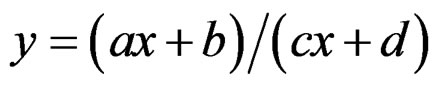
are solutions of the third order nonlinear system
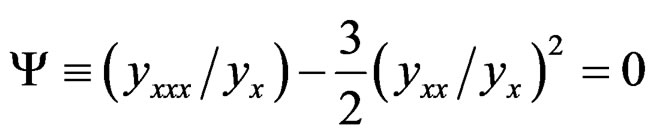 .
.
The sections of the corresponding linearized systems are respectively satisfying 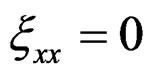 and
and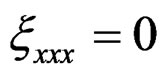 . The generating differential invariant
. The generating differential invariant 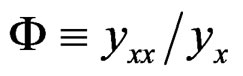 of the affine case transforms like
of the affine case transforms like
when  while
while  transforms like
transforms like
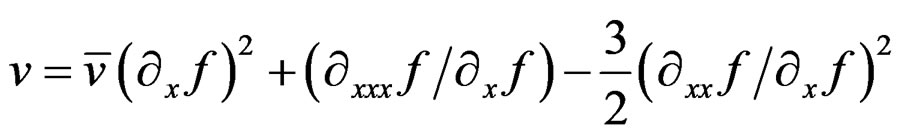 .
.
We now sketch the discovery of Vessiot [8,9] still not known today after more than a century for reasons which are not scientific at all. Roughly, a Lie pseudogroup 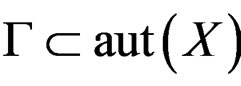 is made by finite transformations
is made by finite transformations  solutions of a (possibly nonlinear) system
solutions of a (possibly nonlinear) system 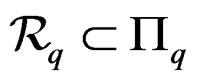 while the infinitesimal transformations
while the infinitesimal transformations 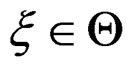 are solutions of the linearized system
are solutions of the linearized system
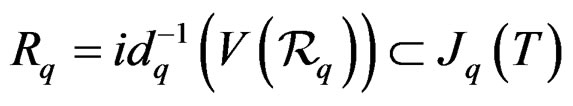
as we have
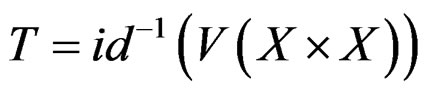 .
.
When ![]() is transitive, there is a canonical epimorphism
is transitive, there is a canonical epimorphism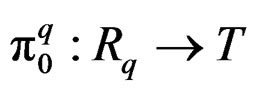 . Also, as changes of source
. Also, as changes of source ![]() commute with changes of target
commute with changes of target![]() , they exchange between themselves any generating set of differential invariants
, they exchange between themselves any generating set of differential invariants 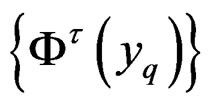 as in the previous example.Then one can introduce a natural bundle
as in the previous example.Then one can introduce a natural bundle 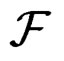 over
over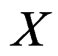 , also called bundle of geomeric objects, by patching changes of coordinates of the form
, also called bundle of geomeric objects, by patching changes of coordinates of the form
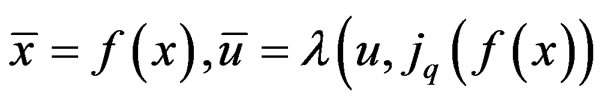
thus obtained. A section ![]() of
of 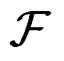 is called a geometric object or structure on
is called a geometric object or structure on 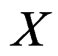 and transforms like
and transforms like
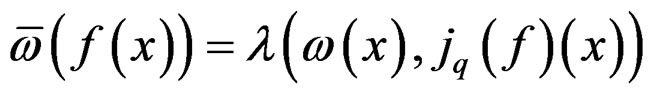
or simply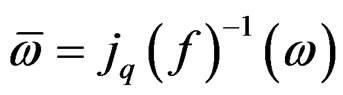 . This is a way to generalize vectors and tensors
. This is a way to generalize vectors and tensors 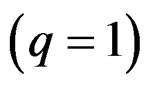 or even connections
or even connections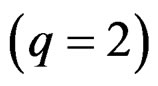 . As a byproduct we have
. As a byproduct we have
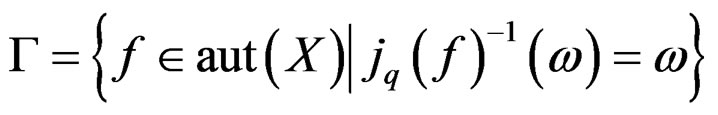
and we may say that ![]() preserves
preserves![]() . Replacing
. Replacing  by
by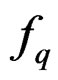 , we also obtain
, we also obtain
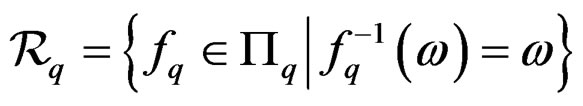 .
.
Coming back to the infinitesimal point of view and setting
 we may define the ordinary Lie derivative with value in the vector bundle
we may define the ordinary Lie derivative with value in the vector bundle 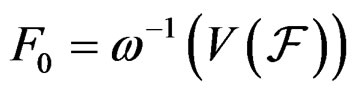 by the formula:
by the formula:
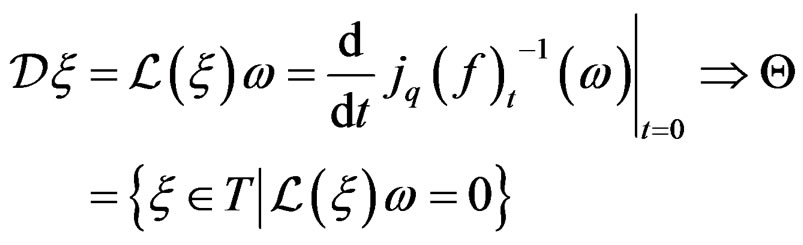
and we say that 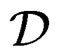 is a Lie operator because
is a Lie operator because 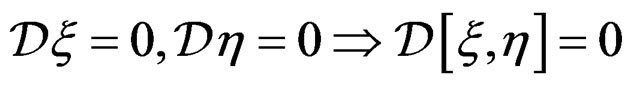 as we already saw.
as we already saw.
Differentiating  times the equations of
times the equations of 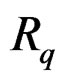 that only depend on
that only depend on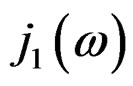 , we may obtain the
, we may obtain the 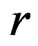 - prolongation
- prolongation
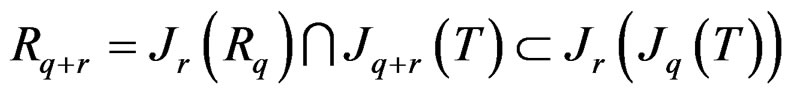 .
.
The problem is then to know under what conditions on ![]() all the equations of order
all the equations of order 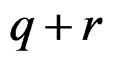 are obtained by
are obtained by 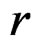 prolongations only,
prolongations only, 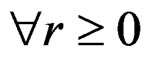 or, equivalently,
or, equivalently, 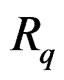 is formally integrable (FI). The solution, found by Vessiot, has been to exhibit another natural vector bundle
is formally integrable (FI). The solution, found by Vessiot, has been to exhibit another natural vector bundle 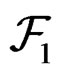 with local coordinates
with local coordinates 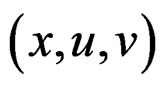 over
over 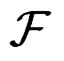 with local coordinates
with local coordinates 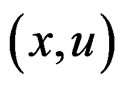 and to prove that an equivariant section
and to prove that an equivariant section 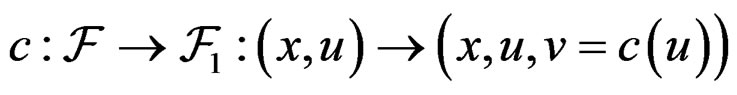 only depends on a finite number of constants called structure constants. The integrability conditions (IC) of
only depends on a finite number of constants called structure constants. The integrability conditions (IC) of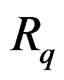 , called Vessiot structure equations, are of the form
, called Vessiot structure equations, are of the form 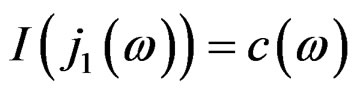 and are invariant under any change of source.
and are invariant under any change of source.
We provide in a self-contained way and parallel manners the following five striking examples which are among the best nontrivial ones we know and invite the reader to imagine at this stage any possible link that could exist between them (A few specific definitions will be given later on).
EXAMPLE 1.7: Coming back to the last example, we show that Vessiot structure equations may even exist when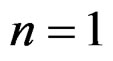 . For this, if
. For this, if 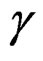 is the geometric object of the affine group
is the geometric object of the affine group 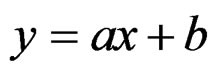 and
and 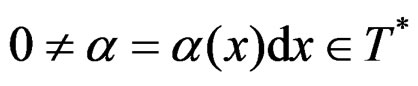 is a
is a  -form, we consider the object
-form, we consider the object 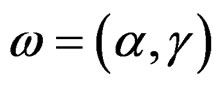 and get at once the two second order Medolaghi equations:
and get at once the two second order Medolaghi equations:
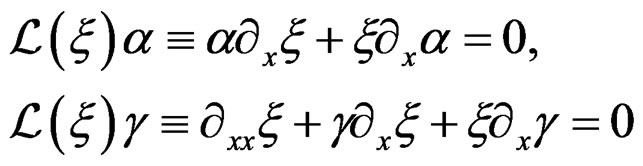
Differentiating the first equation and substituting the second, we get the zero order equation:
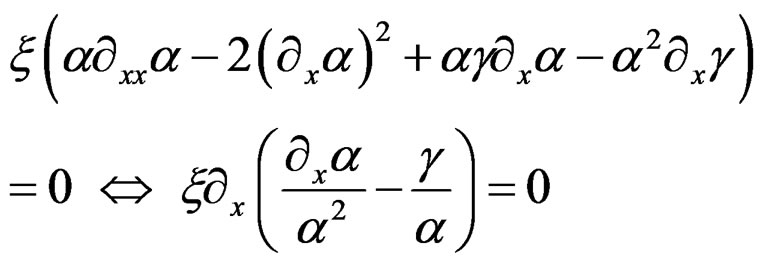
and the Vessiot structure equation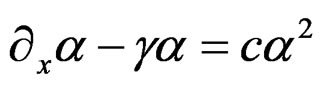 . Alternatively, setting
. Alternatively, setting
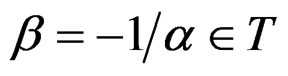 we get
we get
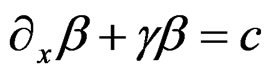 .
.
With
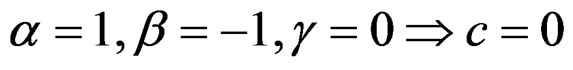
we get the translation subgroup  while, with
while, with
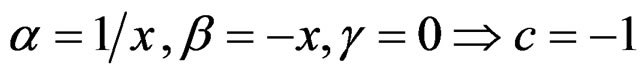
we get the dilatation subgroup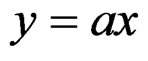 . Similarly, if
. Similarly, if ![]() is the geometric object of the projective group and we consider the new geometric object
is the geometric object of the projective group and we consider the new geometric object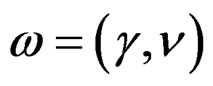 , we get the only Vessiot structure equation
, we get the only Vessiot structure equation
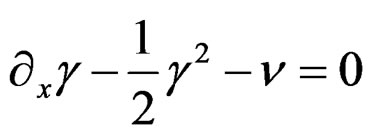
without any structure constant.
EXAMPLE 1.8: (Principal homogeneous structure) When ![]() is the Lie group of transformations made by the constant translations
is the Lie group of transformations made by the constant translations 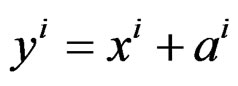 for
for 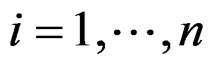 of a manifold
of a manifold 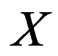 with
with , the characteristic object invariant by
, the characteristic object invariant by ![]() is a family
is a family
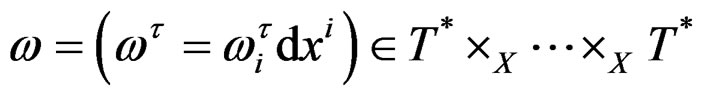
of ![]()
 -forms with
-forms with 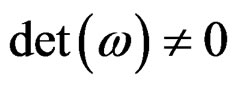 in such a way that
in such a way that
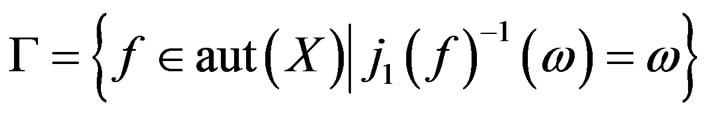
where 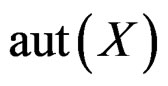 denotes the pseudogroup of local diffeomorphisms of
denotes the pseudogroup of local diffeomorphisms of ,
, 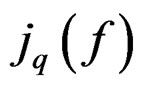 denotes the derivatives of
denotes the derivatives of
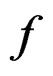 up to order
up to order 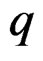 and
and 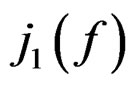 acts in the usual way on covariant tensors. For any vector field
acts in the usual way on covariant tensors. For any vector field 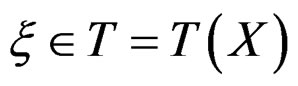 the tangent bundle to
the tangent bundle to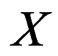 , introducing the standard Lie derivative
, introducing the standard Lie derivative 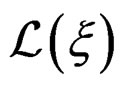 of forms with respect to
of forms with respect to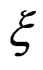 , we may consider the
, we may consider the 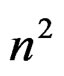 first order Medolaghi equations:
first order Medolaghi equations:
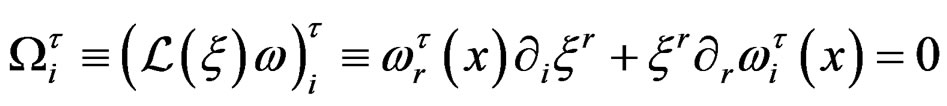 .
.
The particular situation is found with the special choice 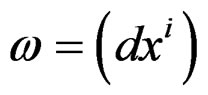 that leads to the involutive system
that leads to the involutive system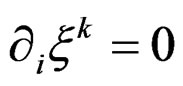 . Introducing the inverse matrix
. Introducing the inverse matrix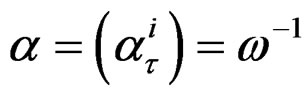 , the above equations amount to the bracket relations
, the above equations amount to the bracket relations 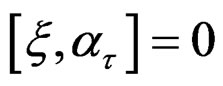 and, using crossed derivatives on the solved form
and, using crossed derivatives on the solved form
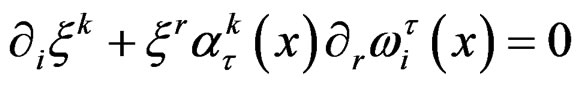 we obtain the
we obtain the 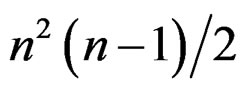 zero order equations:
zero order equations:
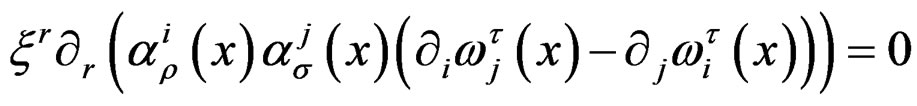 .
.
The integrability conditions (IC), that is the conditions under which these equations do not bring new equations, are thus the 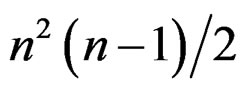 Vessiot structure equations:
Vessiot structure equations:
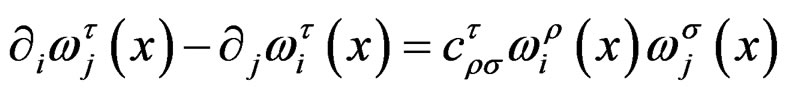
with 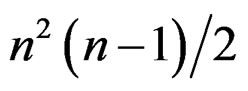 structure constants
structure constants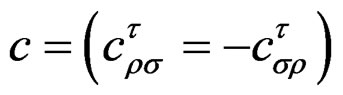 .
.
When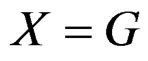 , these equations can be identified with the Maurer-Cartan equations (MC) existing in the theory of Lie groups, on the condition to change the sign of the structure constants involved because we have
, these equations can be identified with the Maurer-Cartan equations (MC) existing in the theory of Lie groups, on the condition to change the sign of the structure constants involved because we have
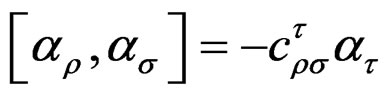 .
.
Writing these equations in the form of the exterior system 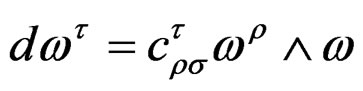 and closing this system by applying once more the exterior derivative
and closing this system by applying once more the exterior derivative![]() , we obtain the quadratic IC:
, we obtain the quadratic IC:
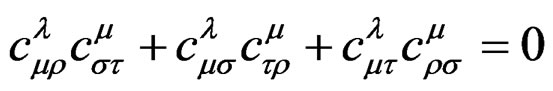
also called Jacobi relations .
.
EXAMPLE 1.9: (Riemann structure) If
is a metric on a manifold  with
with 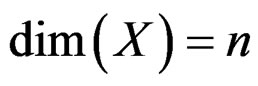 such that
such that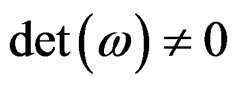 , the Lie pseudogroup of transformations preserving
, the Lie pseudogroup of transformations preserving ![]() is
is
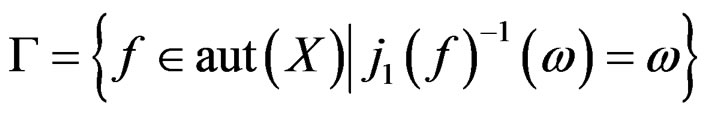
and is a Lie group with a maximum number of 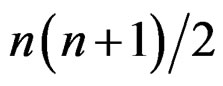 parameters. A special metric could be the Euclidean metric when
parameters. A special metric could be the Euclidean metric when 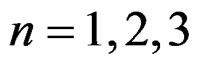 as in elasticity theory or the Minkowski metric when
as in elasticity theory or the Minkowski metric when 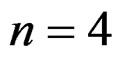 as in special relativity [10]. The first order Medolaghi equations:
as in special relativity [10]. The first order Medolaghi equations:
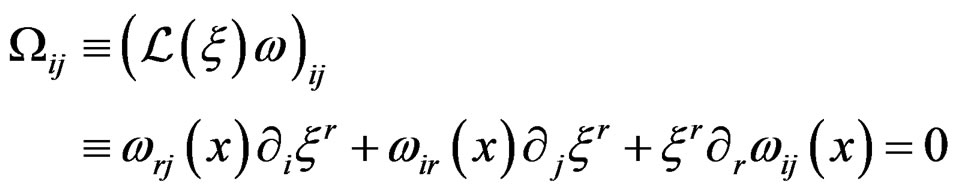
are also called classical Killing equations for historical reasons. The main problem is that this system is not involutive unless we prolong it to order two by differentiating once the equations. For such a purpose, introducing 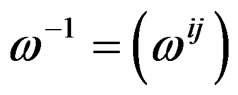 as usual, we may define the Christoffel symbols:
as usual, we may define the Christoffel symbols:
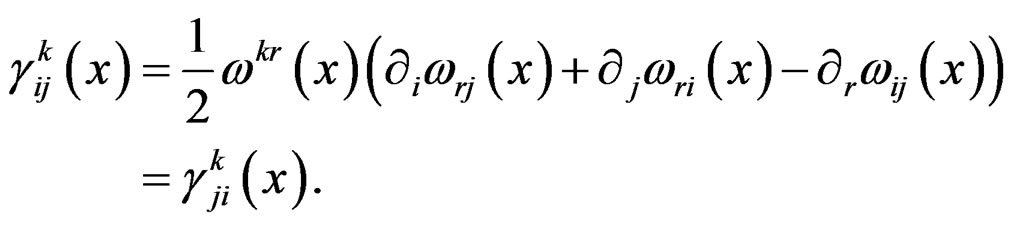
This is a new geometric object of order 2 providing the Levi-Civita isomorphism 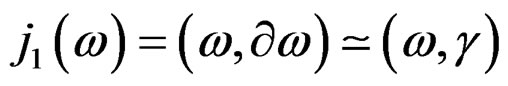 of affine bundles and allowing to obtain the second order Medolaghi equations:
of affine bundles and allowing to obtain the second order Medolaghi equations:
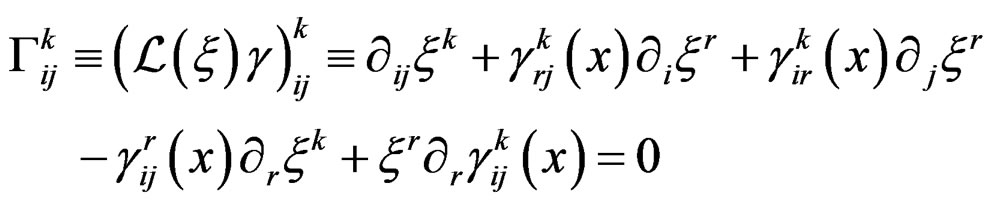
Surprisingly, the following expression called Riemann tensor:
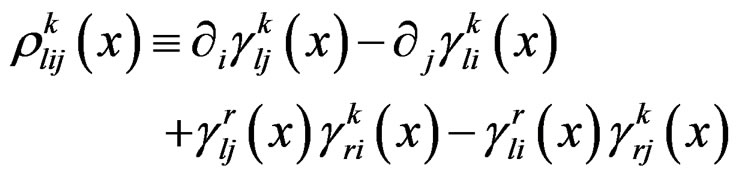
is still a first order geometric object and even a  -tensor with
-tensor with 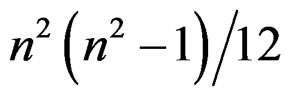 independent components satisfying the purely algebraic relations:
independent components satisfying the purely algebraic relations:
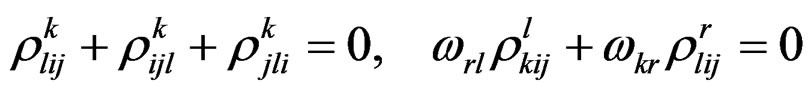 .
.
Accordingly, the IC must express that the new first order equations 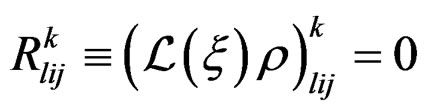 are only linear combinations of the previous ones and we get the Vessiot structure equations:
are only linear combinations of the previous ones and we get the Vessiot structure equations:
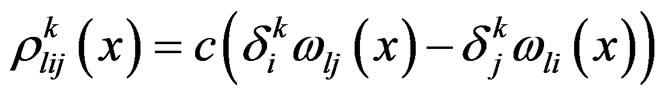
with the only structure constant ![]() describing the constant Riemannian curvature condition of Eisenhart [11,12]. One can proceed similarly for the conformal Killing system
describing the constant Riemannian curvature condition of Eisenhart [11,12]. One can proceed similarly for the conformal Killing system 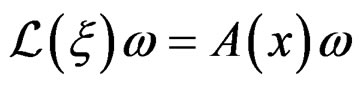 and obtain that the Weyl tensor must vanish, without any structure constant [12].
and obtain that the Weyl tensor must vanish, without any structure constant [12].
EXAMPLE 1.10: (Contact structure) We only treat the case 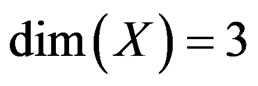 as the case
as the case 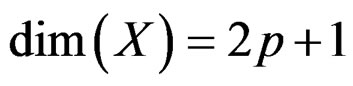 needs much more work [6]. Let us consider the so-called contact
needs much more work [6]. Let us consider the so-called contact  -form
-form 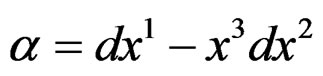 and consider the Lie pseudogroup
and consider the Lie pseudogroup 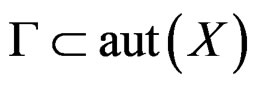 of (local) transformations preserving
of (local) transformations preserving ![]() up to a function factor, that is
up to a function factor, that is
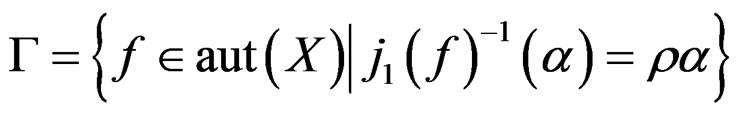
where again 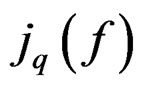 is a symbolic way for writing out the derivatives of
is a symbolic way for writing out the derivatives of 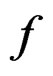 up to order
up to order 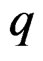 and
and ![]() transforms like a
transforms like a 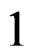 -covariant tensor. It may be tempting to look for a kind of “object” the invariance of which should characterize
-covariant tensor. It may be tempting to look for a kind of “object” the invariance of which should characterize![]() . Introducing the exterior derivative
. Introducing the exterior derivative 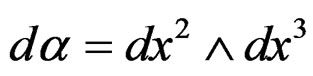 as a
as a 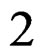 -form, we obtain the volume
-form, we obtain the volume 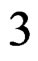 -form
-form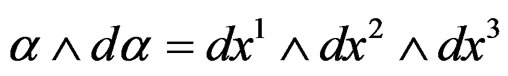 . As it is well known that the exterior derivative commutes with any diffeomorphism, we obtain sucessively:
. As it is well known that the exterior derivative commutes with any diffeomorphism, we obtain sucessively:
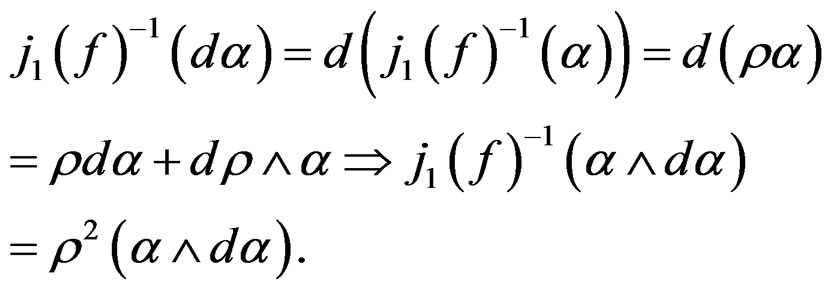
As the volume 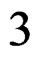 -form
-form 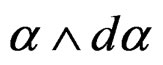 transforms through a division by the Jacobian determinant
transforms through a division by the Jacobian determinant
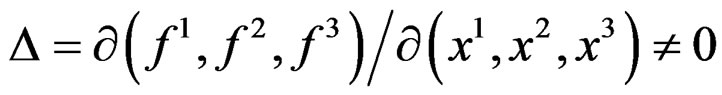
of the transformation 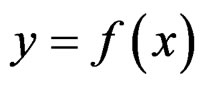 with inverse
with inverse
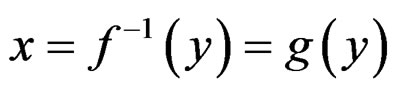 the desired object is thus no longer a 1-form but a 1- form density
the desired object is thus no longer a 1-form but a 1- form density 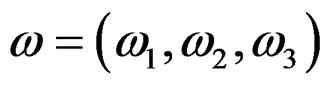 transforming like a 1- form but up to a division by the square root of the Jacobian determinant. It follows that the infinitesimal contact transformations are vector fields
transforming like a 1- form but up to a division by the square root of the Jacobian determinant. It follows that the infinitesimal contact transformations are vector fields 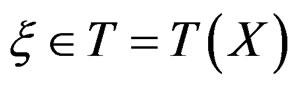 the tangent bundle of
the tangent bundle of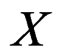 , satisfying the 3 so-called first order Medolaghi equations:
, satisfying the 3 so-called first order Medolaghi equations:
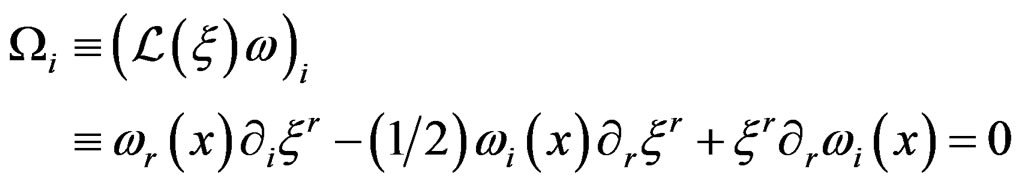 .
.
When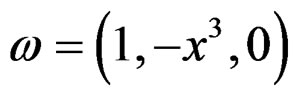 , we obtain the special involutive system:
, we obtain the special involutive system:
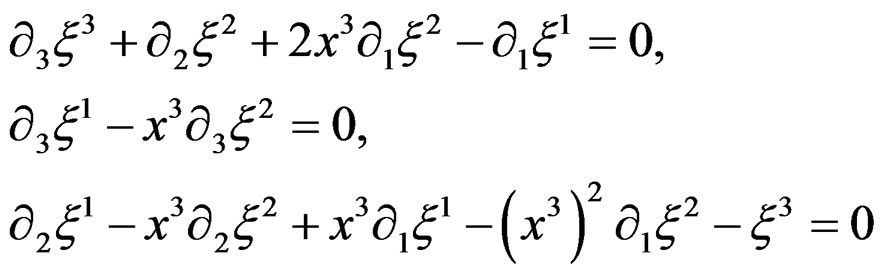
with 2 equations of class 3 and 1 equation of class 2 (see later on for a precise definition) and thus only 1 compatibility conditions (CC) for the second members.
For an arbitrary![]() , we may ask about the differential conditions on
, we may ask about the differential conditions on ![]() such that all the equations of order
such that all the equations of order  are only obtained by differentiating
are only obtained by differentiating 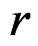 times the first order equations, exactly like in the special situation just considered where the system is involutive. We notice that, in a symbolic way,
times the first order equations, exactly like in the special situation just considered where the system is involutive. We notice that, in a symbolic way, 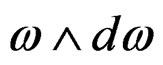 is now a scalar
is now a scalar 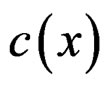 providing the zero order equation
providing the zero order equation 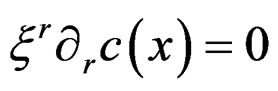 and the condition is
and the condition is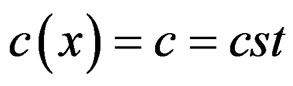 . The integrability condition (IC) is the Vessiot structure equation:
. The integrability condition (IC) is the Vessiot structure equation:
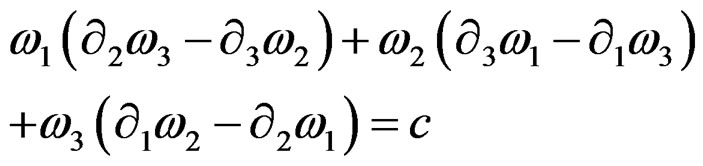
involving the only structure constant![]() .
.
For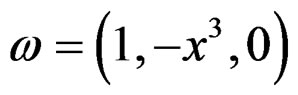 , we get
, we get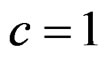 . If we choose
. If we choose 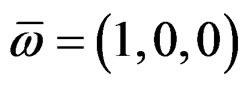 leading to
leading to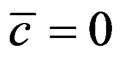 , we may define
, we may define
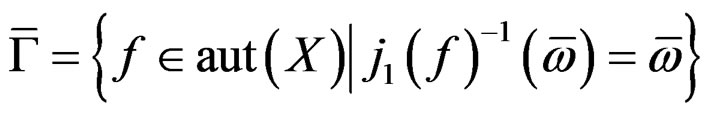
with infinitesimal transformations satisfying the involutive system:
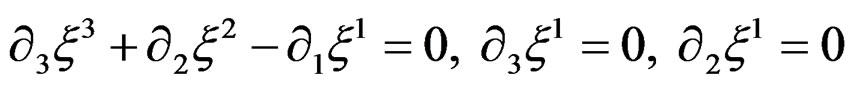
with again 2 equations of class 3 and 1 equation of class 2.
EXAMPLE 1.11: (Unimodular contact structure) With similar notations, let us again set
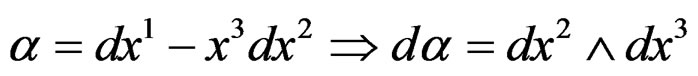
but let us now consider the new Lie pseudogroup of transformations preserving ![]() and thus
and thus 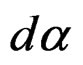 too, that is preserving the mixed object
too, that is preserving the mixed object
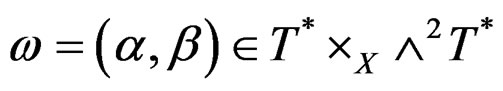
made up by a 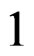 -form
-form ![]() and a
and a 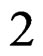 -form
-form 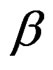 with
with
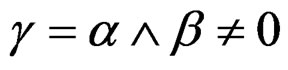 and
and .
.
Then ![]() is a Lie subpseudogroup of the one just considered in the previous example and the corresponding infinitesimal transformations now satisfy the involutive system:
is a Lie subpseudogroup of the one just considered in the previous example and the corresponding infinitesimal transformations now satisfy the involutive system:

with 3 equations of class 3, 2 equations of class 2 and 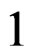 equation of class 1 if we exchange
equation of class 1 if we exchange 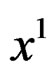 with
with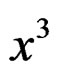 , a result leading now to 4 CC.
, a result leading now to 4 CC.
More generally, when 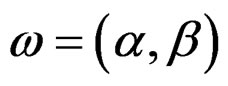 where
where ![]() is a 1- form and
is a 1- form and 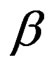 is a
is a  -form satifying
-form satifying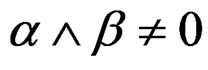 , we may study the same problem as before for the general system
, we may study the same problem as before for the general system
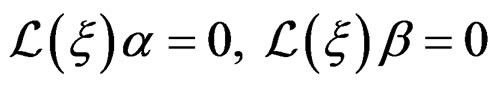 .
.
We let the reader provide the details of the tedious computation involved as it is at this point that computer algebra may be used [13]. The result, not evident at first sight, is that the 2-form 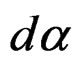 must be proportional to the 2-form
must be proportional to the 2-form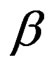 , that is
, that is 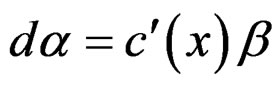 and thus
and thus
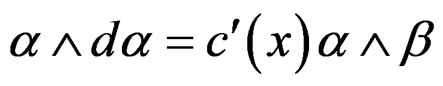 .
.
As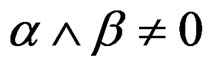 , we must have
, we must have 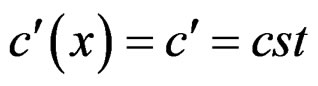 and thus
and thus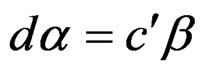 . Similarly, we get
. Similarly, we get 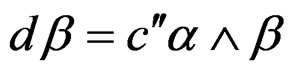 and obtain finally the
and obtain finally the  Vessiot structure equations
Vessiot structure equations
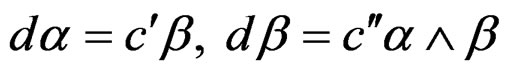
involving 2 structure constants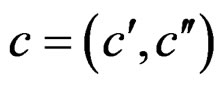 . Contrary to the previous situation (but like in the Riemann case!) we notice that we have now 2 structure equations not containing any constant (called first kind by Vessiot) and 2 structure equations with the same number of different constants (called second kind by Vessiot), namely
. Contrary to the previous situation (but like in the Riemann case!) we notice that we have now 2 structure equations not containing any constant (called first kind by Vessiot) and 2 structure equations with the same number of different constants (called second kind by Vessiot), namely
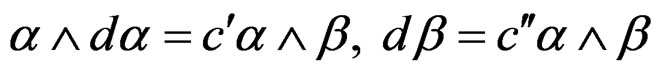 .
.
Finally, closing this system by taking once more the exterior derivative, we get
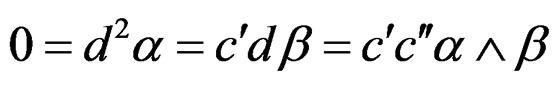
and thus the unexpected purely algebraic Jacobi condition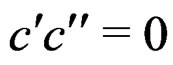 . For the special choice
. For the special choice
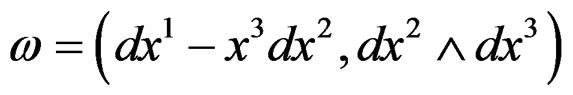
we get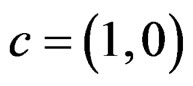 , for the second special choice
, for the second special choice
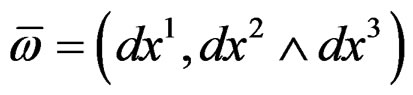
we get 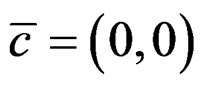 and for the third special choice
and for the third special choice
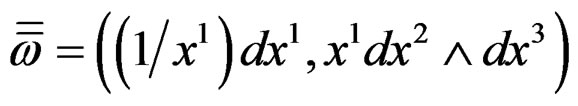
we get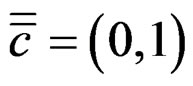 .
.
FIRST FUNDAMENTAL RESULT: Comparing the various Vessiot structure equations containing structure constants that we have just presented and that we recall below in a symbolic way, we notice that these structure constants are absolutely on equal footing though they have in general nothing to do with any Lie algebra.
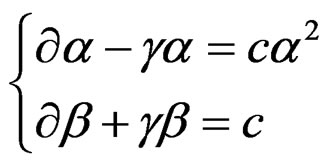
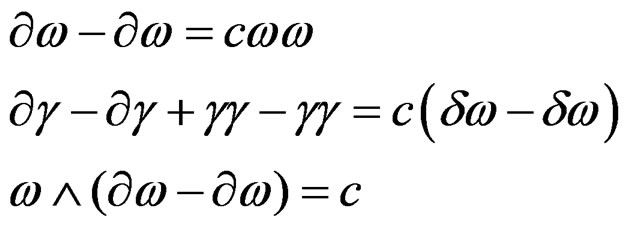
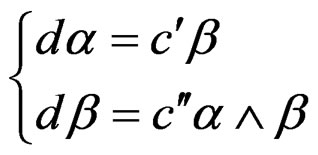 .
.
Accordingly, the fact that the ones appearing in the MC equations are related to a Lie algebra is a coincidence and the Cartan structure equations have nothing to do with the Vessiot structure equations. Also, as their factors are either constant, linear or quadratic, any identification of the quadratic terms appearing in the Riemann tensor with the quadratic terms appearing in the MC equations is definitively not correct [7]. We also understand why the torsion is automatically combined with curvature in the Cartan structure equations but totally absent from the Vessiot structure equations, even though the underlying group (translations + rotations) is the same.
HISTORICAL REMARK 1.12: Despite the prophetic comments of the italian mathematician Ugo Amaldi in 1909 [12], it has been a pity that Cartan deliberately ignored the work of Vessiot at the beginning of the last century and that the things did not improve afterwards in the eighties with Spencer and coworkers (Compare MR 720863 (85 m: 12004) and MR 954613 (90e: 58166)).
3. Second Part: The Janet and Spencer Sequences
Let 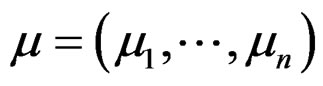 be a multi-index with length
be a multi-index with length
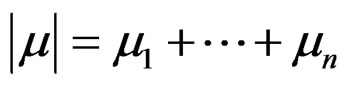
class 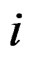 if
if
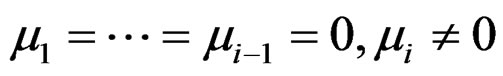
and
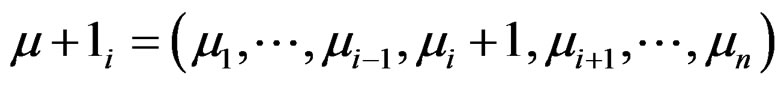 .
.
We set
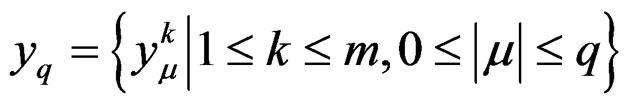
with 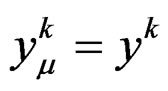 when
when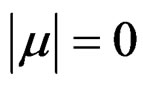 . If
. If 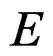 is a vector bundle over
is a vector bundle over 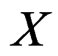 with local coordinates
with local coordinates 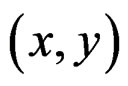 and
and 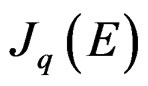 is the
is the 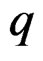 -jet bundle of
-jet bundle of 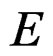 with local coordinates
with local coordinates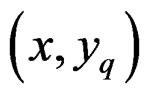 the Spencer operator just allows to distinguish a section
the Spencer operator just allows to distinguish a section 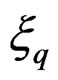 from a section
from a section 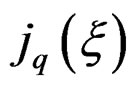 by introducing a kind of “difference” through the operator
by introducing a kind of “difference” through the operator
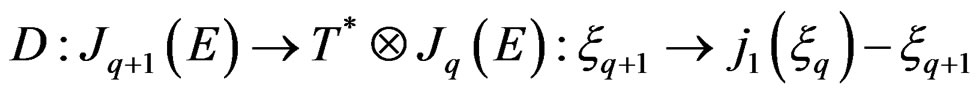
with local components
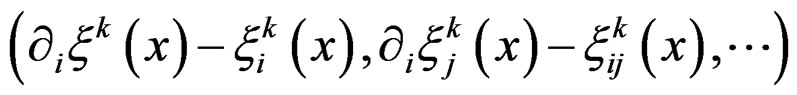
and more generally
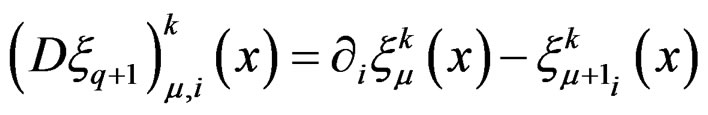 .
.
Minus the restriction of 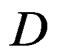 to the kernel
to the kernel 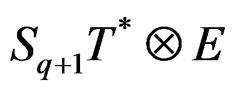 of the canonical projection
of the canonical projection
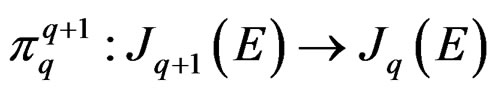
can be extended to the Spencer map
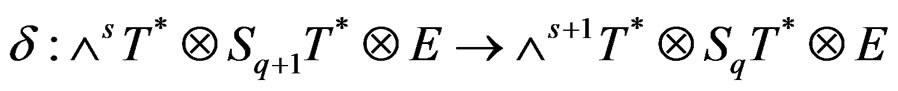
defined by
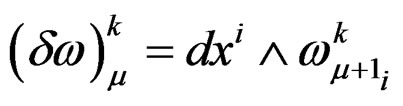 .
.
The kernel of  is made by sections such that
is made by sections such that
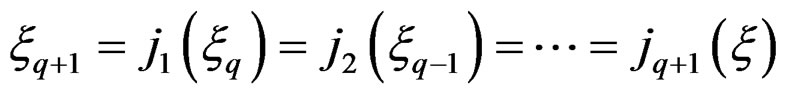 .
.
Finally, if 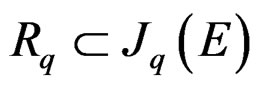 is a system of order
is a system of order 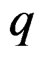 on
on 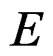 locally defined by linear equations
locally defined by linear equations
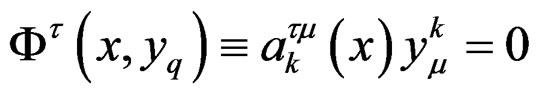 the
the 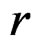 -prolongation
-prolongation
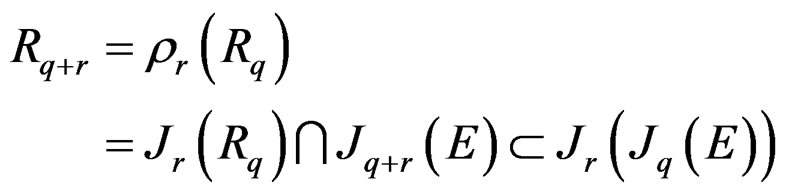
is locally defined when 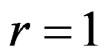 by the linear equations
by the linear equations
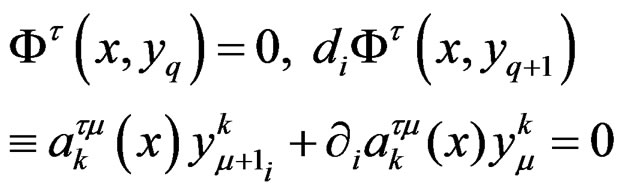
and has symbol
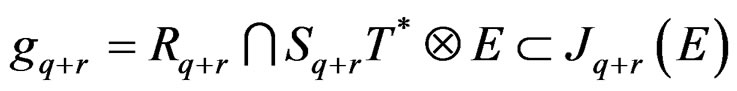
locally defined by
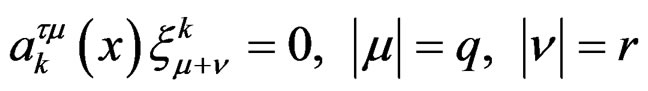
if one looks at the top order terms. If 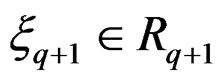 is over
is over
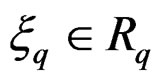 , differentiating the identity
, differentiating the identity
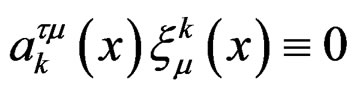
with respect to 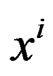 and substracting the identity
and substracting the identity
![]() we obtain the identity
we obtain the identity
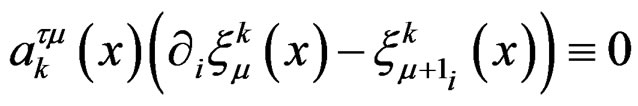
and thus the restriction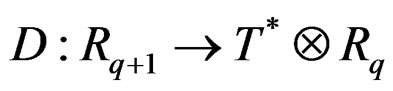 . This first order operator induces, up to sign, the purely algebraic monomorphism
. This first order operator induces, up to sign, the purely algebraic monomorphism 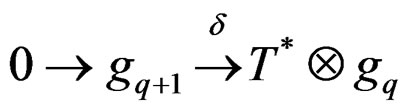 on the symbol level
on the symbol level
[8,14]. The Spencer operator has never been used in GR though an accelerometer in a rocket merely measures one of the components of the Spencer operator involving second order jets.
DEFINITION 2.1: 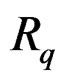 is said to be formally integrable (FI) when the restriction
is said to be formally integrable (FI) when the restriction
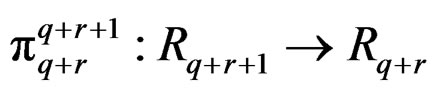
is an epimorphism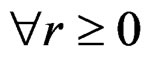 . In that case, the Spencer form
. In that case, the Spencer form 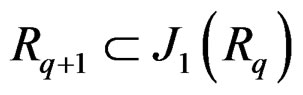 is a canonical equivalent formally integrable first order system on
is a canonical equivalent formally integrable first order system on 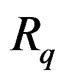 with no zero order equations.
with no zero order equations.
DEFINITION 2.2: 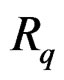 is said to be involutive when it is formally integrable and the symbol
is said to be involutive when it is formally integrable and the symbol 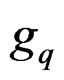 is involutive, that is all the sequences
is involutive, that is all the sequences
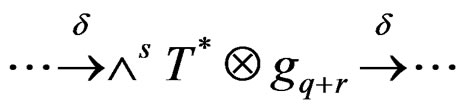
are exact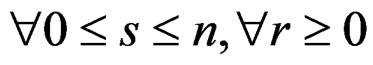 . Equivalently, using a linear change of local coordinates if necessary, we may successively solve the maximum number
. Equivalently, using a linear change of local coordinates if necessary, we may successively solve the maximum number 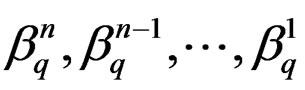 of equations with respect to the leading or principal jet coordinates of strict order
of equations with respect to the leading or principal jet coordinates of strict order 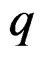 and class
and class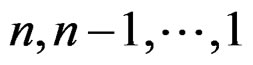 . Then
. Then 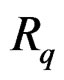 is involutive if
is involutive if 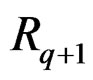 is obtained by only prolonging the
is obtained by only prolonging the 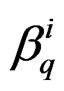 equations of class
equations of class 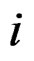 with respect to
with respect to 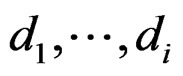 for
for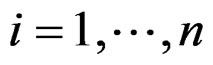 . In that case, such a prolongation procedure allows to compute in a unique way the principal jets from the parametric other ones and may also be applied to nonlinear systems as well [8,15].
. In that case, such a prolongation procedure allows to compute in a unique way the principal jets from the parametric other ones and may also be applied to nonlinear systems as well [8,15].
When 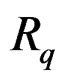 is involutive, the linear differential operator
is involutive, the linear differential operator
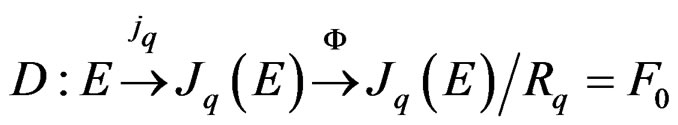
of order 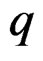 with space of solutions
with space of solutions 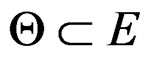 is said to be involutive and one has the canonical linear Janet sequence [8]:
is said to be involutive and one has the canonical linear Janet sequence [8]:
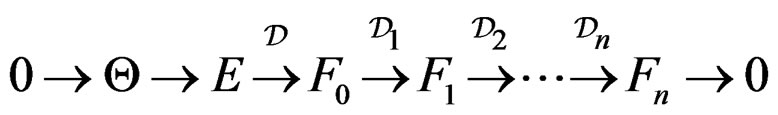
with Janet bundles
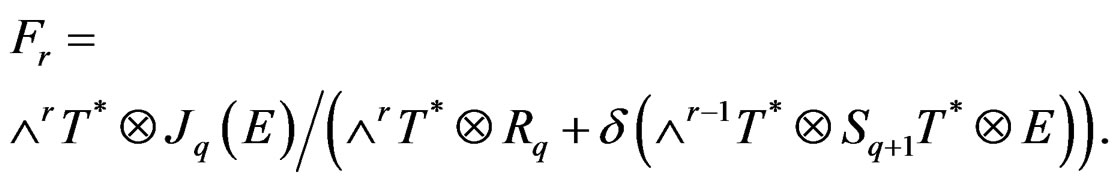
Each operator 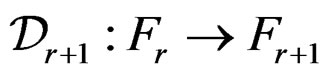 is first order involutive as it is induced by
is first order involutive as it is induced by
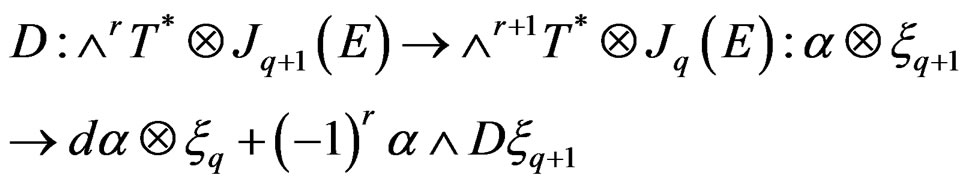
and generates the compatibility conditions (CC) of the preceding one. As the Janet sequence can be cut at any place, the numbering of the Janet bundles has nothing to do with that of the Poincaré sequence, contrary to what many people believe in GR.
Similarly, we have the involutive first Spencer operator
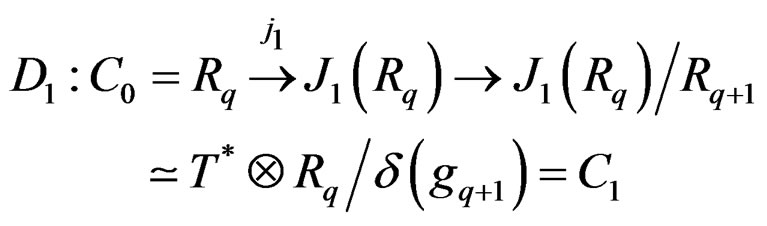
of order one induced by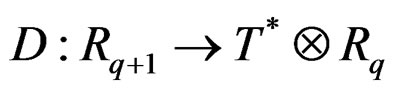 . Introducing the Spencer bundles
. Introducing the Spencer bundles
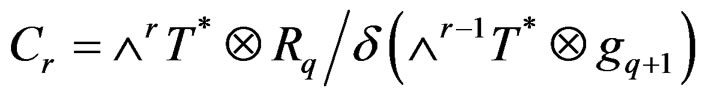 the first order involutive
the first order involutive  Spencer operator
Spencer operator 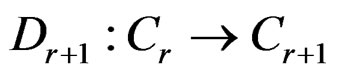 is induced by
is induced by
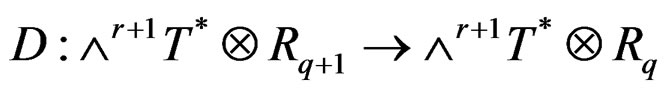
and we obtain the canonical linear Spencer sequence [8,14]:
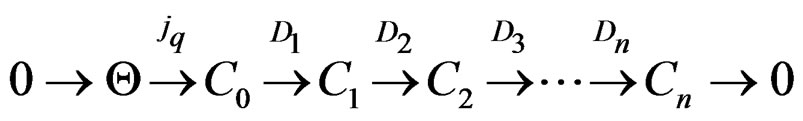
as the Janet sequence for the first order involutive system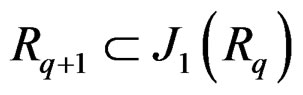 . Introducing the other Spencer bundles
. Introducing the other Spencer bundles
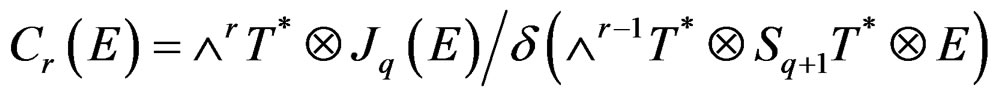
with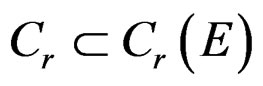 , the linear Spencer sequence is induced by the linear hybrid sequence:
, the linear Spencer sequence is induced by the linear hybrid sequence:
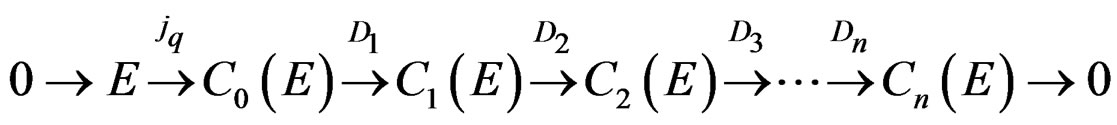
which is at the same time the Janet sequence for 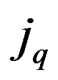 and the Spencer sequence for
and the Spencer sequence for
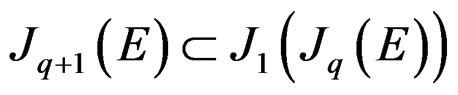
[8,14]. Such a sequence projects onto the Janet sequence and we have the following commutative diagram with exact columns:

In this diagram, only depending on the linear differential operator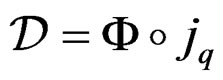 , the epimorhisms
, the epimorhisms
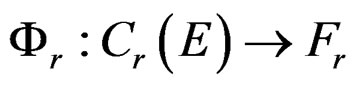 for
for 
are induced by the canonical projection
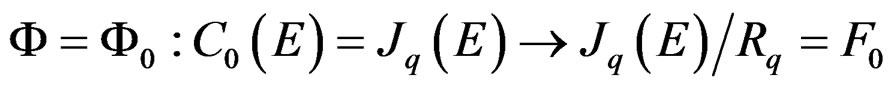
if we start with the knowledge of 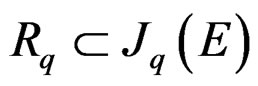 or from the knowledge of an epimorphism
or from the knowledge of an epimorphism
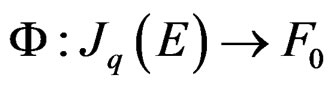
if we set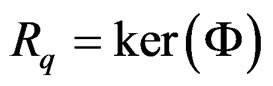 . In the theory of Lie equations considered,
. In the theory of Lie equations considered, 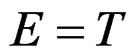 ,
, 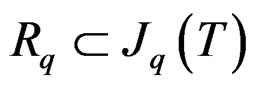 is a transitive involutive system of infinitesimal Lie equations of order
is a transitive involutive system of infinitesimal Lie equations of order 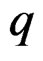 and the corresponding operator
and the corresponding operator 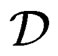 is a Lie operator. As an exercise, we invite the reader to draw this diagram in the affine and projective 1-dimensional cases.
is a Lie operator. As an exercise, we invite the reader to draw this diagram in the affine and projective 1-dimensional cases.
EXAMPLE 2.3: If we restrict our study to the group of isometries of the euclidean metric ![]() in dimension
in dimension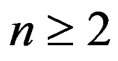 , exhibiting the Janet and the Spencer sequences is not easy at all, even when
, exhibiting the Janet and the Spencer sequences is not easy at all, even when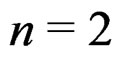 , because the corresponding Killing operator
, because the corresponding Killing operator
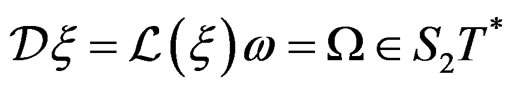 involving the Lie derivative
involving the Lie derivative 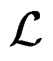 and providing twice the so-called infinitesimal deformation tensor
and providing twice the so-called infinitesimal deformation tensor ![]() of continuum mechanics, is not involutive. In order to overcome this problem, one must differentiate once by considering also the Christoffel symbols
of continuum mechanics, is not involutive. In order to overcome this problem, one must differentiate once by considering also the Christoffel symbols 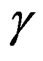 and add the operator
and add the operator
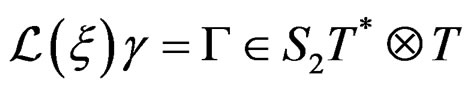 .
.
Now, one can prove that the Spencer sequence for Lie groups of transformations is locally isomorphic to the tensor product of the Poincaré sequence by the Lie algebra of the underlying Lie group [7,8]. Hence, if two Lie groups 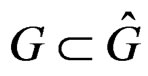 act on
act on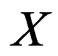 , it follows from the definition of the Janet and Spencer bundles that the Spencer sequence for
, it follows from the definition of the Janet and Spencer bundles that the Spencer sequence for 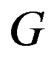 is embedded into the Spencer sequence for
is embedded into the Spencer sequence for 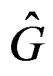 while the Janet sequence for
while the Janet sequence for 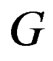 projects onto the Janet sequence for
projects onto the Janet sequence for 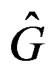 but the common differences are isomorphic to
but the common differences are isomorphic to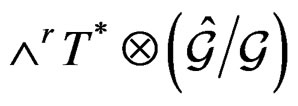 . This rather philosophical comment, namely to replace the Janet sequence by the Spencer sequence, must be considered as the crucial key for understanding the work of the brothers E. and F. Cosserat in 1909 [7,17-19] or H. Weyl in 1918 [7,16], the best picture being that of Janet and Spencer playing at see-saw. Indeed, when
. This rather philosophical comment, namely to replace the Janet sequence by the Spencer sequence, must be considered as the crucial key for understanding the work of the brothers E. and F. Cosserat in 1909 [7,17-19] or H. Weyl in 1918 [7,16], the best picture being that of Janet and Spencer playing at see-saw. Indeed, when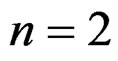 , one has 3 parameters (2 translations + 1 rotation) and the following commutative diagram which only depends on the left commutative square:
, one has 3 parameters (2 translations + 1 rotation) and the following commutative diagram which only depends on the left commutative square:

In this diagram, there is no way to compare 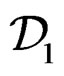 (curvature alone as in Vessiot) with
(curvature alone as in Vessiot) with 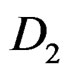 (curvature + torsion as in Cartan).
(curvature + torsion as in Cartan).
For proving that the adjoint of 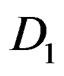 provides the Cosserat equations which can be parametrized by the adjoint of
provides the Cosserat equations which can be parametrized by the adjoint of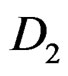 , we may lower the upper indices by means of the constant euclidean metric and look for the factors of
, we may lower the upper indices by means of the constant euclidean metric and look for the factors of 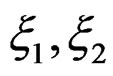 and
and 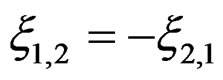 in the integration by parts of the sum:
in the integration by parts of the sum:
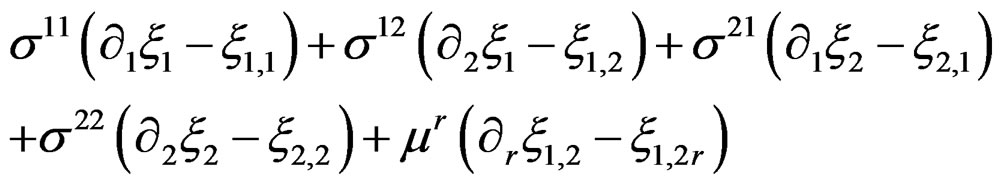
in order to obtain:
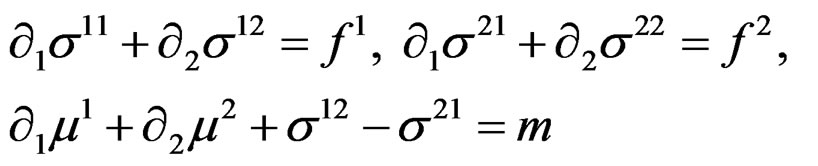
Finally, we get the nontrivial first order parametrization
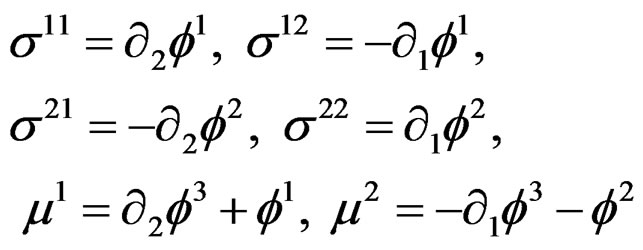
by means of the three arbitrary functions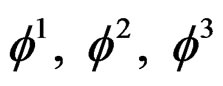 , in a coherent way with the Airy second order parametrization obtained if we set
, in a coherent way with the Airy second order parametrization obtained if we set
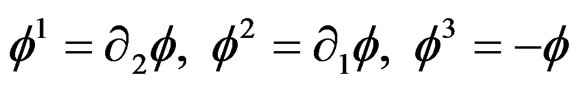
when 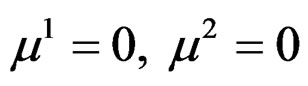 as we shall see in the third part.
as we shall see in the third part.
The link between the FI of 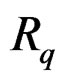 and the CC of
and the CC of 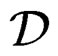 is expressed by the following diagram that may be used inductively:
is expressed by the following diagram that may be used inductively:
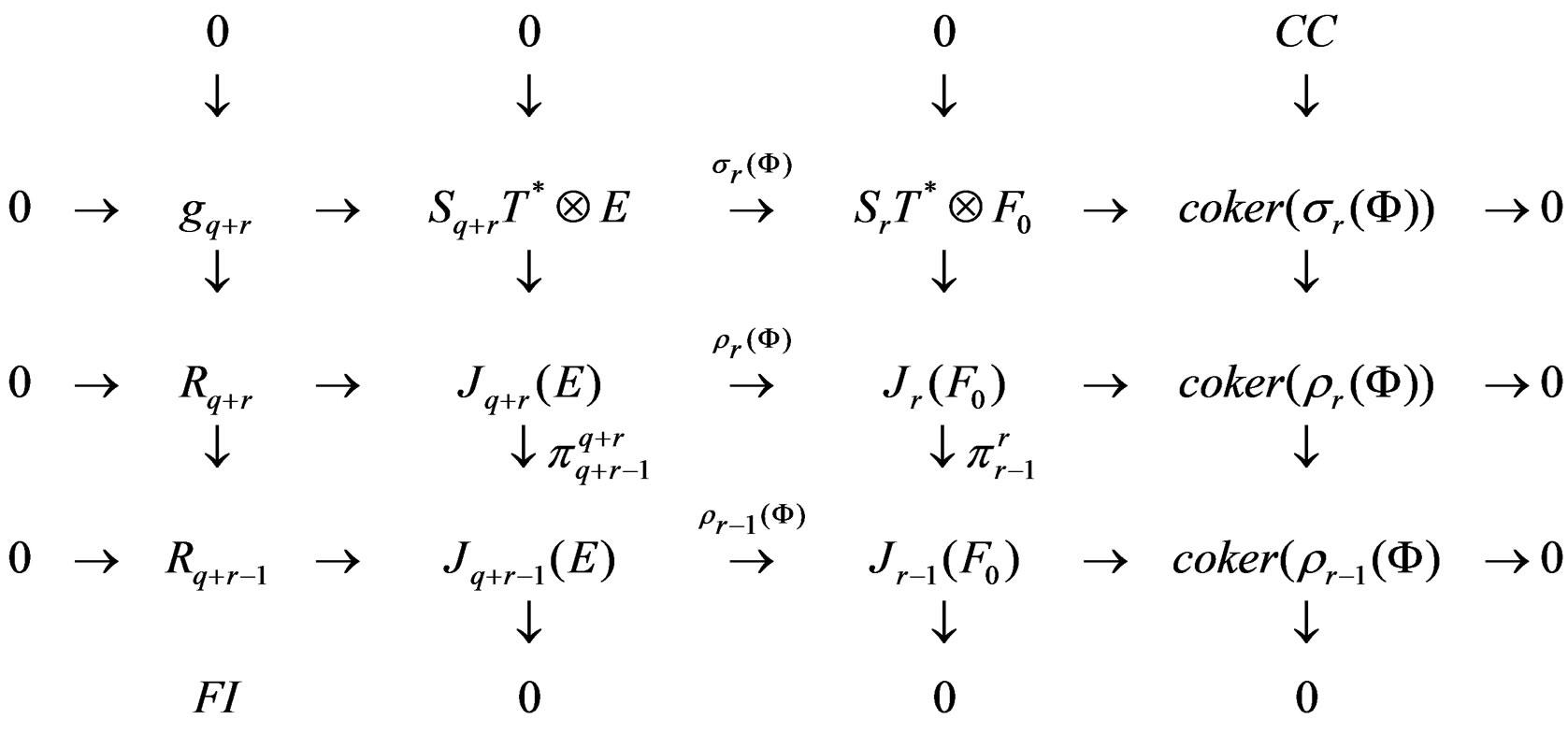
The “snake theorem” [8,20] then provides the long exact connecting sequence:
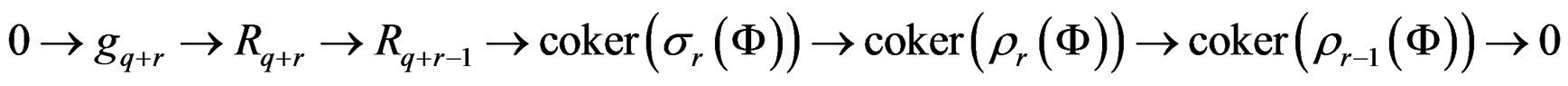 .
.
If we apply such a diagram to first order Lie equations with no zero or first order CC, we have  and we may apply the Spencer
and we may apply the Spencer ![]() -map to the top row obtained with r = 2 in order to get the commutative diagram:
-map to the top row obtained with r = 2 in order to get the commutative diagram:
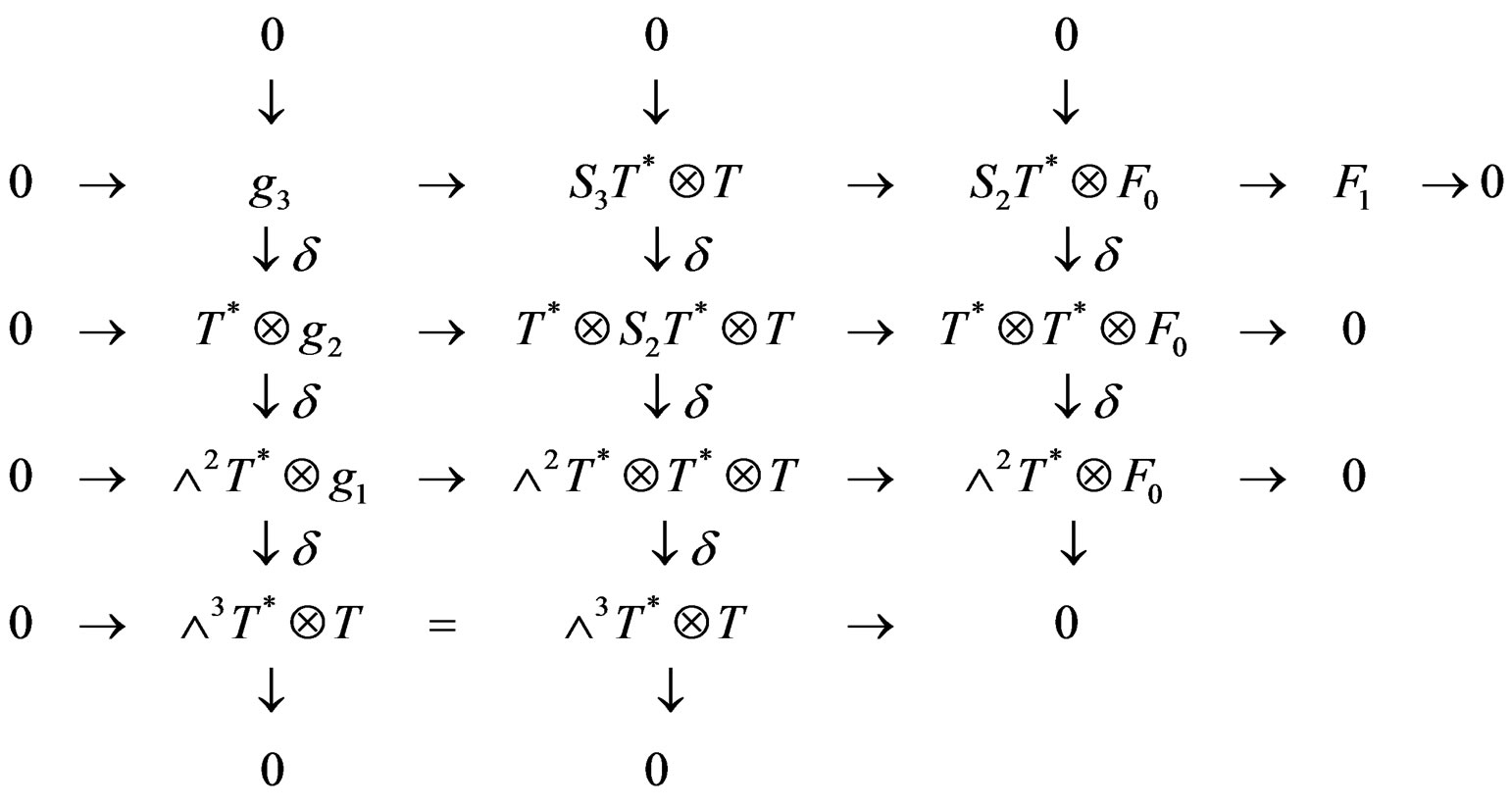
with exact rows and exact columns but the first that may not be exact at . We shall denote by
. We shall denote by 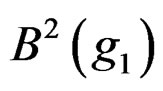 the coboundary as the image of the central
the coboundary as the image of the central![]() , by
, by 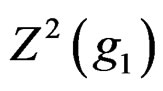 the cocycle as the kernel of the lower
the cocycle as the kernel of the lower ![]() and by
and by 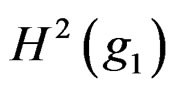 the Spencer
the Spencer ![]() -cohomology at
-cohomology at 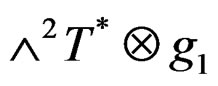 as the quotient.
as the quotient.
In the classical Killing system, 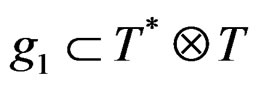 is defined by
is defined by
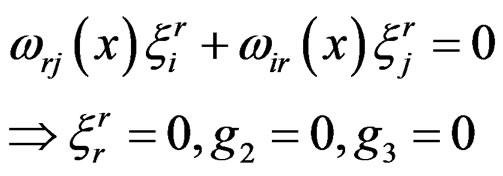
Applying the previous diagram, we discover that the Riemann tensor is a section of the bundle
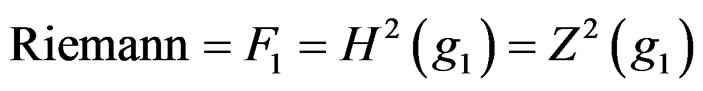
with
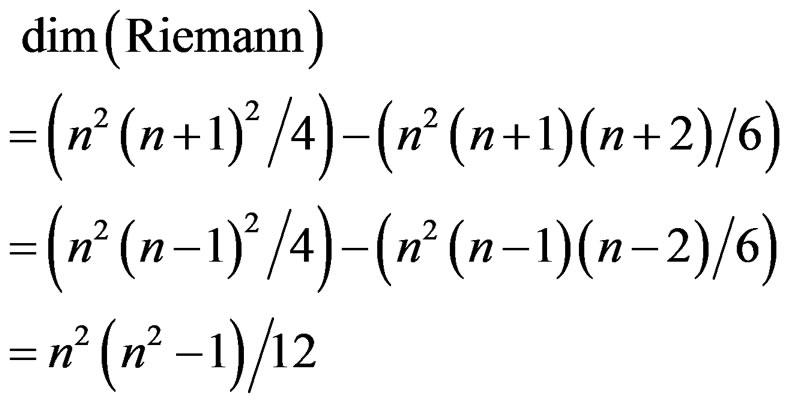
by using the top row or the left column. Though we discover the two properties of the Riemann tensor through the chase involved, we have no indices and cannot therefore exhibit the Ricci tensor of GR by means of the usual contraction or trace.
Let us proceed the same way with the conformal Killing system
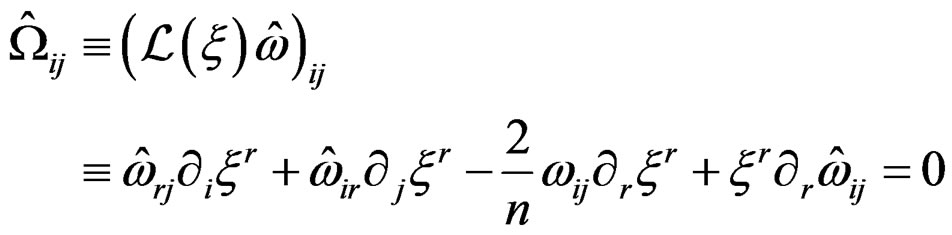
obtained by introducing
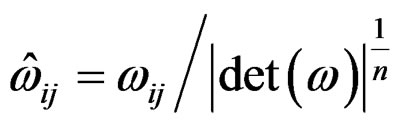
or, equivalently, by eliminating 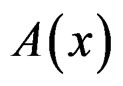 in
in
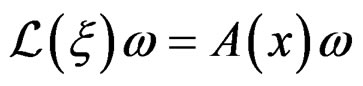 .
.
Now 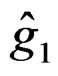 is defined by
is defined by
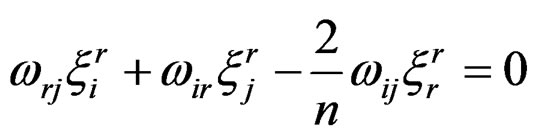
but we have 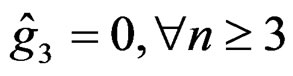 with
with 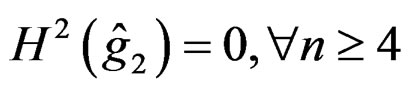 and the Weyl tensor is a section of the bundle
and the Weyl tensor is a section of the bundle
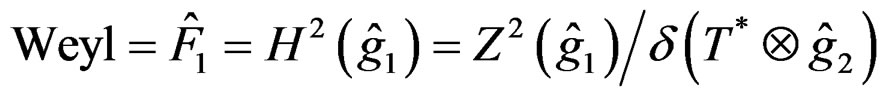
with
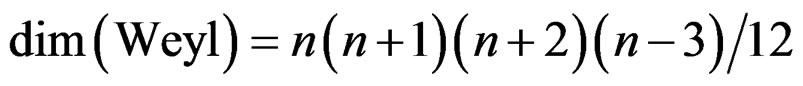 .
.
Similarly, we have no indices and cannot therefore exhibit the Ricci tensor. However, when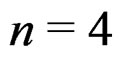 , among the components of the Spencer operator we have
, among the components of the Spencer operator we have
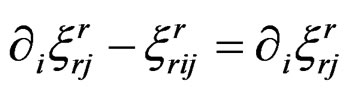
and thus
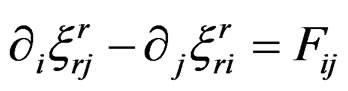 .
.
Such a result allows to recover the electromagnetic field in the image of the Spencer operator  and Maxwell equations by duality along the way proposed by Weyl in [16] but the use of the Spencer operator provides the only possibility to exhibit a link with Cosserat equations.
and Maxwell equations by duality along the way proposed by Weyl in [16] but the use of the Spencer operator provides the only possibility to exhibit a link with Cosserat equations.
Comparing the classical and conformal Killing systems by using the inclusions
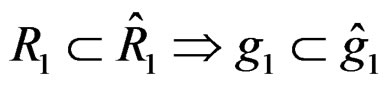 we finally obtain the following commutative and exact diagram where a diagonal chase allows to identify
we finally obtain the following commutative and exact diagram where a diagonal chase allows to identify  with
with
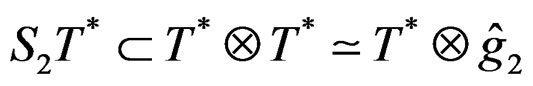
and to split the right column [7,12,20]:
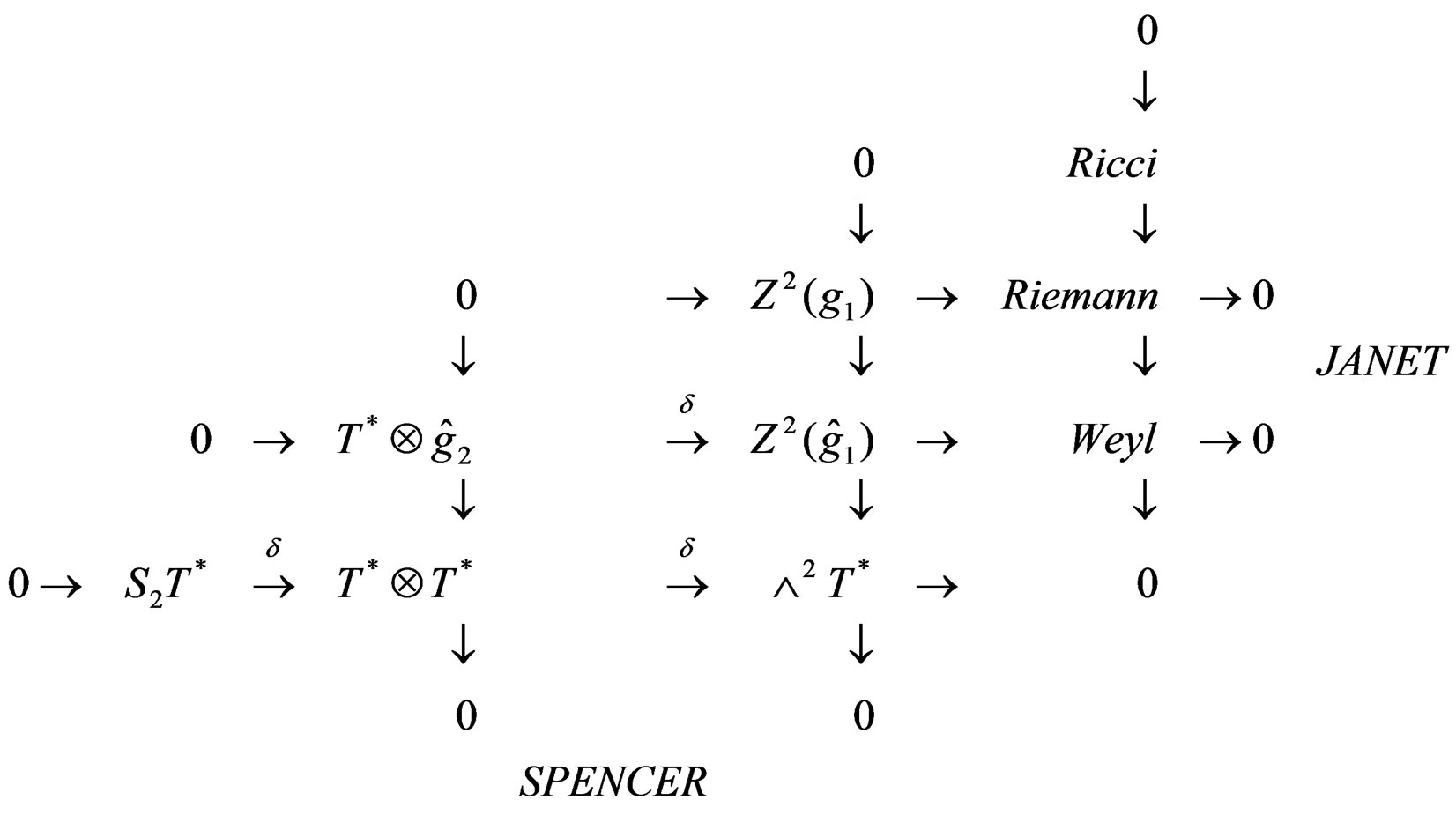
SECOND FUNDAMENTAL RESULT: The Ricci tensor only depends on the “difference” existing between the clasical Killing system and the conformal Killing system, namely the ![]() second order jets (elations once more). The Ricci tensor, thus obtained without contracting the indices as usual, may be embedded in the image of the Spencer operator made by 1-forms with value in 1-forms that we have already exhibited for describing EM. It follows that the foundations of both EM and GR are not coherent with jet theory and must therefore be revisited within this new framework.
second order jets (elations once more). The Ricci tensor, thus obtained without contracting the indices as usual, may be embedded in the image of the Spencer operator made by 1-forms with value in 1-forms that we have already exhibited for describing EM. It follows that the foundations of both EM and GR are not coherent with jet theory and must therefore be revisited within this new framework.
4. Third Part: Algebraic Analysis
EXAMPLE 3.1: Let a rigid bar be able to slide along an horizontal axis with reference position ![]() and attach two pendula, one at each end, with lengths
and attach two pendula, one at each end, with lengths 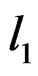 and
and![]() , having small angles
, having small angles 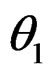 and
and 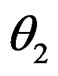 with respect to the vertical. If we project Newton law with gravity
with respect to the vertical. If we project Newton law with gravity ![]() on the perpendicular to each pendulum in order to eliminate the tension of the threads and denote the time derivative with a dot, we get the two equations:
on the perpendicular to each pendulum in order to eliminate the tension of the threads and denote the time derivative with a dot, we get the two equations:
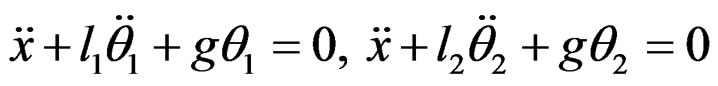
As an experimental fact, starting from an arbitrary movement of the pendula, we can stop them by moving the bar if and only if 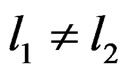 and we say that the system is controllable.
and we say that the system is controllable.
More generally, we can bring the OD equations describing the behaviour of a mechanical or electrical system to the Kalman form 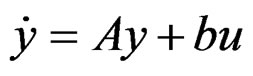 with input
with input 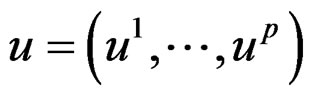 and output
and output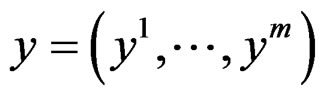 . We say that the system is controllable if, for any given
. We say that the system is controllable if, for any given
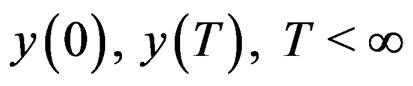 one can find
one can find 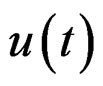 such that a coherent trajectory
such that a coherent trajectory 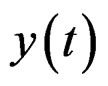 may be found. In 1963 [21], R. E. Kalman discovered that the system is controllable if and only if
may be found. In 1963 [21], R. E. Kalman discovered that the system is controllable if and only if
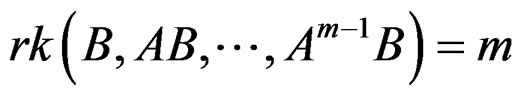 .
.
Surprisingly, such a functional definition admits a formal test which is only valid for Kalman type systems with constant coefficients and is thus far from being intrinsic. In the PD case, the Spencer form will replace the Kalman form.
EXAMPLE 3.2:
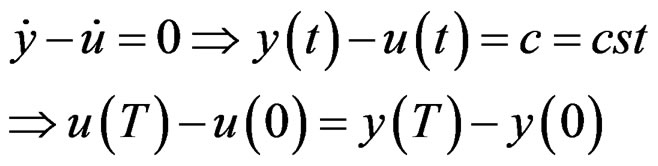
can always be achieved and the system is thus controllable in the sense of the definition but 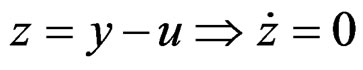 is not controllable in the sense of the test.
is not controllable in the sense of the test.
EXAMPLE 3.3:
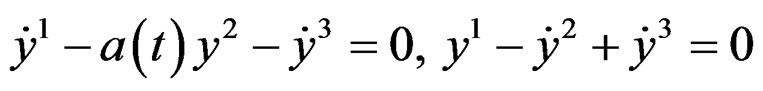 .
.
Any way to bring this system to Kalman form provides the controllability condition 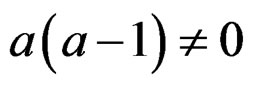 if
if 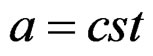 but nothing can be said if
but nothing can be said if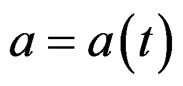 . Also, getting
. Also, getting 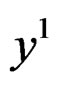 from the second equation and substituting in the first, we get the second order OD equation
from the second equation and substituting in the first, we get the second order OD equation
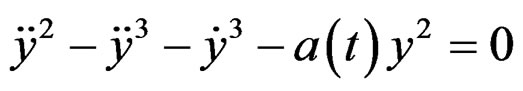
for which nothing can be said at first sight.
PROBLEM 1: Is a SYSTEM of OD or PD equations “controllable” (answer must be YES or NO) and how can we define controllability?
Now, if a differential operator  is given, a direct problem is to find (generating) compatibility conditions (CC) as an operator
is given, a direct problem is to find (generating) compatibility conditions (CC) as an operator  such that
such that
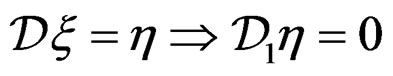 .
.
Conversely, the inverse problem will be to find 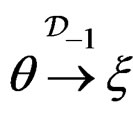
such that 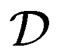 generates the CC of
generates the CC of 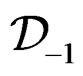 and we shall say that
and we shall say that 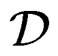 is parametrized by
is parametrized by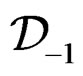 . Of course, solving the direct problem (Janet, Spencer) is necessary for solving the inverse problem.
. Of course, solving the direct problem (Janet, Spencer) is necessary for solving the inverse problem.
EXAMPLE 3.4: When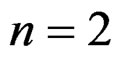 , the Cauchy equations for the stress in continuum mechanics are
, the Cauchy equations for the stress in continuum mechanics are
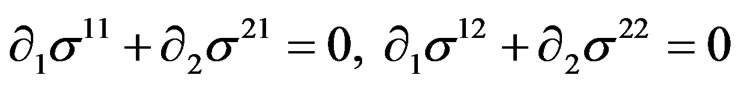
with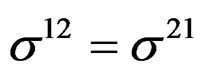 .
.
Their parametrization
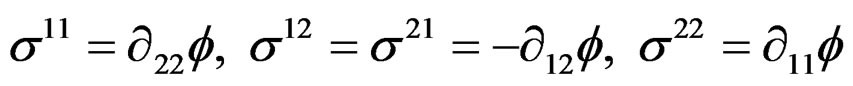
has been discovered by Airy in 1862 and 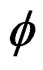 is called the Airy function. When
is called the Airy function. When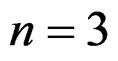 , Maxwell and Morera discovered a similar parametrization with 3 potentials (exercise).
, Maxwell and Morera discovered a similar parametrization with 3 potentials (exercise).
EXAMPLE 3.5: When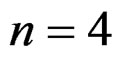 , the Maxwell equations
, the Maxwell equations 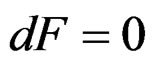 where
where 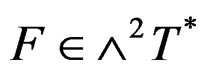 is the EM field are parametrized by
is the EM field are parametrized by 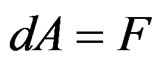 where
where 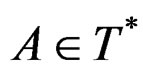 is the 4-potential. The second set of Maxwell equations can also be parametrized by the so-called pseudopotential which is a pseudovector density (exercise).
is the 4-potential. The second set of Maxwell equations can also be parametrized by the so-called pseudopotential which is a pseudovector density (exercise).
EXAMPLE 3.5: If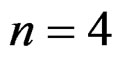 ,
, ![]() is the Minkowski metric and
is the Minkowski metric and 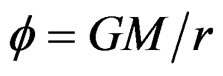 is the gravitational potential, then
is the gravitational potential, then 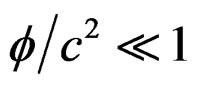 and a perturbation
and a perturbation  of
of ![]() may satisfy in vacuum the 10 second order Einstein equations for the 10
may satisfy in vacuum the 10 second order Einstein equations for the 10 :
:
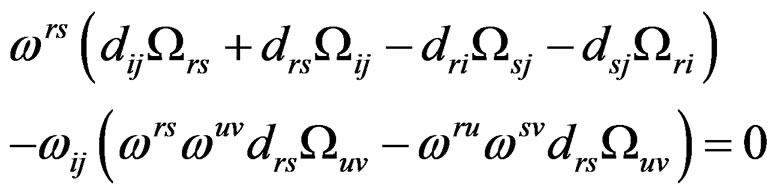
The parametrizing challenge has been proposed in 1970 by J. Wheeler for 1000 $ and solved negatively in 1995 by the author who only received 1 $.
PROBLEM 2: Is an OPERATOR parametrizable (answer must be YES or NO) and how can we find a parametrization?
Let 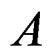 be a unitary ring, that is
be a unitary ring, that is
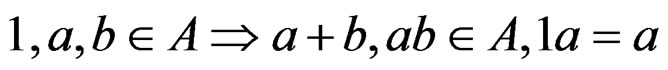
and even an integral domain, that is
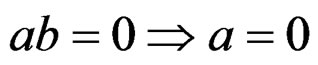 or
or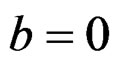 .
.
We say that 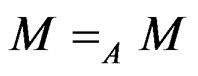 is a left module over
is a left module over 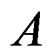 if
if
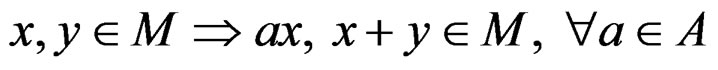
and we denote by 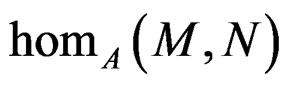 the set of morphisms
the set of morphisms
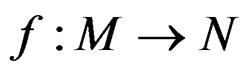 such that
such that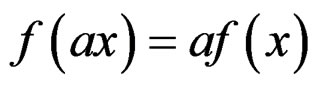 .
.
DEFINITION 3.6: We define the torsion submodule
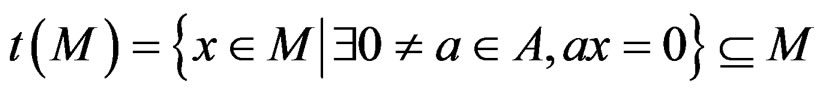 .
.
There is a sequence
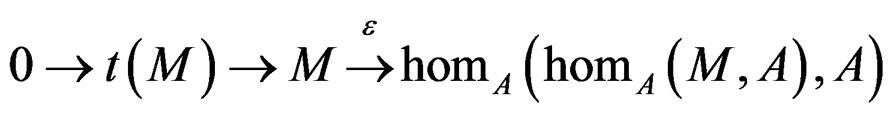
where the morphism ![]() is defined by
is defined by
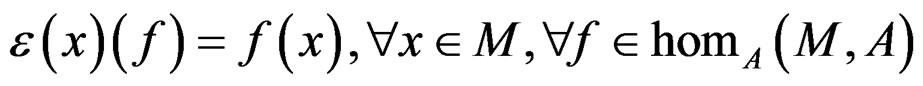
because we have at once
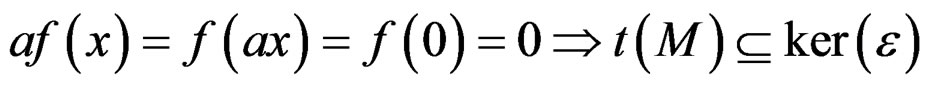 .
.
PROBLEM 3: Is a MODULE 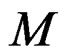 torsion-free, that is
torsion-free, that is 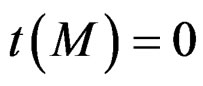 (answer must be YES or NO) and how can we test such a property?
(answer must be YES or NO) and how can we test such a property?
In the remaining of this paper we shall prove that the three problems are indeed identical and that only the solution of the third will provide the solution of the two others [1,22-24].
Let 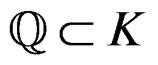 be a differential field, that is a field
be a differential field, that is a field
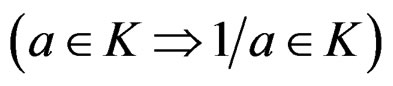
with ![]() commuting derivations
commuting derivations 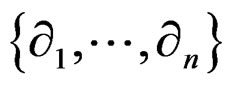 with
with
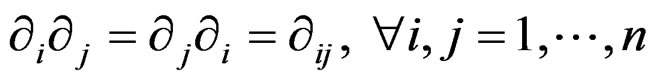
such that
and
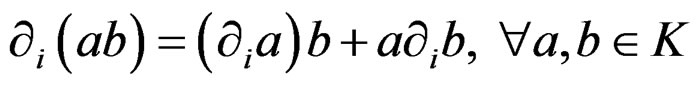 .
.
Using an implicit summation on multiindices, we may introduce the (noncommutative) ring of differential operators
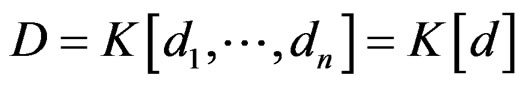
with elements 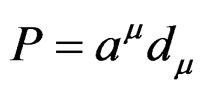 such that
such that 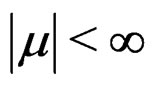 and
and 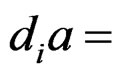
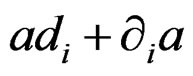 . Now, if we introduce differential indeterminates
. Now, if we introduce differential indeterminates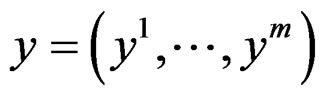 , we may extend
, we may extend ![]() to
to
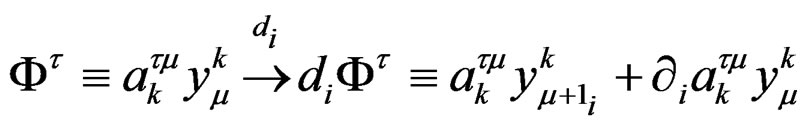
for . Therefore, setting
. Therefore, setting
 we obtain by residue the differential module or
we obtain by residue the differential module or 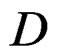 - module
- module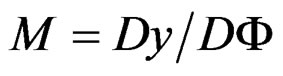 . Introducing the two free differential modules
. Introducing the two free differential modules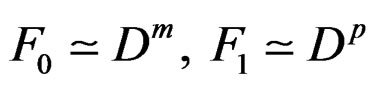 , we obtain equivalently the free presentation
, we obtain equivalently the free presentation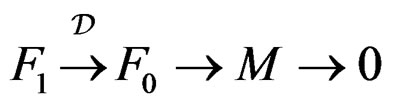 . More generally, introducing the successive CC as in the preceding section, we may finally obtain the free resolution of
. More generally, introducing the successive CC as in the preceding section, we may finally obtain the free resolution of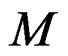 , namely the exact sequence
, namely the exact sequence
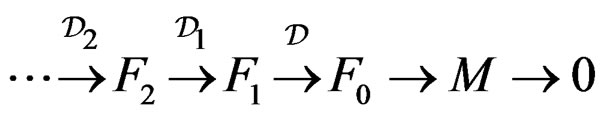 .
.
The “trick” is to let 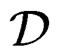 act on the left on column vectors in the operator case and on the right on row vectors in the module case. Homological algebra has been created for finding intrinsic properties of modules not depending on their presentation or even on their resolution.
act on the left on column vectors in the operator case and on the right on row vectors in the module case. Homological algebra has been created for finding intrinsic properties of modules not depending on their presentation or even on their resolution.
EXAMPLE 3.7: In order to understand that different presentations may nevertheless provide isomorphic modules, let us consider the linear inhomogeneous system 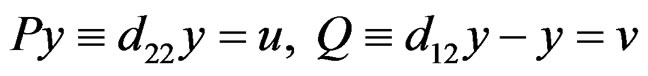 with
with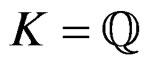 . Differentiating twice, we get
. Differentiating twice, we get 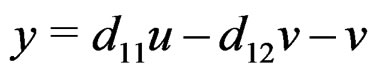 and the two fourth order CC:
and the two fourth order CC:
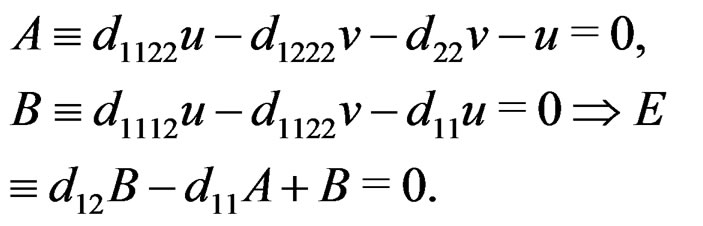
However, as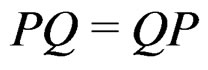 , we also get the CC
, we also get the CC 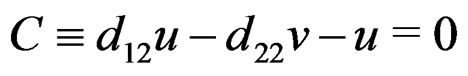 and the two resolutions:
and the two resolutions:
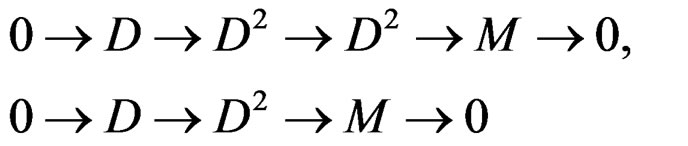
where we can identify the two differential modules involved on the right with 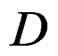 because:
because:
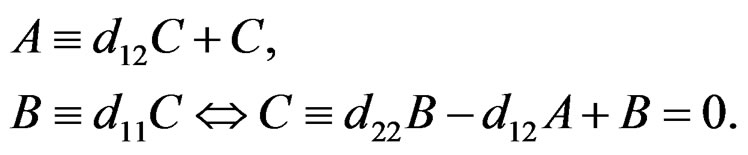
We now exhibit another approach by defining the formal adjoint of an operartor 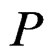 and an operator matrix
and an operator matrix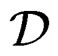 :
:
DEFINITION 3.8:
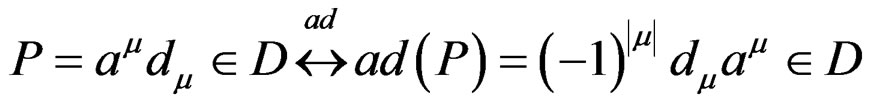
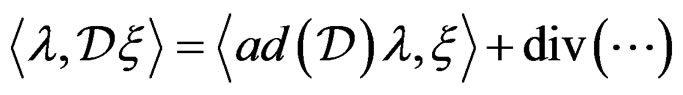
from integration by part, where ![]() is a row vector of test functions and
is a row vector of test functions and  the usual contraction.
the usual contraction.
PROPOSITION 3.9: If we have an operator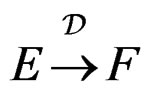 , we obtain by duality an operator
, we obtain by duality an operator
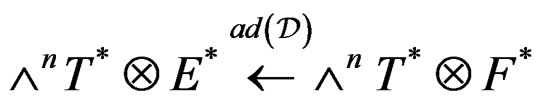
where 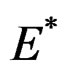 is obtained from
is obtained from 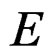 by inverting the transition matrix and EM provides a fine example of such a procedure [10].
by inverting the transition matrix and EM provides a fine example of such a procedure [10].
Now, with operational notations, let us consider the two differential sequences:
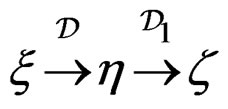
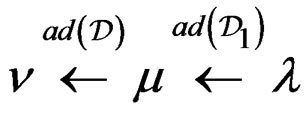
where 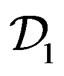 generates all the CC of
generates all the CC of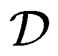 . Then
. Then
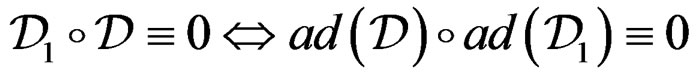
but 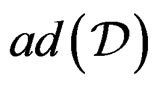 may not generate all the CC of
may not generate all the CC of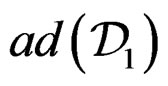 .
.
EXAMPLE 3.10: With 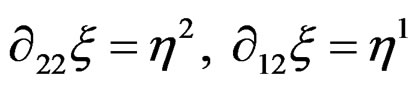 for
for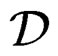 , we get
, we get  for
for . Then
. Then 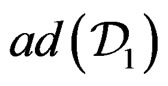 is defined by
is defined by 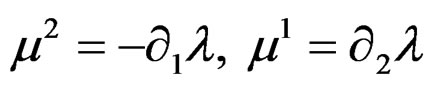 while
while 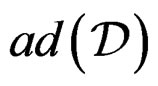 is defined by
is defined by 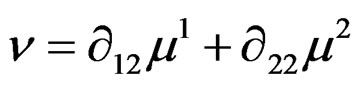 but the CC of
but the CC of 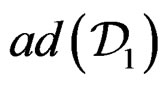 are generated by
are generated by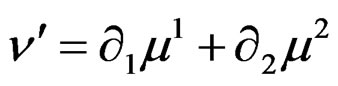 . Passing to the module framework, we obtain the sequences:
. Passing to the module framework, we obtain the sequences:
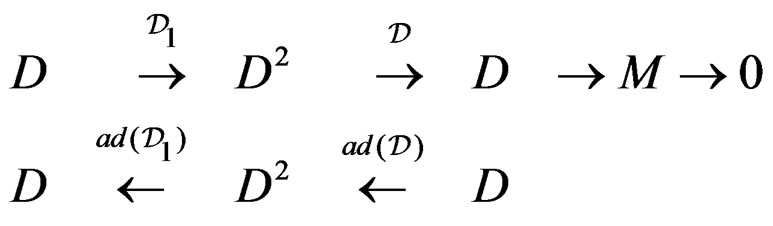
THEOREM 3.11: The cohomology 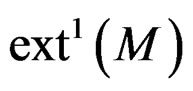 at
at 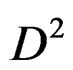 of the lower sequence does not depend on the resolution of
of the lower sequence does not depend on the resolution of  and is a torsion module called the first extension module of
and is a torsion module called the first extension module of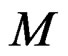 .
.
Exactly like we defined the differential module 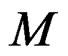 from
from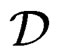 , let us define the differential module
, let us define the differential module 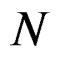 from
from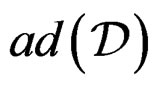 . The proof of the next theorem is quite tricky and out of the scope of this paper [1,22-24]:
. The proof of the next theorem is quite tricky and out of the scope of this paper [1,22-24]:
MAIN THEOREM 3.12: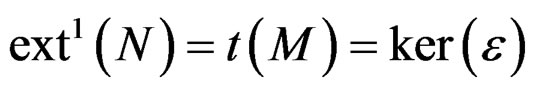 .
.
FORMAL TEST 3.13: The double duality test needed in order to check whether 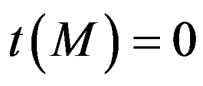 or not and to find out a parametrization if
or not and to find out a parametrization if 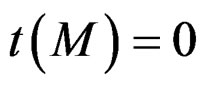 has 5 steps which are drawn in the following diagram where
has 5 steps which are drawn in the following diagram where 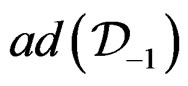 generates the CC of
generates the CC of 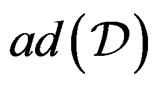 and
and 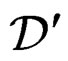 generates the CC of
generates the CC of :
:
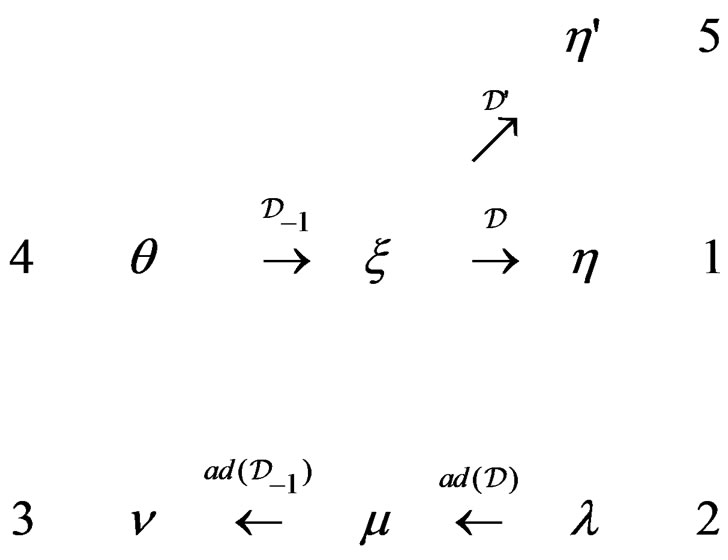
THEOREM 3.14:  parametrized by
parametrized by
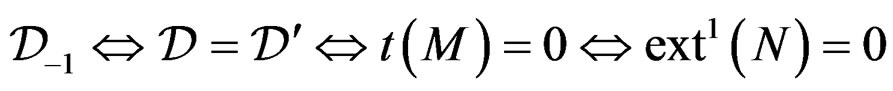 .
.
COROLLARY 3.15: If 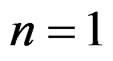 and
and 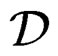 is surjective, then
is surjective, then 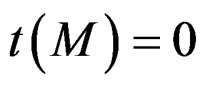 if and only if
if and only if 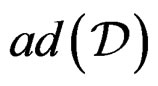 is injective [24,25].
is injective [24,25].
EXAMPLE 3.16: (Kalman test revisited) If we multiply the Kalman system 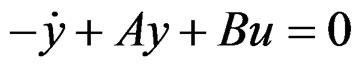 on the left by a test row vector
on the left by a test row vector![]() , we obtain:
, we obtain:
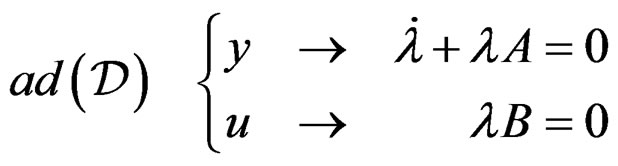
Differentiating the zero order equations and using the first order ones, we get 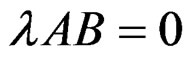 and so on. Using the Cayley-Hamilton theorem, we stop at
and so on. Using the Cayley-Hamilton theorem, we stop at 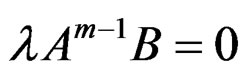 and find back exactly the Kalman test but in a completely different intrinsic framework.
and find back exactly the Kalman test but in a completely different intrinsic framework.
EXAMPLE 3.17: (Double pendulum revisited) Using two test functions 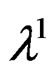 and
and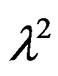 , we get:
, we get:
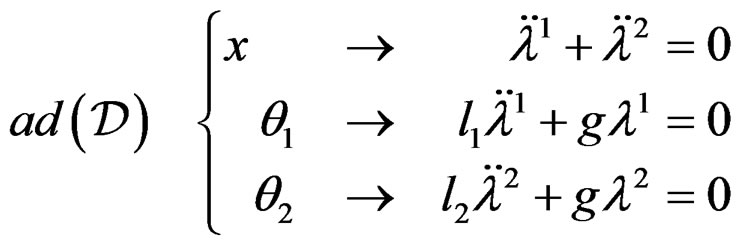
and obtain at once the zero order equation
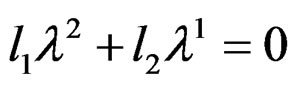 .
.
Differentiating twice and substituting, we also get
 and
and 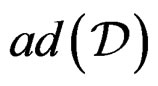 is injective if and only if
is injective if and only if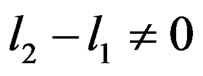 .
.
EXAMPLE 3.18: (Airy parametrization revisited) When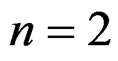 , we may study the infinitesimal deformation
, we may study the infinitesimal deformation 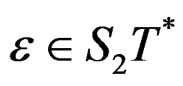 by means of the Killing operator
by means of the Killing operator 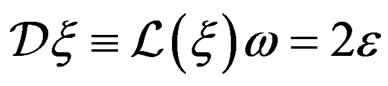 when
when ![]() is the euclidean metric. Then
is the euclidean metric. Then 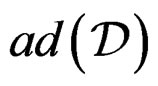 provides (up to sign and factor
provides (up to sign and factor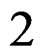 ) the Cauchy equations
) the Cauchy equations 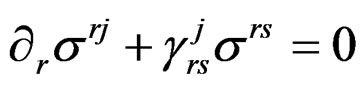 for the stress tensor density [12,16,26]. The following diagram describes the Poincaré scheme:
for the stress tensor density [12,16,26]. The following diagram describes the Poincaré scheme:
 .
.
Accordingly, the second order Airy parametrization is nothing else than the adjoint of the only Riemann CC involved, namely 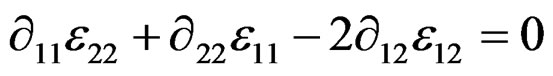 which is the linearization of the Riemann tensor of Example 1.9.
which is the linearization of the Riemann tensor of Example 1.9.
EXAMPLE 3.19: (Einstein equations revisited) Contrary to the Ricci operator, the Einstein operator is selfadjoint because it comes from a variational procedure, the sixth terms being exchanged between themselves under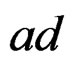 . For example, we have:
. For example, we have:
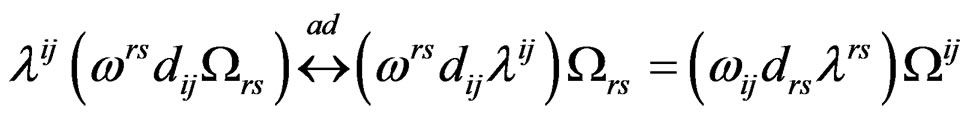
and the adjoint of the first operator is the sixth. Accordingly, one has the following diagram where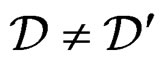 :
:
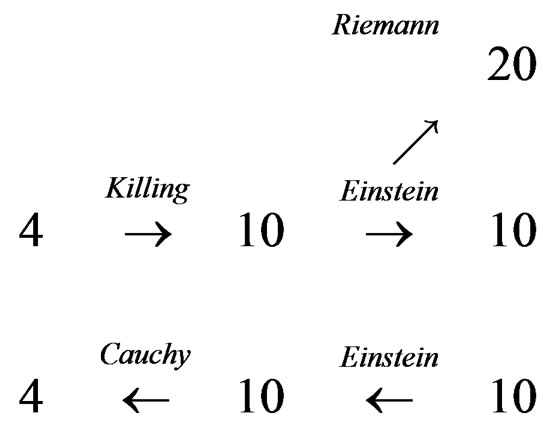
THIRD FUNDAMENTAL RESULT: Comparing this diagram to the previous one proves that Einstein equations are not coherent with Janet and Spencer sequences as conformal geometry has not been introduced in this last part.
EXERCISE 3.20: Prove that
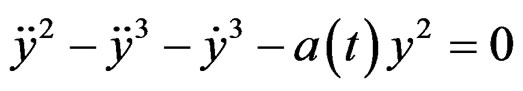
is controllable if and only if 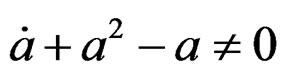 (Riccati) and find a parametrization.
(Riccati) and find a parametrization.
EXERCISE 3.21: Prove that the infinitesimal contact transformations of Example 1.10 admit the injective parametrization
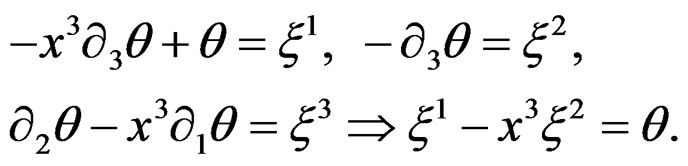
5. Conclusion
The mathematical foundations of General Relativity leading to Einstein equations are always presented in textbooks or papers without any reference to conformal geometry. However, comparing the classical Killing equations to the conformal Killing equations while constructing corresponding differential sequences, the Ricci tensor appears as the kernel of the canonical projection of the Riemann tensor onto the Weyl tensor. After obtaining such a result in a purely intrinsic way, that is without using indices, we have been able to introduce “diagram chasing” in order to relate for the first time electromagnetism and gravitation to the Spencer ![]() -cohomology of the classical and conformal Killing symbols. Accordingly, the mathematical foundations of general relativity are not coherent with jet theory and must therefore be revisited within this new framework along the lines we have sketched. Finally, the fact that Einstein equations cannot be parametrized, contrary to most other equations of physics or engineering, also brings a deep structural question on these equations that will have to be solved in the future by means of algebraic analysis.
-cohomology of the classical and conformal Killing symbols. Accordingly, the mathematical foundations of general relativity are not coherent with jet theory and must therefore be revisited within this new framework along the lines we have sketched. Finally, the fact that Einstein equations cannot be parametrized, contrary to most other equations of physics or engineering, also brings a deep structural question on these equations that will have to be solved in the future by means of algebraic analysis.
REFERENCES
- J.-F. Pommaret, “Partial Differential Control Theory,” Kluwer, Dordrecht, 2001. doi:10.1007/978-94-010-0854-9
- E. Cartan, Annales Scientifiques de l’École Normale Supérieure, Vol. 21, 1904, pp. 153-206.
- E. Cartan, Annales Scientifiques de l’École Normale Supérieure, Vol. 40, 1923, pp. 325-412.
- H. Goldschmidt, Journal of Differential Geometry, Vol. 6, 1972, pp. 357-373,
- A. Kumpera and D. C. Spencer, “Lie Equations,” Annals of Mathematics Studies 73, Princeton University Press, Princeton, 1972.
- J.-F. Pommaret, “Differential Galois Theory,” Gordon and Breach, New York, 1983.
- J.-F. Pommaret, “Spencer Operator and Applications: From Continuum Mechanics to Mathematical Physics,” In: Y. Gan, Ed., Continuum Mechanics-Progress in Fundamentals and Engineering Applications, InTech, 2012. http://www.intechopen.com/books/continuum-mechanics-progress-in-fundamentals-and-engineering-applications/spencer-operator-and-applications-from-continuum-mechanics-to-mathematical-physics
- J.-F. Pommaret, “Partial Differential Equations and Group Theory,” Kluwer, 1994. doi:10.1007/978-94-017-2539-2
- E. Vessiot, Annales scientifiques de l’École Normale Supérieure, Vol. 20, 1903, pp. 411-451.
- V. Ougarov, “Théorie de la Relativité Restreinte,” MIR, Moscow, 1969.
- L. P. Eisenhart, “Riemannian Geometry,” Princeton University Press, Princeton, 1926.
- J.-F. Pommaret, “Lie Pseudogroups and Mechanics,” Gordon and Breach, New York, 1988.
- A. Lorenz, “Jet Groupoids, Natural Bundles and the Vessiot Equivalence Method,” Acta Applicandae Mathematicae, Vol. 1, 2008, pp. 205-213. doi:10.1007/s10440-008-9193-7
- D. C. Spencer, Bulletin of the American Mathematical Society, Vol. 75, 1965, pp. 1-114.
- M. Janet, Journal de Mathématiques Pures et Appliquées, Vol. 8, 1920, pp. 65-151.
- H. Weyl, “Space, Time, Matter,” Berlin, 1918.
- E. Cosserat and F. Cosserat, “Théorie des Corps Déformables,” Hermann, Paris, 1909.
- J.-F. Pommaret, Acta Mechanica, Vol. 149, 2001, pp. 23-39. doi:10.1007/BF01261661
- J.-F. Pommaret, Acta Mechanica, Vol. 215, 2010, pp. 43- 55. doi:10.1007/s00707-010-0292-y
- J. J. Rotman, “An Introduction to Homological Algebra,” Academic Press, Cambridge, 1979.
- R. E. Kalman, Y. C. Yo and K. S. Narenda, Journal of Differential Equations, Vol. 1, 1963, pp. 189-213.
- M. Kashiwara, Mémoires de la Société Mathématique de France, Vol. 63, 1995, pp. 1-72.
- V. P. Palamodov, “Linear Differential Operators with Constant Coefficients,” Grundlehren der Mathematischen Wissenschaften 168, Springer, 1970. doi:10.1007/978-3-642-46219-1
- J.-F. Pommaret, “Algebraic Analysis of Control Systems Defined by Partial Differential Equations,” Advanced Topics in Control Systems Theory, Springer, Lecture Notes in Control and Information Sciences 311, 2005, pp. 155-223.
- E. Kunz, “Introduction to Commutative Algebra and Algebraic Geometry,” Birkhäuser, 1985.
- W. Pauli, “Theory of Relativity,” Pergamon Press, London, 1958.

