Journal of Modern Physics
Vol.4 No.6(2013), Article ID:33467,10 pages DOI:10.4236/jmp.2013.46118
Charged Gravastar in a Dark Energy Universe
1Departamento de Fisica Teórica, Instituto de Fisica, Universidade do Estado do Rio de Janeiro, Rua São Francisco Xavier 524, Maracanã, Rio de Janeiro-RJ, Brasil
2Coordenação de Astronomia e Astrofisica, Observatório Nacional, Rua General José Cristino, 77, São Cristóvão, Rio de Janeiro, RJ, Brazil
3IST-Instituto Superior de Tecnologia de Paracambi, FAETEC, Rua Sebastião de Lacerda s/n, Bairro da Fábrica, Paracambi, RJ, Brazil
Email: fredcharret@yahoo.com.br, chan@on.br, mfasnic@gmail.com, pedrosennarocha@gmail.com
Copyright © 2013 C. F. C. Brandt et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 15, 2013; revised April 17, 2013; accepted May 11, 2013
Keywords: Gravastar; Charge; De Sitter-Reissner-Nordstrom Spacetime; Black Hole; Naked Singularity; Dark Energy
ABSTRACT
Here we constructed a charged gravastar model formed by an interior de Sitter spacetime, a charged dynamical infinitely thin shell with an equation of state and an exterior de Sitter-Reissner-Nordström spacetime. We find that the presence of the charge is crucial to the stability of these structures. It can as much favor the stability of a bounded excursion gravastar, and still converting it in a stable gravastar, as make disappear a stable gravastar, depending on the range of the charge considered. There is also formation of black holes and, above certain values, the presence of the charge allows the formation of naked singularity. This is an important example in which a naked singularity emerges as a consequence of unstabilities of a gravastar model, which reinforces that gravastar is not an alternative model to black hole.
1. Introduction
Although we have strong theoretical and experimental evidences in favor of the existence of black holes, lots of paradoxical problems about them do exist [1]. Besides, it was shown recently that observational data could give strong arguments in the existence of event horizons, but we can not prove it directly [2].
We also have the fact that the picture of gravitational collapse provided by Einstein’s General Relativity cannot be completely correct since in the final stages of collapse quantum effects must be taken into account at high curvature values, or short distances, compared with the Planck length scale, as pointed out by Chapline [3] and other researchers.
These facts frequently motivated authors to try to find new alternatives for the final state of a collapsing star without horizons. Among these models we can mention Bose superfluid [4], dark stars [5] and holostars [6-11].
There are many other additional models proposed as black holes mimickers, but among the alternative models to these compact objects, the gravitational vacuum stars (gravastars) [12] received special attention, partially due to the tight connection between the cosmological constant and our accelerated expanding universe, although it is very difficult to distinguish these objects from black holes.
In the original model of Mazur and Mottola (MM) [12], gravastars consist of five layers. To study the dynamical stability of such compact object, Visser and Wiltshire (VW) [13] argued that such five-layer models can be simplified to three-layer ones. They also pointed out that there are two different types of stable gravastars which are stable gravastars and “bounded excursion” gravastars. The first one represents a stable structure already formed, while the second one is a system with a shell which oscillates around a equilibrium position which can loose energy and stabilize at the end.
Recently we have studied the stability of some three layer gravastar models [14-19]. The first model [14] consisted of an internal de Sitter spacetime, a dynamical infinitely thin shell of stiff fluid, and an external Schwarzschild spacetime, as proposed by VW [13]. We have shown explicitly that the final output can be a black hole, a “bounded excursion” stable gravastar, a Minkowski, or a de Sitter spacetime, depending on the total mass  of the system, the cosmological constant
of the system, the cosmological constant  and the initial position
and the initial position 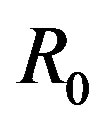 of the dynamical shell. We have concluded that although it does exist a region of the space of the initial parameters where it is always formed stable gravastars, it still exists a large region of this space where we can find black hole formation. In the sequence, considering after an equation of state
of the dynamical shell. We have concluded that although it does exist a region of the space of the initial parameters where it is always formed stable gravastars, it still exists a large region of this space where we can find black hole formation. In the sequence, considering after an equation of state  for the shell [15], instead of only using a stiff fluid
for the shell [15], instead of only using a stiff fluid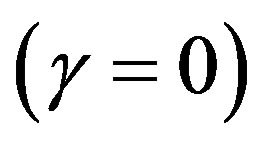 , we concluded that gravastar really is not an alternative model to black hole.
, we concluded that gravastar really is not an alternative model to black hole.
We also have generalized the former one considering an interior constituted by an anisotropic dark energy fluid [16,19]. We have again confirmed the previous results, i.e., that both gravastars and black holes can be formed, depending on the initial parameters. It is remarkable that for this case we have an interior fulfilled by a physical matter, instead of a de Sitter vacuum. Thus, it is similar to dark energy star models.
Recently, Carter [20] studied spherically symmetric gravastar solutions which possess an (anti) de Sitter interior and a (anti) de Sitter-Schwarzschild or ReissnerNordström exterior, separately. He followed the same approach that Visser and Wiltshire took in their work [13] assuming a potential 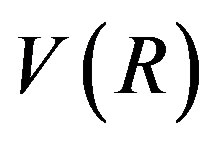 and then founding the equation of state of the shell. He found a wide range of parameters which allow stable gravastar solutions, and presented the different qualitative behaviors of the equation of state for these parameters, for both cases, those are, a (anti) de Sitter-Schwarzschild or Reissner-Nordström exterior.
and then founding the equation of state of the shell. He found a wide range of parameters which allow stable gravastar solutions, and presented the different qualitative behaviors of the equation of state for these parameters, for both cases, those are, a (anti) de Sitter-Schwarzschild or Reissner-Nordström exterior.
Differently from Carter’s work [20], we consider here a different approach, as in the previous works. In a first step, we generalized our second work on gravastars [15], introducing an external de Sitter-Schwarzschild spacetime [17]. The aim was to study how the cosmological constant affects the gravastar formation, and we found that the exterior cosmological constant imposes a limit on the gravastar formation since the dark energy density inside the gravastar has to be greater than the surrounding spacetime. Now we are interested in the influence of the charge, combined with the influence of an exterior cosmological constant, considering a de Sitter-ReissnerNordström exterior spacetime. For this configuration we showed that the presence of the charge can change considerably the stability conditions of these structures. It can as much favor the stability of a bounded excursion gravastar, converting it in a stable gravastar, as make disappear a stable gravastar or even to allow a naked singularity formation.
In a previous work [18] we have already considered the exterior of the gravastar is a Reissner-Nordström spacetime, but with zero total mass and, depending on the parameter 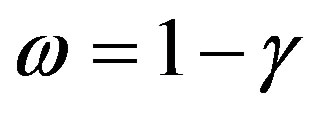 of the equation of state of the shell, and the charge, a gravastar structure can be formed. We have found that the presence of the charge contributes to the stability of the gravastar, if the charge is greater than a critical value.
of the equation of state of the shell, and the charge, a gravastar structure can be formed. We have found that the presence of the charge contributes to the stability of the gravastar, if the charge is greater than a critical value.
The paper is organized as follows: In Section 2 we present the metrics of the interior and exterior spacetimes, with their extrinsic curvatures, the equation of motion of the shell and the potential of the system. In Section 3 we analyze the influence of the presence of the charge in the gravastar model confirming the existence of naked singularity formation and we investigate the formation of gravastar from numerical analysis of the general potential. Finally, in Section 4 we present our conclusions.
2. Formation of Gravastars in a De Sitter-Reissner-Nordström Spacetime
This gravastar model is described by an interior spacetime with a cosmological constant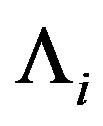 , given by the de Sitter metric,
, given by the de Sitter metric,
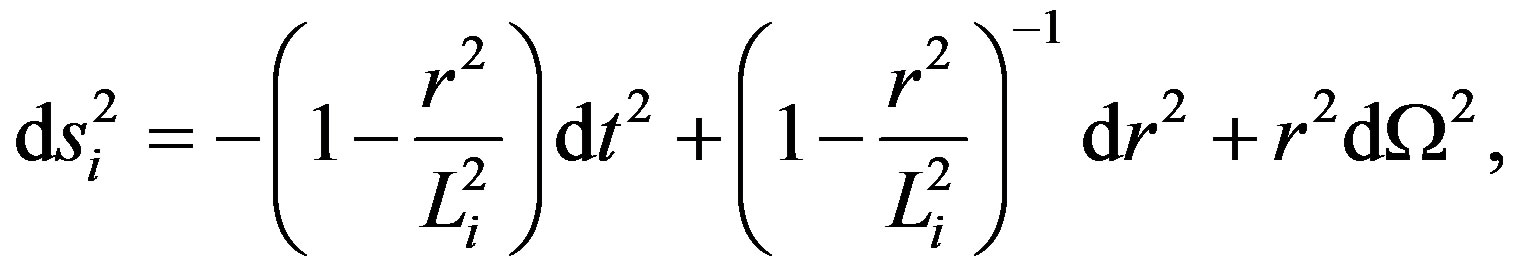 (1)
(1)
where, 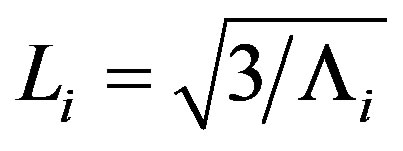 and
and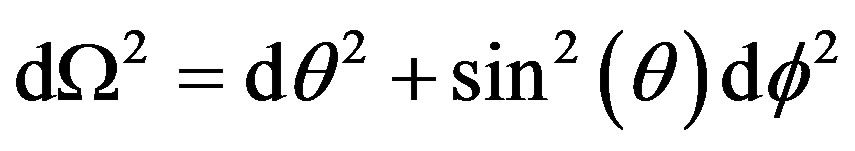 .
.
Differently from the previous models, here we consider a charged shell and a cosmological constant 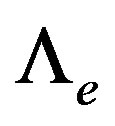 generating a vacuum exterior spacetime described by the de Sitter-Schwarzschild-Reissner-Nordström metric,
generating a vacuum exterior spacetime described by the de Sitter-Schwarzschild-Reissner-Nordström metric,
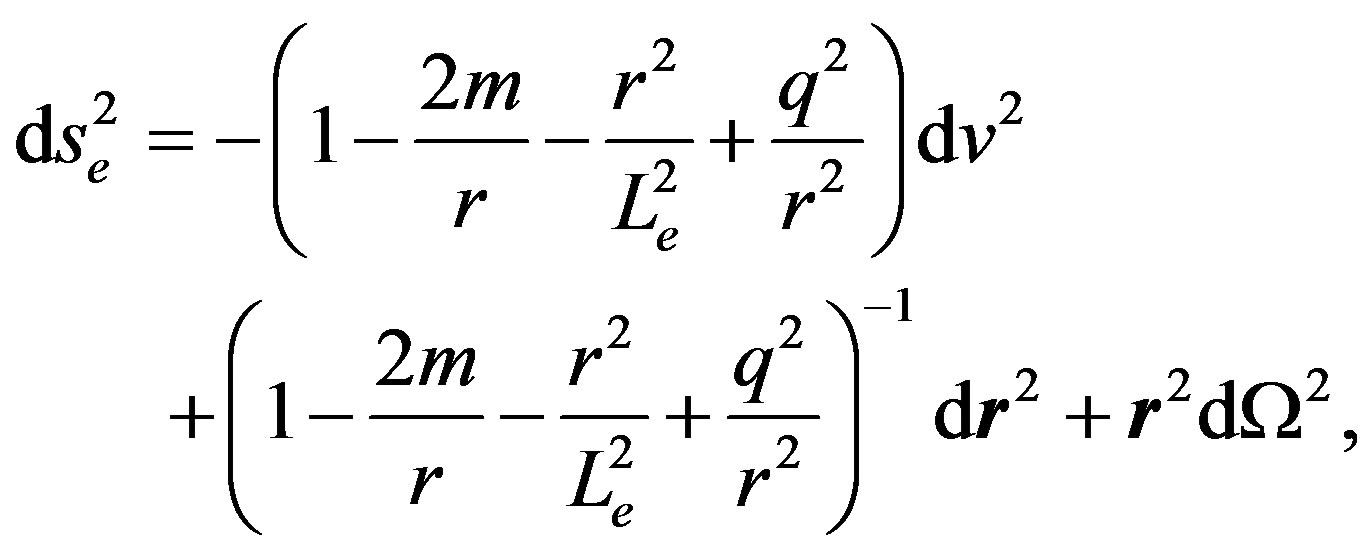 (2)
(2)
where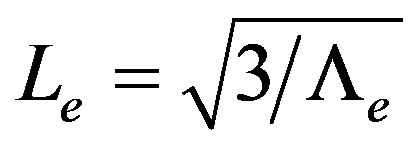 .
.
The thin shell is characterized by the hypersurface  and given by the metric
and given by the metric
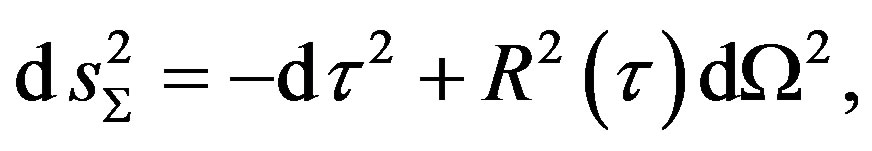 (3)
(3)
where  is the proper time.
is the proper time.
In order to find the mass of the shell, and then its potential, it is necessary to consider the junction conditions.
The continuity of the first fundamental form imposes that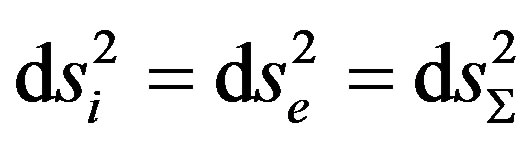 , then
, then 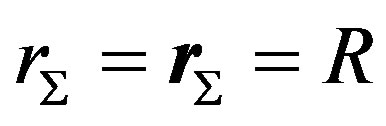 and
and
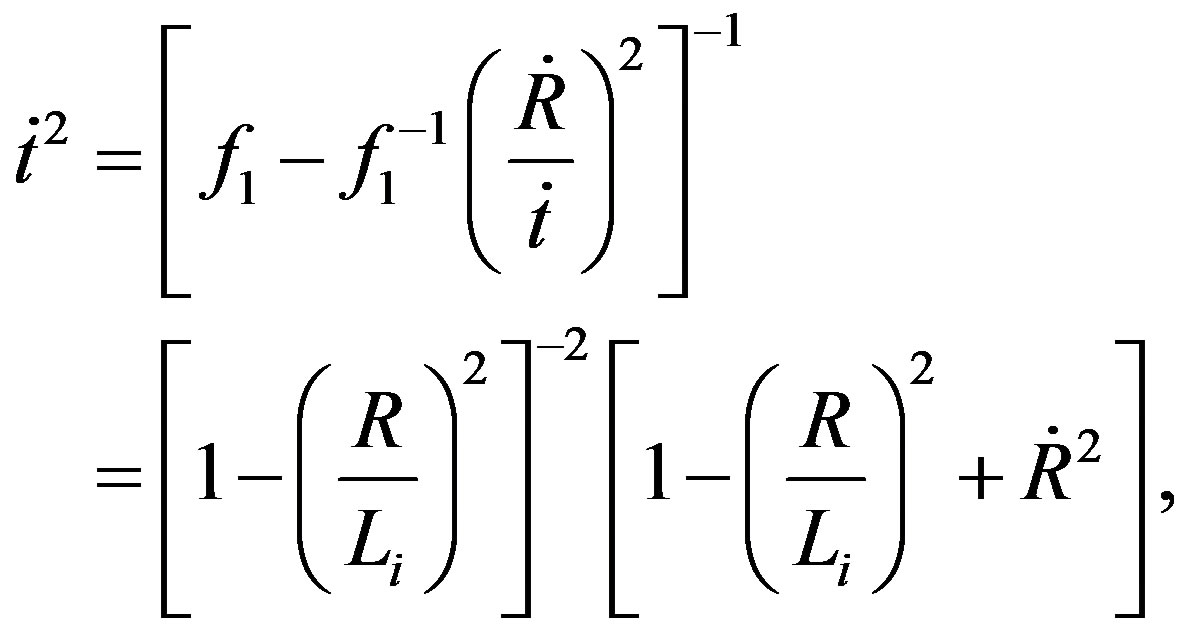 (4)
(4)
and
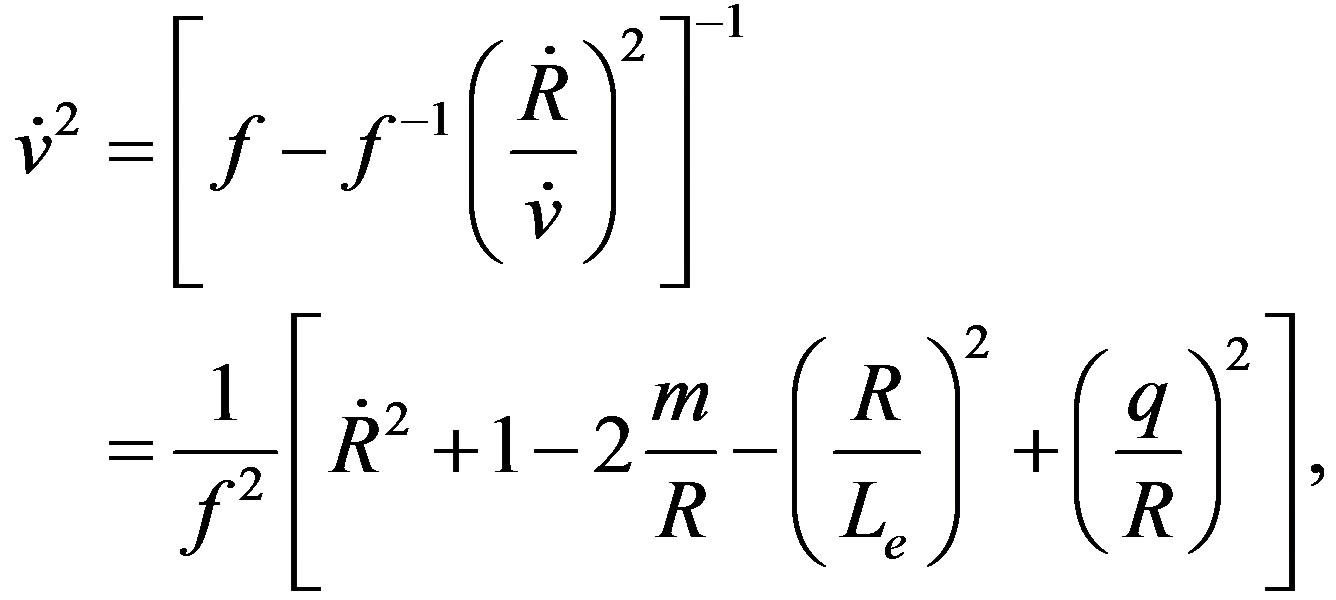 (5)
(5)
where the dot represents the differentiation with respect to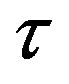 .
.
Thus, the interior and exterior normal vector are given by
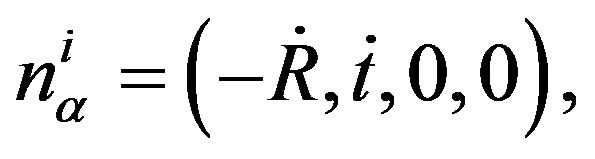 (6)
(6)
and
 (7)
(7)
The interior and exterior extrinsic curvature are given by
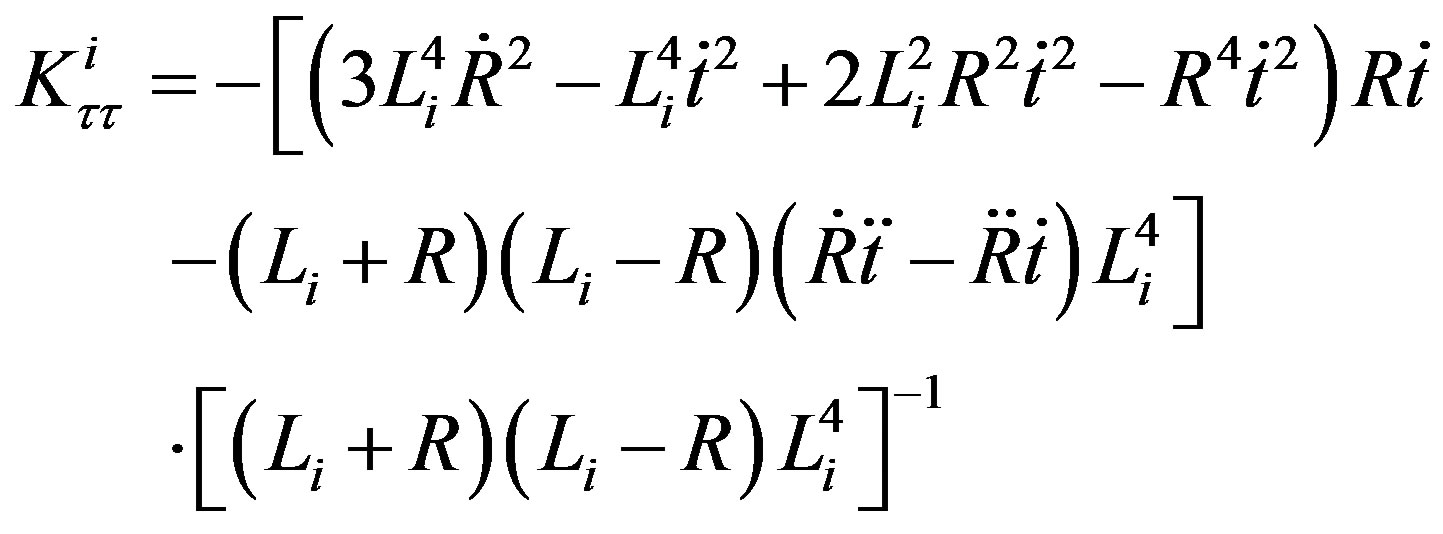 (8)
(8)
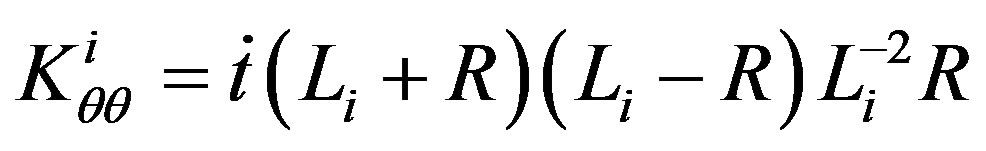 (9)
(9)
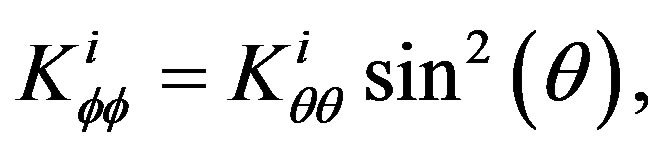 (10)
(10)
 (11)
(11)
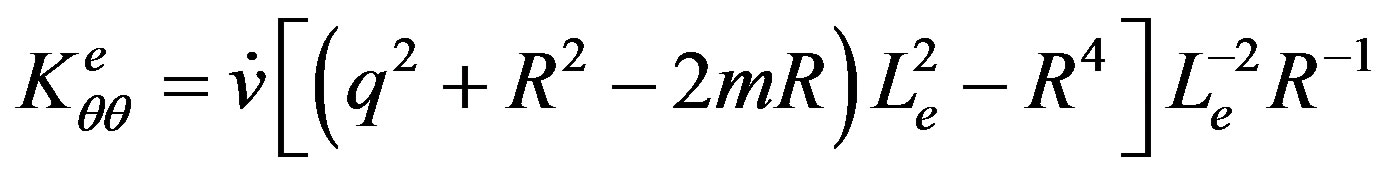 (12)
(12)
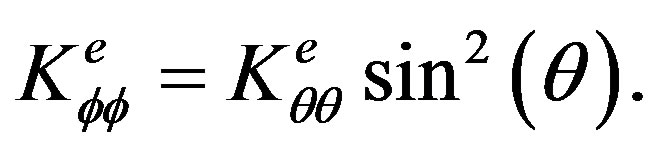 (13)
(13)
Following Lake [21], we have
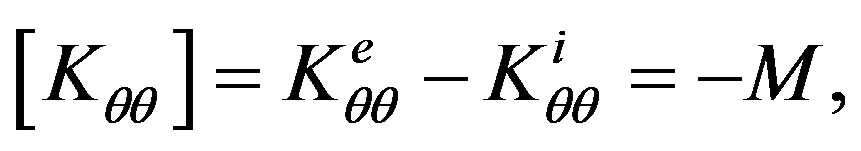 (14)
(14)
where 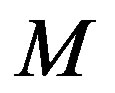 is the mass of the shell. Thus
is the mass of the shell. Thus
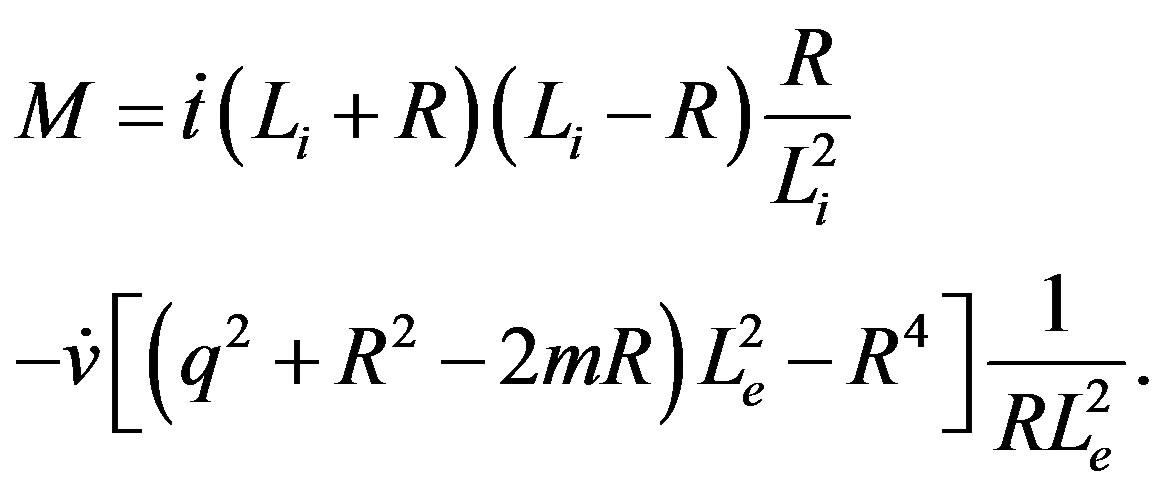 (15)
(15)
Then, substituting Equations (4) and (5) into (15) we get
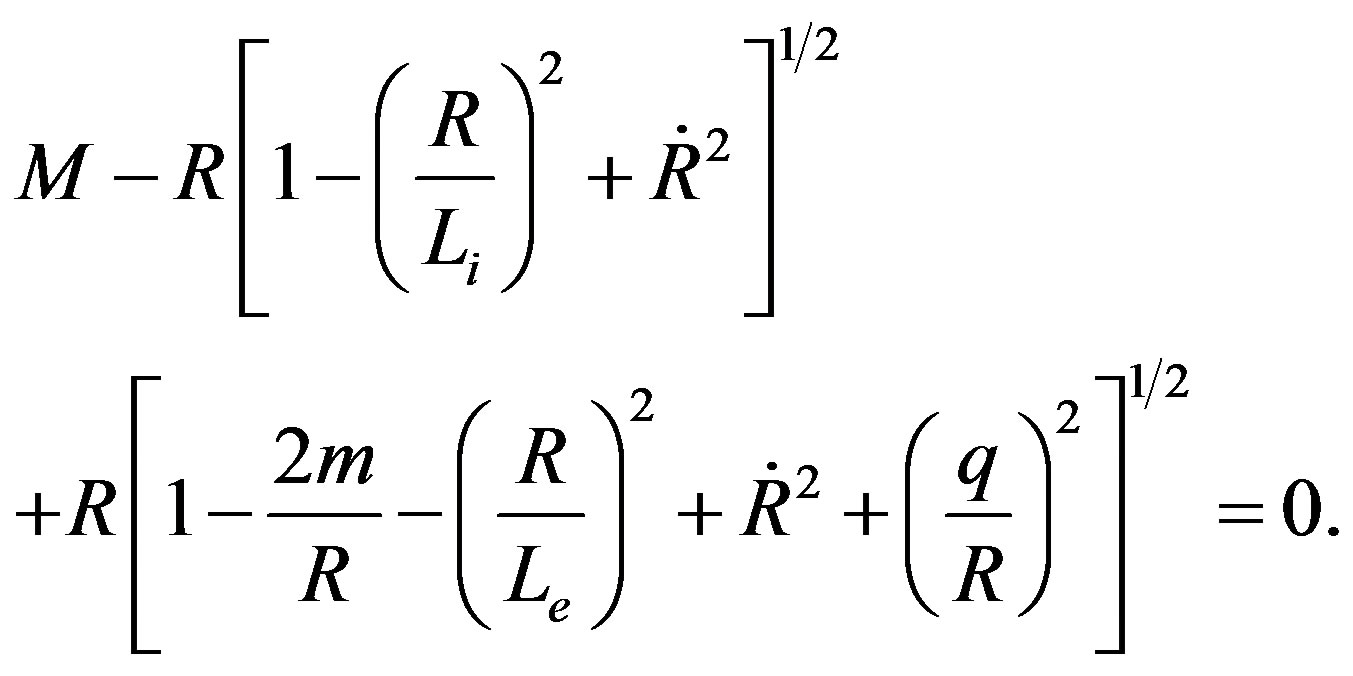 (16)
(16)
Solving the Equation (16) for 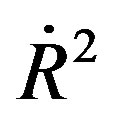 we obtain the potential
we obtain the potential 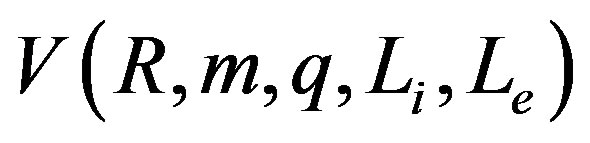 [15]. In order to keep the ideas of our work [15] as much as possible, we consider the thin shell as consisting of a fluid with a equation of state,
[15]. In order to keep the ideas of our work [15] as much as possible, we consider the thin shell as consisting of a fluid with a equation of state, 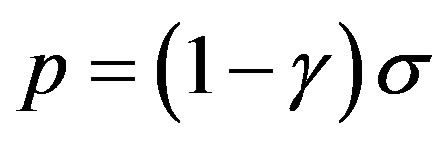 , where
, where  and
and 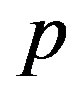 denote, respectively, the surface energy density and pressure of the shell and
denote, respectively, the surface energy density and pressure of the shell and  is a constant. The equation of motion of the shell is given by [21]
is a constant. The equation of motion of the shell is given by [21]
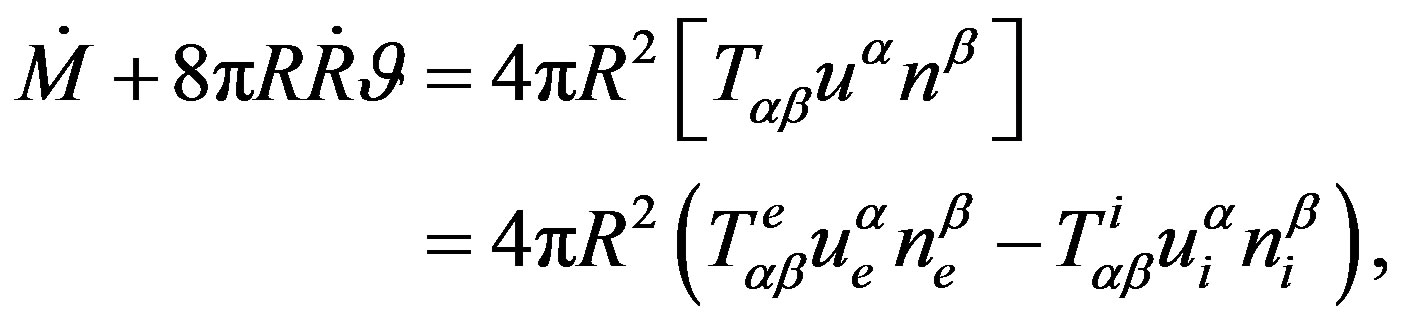 (17)
(17)
where  is the four-velocity. Since the interior region is constituted by a fluid with cosmological constant and the exterior corresponds to a charged spacetime characterized by the Reissner-Nordström with exterior cosmological constant, we get
is the four-velocity. Since the interior region is constituted by a fluid with cosmological constant and the exterior corresponds to a charged spacetime characterized by the Reissner-Nordström with exterior cosmological constant, we get
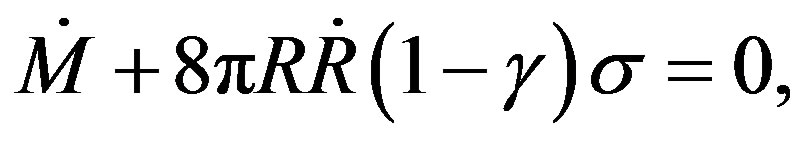 (18)
(18)
since [22]
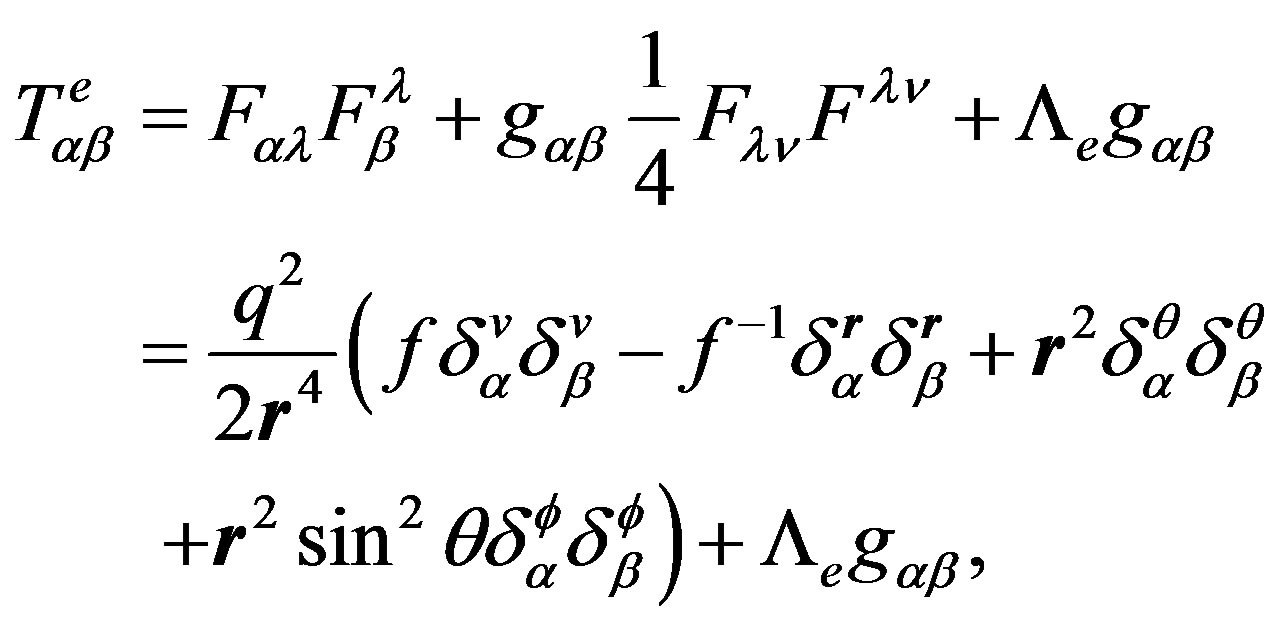 (19)
(19)
where 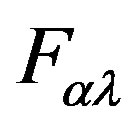 is the Maxwell tensor.
is the Maxwell tensor.
Since  we can solve Equation (18) giving
we can solve Equation (18) giving
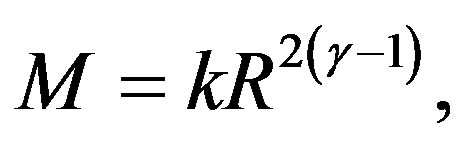 (20)
(20)
where 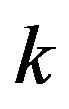 is an integration constant.
is an integration constant.
Substituting Equation (20) into , we obtain the general expression for the potential,
, we obtain the general expression for the potential,
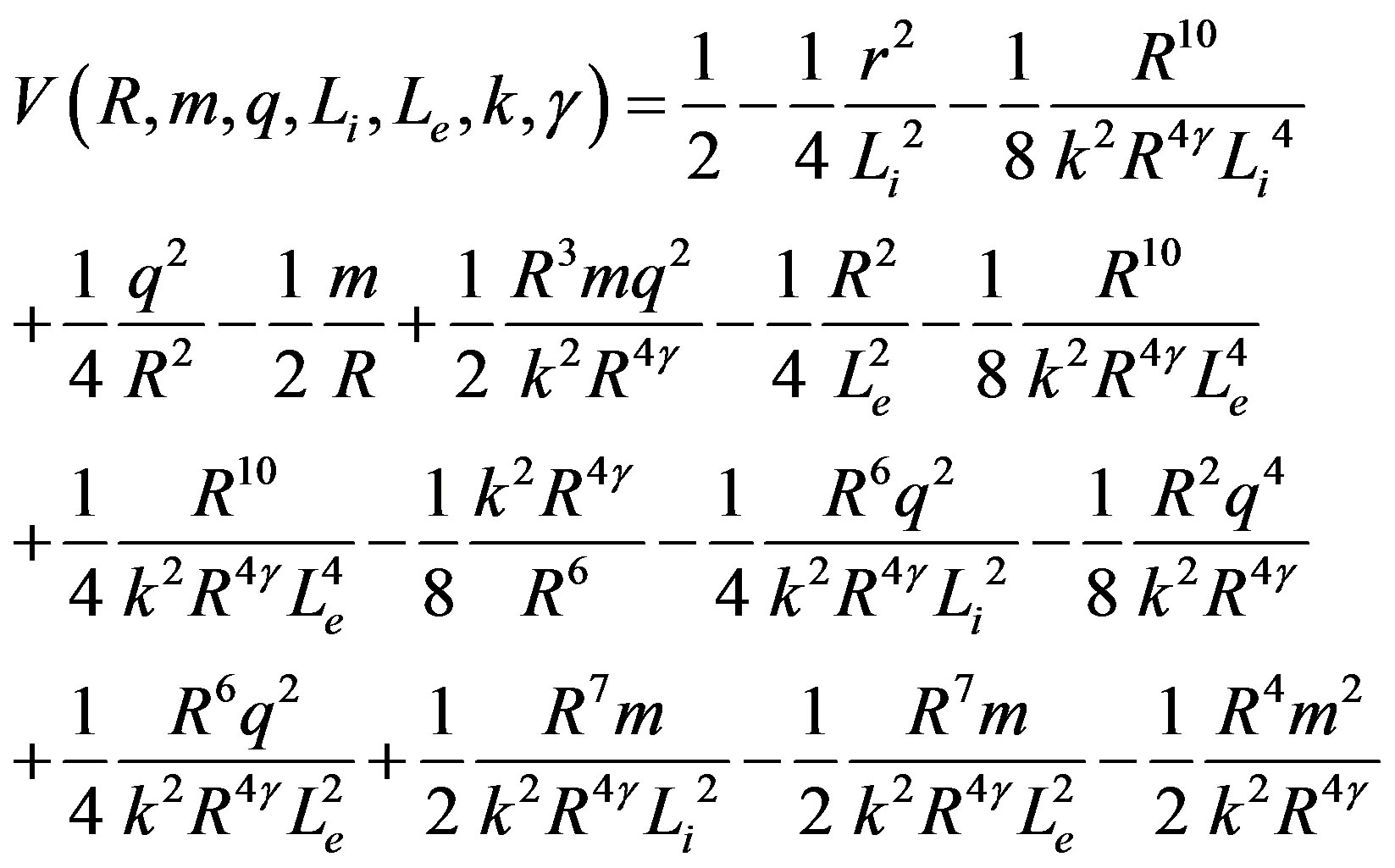 (21)
(21)
Redefining the Schwarzschild mass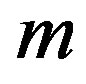 , the charge
, the charge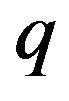 , the cosmological constants
, the cosmological constants 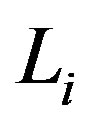 and
and 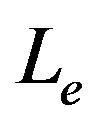 and the radius
and the radius  as
as
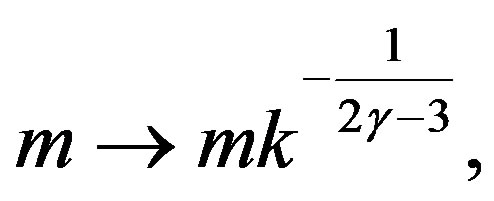 (22)
(22)
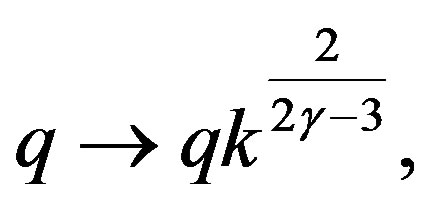 (23)
(23)
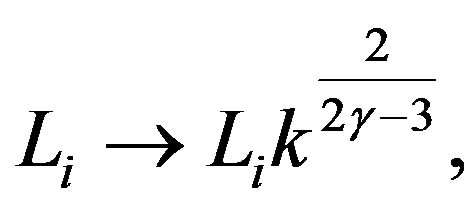 (24)
(24)
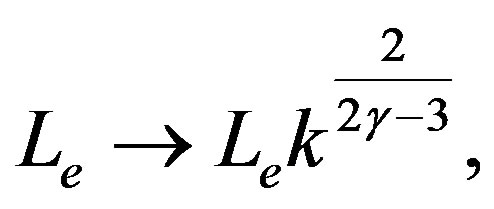 (25)
(25)
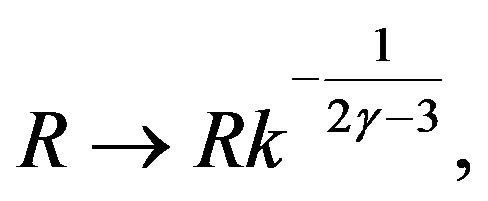 (26)
(26)
we get the potential
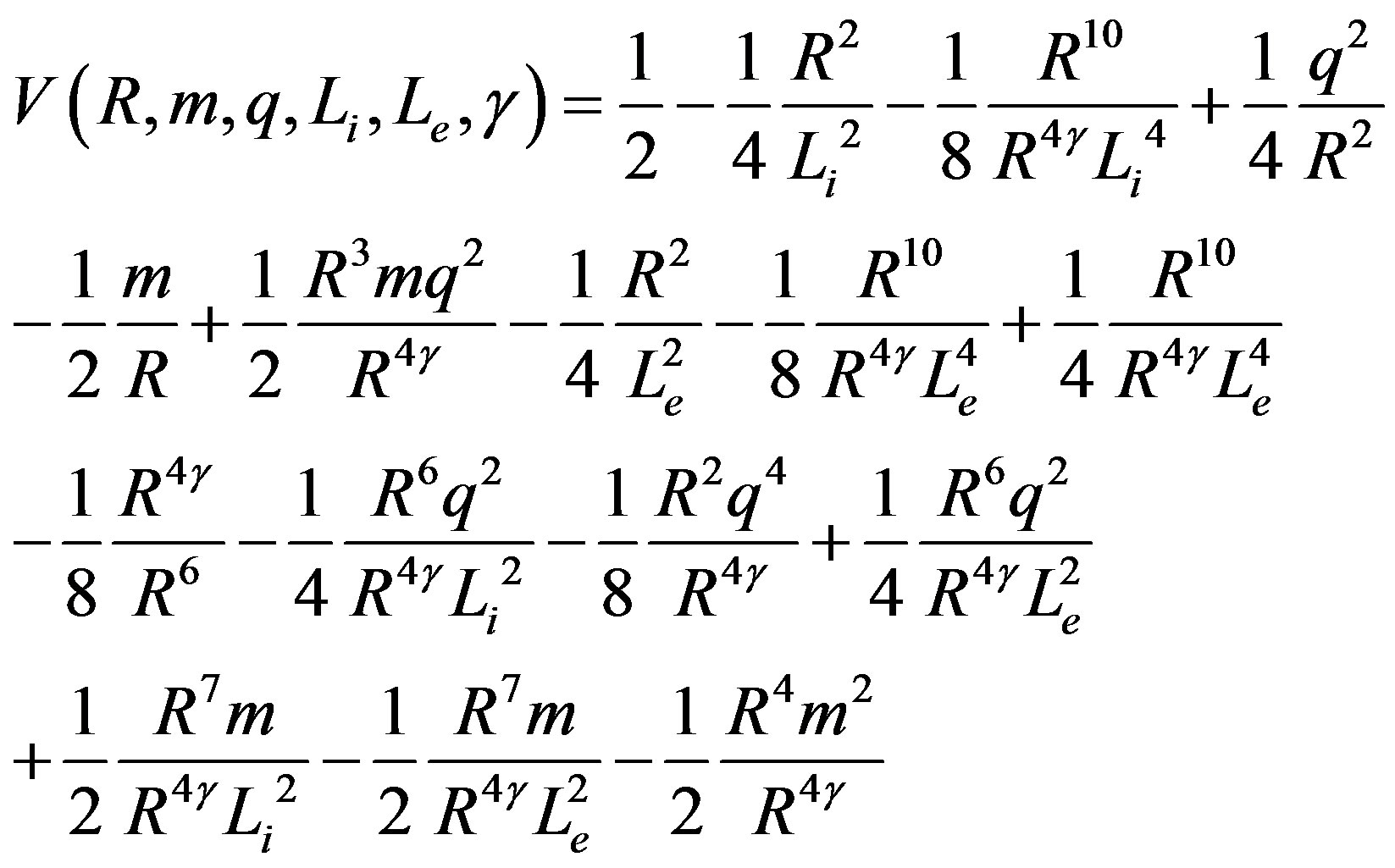 (27)
(27)
Therefore, for any given constants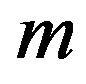 ,
, 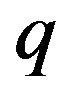 ,
, 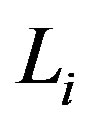 ,
, 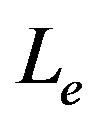 and
and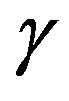 , Equations (21) or (27) uniquely determines the collapse of the shell. Observe that the exponents of the charge, as well as those of
, Equations (21) or (27) uniquely determines the collapse of the shell. Observe that the exponents of the charge, as well as those of  and
and , are always even implying that its sign is irrelevant.
, are always even implying that its sign is irrelevant.
The gravastar model constructed here shows 4 different horizons, which are:
 (28)
(28)
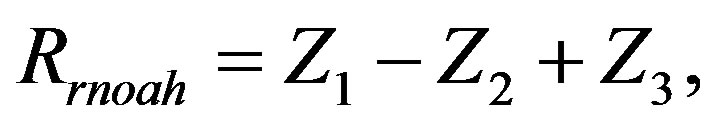 (29)
(29)
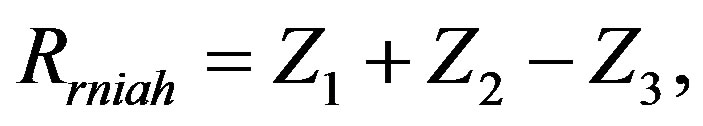 (30)
(30)
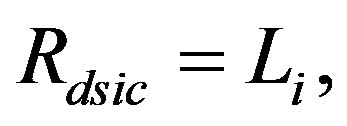 (31)
(31)
where
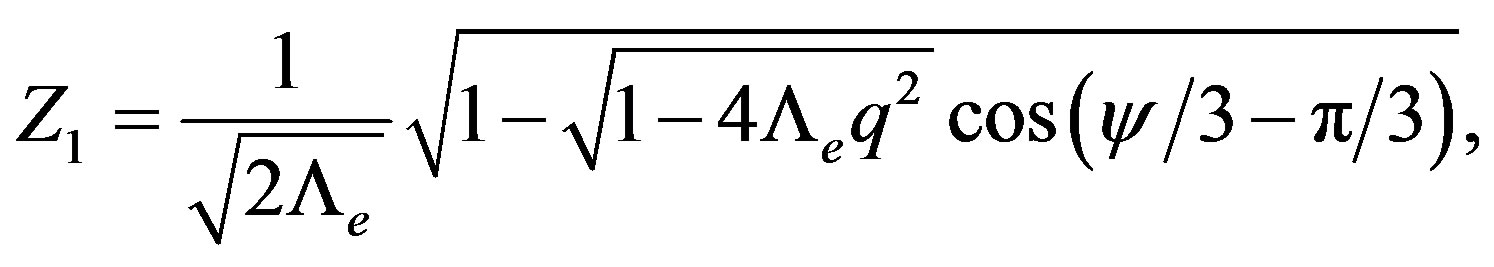 (32)
(32)
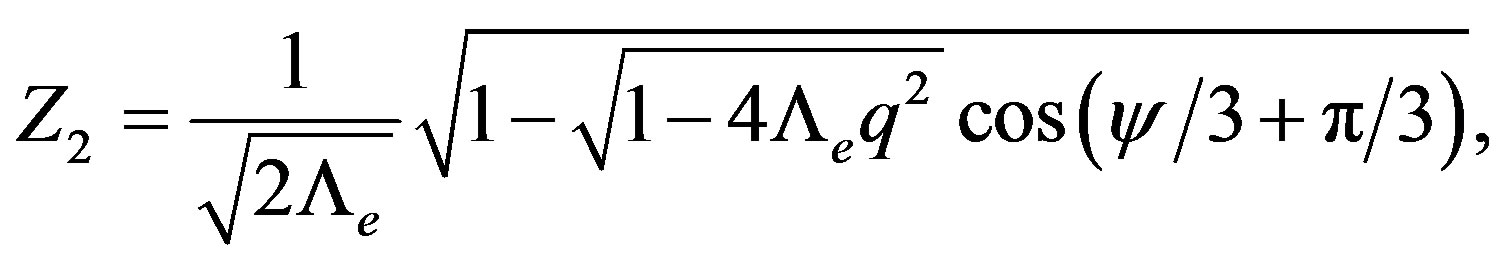 (33)
(33)
 (34)
(34)
and
 (35)
(35)
where
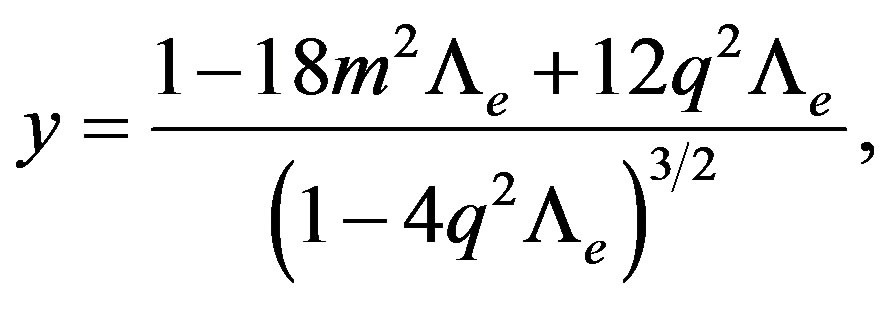 (36)
(36)
where ,
, 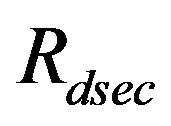 is the exterior cosmological horizon,
is the exterior cosmological horizon,  is the outer apparent horizon,
is the outer apparent horizon, 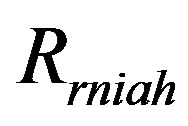 is the inner apparent horizon, all of them for the de-SitterReissner-Nordström exterior spacetime [23] and
is the inner apparent horizon, all of them for the de-SitterReissner-Nordström exterior spacetime [23] and 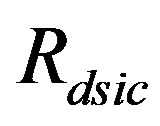 is the cosmological horizon for the interior de Sitter spacetime. Note that if
is the cosmological horizon for the interior de Sitter spacetime. Note that if 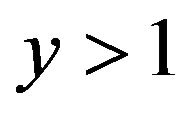 this gives us an imaginary angle
this gives us an imaginary angle . In this case, the horizons
. In this case, the horizons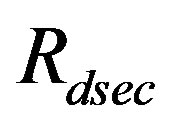 ,
,  and
and  are imaginary. Since any spacetime is defined only for real and non-negative radii, horizons obtained from Equations (28)-(31) can not be negative or imaginary. When this occurs it means that the spacetime is horizonfree.
are imaginary. Since any spacetime is defined only for real and non-negative radii, horizons obtained from Equations (28)-(31) can not be negative or imaginary. When this occurs it means that the spacetime is horizonfree.
To guarantee that initially the spacetime does not have any kind of horizons, cosmological or event, in general, we must restrict 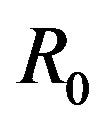 to the ranges simultaneously,
to the ranges simultaneously,
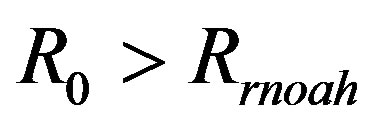 and
and
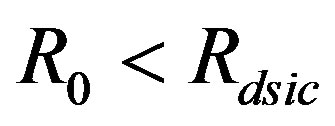 , if
, if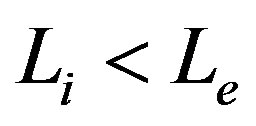 where
where 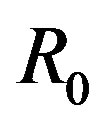 is the initial collapse radius.
is the initial collapse radius.
In the particular case of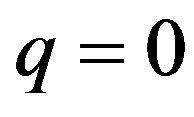 , the exterior horizons are given by [24]
, the exterior horizons are given by [24]
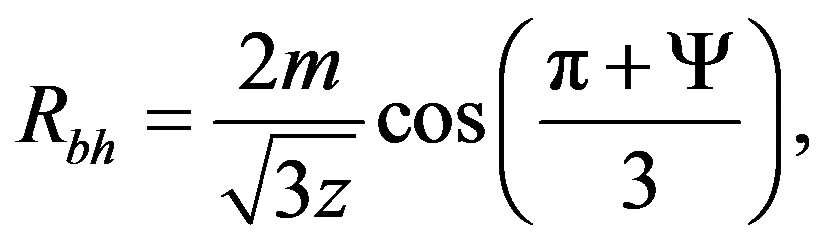 (37)
(37)
 (38)
(38)
where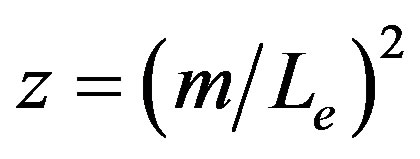 ,
, 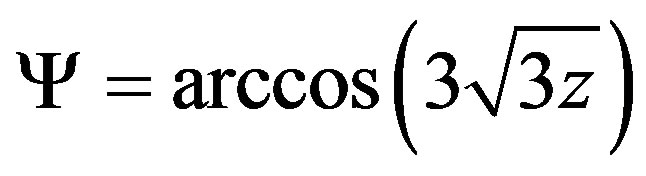 ,
, 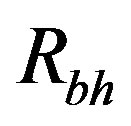 denotes the black hole horizon and
denotes the black hole horizon and  denotes the cosmological horizon. Note that if
denotes the cosmological horizon. Note that if 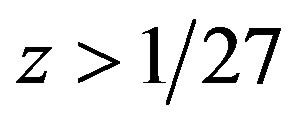 the quantity
the quantity 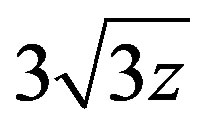 is greater than 1, giving an imaginary angle
is greater than 1, giving an imaginary angle . Thus, the horizons
. Thus, the horizons 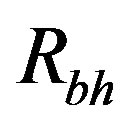 and
and 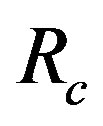 are imaginary and the spacetime becomes free of horizons.
are imaginary and the spacetime becomes free of horizons.
Since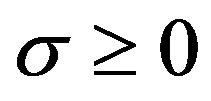 , in order to avoid dark energy fluids, we must to have
, in order to avoid dark energy fluids, we must to have 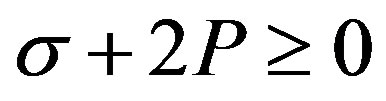 for the shell and assuming that
for the shell and assuming that 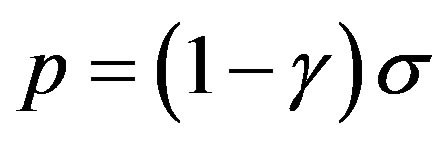 we must have
we must have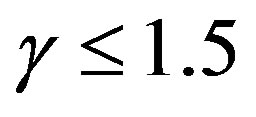 . On the other hand, in order to satisfy the condition
. On the other hand, in order to satisfy the condition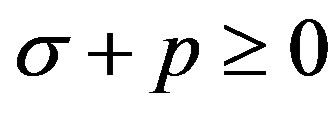 , we get that
, we get that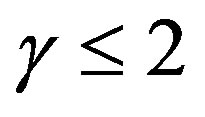 . The dominant energy condition is only satisfied for
. The dominant energy condition is only satisfied for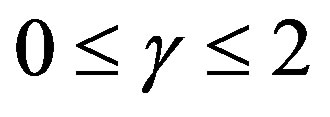 . Although the phantom energy is usually considered as a kind of dark energy, in this paper we will use the expression dark energy for the case where the condition
. Although the phantom energy is usually considered as a kind of dark energy, in this paper we will use the expression dark energy for the case where the condition 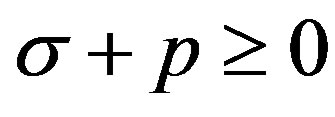 is satisfied and phantom energy otherwise. Hereinafter, we will use only some particular values of the parameter
is satisfied and phantom energy otherwise. Hereinafter, we will use only some particular values of the parameter 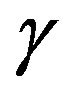 which are analyzed in this work. See Table 1.
which are analyzed in this work. See Table 1.
3. General Case
In the following have done a graphical analysis of several special cases. The influence of the cosmological constant was deeply discussed in a previous work [17], where 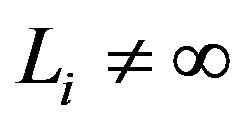 and
and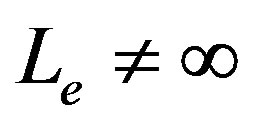 , but
, but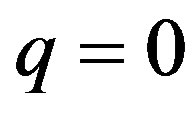 , we showed that there is a limit on
, we showed that there is a limit on 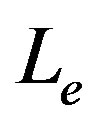 in order to form a gravastar, i.e., the formation of gravastars depends on the value of
in order to form a gravastar, i.e., the formation of gravastars depends on the value of  (
(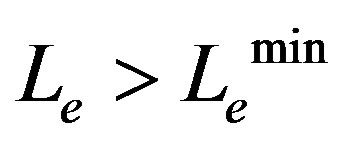 , with
, with ) in a such way that, instead of what occurs for
) in a such way that, instead of what occurs for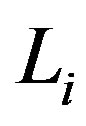 , as smaller is
, as smaller is 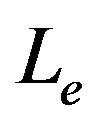 as bigger is the tendency to the collapse. Now, our main aim is to study the role of the charge in the dynamic of the gravastar. Our strategy is to start with values of
as bigger is the tendency to the collapse. Now, our main aim is to study the role of the charge in the dynamic of the gravastar. Our strategy is to start with values of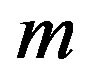 ,
, 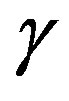 ,
, 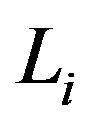 and
and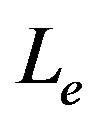 , for which we had a bounded excursion or a stable gravastar for chargeless configurations and, then, gradually introduce and increase the value of the charge. Thus, we can investigate if there is a range for the charge favoring the formation any kind of structure.
, for which we had a bounded excursion or a stable gravastar for chargeless configurations and, then, gradually introduce and increase the value of the charge. Thus, we can investigate if there is a range for the charge favoring the formation any kind of structure.
In order to analyze the effect of the charge we have started from the cases with q = 0, considered in the previous work [17], and we have used the critical mass, when a stable gravastar was formed, changing the value of the charge. Recalling that the critical mass is defined as the mass for which 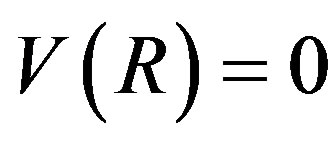 and
and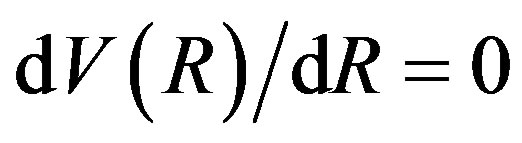 , for a fixed value of the charge. The results are shown in the Tables 2-6, and the respective potential are in the Figure 1 and Figures 2-5. In particular, in the Figure 1, we have lost the stable configuration when we increase the value of the charge. In order to check if it is possible to have a charged stable gravastar we plotted the Figure 6. In this figure we have fixed the value of the mass and we searched for the critical charge. The critical charge is defined as the charge for which
, for a fixed value of the charge. The results are shown in the Tables 2-6, and the respective potential are in the Figure 1 and Figures 2-5. In particular, in the Figure 1, we have lost the stable configuration when we increase the value of the charge. In order to check if it is possible to have a charged stable gravastar we plotted the Figure 6. In this figure we have fixed the value of the mass and we searched for the critical charge. The critical charge is defined as the charge for which  and
and , for a fixed value of the mass. It is remarkable the crucial role of the charge. Note that there is an approximated interval
, for a fixed value of the mass. It is remarkable the crucial role of the charge. Note that there is an approximated interval  in which we can always find bounded excursion or stable gravastar, where the value
in which we can always find bounded excursion or stable gravastar, where the value  corresponds to the stable gravastar. For the values outside of this interval, we always have the collapse of the shell. In the Figure 7 we show that a similar interval for the mass can be also found for a fixed value of charge
corresponds to the stable gravastar. For the values outside of this interval, we always have the collapse of the shell. In the Figure 7 we show that a similar interval for the mass can be also found for a fixed value of charge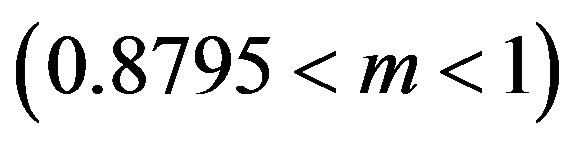 . Thus we can have stable or bounded excursion gravastar depending on the combination of charge and mass.
. Thus we can have stable or bounded excursion gravastar depending on the combination of charge and mass.

Table 1. This table summarizes the matter classification based on the energy conditions of the shell, in terms of the parameter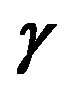 .
.
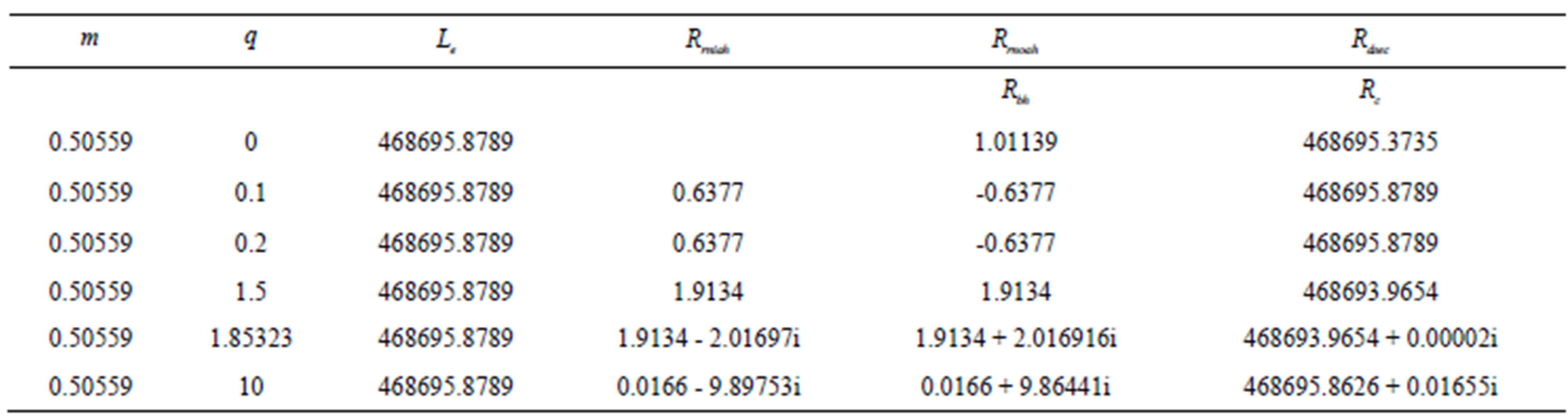
Table 2. This table shows the calculated horizons using the Equations (28)-(30). When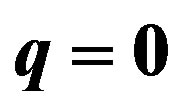 , we have used the Equations (37) and (38). Hereinafter, the symbol
, we have used the Equations (37) and (38). Hereinafter, the symbol 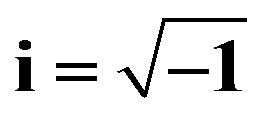 denotes the imaginary unit.
denotes the imaginary unit.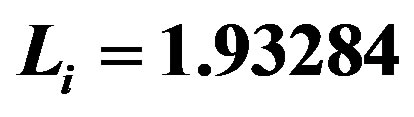 ,
,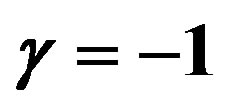 . See Figure 1.
. See Figure 1.

Table 3. This table shows the calculated horizons using the Equations (28)-(30). When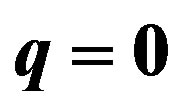 , we have used the Equations (37) and (38).
, we have used the Equations (37) and (38).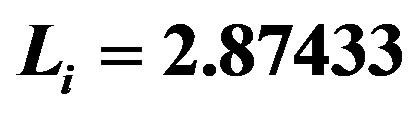 ,
,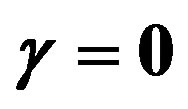 . See Figure 2.
. See Figure 2.

Table 4. This table shows the calculated horizons using the Equations (28-(30). When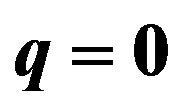 , we have used the Equations (37) and (38).
, we have used the Equations (37) and (38).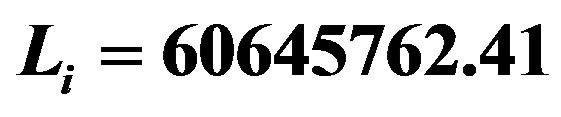 ,
, . See Figure 3.
. See Figure 3.
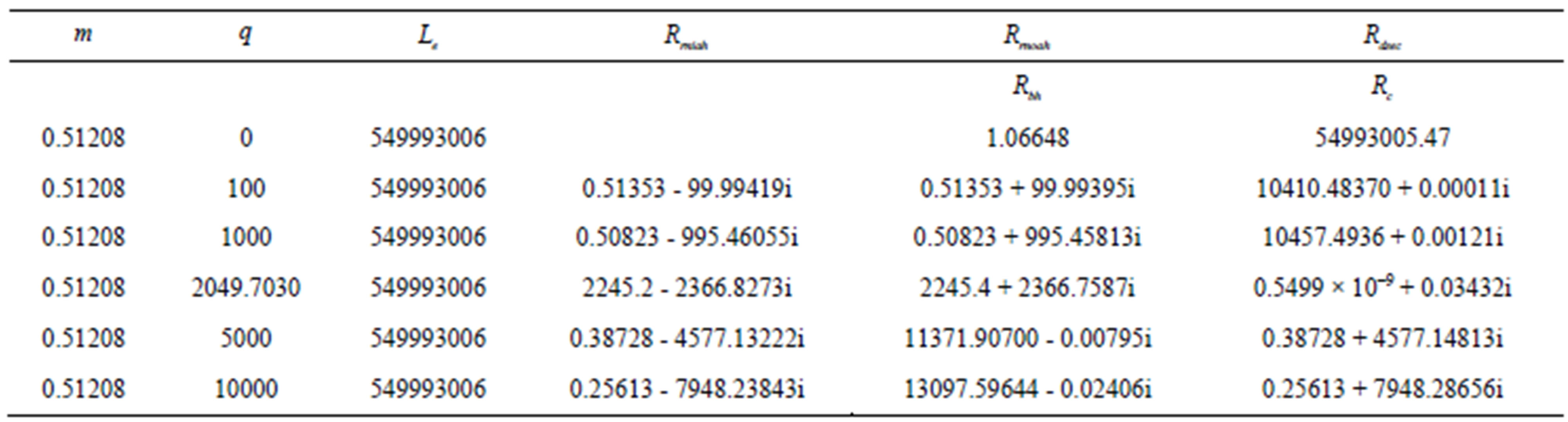
Table 5. This table shows the calculated horizons using the Equations (28)-(30). When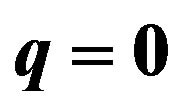 , we have used the Equations (37) and (38).
, we have used the Equations (37) and (38).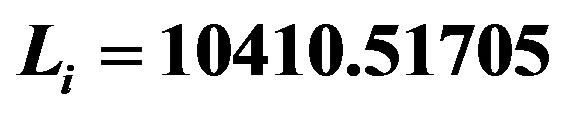 ,
,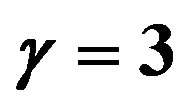 . See Figure 4.
. See Figure 4.
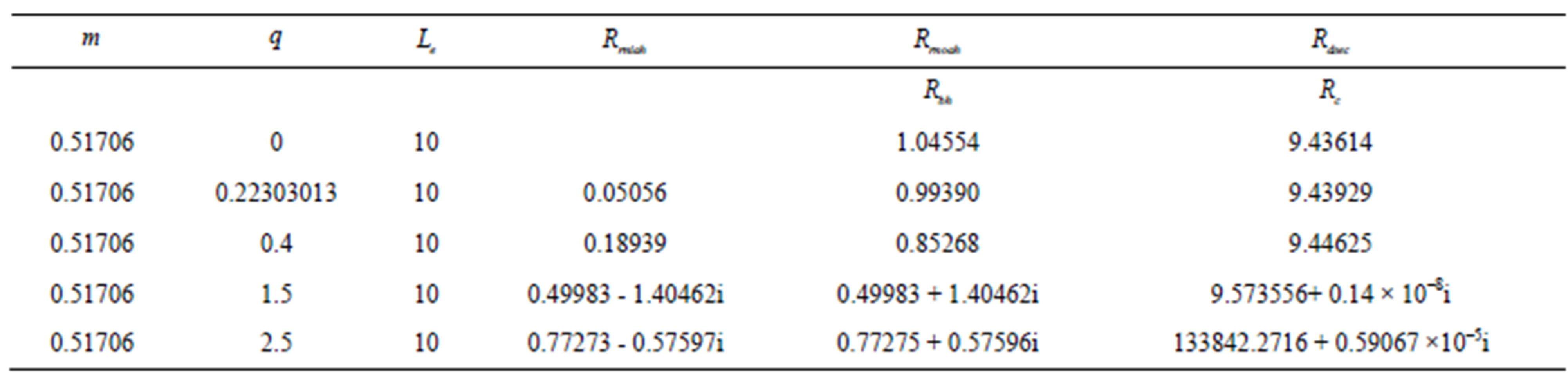
Table 6. This table shows the calculated horizons using the Equations (28)-(30). When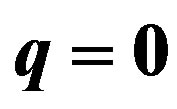 , we have used the Equations (37) and (38).
, we have used the Equations (37) and (38). ,
, . See Figure 5.
. See Figure 5.
We call attention that in all the cases studied here, the formation of the apparent horizon can be avoided increasing the value of the charge, indicating that the shell can collapse to form naked singularity.
4. Conclusions
We constructed a gravastar model consisting by an interior de Sitter spacetime and an exterior spacetime with an external cosmological constant, described by a de Sitter-Reissner-Nordström metric. The charge is localized on the shell. Restricting the range of the initial radius, we obtain as the final structure bounded excursions, stable gravastars and also naked singularities.
We investigated the influence of the charge and we observed that increasing its value, and fixing a value for the mass, we can obtain a stable gravastar from a bounded excursion gravastar. For even higher values of

Figure 1. The potential 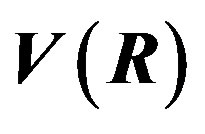 for
for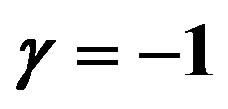 ,
, 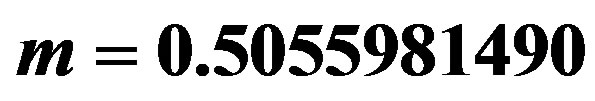 ,
, 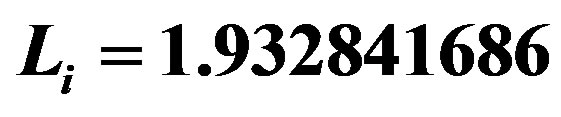 and
and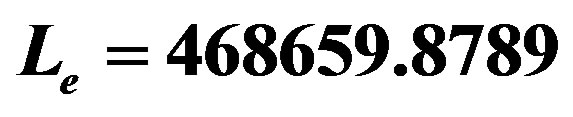 . The horizons are given in Table 1. The growth of the charge eliminates the stable structure. In addition, note that for
. The horizons are given in Table 1. The growth of the charge eliminates the stable structure. In addition, note that for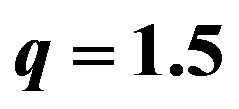 , the shell collapses to a black hole, while for
, the shell collapses to a black hole, while for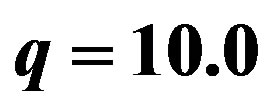 , we have the collapse of the shell in a naked singularity.
, we have the collapse of the shell in a naked singularity.
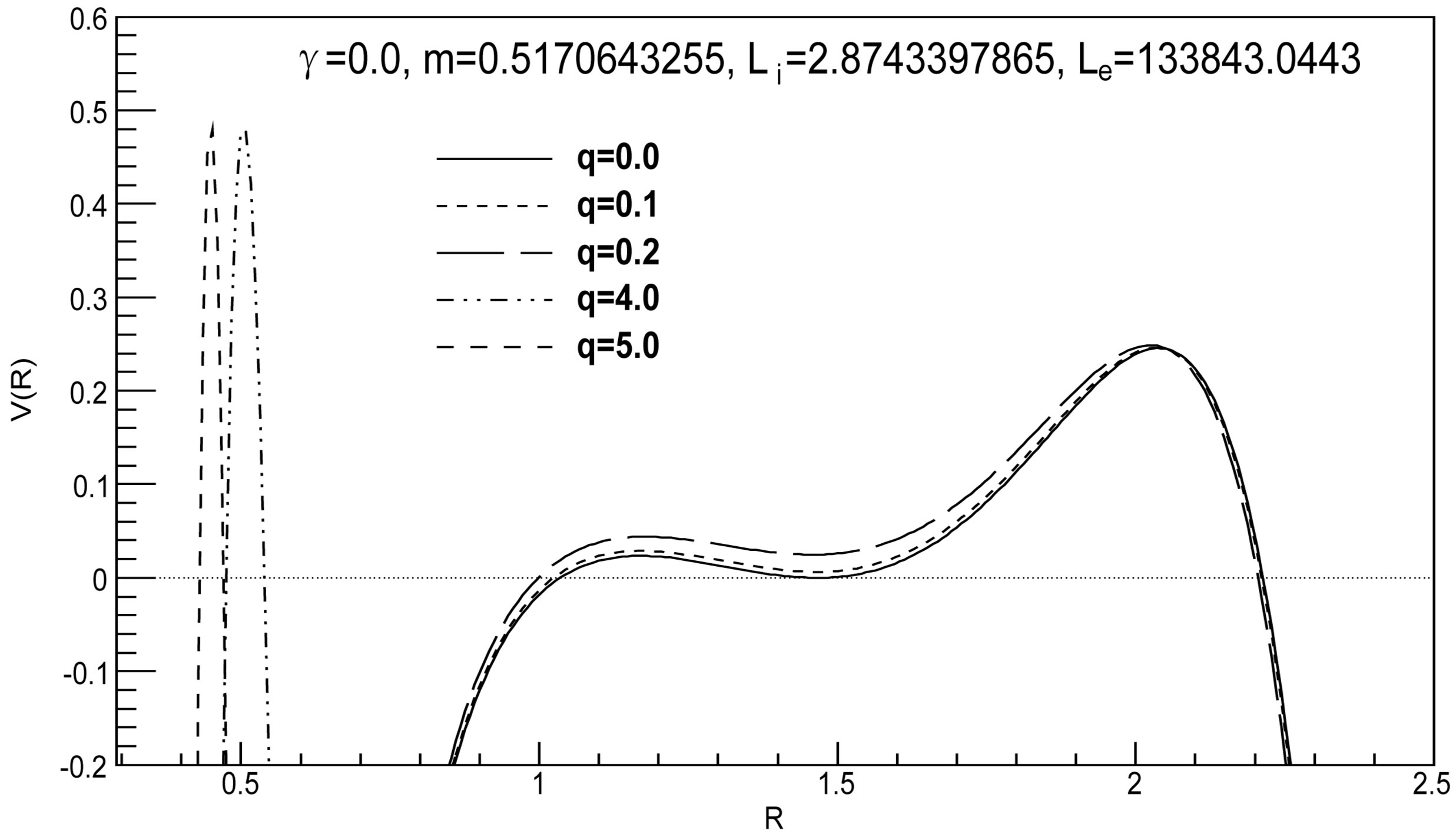
Figure 2. The potential  for
for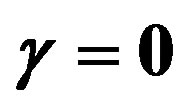 ,
,  ,
,  and
and . The horizons are given in Table 2. For
. The horizons are given in Table 2. For 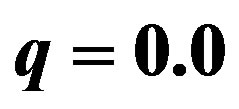 a stable gravastar is formed if
a stable gravastar is formed if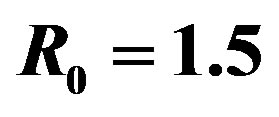 , but for bigger charges, the shell collapses to a naked singularity.
, but for bigger charges, the shell collapses to a naked singularity.
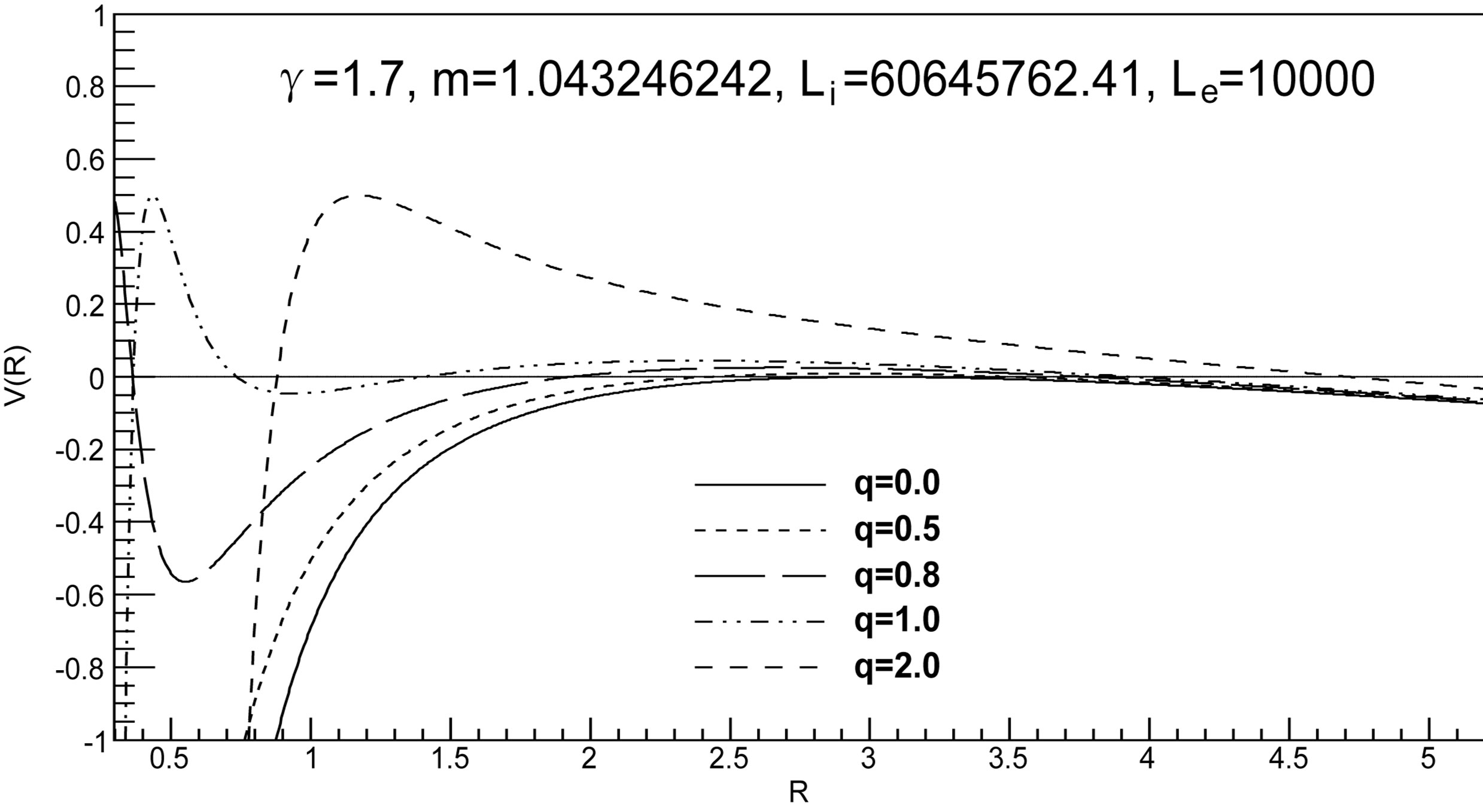
Figure 3. The potential 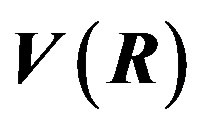 for
for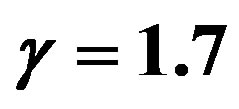 ,
,  ,
, 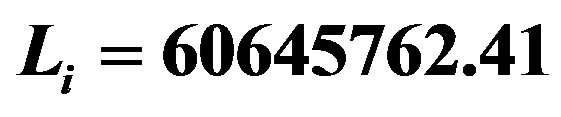 and
and . The horizons are given in Table 3. Note that we have a bounded excursion gravastar for
. The horizons are given in Table 3. Note that we have a bounded excursion gravastar for  and
and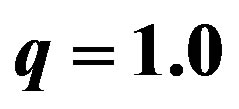 , and a naked singularity for
, and a naked singularity for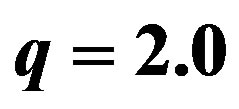 .
.
Figure 4. The potential  for
for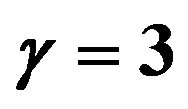 ,
, 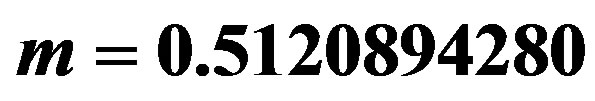 ,
, 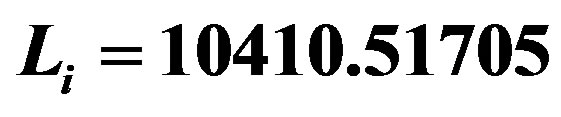 and
and . The horizons are given in Table 4. In this example, the shell is constituted by phantom energy and none stable structure is formed.
. The horizons are given in Table 4. In this example, the shell is constituted by phantom energy and none stable structure is formed.
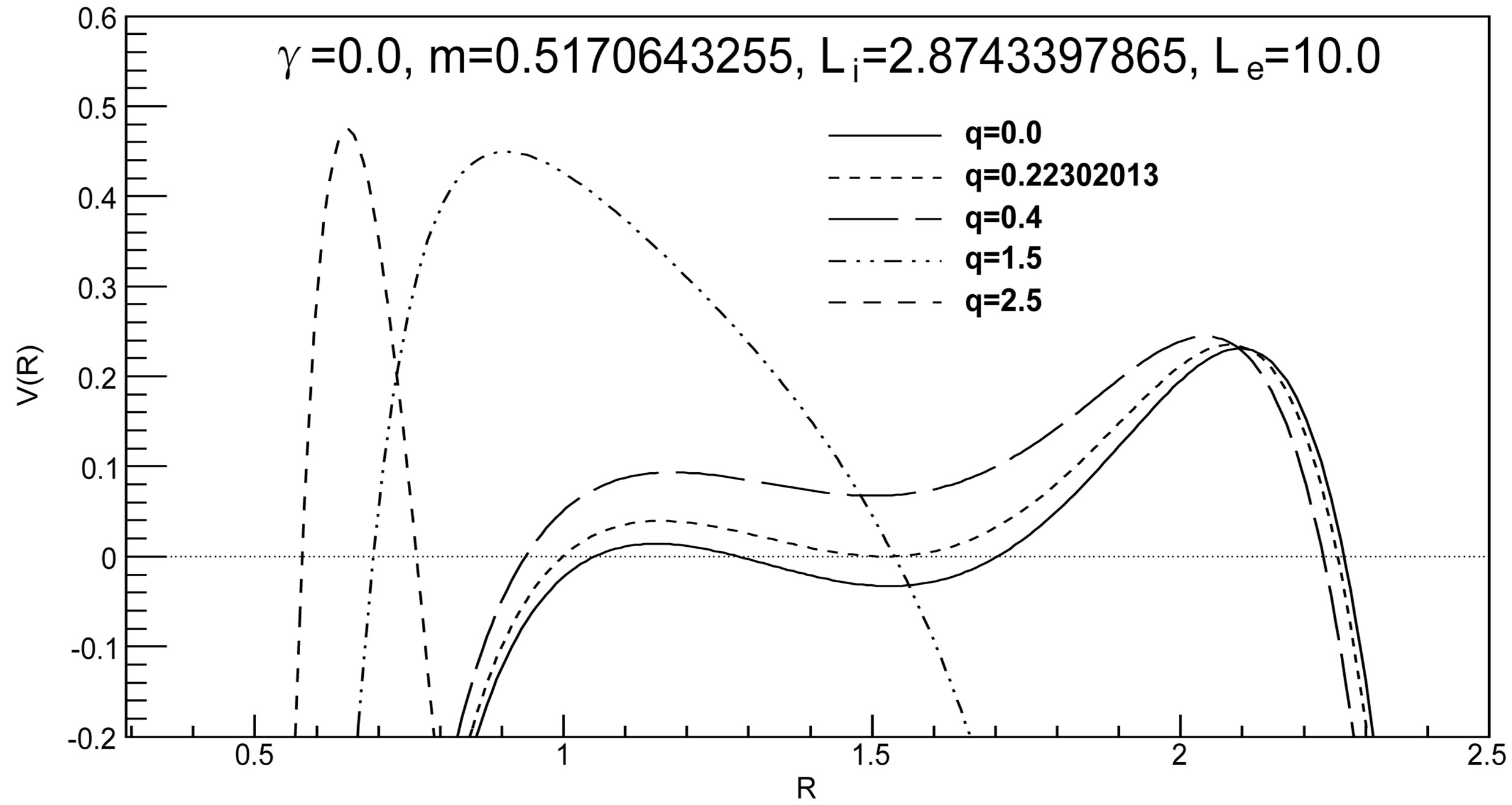
Figure 5. The potential  for
for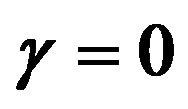 ,
, 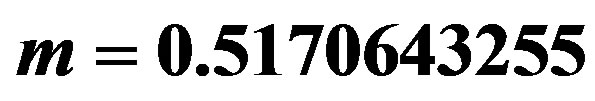 ,
,  and
and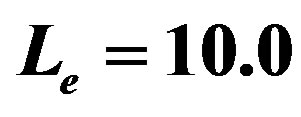 . The horizons are given in Table 5. Note that we have a gravastar enclosing a naked singularity.
. The horizons are given in Table 5. Note that we have a gravastar enclosing a naked singularity.
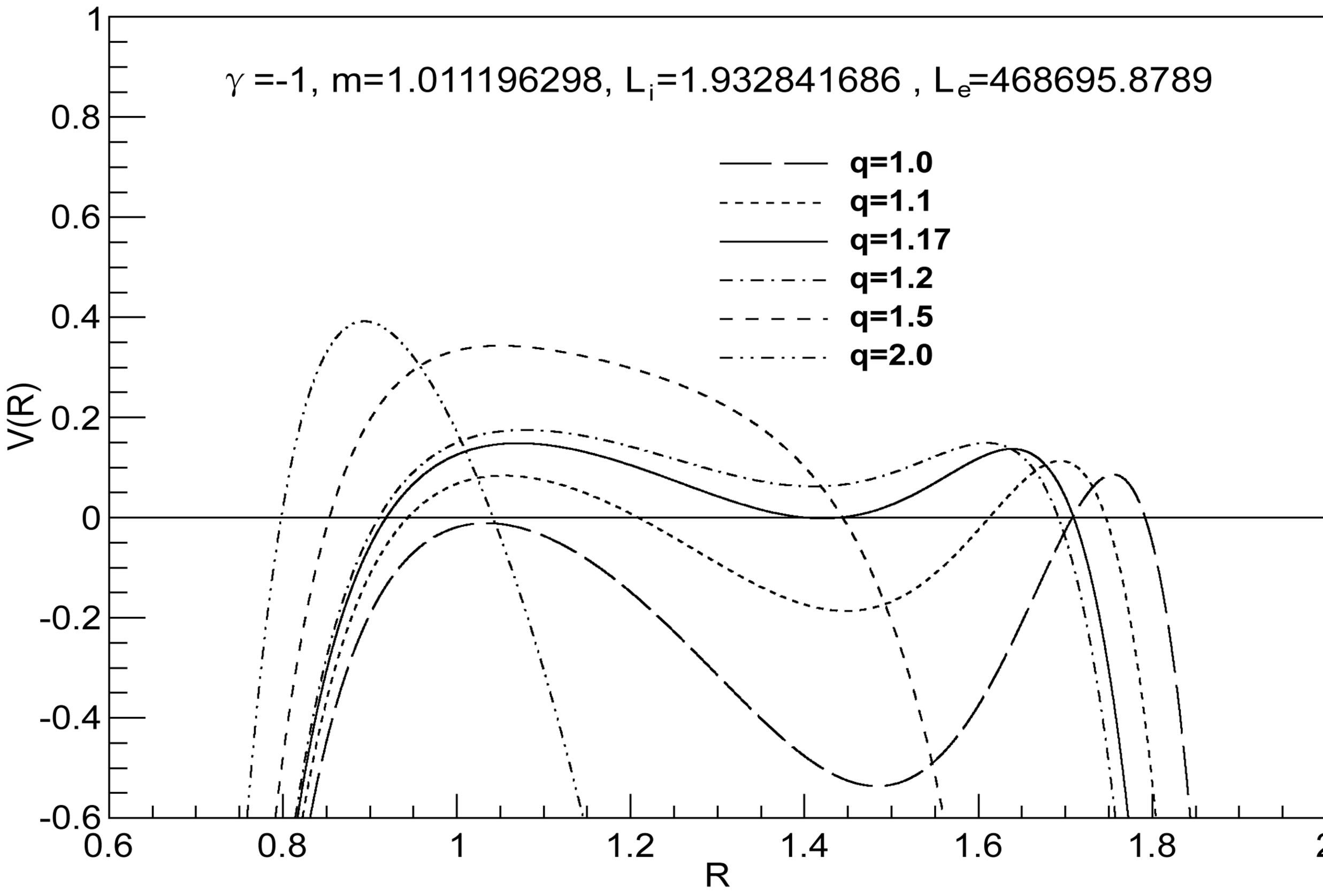
Figure 6. The potential 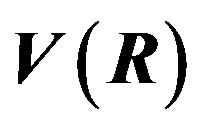 for
for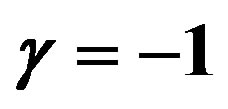 ,
, 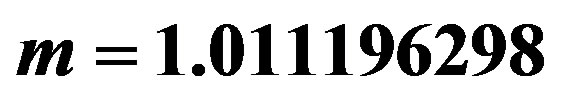 ,
, 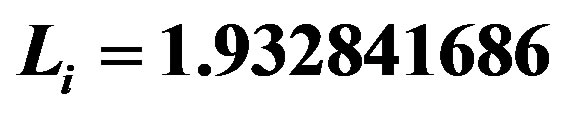 and
and . This figure shows the influence of the charge for the stability of the shell. As showed in the figure 1, the increase of the charge implies in the loss of the stability.
. This figure shows the influence of the charge for the stability of the shell. As showed in the figure 1, the increase of the charge implies in the loss of the stability.
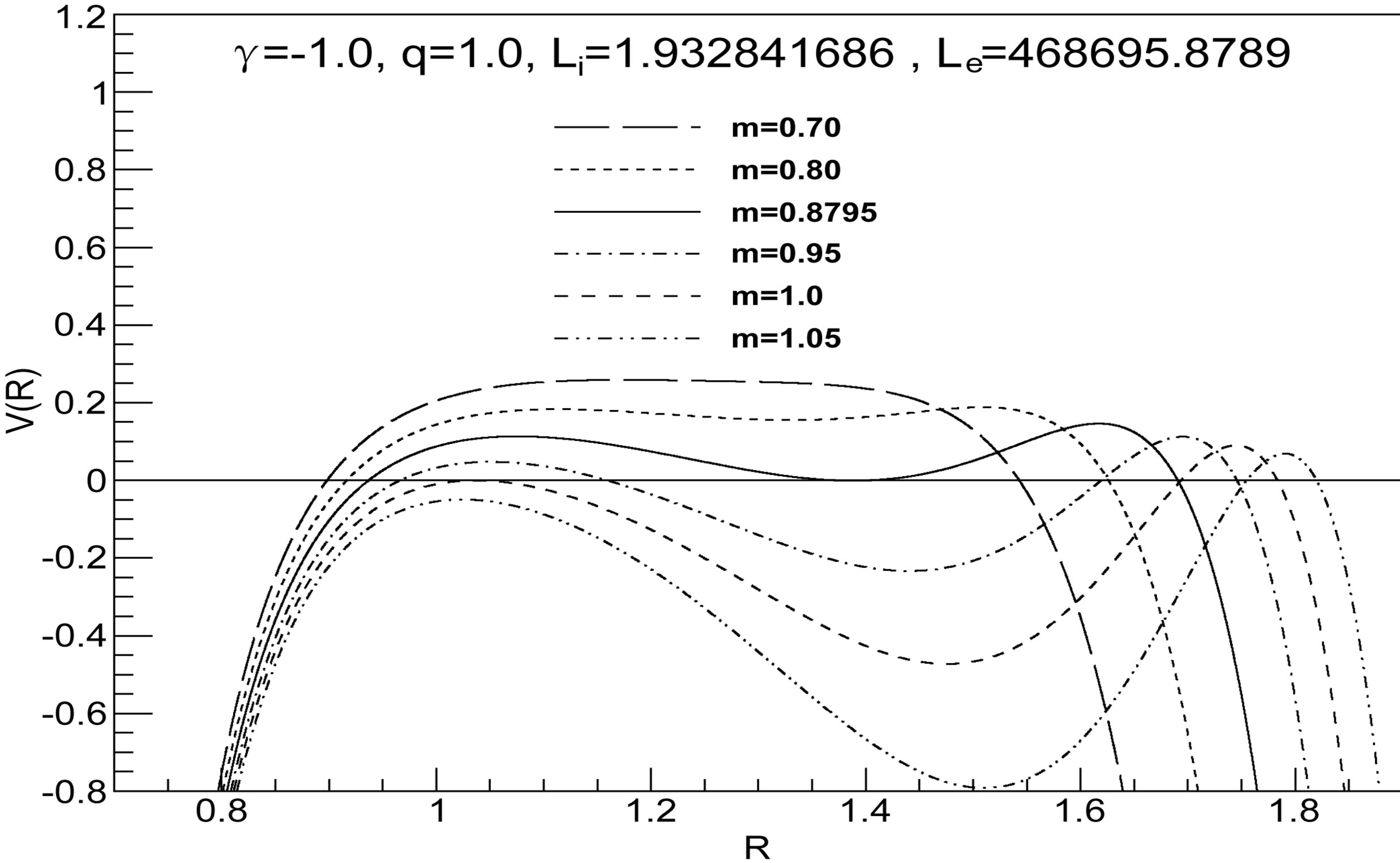
Figure 7. The potential  for
for ,
,  ,
,  and
and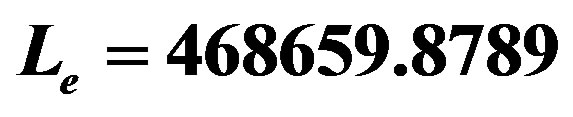 . This figure shows as the mass, for a given charge, contributes for the stability of the shell.
. This figure shows as the mass, for a given charge, contributes for the stability of the shell.
the charge the apparent horizon can be avoided, which leads the formation of a naked singularity.
In the case of a shell formed by standard energy, with 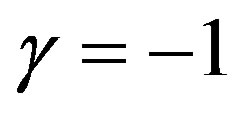 in its state equation (Figures 1, 6 and 7), for some fixed values of charge, above a lower limit
in its state equation (Figures 1, 6 and 7), for some fixed values of charge, above a lower limit 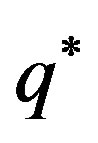 dependent on the mass and on cosmological constants, and small initial values of radius, the shell can collapse and form a naked singularity. There is also a possibly formation of black holes for some values of the charge, below
dependent on the mass and on cosmological constants, and small initial values of radius, the shell can collapse and form a naked singularity. There is also a possibly formation of black holes for some values of the charge, below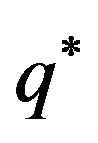 , for fixed values of the mass. Increasing the value of the charge, we verify that initially bounded excursion configurations become more stable and there is another limit for the charge,
, for fixed values of the mass. Increasing the value of the charge, we verify that initially bounded excursion configurations become more stable and there is another limit for the charge,  , for which the structure becomes a stable gravastar. For charges upper than
, for which the structure becomes a stable gravastar. For charges upper than  the shell collapses. Moreover, fixing the mass and varying the charge, we have a similar behavior, that is, a bounded excursion becomes more stable increasing the charge until reaches a stable gravastar and for other values of the charge, we have black holes and naked singularities. In the case of
the shell collapses. Moreover, fixing the mass and varying the charge, we have a similar behavior, that is, a bounded excursion becomes more stable increasing the charge until reaches a stable gravastar and for other values of the charge, we have black holes and naked singularities. In the case of 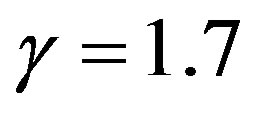 (Figure 3), the shell is constituted by dark energy and for small values of the initial radius there is also a naked singularity formation. The same is found for a phantom dark energy shell with
(Figure 3), the shell is constituted by dark energy and for small values of the initial radius there is also a naked singularity formation. The same is found for a phantom dark energy shell with 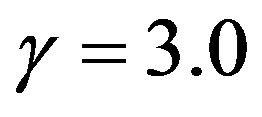 (Figure 4). Finally, for a stiff fluid shell with
(Figure 4). Finally, for a stiff fluid shell with 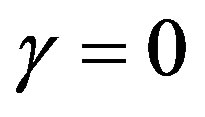 (Figures 2 and 5), we have bounded excursion formation, stable gravastar, black hole and naked singularity formation according to the values of the charge and for some values of initial radius. It is remarkable that the naked singularity formation appeared in this gravastar model is completely new. Then, beginning with a shell linking two spacetimes (de Sitter and de Sitter-ReissnerNordström) in order to eliminate the horizons, as proposed by the gravastar’s model, except for the cosmological horizon of the exterior spacetime, the shell can stay stable, forming a gravastar, or collapsing in a black hole or even a naked singularity, representing a new counterexample to the Cosmic Censorship. Then, this model definitively is not an alternative to the black hole, even naked singularities.
(Figures 2 and 5), we have bounded excursion formation, stable gravastar, black hole and naked singularity formation according to the values of the charge and for some values of initial radius. It is remarkable that the naked singularity formation appeared in this gravastar model is completely new. Then, beginning with a shell linking two spacetimes (de Sitter and de Sitter-ReissnerNordström) in order to eliminate the horizons, as proposed by the gravastar’s model, except for the cosmological horizon of the exterior spacetime, the shell can stay stable, forming a gravastar, or collapsing in a black hole or even a naked singularity, representing a new counterexample to the Cosmic Censorship. Then, this model definitively is not an alternative to the black hole, even naked singularities.
5. Acknowledgements
The financial assistance from FAPERJ/UERJ (CFCB and MFAdaS) is gratefully acknowledged. The authors (RC, MFAdaS) acknowledge the financial support from FAPERJ (no. E-26/171.754/2000, E-26/171.533/2002, E-26/ 170.951/2006, E-26/110.432/2009 and E-26/111.714/ 2010). The authors (RC and MFAdaS) also acknowledge the financial support from Conselho Nacional de Desenvolvimento Científico e Tecnológico-CNPq-Brazil (no. 450572/2009-9, 301973/2009-1 and 477268/ 2010-2). The author (MFAdaS) also acknowledges the financial support from Financiadora de Estudos e Projetos-FINEPBrazil (Ref. 2399/03).
REFERENCES
- R. M. Wald, Living Reviews in Relativity, Vol. 4, 2001, p. 6. [arXiv:gr-qc/9912119]
- M. A. Abramowicz, W. Kluzniak and J.-P. Lasota, Astronomy & Astrophysics, Vol. 396, 2002, pp. L31-34. doi:10.1051/0004-6361:20021645
- G. Chapline, “Dark Energy Stars and AdS/CFT,” Talk at the 12th Marcel Grossman Meeting, 2009. [arXiv:gr-qc/0907.4397]
- G. Chapline, E. Hohlfeld, R. B. Laughlin and D. I. Santiago, International Journal of Modern Physics A, Vol. 18, 2003, p. 3587. [arXiv:gr-qc/0012094]. doi:10.1142/S0217751X03016380
- T. Vachaspati, “Black Stars and Gamma Ray Bursts,” arXiv:0706.1203
- M. Petri, “Charged Holostars,” 2003. gr-qc/0306068
- M. Petri, “Compact Anisotropic Stars with Membrane: A New Class of Exact Solutions to the Einstein Field Equations,” 2003. gr-qc/0306063.
- M. Petri, “The Holographic Solution: Why General Relativity must Be Understood in Terms of Strings,” 2004. gr-qc/0405007
- M. Petri, “Holostar thermodynamics,” 2003. gr-qc/0306067
- M. Petri, “Are We Living in a String Dominated Universe?” 2004. gr-qc/0405011.
- M. Petri, “On the Origin of the Matter-Antimatter Asymmetry in Self-Gravitating Systems at Ultra-High Temperatures,” 2004. gr-qc/0405010.
- P. O. Mazur and E. Mottola, “Gravitational Condensate Stars: An Alternative to Black Holes,” Proceedings of the National Academy of Sciences, Vol. 101, 2004, p. 9545. [arXiv:gr-qc/0407075]
- M. Visser and D. L. Wiltshire, Classical and Quantum Gravity, Vol. 21, 2004, p. 1135. [arXiv:gr-qc/0310107] doi:10.1088/0264-9381/21/4/027
- P. Rocha, A. Y. Miguelote, R. Chan, M. F. da Silva, N. O. Santos and A. Wang, Journal of Cosmology and Astroparticle Physics, Vol. 6, 2008, p. 25. [arXiv:gr-qc/08034200] doi:10.1088/1475-7516/2008/06/025
- P. Rocha, R. Chan, M. F. da Silva and A. Wang, Journal of Cosmology and Astroparticle Physics, Vol. 11, 2008, p. 10. [arXiv:gr-qc/08094879] doi:10.1088/1475-7516/2008/11/010
- R. Chan, M. F. da Silva, P. Rocha and A. Wang, Journal of Cosmology and Astroparticle Physics, Vol. 3, 2009, p. 10. [arXiv:gr-qc/08124924] doi:10.1088/1475-7516/2009/03/010
- R. Chan, M. F. A. da Silva and P. Rocha, Journal of Cosmology and Astroparticle Physics, Vol. 12, 2009, p. 17. [arXiv:gr-qc/09102054] doi:10.1088/1475-7516/2009/12/017
- R. Chan and M. F. A. da Silva, Journal of Cosmology and Astroparticle Physics, Vol. 7, 2010, p. 29. [arXiv:gr-qc/10053703] doi:10.1088/1475-7516/2010/07/029
- R. Chan, M. F. A. da Silva and P. Rocha, General Relativity and Gravitation, Vol. 43, 2011, p. 8. [arXiv:gr-qc/10094403] doi:10.1007/s10714-011-1178-6
- B. M. N. Carter, Class. Classical and Quantum Gravity, Vol. 22, 2005, p. 4551. doi:10.1088/0264-9381/22/21/007
- K. Lake, Physical Review D, Vol. 19, 1979, pp. 2847- 2849. doi:10.1103/PhysRevD.19.2847
- R. Adler, M. Bazin and M. Schiffer, “Introduction to General Relativity,” McGraw-Hill Inc., 1975, p. 489.
- B. D. Koberlein and R. L. Mallet, Physical Review D, Vol. 49, 1994, pp. 5111-5114. doi:10.1103/PhysRevD.49.5111
- S. Shankaranarayanan, Physical Review D, Vol. 67, 2003, Article ID: 084026. doi:10.1103/PhysRevD.67.084026

