Journal of Modern Physics
Vol.3 No.9A(2012), Article ID:23117,4 pages DOI:10.4236/jmp.2012.329165
Investigating Initial Conditions of the WdW Equation in Flat Space in a Transition from the Pre-Planckian Physics Era to the Electroweak Regime of Space-Time
Physics Department, Chongqing University, Chongqing, China
Email: abeckwith@uh.edu
Received June 5, 2012; revised July 30, 2012; accepted August 6, 2012
Keywords: Wheeler De Witt Equation; Planck’s Constant; Wavefunction of the Universe; Octonionic Geometry; Quantum Mechanics
ABSTRACT
This document is due to reviewing an article by Maydanyuk and Olkhovsky, of a Nova Science conpendium as of “The big bang, theory assumptions and Problems”, as of 2012, which uses the Wheeler De Witt equation as an evolution equation assuming a closed universe. Having the value of k, not as the closed universe, but nearly zero of a nearly flat universe, which leads to serious problems of interpretation of what initial conditions are. These problems of interpretations of initial conditions tie in with difficulties in using QM as an initial driver of inflation. And argue in favor of using a different procedure as far as forming a wave function of the universe initially. The author wishes to thank Abhay Ashtekar for his well thought out criticism but asserts that limitations in space-time geometry largely due to when 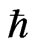 is formed from semi classical reasoning, i.e. Maxwell’s equation involving a close boundary value regime between Octonionic geometry and flat space non Octonionic geometry is a datum which Abhay Ashekhar may wish to consider in his quantum bounce model and in loop quantum gravity in the future.
is formed from semi classical reasoning, i.e. Maxwell’s equation involving a close boundary value regime between Octonionic geometry and flat space non Octonionic geometry is a datum which Abhay Ashekhar may wish to consider in his quantum bounce model and in loop quantum gravity in the future.
1. Introduction
What we are looking at, in Maydanyuk and Olkhovsky [1], is a way to define the initial Wheeler De Witt equation, not as what they did, for a closed universe, but to get to the actual nearly flat space Euclidian universe conditions which suggest that quantum mechanics will not work well as to initial conditions, and that a different procedure than what was done for closed universe conditions [1] needs to be considered for the start of cosmological evolution. Note that the difficulty in initial conditions has startling similarities as to the problem with gravitions having mass as noted by Maggiorie [2] which specifically delineated for non zero graviton mass, where 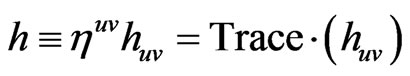 and
and 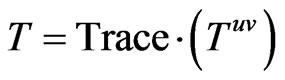 that
that
 (1)
(1)
As noted by Maggiore, one gets into serious analytical difficulties from the beginning, with (1) and the reader is invited to look at his massive Graviton section [2] which delineates some of the problems. In a similar manner, the closed universe analysis done in [1] encounters serious problems in initial conditions if we used flat space in the onset which sheds light upon the vulnerabilities of quantum mechanics in forming appropriate initial conditions, which we will comment upon and offer a solution for.
2. Looking at the Way to Form a Wheeler De Witt Equation via a Nearly Flat Space Model
The author is quite aware of work discussed with him in conferences, noticiably Rencontres De Moriond, in the experimental gravity conference, which alledges that from the initial conditions that inflation mandated almost completely flat space. For the sake of argument in this work, we will work with flat space, and will commence a derivation which shows serious issues with the Wheeler De Witt analysis of Quantum space time offered in [1] which works passably well in a closed universe condition.
To do this, we will reproduce, using instead of k = 1 (closed universe), 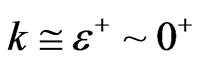 , and use that to reproduce the Wheeler De Witt argument and wave functions in [1], designating what we think are serious initial condition problems inherient in the
, and use that to reproduce the Wheeler De Witt argument and wave functions in [1], designating what we think are serious initial condition problems inherient in the  nearly flat space conditions, so as to look at first the mini super space Langrangian. This document is due to reviewing an article by Maydanyuk and Olkhovsky, of a Nova Science conpendium as of “The big bang, theory assumptions and Problems”, as of 2012, which uses the Wheeler De Witt equation as an evolution equation assuming a closed universe. Having the value of k, not as the closed universe, but nearly zero of a nearly flat universe, which leads to serious problems of interpretation of what initial conditions are. These problems of interpretations of initial conditions tie in with difficulties in using QM as an initial driver of inflation. And argue in favor of using a different proceedure as far as forming a wave function of the universe initially, which is written in [1] as for a mini superspace lagrangian
nearly flat space conditions, so as to look at first the mini super space Langrangian. This document is due to reviewing an article by Maydanyuk and Olkhovsky, of a Nova Science conpendium as of “The big bang, theory assumptions and Problems”, as of 2012, which uses the Wheeler De Witt equation as an evolution equation assuming a closed universe. Having the value of k, not as the closed universe, but nearly zero of a nearly flat universe, which leads to serious problems of interpretation of what initial conditions are. These problems of interpretations of initial conditions tie in with difficulties in using QM as an initial driver of inflation. And argue in favor of using a different proceedure as far as forming a wave function of the universe initially, which is written in [1] as for a mini superspace lagrangian
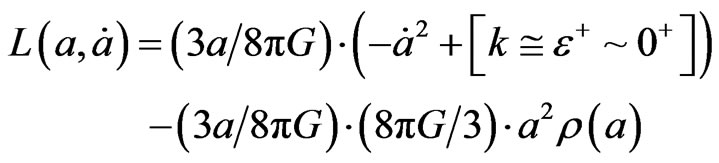 (2)
(2)
A Chapylgin gas equation of state was used, in working with Equation (2) using 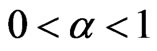 so that
so that
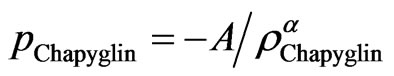 (3)
(3)
And, in conditions which specify 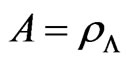 and
and 
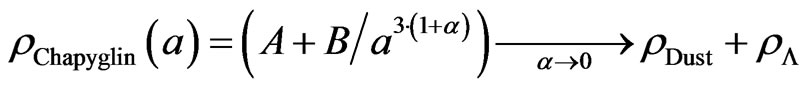 (4)
(4)
and a general density equation we will write up as
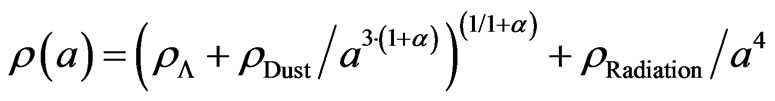 (5)
(5)
The end result as given is that [3] one has a S.E. with a wavefunction 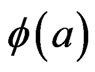
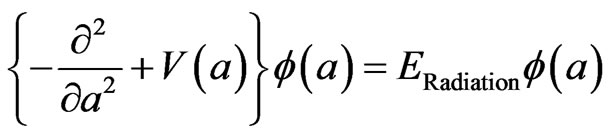 (6)
(6)
with
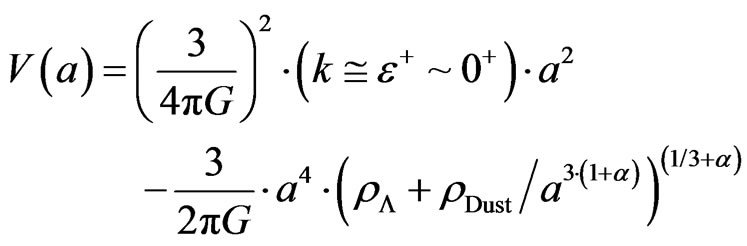 (7)
(7)
The difficulty in the change of variables comes next and is attributed to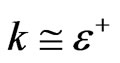 . Set
. Set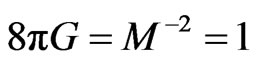 , and then the Equation (7) becomes, instead, if
, and then the Equation (7) becomes, instead, if
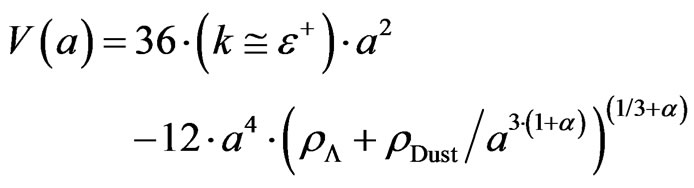 (8)
(8)
This potential is almost identitcal to what was done in [1] but the term  is what creates initial conditions which simply do not work out and are to be commented upon directly. If one does an expansion of Equation (8) as given above by
is what creates initial conditions which simply do not work out and are to be commented upon directly. If one does an expansion of Equation (8) as given above by  then by [1]
then by [1]
 (9)
(9)
 ;
;
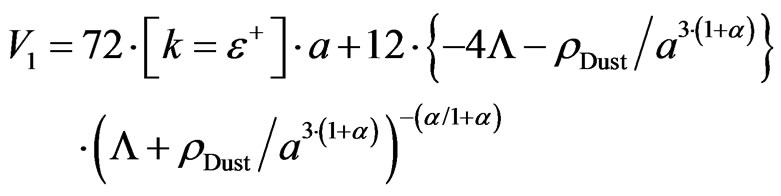 (10)
(10)
Then Equation (6) becomes, with  a wave function of the universe for
a wave function of the universe for 
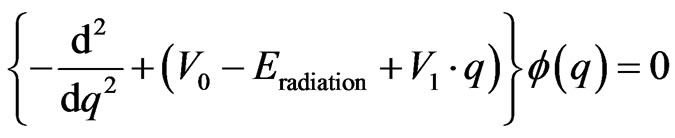 (11)
(11)
The following change of variables is where the problem in the Planckian regime becomes acute. i.e. set
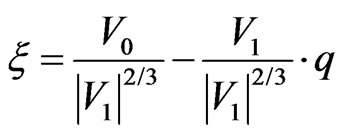 (12)
(12)
Then, Equation (11) become an Airy style differential equation with
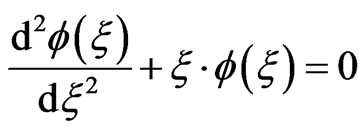 (13)
(13)
The following change of variables is where the problem in the Planckian regime becomes acute. Equation (13) above becomes undefinable, in the Planck regime of space time due to working with
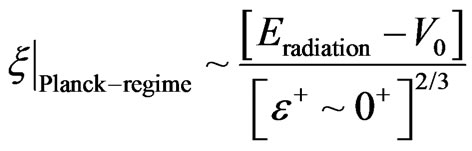 (14)
(14)
In this case, the 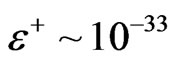 centimeters is so small, that it is next to impossible to define Equation (14) , with a solution as given in [1] via
centimeters is so small, that it is next to impossible to define Equation (14) , with a solution as given in [1] via
 ;
;
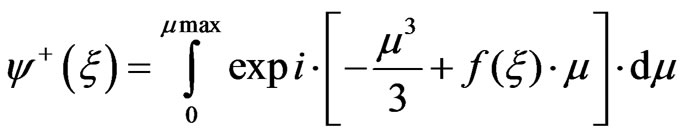 (15)
(15)
If we do a power series expansion of the function , [1] asserts that Equation (15) becomes proportional to an airy function with
, [1] asserts that Equation (15) becomes proportional to an airy function with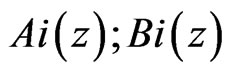 , provided
, provided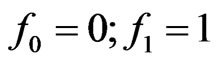 .
.
3. Criticism of the Above Methodology by Abhay Ashtekar
We introduce several criticisms of the above methodology leading to what was said about Equation (14) by Abhay Ashtekar, in private communication with the author [4].
“There are several technical problems. For instance, the substitution from (11)-(13), introducing (12), seems to overlook the fact that the new variable xi in (12) depends on q or a not just by the explicit factor but also via the potentials. And even if there is a coefficient dividing by a small epsilon (related to k), this value is not zero and there is no problem with well-defined equations. One would simply make a poor choice of variables in which some coefficients are unnaturally large (After all, a flat universe with k = 0 has a well-defined formulation)”.
4. The Author’s Answer to Abhay Ashtekar
First of all the author wishes to thank Abhay Astekar for his direct communications to correct what he perceived as sloppy thinking. The first place to start is to look at (12) above again, and to ask what is possibly driving
 (16)
(16)
Recall Equation (11)
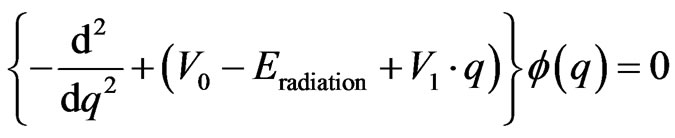 (11)
(11)
This presumably would happen when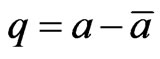 , and then we would be really looking at
, and then we would be really looking at
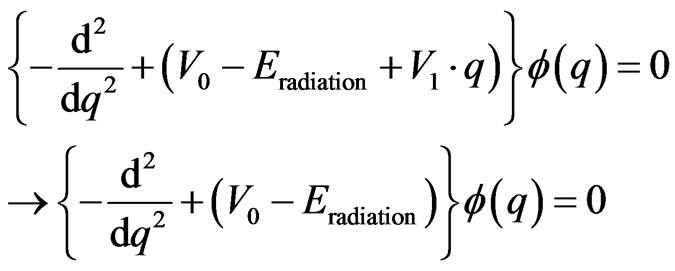 (17)
(17)
The transition from the left to the right hand side in Equation (20) above is tandem to what was said by Beckwith [5,6] as to formation of Planck’s constant.
5. Criticism of Forming Wave Function of Equation (15) if an Airy Function, with Using Equation (14)
We assert that in the Planck regime of space time, that Equation (14) is in reality undefinable due to the denominator of 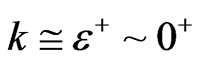 at or below 10 ^ - 33 centimeters of space time. The value of this parameter is so small, in fact, that what really needs to be addressed, to make any sense out of how small Equation (14) really is, is the following observation. Namely in looking at an evolution of a Wheeler De Witt equation of space time, that we can define a spatial evolution, via expansion of the scale factor a, as in Equation (11), but we have to put in by hand the initial time step i.e. the exact same problem shows up in Loop quantum gravity. In the case of scale factor
at or below 10 ^ - 33 centimeters of space time. The value of this parameter is so small, in fact, that what really needs to be addressed, to make any sense out of how small Equation (14) really is, is the following observation. Namely in looking at an evolution of a Wheeler De Witt equation of space time, that we can define a spatial evolution, via expansion of the scale factor a, as in Equation (11), but we have to put in by hand the initial time step i.e. the exact same problem shows up in Loop quantum gravity. In the case of scale factor , the spatial evolution is amendable by QM, but there is no idea as to how to get about putting in “by hand” the initial time step, which we presume would be a Planck time interval.
, the spatial evolution is amendable by QM, but there is no idea as to how to get about putting in “by hand” the initial time step, which we presume would be a Planck time interval.
6. So If a Domain Wall Enters the Picture, Then What Does This Do to Structure Formation and also Plank’s Constant?
In [5] we are stuck with how a semi classical argument can be used to construct Table 1 above. In particular, we look at how Planck’s constant is derived, as in the electroweak regime of space time, namely that given the prime in both Equations (16) and (17) is for a total derivative [7,8]
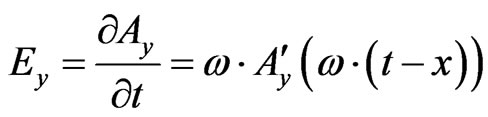 (18)
(18)
Similarly [15]
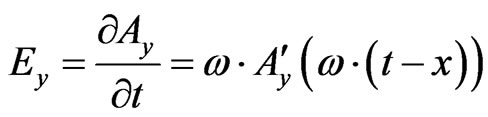 (19)
(19)
The A field so given would be part of the Maxwell’s equations given by [7] as, when  represents a D’Albertain operator, that in a vacuum, one would have for an A field [7,8]
represents a D’Albertain operator, that in a vacuum, one would have for an A field [7,8]
 (20)
(20)
And for a scalar field 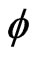
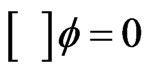 (21)
(21)
Following this line of thought we then would have an energy density given by, if 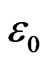 is the early universe permeability [7]
is the early universe permeability [7]
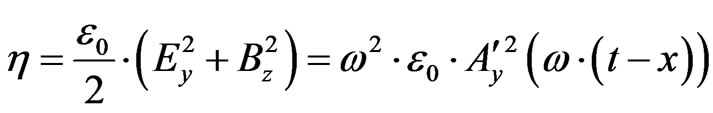 (22)
(22)

Table 1. Organizing WdW evolution.
We integrate (20) over a specified E and M boundary, so that, then we can write the following condition namely [7,8].
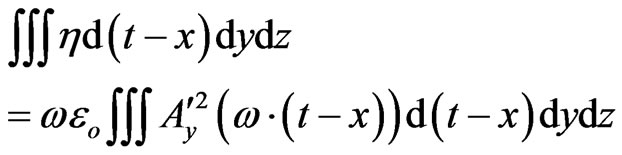 (23)
(23)
(21) would be integrated over the boundary regime from the transition from the Octonionic regime of space time, to the non Octonionic regime, assuming an abrupt transition occurs, and we can write, the volume integral as representing [7,8]
 (24)
(24)
Our contention for the rest of this paper, is that Mach’s principle will be necessary as an information storage container so as to keep the following, i.e. having no variation in the Planck’s parameter after its formation from electrodynamics considerations as in (21) and (22). Then by applying [7,8]
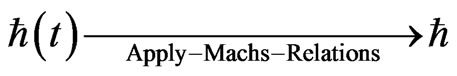 (Constant value)(25)
(Constant value)(25)
7. Conclusions. We Need to Reconsider the Role of Quantum Gravity Models at the Onset of Inflation
We are stuck in all Quantum gravity models as of putting in an initial time step “by hand” so to speak which raises fundamental issues of what would form an initial time step in Quantum gravity. How the transtion from the left to the right hand side of Equation (17) occurs is crucial and it comes about because of a transition from Octonionic geometry to quantum accessible and analyzable flat space geometry. The key equation to understand is Equation (17) which delineates how one can have Equation (11), Equation (16), and Equation (17) happen. This indeterminate nature of time, itself, at the onset of Quantum gravity models of space time may be seen as a fundamental defect killing off all initial QM influences at the start of inflation. The other way to look at the role of an undefined initial starting point for time, which we put in by “hand” is that the special nature of time itself may be if experimentally verified, via observations, the best hope we have of falsifiable measurements of t’Hoofts conjecture [9,10] that quantum mechanics is embedded within a classical physics frame work which we have yet to fully develop. To do that would also, if the Gravition exists with initial measurements, such as given by
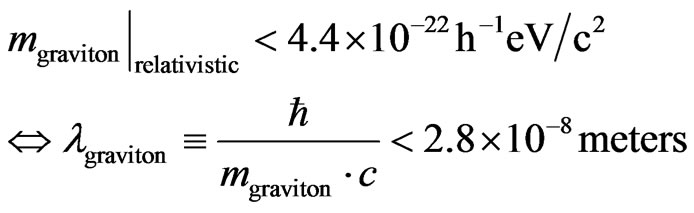 (26)
(26)
Perhaps lead to signals from early universe gravitational waves which may confirm or falsify the role of quantum mechanics in initial univese conditions. As well as the role that set as a working approximation [6].
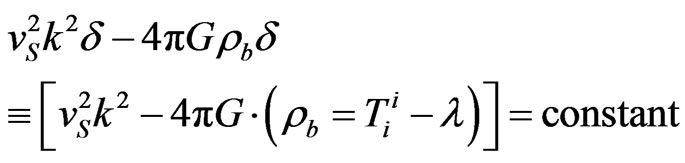 (27)
(27)
Affects the formation of baryonic matter fluctuations, which may play a role in the formation of Table 1.
8. Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No.110752.
REFERENCES
- S. Maydanyuk and V. Olkhovsky, “Fully Quantum Study of the FRW Model with Radiation and Chaplygin Gas,” In: J. O’Connell and A. Hale, Eds., The Big Bang, Theory, Assumptions and Problems, Nova Science Publishers, New York, 2012, pp. 185-196.
- M. Maggiore, “Gravitational Waves, Volume 1: Theory and Experiment,” Oxford University Press, Oxford, 2008.
- G. A. Monerat, et al., “Dynamics of the Early Universe and the Initial Conditions for Inflation in a Model with Radiation and a Chaplygin Gas,” Physical Review D, Vol. 76, No. 2, 2007, Article ID: 024017. doi:10.1103/PhysRevD.76.024017
- A. Ashtekar, “Private Communications with the Author,” Monday, 9 July 2012.
- A. Beckwith, “Is Quantum Mechanics Involved at the Start of Cosmological Evolution? Does a Machian Relationship between Gravitons and Gravitinos Answer This Question?” 2012. http://vixra.org/abs/1206.0023
- A. W. Beckwith, “Is There a Change in the Baryonic Structure Formation if Quark Strings and Domain Walls Exist at about the Electro-Weak Era?” 2012. http://vixra.org/abs/1207.0034
- U. Bruchholz, “Derivation of Planck’s Constant from Maxwell’s Electrodynamics,” Progress in Physics, Vol. 4, 2009, p. 67.
- U. Bruzchholz, “Key Notes on a Geometric Theory of Fields,” Progress in Physics, Vol. 2, 2009, pp. 107-113.
- G. ‘t Hooft, “Determinism beneath Quantum Mechanics,” In: Beyond the Quantum, Th. M. Nieuwenhuizen, et al., Eds., World Press Scientific, Singapore, 2002. http://arxiv.org/PS_cache/quant-ph/pdf/0212/0212095v1.pdf
- G. ‘t Hooft, “The Mathematical Basis for Deterministic Quantum Mechanics,” In: Th. M. Nieuwenhuizen, et al., Eds., Beyond the Quantum, World Press Scientific, Singapore, 2006. http://arxiv.org/PS_cache/quant-ph/pdf/0604/0604008v2.pdf

