Journal of Modern Physics
Vol. 2 No. 11 (2011) , Article ID: 8649 , 5 pages DOI:10.4236/jmp.2011.211174
Electromagnetic Radiation Reaction and Stability of the Hydrogen-Like Atoms
Department of Physics, Ilam University, Ilam, Iran
E-mail: dehghan22@gmail.com
Received September 15, 2011; revised October 6, 2011; accepted October 29, 2011
Keywords: Radiation Reaction, Hydrogen Atom, Electromagnetic Potentials, Maxwell Equations
ABSTRACT
Based on a suitable linear combination of the physical and un-physical electromagnetic potentials, the radiation reaction potentials have been calculated. Through the near zone expansion of the potentials, it has been shown that in either of the relativistic and non-relativistic cases the outgoing (radiated) energy of the electrons orbiting the nucleus is substituted by incoming (electromagnetic radiation reaction) energy. This means that energy is conserved and the classical hydrogen-like atoms are stable.
1. Introduction
The interaction of a particle with it’s own field produces the phenomenon of radiation reaction. This phenomenon results in an extra force on the particle; a self-force which changes the equations of motion. The non-relativistic equation of motion for a point charge including radiation reaction was found by Lorentz [1]. Its relativistic generalization was first derived by Abraham [2] and later covariantly by Dirac [3]. A modern review of Abraham-Lorentz-Dirac equation has been presented in Ref. [4]. The generalized version of the Abraham-LorentzDirac equation to the curved space times has been derived by De Witt and Brehme [5], which was corrected by some additional terms by Hobbs [6].
The Abraham-Lorentz-Dirac equation is not without its problems: a third order rather than of second order differential equation, allowing self force in the absence of an external force and appearance of runaway solutions. A corrected version of Abraham-Lorentz-Dirac equation has been given by Rohrlich [7]. By the consideration of emitted radiation from the magnetic moment in addition to that of electric charge of an accelerating electron, Heras showed that Abraham-Lorentz-Dirac equation predicts non-runaway solutions provided that suitable initial conditions are proposed [8].
However, the radiation reaction phenomenon is a more interesting subject and it has been studied extensively in the frameworks of classical electrodynamics, quantum electrodynamics and quantum field theory by many authors [9-15].
In this article, I study the stability of the relativistic and non-relativistic hydrogen-like atoms from a different point of view. The method utilized is based on a suitable linear combination of the retarded and advanced solutions of the Maxwell equations, introduced by Poisson [4,16].
A point electric charge moving in flat space-time produces an electromagnetic potential 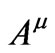 that satisfies the wave equation
that satisfies the wave equation
 (1.1)
(1.1)
together with the Lorentz gauge condition .
.
The four-vector  is the charge’s current density which is formally written in terms of a four-dimensional Dirac’s delta function supported on the charge’s world line. An immediate difficulty is that the electromagnetic potential, and also the electromagnetic field tensor diverge on the particle’s world line because the field of a point charge is necessarily infinite at the charge’s position.
is the charge’s current density which is formally written in terms of a four-dimensional Dirac’s delta function supported on the charge’s world line. An immediate difficulty is that the electromagnetic potential, and also the electromagnetic field tensor diverge on the particle’s world line because the field of a point charge is necessarily infinite at the charge’s position.
The situation in which the radiation is propagating outward and the charge is spiraling inward, breaks the time-reversal invariance of Maxwell’s theory. A specific time direction was adopted when, among all possible solutions to the wave equation, we choose , the retarded solution as the physically-relevant solution. Choosing instead the advanced solution
, the retarded solution as the physically-relevant solution. Choosing instead the advanced solution , would produce a time-reversed picture in which the radiation is propagateing inward and the charge is spiraling outward. Alternatively, choosing the linear superposition [16]
, would produce a time-reversed picture in which the radiation is propagateing inward and the charge is spiraling outward. Alternatively, choosing the linear superposition [16]
 (1.2)
(1.2)
would restore time-reversal invariance, outgoing and incoming radiation would be present in equal amounts, there would be no net loss nor gain of energy by the system, and the charge would not undergo any radiation reaction. In Equation (1.2) the subscript S stands for symmetric, as the vector potential depends symmetrically upon future and past.
On the other hand, while the potential of Equation (1.2) does not exert a force on the charged particle, it is just as singular as the retarded potential in the vicinity of the world line. This follows from the fact that ,
,  and
and  all satisfy Equation (1.1), whose source term is infinite on the world line. So while the wave-zone behaviors of these solutions are very different (with the retarded solution describing outgoing waves, the advanced solution describing incoming waves, and the symmetric solution describing standing waves), the three vector potentials share the same singular behavior near the world line. Thus the subscript S in Equation (1.2) stands for singular as well as symmetric. Because
all satisfy Equation (1.1), whose source term is infinite on the world line. So while the wave-zone behaviors of these solutions are very different (with the retarded solution describing outgoing waves, the advanced solution describing incoming waves, and the symmetric solution describing standing waves), the three vector potentials share the same singular behavior near the world line. Thus the subscript S in Equation (1.2) stands for singular as well as symmetric. Because 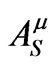 is just as singular as
is just as singular as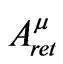 , removing it from the retarded solution gives rise to a potential that is well behaved in a neighborhood of the world line and because
, removing it from the retarded solution gives rise to a potential that is well behaved in a neighborhood of the world line and because  not to affect the motion of the charged particle, this new potential must be entirely responsible for the radiation reaction. Now we introduce the new potential
not to affect the motion of the charged particle, this new potential must be entirely responsible for the radiation reaction. Now we introduce the new potential
 (1.3)
(1.3)
and postulate that it, and it alone, exerts a force on the particle.  is nonsingular (regular) on the world line. This property can be directly inferred from the fact that the regular potential satisfies the homogeneous version of Equation (1.1). Since
is nonsingular (regular) on the world line. This property can be directly inferred from the fact that the regular potential satisfies the homogeneous version of Equation (1.1). Since 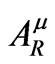 satisfies the homogeneous wave equation, it can be thought of as a free radiation field, and the subscript R could also stand for radiative. Thus the radiation reaction part of the electromagnetic fields can be written as [4,16]
satisfies the homogeneous wave equation, it can be thought of as a free radiation field, and the subscript R could also stand for radiative. Thus the radiation reaction part of the electromagnetic fields can be written as [4,16]
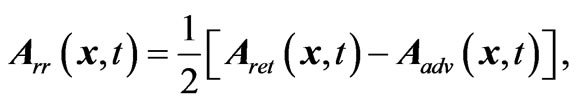 (1.4)
(1.4)
 (1.5)
(1.5)
In the following, using the radiation reaction electromagnetic potentials, I will calculate the rate at which the work is done by the radiation reaction force, or the rate at which energy comes in, and show that it is equal to the outgoing energy through the electromagnetic radiation. The results show that in either of the relativistic and non-relativistic cases, the energy is conserved and the classical hydrogen-like atoms are stable.
2. Non-Relativistic Hydrogen-Like Atoms
A classical electron orbiting the nucleus emits electromagnetic radiation. As a result the non-relativistic hydrogen-like atoms loss energy in a rate determines by Larmor’s formula [17,18],
 (2.1)
(2.1)
The physical solution to Maxwell’s equations is the retarded solution,
 (2.2)
(2.2)
where J is the current density. This describes waves that are outgoing in the wave zone. These waves remove energy from the system, and the radiation reaction drives the electron inward. A so-called un-physical solution to the Maxwell's equations is the advanced solution,
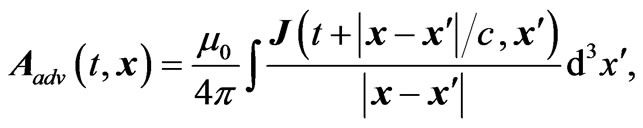 (2.3)
(2.3)
and this describes the waves that are incoming the wave zone. These waves bring energy to the system, and the radiation reaction drives the electron outward. For the scalar potential we have also the two solutions,
 (2.4)
(2.4)
we need to evaluate 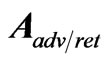 and
and 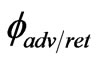 near the electron. We can therefore take
near the electron. We can therefore take  to be small, and Taylor-expand current and charge densities
to be small, and Taylor-expand current and charge densities
 (2.5)
(2.5)
 (2.6)
(2.6)
We have for the retarded and advanced vector potentials,
 (2.7)
(2.7)
The second term is of order  and this mean that we are working in the non-relativistic regime. The radiation reaction part of the vector and scalar potentials are
and this mean that we are working in the non-relativistic regime. The radiation reaction part of the vector and scalar potentials are
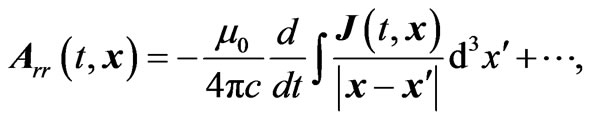 (2.8)
(2.8)
 (2.9)
(2.9)
For a point charge q we set  and
and  where
where 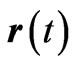 is the particle’s trajectory and
is the particle’s trajectory and  Substituting these into Equations (2.8) and (2.9) we have
Substituting these into Equations (2.8) and (2.9) we have
 (2.10)
(2.10)

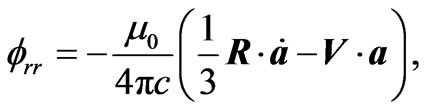 (2.11)
(2.11)
where  and
and 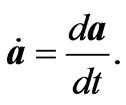 The radiation reaction part of the electric and magnetic fields are
The radiation reaction part of the electric and magnetic fields are
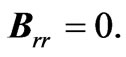
 (2.12)
(2.12)
The radiation reaction force is therefore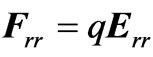 , or
, or
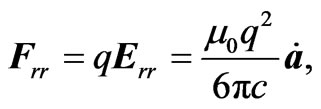 (2.13)
(2.13)
As the charge moves with velocity V this force does work at a rate
 (2.14)
(2.14)
where p is the power radiated by the point charge, as given by Larmor’s formula (2.1). The work done by the radiation reaction force therefore matches the energy taken away by electromagnetic radiation, and we have energy conservation.
3. Relativistic Hydrogen-Like Atoms
The relativistic generalization of the Larmor’s formula is known as the Lienard’s formula [17,18]
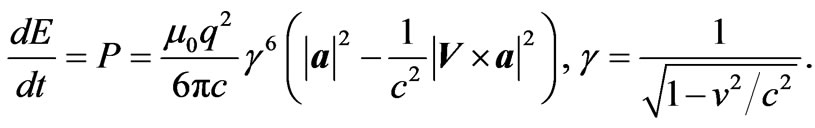 (3.1)
(3.1)
To study the relativistic regime, the upper terms in Equations (2.5) and (2.6) must be taken into account,
 (3.2)
(3.2)
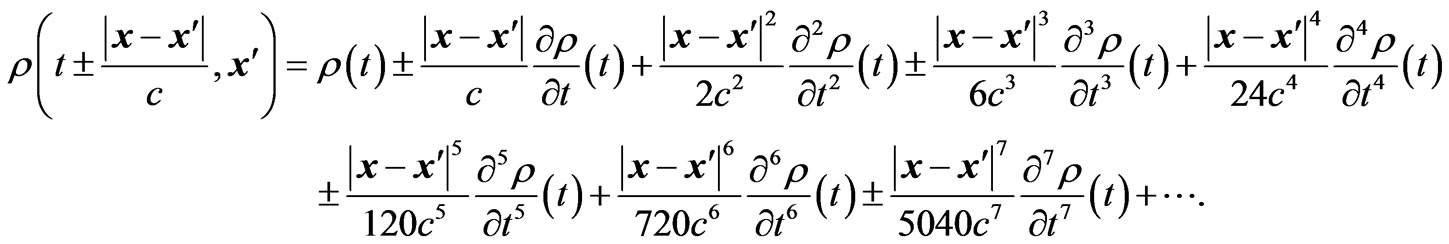 (3.3)
(3.3) Substituting Equations (3.2) and (3.3) in Equations (2.2), (2.3) and (2.4), and then in Equations (1.4) and (1.5), we obtain the radiation reaction vector and scalar potentials as
 (3.4)
(3.4)
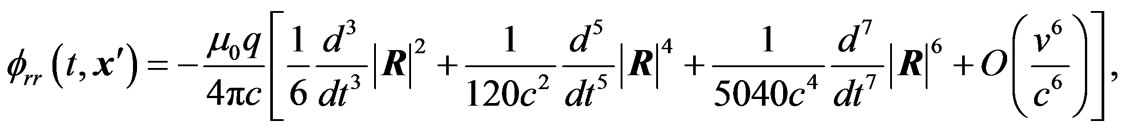 (3.5)
(3.5)
After taking the limit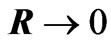 , we obtain (Appendix-A)
, we obtain (Appendix-A)
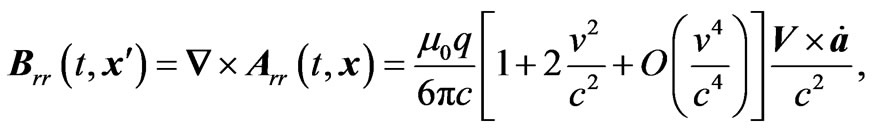 (3.6)
(3.6)
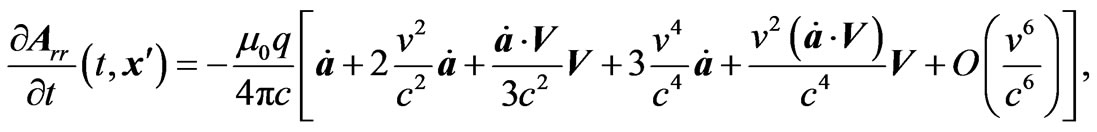 (3.7)
(3.7)
 (3.8)
(3.8)
Combining these relations, we have
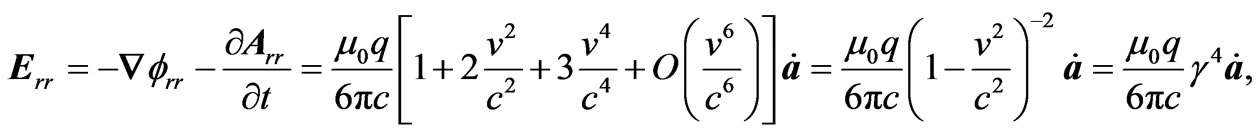 (3.9)
(3.9) where, we have used the binomial expansion relation . The radiation reaction force acting on the charge q is
. The radiation reaction force acting on the charge q is
 (3.10)
(3.10)
and the rate at which the work is down on the moving charge q is
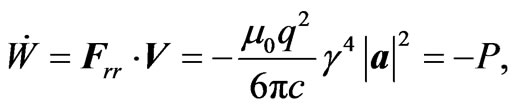 (3.11)
(3.11)
where P is the radiated power by a relativistic point charge, given in (3.1). This means that the work done by the radiation reaction force (incoming energy), is equal to the energy taken away by electromagnetic radiation, and we have energy conservation, once again.
4. Conclusions
Based on a suitable linear combination of the physical and un-physical electromagnetic potentials, with the properties: 1) not diverging (i.e. regular) on the charge's position, 2) preserving the time-reversal symmetry of the Maxwell’s theory of electromagnetism, and 3) satisfying the homogeneous (i.e. radiative) wave equation, the radiation reaction vector and scalar potentials are calculated for the electrons orbiting the nucleus in the relativistic and non-relativistic hydrogen-like atoms. Through the near zone expansion of radiation reaction potentials, it was shown that for the non-relativistic hydrogen-like atoms the incoming (electromagnetic radiation reaction) energy is equal and opposite sign to the outgoing (radiated) energy given by Larmor’s formula. Also, in the relativistic case the radiated energy of the electron orbiting the nucleus, which is given by Lienard’s formula, is substituted by incoming (electromagnetic radiation reaction) energy. This means that energy is conserved and the classical hydrogen-like atoms are stable. This method can be generalized to the gravitational waves and the consideration of the gravitational radiation reaction.
REFERENCES
- H. A. Lorentz, “La theorie electromagnetique de Maxwell et son application aux corps mouvants,” Archives néerlandaises des Sciences exactes er naturelles, Vol. 25, 1892, pp. 363-552.
- M. Abraham and R. Becker, “Theorie der Elektrizitat,” Vol. II, Teubner, Leipzig, 1905.
- P. A. M. Dirac, “Classical Theory of Radiative Electrons,” Proceeding of the Royal Society London A, Vol. 167, 1938, pp. 148-169. doi:10.1098/rspa.1938.0124
- E. Poisson, “An Introduction to the Lorentz-Dirac Equation,” 1999. arXiv:gr-qc/9912045
- B. S. De Witt and R. Brehme, “Radiation Damping in a Gravitational Field,” Annals of Physics, Vol. 9, No. 2, 1960, pp. 220-259. doi:10.1016/0003-4916(60)90030-0
- J. Hobbs, “A Vierbein Formalism of Radiation Damping,” Annals of Physics, Vol. 47, No. 1, 1968, pp. 141- 165. doi:10.1016/0003-4916(68)90231-5
- F. Rohrlich, “The Correct Equation of Motion of a Classical Point Charge,” Physics Letters A, Vol. 283, No. 5-6, 2001, pp. 276-278. doi:10.1016/S0375-9601(01)00264-X
- J. A. Heras, “The Radiation Reaction Force on an Electron Reexamined,” Physics Letters A, Vol. 314, No. 4, 2003, pp. 272-277. doi:10.1016/S0375-9601(03)00907-1
- A. Higuchi and P. J. Walker, “Classical and Quantum Radiation Reaction in Conformally Flat Spacetime,” Physical Review D, Vol. 79, No. 10, 2009, Article ID 105023. doi:10.1103/PhysRevD.79.105023
- C. R. Gally and M. Tiglio, “Radiation Reaction and Gravitational Waves in the Effective Field Theory Approach,” Physical Review D, Vol. 79, No. 12, 2009, Article ID 124027. doi:10.1103/PhysRevD.79.124027
- C. Harvey, T. Heinzl, N. Iji and K. Langfeld, “Covariant Worldline Numerics for Charge Motion with Radiation Reaction,” Physical Review D, Vol. 83, No. 7, 2011, Article ID 076013. doi:10.1103/PhysRevD.83.076013
- A. Higuchi and G. D. R. Martin, “Radiation Reaction on Charged Particles in Three-Dimensional Motion in Classical and Quantum Electrodynamics,” Physical Review D, Vol. 73, No. 2, 2006, Article ID 025019. doi:10.1103/PhysRevD.73.025019
- A. Higuchi and G. D. R. Martin, “Quantum Radiation Reaction and the Green’s Function Decomposition,” Physical Review D, Vol. 74, No. 12, 2006, Article ID 125002. doi:10.1103/PhysRevD.74.125002
- A. Higuchi and P. J. Walker, “Quantum Corrections to the Larmor Radiation Formula in Scalar Electrodynamics,” Physical Review D, Vol. 80, No. 10, 2009, Article ID 105019.
- F. Rohrlich, “Dynamics of a Classical Quasi-Point Charge,” Physics Letters A, Vol. 303, No. 5-6, 2002, pp. 307-310. doi:10.1016/S0375-9601(02)01311-7
- E. Poisson, “The Motion of Point Particles in Curved Spacetime,” Living Reviews in Relativity, Vol. 7, 2004, p. 6.
- J. D. Jackson, “Classical Electrodynamics,” Third Edition, John Wiley and Sons, Inc., New York, 1982.
- J. D. Griffiths, “Introduction to Electrodynamics,” Second Edition, New Delhi, 1982.
Some Useful Mathematical Formula
In obtaining the radiation reaction electromagnetic fields given in Equations (2.12) and (3.6)-(3.9) the following relations have been used
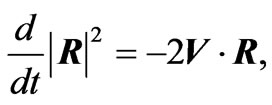 (A.1)
(A.1)
 (A.2)
(A.2)
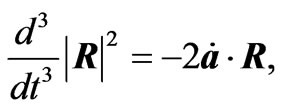 (A.3)
(A.3)
 (A.4)
(A.4)
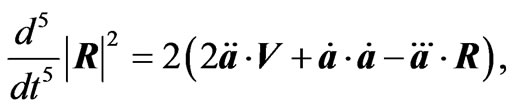 (A.5)
(A.5)
 (A.6)
(A.6)
 (A.7)
(A.7)
 (A.8)
(A.8)
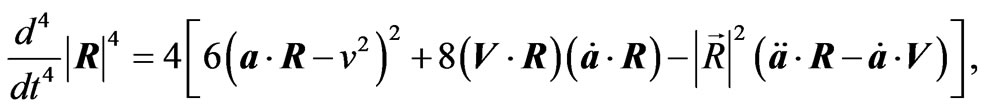 (A.9)
(A.9)
 (A.10)
(A.10)  (A.11)
(A.11) 
