Received 11 September 2014; revised 15 October 2014; accepted 29 October 2014

ABSTRACT

We propose and analyze an epidemiological model to evaluate the effectiveness of bed nets as a prophylactic measure in malaria-endemic areas. The main purpose in this work is the modeling of the aggressiveness of anopheles mosquitoes relative to the way humans use to protect themselves against bites of mosquitoes. This model is a system of several differential equations: the number of equations depends on the particular assumptions of the model. 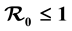We compute the basic re- production number, and show that if, the disease free equilibrium (DFE) is globally asymptotically stable on the non-negative orthant. If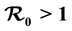, the system admits a unique endemic equilibrium (EE) that is globally and asymptotically stable. Numerical simulations are presented corresponding to scenarios typical of malaria-endemic areas, based on data collected in the literature. Finally, we discuss the relative effectiveness of different kinds of bed nets.

Keywords:

Epidemiological Model, Malaria, Basic Reproduction Number, Lyapunov Function, Global Asymptotic Stability, Non-Standard Finite Difference Scheme (NFDS), Simulation

1. Introduction

Malaria is a vector-borne infectious disease that is widespread in tropical regions, including parts of America, Asia and much of Africa. Humans contract malaria following effective bites of infected Anopheles female mosquitoes during blood feeding. Plasmodium falciparum is the most common cause of malaria mortality in Africa, and the chain of transmission can be broken through the use of insecticide-treated bed nets and anti-malarial drugs, as well as other control strategies.

Malaria accounts for more than 207 million infections and results in over 627,000 deaths globally in 2012 [1] . About 90% of these fatalities occur in Sub-Saharan Africa [1] [2] . Despite intensive social and medical research and numerous programs to combat malaria, the incidence of malaria across the African continent remains high.

In the field of mathematical epidemiology, numerous models have been proposed with the purpose of under- standing various aspects of the disease. The foundation model of Sir Ronald Ross, originally proposed in 1911 [3] and extended by MacDonald in 1957 [4] , serves as the basis for many mathematical investigations into the epidemiology of malaria. A prominent example is the model of Ngwa and Shu [5] , which introduces susceptible (S), exposed (E), and infectious (I) classes for both humans and mosquitoes, plus an additional Immune class (R) for humans. This model is extended in the Ph.D. theses of Chitnis [6] and Zongo [7] (these two theses also provide comprehensive reviews on the state of the art). Chitnis introduces immigration into the host population, which is a significant effect since hosts migrating from a naive region to a region with high endemicity are especially susceptible to infection. Zongo further extends the model by dividing the human population into non- immune and semi-immune sub-populations, which are modeled using (SEIS) and (SEIRS) model types, respectively.

In his thesis, Chitnis espoused the use of insecticide-treated bed nets, coupled with rapid medical treatment of new cases of infection, as the best strategy to combat malaria transmission. In this paper we make further extensions to the model to include the effects of bed-net use on malaria transmission. In particular, we divide the human population into groups that are characterized by the methods they use to protect themselves against the mosquito bites. These assumptions are consistent with the observable situation in many endemic areas, parti- cularly in poor countries. We believe that the current study represents the first systematic model-based analysis of the impact of bed nets on the dynamics of malaria transmission.

Malaria is highly seasonal [8] [9] : the highest endemicity typically occurs during rainy seasons, when mosquito density is high due to high humidity and the presence of standing water where mosquitoes can breed. During this period, even people with immune predisposition to malaria infection are at risk of attaining the critical level of malaria parasites in their bloodstream that could make them fall sick. In our model, we consider conditions characteristic of a rainy season in a region of high malaria endemicity: typically, such conditions last for a period between three to six months. Because of the brevity of the period being considered, we neglect the effects of death, birth and migration of hosts. We also omit exposed and recovered classes for hosts: due to the high density of anopheles mosquitoes during such periods, exposed individuals rapidly become infectious, and the partial immunity of hosts following recovery has negligible effect. Results for more sophisticated models that include exposed and/or recovered state(s) are reserved for forthcoming papers.

The paper is organized as follows. Section 2 describes our model and gives the corresponding system of differential equations. Section 3 establishes the well-posedness of the model by demonstrating invariance of the set of non-negative states, as well as boundedness properties of the solution. The equilibriums of the system are calculated, and a threshold condition for the stability of the disease free equilibrium (DFE) is calculated, which is based on the basic reproduction number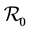. The method used to derive the basic reproduction number is different for the method of the next generation operator of Van Den Driesshe and Watmough [10] currently used in literature. Section 4 analyzes the stability of equilibriums. We prove in Section 4.1 the global asymptotic stability (GAS) of the disease free equilibrium (DFE) when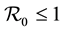; in Section 4.2 we prove the GAS of the endemic equilibrium (EE) when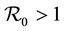. Section 5 provides graphs of trajectories corresponding to various parameter sets computed based on data obtained from the literature. Section 6 discusses the significance of our results. Finally, the Appendix contains detailed proofs and computations required by the analysis.

2. Model Description and Mathematical Specification

The model assumes an area populated by 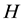human hosts and female mosquitoes (disease vectors) under conditions of higher endemicity of malaria. The human and mosquito populations are homogeneously mixed. In the following subsections, we provide a detailed description of the population structure and dynamics of hosts and vectors.

2.1. Host Population Structure and Dynamics

The human population is divided into 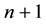groups. One of these groups consists of humans who do not use bed nets, while the other 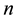groups correspond to the various types of bed nets used as protection against mosquito bites. Some nets are untreated; others are treated with repellent; others are treated with insecticides, with varying degrees of toxicity (toxicity typically decreases with use). We let 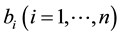denote the proportion

of the human population that is in the protected group, and is the proportion of humans that

use no protection.

The dynamics of the host population 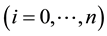is described by a SIS-based compartment model as shown in Figure 1. As explained in the Introduction, we omit exposed and recovered classes, as well as the ef-

fects of birth, death, and migration. The incidence of infection for humans in the 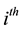group is given by,

where a is the average number of bites per mosquito per unit time (the entomological inoculation rate); is the number of infectious mosquitoes; H is the human population; and is the infectivity of the mosquito within the contact with human of the group, that is the probability that the bites of an infected mosquito on a susceptible human of the group will transfer infection to the bitten human.

2.2. Mosquito Population Structure and Dynamics

The population of disease vectors (adult female anopheles mosquitoes) is characterized by several classes, where each mosquito’s class membership is determined by its own history of past activity. Newly-emerged adult mosquitoes initially enter the susceptible class: the rate of entry (that is, the recruitment rate) is. Also included within the susceptible class are all uninfected mosquitoes: this includes mosquitoes that have never fed, as well as those that have fed but have never become infected. This is a reasonable approximation, since all such mosquitoes are in the same state with respect to progress of the infection. The natural death rate for mosquitoes (apart from mortality due to being killed while feeding) is.

Adult mosquitoes alternate between two activities: questing (that is, seeking a host to bite for its blood meal) and resting (to lay down eggs, or to digest a blood meal). In the current model we assume that all susceptible mosquitoes are in the questing state: the presence of susceptible resting mosquitoes can be approximately accommodated by reducing to account for recruited mosquitoes that are resting and not questing. We are currently working on an improved model that explicitly includes the class of susceptible resting mosquitoes.

Questing mosquitoes are equally likely to feed on any human, regardless of his/her protection method. Thus for any given blood meal, the probability that the human host belongs to the group is. During a blood meal on a human in the group, the mosquito is killed with probability, survives with probability, and succeeds in feeding with probability. Letting denote the average number of bites per mosquito per unit time (the entomological inoculation rate) it follows that the incidence rate of successful blood meals is

, while the additive death rate caused by the questing activity of mosquitoes is. If

we let and denote respectively the number of infected humans in group and the probability that the bite of a mosquito on humans in group will infect the mosquito, then the incidence rate for mosquitoes be-

coming infected is.

Susceptible mosquitoes that become infected enter the first exposed resting class. Following initial infection, the mosquito must remain alive for a certain period before becoming infectious. This period is known in biological and medical literature as extrinsic incubation period [11] . During this period, the mosquito experiences a certain number of periods of questing and resting. In our model, we suppose that a mosquito becomes

infectious after a fixed number l of resting/questing cycles following initial infection. These successive resting/

questing cycles are modeled as a sequence of exposed states, and are denoted by.

If a mosquito survives through all of these state, it then enters the infectious class, which is further divided into questing and resting sub-classes (and, respectively). Once a mosquito enters the infectious class, it remains there for the rest of its life, alternating between questing and resting states.

The overall dynamics of the mosquito population is depicted in the multi compartment diagram in Figure 2: The fundamental model parameters are summarized in Table 1, while derived parameters are summarized in Table 2.

2.3. Model Equations

The system of ordinary differential equations that characterize the model are given as follows:

(1)

The system (1) together with initial conditions completely specifies the evolution of the multi-compartment system shown in Figure 1 and Figure 2. Note that system (1) also determines (susceptible hosts of the hosts group, since each host sub population is closed and.

3. Well-Posedness, Dissipativity and Equilibria of the System

In this section we demonstrate well-posedness of the model by demonstrating invariance of the set of non- negative states, as well as boundedness properties of the solution. We also calculate the equilibriums of the system, whose stability properties will be examined in the following section.

3.1. Positive Invariance of the Non-Negative Cone in State Space

The system (1) can be rewritten in matrix form as

(2)

Equation (2) is defined for values of the state variable lying in the non-negative cone of , which we denote as. Here represents the naive vector component, and

represents the non-naive components of the state of the system. This notation is consistent with the notation of reference ([12] ), and we use results from this reference in our analysis.

The matrix may be written in block form as

(3)

where the four matrices blocks may be described as follows:

The matrix expresses the interaction between non-infected components of the system. It is a 2-banded matrix whose diagonal and sub-diagonal elements are given by the vectors and respectively, defined by

(4)

The matrix gives the dependence of the exposed components on the infected components. The only nonzero entries in this matrix are the first

terms of the first row, which are given by: these terms characterize the transition of

vectors from the susceptible to the first exposed state, which depends on infectious the host components. The matrix gives the dependence of infectious components on exposed components. All

entries are zero except the entry, which is equal to reflecting the transition rate of vectors

from state to state.

The matrix may be written in block form as, with;;.

Remark 3.1. The second matrix form given in (2) can also be written in the form

(5)

where, , and is the component of

the DFE (see Proposition 3.5 below) in the disease free sub-variety For such a system, Kamgang et al. in [12] gives a threshold condition for the stability of the DFE and an analysis of global asymptotic stability that we may apply to the current system.

For a given, the matrices, and are Metzler matrices.

The following proposition establishes that system (2) is epidemiologically well posed.

Proposition 3.1. The non-negative cone is positively invariant for the system (2).

Proof. For any, the matrix is a Metzler matrix (see Appendix); and it is well-known that systems determined by Metzler matrices preserve invariance of the non-negative cone. □

3.2. Boundedness and Dissipativity of the Trajectories

We have the following proposition.

Proposition 3.2. The simplex

(6)

where and is a compact forward-invariant and absorb-

ing set for the system (1).

Note that is the overall population of non-naive mosquitoes; while is the maximum incidence rate of infection for questing susceptible mosquitoes.

Proof. From (1) we have as dynamic of susceptible mosquitoes; thus. It

follows that. From (1) we also have, , so similarly. Finally, by adding together the equations for exposed and infectious vector populations in system (1) we obtain; and since and we ob- tain. It follows that, which completes the proof. □

As a result of Proposition 2, we may limit our study to the simplex specified in (6).

3.3. Computation of the Threshold Condition

Several techniques exist for computing the basic reproduction number and threshold conditions for the local asymptotic stability of the disease free equilibrium of epidemiological models represented by systems of ordinary differential equations. In [10] the maximum eigenvalue of next generation operator is proposed. In many other papers in the literature, either the technique in [10] , or the Routh-Hurwitz criterion are used [13] - [15] . Unfortunately, these are not suitable for large-scale systems that may possess many equations. Instead, we use the technique in [12] to compute the threshold condition for the system under consideration, which also enables the evaluation of the basic reproduction number. Specifically, we have:

Proposition 3.3 ([12] ). Let be a Metzler matrix with block decomposition where and

D are square matrices. Then is Metzler stable if and only if A and (or and) are Metzler stable.

We refer the reader to reference [12] for the proof of the proposition. This result enables the reduction of the large-scale matrix to a number of smaller-scale matrices, to which more classical methods may be applied.

Proposition 3.4. The basic reproduction number for the system (1) is

(7)

where and are respectively the questing and the resting frequencies of mosquitoes.

The proof of the above proposition is postponed to Appendix B.

3.4. System Equilibria

Steady states of the system are specified by the following proposition.

Proposition 3.5. System (2) admits two equilibriums. The first (called the disease free equilibrium or DFE) is

given by, where with and. The second (called the en-

demic equilibrium or EE) is given by

(8)

where is the finite root of the equation

(9)

The proof of Proposition 3.5 is postponed to Appendix C.

Remark 3.2. Equation (9) shows that the dynamics of the mosquito population (expressed in the parameters, and) as well as the protection means used by the population (expressed in the parameter) strongly influence the location of the EE. This justifies our assertion that mosquito dynamics and host protection means are important practical factors in determining the prevalence of infection.

4. Stability of System Equilibria

In this section we analyze the stability of the system equilibriums given in Proposition 3.5.

4.1. Global Asymptotic Stability of the Disease Free Equilibrium (DFE)

We have the following result for the global asymptotic stability of the disease free equilibrium:

Theorem 4.1. When, then the DFE for system (2) is GAS in.

Proof. Our proof is based on Theorem 4.3 of [12] , which establishes global asymptotic stability for epidemiological systems that can be expressed in the matrix form (5). This theorem is restated as Theorem A.1 in the Appendix: for the proof, the reader may consult [12] . To complete the proof, we need only establish for the system (2) that the five conditions (h1)-(h5) required in Theorem A.1 are satisfied when.

(h1) This condition is satisfied for the system (2) as a result of Proposition 2.

(h2) We note first that, and the canonical projection of on is; the system (2) re-

duced to this sub variety is, which is obviously GAS at on and thus on since;

(h3) We consider first the case and. In this case, the matrix in the system (2) is

In this case, the two properties required for condition (h3) follow immediately: off-diagonal terms of the matrix are non-positive; and Figure 3 shows the associated direct graph, which is evidently connected, thus establishing irreducibility. For general and the proof of (h₃) is similar.

(h4) Defining, we have , and; thus the upper bound of is attained at the DFE which is a point on the boundary of, and condition (h₄) is satisfied.

(h5) We first observe that is the block matrix of the Jacobian matrix of the system (1) corresponding to the infected sub-manifold, taken at the DFE. As has been pointed in [12] , the condition, which is equivalent to the condition that is a stable Metzler matrix, is also equivalent to the condition. This fact is developed in the proof of Proposition 3.4 (see Appendix) where we compute the value of by ex- pressing the stability of the Metzler matrix.

Since the five conditions for Theorem 4.3 of [12] are satisfied, the theorem follows. □

4.2. Stability Analysis of Endemic Equilibrium (EE)

In this section we address the analysis of the behavior of the system when the condition holds. It is obvious that in this case the DFE is not a stable steady state of the system (1); and as stated in Proposition 3.5, the system (1) admits a unique nontrivial biologically feasible equilibrium (the EE). In the remainder of this subsection, we establish the global asymptotic stability of the EE.

Theorem 4.2. When, the EE of the system (1) defined in Equation (8) is GAS on.

Remark 4.1. The above theorem implies the GAS of the EE in the non-negative cone, since the positive cone is absorbing for the system (1).

Proof. Considering the system (1) when, there is a unique EE with respective components given as in (8). As it is usual in the study of the stability of EE of epidemiological system in the literature [16] - [28] , let be the function defined on as follows:

(10)

where the coefficients, for, are positive constants to be determined such that the derivative of along the trajectories of the system (1) is non-positive. The technique adopted in the determination of the is that of Guo et al. [16] [17] using graph-theoretic approach to determine the global Lyapunov function for the global asymptotic stability of the EE in models involving multi-group. In their models and examples, the dynamic in divers sub-group were describe in the same shape. here is a case where it appears that this technique works also when the shape or sub-group involved in the dynamic can be different.

With these positive constants, is positive definite function on; its derivative along the trajectories of the system (1) is:

Substituting the value of, i.e., after some algebraic manipulations, the above becomes:

Using relations between values of components of the state of the model at the EE given in Equation (8) (see Proposition 3.5) specifically

and after few algebraic arrangements, the above becomes:

Taking; with this values of we have; exploiting for identities, the above becomes

(11)

The terms, , for each, and are non-positives by the Corollary A.1 of the Lemma A.1 (of arithmetic-geometric means inequality). is null whenever holds; for each, is null

whenever holds; is null on the subset of where; for each, is null on

the on the subset of where equalities given in (12) below hold.

(12)

Using the fact that is null whenever (or what should have been the same each is null when- ever) and scanning equalities given in (12), we have obviously that the subset of on which is reduced to.

It comes out that is a strict Lyapunov function for the system (1) on. By LaSalle invariance principle, we conclude to the GAS of the EE of the system (1) [29] -[32] . □

5. Numerical Simulation

To illustrate results in this work, the system (1) is simulated using parameters value/range in the following Table 3 and Table 4. We assume in all our simulations the initial ratio of fifty vectors for one human, since the model assume an episode of high endemicity of the disease (i.e.). We also assume the birth rate of the vectors slightly higher than the death rate (i.e. the hatching rate of the mosquitoes is); this establish how the consideration in the model can enforce saturation in exponential growth of the population of vectors. Certain coefficients have been assumed (i.e. for the host sub-population: probability of “feed and survive”, probability of “being killed during their questing activities” for mosquitoes). The remaining parameters are collected in the literature. The number of questing/resting steps before the infectious class of mosquitoes (i.e. the) comes from entomological literature [11] where there are well coined number of days for the extrinsic incubation period for vectors depending on the temperature. We have used some data always estimated from [6] [7] ; references relative to data can be found in there. The coefficient of the infectivity of mosquitoes relative to people of the group (i.e.) depends on the protecting strategy used in the group (i.e. since are coefficients modeling the protection strategy in the group is an increasing function). We assume that. With this function values of are in the interval of proposed data for. This assumption is only for simulation purpose, since we have not found data to evaluate this parameter.

Note. Source of the estimation:: [11] .

We also assume different values of coefficients and depend on the protecting strategy. Their values in simulations are taken in the range given in the Table 3 and Table 4 respecting the assumption that less people are bitten, less longer they stay infectious, and less they contribute to the infection of vectors.

We use for simulation Non-standard Finite Difference Scheme (NFDS) instead of classical ordinary differential packages that can be found in various scientific programming environment. The NFDS used is given in the Appendix D. As a matter of fact, the technique involved is designed by R. Anguelov et al. [33] as a numerical companion of [12] , that is well designed for system as ours (i.e. large scale system). Simulation using ode packages takes much time and solutions obtained, compared to those computed using NFDS are really less accurate.

5.1. Figures of Trajectories of Significatives Components of the States

Below, are plots of trajectories of significant components (when the time of the realization of the asymptotic stability is reasonable) of the states of the model (infectious hosts and infectious questing vector) or parametric curves (when the time of the realization of the asymptotic stability is very long) between significant components accompany by finishing sections of trajectories (to show how accurate the result produced by numerical scheme is) representing scenarios corresponding to set of data (with the corresponding values of the computed) given below each figure. The shows in these plots are the asymptotic stability (each scenario is based on three initial states); the effectiveness of the manner various combination of parameters values acts to lower the endemicity of the malaria in the area. These plots are organized in scenarios based on protecting skills.

5.1.1. Scenarios with One Protected Skill of Two Third of the Hosts with Net with Poor Killing Effect

Figures 4-11 show scenarios where humans are protected with bed nets with small killing effect (i.e.)

and a repelling effect that increases from poor (see Figure 4, Figure 5, where) to a quite high (see Figure 10, Figure 11, where).

5.1.2. Scenarios with One Protected Skill of Two Third of the Hosts Using Net with Killing Effect

Figures 12-19 show scenarios where the killing effect of bed nets in protection skills is better () than those in scenario in Figures 4-11.

Figures 20-27 are scenarios with one protection skill not corresponding to the section, and which, with parameters values have been chosen in order to compute situation of closed to one. Figures 20-23 are parametric curves (Figure 20, Figure 21 when and Figure 22, Figure 23 when closed to one) of the dependence between infectious hosts and infectious vectors components of the state of the model, with the finishing section of the corresponding components (Figure 24, Figure 25 when and Figure 26, Figure 27 when closed to one). What is fascinating in these figures is the accuracy of the results produced by the numerical scheme used.

5.1.3. Scenarios with One Protected Skill of Six Seventh of the Hosts Using Net

We now change the proportion of bed net users from two third to six seventh in scenarios corresponding to lowest feeding effects in figures (scenarios in Figure 10, Figure 18). Figures 28-31 show how important this impacts trajectories presented. It can be observed that the drop down of the endemicity happens quickly and strongly. e.g. in Figure 29, despite the value of is greater than one and the killing capability of the protection of protected hosts is weak, at the fiftieth day the area is cleared of the infected questing mosquitoes and consequently cleared of principal factor of the disease.

5.1.4. Scenarios with Two Protected Skills; Half Protected and Full Protected

For scenarios with two protections (for half protected, and for full protected), since the components of infectious vectors behave nearly the same as what appears in scenarios with one protection in Figures 4-31 above, we present only figures of trajectories of the infectious hosts components of the state of the system (Figure 32, Figure 33). For chosen values of parameters such that is closed to unity, parametric curves representing infectious hosts variations for three initial states (Figure 34,), (Figure 35,); since for each, the time of the realization of the asymptotic stability is quite long, the respective finishing sections of each case is also presented for the obviousness of the point each tends to, since the two figures look the same (Figure 36,), (Figure 37,). In Figure 38 is trajectories of infected hosts with parameters of scenarios in Figures 33 with modification in the proportion of protected hosts as a show of how the proportion of bed net users impact on the level of endemicity.

5.1.5. Scenarios with Three Protected Capabilities; Poor Protected, Middle Protected and Full Protected

For scenarios with three protections (for poor protected, for middle protected and for full protected),

since the components of infectious vectors behave nearly the same as what appears in scenarios with one protection in Figures 4-33 above, we present only figures of trajectories of the infectious hosts components of the state of the system (Figures 39). For chosen set of parameters such that is closed to one, parametric plots of curves representing infectious hosts variations for three initial states (Figure 40, Figure 41, , Figure 42, Figure 43,) since for each, the time of the realization of the asymptotic stability is quite long. Since there are four infectious hosts components (i.e., , and), each of the four curves in scenarios presented above is a combination of three infectious components. Finishing sections of trajectories of infectious hosts components of the state are also presented for the obviousness of the equilibrium in each case since plots of parametric curves are nearly similar (Figure 44, , Figure 45,). In Figure 46 is a scenario with parameters of scenario in Figure 40 with modification of proportion in bed net users as a show of how the proportion of bed net users impact on the level of endemicity.

5.2. Comments on Figures

In the Graphical representation (Subsection 5.1 here above), we assumed a human population constituted in a

thousand of individuals and at any initial state, the size of vectors population is fifty time the size of the hosts population. We also assumed the hatching force of mosquitoes sufficiently high to figure situation of an area of higher malaria endemicity.

In all figures, we choose to present only coordinates of the states of the model corresponding to the infectious humans and infectious questing vectors, since they are the most relevant from the analysis in this paper. Figures 4-31 are plots of trajectories and parametric curves with the same initial states (three initial states) corresponding to scenarios based on one protection strategy. For values of (see Figures 4-25, Figure 28 and Figure 29), we have couples of figures (figures with odd numbers representing trajectories of infectious hosts components, and those with even numbers representing trajectories of the infectious questing vectors of the state of the model). Figures 4-11 show scenarios where humans are protected with bed nets with small killing effect (i.e.) and a repelling effect that increases from poor (see Figure 5, Figure 6, where) to a quite high (see Figure 11, Figure 12, where). The repelling effect is characterized by the probability that mosquitoes must not be able to feed (i.e. for). Values of computed in Figures 4-11 are high (). A certain drop down is observed in the level of the, but

the endemicity regarding the level of the infectious hosts is still high. Figures 12-19 that correspond to scenarios where peoples are protected with bed nets with the killing effect, following the same reasoning that is done for Figures 4-11, we observe significant drops of values of computed (). This establishes how important the killing effect of the bed net protection is. Figures 4-19 exhibit also how combination of and, associated to choices of others parameters influence the endemicity of the disease and the saturation of the area with infectious questing mosquitoes. Scenarios presented in Figures 20-25 correspond to parameters chosen such to realize the result of global asymptotic stability of the endemic equilibrium when the condition and the closed to one hold. Parametric curves (Figure 20, Figure 21) have been preferred to trajectories since the time of the realization of this stability was quite long and the finishing sections of trajectories (Figures 24, Figure 25) have been presented to let the obviousness this stability appeared. In the same way, scenarios presented in Figure 22, Figure 27 correspond to parameters chosen such to realize the result of global asymptotic stability of the disease free equilibrium when the condition and the closed to one hold. Parametric curves (Figure 22, Figure 23) have been preferred to trajectories

since the time of the realization of this stability was quite long and the finishing sections of trajectories (Figure 26, Figure 27) have been presented to let the obviousness of this stability appeared. What is enlightened in the presentation of these figures is the efficacy of the scheme used for our simulations. The Non Standard Finite Difference Scheme (NSFDS) of Anguelov et al. [33] is definitely established here as the unchangeable scheme for simulation of system like ours. (more than seventeen equations). Coming back to our initial goal, scenarios in Figures 28-31 are made up by increasing the proportion of protected bed net users in scenarios in Figure 10, Figure 11 and in Figure 18, and Figure 19 respectively. In these figures, it appears obviously and in all proportion how, when the great majority of hosts are bed net users, this impacts the endemicity of malaria. The area is quickly cleared from vectors, and the endemicity in term of the quantity of infected host drops down quickly.

Figures 32-38 are plots of trajectories (Figure 32, Figure 33 and Figure 38) and parametric curves with finishing sections of trajectories (Figures 34-37) with the same initial states (three initial states) representing scenarios based on two protection strategies (half protection indexed by and full protection indexed by). In these strategies, plots presented are only those of infectious host components of the state of the model; the

infectious questing mosquitoes component behave nearly in the same manner as those in plots of infectious questing mosquitoes components in Figures 4-31; we exclude them since they are very large files. Comparing Figure 32 and Figure 33, it comes out another presentation of the influence of the killing effect of the bed net protection on the prevalence of the disease. A minor modification of makes a remarkable drop down of the value of and significant modification in trajectories as presented in the two figures. Figure 34 and Figure 35 are three dimensional plots of curves representing the dependence between, and, the three infectious hosts components of the state of the model. We present this curves since the time of the realization of the asymptotic stability is quite long; Figure 36 and Figure 37 are the respective finishing sections of trajectories of components in Figure 34 and Figure 36. The purpose in the four figures is the presentation of the global asymptotic stability of the model in conditions and with closed to one. The Figure 38 shows how the level the endemicity is affected by the modification of the proportion of protected hosts; we have considered the scenario corresponding to Figure 33 in which we have reduced the proportion of non-protected hosts, and increase the proportion of the two other host sub-populations in the scenario; in all proportions, the level of the endemicity goes down.

Figures 39-46 are plots of trajectories (Figure 39 and Figure 46), parametric curves (Figures 40-43) and respective finishing sections of trajectories in scenarios represented with parametric curves (Figure 44 and Figure 45), with the same initial states (three initial states) representing scenarios based on three protection strategies (poor protection indexed by, middle protection indexed by and full protection indexed by). In these strategies, plots presented are those of infectious host components of the state of the model, motivated by the same reasons as the presentation of scenarios based on two protection strategies. Figure 39 shows how combining several strategies of protection impacts on the value of and the prevalence of the disease in the given area. Figures 40-43 are three dimensional plots of curves representing the dependence between each of the four combinations of three of the four infectious hosts components of the state of the model. We consider presenting this curves since the time of the realization of the asymptotic stability is quite long. The purpose in Figures 40-43 is the presentation of the global asymptotic stability of the model in conditions (Figure 40, Figure 41) and (Figures 42, Figure 43) with closed to one; we have joined Figure 44 and Figure 45, the respective finishing section of each of the pair of preceding figures to let what happen in each case be obvious. Figure 46 is plots of trajectories of components of infectious hosts in a scenario made by

modifying the proportion of host with in data of the scenario in Figure 39. It obviously appear how in all proportions, the level of the endemicity goes down.

6. Discussion on the Contribution

This paper stands as a mathematical contribution in order to evaluate how effective the utilization of bed nets in the fight against malaria in endemic areas can be. We proposed a model of the dynamic of malaria transmission involving a population of vectors and a population of humans as hosts subdivided into several sub-populations depending on the way they usually protect themselves against mosquito bites. Even though the model is made of a generic number of equations that can be high, the model is sufficiently simple to capture what is essential (i.e. how the protecting factors (and) and the probabilities of the transmission from the vectors to hosts

and probabilities of the transmission from host to vectors act on the value of the basic reproduction number, and act also on the level of the endemicity that corresponds to cases where). The level of the endemicity is materialized by how the value of at the endemic equilibrium that is can be small. Even though we do not have its explicit value, we know its upper bound that depends on parameters of the model (see (8)); it depends on the duration of the extrinsic incubation period represented by the; the longer is the extrinsic incubation period the smaller is the upper bound of the. It depends also in a more delicate way on all other parameters since they participate in the computation of the frequencies, and also; this dependence is shown in simulations and presented here in various figures. The smaller is the, the smaller is the value of. It appears also in simulations how the drop down of the endemicity in host sub-populations happen depending on the drop down of the endemicity in the vectors population and subsequently on the

combination of parameters. If the highest proportion of hosts uses insecticide treated bed nets with good protection capability (i.e. if hosts use bed nets treated with insecticide with good repelling and killing capabilities), this acts on the level of the endemicity. As it appears in simulations in scenarios of more than three sub-populations of hosts, even though there are sub-populations that use low level protection, the impact of the high proportion of bed nets users that use well-protecting bed nets on the level of endemicity is obvious. The policy in countries in endemic area is founding the ownership of mosquitoes―treated net and advertising by various media for its large utilization by people. In Cameroon Mosquitoes―treated nets that are freely distributed are called MILDA (i.e. Moustiquaire Imprégnée à Longue Durée d’Action), meaning Bed Nets with long lasting protection against mosquitoes. Even though there is some doubt for its long lasting protective and killing capability, there is no concern regarding hypothetical regain of endemicity of the malaria. There is no

need of changing old one for new one. The long lasting protecting capability of those Bed Nets can be also based on the fact of continuing of sleeping under the protection of a bed net, and the continuation of the policy of the distribution of “MILDA”.

An interesting research topic that can follow this paper is studying the regain of endemicity that can be observed, in certain malaria endemic regions. In the far north region of Cameroon, after the rainy season, months August to November 2013, there have been an increase on the level of endemicity of the malaria that have resulted in many deaths. A naive explanation of this fact can be the stopping of the utilization of bed net protecting measures associated with the profusion of the area by new hatching mosquitoes that happens with seasonal weather changes to dry to rainy and rainy to dry. People that have lost the immunity due to long term protection become totally susceptible and are exposed again.

In simulations, we made a strong focus on scenarios of endemicity (i.e. scenarios with). The study is about regions with high endemicity with the goal to lower the endemicity. Simulations show how combination of factors in the model can help weaken the endemicity. Extended simulations to cases of low values of would have been also good; but this would have substantially increased a lot the number of case studies. A focus is also made on the shows of the asymptotic stability of endemic equilibrium. This is the reason for the consideration of three different initial states for each figure, and the presentation of finishing sections in figures corresponding to choices parameter values related to close to one; for those chosen values, the time to run to the shows of the stability is quite long; the finishing sections were to establish the global stability of equilibrium; the DFE in cases of, and the endemic equilibrium is cases of. For this Non Standard

Finite Difference Scheme (NSFDS) has been used for the effectiveness of the shows. NSFDS is the scheme highly adapted for the integration of system with many equations like our models. Ode packages are less efficient (i.e. much longer processing time, and results with less accuracies).

7. Conclusion and Perspective

We have considered the problem of analyzing the model of the utilization of bed net in the fight against malaria. The proposed model takes into account multiple levels of protection with bed net in human population, multiple (questing, resting) steps between the first successful infected blood meal and the infectious state of mosquitoes. This consideration is a modeling of the activity of vectors in the dynamic of the malaria, which has not yet been

considered by modelers of vectors borne diseases. As it appears in the analysis that we addressed, this can be a considerable step in the understanding of the complexity of vector borne diseases. We have obtained the basic reproduction number, whatever is the scale of the system; we have established that the DFE of the model is GAS providing that. This is an improvement of a result always in the literature in [34] , where the condition of the stability of the DFE is not based on the above inequality. We also analyzed the behavior of the model when. In this last case, we establish that there is a unique EE, and we prove that this equilibrium is GAS for our system. We are aware of the fact that this is still far away from the ideal deterministic model on the same subject; as a matter of fact, malaria is one of the principal disasters and one of the first causes of death in

African countries. A more realistic model must take into account parameters of death, birth and migration in human sub-populations, and the account must also be taken for exposed and removed states in human sub- populations. Our work seems non-negligible to us, since the endemicity of malaria happens by episodes, and in different episodes, values of parameters must not be the same. It is also the first time that the activity of vectors is used in the modeling of a vector borne disease.

Cite this paper

Jean ClaudeKamgang,Vivient CorneilleKamla,Stéphane YanickTchoumi, (2014) Modeling the Dynamics of Malaria Transmission with Bed Net Protection Perspective. Applied Mathematics,05,3156-3205. doi: 10.4236/am.2014.519298

References

Appendix

A. Useful Definitions and Results

Herein, one finds definition of terms and notions used throughout the paper; some results, useful in our proof found here and there in the literature are also included; this in order to avoid frequent interruption of the exposition and to make the paper as self-contained as possible. The readers are pleased to refer to the cited reference for the proof of results.

Definition A.1 (Metzler matrix [35] -[37] ). A given real matrix is said to be a Metzler matrix if all its off-diagonal terms are non-negative.

The qualification currently used to such matrix is the “-matrix”; a given square matrix with real coefficients is said to be a Metzler matrix if and only if is an -matrix. The essential property of Metzler matrices used in this paper is the fact that every dynamical system described by ordinary differential equations which Jacobian matrix is a Metzler matrix keeps invariant the positive cone in its space state.

Definition A.2 (Irreducible matrix). A given matrix is said to be an reducible matrix if there exists

a matrix of permutation such that the matrix has the block matrix form

where and are square matrices. The matrix is said to be irreducible otherwise.

Irreducibility of can be checked using the associated directed graphs. The directed graph associated with has vertices with a directed arc from to j if and only if. It is strongly connected if any two distinct vertices are joined by an oriented path. The matrix is irreducible if and only if is strongly connected [17] .

Lemma A.1 (Arithmetic-Geometric Means Inequality[38] ).

Let be positive real numbers. Then

Furthermore, exact equality only occurs if.

An immediate consequence of the Arithmetic-Geometric Means Inequality follows.

Corollary A.1 ([38] ). Let be positive real numbers such that their product is 1. Then

.

Furthermore, exact equality only occurs if.

Theorem A.1 ([12] ). Consider the system (5) defined on a positively invariant set. Assuming

h₁: The system is dissipative on.

h₂: The equilibrium of the sub-system of the system (5) is GAS on the canonical projection of on.

h₃: The matrix is Metzler matrix and irreducible for each.

h₄: There is an upper-bound matrix (in the sense of point wise order) for the set of square ma-

trices with the property that either or if, then for any such

that, we have.

h₅:.

Then, the DFE is GAS for the system (5) in.

B. Proof of Proposition 3.4

Since the system reduced on the infection free sub-variety of , system has a unique equilibrium that is GAS (we recall here that the DFE is as stated in the proposition), we seek for conditions under which the matrix , that is the sub matrix of the Jacobian matrix of the system (2) reduced to the infected sub variety at the DFE is stable. This matrix is a Metzler matrix, so we must seek for conditions, for which the matrix is Metzler stable matrix. We apply the algorithm given in the proposition 3.3 to the matrix ; we have: is Metzler stable matrix if and only if

and are Metzler stable matrix. Since is always a Metzler stable matrix, is Me- tzler stable matrix if and only if

is Metzler stable matrix.

is a matrix that can be decomposed into the following block matrix form:

with , , and is a matrix with each entry of the second row equal to zero, and each entry on the first row equal respectively to

We make another iteration of the algorithm given by the proposition 3.3 above; we have: is Metzler

stable if and only if and are Metzler stable matrices. Since

is always a Metzler stable matrix, we have: is a Metzler stable if and only if

is a Metzler stable matrix.

with

(13)

For the last iteration of the algorithm, since is negative coefficient (i.e. a Metzler stable matrix),

We have that the necessary and sufficient condition of the matrix is the unique condition

i.e.

with the expression of given in (13) we have:

this inequality is rewritten as

with the value of given in the proof of the proposition the above is rewritten:

After few algebraic arrangements in the above, we have

(14)

Thus the Matrix is Metzler stable if and only if the condition (14) holds.

We recall that and denote the questing and the resting frequencies of mosquitoes respectively.

By biological means, the coefficient in the left of the condition (14) is the basic reproduction number. As a matter of fact, following the description in [6] of different factors that must be taken in account in the expressions of the basic reproduction number, we have the coefficient

that describes the successfulness for mosquitoes of crossing the steps of questing resting without been killed. Mosquitoes which cross those step reach the last exposed compartment, say . So the due time to get

from the susceptible state to the infectious state is . Multiplying this coefficient by

gives the average number of secondary cases of mosquitoes which are infectious from primary infection within the contact with one infectious host of the group. It corresponds to

of [6] . Straightforwardly the average number of secondary cases of host of the group within the contacts with an infectious questing vector is:

.

It comes out as it is usual while dealing with vector born diseases that

represents the average number of secondary cases of infectious vectors (respectively hosts) that are occasioned by one infectious vector (respectively host) introduced in a population of susceptible vectors (respectively hosts). i.e. for the population of vectors and also for the population of hosts. When this number is computed with the technique of the next generation matrix of van den Driessche et al. [10] , it appears usually with a square root; it is so common to find, even if it is not computed with the next generation matrix technique a square root coming from nowhere appearing in the expression at the end on the number. There is a paper of J. Li et al. [39] talking about possible failure of the next generation matrix technique. specially in cases of diseases with three actors or more, like vector borne diseases. We have tried with the technique in [10] with reasonable choice of and and the result was the square root of the here above. □

C. Proof of Proposition 3.5

The purpose of Proposition 3.5 is to determine possible steady states of the system (1).

The disease free equilibrium occur at a state , with components representing non-naive classes equal to zero i.e. with . The characteristic equation of steady state of the system (1) with the constraint is

this is a linear equation which admits the unique solution .

The endemic equilibriums would happen at probable states of the model where at least one of the infected or infectious components is non-zero. Since disease begins with the presence of a questing infectious vectors that successfully transmits disease to a host in one of the host sub-population, we assume that where is the component of corresponding to the infectious questing mosquitoes; scanning equations in the system (1), it comes out the values:

make components of the vector field that describe variations of infected and infectious components of the state of the model vanish.

The value of is obtained by merging equation of and at the equilibrium on the expression of . As a matter of fact, at the endemic equilibrium, we have:

substituting this value in the expression of at the equilibrium gives

and thus,

.

For each , the component of steady state is ruled by the equality: this yields:

.

All components given above assume that there is a feasible non-zero . To determine this component, we use the two expressions of take at this steady state.

The first comes from the equality (second Equation of (1)) we have:

(15)

The second comes from the expression of issued from the construction of the model

(16)

and the two expressions depends on .

Merging (15) and (16) gives the following equation with as unknown

(17)

Setting as the new unknown, and , with the relation:

(18)

made by the expression of (7), the expression (17) becomes:

(19)

Classically, at this stage, a rational function is derived; the property of the solution is obtained from the function in the numerator of the rational function, using the Descartes criterion that depends on the value of . The Descartes criterion gives the number of probable roots of the function in the numerator, but does not point the scale of the hypothetical roots. In the case in which we are interested here, we need more than the existence of roots of the function in the numerator of the rational function; it is also important to know more about their scale. For this we have thought about some basic knowledge of the elementary mathematics specifically the intermediate value property that is to be used applied on the hall rational function.

Setting

we have that is a rational function, which is thus of class on ; The part of this set that is interesting to us is ; we also have ; obviously, whenever . We have also that , ; and ; The derivative of the function is which is a positive function on ; is thus an increasing function on . Using the intermediate value property of elementary mathematics, it comes out that there are two solutions for Equation (19), with the biologically feasible one in the interval , and the second solution situated at the infinity, that is not biologically feasible. this ends the proof. □

D. Non Standard Finite Difference Scheme Used in Simulations

The Non Standard Finite Difference Scheme uses for simulations is:

(20)

with; solved in the term give the semi implicit system of difference equations

(21)

The time step function corresponding is, with.

The equation above can be written in the short form as

(22)

where

.

The matrix may be written in in block matrix form as:

with the two bands diagonal square matrix, where diagonal and sub-diagonal terms are components of the vectors and respectively defined by:

and

and are respectively and matrices given by:

is the matrix with only the last component of the first row equal to , and the other components equal to zero.