Applied Mathematics
Vol.5 No.13(2014), Article
ID:47931,5
pages
DOI:10.4236/am.2014.513199
Truncated Geometric Bootstrap Method for Time Series Stationary Process
T. O. Olatayo
Department of Mathematical Science, Olabisi Onabanjo University, Ago-Iwoye, Nigeria
Email: otimtoy@yahoo.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 April 2014; revised 30 May 2014; accepted 10 June 2014
ABSTRACT
This paper introduced a bootstrap method called truncated geometric bootstrap method for time series stationary process. We estimate the parameters of a geometric distribution which has been truncated as a probability model for the bootstrap algorithm. This probability model was used in resampling blocks of random length, where the length of each blocks has a truncated geometric distribution. The method was able to determine the block sizes b and probability p attached to its random selections. The mean and variance were estimated for the truncated geometric distribution and the bootstrap algorithm developed based on the proposed probability model.
Keywords:Truncated Geometric Bootstrap Method, Stationary Process, Moving Block and Geometric Stationary Bootstrap Method

1. Introduction
Several studies have been made of truncated distribution. [1] has treated the truncated binomial distribution. [2] [3] also treated the truncated binomial and negative binomial distribution and truncated Poisson distribution and has shown how to estimate the parameter of distributions. The first part of the present paper shows how to estimate the parameter of truncated geometric distribution as a true probability model, by method of moment. The second part of the paper uses the distribution to developed bootstrap algorithm for stationary time series process to overcome the difficulties of moving block scheme [4] [5] and geometric Bootstrap scheme of [6] in determining probability p and block size b respectively. The heart of the bootstrap is not simply computer simulation, and bootstrapping is not perfectly synonymous with Monte Carlo. Bootstrap method relies on using an original sample or some part of it, such as residuals as an artificial population from which to randomly resample [7] . Bootstrap resampling methods have emerged as powerful tools for constructing inferential procedures in modern statistical data analysis. The Bootstrap approach, as initiated by [8] , avoids having to derive formulas via different analytical arguments by taking advantage of fast computers. The bootstrap methods have and will continue to have a profound influence throughout science; as the availability of fast, inexpensive computing has enhanced our abilities to make valid statistical inferences about the world without the need for using unrealistic or unverifiable assumptions [9] .
An excellent introduction to the bootstrap may be found in the work of [10] -[13] . Recently, [4] and [5] have independently introduced non-parametric versions of the bootstrap that are applicable to weakly dependent stationary observations. Their sampling procedure have been generalized by [6] by resampling “blocks of blocks” of observations for the stationary time series process. On this note we propose a stationary bootstrap method generated by resampling blocks of random size, where the length of each block has a “truncated geometric distribution”.
2. Materials and Method
The truncation is more than just theoretical interest as a number of applications have been reported in [14] .
Estimating the Parameter of Truncated Geometric Distribution.
A random variable X may be defined to have a truncated geometric distribution, with parameter p. and N terms, when it has the probability distribution.
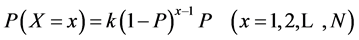 (2.1)
(2.1)
The constant K is found, using condition
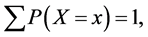 to be
to be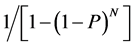 .
.
We shall introduce a truncated form of the geometric distribution and then demonstrate that it is suitable model for a probability distribution. Hence, the probability density function is:
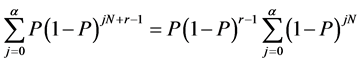 (2.2)
(2.2)
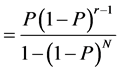 (2.3)
(2.3)
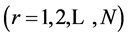
These are the probabilities of truncated geometric distribution with parameter P and N terms. Therefore we intend to derive the distributional properties of our estimates by looking at the expectation and variance of truncated geometric distribution.
Thus,
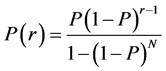
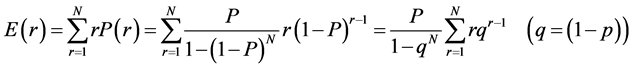 (2.4)
(2.4)
Recall some facts on geometric series,
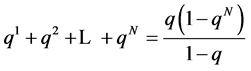 (2.5)
(2.5)
Using method of moment we have;
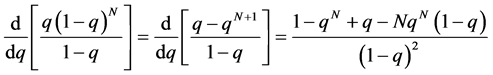 (2.6a)
(2.6a)
 (2.6b)
(2.6b)
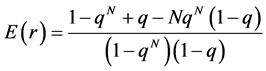 (2.7)
(2.7)
Thus, 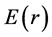 is the sample mean, as demonstrated by [15] .
is the sample mean, as demonstrated by [15] .
In this paper, we derived the second moment further.
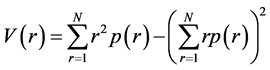 (2.8)
(2.8)
Thus,
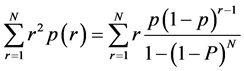
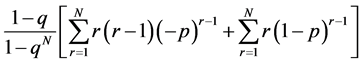
For the second moment and by second differentiation we have,

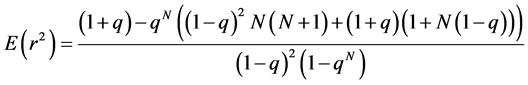 (2.9)
(2.9)
For the variance
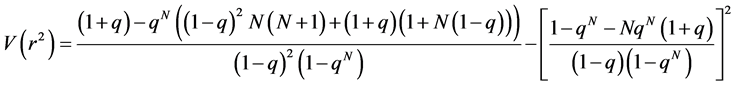
The variance for truncated geometric distribution is:
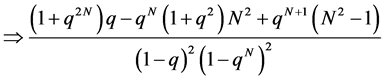
Therefore, when N = 0 we have 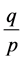 and
and 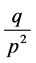 corresponding to the mean and variance of geometric distribution.
corresponding to the mean and variance of geometric distribution.
Suppose that length L, numbered 1 to N are to be selected randomly with replacement which is the principle of bootstrap as introduced by [8] . Then the process continues until it is truncated geometrically at r with an appropriate probability p attached to its random selections in form of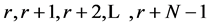 .
.
3. Results and Discussions
In this paper, we take our N to be 4, that is, the random selections could be truncated between 1 to 4 at an appropriate probability attached to each of them respectively.
Using Equation (2.3) and from any fixed value of p in (0, 1). Different values of p can be generated for any values of r. Therefore our r here will represent the number of blocks to be selected and the appropriate values of p attached to it are the probabilities of being selected at each random selection with replacement.
Below are the table value generated for a number of fixed number of p in (0, 1), for different values of rth truncation geometrically.
From the Table 1, each value r = 1 to N will be our b (block sizes) and each values of p (probability) for each various random selections.
Table 1. Summary Statistics values for truncated geometric distribution
Suppose that L length, numbers 1 to N are to be selected randomly with replacement. Then, the process continues until it is truncated geometrically at r with an appropriate probability P attached to its random selection in form of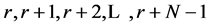 . We take our N to be 4, that is, the random selections could be truncated between 1 to 4 at an appropriate probability.
. We take our N to be 4, that is, the random selections could be truncated between 1 to 4 at an appropriate probability.
Then, a description of the resampling algorithm when r > 1 is as follows:
1) Let 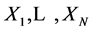 be a random variables 2) Let
be a random variables 2) Let 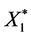 be determined by the r-th truncated observation Xr in the original time series3) Let
be determined by the r-th truncated observation Xr in the original time series3) Let 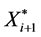 be equal to Xr+1 with probability 1 − P and picked at random from the original N observations with probability p.
be equal to Xr+1 with probability 1 − P and picked at random from the original N observations with probability p.
4) Let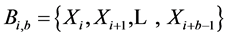 , be the block consisting of b observation starting from Xi
, be the block consisting of b observation starting from Xi
5) Let 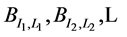 be a sequence of blocks of random length determined by truncated geometric distribution.
be a sequence of blocks of random length determined by truncated geometric distribution.
6) The first L1, observations in the pseudo time series 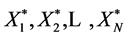 are determined by the first block
are determined by the first block 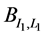 of observation
of observation 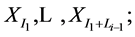 the next L2 observations in the pseudo time series are the observations in the second sampled block
the next L2 observations in the pseudo time series are the observations in the second sampled block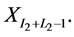 .
.
7) The process is resampled with replacement, until the process is stopped once N observation in the pseudo time series have been generated.
8) Once 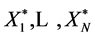 has been generated, one can compute the quantities of interest for the pseudo time series.
has been generated, one can compute the quantities of interest for the pseudo time series.
The algorithm has two major components, the construction of a bootstrap sample and the computation of statistics on this bootstrap sample, and repeats these operation many times through some kinds of a loop.
Proposition 1. Conditional on  is stationary.
is stationary.
If the original observations  are all distinct, then the new series
are all distinct, then the new series 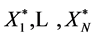 is, conditional on
is, conditional on 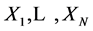 a stationary Markov chain. If, on the other hand, two of the original observations are identical and the remaining are distinct, then the new series
a stationary Markov chain. If, on the other hand, two of the original observations are identical and the remaining are distinct, then the new series 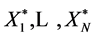 is a stationary second order Markov chain. The stationary bootstrap resampling scheme proposed here is distinct from the proposed by [4] [5] , but posses the same properties with that proposed by [2] .
is a stationary second order Markov chain. The stationary bootstrap resampling scheme proposed here is distinct from the proposed by [4] [5] , but posses the same properties with that proposed by [2] .
4. Conclusion
The truncated geometric bootstrap method proposed in this paper is a true probability model with the estimated parameters. The method was able to determine the block sizes b and probability p attached to its random selections. The mean and variance were estimated for the truncated geometric distribution and the bootstrap algorithm developed based on the proposed probability model.
References
- Finney, D.J. (1949) The Truncated Binomial Distribution. Annals of Eugenics, 14, 319-328. http://dx.doi.org/10.1111/j.1469-1809.1947.tb02410.x
- Rider, P.R. (1953) Truncated Poisson Distribution. Journal of the American Statistical Association, 48, 826-830. http://dx.doi.org/10.1080/01621459.1953.10501204
- Rider, P.R. (1955) Truncated Binomial and Negative Binomial Distribution. Journal of the American Statistical Association, 50, 877-883. http://dx.doi.org/10.1080/01621459.1955.10501973
- Kunsch, H.R. (1989) The Jacknife and the Bootstrap for General Stationary Observations. The Annals of Statistics, 17, 1217-1241. http://dx.doi.org/10.1214/aos/1176347265
- Liu, R.Y. and Singh, K. (1992) Moving Blocks Jackknife and Bootstrap Capture Weak Dependence. In: R. Lepage and L. Billard, Eds., Exploring the Limits of Bootstrap, John Wiley, New York.
- Politis, D.N. and Romano, J.O. (1994) The Stationary Bootstrap. Journal of American Statistical Association, 89, 303-1313. http://dx.doi.org/10.1080/01621459.1994.10476870
- Barreto, H. and Howland, F.M. (2005) Introductory Econometrics, Using Monte Carlo simulation with Microsoft Excel. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511809231
- Efron, B. (1979) Bootstrap Methods: Another Look at the Jacknife. The Annals of Statistics, 7, 1-26. http://dx.doi.org/10.1214/aos/1176344552
- Leger, C., Politis, D. and Romano, J. (1992) Bootstrap Technology and Applications. Technometrics, 34, 378-398. http://dx.doi.org/10.1080/00401706.1992.10484950
- Efron, B. and Tibshirani, R. (1986) Bootstrap Measures for Standard Errors, Confidence Intervals, and Other Measures of Statistical Accuracy. Statistical Science, 1, 54-77. http://dx.doi.org/10.1214/ss/1177013815
- Efron, B. and Tibshirani, R. (1993) An Introduction to the Bootstrap. Chapman and Hall/CRC, London
- Diciccio, T. and Romano, J. (1988) A Review of Bootstrap Confidence Intervals (with Discussion). Journal of the Royal Statistical Society B, 50, 338-370.
- Davison, A.C. and Hinkley, D.V. (1997) Bootstrap Methods and their Application. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511802843
- Bancroft, G.A., Colwell, D.J. and Gillet, J.R. (1983) A Truncated Poisson Distribution. The Mathematical Gazette, 66, 216-218.
- Kapadia, C.H. and Thomasson, R.L. (1975) On Estimating the Parameter of the Truncated Geometric Distribution by the Method of Moments. Annals of the Institute of Statistical Mathematics, 20, 519-532.


