ABSTRACT

Received December 20, 2013; revised January 20, 2014; accepted January 27, 2014

The Schwarz method for a class of elliptic variational inequalities with noncoercive operator was studied in this work. The author proved the error estimate in L^∞-norm for two domains with overlapping nonmatching grids using the geometrical convergence of solutions and the uniform convergence of subsolutions.

Keywords:

Variational Inequalities; Schwarz Method; Subsolutions; L^∞-Error Estimates

1. Introduction

More than one hundred years ago, Schwarz algorithms were proposed for proving the solvability of PDEs on a complicated domain. With parallel calculators, this rediscovery of these methods as algorithms of calculations was based on a modern variational approach. Pierre-Louis Lions was the starting point of an intense research activity to develop this tool of calculation, see, e.g., [1,2] and the references therein [3-9].

In this paper, we give a new approach to the finite element approximation for the problem of variational in- equality with noncoercive operator. This problem arises in stochastic control (see [10]). We consider a domain which is the union of two overlapping sub-domains where each sub-domain has its own generated triangulation. To prove the main result of this work, we construct two sequences of subsolutions and we estimate the errors between Schwarz iterates and the subsolutions. The proof stands on a Lipschitz continuous dependency with respect to the source term for variational inequality, while in [5] the proof stands on a Lipschitz continuous dependency with respect to the boundary condition.

The paper is organized as follows. In Sections 2, we introduce the continuous and discrete obstacle problem as well as Schwarz algorithm with two sub-domains and give the geometrical convergence theorem. In Section 3, we establish two sequences of subsolutions and their error estimates and prove a main result concerning the error estimate of solution in the -norm, taking into account the combination of geometrical convergence and uniform convergence [11,12] of finite element approximation.

2. Schwarz Algorithm for Variational Inequalities with Noncoercive Operator

2.1. Notations and Assumptions

Let’s consider functions

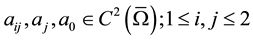(1)

such that

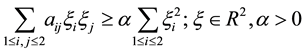(2)

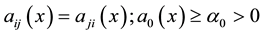(3)

where is a connected bounded domain in 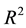with sufficiently regular boundary.

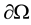We define a second order differential operator

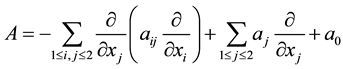(4)

where the bilinear form associated:

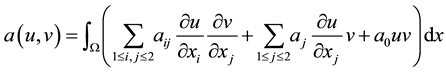(5)

Let 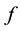be a function in

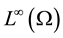(6)

an obstacle

(7)

a regular function defined on 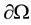such that

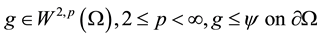(8)

AM and a nonempty convex set

(9)

We assume there exists 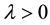large enough and a constant such that

(10)

Putting

(11)

then the bilinear form is strongly coercive.

Let be the solution of variational inequality (V.I)

(12)

which is equivalent to

(13)

denotes the usual inner product in

We define the solution of the following V.I

(14)

where and is a mapping from into itself.

Remark 1. We call quasi-variational inequality (Q.V.I) if the right hand side depends of solution, in the contrary case we call variational inequality (V.I).

2.2. Some Preliminary Results on the V.I Noncoercive

Thanks to [10], the problem (12) has one and only one solution, moreover satisfies the regularity property

We give a monotonicity property of the solution with respect to both the source term, the boundary condition and the obstacle. Let be a pair of data and the correspond- ing solution of V.I (12).

Lemma 1 [10] Under the preceding notations and assumptions (1) to (11), if and, then.

Let be the set of sub-solutions of the Q.V.I, ie all the such that

(15)

that is equivalent to

Lemma 2 [10] Under the preceding notations and assumptions (1) to (11), the solution of problem (12) is the maximum element of the set.

We show the Lipschitz property, which gives the continuous dependance to the data.

Lemma 3 Under the preceding notations and assumptions (1) to (11), we have

where is an independent constant of data.

Proof Firstly, let

we have

then

and

if we put

then

therefore

Secondly, it is clear that

and

so, due to lemma 1, we get

which gives

by changing the roles of and we obtain

which completes the proof.

Remark 2 If and, then we have

Let be decomposed into triangles and let denote the set of those elements; is the mesh-size. We assume the triangulation is regular and quasi-uniform. Let denote the standard piecewise linear finite element space and by the basis functions of the space. Let be the usual restriction operator in. The discrete counterpart of (13) consists of finding solution of

(16)

where

(17)

is an interpolation operator on

We shall assume that the matrix defined by

(18)

is -matrix [13] (i.e. angles of triangles of are).

2.3. The Continuous Schwarz Algorithm

Consider the model obstacle problem: find such that

(19)

where defined in (9) with.

We decompose into two overlapping polygonal subdomains and such that

and satisfies the local regularity property

we denote the boundary of and The intersection of and is assumed to be empty. We will always assume to simplify that are smooth.

For we define

We associate with problem (19) the following system: find solution of

(20)

where

Starting from we define the continuous Schwarz sequences on such that solves

(21)

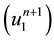
and on such that solves

(22)

where

The following geometrical convergence is due to ([2], pages 51-63)

Theorem 1 The sequences and of the Schwarz algorithm converge geometrically to the solution of the problem (20). More precisely, there exist two constants such that for all

2.4. The Discretization

For; let be a standard regular and quasi-uniform finite element triangulation in, being the mesh size. We assume that the two triangulations are mutually independent on where a triangle belonging to one triangulation does not necessarily belong to the other. Let be the space of continuous piecewise linear functions on which vanish on For we define

where denotes a suitable interpolation operator on We give the discrete counterparts of Schwarz algorithm defined in (21) and (22) as follows.

Starting from we define the discrete Schwarz sequence on such that solves

(23)

and on the sequence solves

(24)

We will also always assume that the respective matrices resulting from problems (23) and (24) are - matrices.

3. Error Analysis

This section is devoted to the proof of the main result of this work. For that, we begin by introducing two auxi- liary sequences.

3.1. Auxiliary Schwarz Sequences

To simplify the notation, we take

Let be the solution of discrete V.I

(25)

where is the solution of continuous V.I (21) (resp. (22)) and let

be the solution of continuous V.I

(26)

where is the solution of discrete V.I. (23) (resp. (24)).

It is clear that is the finite element approximation of Then, as (independent of), therefore, we apply the error estimate for variational inequality (see [11,12]), we get

(27)

similarly, we have

(28)

3.2. Sequences of Sub-Solutions

The following theorems will play a important role in proving the main result of this paper.

3.2.1. Part One―Discrete Sub-Solution

We construct a discrete function near such that:

Theorem 2 Let be the solution of (25). Then there exists a function and a constant independent of and such that

Proof Let us give the proof for. The one for is similar. Indeed, being the solution of V.I (25) for, it is easy to show that is also a subsolution, i.e

then

so, due to lemma 2 (discrete case), it follows that

(29)

where

setting and using both remak2 (discrete case) and estimate (27), we get

(30)

which combined with (29) yields

Thus, we choose

then

and

3.2.2. Part Two―Continuous Sub-Solution

We construct a continuous function near such that:

Theorem 3 Let be the solution of (26). Then there exists a function and a constant independent of and such that

Proof Let us give the proof for. The one for is similar. indeed, being the solution of V.I (26) for, it is also a subsolution, i.e.

then

so, making use of lemma 2, we obtain

(31)

where

Setting and using both Remark 2 and estimate (28), we get

(32)

so, combining (31) with estimate (32) yields

Finally, choosing

we get immediately the results.

3.3. L^∞-Error Estimate

Theorem 4 Let (resp.) be the solution of (21), (22) (resp. (23), (24)). Then there exists a constant independent of and such that

Proof Thanks to theorem 2 and theorem 3, we have

therefore

(33)

moreover

let then making use of Theorem 1 and estimate (33), we get

we choose such that

then

and by inverse inequality, we get

4. Conclusion

We have established a convergence order of Schwarz algorithm for two overlapping subdomains with non- matching grids. This approach developed in this paper relies on the geometrical convergence and the error estimate between the continuous and discrete Schwarz iterates. The constant c in error estimate is independent of Schwarz iterate n.

References