Applied Mathematics
Vol.3 No.12(2012), Article ID:25597,6 pages DOI:10.4236/am.2012.312272
Generalized Entropy of Order Statistics
Department of Applied Mathematics, Delhi Technological University, Delhi, India
Email: richa31aug@gmail.com; hctaneja@rediffmail.com
Received September 4, 2012; revised October 12, 2012; accepted October 20, 2012
Keywords: Entropy; Order Statistics; Probability Integral Transformation; Residual Entropy; Generalized Information
ABSTRACT
In this communication, we consider and study a generalized two parameters entropy of order statistics and derive bounds for it. The generalized residual entropy using order statistics has also been discussed.
1. Introduction
Suppose 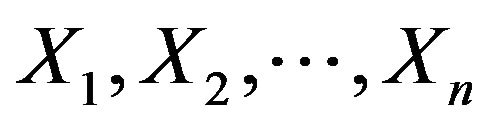 are
are ![]() independent and identically distributed observations from a distribution
independent and identically distributed observations from a distribution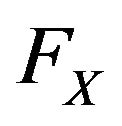 , where
, where 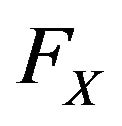 is differentiable with a density
is differentiable with a density 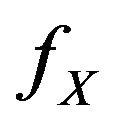 which is positive in an interval and zero elsewhere. The order statistics of the sample is defined by the arrangement of
which is positive in an interval and zero elsewhere. The order statistics of the sample is defined by the arrangement of 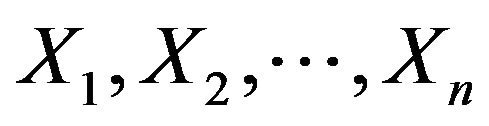 from the smallest to largest denoted as
from the smallest to largest denoted as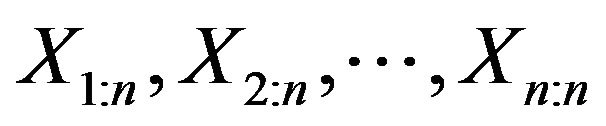 . Then the p.d.f. of the
. Then the p.d.f. of the  order statistics
order statistics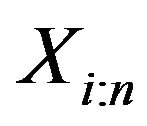 , is given by
, is given by
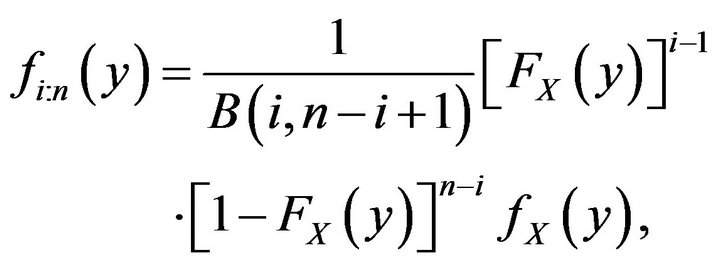 (1)
(1)
for details refer to [1].
Order statistics has been studied by statisticians for some time and has been applied to problems of statistical estimation [2], reliability analysis, image coding [3] etc. Some information theoretic aspects of order statistics have been discussed in the literature. Wong and Chen [4] showed that the difference between average entropy of order statistics and the entropy of a data distribution is a constant. Park [5] showed some recurrence relations for entropy of order statistics. Information properties of order statistics based on Shannon entropy [6] and Kullback-Leibler [7] measure using probability integral transformation have been studied by Ebrahimi et al. [8]. Arghami and Abbasnejad [9] studied Renyi entropy properties based on order statistics. The Renyi [10] entropy is a single parameter entropy. We consider a generalized two parameter, the Verma entropy [11], and study it in context with order statistics. Verma entropy plays a vital role as a measure of complexity and uncertainty in different areas such as physics, electronics and engineering to describe many chaotic systems. Considering the importance of this entropy measure, it will be worthwhile to study it in case of order statistics. The rest of the article is organized as follows:
In Section 2, we express generalized entropy of  order statistics in terms of generalized entropy of
order statistics in terms of generalized entropy of  order statistics of uniform distribution and study some of its properties. Section 3 provides bounds for entropy of order statistics. In Section 4, we derive an expression for residual generalized entropy of order statistics using residual generalized entropy for uniform distribution.
order statistics of uniform distribution and study some of its properties. Section 3 provides bounds for entropy of order statistics. In Section 4, we derive an expression for residual generalized entropy of order statistics using residual generalized entropy for uniform distribution.
2. Generalized Entropy of Order Statistics
Let 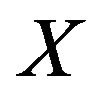 be a random variable having an absolutely continuous cdf
be a random variable having an absolutely continuous cdf 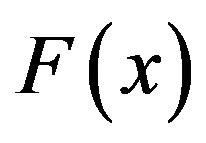 and pdf
and pdf , then Verma [11] entropy of the random variable
, then Verma [11] entropy of the random variable 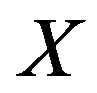 with parameters
with parameters 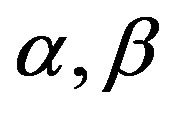 is defined as:
is defined as:
 (2)
(2)
where
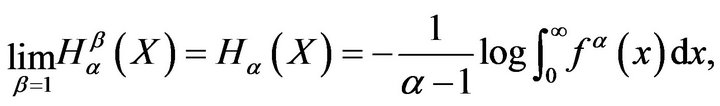
is the Renyi entropy, and
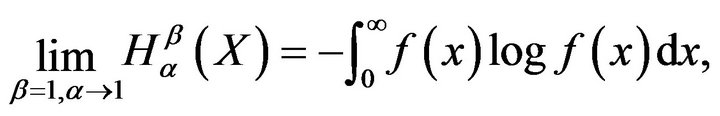
is the Shannon entropy .
We use the probability integral transformation of the random variable 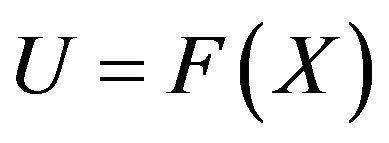 where the distribution of U is the standard uniform distribution. If
where the distribution of U is the standard uniform distribution. If 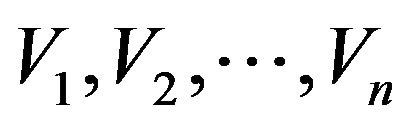 are the order statistics of a random sample
are the order statistics of a random sample 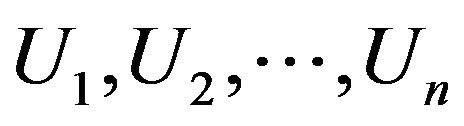 from uniform distribution, then it is easy to see using (1) that
from uniform distribution, then it is easy to see using (1) that 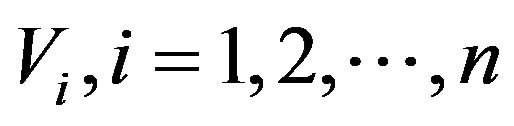 has beta distribution with parameters
has beta distribution with parameters 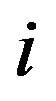 and
and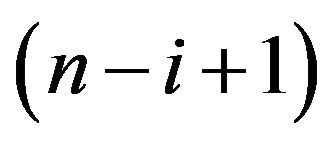 . Using probability integral transformation, entropy (2) of the random variable
. Using probability integral transformation, entropy (2) of the random variable 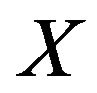 can be represented as
can be represented as
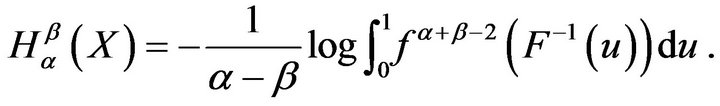 (3)
(3)
Next, we prove the following result:
Theorem 2.1 The generalized entropy of 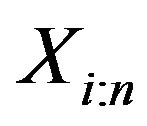 can be expressed as
can be expressed as
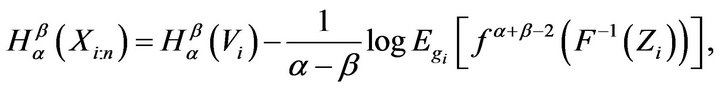 (4)
(4)
where 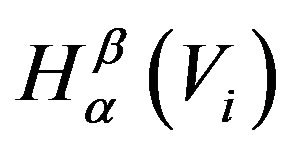 denotes the entropy of the beta distribution with parameters
denotes the entropy of the beta distribution with parameters 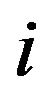 and
and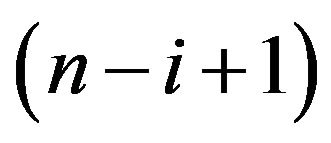 ,
, 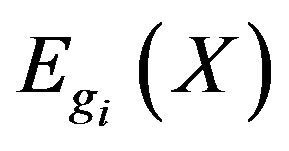 denotes expectation of
denotes expectation of 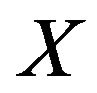 over
over 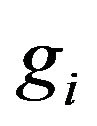 and
and 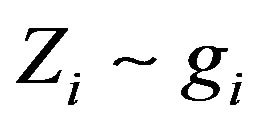 is the beta density with parameters
is the beta density with parameters 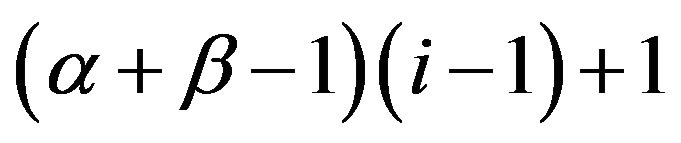 and
and
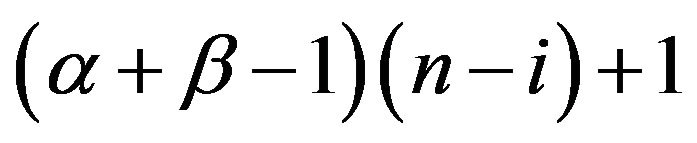 .
.
Proof: Since 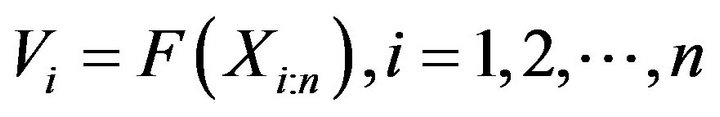 which implies
which implies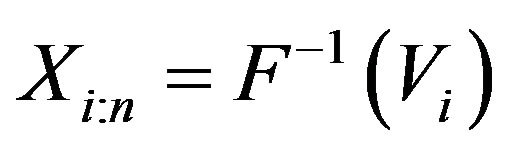 . Thus, from (3) we have
. Thus, from (3) we have
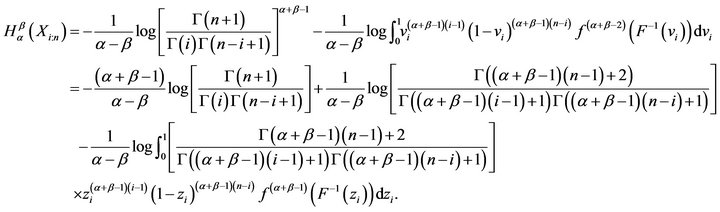 (5)
(5)
It is easy to see that the entropy (2) for the beta distribution with parameters 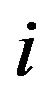 and
and 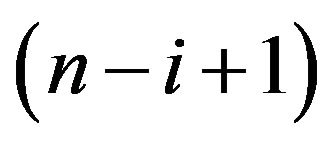 (that is, the
(that is, the 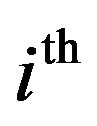 order statistics of uniform distribution) is given by
order statistics of uniform distribution) is given by
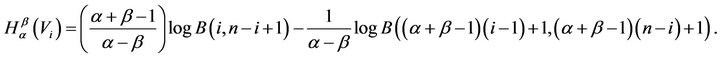 (6)
(6)
Using (6) in (5), the desired result (4) follows.
In particular, by taking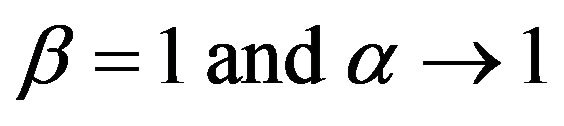 , (4) reduces to
, (4) reduces to
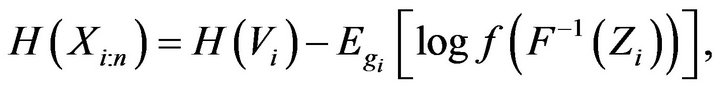
a result derived by Ebrahimi et al. [8].
Remark: In reliability engineering 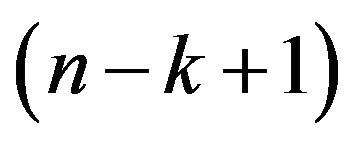 -outof-
-outof-![]() systems are very important kind of structures. A
systems are very important kind of structures. A 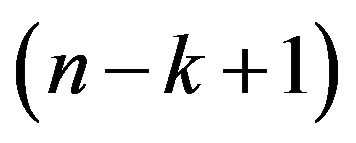 -out-of-
-out-of-![]() system functions iff atleast
system functions iff atleast
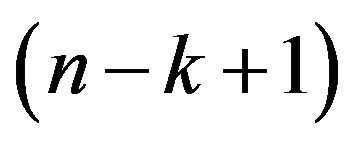 components out of
components out of ![]() components function. If
components function. If 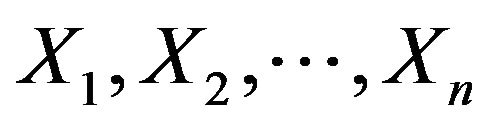 denote the independent lifetimes of the components of such system, then the lifetime of the system is equal to the order statistic
denote the independent lifetimes of the components of such system, then the lifetime of the system is equal to the order statistic![]() . The special case of
. The special case of 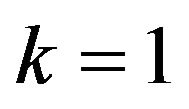 and
and![]() , that is for sample minima and maxima correspond to series and parallel systems respectively. In the following example, we calculate entropy (4) for sample maxima and minima for an exponential distribution.
, that is for sample minima and maxima correspond to series and parallel systems respectively. In the following example, we calculate entropy (4) for sample maxima and minima for an exponential distribution.
Example 2.1 Let 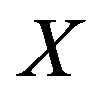 be a random variable having the exponential distribution with pdf
be a random variable having the exponential distribution with pdf
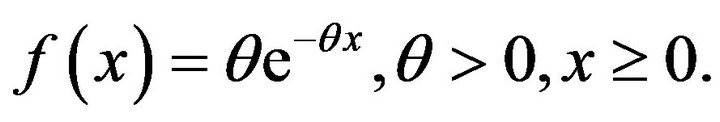
Here, 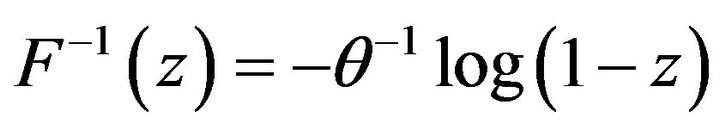 and the expectation term is given by
and the expectation term is given by
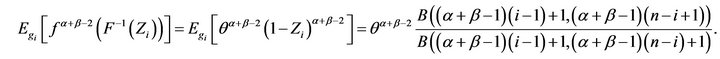
For![]() , from (6), we have
, from (6), we have
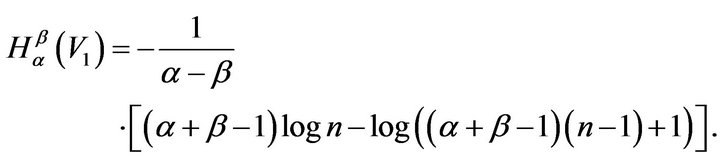
Hence, using (4)
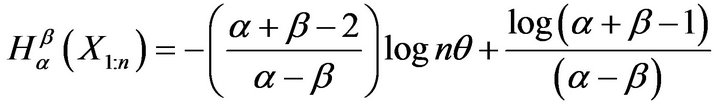 which confirms that the sample minimum has an exponential distribution with parameter
which confirms that the sample minimum has an exponential distribution with parameter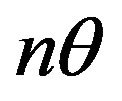 , since
, since
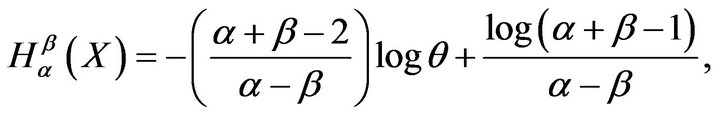
where 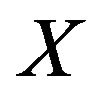 is an exponential variate with parameter
is an exponential variate with parameter . Also
. Also
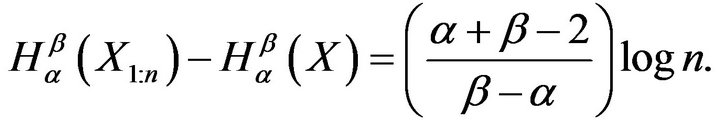
Hence, the difference between the generalized entropy of first order statistics i.e. the sample minimum and the generalized entropy of parent distribution is independent of parameter , but it depends upon sample size
, but it depends upon sample size![]() . Similarly, for sample maximum, we have
. Similarly, for sample maximum, we have
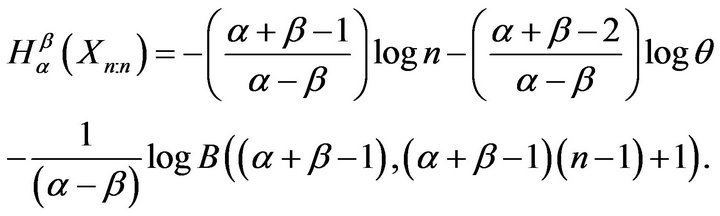
It can be seen easily that the difference between 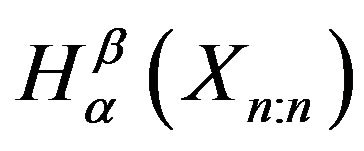 and
and 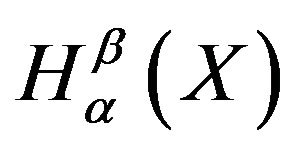 is
is
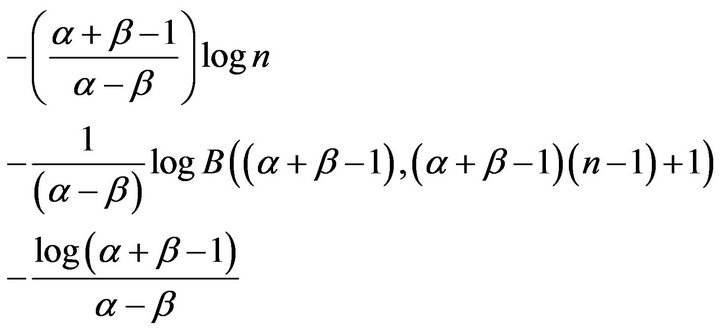
which is also independent of parameter .
.
3. Bounds for the Generalized Entropy of Order Statistics
In this section, we find the bounds for generalized entropy for order statistics (4) in terms of entropy (2). We prove the following result.
Theorem 3.1 For any random variable 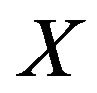 with
with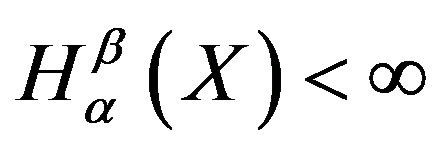 , the entropy of the
, the entropy of the  order statistics
order statistics 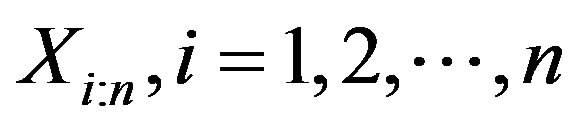 is bounded above as
is bounded above as
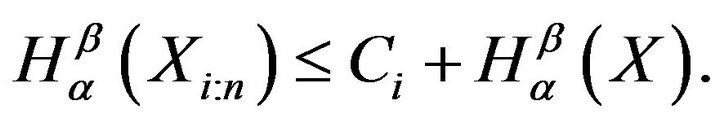 (7)
(7)
where
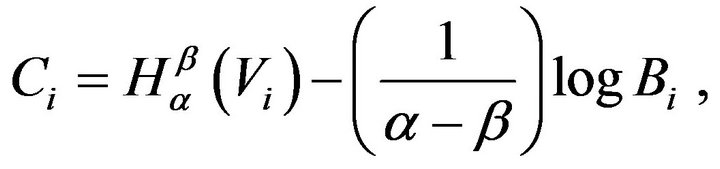
and, bounded below as
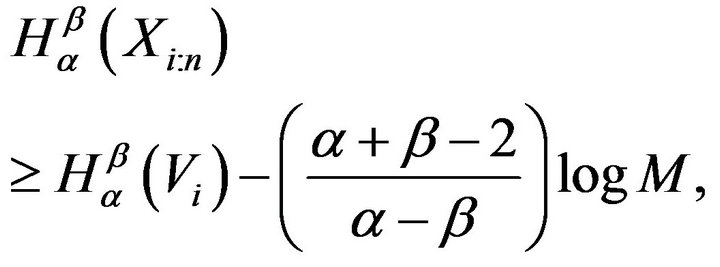 (8)
(8)
where, 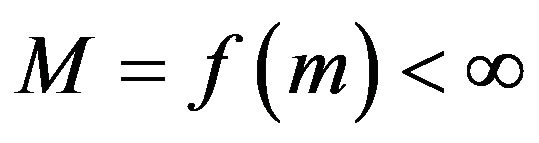 , and
, and ![]() is the mode of the distribution and
is the mode of the distribution and 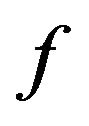 is pdf of the random variable
is pdf of the random variable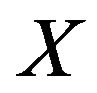 .
.
Proof: The mode of the beta distribution 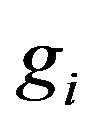 is
is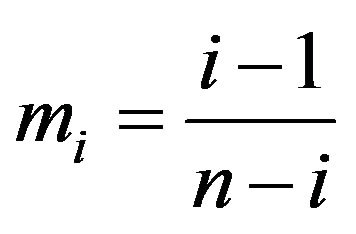 . Thus,
. Thus,
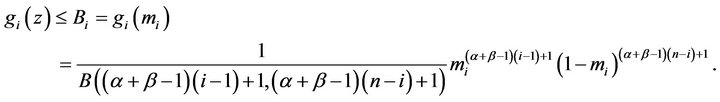
For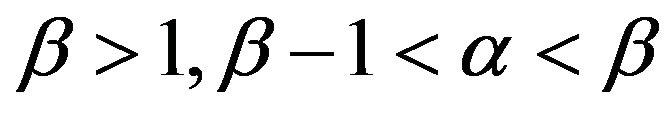 , from (4)
, from (4)
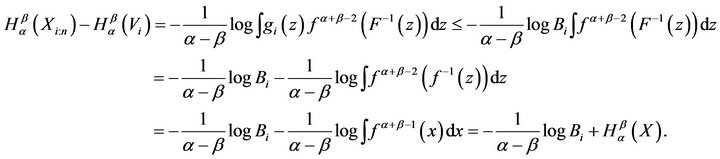
which gives (7).
From (4) we can write
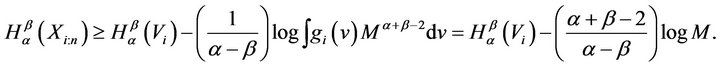
Example 3.1 For the uniform distribution over the interval 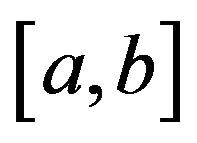 we have
we have
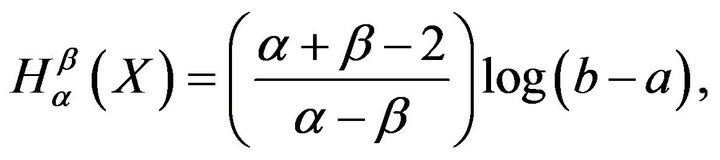
and from (6),
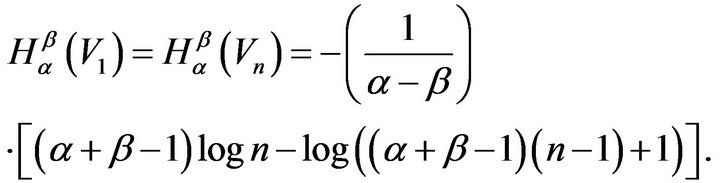
and
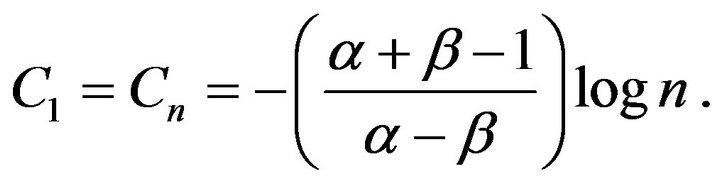
Hence, using (7) we get
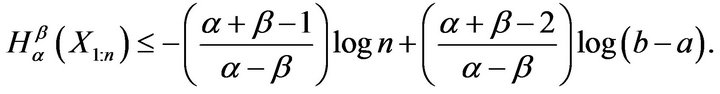
Further, for uniform distribution over the interval
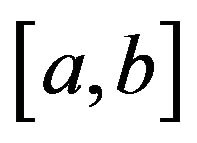 ,
,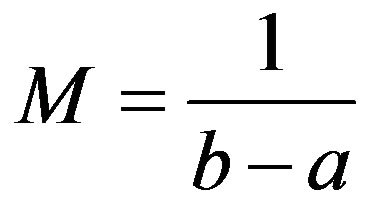 . Using (8) we get
. Using (8) we get
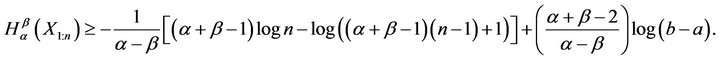
Thus, for uniform distribution, we have
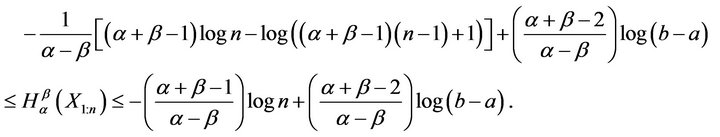
We can check that the bounds for 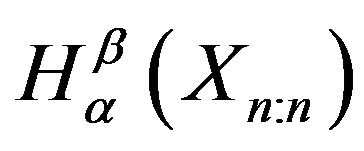 are same as that of
are same as that of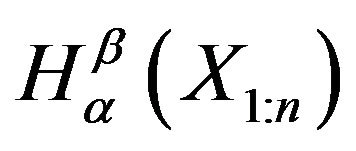 .
.
Example 3.2 For the exponential distribution with parameter , we have
, we have  and
and
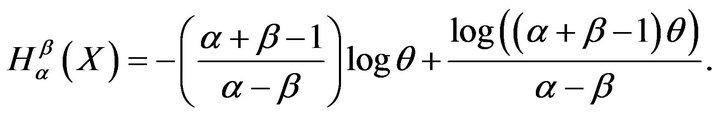
Thus, as calculated in Example 2.1
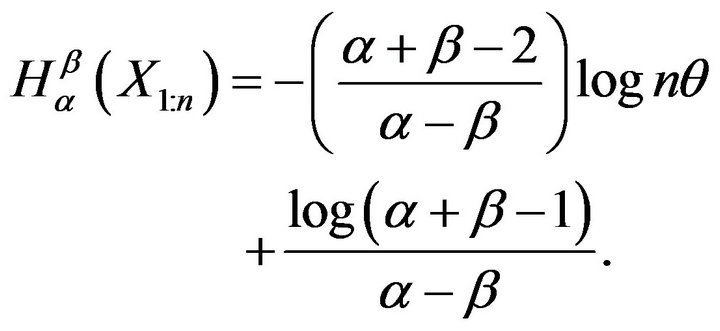
Using Theorem 3.1
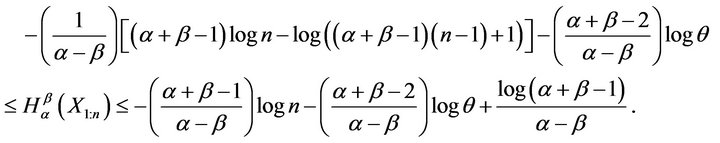
Here we observe that the difference between upper bound and 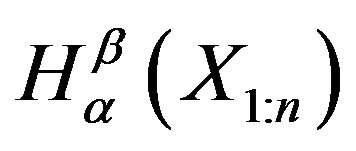 is
is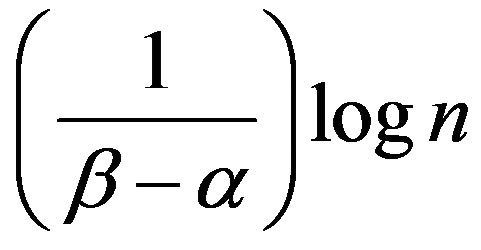 , which is an increasing function of n. Thus, for the exponential distribution upper bound is not useful when sample size is large.
, which is an increasing function of n. Thus, for the exponential distribution upper bound is not useful when sample size is large.
4. The Generalized Residual Entropy of Order Statistics
In reliability theory and survival analysis, 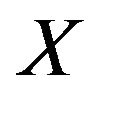 usually denotes a duration such as the lifetime. The residual lifetime of the system when it is still operating at time
usually denotes a duration such as the lifetime. The residual lifetime of the system when it is still operating at time , given by
, given by 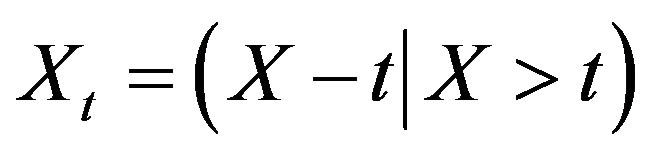 has the probability density
has the probability density
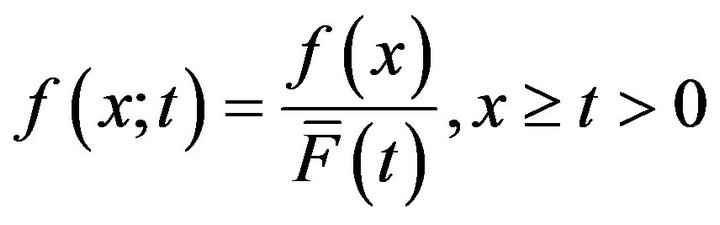 , where
, where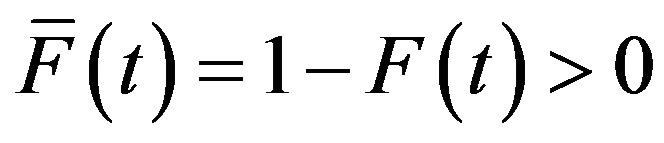 . Ebrahimi [12] proposed the entropy of the residual lifetime
. Ebrahimi [12] proposed the entropy of the residual lifetime 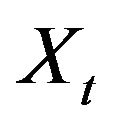 as
as
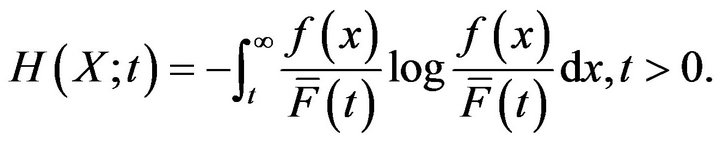 (9)
(9)
Obviously, when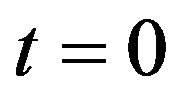 , it reduces to Shannon entropy.
, it reduces to Shannon entropy.
The generalized residual entropy of the type 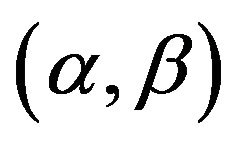 is defined as
is defined as
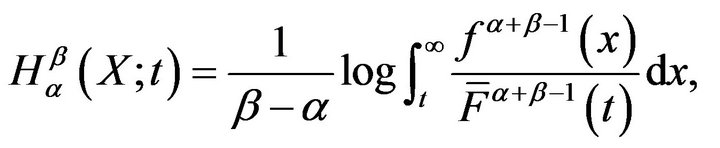 (10)
(10)
where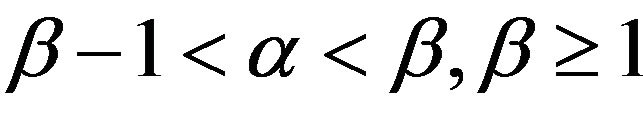 . When
. When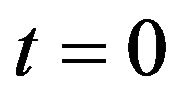 , it reduces to (2).
, it reduces to (2).
We note that the density function and survival function of 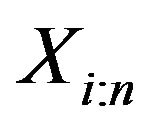 (refer to [13]), denoted by
(refer to [13]), denoted by 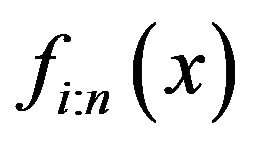 and
and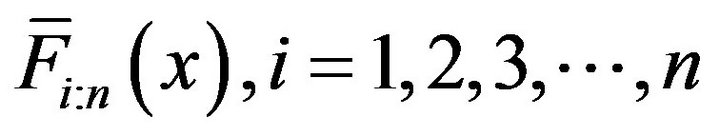 , respectively are
, respectively are
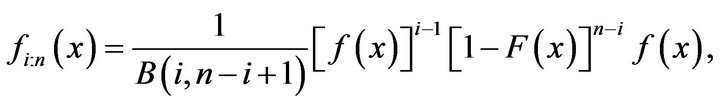 (11)
(11)
where
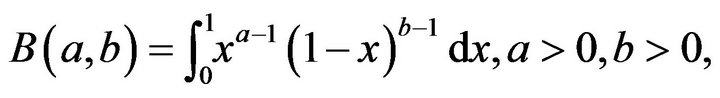 (12)
(12)
and
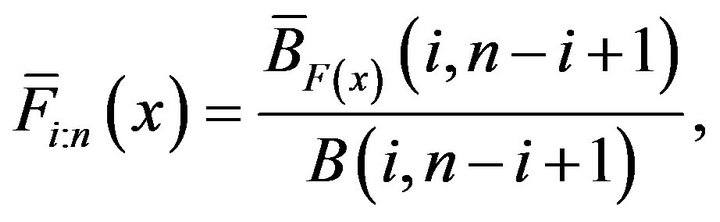 (13)
(13)
where
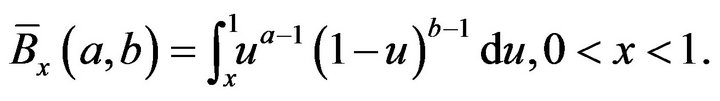 (14)
(14)
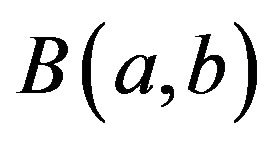 and
and 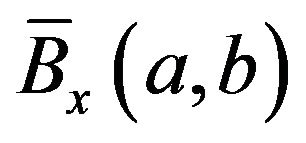 are known as the beta and incomplete beta functions respectively. In the next lemmawe derive an expression for
are known as the beta and incomplete beta functions respectively. In the next lemmawe derive an expression for 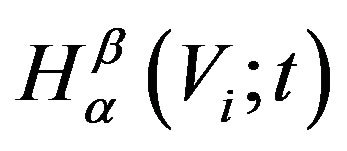 for the dynamic version of
for the dynamic version of 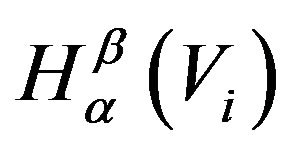 as given by (6).
as given by (6).
Lemma 4.1 Let 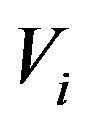 be the
be the 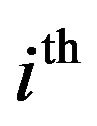 order statistics based on a random sample of size
order statistics based on a random sample of size ![]() from uniform distribution on
from uniform distribution on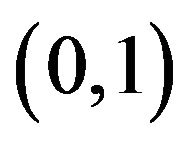 . Then
. Then
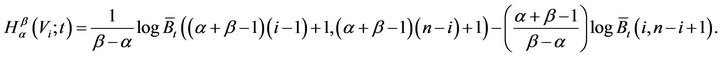 (15)
(15)
Proof: For uniform distribution using (10), we have
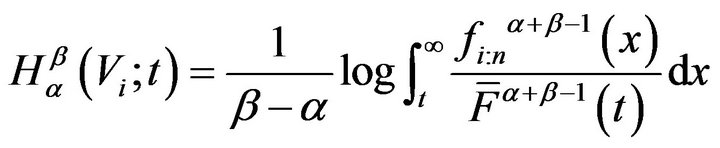 (16)
(16)
Putting values from (11) and (13) in (16), we get the desired result (15).
If we put 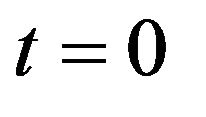 in (15), we get (6).
in (15), we get (6).
Using this, in the following theorem, we will show that the residual entropy of order statistics 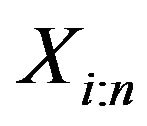 can be represented in terms of residual entropy of uniform distribution.
can be represented in terms of residual entropy of uniform distribution.
Theorem 4.1 Let 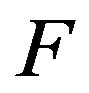 be an absolutely continuous distribution function with density
be an absolutely continuous distribution function with density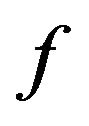 . Then, generalized residual entropy of the
. Then, generalized residual entropy of the 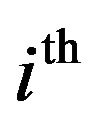 order statistics can be represented as
order statistics can be represented as
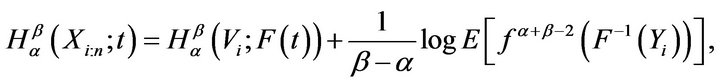 (17)
(17)
where
![]()
Proof: Using the probability integral transformation
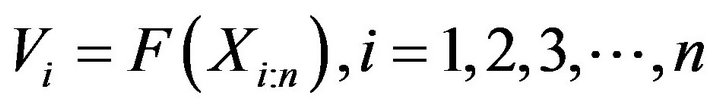
and above lemma, the result follows.
Take 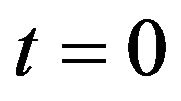 in (17), it reduces to (4).
in (17), it reduces to (4).
Example 4.1 Suppose that 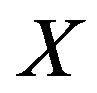 is exponentially distributed random variable with mean
is exponentially distributed random variable with mean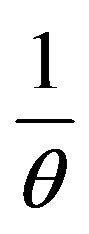 . Then,
. Then,
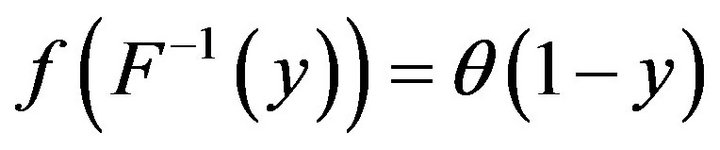
and we have
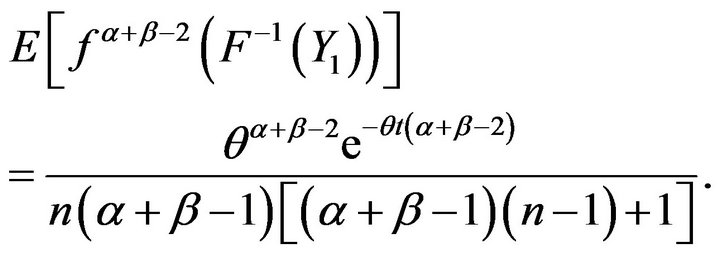
For![]() , Theorem 4.1 gives
, Theorem 4.1 gives
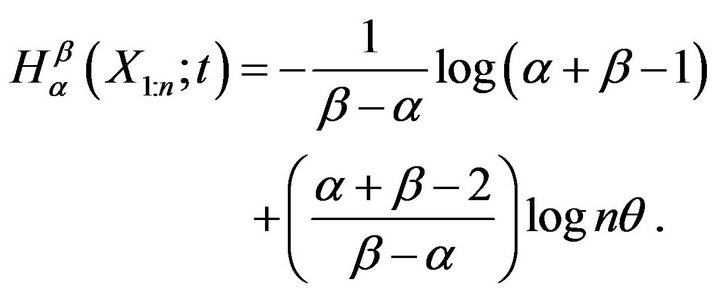
Also
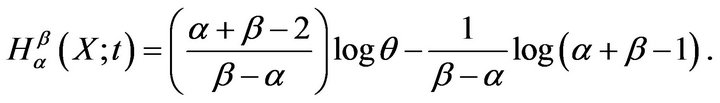
Hence
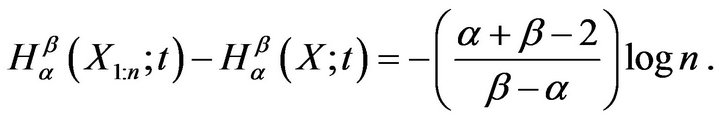
So, in the exponential case the difference between generalized residual entropy of the lifetime of a series system and residual generalized entropy of the lifetime of each component is independent of time.
5. Conclusion
The two parameters generalized entropy plays a vital role as a measure of complexity and uncertainty in different areas such as physics, electronics and engineering to describe many chaotic systems. Using probability integral transformation we have studied the generalized and generalized residual entropies based on order statistics. We have explored some properties of these entropies for exponential distribution.
6. Acknowledgements
The first author is thankful to the Center for Scientific and Industrial Research, India, to provide financial assistance for this work.
REFERENCES
- B. C. Arnold, N. Balakrishnan and H. N. Nagaraja, “A First Course in Order Statistics,” John Wiley and Sons, New York, 1992.
- E. H. Llyod, “Least-Squares Estimation of Location and Scale Parameters Using Order Statistics,” Biometrika, Vol. 39, No. 1-2, 1952, pp. 88-95.
- E. Ataman, V. K. Aatre and K. M. Wong, “Some Statistical Properties of Median Filters,” IEEE Transactions on Acoustics, Speech and Signal Processing, Vol. ASSP-29, No. 5, 1981, pp. 1073-1075.
- K. M. Wong and S. Chen, “The Entropy of Ordered Sequences and Order Statistics,” IEEE Transactions on Information Theory, Vol. 36, No. 2, 1990, pp. 276-284. doi:10.1109/18.52473
- S. Park, “The Entropy of Consecutive Order Statistics,” IEEE Transactions on Information Theory, Vol. 41, No. 6, 1995, pp. 2003-2007. doi:10.1109/18.476325
- C. E. Shannon, “A Mathematical Theory of Communication,” Bell System Technical Journal, Vol. 27, 1948, pp. 379-423 and 623-656.
- S. Kullback, “Information Theory and Statistics,” Wiley, New York, 1959.
- N. Ebrahimi, E. S. Soofi and H. Zahedi, “Information Properties of Order Statistics and Spacings,” IEEE Transactions on Information Theory, Vol. 50, No. 1, 2004, pp. 177-183. doi:10.1109/TIT.2003.821973
- N. R. Arghami and M. Abbasnejad, “Renyi Entropy Properties of Order Statistics,” Communications in Statistics, Vol. 40, No. 1, 2011, pp. 40-52. doi:10.1080/03610920903353683
- A. Renyi, “On Measures of Entropy and Information,” Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkley, 20 June-30 July 1961, pp. 547-561.
- R. S. Verma, “Generalization of Renyi’s Entropy of Order α,” Journal of Mathematical Sciences, Vol. 1, 1966, pp. 34-48.
- N. Ebrahimi, “How to Measure Uncertainty in the Residual Lifetime Distributions,” Sankhya A, Vol. 58, 1996, pp. 48-57.
- H. A. David and H. N. Nagaraja, “Order Statistics,” Wiley, New York, 2003. doi:10.1002/0471722162

