Applied Mathematics
Vol.3 No.10A(2012), Article ID:24125,6 pages DOI:10.4236/am.2012.330198
A New Lagrangian Multiplier Method on Constrained Optimization*
Department of Mathematics, Henan University of Science and Technology, Luoyang, China
Email: #mathshang@sina.com
Received July 8, 2012; revised August 8, 2012; accepted August 15, 2012
Keywords: Nonlinear Programming; NCP Function; Lagrange Function; Multiplier; Convergence
ABSTRACT
In this paper, a new augmented Lagrangian function with 4-piecewise linear NCP function is introduced for solving nonlinear programming problems with equality constrained and inequality constrained. It is proved that a solution of the original constrained problem and corresponding values of Lagrange multipliers can be found by solving an unconstrained minimization of the augmented Lagrange function. Meanwhile, a new Lagrangian multiplier method corresponding with new augmented Lagrangian function is proposed. And this method is implementable and convergent.
1. Introduction
Considering the following nonlinear inequality constrained optimization Problem (NLP):
 (1)
(1)
where  and
and
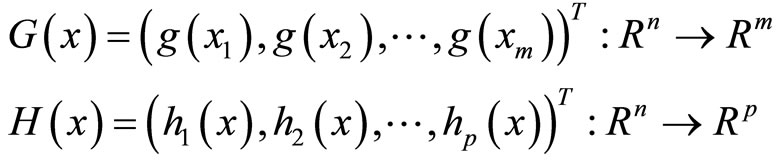
are continuously differentiable functions.
We denote by
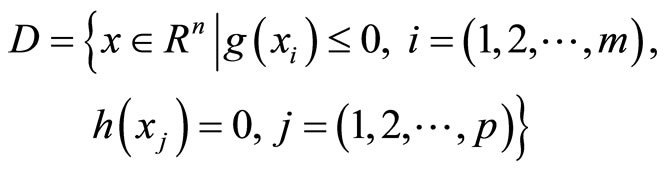
the feasible set of the problem (NLP).
The Lagrangian function associated with the problem (NLP) is the function

where
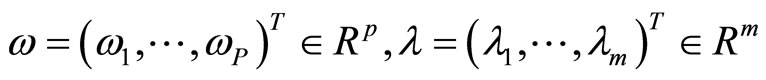
are the multiplier vectors, For simplicity, we use  to denote the column vector
to denote the column vector 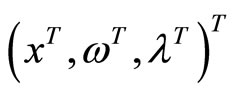
Defintion 1.1. A point 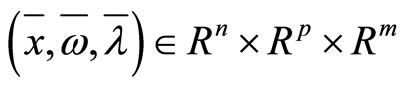 is called a Karush-Kuhn-Tucker (KKT) point or a KKT pair of Problem (NLP), if it satisfies the following conditions:
is called a Karush-Kuhn-Tucker (KKT) point or a KKT pair of Problem (NLP), if it satisfies the following conditions:
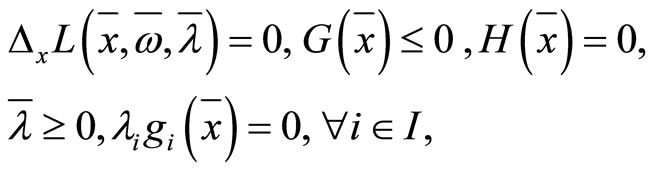 (2)
(2)
where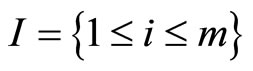 , we also say
, we also say  is a KKT point if there exists a
is a KKT point if there exists a 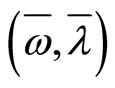 such that
such that  satisfies (2).
satisfies (2).
For the nonlinear inequality constrained optimization problem (NLP), there are many practical methods to solve it, such as augmented Lagrangian function method [1-6], Trust-region filter method [7,8], QP-free feasible method [9,10], Newton iterative method [11,12], etc. As we know, Lagrange multiplier method is one of the efficient methods to solve problem (NLP). Pillo and Grippo in [1-3] proposed a class of augmented Lagrange function methods which have nice equivalence between the unconstrained optimization and the primal constrained problem and get good convergence properties of the related algorithm. However, a max function is used for these methods which may be not differentiable at infinite numbers of points. To overcome this shortcoming, Pu in [4] proposed a augmented Lagrange function with FischerBurmeister nonlinear NCP function and Lagrange multiplier methods. Pu and Ding in [6] proposed a Lagrange multiplier methods with 3-piecewise linear NCP function. In this paper, a new class augmented Lagrange function with 4-piecewise linear NCP function and some Lagrange multiplier methods are proposed for the minimization of a smooth function subject to smooth inequality constraints and equality constrains.
The paper is organized as follows: In the next section we give some definitions and properties about NCP function, and then define a new augmented Lagrange function with 4-piecewise NCP function. In Section three, we give the algorithm. In Section four, we prove convergence of the algorithm. Some conclusions are given in Section five.
2. Preliminaries
In this section, we recall some definitions and define a new Lagrange multiplier function with 4-piecewise NCP function.
Definition 2.1 (NCP pair and SNCP pair). We call a pair (a, b) to be an NCP pair if 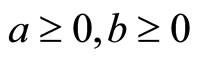 and ab = 0; and call (a, b) to be an SNCP pair if (a, b) is a pair and
and ab = 0; and call (a, b) to be an SNCP pair if (a, b) is a pair and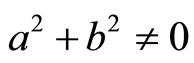 .
.
Definition 2.2 (NCP function). A function 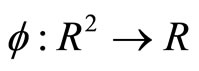 is called an NCP function if
is called an NCP function if 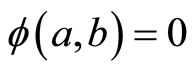 if and only
if and only 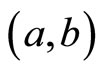 is an NCP pair.
is an NCP pair.
In this paper, we propose a new 4-piecewise linear NCP function  is as follows:
is as follows:
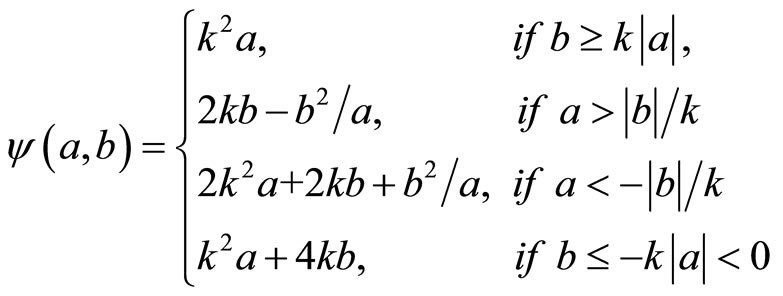 (3)
(3)
If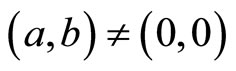 , then
, then
 (4)
(4)
and
 (5)
(5)
It is easy to check the following propositions:
1) ;
;
2) The square of  is continuously differentiable;
is continuously differentiable;
3)  is twice continuously differentiable everywhere except at the origin but it is strongly semi-smooth at the origin.
is twice continuously differentiable everywhere except at the origin but it is strongly semi-smooth at the origin.
Let
where is a parameter.
is a parameter.  if and only if
if and only if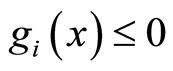 ,
, 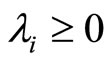 and
and 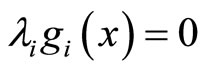 for any
for any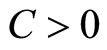 .
.
We construct function:
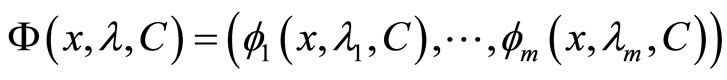
Clearly, the KKT point condition (2) is equivalently reformulate as the condition:
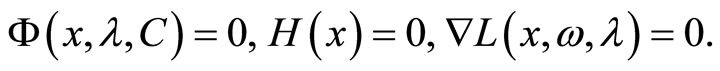
If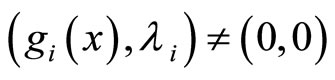 , then
, then 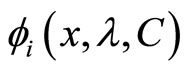 is continuously differentiable at
is continuously differentiable at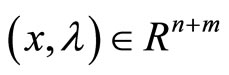 . We have
. We have
 (6)
(6)
where  is the ith column of the unit matrix, its jth element is 1, and other elements are 0, in this paper take k = 1.
is the ith column of the unit matrix, its jth element is 1, and other elements are 0, in this paper take k = 1.
If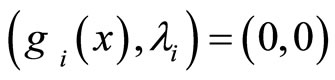 , and then
, and then  is strongly semi-smooth and direction differentiable at
is strongly semi-smooth and direction differentiable at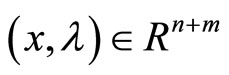 . We have
. We have
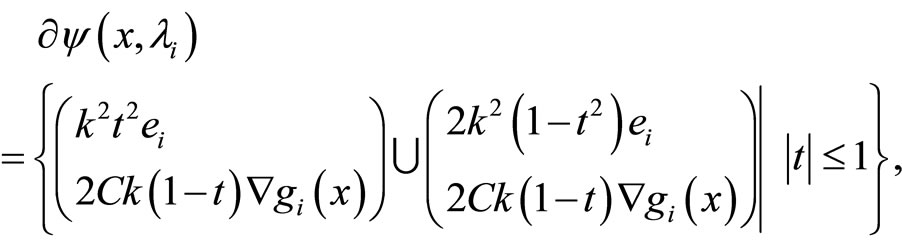 (7)
(7)
For Problem (NLP), we define a Di Pillo and Grippo type Lagrange multiplier function with 4-piecewise linear NCP function is as following:
 (8)
(8)
where
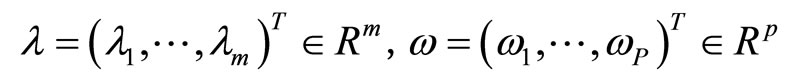 are the Lagrange multiplier, C and D are positive parameters.
are the Lagrange multiplier, C and D are positive parameters.
In this section, we gave some assumptions as follows:
Assumpion 1 f, 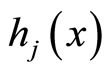 ,
,  ,
, 
 are twice Lipschitz continuously differentiable.
are twice Lipschitz continuously differentiable.
Define index set  and
and 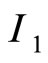 as follows:
as follows:

for any , according to definition of
, according to definition of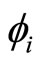 , have
, have
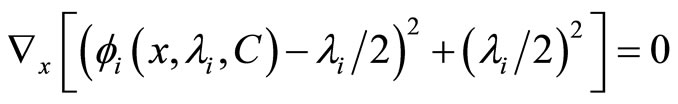
for any , we have 1) if
, we have 1) if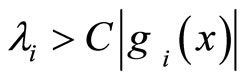 , we have
, we have
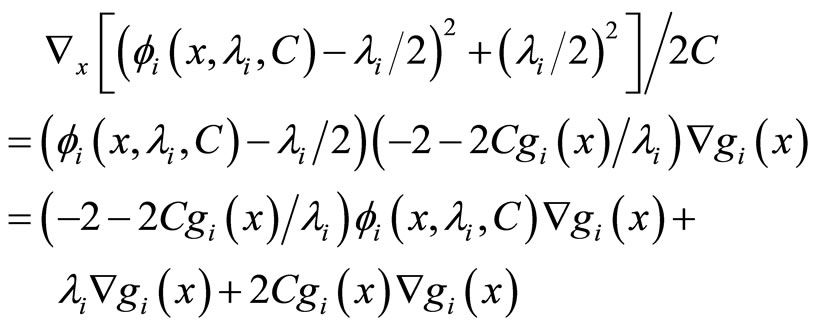 (9)
(9)
The gradient of 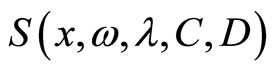 is
is
 (10)
(10)
The Henssian matrix of 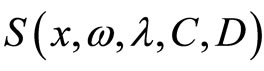 at KKT point
at KKT point  is
is
 (11)
(11)
2) if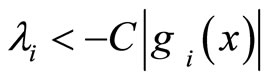 , then
, then
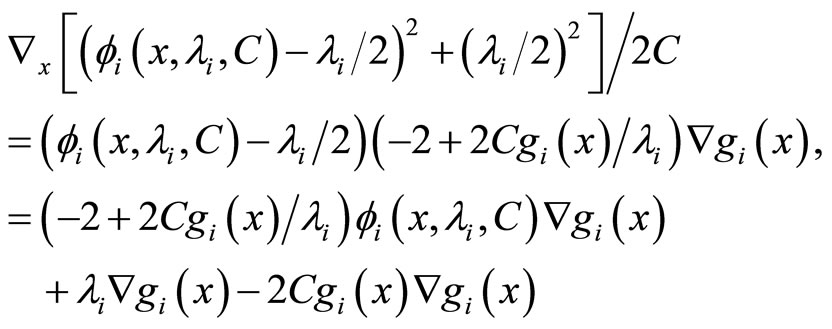 (12)
(12)
The gradient of  is
is
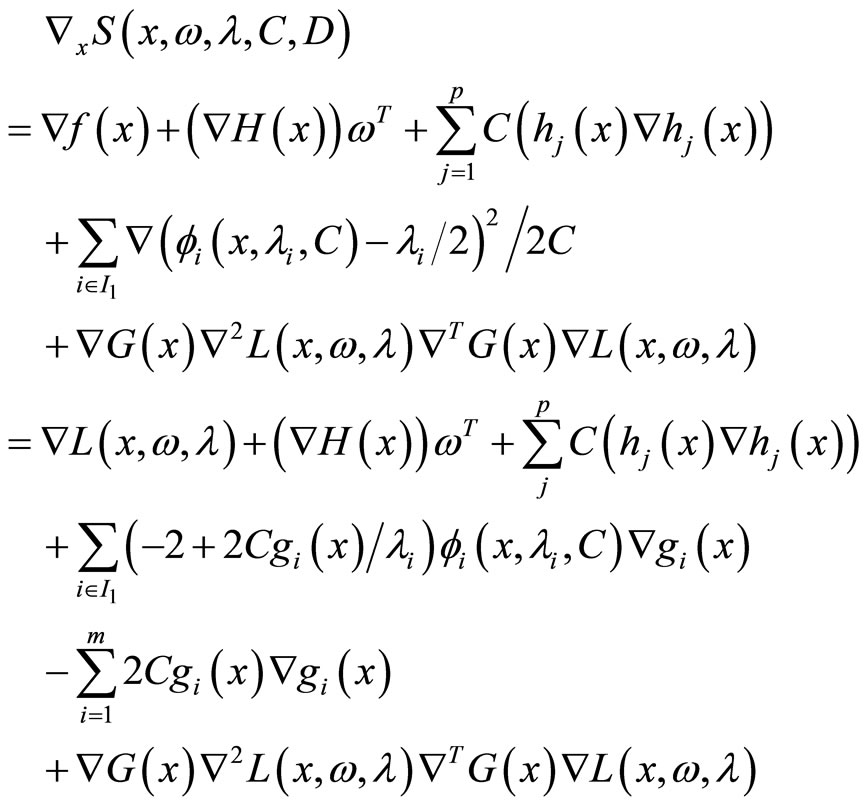 (13)
(13)
The Henssian matrix of  at KKT point
at KKT point  is
is
 (14)
(14)
Definition 2.3 A point  is said to satisfy the strong second-order sufficiency condition for problem (NLP) if it satisfies the first-order KKT condition and if
is said to satisfy the strong second-order sufficiency condition for problem (NLP) if it satisfies the first-order KKT condition and if 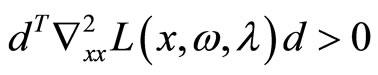 for all
for all
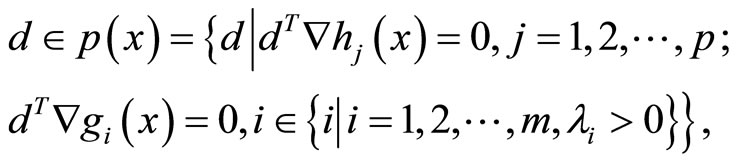
and .
.
Assumption 2 At any KKT point  satisfied strong second-order sufficiency condition.
satisfied strong second-order sufficiency condition.
Lemma If 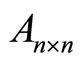 is a positive semi-definite matrix, for any
is a positive semi-definite matrix, for any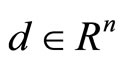 ,
, 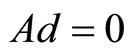 , matrix
, matrix 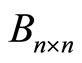 satisfied
satisfied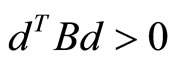 , then exist
, then exist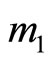 , for any
, for any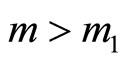 ,
, 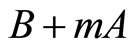 is positive definite matrix (see [4]).
is positive definite matrix (see [4]).
Theorem 2.1 If 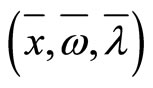 is KKT point of problem (1), then for sufficiently large C and D,
is KKT point of problem (1), then for sufficiently large C and D,  is strong convex function at point
is strong convex function at point .
.
Proof: Let 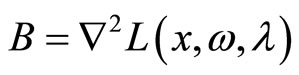
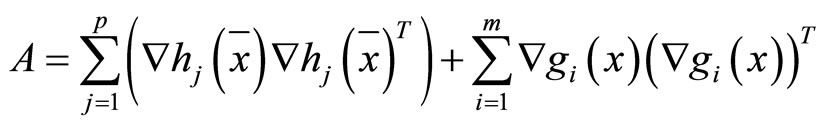
for , we have
, we have

from A2, we have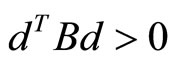 . Furthermore there is
. Furthermore there is 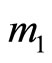 if
if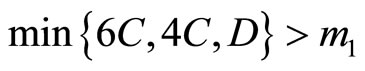 , for any
, for any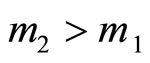 ,
,  is positive definite matrix. And then for any
is positive definite matrix. And then for any 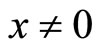 and sufficiently large C and D have
and sufficiently large C and D have
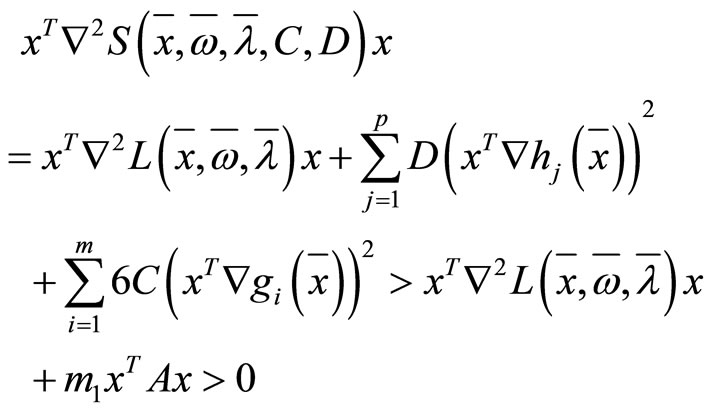
by its continuously, we may obtained that there is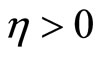 , for all
, for all

we have 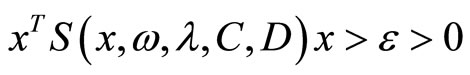 the theorem hold.
the theorem hold.
3. Lagrange Multiplier Algorithm
Step 0 Choose parameters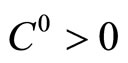 ,
, 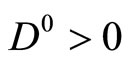 ,
, 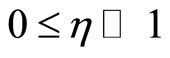 ,
, 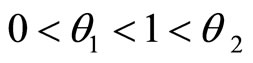 , given point
, given point , and
, and
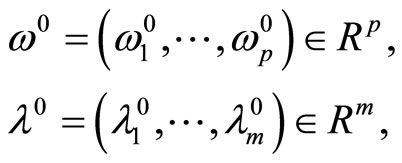
Let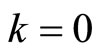 .
.
Step 1 Solve following, we will obtain .
.

if 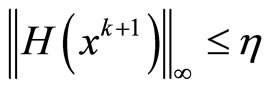 and
and 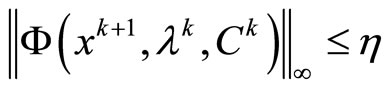 then stop.
then stop.
Step 2 For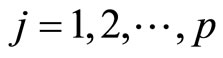 ,
, 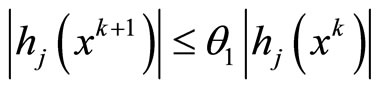 , then
, then 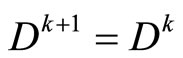 or
or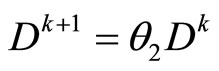 , for
, for , if
, if
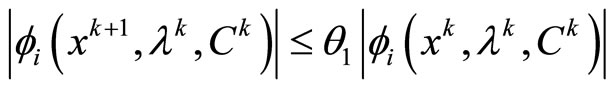 then
then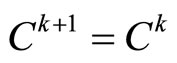 , or
, or 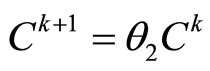
Step 3 Compute 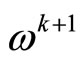 and
and 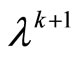

Step 4 Let k = k + 1, go to Step 1.
4. Convergence of the Algorithm
In this section, we make a assumption follow as:
Assumption 3 For any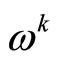 ,
, 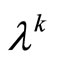 ,
,  ,
, 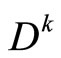 ,
,
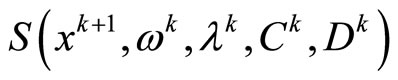 exists a minimizer point
exists a minimizer point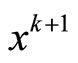 .
.
Theorem 4.1 Assume feasible set of problem (NLP) is non-empty set and  is bounded, then algorithm is bound to stop after finite steps iteration.
is bounded, then algorithm is bound to stop after finite steps iteration.
Proof: Assume that the algorithm can not stop after finite steps iteration, by the sack of convenience, we define index set as following
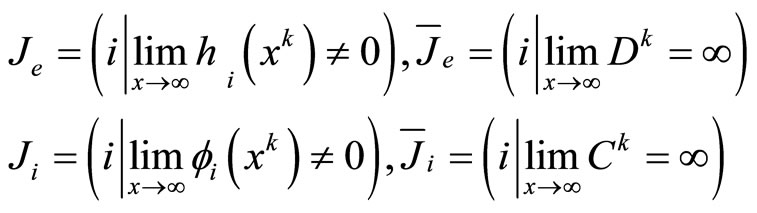
according to assumption A3, it is clearly that  or
or 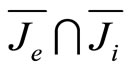 are non-empty set. for any k, obtain
are non-empty set. for any k, obtain

from above assumption, we obtain that for any a  there is
there is , for any
, for any  and
and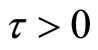 ,
, 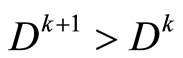 and
and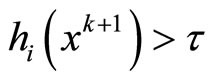 , for sufficiently large k, it is not difficult to see that
, for sufficiently large k, it is not difficult to see that
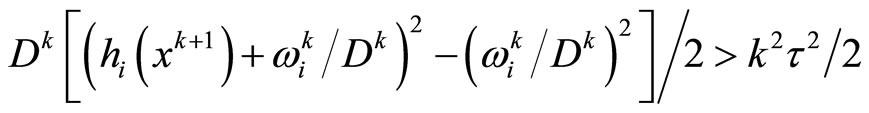
Or for any 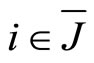 and
and ,
,  and
and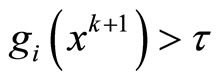 , for sufficiently large k, have
, for sufficiently large k, have
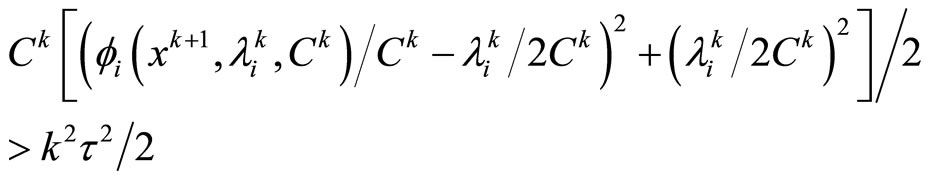
When  we can hold
we can hold
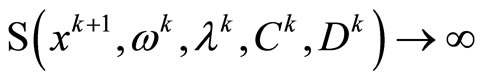
Which contradicts A3, the theorem holds.
Theorem 4.2 Let 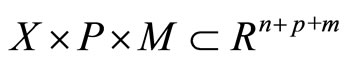 is a compact set, sequence
is a compact set, sequence 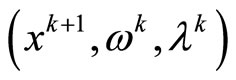 are generated by the algorithm, and
are generated by the algorithm, and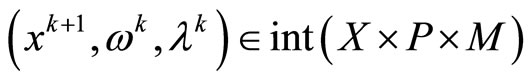 , in algorithm, 0 take the place of
, in algorithm, 0 take the place of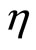 , either algorithm stops at its
, either algorithm stops at its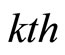 and
and 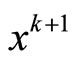 is solution of problem(NLP), or for any an accumulation
is solution of problem(NLP), or for any an accumulation 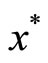 of sequence
of sequence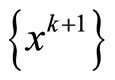 ,
, is solution of problem (NLP).
is solution of problem (NLP).
Proof: Because the algorithm stops at its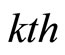 , then we have
, then we have
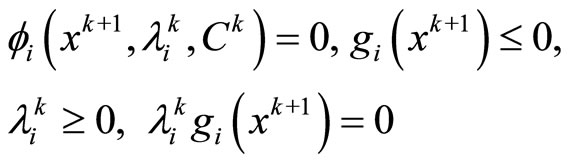 (15)
(15)
for ,
, 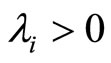 , it is easy to see that for any
, it is easy to see that for any 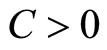 have
have

It is from Step 2 of the algorithm that we have
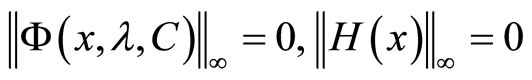 (16)
(16)
putting (15) (16) into (10) or (13), we can obtain
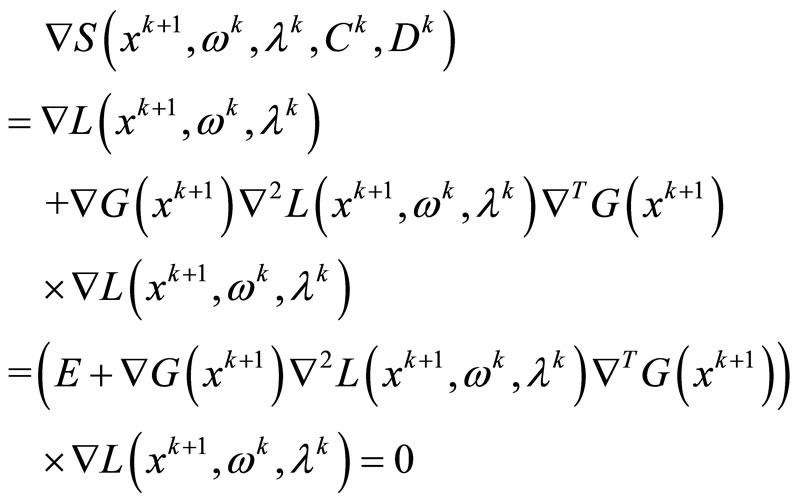
for ,
,  , according to definition of
, according to definition of
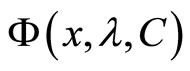 , we can obtain, that
, we can obtain, that
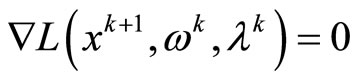
First part of the theorem holds,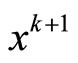 is solution of problem (NLP).
is solution of problem (NLP).
On the other hand, if the algorithm is not stop at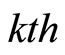 , for any accumulation point
, for any accumulation point 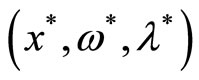 of sequence
of sequence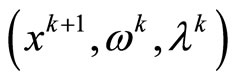 , from theorem 4.1, we can obtain, for any positive number C, that
, from theorem 4.1, we can obtain, for any positive number C, that
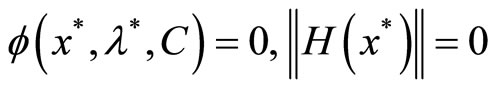
for any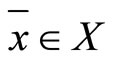 , have
, have
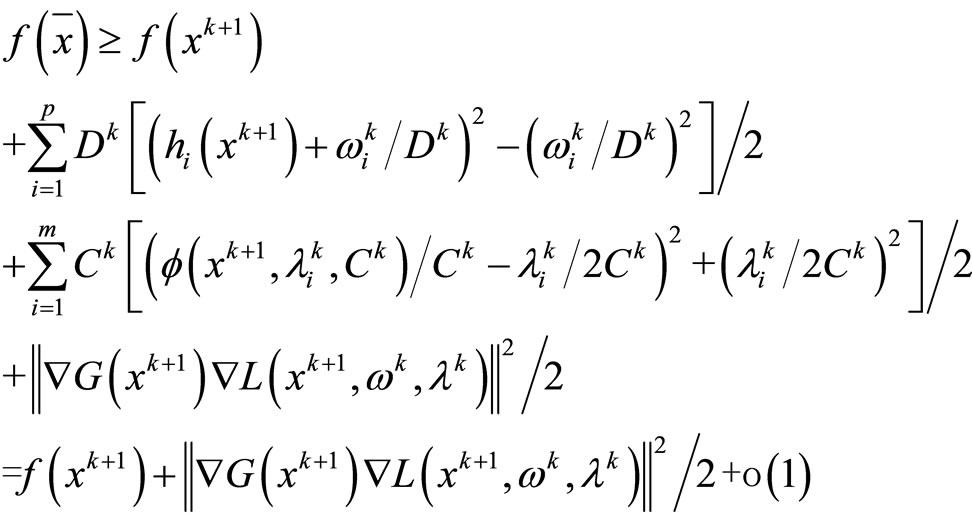
Let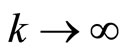 ,have
,have

Clearly, second part of the theorem holds.  is solution of problem (NLP).
is solution of problem (NLP).
5. Conclusion
A new Lagrange multiplier function with 4-piecewise linear NCP function is proposed in this paper which has a nice equivalence between its solution and solution of original problem. We can solve it to obtain solution of original constrained problem, the algorithm corresponding with it be endowed with convergence.
6. Acknowledgements
This paper was partially supported by the NNSF of China under Grant No. 10971053, and NNSF of Henan under Grant No. 094300510050.
REFERENCES
- G. Pillo and L. Grippo, “A New Class of Augmented Lagrangian in Nonlinear Programming,” SIAM Journal on Control and Optimization, Vol. 17, No. 5, 1979, pp. 617- 628.
- G. Pillo and L. Grippo, “An Augmented Lageangian function for Inequlity Constrains in Nonlinear Programming Problems,” Optimization Theorem and Application, Vol. 36, No. 4, 1982, pp. 495-520. doi:10.1007/BF00940544
- G. Pillo and S. Lucidi, “An augmented Lagrange Function with Improved Exactness Properties,” SIAM Journal on Control and Optimization, Vol. 12, No. 2, 2001, pp. 376-406.
- D. G. Pu and Z. Jin, “A New Lagrange Multiplier Method,” Tongji University Journal, Vol. 9, No. 38, 2010, pp. 1384-1391.
- K. D. Li and D. G. Pu, “A class of New Lagrange Multiplier Methods,” OR Transaction, Vol. 10, No. 4, 2006, pp. 9-24.
- X.-W. Du and Y.-L. Shang, “Exact Augmented Lagrange Function for Nonlinear Programming Problems with Inequality and Equality Constraints,” Applied Mathematics and Mechanics, Vol. 26, No. 12, 2005, pp. 1651-1656.
- K. Su, “Trust-Region Filter Method with NCP Function,” Journal of Systems Science and Mathematical Science, Vol. 28, No. 12, 2008, pp. 1525-1534
- D. G. Pu, “A New Filter Method,” OR Transaction, Vol. 1, No. 15, 2011, pp. 46-58.
- W. Hua and D. G. Pu, “A Modified QP-Free Feasible Method,” Applied Mathmatical Modelling, Vol. 35, No. 4, 2011, pp. 1696-1708. doi:10.1016/j.apm.2010.10.002
- K. Li and D. G. Pu, “Filter QP-Free Method with 3-PieceWise Linear NCP Function,” OR Transaction, Vol. 12, No. 2, 2008, pp. 49-57.
- Y. X. Yuan, “Numerical Method for Nonlinear Programming,” Shanghai Science and Technology Press, Shanghai, 1993.
- B. L. Chen, “The Theory of Optimization and Calculate,” 2nd Edition, Tsinghua University Press, Beijing, 2005.
NOTES
*This paper was partially supported by the National Natural Science Foundation of China under Grant No. 10971053, and NNSF of Henan Province under Grant No. 094300510050.
#Corresponding author.

