International Journal of Astronomy and Astrophysics
Vol.4 No.1(2014), Article ID:43984,14 pages DOI:10.4236/ijaa.2014.41022
On the Gravitational Bending of Light
—Was Sir Arthur Stanley Eddington Right?
G. G. Nyambuya, W. Simango
Department of Applied Physics, National University of Science and Technology, Bulawayo, Republic of Zimbabwe
Email: physicist.ggn@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 9 December 2013; revised 10 January 2014; accepted 17 January 2014
ABSTRACT
The paramount British-Led (May 29, 1919) Solar Eclipse Result of Eddington et al. has been tremendous if not an arcane effect in persuading scientists, philosophers and the general public, to accept Einstein’s esoteric General Theory of Relativity (GTR) thereby “deserting” Newtonian gravitation altogether, especially in physical domains of extreme gravitation where Einstein’s GTR is thought or believed to reign supreme. The all-crucial factor “2” predicted by Einstein’s GTR has been “verified” by subsequent measurements, more so by the most impressive and precision modern technology of VLBA measurements using cosmological radio waves to within 99.998% accuracy. From within the most well accepted provinces, confines and domains of Newtonian gravitational theory, herein, we demonstrate that the gravitational to inertial mass ratio of photons in Newtonian gravitational theory where the identities of the inertial and gravitational mass are preserved, the resulting theory is very much compatible with all measurements made of the gravitational bending of light. Actually, this approach posits that these measurements of the gravitational bending of light not only confirm the gravitational bending of electromagnetic waves, but that, on a much more subtler level; rather clandestinely, these measurements are in actual fact a measurement of the gravitational to inertial mass ratio of photons. The significant 19% scatter is seen in the measurements where white-starlight is used, according to the present thesis, this scatter is seen to imply that the gravitational to inertial ratio of photons may very well be variable quantity such that for radio waves, this quantity must—to within 99.998% accuracy, be unity. We strongly believe that the findings of the present reading demonstrate or hint to a much deeper reality that the gravitational and inertial mass, may—after all; not be equal as we have come to strongly believe.
Keywords:Astrometry; Celestial Mechanics; Ephemerides; Planets and Satellites; Formation

1. Introduction
The General Theory of Relativity (GTR)—which was published by the then 37-year-old Albert Einstein [1] after he had submitted his finished manuscript to Germany’s Prussian Academy of Sciences on November 25, 1915, is held and hailed as the best paradigm of gravitation that we have at our disposal. This theory was propped to prominence by the pre-eminent British astronomer, mathematician, physicist and philosopher, Sir Prof. Dr. Stanley Arthur Eddington’s esoteric Solar Eclipse Results of May 29, 1919. Einstein’s GTR predicts that a ray of light just barely grazing the limb of the Sun will suffer a deflection of about 1.75″ from its otherwise straight path. The two Edinginton-led expeditions gave the result 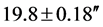 and
and 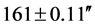 [2] [3] . This result was and has been taken as the first clearest indication yet, of the GTR’s supremacy over Newtonian gravitation and for this reason, Eddington’s Solar expedition is ranked amongst one of the single most important, esoteric and touchstone scientific measurements of 20th century physics (see, e.g., Ref. [4] ).
[2] [3] . This result was and has been taken as the first clearest indication yet, of the GTR’s supremacy over Newtonian gravitation and for this reason, Eddington’s Solar expedition is ranked amongst one of the single most important, esoteric and touchstone scientific measurements of 20th century physics (see, e.g., Ref. [4] ).
In 1919, after the so-called First World War had ended, scientific expeditions were sent to Sobral in South America and Principe in West Africa to make observations and measurements of the Solar eclipse. The reported results were deflections of 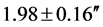 and
and 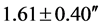 respectively. These results were taken as clear confirmation of Einstein’s GTR prediction of 1.75″. However, the actual combined measurements (from 1919 to 1973) of the bending of starlight show a slight but significant scatter (~19%) about the predicted value of 1.75″. The scatter has been taken as indication of the experimental difficulty in the measurement process. In this reading, we suggest that this scatter may very well be a result of the variation of the gravitational to inertial mass ratio of photons. The present work comes as nothing short of a scientific exegesis to the 1919 Eddington Eclipse Result. We are in complete agreement with the fact that Eddington et al.’s efforts did prove for the first time, that the path of light is altered by a gravitational field. Our bone of contention is whether or not the factor “2” vindicates Einstein’s GTR and eternally puts Newtonian gravitation on the scientific crucifix.
respectively. These results were taken as clear confirmation of Einstein’s GTR prediction of 1.75″. However, the actual combined measurements (from 1919 to 1973) of the bending of starlight show a slight but significant scatter (~19%) about the predicted value of 1.75″. The scatter has been taken as indication of the experimental difficulty in the measurement process. In this reading, we suggest that this scatter may very well be a result of the variation of the gravitational to inertial mass ratio of photons. The present work comes as nothing short of a scientific exegesis to the 1919 Eddington Eclipse Result. We are in complete agreement with the fact that Eddington et al.’s efforts did prove for the first time, that the path of light is altered by a gravitational field. Our bone of contention is whether or not the factor “2” vindicates Einstein’s GTR and eternally puts Newtonian gravitation on the scientific crucifix.
2. Weak Equivalence Principle
As is well known, there is at least two distinct and important kinds of mass that enter Newtonian mechanics. The first is the inertial mass  which enters into physics via Newton’s second law of motion
which enters into physics via Newton’s second law of motion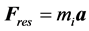 . The second kind of mass enters Newtonian mechanics via Newton’s law of universal gravitation which states that the gravitational force drawing together two objects of gravitational mass
. The second kind of mass enters Newtonian mechanics via Newton’s law of universal gravitation which states that the gravitational force drawing together two objects of gravitational mass ![]() and
and  that are separated by a distance
that are separated by a distance  is:
is:
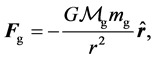 (1)
(1)
where ![]() is Newton’s constant of universal gravitation and
is Newton’s constant of universal gravitation and ![]() is the unit vector along the line joining the centres of mass of these objects and the negative sign is there to denote the fact that the gravitational force is a force of attraction.
is the unit vector along the line joining the centres of mass of these objects and the negative sign is there to denote the fact that the gravitational force is a force of attraction.
The Weak Equivalence Principle (WEP) due to the great Italian astronomer, mathematician, scientist and philosopher—Galileo Galilei (1564-1642), states that test bodies fall with the same acceleration independent of their internal structure or composition: in other words, this means that . Throughout this reading, in order to distinguish between gravitational and inertial mass, we shall use the subscripts “i” and “g” respectively i.e.
. Throughout this reading, in order to distinguish between gravitational and inertial mass, we shall use the subscripts “i” and “g” respectively i.e. 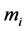 and
and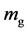 . If by any chance the hypothesis
. If by any chance the hypothesis 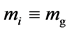 is true, then, this fact must and will come out clean from the resultant equations.
is true, then, this fact must and will come out clean from the resultant equations.
If we are to denote the ratio between the gravitational and inertial mass 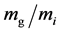 as:
as:
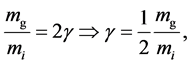 (2)
(2)
then, the acceleration of an object in a gravitational field which is obtained by setting 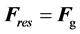 and then dividing the resultant equation throughout by
and then dividing the resultant equation throughout by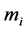 ; will be such that:
; will be such that:
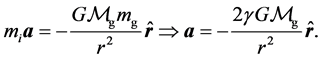 (3)
(3)
The factor 1/2 (or 2) in (2) has been inserted for convenience purposes. That is, written with this factor 1/2, numerically speaking, ![]() has the same meaning as it has in Post-Parametrised Newtonian (PPN) gravitation. For example, if we are to set
has the same meaning as it has in Post-Parametrised Newtonian (PPN) gravitation. For example, if we are to set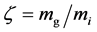 , then, a comparison of this
, then, a comparison of this 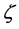 -factor with PPN gravitation’s
-factor with PPN gravitation’s ![]() -factor requires that
-factor requires that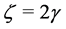 . So, in order that we have a direct comparison without the hindrance of this factor 2, one can deal with this once and for altime by inserting the factor 1/2 as has been done in (2). This is the reason for inclusion of this factor 1/2 (or 2). As already stated, under the Newtonian scheme where
. So, in order that we have a direct comparison without the hindrance of this factor 2, one can deal with this once and for altime by inserting the factor 1/2 as has been done in (2). This is the reason for inclusion of this factor 1/2 (or 2). As already stated, under the Newtonian scheme where 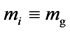 is assumped, it follows that
is assumped, it follows that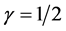 . This is a fundamental assumption of Newtonian mechanics.
. This is a fundamental assumption of Newtonian mechanics.
3. Newtonian Bending of Light (I)
It is only for instructive purposes that we go through this exercise of deriving the equation of orbit for a test particle in a Newtonian gravitational field. This derivation is found in every good textbook dealing with Classical/Newtonian Mechanics. In polar coordinates, the acceleration 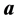 for a two dimensional surface (i.e. along a plane) is given by:
for a two dimensional surface (i.e. along a plane) is given by:
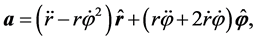 (4)
(4)
so that Equation (3) under the assumptions 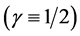 results in the equation of motion:
results in the equation of motion:
 (5)
(5)
where 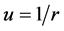 and
and 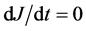 (which implies that
(which implies that ![]() is a conserved quantity). A solution to this equation is given by:
is a conserved quantity). A solution to this equation is given by:
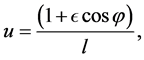 (6)
(6)
where 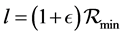 is a constant and is twice the distance when or the particle in orbit when
is a constant and is twice the distance when or the particle in orbit when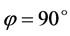 ,
, 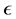 is the eccentricity of the orbit and
is the eccentricity of the orbit and 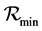 is the perigee distance of the orbit. Substituting
is the perigee distance of the orbit. Substituting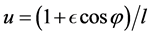 , into (5), one obtains that the specific orbital angular momentum is given by:
, into (5), one obtains that the specific orbital angular momentum is given by:
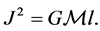 (7)
(7)
As will be seen when we arrive at (13), this Equation (7) is very important for the purposes of what we seek to achieve. From all this, one can show that:
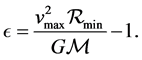 (8)
(8)
Now, we have to apply all the above ideas to the gravitational bending of light as is usually done or as has been done by past researchers. There is nothing new so far. In this application, light is treated as a beam composed of a stream of massive particles called photons. These photons move inside the gravitational field at a constant speed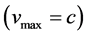 . For the eccentricity of this hyperbolic orbit
. For the eccentricity of this hyperbolic orbit , so that:
, so that:
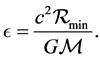 (9)
(9)
On grazing the Solar limb, the distance of the ray of light is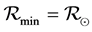 , this implies that this Newtonian angle of deflection
, this implies that this Newtonian angle of deflection 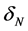 will be:
will be:
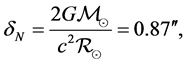 (10)
(10)
where the subscript “![]() ” has been inserted on
” has been inserted on ![]() so as to identity this result as a Newtonian result. This is the famous Newtonian result that is a factor “2” less than that obtained from Einstein’s GTR.
so as to identity this result as a Newtonian result. This is the famous Newtonian result that is a factor “2” less than that obtained from Einstein’s GTR.
4. Einsteinian Bending of Light
As stated in the introductory section, Einstein applied his newly found Equivalence Principle to the motion of light in a gravitational field. For light grazing the Solar limb, Einstein obtained the same value as that obtained from Newtonian gravitational under the assumption . After the completion of the GTR, he revised the same problem, and this time he obtained:
. After the completion of the GTR, he revised the same problem, and this time he obtained:
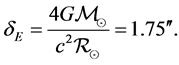 (11)
(11)
We are not—as we did in the Newtonian case; going to derive this result but simple state it as we have done above. This value is twice the Newtonian value i.e.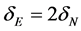 . What this meant is that now, it was possible to experimentally differentiate Newtonian gravitation from Einsteinian gravitational. The factor two is now a very crucial arbiter. As already stated in the introductory section, on November 19, 1919, Eddington’s expedition reported their now world famous result that posted Einstein into a scientific superstar on a scale never witnessed before for any scientist—i.e., both living and dead. They reported that their observations had given the deflection values of
. What this meant is that now, it was possible to experimentally differentiate Newtonian gravitation from Einsteinian gravitational. The factor two is now a very crucial arbiter. As already stated in the introductory section, on November 19, 1919, Eddington’s expedition reported their now world famous result that posted Einstein into a scientific superstar on a scale never witnessed before for any scientist—i.e., both living and dead. They reported that their observations had given the deflection values of 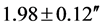 for the West African expedition, while the Principe observations yielded a value of
for the West African expedition, while the Principe observations yielded a value of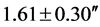 . These measurements clearly showed that the first two initial possibilities could be rejected, leaving the predictions of the GTR as the most plausible.
. These measurements clearly showed that the first two initial possibilities could be rejected, leaving the predictions of the GTR as the most plausible.
As shown in Table 1, in the years that followed, i.e. from 1922 up to 1973, eleven similar experiments were conducted. These measurements always recover Einstein’s 1.75″ prediction in the margins of error. Additionally, these deflection values display a scatter in the range 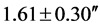 to
to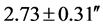 . The deflection value
. The deflection value 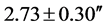 measured in 1936 in the then United Soviet Socialist Republic (USSR), is significantly larger than the Einsteinian deflection value of 1.75″. Einstein’s prediction is not even recovered in the margins of error for this measurement. Even in Eddington’s West African result (i.e.
measured in 1936 in the then United Soviet Socialist Republic (USSR), is significantly larger than the Einsteinian deflection value of 1.75″. Einstein’s prediction is not even recovered in the margins of error for this measurement. Even in Eddington’s West African result (i.e.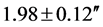 ), Einstein’s prediction is not even recovered in the margins of error. The usual explanation is that these experiments are very difficult to conduct. This “excuse” explains that scatter and the reason why the Einsteinian 1.75″ prediction is mostly recovered in the margins of error. Is this really the reason? Soon, we shall suggest otherwise. About the VLBA measurements that fervently confirm convincingly the Einsteinian 1.75″ prediction, we say unto our reader, for now, behold. We shall come to this in §’s (7) and (8). In the next section, we shall derive our major result that will cast some real doubt on the way researchers since 1919 have come to understand Eddington’s result and the subsequent sister experiments.
), Einstein’s prediction is not even recovered in the margins of error. The usual explanation is that these experiments are very difficult to conduct. This “excuse” explains that scatter and the reason why the Einsteinian 1.75″ prediction is mostly recovered in the margins of error. Is this really the reason? Soon, we shall suggest otherwise. About the VLBA measurements that fervently confirm convincingly the Einsteinian 1.75″ prediction, we say unto our reader, for now, behold. We shall come to this in §’s (7) and (8). In the next section, we shall derive our major result that will cast some real doubt on the way researchers since 1919 have come to understand Eddington’s result and the subsequent sister experiments.
5. Newtonian Bending of Light (II)
As already stated earlier, the strongest reason for setting 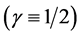 began with Galileo’s legendary experiments
began with Galileo’s legendary experiments
Table 1. Column (1) gives the number of the observation in the table. Column (2) and (3) gives the date and location of execution of the eclipse observations. Column (4) gives the actual measurements made, while column (5) and (6) gives the γ-factor and the ratio λc /λ as determined from Equation (19). Column (7) gives the deviation of the measurement from Einstein’s expected 1.75″ Solar deflection.
References: For the measurements given column (4), see: aDyson et al. ; b,c,d,eCampbell & Trumpler ; fFreundlich ; gMikhailov ; hmissing; i ; jvan Biesbroeck ; kBrune et al. and Jones .
at the Learning Tower of Pisa in Italy. He demonstrated—contrary to conventional wisdom of his day; that different masses will take the same amount of time to fall the same distance in a gravitational field. Before the reader proceeds, s/he must once again ask themselves the question “Is there anything wrong in writing the Newtonian gravitational equation of motion as?”: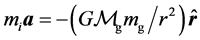 . By so doing, all that we have done is merely preserve the identity of the gravitational and inertial mass. Clearly, the most honest answer is that—if any at all; there is no reason whatsoever to reject the above equation because if
. By so doing, all that we have done is merely preserve the identity of the gravitational and inertial mass. Clearly, the most honest answer is that—if any at all; there is no reason whatsoever to reject the above equation because if , this will emerge from the resultant equations of motions upon weighing this equation against the test of experience as the resultant equations of motion sensitively depend on
, this will emerge from the resultant equations of motions upon weighing this equation against the test of experience as the resultant equations of motion sensitively depend on![]() . As will be demonstrated shorty, the inequality or equity of the gravitational and inertial mass is something that can be answered conclusively within the realm of Newtonian School of Mechanical Thought.
. As will be demonstrated shorty, the inequality or equity of the gravitational and inertial mass is something that can be answered conclusively within the realm of Newtonian School of Mechanical Thought.
Surely, if the afore-stated is the case i.e. 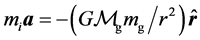 and that we shall assume that
and that we shall assume that , then, it follows that there should be no reason whatsoever to reject the final equations of motion which predict that the gravitational bending of light will depend on the
, then, it follows that there should be no reason whatsoever to reject the final equations of motion which predict that the gravitational bending of light will depend on the ![]() -factor. This is about the only “modification” that we make to Newtonian gravitation. We simple say to ourself, let us identify the gravitational and inertial mass of the objects and thereafter preserve these identities as we derive the resulting equations of motion in exactly the same manner as has been done since the time of Sir Isaac Newton’s derivation of the equation of the orbit of a test particle in a Newtonian gravitational field.
-factor. This is about the only “modification” that we make to Newtonian gravitation. We simple say to ourself, let us identify the gravitational and inertial mass of the objects and thereafter preserve these identities as we derive the resulting equations of motion in exactly the same manner as has been done since the time of Sir Isaac Newton’s derivation of the equation of the orbit of a test particle in a Newtonian gravitational field.
The result that we obtain from the resultant equations of motion have a rich mean meaning insofar as the WEP and the gravitational bending of light measurements are concerned. To dismiss this meticulous observations that Newtonian gravitation has something significant to say about ![]() is nothing-but logic denied. It is nothing but a deliberate denial of the truth emergent from clearly acceptable facts. Instead of rejecting this result, we must try to comprehend it, i.e. what does it mean insofar as our present understanding of gravitation is concerned? This is the approach that we take, we would like to understand this result in the light of our present understanding of gravitational theories.
is nothing-but logic denied. It is nothing but a deliberate denial of the truth emergent from clearly acceptable facts. Instead of rejecting this result, we must try to comprehend it, i.e. what does it mean insofar as our present understanding of gravitation is concerned? This is the approach that we take, we would like to understand this result in the light of our present understanding of gravitational theories.
Now, the corresponding equation to (5) under the assumption 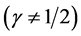 is:
is:
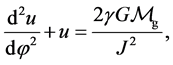 (12)
(12)
and a solution to this equation is the same as that to (5) i.e. . The major an all-important difference is the equation corresponding to (7). By substituting
. The major an all-important difference is the equation corresponding to (7). By substituting 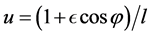 into (12), one interestingly and surprisingly, finds that:
into (12), one interestingly and surprisingly, finds that:
![]() (13)
(13)
This is the central result of the present reading as the main theme and conclusion to be derived herein flows from this result.
First and most important of all, notice that; in (13) the ![]() -factor has just entered Newtonian gravitational physics in a very significant way. The
-factor has just entered Newtonian gravitational physics in a very significant way. The ![]() -factor is now an inalienable and intricate part and parcel of the measurable equations of motion. This is were all the important difference comes in. However trivial this result may appear, we are certain that it is found nowhere else in the literature. It is the first time it is appearing. If not, then, its true significance has not been understood or appreciated. This reading shall demonstrate that, indeed, this result brings a whole new meaning to the equity of gravitational and inertial mass in Newtonian gravitational theory. It is imperative that the reader takes note of this.
-factor is now an inalienable and intricate part and parcel of the measurable equations of motion. This is were all the important difference comes in. However trivial this result may appear, we are certain that it is found nowhere else in the literature. It is the first time it is appearing. If not, then, its true significance has not been understood or appreciated. This reading shall demonstrate that, indeed, this result brings a whole new meaning to the equity of gravitational and inertial mass in Newtonian gravitational theory. It is imperative that the reader takes note of this.
We are certain the reader does not object to the result (13). On that footing and pedestal, we do not expect the reader to object to the final findings of the reading as these findings flow smoothly from the logic thereof. Yes, the results are difficult to believe at first sight, but, they flow smoothly from the logic of the mathematics whose nomothetic physical foundations are credible. Are we to go to war with logic in the hope of emerging victorious? We think not, we must accept results deduced from logic, its the only logical thing to do. The new finding (13), leads to the eccentricity now being given by:
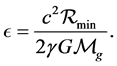 (14)
(14)
With the eccentricity now defined for the case , one can show that the new deflection angle
, one can show that the new deflection angle ![]() is given by:
is given by:
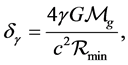 (15)
(15)
where the subscript “![]() ” has been inserted onto
” has been inserted onto ![]() so as to highlight that this result now in-cooperates the
so as to highlight that this result now in-cooperates the ![]() - factor. For electromagnetic waves grazing the Solar limb, we will have:
- factor. For electromagnetic waves grazing the Solar limb, we will have:
![]() (16)
(16)
Thus, any deviation from Einstein’s 1.75″ deflection can now be attributed to the ![]() -factor being different from unity—there is no escape from this.
-factor being different from unity—there is no escape from this.
6. The Scatter
If as in the cases (10) & (11), the new formula (15) is applicable to the motion of light, then, the ![]() -factor brings in a new meaning to the bending of light measurements. There is no reason whatsoever to reject (15) as it has been derived in exactly the same way as (10). The only difference has been to drop the hypothesis
-factor brings in a new meaning to the bending of light measurements. There is no reason whatsoever to reject (15) as it has been derived in exactly the same way as (10). The only difference has been to drop the hypothesis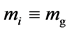 . Dropping this hypothesis is not in any way a modification of Newtonian gravitation but merely taking Newtonian gravitation in its bare form without making any hypothesis about the equity of inequity of gravitational to inertial mass. We have merely preserved the identities of these masses. What distinguishes our approach as unique, novel and ingenious, is our observation that when the identities of the gravitational and inertial mass are preserved, the specific angular momentum becomes dependent on
. Dropping this hypothesis is not in any way a modification of Newtonian gravitation but merely taking Newtonian gravitation in its bare form without making any hypothesis about the equity of inequity of gravitational to inertial mass. We have merely preserved the identities of these masses. What distinguishes our approach as unique, novel and ingenious, is our observation that when the identities of the gravitational and inertial mass are preserved, the specific angular momentum becomes dependent on ![]() as given in (13), and via this equation, one can now justly, formally and logically slip in this factor into the equations of motion. We shall now proceed to make the endeavour to associate the
as given in (13), and via this equation, one can now justly, formally and logically slip in this factor into the equations of motion. We shall now proceed to make the endeavour to associate the ![]() -factor with the scatter of the light bending measurements.
-factor with the scatter of the light bending measurements.
As a first step, let us define a measure for the deviation of the observational result 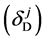 from that expected from theory
from that expected from theory 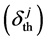 as:
as:
 (17)
(17)
Further, let us define a measure for the scatter, that is, the overall deviation of the observational result to that expected from theory as:
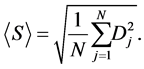 (18)
(18)
Now, with the above given, the new meaning brought in by the ![]() -factor in the bending of light measurements is that these measurements actually measure the
-factor in the bending of light measurements is that these measurements actually measure the ![]() -factor for photons. That is to say, for photons grazing the limb of the Sun, we will have:
-factor for photons. That is to say, for photons grazing the limb of the Sun, we will have:
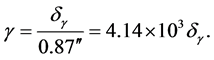 (19)
(19)
If the above proposal is accepted, then, the scatter seen in the bending of light measurements (see column three of Table 1 and as-well the plot in Figure 1) implies that ![]() is variable for these photons.
is variable for these photons.
The mean in the twelve eclipse deflection measurements listed in Table 1 and as-well their mean percentage error is 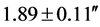 and 10% respectively. For both Einsteinian and Newtonian gravitation under the assumption that
and 10% respectively. For both Einsteinian and Newtonian gravitation under the assumption that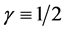 , one has the right to calculate the mean since this value must be the same for all the twelve measurements. Judging from this mean value, the Einstein value of 1.75” is recovered in the error margins. However, for Newtonian gravitation where the assumption
, one has the right to calculate the mean since this value must be the same for all the twelve measurements. Judging from this mean value, the Einstein value of 1.75” is recovered in the error margins. However, for Newtonian gravitation where the assumption 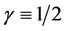 has been dropped, there is no priori nor posteriori justification for assuming that
has been dropped, there is no priori nor posteriori justification for assuming that ![]() must be constant. We simple have to take it as is. From these results, one can safely say that
must be constant. We simple have to take it as is. From these results, one can safely say that ![]() must be a variable quantity.
must be a variable quantity.
A value of  certainly favours the Einsteinian result (1.75″). But now, in the light of the new proposal that the assumption that
certainly favours the Einsteinian result (1.75″). But now, in the light of the new proposal that the assumption that 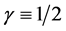 be dropped, the eclipse measurements no longer exclusively favour the Einsteinian result because under this new assumption, the eclipse measurements; while they measure the gravitational deflection of light, the effective measurement of these measurements according to (19), is that they measure the
be dropped, the eclipse measurements no longer exclusively favour the Einsteinian result because under this new assumption, the eclipse measurements; while they measure the gravitational deflection of light, the effective measurement of these measurements according to (19), is that they measure the ![]() -factor for the light under observation.
-factor for the light under observation.
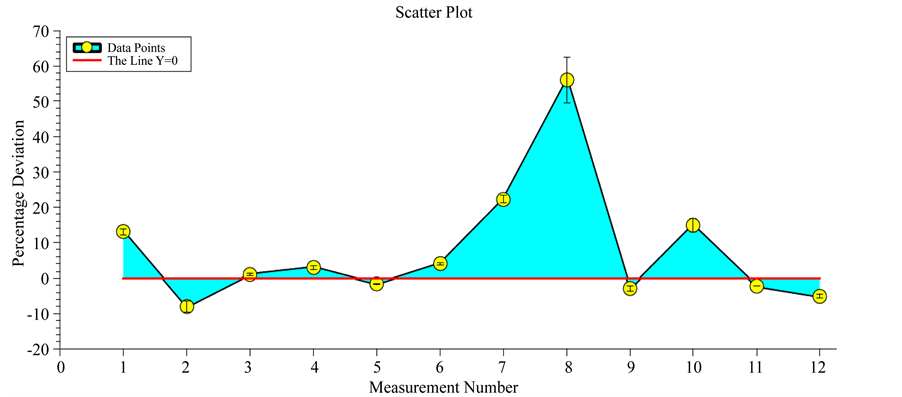
Figure 1. A scatter plot of the twelve Solar eclipse measurements presented in Table 1. The scatter is measured relative to the Einsteinian value 1.75″. Of the twelve, seven measurements have a positive deviation while five have a negative deviation. At about 56% deviation, the Japan (Sedul) measurement has the largest deviation. On average, all the twelve measurements have a scatter of 12.00% ± 7.00%.
6.1. Statistical Analysis
In order to obtain an objective view on the nature of the deviation of the 12-light bending measurement presented in Table 1, we shall submit these to some objective statistical analysis. Obviously, underlying our statistical analysis are some basic and fundamental assumptions. The conclusions draw thereof hinge on these assumptions.
6.1.1. Best Value
In our statistical analysis, our first port-of-call is to ask, what is the best value of Solar light bending can one derive from these 12-light bending measurement presented in Table 1? The best estimate can be obtained by taking the weighted mean of the two values. For example if 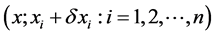 is set of
is set of 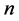 measurements of a constant quantity
measurements of a constant quantity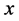 , where
, where  is the best value of for the
is the best value of for the  measurement and
measurement and 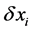 is its accompanying error margin, then, the best estimate of
is its accompanying error margin, then, the best estimate of 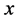 from this set is
from this set is 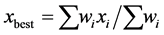 where
where ![]() are the weights such that
are the weights such that 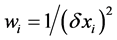 and the best estimate in the error margin
and the best estimate in the error margin 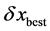 is
is 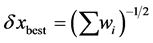 (see, e.g., Ref. [12] , p. 150). Applying this prescription to the 12-light bending measurements in Table 1, we obtain:
(see, e.g., Ref. [12] , p. 150). Applying this prescription to the 12-light bending measurements in Table 1, we obtain:
![]() (20)
(20)
We shall hereafter adopt this value as the best value representing the mean value of the 12-light bending measurements. This value 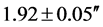 is a significant 10% higher than the expected Einsteinian value of 1.75″.
is a significant 10% higher than the expected Einsteinian value of 1.75″.
6.1.2. χ2 Statistical Analysis
If one has a sizeable set of  measurements where
measurements where 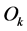 is the
is the 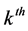 observation and
observation and 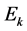 is the corresponding expected value, then, one can calculate
is the corresponding expected value, then, one can calculate 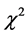 as follows
as follows 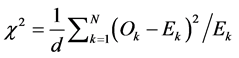 where
where 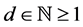 is the number of degrees of freedom of the given dataset. The number of degrees of freedom
is the number of degrees of freedom of the given dataset. The number of degrees of freedom 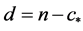 where
where 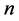 is the sample size and
is the sample size and 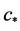 is the number of constraints required to derive or compute
is the number of constraints required to derive or compute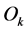 . If we are testing whether a particular hypothesis holds, then, if
. If we are testing whether a particular hypothesis holds, then, if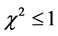 , there is no reason to believe the hypothesis under probe does not hold. If
, there is no reason to believe the hypothesis under probe does not hold. If , we have reasons to doubt our hypothesis. This is the so-called null hypothesis test or the
, we have reasons to doubt our hypothesis. This is the so-called null hypothesis test or the 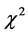 -test statistics (e.g., Ref. [12] , pp. 228-236). We shall apply this test to the 12-light bending measurements in Table 1.
-test statistics (e.g., Ref. [12] , pp. 228-236). We shall apply this test to the 12-light bending measurements in Table 1.
6.1.3. Gaussian Statistical Analysis
Whether or not the scatter in the 12-light bending measurements is a reflection or indicator of the level difficulty of the data procurement process, one fact that is clear is that, if the scatter were due to random natural causes, the distribution of the 12 measurements would be normally distributed. Inspection of Figure 2 reveals the measurements are not normally distributed. Yes, 75% of them fall within one standard deviation from the Einsteinian value 1.75″ while 25% are above this level. Below the one 1s-level of the Einsteinian value 1.75″, there are no measurements. The distribution of the 12 measurements is not Gaussian. Applying a 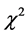 -test to ascertain whether or not the distribution is Gaussian, one finds that
-test to ascertain whether or not the distribution is Gaussian, one finds that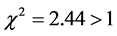 , the answer of which is that the distribution is certainly not Gaussian in nature.
, the answer of which is that the distribution is certainly not Gaussian in nature.
The standard deviation 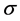 was computed by taking the Einsteinian value 1.75″ as the mean i.e.
was computed by taking the Einsteinian value 1.75″ as the mean i.e. 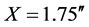 where-after, it was found that
where-after, it was found that![]() . With this, the data was binned as shown in Table 2. Clearly, from this table and from Figure 2, the odds are against the Newtonian value of 0.87″ and very much in favour of the Einstein value of 1.75″. Our major concern here is not the (75% of the) observations that seem to support Einstein’s 1.75″ but the 25% that are significantly well in excess of this value. What is the cause of this? This is something to be concerned about. If the scatter was truly of a random statistical nature, we would expect some of the observations to fall at least below the 1s-level of the mean. From this, one can, with equanimity say, there is reason to suspect that the 25% of the observations that are significantly well in excess of this value of 1s-level of the mean may very well be something inherent in the data and not of a statistical random nature.
. With this, the data was binned as shown in Table 2. Clearly, from this table and from Figure 2, the odds are against the Newtonian value of 0.87″ and very much in favour of the Einstein value of 1.75″. Our major concern here is not the (75% of the) observations that seem to support Einstein’s 1.75″ but the 25% that are significantly well in excess of this value. What is the cause of this? This is something to be concerned about. If the scatter was truly of a random statistical nature, we would expect some of the observations to fall at least below the 1s-level of the mean. From this, one can, with equanimity say, there is reason to suspect that the 25% of the observations that are significantly well in excess of this value of 1s-level of the mean may very well be something inherent in the data and not of a statistical random nature.

Figure 2. A histogram showing the statistical distribution of the 12 Solar bending of light measurements appearing in Table 1. In the histogram, Series 1 is the expected Gaussian distribution if the scatter in the measurements were a result of natural randomness while Series 2 is the actual distribution.
Table 2. Gaussian statistical analysis table.
6.1.4. Conclusion
If the observed scatter in the data was truly of a random statistical nature, we would expect some of the observations to fall at least below the 1s-level of the mean 1.75″. However, this is not the case. From this—with judicious equanimity, we draw the conclusion that there is reason to suspect that the 25% of the observations that are significantly well in excess of this value of 1s-level of the mean may very well be due to something inherent in the data; the cause of the excess may not be of a statistical random nature but systematic and inherent and due to a hitherto unbeknown phenomenon.
7. VLBA Experiments with Radio Waves
Beginning in about 1991, radio-interferometric using the Very-Long-Baseline Interferometry (VLBI) methods impressively determined that Einstein’s GTR was in excellent agreement with experience to within 0.02% [13] . That is to say, if 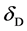 is the deflection angle from measurements, and
is the deflection angle from measurements, and 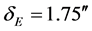 is the Einsteinian prediction, we can define the ratio
is the Einsteinian prediction, we can define the ratio ; then, the said VLBI observations gave
; then, the said VLBI observations gave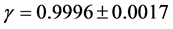 . This is an excellent agreement between observations and theory. If observations are to agree 100% with Einstein’s theory, then
. This is an excellent agreement between observations and theory. If observations are to agree 100% with Einstein’s theory, then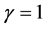 . The value
. The value 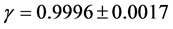 is obviously unprecedented. This
is obviously unprecedented. This ![]() -value for these VBLA measurements can be given the same meaning as the
-value for these VBLA measurements can be given the same meaning as the ![]() -value as defined herein. The factor 1/2 (or 2: depends on how one envisions this factor) that we inserted in (2) has been inserted so that the
-value as defined herein. The factor 1/2 (or 2: depends on how one envisions this factor) that we inserted in (2) has been inserted so that the ![]() -value for these VBLA measurements the
-value for these VBLA measurements the ![]() -value as defined herein will have the same meaning—or at least these two
-value as defined herein will have the same meaning—or at least these two![]() ’s are comparable.
’s are comparable.
Lebach et al. [13] obtained their impressive result by observing the gravitational deflection of radio waves from the strong radio source—the famous Quasar, 3C279. Other than the measurements of the Quasar, 3C279, several measurements using radio waves have been conducted to test Einstein’s gravitational bending of light (see, e.g., Ref. [14] -[21] ). All these measurements give excellent results. They confirm Einstein’s prediction to better than 1 part in 105. In comparison to measurements using white-light during Solar eclipses, the “improved accuracy” or the closeness of the deflection angle to that expected from the GTR may very well be that radio waves and visible light may have a different ![]() -values. These are matters that we will look at much more closely in the section that follows.
-values. These are matters that we will look at much more closely in the section that follows.
8. Massive Long Range Photons
If our proposal herein is to be accepted, namely that for photons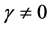 , then photons must have a mass! Generally, photons are considered to be massless. This means that their rest mass is assumed (or taken) to be identically zero. This wisdom is drawn from both Einstein’s Special Theory of Relativity and our palatable experience. Not only are photons held as massless particles, this is extented to apply to every particle that travels at the speed of light—accordingly, it is believed that such particles must be massless. This view has critically been brought into the scientific dock in the reading [22] . Another strong reason for ascribing photons a mass of zero is that the electromagnetic interaction is long range and for this to be so, the photon must be massless. This requirement—that for a long range interaction, there is need for its intermediate gauge Boson to be massless; this seemingly sacrosanct requirement has been shown in [23] to be not a sine qua non. Thus, according to [22] and [23] , massive photons that travel at the speed of light—can, in-principle exist without much difficultly.
, then photons must have a mass! Generally, photons are considered to be massless. This means that their rest mass is assumed (or taken) to be identically zero. This wisdom is drawn from both Einstein’s Special Theory of Relativity and our palatable experience. Not only are photons held as massless particles, this is extented to apply to every particle that travels at the speed of light—accordingly, it is believed that such particles must be massless. This view has critically been brought into the scientific dock in the reading [22] . Another strong reason for ascribing photons a mass of zero is that the electromagnetic interaction is long range and for this to be so, the photon must be massless. This requirement—that for a long range interaction, there is need for its intermediate gauge Boson to be massless; this seemingly sacrosanct requirement has been shown in [23] to be not a sine qua non. Thus, according to [22] and [23] , massive photons that travel at the speed of light—can, in-principle exist without much difficultly.
It is not difficult to make this deduction. For example, given the dispersion relation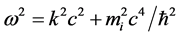 , where
, where ![]() is Planck’s normalised constant,
is Planck’s normalised constant, 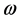 and
and  are the angular frequency and the wave-number of a massive photon, then, if the mass
are the angular frequency and the wave-number of a massive photon, then, if the mass  of the photon is—say, dependent on the wave-number i.e.
of the photon is—say, dependent on the wave-number i.e. 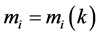 [consequently
[consequently 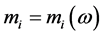 as-well], then, the group velocity
as-well], then, the group velocity 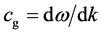 of such photons is given by:
of such photons is given by:
 (21)
(21)
The above relation assumes that, for all electromagnetic waves, the phase or particle velocity 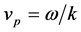 is a constant and is equal to the usual speed of light i.e.
is a constant and is equal to the usual speed of light i.e.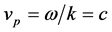 . Now, notice that in the above relation, if
. Now, notice that in the above relation, if  and is not a function of
and is not a function of  (or
(or ), then
), then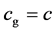 . This means that, a massive photon can indeed travel at the speed of light
. This means that, a massive photon can indeed travel at the speed of light 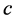 for as long as the mass
for as long as the mass 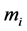 is not a function of the wave-number. Our aim in the present section has been to demonstrate this simple yet profound fact that massive photons can—indeed, travel at the speed of light. For a more detailed analysis of some interesting thoughts on the matter of massive photons, we refer the reader to the readings [22] [23] . Thus, in-principle and in theory, there is no priori nor posteriori justified reason to “fear” nor exclude the possibility of massive photons, especially massive long range photons that travel at the speed of light
is not a function of the wave-number. Our aim in the present section has been to demonstrate this simple yet profound fact that massive photons can—indeed, travel at the speed of light. For a more detailed analysis of some interesting thoughts on the matter of massive photons, we refer the reader to the readings [22] [23] . Thus, in-principle and in theory, there is no priori nor posteriori justified reason to “fear” nor exclude the possibility of massive photons, especially massive long range photons that travel at the speed of light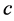 .
.
9. Status of Einstein’s Principle of Equivalence
At the very heart and nimbus of Einstein’s GTR is Einstein’s seemingly sacrosanct Equivalence Principle (EP). Interwoven and intertwine in Einstein’s EP are three separate principles (see, e.g., Ref. [24] ): that is, (1) The WEP, and (2) the principles of Local Lorentz Invariance (LLI) and (3) Local Position Invariance (LPI). More explicitly:
1. WEP: Test bodies fall with the same acceleration independently of their internal structure or composition. This is the WEP first set into motion by Galileo’s famous experiment at the Learning Tower of Pisa in Italy.
2. LLI: The outcome of any local non-gravitational experiment is independent of the velocity and acceleration of the freely-falling reference system in which it is performed. This is the Local Lorentz Invariance principle.
3. LPI: The outcome of any local non-gravitational experiment is independent of where and when in the Universe it is performed. This is the Local Position Invariance.
Now, for as long as all material bodies have the same value of ![]() at a given point
at a given point 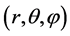 in a gravitational field, they will fall at the same rate, thus, Galileo’s falling bodies experiments at the Learning Tower of Pisa in Italy, will hold exactly leading to the same conclusion everywhere in the Universe. The present ideas suggest that for matter
in a gravitational field, they will fall at the same rate, thus, Galileo’s falling bodies experiments at the Learning Tower of Pisa in Italy, will hold exactly leading to the same conclusion everywhere in the Universe. The present ideas suggest that for matter  [or more generally
[or more generally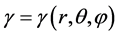 ], so all material bodies have the same value of
], so all material bodies have the same value of ![]() at a given point in a gravitational field. For both matter and radiation, in the local neighbour of a freely falling cabin in a gravitational field, the LLI and the LPI principles will hold exactly. For an observer in a closed freely falling cabin, they will not be able to distinguish whether they are in a gravitational field or they are experiencing an inertia generated acceleration. They will however be able to tell that their closed freely falling cabin is undergoing an acceleration by measuring the deflection of light rays of different wavelength.
at a given point in a gravitational field. For both matter and radiation, in the local neighbour of a freely falling cabin in a gravitational field, the LLI and the LPI principles will hold exactly. For an observer in a closed freely falling cabin, they will not be able to distinguish whether they are in a gravitational field or they are experiencing an inertia generated acceleration. They will however be able to tell that their closed freely falling cabin is undergoing an acceleration by measuring the deflection of light rays of different wavelength.
Now, given the violation of the WEP by radiation, the question arises “Does this mean that Einstein’s EP does not hold any longer?” Further, “Does this mean that Einstein’s GTR is not correct?” We strongly believe that Einstein’s GTR requires the survival of only the LLI and the LPI principles. These two principles i.e. the LLI and the LPI principles should be sufficient to uphold the Principle of Relativity. In its depth and breath, the EP’s ultimate endeavour is to uphold the LLI and the LPI principles, that is:
for as long as the outcome of any local non-gravitational experiment is independent of the velocity and acceleration of the freely-falling reference system in which it is performed Einstein’s GTR is safe. Actually, in-order to in-cooperate the new development, there is a way out. Einstein’s bare GTR will have to be transformed into a conformal theory of gravitation much akin to Weyl [25] -[27] ’s conformal theory of gravitation i.e., in Riemann geometry, the metric ![]() will have to be transformed into
will have to be transformed into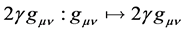 , so that the line element of spacetime
, so that the line element of spacetime 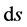 now becomes:
now becomes:
![]() (22)
(22)
where 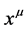 is the four position in spacetime. Under such a setting,
is the four position in spacetime. Under such a setting, ![]() is now a scalar field. The geodesic equation in such kind of a spacetime is:
is now a scalar field. The geodesic equation in such kind of a spacetime is:
 (23)
(23)
where ![]() is the usual Christophel three symbol in Reimann geometry and:
is the usual Christophel three symbol in Reimann geometry and:
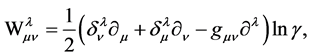 (24)
(24)
is the corresponding Weyl conformal affine connection. To first order approximation, in the weak field approximation where the Weyl conformal affine connection![]() , (23) reproduces the equation of motion (12) which leads directly to the main result (15) of the present work. Obviously, there is need for more work than has been conducted here in-order to get these ideas on a firm pedestal.
, (23) reproduces the equation of motion (12) which leads directly to the main result (15) of the present work. Obviously, there is need for more work than has been conducted here in-order to get these ideas on a firm pedestal.
10. Discussion
At any rate imaginable, we do not doubt that the path of light (or in general, an electromagnetic wave) is altered by a gravitational field nor do we doubt that experience as revealed by the gravitational deflection of radio waves strongly and clearly favours Einstein’s GTR. Our bone of contention is what this deflection really measures? As presented herein, other than a confirmation that gravity does indeed alter the path of light, we have asked a rather disturbing question: “Are these experiments not also a measure of the gravitational to inertial mass ratio of photons? Why do we have a scatter (~20%) that is one and half times the average margin of error (~13%) of all the twelve experiments from 1919 to 1973?” If anything, these (seemingly) simple questions need solid answers. This is what we have tried to provide herein.
The findings of this reading if correct (as we believe them to be), then, it is without doubt that they have serious implications on the foundations of physics—at the very least, they call for nothing short of a rethink on our understanding of these foundations. For example, “Truly, does the all-embellished WEP hold universally? That is, does it hold for all matter and radiation?” In the light of what has been presented, this is just but one of the many deep, important foundational questions that come to the deeply enquiring mind seeking understanding of the most fundamental Laws of Nature. In our modest and humble of opinion, we strongly believe that we have shown herein that, from its own internal logic and consistency, Newton’s gravitational theory strongly suggests that the WEP may not hold, especially with electromagnetic radiation were we have clearly demonstrated that the factor ![]() is not necessarily equal one half has required for this to be so.
is not necessarily equal one half has required for this to be so.
In short, the main thrust of this work has been to rise the point that the ![]() -factor (as defined herein) may be used in Newtonian gravitation to furnish any deficiency that may arise from measurements of the deflection of light by a gravitational field. Solar gravitational deflection of light is not constrained to Einstein’s 1.75″ deflection but any arbitrary amount depending on the photon’s
-factor (as defined herein) may be used in Newtonian gravitation to furnish any deficiency that may arise from measurements of the deflection of light by a gravitational field. Solar gravitational deflection of light is not constrained to Einstein’s 1.75″ deflection but any arbitrary amount depending on the photon’s ![]() -value. Naturally, unwillingly and involuntarily, this rises the rather contentious and polemical question of:
-value. Naturally, unwillingly and involuntarily, this rises the rather contentious and polemical question of:
What one is to make of Sir Professor Eddington’s efforts... and as-well, what one is to make of similar efforts?
Are these efforts to be understood as confirming Einstein’s 1.75″ deflection? or are they to be understood as confirming that the gravitational field does alter the path of an electromagnetic wave in such a manner that this deflection angle is a direct measure of the photon’s gravitational to inertial mass ration ![]() as defined herein? Are we to be content with the 20% scatter about Einstein’s 1.75″ as reflective of the level difficulty in the measurements or are we to understand this scatter as reflective of a variable
as defined herein? Are we to be content with the 20% scatter about Einstein’s 1.75″ as reflective of the level difficulty in the measurements or are we to understand this scatter as reflective of a variable ![]() that deviates from the expected
that deviates from the expected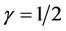 ?
?
As tabled in Table 1, the average value for the displacement of the stellar images from the Sobral observations was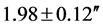 , and the Principe observations yielded a value of
, and the Principe observations yielded a value of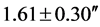 . These measurements clearly showed that two of the initial possibilities could be rejected, leaving the predictions of the GTR as the most plausible. It is now common knowledge that this expedition determined Einstein’s findings to be correct to within 8% to 34%. In 1995 the accuracy was greatly improved. It was determined by radiointerferometric (Very-Long-Baseline Interferometry; VLBI) methods that and these measurements indicated that Einstein’s GTR was correct to within 0.02% [13] . The “improved accuracy” or the closeness of the deflection angle to that expected from the GTR may very well be that radio waves and visible light may have a different
. These measurements clearly showed that two of the initial possibilities could be rejected, leaving the predictions of the GTR as the most plausible. It is now common knowledge that this expedition determined Einstein’s findings to be correct to within 8% to 34%. In 1995 the accuracy was greatly improved. It was determined by radiointerferometric (Very-Long-Baseline Interferometry; VLBI) methods that and these measurements indicated that Einstein’s GTR was correct to within 0.02% [13] . The “improved accuracy” or the closeness of the deflection angle to that expected from the GTR may very well be that radio waves and visible light may have a different ![]() -values. These are matters that will require to be looked at much more closely in-order to establish the truth.
-values. These are matters that will require to be looked at much more closely in-order to establish the truth.
If, truly, it occurs that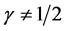 , invariably, this means, once the WEP is found wanting, so is Einstein’s GTR, it must be found wanting too. Is this the case? The answer is yes, Einstein’s GTR will be found in a wantingstate. To see this, for a minute, imagine or suppose one is inside a freely falling cabin and in this cabin, they hold two relatively small masses that have differing
, invariably, this means, once the WEP is found wanting, so is Einstein’s GTR, it must be found wanting too. Is this the case? The answer is yes, Einstein’s GTR will be found in a wantingstate. To see this, for a minute, imagine or suppose one is inside a freely falling cabin and in this cabin, they hold two relatively small masses that have differing![]() ’s. Further, the
’s. Further, the ![]() of the cabin itself is different from that of the two masses—lets suppose it is much less than that of the two masses. Clearly, these two masses if let loose, they will not remain at rest relative to the freely falling cabin, but will begin to move. The mass with a much higher
of the cabin itself is different from that of the two masses—lets suppose it is much less than that of the two masses. Clearly, these two masses if let loose, they will not remain at rest relative to the freely falling cabin, but will begin to move. The mass with a much higher ![]() will be seen to accelerate toward the fall of the cabin much faster than the other mass with a lower
will be seen to accelerate toward the fall of the cabin much faster than the other mass with a lower![]() . The freely falling cabin is no longer an inertial reference system. But, if the
. The freely falling cabin is no longer an inertial reference system. But, if the ![]() of the cabin and the two masses are the same, the cabin will behave like an inertial reference system exactly as Einstein [28] imagined.
of the cabin and the two masses are the same, the cabin will behave like an inertial reference system exactly as Einstein [28] imagined.
In the light of the present reading—unless off-cause one has sufficiently reasonable ground to do so; one can not arbitrarily set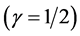 , because, the very fact that the bending angle, as procured from experience, is not compatible with the setting
, because, the very fact that the bending angle, as procured from experience, is not compatible with the setting 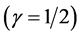 as evidenced by the significant scatter in the observational measurements of
as evidenced by the significant scatter in the observational measurements of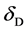 , this may very well be that the value of
, this may very well be that the value of ![]() that restores agreement between experience and theory is the
that restores agreement between experience and theory is the ![]() -value of the photons under observation.
-value of the photons under observation.
In-closing, allow us to say that if we were asked whether or not the WEP holds, without hesitation, our answer to this is that:
“it is very possible that this principle—as commonly understood i.e. were ![]() is the same for all material bodies everywhen and everywhere; may not hold as we have come to believe”.
is the same for all material bodies everywhen and everywhere; may not hold as we have come to believe”.
The justification is what we have presented herein. In the light of this, we do not know what interesting answer our reader(s) would give to this same question. As to whether Einstein’s GTR falls apart or not, we would say no, it does not fall apart as it has been argued herein that the violation of the WEP in its popular understanding, this does not translate nor entail a violation of the EP by matter. However, Einstein’s GTR will need to be revisited if the ![]() -factor is accepted or shown to actually explain the scatter in the deflection measurements because Einstein’s GTR will have to successfully stand to these data. This will certainly require a modification of the GTR.
-factor is accepted or shown to actually explain the scatter in the deflection measurements because Einstein’s GTR will have to successfully stand to these data. This will certainly require a modification of the GTR.
11. Conclusions
Assuming the correctness (or acceptability) of the thesis set-forth herein, we hereby make the following conclusions:
1. As is widely believed, the eclipse results of the Solar gravitational bending of light carried by Eddington and his team in 1919 and all subsequent eclipse measurement results from 1922 to 1973; these measurements do not point to Einstein’s GTR being a superior theory to Newtonian gravitational theory, because, according to the Newtonian gravitational theory under the WEP violation, the eclipse results of the Solar gravitational bending of light actually measure the ![]() -factor for light and the deflection angle. To predict the deflection angle, one will need to know forehand that value of
-factor for light and the deflection angle. To predict the deflection angle, one will need to know forehand that value of ![]() for light. There is no priori justification to set this value to unity thus, from these eclipse measurements, one can safely say that it strongly appears that
for light. There is no priori justification to set this value to unity thus, from these eclipse measurements, one can safely say that it strongly appears that ![]() varies markedly for white-light while for radio wave waves this ratio appears to be constant.
varies markedly for white-light while for radio wave waves this ratio appears to be constant.
2. The excellent results of the VLBA measurements leading to researchers to fervently claim that these excellent measurements vindicate Einstein’s GTR; this may very well suggest that for these waves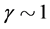 , which would for the Sun mean
, which would for the Sun mean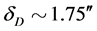 .
.
3. The “poor” eclipse measurements leading to researchers suggest that these “poor” results are a reflection of the level difficulty in the measurement process itself; these results, may very well suggest that the gravitational to inertial mass ratio of photons depends on the wavelength. Since white-light grazing the Solar limb comes from light sources emitting in varying frequency range in the visible part of the electromagnetic spectrum, these photons will have different ![]() -ratios, leading to varying deflection angles. The variation of the deflection angle is perhaps what we observe as a 20% scatter in the twelve Eclipse measurements so far made from 1919 right up to 1973. This scatter is a significant 1.46 times the average margin of error of the twelve Eclipse measurements.
-ratios, leading to varying deflection angles. The variation of the deflection angle is perhaps what we observe as a 20% scatter in the twelve Eclipse measurements so far made from 1919 right up to 1973. This scatter is a significant 1.46 times the average margin of error of the twelve Eclipse measurements.
4. It strongly appears that the WEP may very well not hold. However, its violation does not lead to a violation of the Local Position Invariance which is necessary for the survival of Einsten’s GTR. Consequently, Einstein’s GTR holds, albeit, it will have to be modified so that it takes into account the hypothesised positional variation of![]() . We have briefly shown herein that a conformal metric theory of gravitation akin to that of Weyl can replace Einstein’s GTR with relative ease. They resulting theory needs to be worked out properly to put it on a firm footing and pedestal.
. We have briefly shown herein that a conformal metric theory of gravitation akin to that of Weyl can replace Einstein’s GTR with relative ease. They resulting theory needs to be worked out properly to put it on a firm footing and pedestal.
12. Recommendations
Assuming the correctness (acceptability/plausibleness) of the ideas laid down herein, we hereby put forward the following recommendations:
1. There is need for renewed efforts to measure much more accurately the gravitational deflection of light at every eclipse opportune in the future in-order to ascertain for sure that Einstein’s GTR exclusively explains this phenomenon. It must be demanded of these precision measurements that the deflection angle must not vary markedly from Einstein’s prediction. Any scatter in these results only support the thesis set-forth herein that ![]() is constrained to unity; this factor varies depending on the light mixture under probe. Given that there is the upcoming GAIA mission which amongst others aims to measure over all the sky, the apparent positions (due to Solar gravitational deflection) of stars so accurately and precisely, so much that the gravitational deflection due to the Sun will be a large signal, there is all hope that this scatter may or deviation from the Einsteinian-1.75″ prediction, may come to full notice and attention of the agile and diligent observer.
is constrained to unity; this factor varies depending on the light mixture under probe. Given that there is the upcoming GAIA mission which amongst others aims to measure over all the sky, the apparent positions (due to Solar gravitational deflection) of stars so accurately and precisely, so much that the gravitational deflection due to the Sun will be a large signal, there is all hope that this scatter may or deviation from the Einsteinian-1.75″ prediction, may come to full notice and attention of the agile and diligent observer.
2. In the light of the new ideas set-forth herein, the need for a thorough reanalysis of all the available eclipse data can not be overstated. Such a study needs to treat the deflection of each star individually and not what has been happening where the individually measured deflections of stars belonging to a set of given a eclipse data set, one averages the deflection of all the stars on the plate after which a single value for the deflection for that dataset is given as representative of the overall Solar gravitational deflection of light. The thrust of such a study would be to unearth the true nature of the scatter of these deflections about the predicted Einsteinian value of 1.75″.
3. To avoid and reduce—if not eliminate all public scepticism; in the true spirit of science, raw data from the eclipse measurements must be published so as to allow and afford scientifically minded and able members of the general public to verify for themselves the true nature and extend of Solar gravitational deflection. Eddington and some latter eclipse observers, have discarded some of the plates with the simple remark that “these plates were bad, so bad that no useful data could be derived from them”. The able and agile members of the general public must be given the opportunity to judge for themselves whether or not these plates are really bad, so bad so much that no useful data can be derived from them. This is important for the progress of science and as-well for progress on this matter of the Solar gravitational bending of light vis whether or not these measurements vindicate 100% Einstein and place his GTR on an exclusive, distinct and superior pedestal to Newton’s gravitational theory.
4. Given that currently, Einstein’s GTR is an all-embellished and seemingly sacrosanct touchstone of gravitation—at this juncture in its history and development; could there be something Einsteinian gravitation can learn from its predecessor i.e. Newtonian gravitation? We pause or ask this question to our dear reader because we solemnly hold that, in the light of the new ideas presented herein, a thorough non-biased publishing of raw data will certainly lead to a scenario where Einstein’s GTR may learn one or two things from Newtonian gravitation. As to ourself on this matter—i.e. on Einstein’s GTR learning from Newtonian gravitation; confidently, without an iota or dot of doubt; we think, believe and hold that:
Yes, there is!
Acknowledgements
We are grateful to the National University of Science & Technology (NUST)’s Research & Innovation Department and Research Board for their unremitting support rendered toward our research endeavours; of particular mention, Dr. P. Makoni and Prof. Y. S. Naik’s unwavering support.
References
- Einstein, A. (1916) Grundlage der Allgemeinen Relativitätstheorie (The Foundation of the General Theory of Relativity). Annalen der Physik (Leipzig), 354, 769-822. http://dx.doi.org/10.1002/andp.19163540702
- Dyson, F.W., Eddington, A.S. and Davidson, C. (1920) A Determination of the Deflection of Light by the Sun’s Gravitational Field, from Observations Made at the Total Eclipse of May 29, 1919. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character, 220, 291-333.
- Dyson, F.W., Eddington, A.S. and Davidson, C. (1920) Relativity and the Eclipse Observations of May, 1919. Nature, 106, 786-787. http://dx.doi.org/10.1038/106786a0
- Kennefick, D. (2009) Testing Relativity from the 1919 Eclipse—A Question of Bias. Physics Today, 62, 37-42. http://dx.doi.org/10.1063/1.3099578
- Campbell, W.W. and Trumpler, R. (1923) The Total Eclipse of the Sun, September 21, 1922. Publications of the Astronomical Society of the Pacific, 35, 11. http://dx.doi.org/10.1086/123262
- Freundlich, E.F., von Klüber, H. and von Brunn, A. (1929) Ergebnisse der Potsdamer Expedition zur Beobachtung der Son-Nenfinsternis von 1929, Mai 9, in Takengon (Nordsumatra). 5. Mitteilung. Ober die Ablenkung des Lichtes im Schwerefeld der Sonne, ZAP, 3, 171-198.
- Mikhailov, A.A. (1940) Measurement of the Deflection of Light by the Sun’s Gravitational Field during the Eclipse of June 19, 1936. DokIady Akademii Nauk, USSR, 29, 189-190.
- van Biesbroeck, G. (1950) The Einstein Shift at the Eclipse of May 20, 1947, in Brazil. Astronomical Journal, 55, 49- 52. http://dx.doi.org/10.1086/106328
- Van Biesbroeck, G. (1953) The Relativity Shift at the 1952 February 25 Eclipse of the Sun. Astronomical Journal, 58, 87. http://dx.doi.org/10.1086/106825
- Allen Brune Jr., R., Cobb, C.L., De-Witt, B.S., De-Witt-Morette, C., Evans, D.S., Floyd, J.E., Jones, B.F., Lazenby, R.V., Marin, M., Matzner, R.A., Mikesell, A.H., Mikesell, M.R., Mitchell, R., Ryan, M.P., Smith, H.J., Sy, A. and Thompson, C.D. (1976) Gravitational Deflection of Light: Solar Eclipse of 30 June 1973 I. Description of Procedures and Final Results. Astronomical Journal, 81, 452.
- Jones, B.F. (1976) Gravitational bending of light: Solar Eclipse of 30 June 1973 II. Plate Reductions. Astronomical Journal, 81, 455-463. http://dx.doi.org/10.1086/111907
- Taylor, J.R. (1982) Introduction to Error Analysis. University Science Books, Sausalito.
- Lebach, D.E., Corey, B.E., Shapiro, I.I., Ratner, M.I., Webber, J.C., Rogers, A.E.E., Davis, J.L. and Herring, T.A. (1995) Measurement of the Solar Gravitational Deflection of Radio Waves Using Very-Long-Baseline Interferometry. Physical Review Letters, 75, 1439-1442. http://dx.doi.org/10.1103/PhysRevLett.75.1439
- Anderson, J.D., Lau, E.L. and Gaipieri, G. (2004) Measurement of the ppn Parameter with Radio Signals from the Cassini Spacecraft at xand ka-Bands. 22nd Texas Symposium on Relativistic Astrophysics at Stanford University, 13-17 December 2004.
- Bertotti, B., Iess, L. and Tortora, P. (2003) A Test of General Relativity Using Radio Links with the Cassini Spacecraft. Nature, 425, 374-376. http://dx.doi.org/10.1038/nature01997
- Fomalont, E.B. and Sramek, R.A. (1976) Measurements of the Solar Gravitational Deflection of Radio Waves in Agreement with General Relativity. Physical Review Letters, 36, 1475-1478. http://dx.doi.org/10.1103/PhysRevLett.36.1475
- Robertson, D.S., Carter, W.E. and Dillinger, W.H. (1991) New Measurement of Solar Gravitational Deflection of Radio Signals Using VLBI. Nature, 349, 768-770. http://dx.doi.org/10.1038/349768a0`
- Counselman, C.C., Kent, S.M., Knight, C.A., Shapiro, I.I., Clark, T.A., Hinteregger, H.F., Rogers, A.E.E. and Whitney, A.R. (1974) Solar Gravitational Deflection of Radio Waves Measured by Very-Long-Baseline Interferometry. Physical Review Letters, 33, 1621-1623. http://dx.doi.org/10.1103/PhysRevLett.33.1621
- Muhleman, D.O., Ekers, R.D. and Fomalont, E.B. (1970) Radio Interferometric Test of the General Relativistic Light Bending Near the Sun. Physical Review Letters, 24, 1377-1380. http://dx.doi.org/10.1103/PhysRevLett.24.1377
- Shapiro, I.I. (1964) Fourth Test of General Relativity. Physical Review Letters, 13, 789-791. http://dx.doi.org/10.1103/PhysRevLett.13.789
- Shapiro, S.S., Davis, J.L., Lebach, D.E. and Gregory, J.S. (2004) Measurement of the Solar Gravitational Deflection of Radio Waves Using Geodetic Very-Long-Baseline Interferometry Data, 1979-1999. Physical Review Letters, 92, 121101. http://dx.doi.org/10.1103/PhysRevLett.92.121101
- Nyambuya, G.G. (2013) Are Photons Massless of Massive? viXra:1301.0061.
- Nyambuya, G.G. (2013) Massive Long Range Photons and the Variation of the Fine Structure Constant. viXra: 1302. 0168.
- Will, C.M. (2009) The Confrontation between General Relativity and Experiment. Space Science Reviews, 148, 3-13. http://dx.doi.org/10.1007/s11214-009-9541-6
- Weyl, H.K.H. (1918) Gravitation und Elektrizität, Sitzungsber. Preuss. Akad. Wiss, 26, 465-478.
- Weyl, H.K.H. (1927) Elektron und Gravitation I. Zeitschrift für Physik, 56, 330-352. http://dx.doi.org/10.1007/BF01339504
- Weyl, H.K.H. (1927) Gravitation and the Electron. Proceedings of the National Academy of Sciences, 15, 323-334. http://dx.doi.org/10.1073/pnas.15.4.323
- Einstein, A. (1977) Grundlage der Allgemeinen Relativitätstheorie (The Foundation of the General Theory of Relativity). Annalen der Physik (Leipzig), 49, 769-822.


