Applied Mathematics
Vol. 3 No. 6 (2012) , Article ID: 20358 , 4 pages DOI:10.4236/am.2012.36097
The Many-on-One Stochastic Duel Model with Information-Sharing*
School of Science, Nanjing University of Science & Technology, Nanjing, China
Email: j_jli@163.com, lwliu@mail.njust.edu.cn
Received April 25, 2012; revised May 25, 2012; accepted June 2, 2012
Keywords: Stochastic Dule; Information-Sharing; Probability Density Function
ABSTRACT
In this paper we extend the one-on-one stochastic duel model with searching to the many-on-one case based on information-sharing. We have derived the probability density function of the time to kill the target in many-on-one model. It is illustrated by an example in which the firing time and the searching time are of different exponential distributions.
1. Introduction
The stochastic duel problem has been studied extensively in the past. Ancker [1] studied the fundamental one-onone stochastic duel model, and provided a good review of such model. The general two-on-one stochastic duel model was considered by Gafarian and Ancker [2]. They obtained the general solution for the duel state probabilities, and derived the winning probabilities.
Friedman [3] and Kikuta [4] considered the many-onone stochastic duel model. They have got an optimal firing policy for the single unit side. Subsequently, Kress [5] investigated the general many-on-one stochastic duel conditioned on the order in which targets are attacked.
Wand et al. [6] revisited the one-on-one stochastic duel model and took account of searching in their model. Liu [7,8] studied the one-on-one stochastic duel model with searching and deduced the density function of the time needed for killing the target, and calculated the winning probabilities for the both sides.
In this paper we extend the one-on-one stochastic duel model with searching given in [7] to the many-on-one case based on information-sharing. The scenario envisaged is many hidden defenders and one of a hidden attacker. In this scenario, when one of the defenders detects the attacker after some random time interval, all the defenders share the information about the attacker at the same time. The defenders start their firing process immediately after the attacker being detected. Assuming the defenders are well dug-in, it would be extremely difficult for the attacker to detect the defenders. We assume that the attacker will be killed before he can return fire. That is to say, the attacker is a passive target after being detected.
The remainder of this paper is organized as follows. The notation is described in Section 2. Then, in Section 3, the probability model is developed. In Section 4, this model is restricted to the negative exponential distribution case to allow ease of computation. Finally, we draw some concluding remarks and a brief discussion of some possible extensions in Section 5.
2. Assumptions and Notations
Suppose that the two sides in the duel are A and B, respectively. There are k combatants on side A which are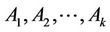 . They are hidden defenders, and their mission is to kill the invaders or the attackers. Side B only has one hidden attacker.
. They are hidden defenders, and their mission is to kill the invaders or the attackers. Side B only has one hidden attacker.
Two sides, A and B, conduct a duel satisfying the following assumptions:
1) All the information about B is shared among A’s members. When one of them detects B, every one will know.
2) Each combatant 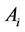 fires simultaneously until B is killed after B being detected.
fires simultaneously until B is killed after B being detected.
3) Every member of side A has the same fixed probability, p, of killing B.
4) A’s firing time (that is, the time between rounds) is a random variable with a known probability density function,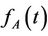 . And each firing time is selected from
. And each firing time is selected from , independently and at random.
, independently and at random.
5) Side B is a passive target.
Other notations which we will use are as follows.
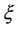 : The time for A to detect B. It is a positive random variable.
: The time for A to detect B. It is a positive random variable.
 : The probability density function (pdf) of
: The probability density function (pdf) of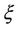 .
.
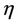 : A’s firing time. The pdf of
: A’s firing time. The pdf of 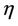 is
is 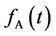 (see above 4)). It is a positive random variable too.
(see above 4)). It is a positive random variable too.
 : The characteristic function of
: The characteristic function of .
.
 : The time for A to kill B, measured from the beginning of A’s searching B.
: The time for A to kill B, measured from the beginning of A’s searching B.
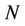 : The firing round times of A until killing B.
: The firing round times of A until killing B.
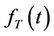 : The pdf of
: The pdf of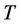 .
.
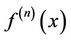 : The
: The  multiple convolution of the density function
multiple convolution of the density function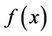 . That is,
. That is,
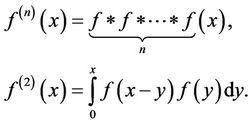
3. The Model
Consider the pdf of random variable 
 . (1)
. (1)
The probability,  , that A takes between time t and
, that A takes between time t and 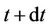 to kill B in the condition of
to kill B in the condition of 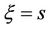 is the probability of a kill on the first round times the probability side A took between time t and
is the probability of a kill on the first round times the probability side A took between time t and  to fire the first round, plus the probability of a kill on the second round times the probability side A took between time t and
to fire the first round, plus the probability of a kill on the second round times the probability side A took between time t and 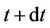 to fire the two rounds and so on; thus
to fire the two rounds and so on; thus
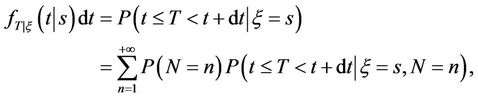 (2)
(2)
where
 (3)
(3)
where . Since A’s firing time,
. Since A’s firing time,  , density function is
, density function is , the time at which the nth round is fired is the sum of n independent selections from
, the time at which the nth round is fired is the sum of n independent selections from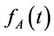 , so we have
, so we have
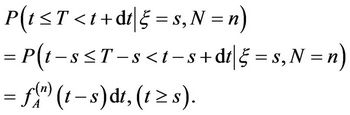 (4)
(4)
When (3) and (4) are substituted into (2), we have
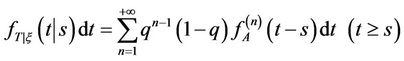
or
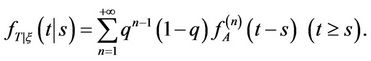 (5)
(5)
Before continuing we shall give the characteristic function of firing time distribution. The characteristic function of  is
is
 (6)
(6)
The following properties of 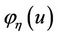 are readily demonstrated.
are readily demonstrated.
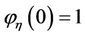 , (7)
, (7)
 . (8)
. (8)
Let 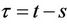 and
and . Then (5) can be rewritten as
. Then (5) can be rewritten as
 (9)
(9)
The characteristic function for the conditional density function 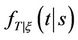 (or
(or ) is denoted by
) is denoted by  From the convolution property of characteristic functions, (9) may be transformed into
From the convolution property of characteristic functions, (9) may be transformed into
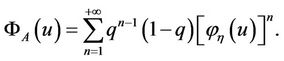 (10)
(10)
From (8), (10) and , we have
, we have

The inversion of 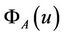 is as follows:
is as follows:
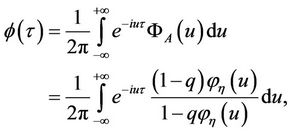
then
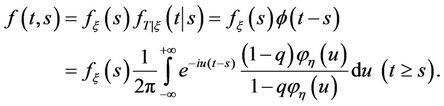 (11)
(11)
From (11), we can derive the probability density function of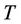 ,
, .
.
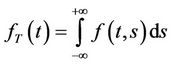 (12)
(12)
When (11) is substituted into (12), we have
 (13)
(13)
4. Example
Suppose that the probability density functions of 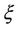 and
and 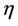 are of exponentials with parameters
are of exponentials with parameters 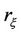 and
and , respectively, then
, respectively, then
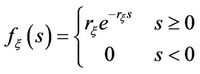 and
and
 where
where ,
,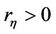 . The characteristic function of
. The characteristic function of  is
is

From (13), we obtain that
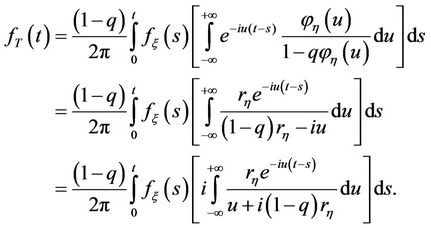
Applying the residue theorem, we have
 (14)
(14)
It is readily demonstrated that 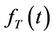 has the following properties:
has the following properties:
1)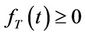 2)
2)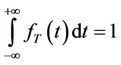 3)
3) .
.
Proof of property 3): When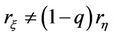 , we have
, we have

when , the same result can be derived.
, the same result can be derived.
5. Conclusion
In this article we extend the one-on-one stochastic duel model with searching to the many-on-one case based on information sharing. The probability density function of the time to kill the target is obtained in integral form. And it is illustrated by an example where the firing time and the searching time are of different exponential distributions.
REFERENCES
- C. J. Ancker, “One-on-One Stochastic Duels,” Research Monograph, Military Applications Section, Operations Research Society of America (now INFORMS), Arlington, 1982.
- A. V. Gafarian and C. J. Ancker, “The Two-on-One Stochastic Duel,” Naval Research Logistics Quarterly, Vol. 31, 1984, pp. 309-324. doi:10.1002/nav.3800310213
- Y. Friedman, “Optimal Strategy for the One-againstMany Battle,” Operations Research, Vol. 25, No. 5, 1977, pp. 884-888. doi:10.1287/opre.25.5.884
- K. Kikuta, “A Note on the One-against-Many Battle,” Operations Research, Vol. 31, No. 5, 1983, pp. 952-956. doi:10.1287/opre.31.5.952
- M. Kress, “The Many-on-One Stochastic Duel,” Naval Research Logistics Quarterly, Vol. 31, 1987, pp. 713- 720.
- K. Wand, S. Humble and R. J. T. Wilson, “Explicit Modelling of Detection within a Stochastic Duel,” Naval Research Logistics Quarterly, Vol. 40, 1993, pp. 431-450. doi:10.1002/1520-6750(199306)40:4<431::AID-NAV3220400402>3.0.CO;2-S
- L. W. Liu, “Density Function of the Time for Target Killing Involving the Target Detection Time,” Acta Armamentarii, Vol. 23, No. 3, 2002, pp. 370-373.
- L. W. Liu, “A Kind of Stochastic Duel Model for Guerrilla War,” European Journal of Operational Research, Vol. 171, No. 1, 2006, pp. 430-438. doi:10.1016/j.ejor.2004.09.032
NOTES
*Supported by National Natural Science Foundation of China under Grant No.60874118.

