Agricultural Sciences
Vol.06 No.09(2015), Article ID:60059,8 pages
10.4236/as.2015.69106
Estimating Chlorophyll Content of Apple Leaves Based on Different Scales in Differential Window
Zhaoying Han1, Xicun Zhu1,2*, Zhuoyuan Wang1, Gengxing Zhao1, Ling Wang1
1College of Resources and Environment, Shandong Agricultural University, Tai’an, China
2Key Laboratory of Agricultural Ecology Environment of Shandong Agricultural University, Tai’an, China
Email: *HAN20095759@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 August 2015; accepted 24 September 2015; published 29 September 2015
ABSTRACT
The aims of this study are to explore the effect of different scales in the high spectral data on the estimation of chlorophyll content of apple leaves, to find out the optimal differential window scale and to establish a model for estimating the chlorophyll content of apple leaves. Taking the apple leaves as the research object, the actual spectral reflectance of the leaves was determined by the ASD Field Spec 3 spectrometer and the chlorophyll contents of the leaves were measured in the laboratory. Firstly, the differential transformations from 1 to 30 window scales were done for actual spectral data respectively, and correlation analyses were done between apple leaf chlorophyll content and differential data, then two sensitive wavelengths were chosen under each window. Secondly, taking five consecutive differential windows as a group, the best differential window was selected in each group. Lastly, after the conversion of two sensitive wavelengths in six differential windows, relationship analyses between chlorophyll content of apple leaves and two sensitive wavelengths were done, then two new parameters with the largest correlation coefficient were chosen to establish estimation model. Results showed that with increasing differential window, the determination coefficient (R2) of estimation model decreased after an initial increase, the tipping point was at the 13th differential window scale. Testing the partial least squares (PLS) model and the stepwise regression (SR) model established under differential window scale of the 13th, the R2 of the SR model was higher than that of the PLS model. The RMSE and RE% of the SR model were lower than that of the PLS model, which showed that SR model was more suitable to estimate chlorophyll content.
Keywords:
Differential Window, Hyperspectral, Chlorophyll Content, Estimation Model

1. Introduction
Chlorophyll content in plant leaves is a good indicator for plant nutrition, photosynthetic capacity, growth and development [1] [2] . Most traditional chlorophyll content diagnosis of vegetation was sampled and analyzed in the laboratory. Though the results are more accurate, it can’t meet the demand of fast and efficient precision agriculture because of time-consuming and high cost. In recent years, with the continuous development of hyper- spectral remote sensing technology, to monitor vegetation biochemical components in real-time, accurate and rapid has become possible. At present, the hyperspectral estimations of chlorophyll content of crops have been studied in corn [3] [4] , wheat [5] [6] , soybean [7] [8] , cotton [9] -[12] , rice [13] [14] and other crops. In the study of fruit trees, Zhu et al. analyzed the hyperspectral characteristics of apple leaves, and established a model for monitoring the pigment content based on spectral parameters [15] . Li et al. researched the correlation between SPAD and chlorophyll contents of apple leaves and built the regression models between the Soil and Plant Analyzer Development (SPAD) value and chlorophyll contents of apple leaves based on first differential spectral value [16] . Liang et al. found that the estimation models, which leaf chlorophyll index (LCI), the combinations of 521 nm and 523 nm first differential value as variables, have the highest accuracy [17] . Fang et al., Pan et al. constructed the quantitative relationship model between apple canopy chlorophyll content and canopy spectral characteristics parameters [18] [19] . The above studies on chlorophyll content, the differential scale used in the transformation of the actual spectral data was the 2nd, there was no research on the different differential scale of spectral data transformation and the selection of the best differential scale. Taking Qixia County of Shandong Province as the study area, Red Fuji apple tree of full bearing fruit was selected to be the research object. The hyperspectral data and chlorophyll content of apple leaves were determined. The differential transformation of different window scales was done to actual spectral data. Sensitive wavelengths were selected and the models of spectral parameters were constructed. After comparison, the estimation model and the best first differential window of chlorophyll content in apple leaves were determined.
2. Materials and Methods
2.1. Study Area
Apple leaves were collected from Qixia County of Shandong Province (37˚05'N to 37˚32'N, 120˚33'E to 121˚15'E). It is located in the center of the Jiaodong Peninsula. Its territory is dominated by mountain hills in which the mountain accounted for 72.1%, the hills accounted for 21.8% and plain accounted for 6.1%. Average altitude is 178 meters. Its climate is defined as sub-humid monsoon. The average annual rainfall is 754 mm. The average annual temperature is 11.3˚C, frost-free season of 207 d and total annual sunshine of 2690 h. It is a large temperature difference between day and night in autumn, the natural environment is very suitable for apple growth.
2.2. Sample Collection
In September 2013, 90 samples of autumn shoots stop growing stage were collected from thirty orchards, randomly selected from the study area, in Qixia County of Shandong Province three trees were randomly chosen from each fuji apple orchard. Eight healthy leaves were taken from apple tree growing branches in four orientations and placed into a numbered valve bag. The valve bag was kept in the foam box. The samples were taken back to the laboratory for subsequent measurement.
2.3. Leaf Hyperspectra Measurements
The diffuse reflectance spectra of apple leaves were scanned by ASD Field Spec 3. The portable object spectrometer has a spectral range of 350 - 2500 nm. At 350 - 1000 nm, the sampling interval was 1.4 nm and the spectral resolution was 3 nm; at 1001 - 2500 nm, the sampling interval was 2 nm and the spectral resolution was 10 nm. Before measuring the reflectance spectra of the leaf stacks, a white spectral on panel was measured for spectral standardization, after which the reflectance spectra of the fresh apple leaves were measured. When measuring the spectrum, the leaves were wiped with a clean paper. Blade clamp respectively clipped three parts (upper, middle and lower) of each leaf to measure reflectance spectra 10 times. The spectral reflectance of per leaf was determined as the mean of 30 spectral data.
2.4. Chemical Analysis of Chlorophyll Concentrations
The chlorophyll content of the leaves was determined after spectral measurement. About 0.2 g apple leaves were cut from each leaf sample for grinding in 6 mL 95% alcohol with a small amount of quartz sand and calcium carbonate powder, until the grinding blade into liquid, then filtered by adding alcohol for a total of 25 mL in each tube [20] . Each sample for analysis of chlorophyll concentration was placed in a cuvette and absorbance was measured between 200 nm and 1000 nm with 2.0 nm wavelength accuracy and 1nm wavelength repeatability using a UV-2100 UV/V is Spectrophotometer [21] . For each sample, three replicates were analyzed. Ca, Cb, and Ca+b concentrations were calculated as follows:
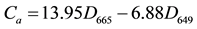 (1)
(1)
 (2)
(2)
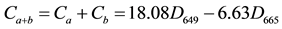 (3)
(3)
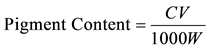 (4)
(4)
where Ca, Cb and Ca+b were the concentration of chlorophyll a, chlorophyll b and total chlorophyll a + b. D649 and D665 were the absorbance of wavelength at 649 nm and 665 nm. C was pigment concentration (mg/L), V was extract volume (ML) and W was fresh weight (g) of the leaves.
2.5. Data Processing and Analysis
The differential transformations from 1 to 30 windows were done to actual spectral data respectively, the differential transformation formula as follows:
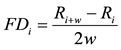 (5)
(5)
where FDi was differential value of wavelength i, Ri was the spectral reflectivity of wavelength i and w was the differential window. Correlation analysis of the chlorophyll content and the first differential spectrum of apple leaves were done. The sensitive wavelength of chlorophyll content was determined by 30 kinds of differential window scales. Spectral parameters of chlorophyll content in apple leaves were established.
There were 90 samples in the experiment, 70 samples were randomly selected to establish the estimation model, and 20 samples were used for model validation. The accuracy of estimation model was explained by determination coefficient (R2), root mean square error (RMSE) and relative error (RE). The statistical results were shown in Table 1.
2.6. The Methods of Modeling
Partial least squares (PLS) and Stepwise regression (SR) analysis were used to establish models for predicting the apple leaf chlorophyll content.
PLS is a new multivariate data analysis technique proposed in the application domain. In the last ten years, it has been developed rapidly, which can effectively overcome many practical problems of current regression modeling. In addition to overcoming the multiple correlations of multiple independent variables and dependent variables in traditional linear regression, PLS adopted the component extraction method; t1 and u1 were extracted
from independent variable 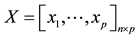 and dependent variable
and dependent variable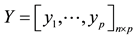 . The correlation
. The correlation
degree of t1 and u1 reached the maximum, while t1 and u1 carried the variant information in each data table as
Table 1. Statistical analysis of research data.
much as possible. It repeated iteration and extraction until the regression equation achieves satisfactory accuracy.
SR analysis was started from a variable, then according to the order of the significant degree from large to small independent variable effect on Y, the independent variable was introduced one by one. While, if the introduction of the latter, the introduction of the independent variable was not significant to Y, it would be removed. An independent variable was introduced or removed by F-measure to make sure that every time the introduction of new variables had statistical significance, so the regression equation only contained variables significantly effect on Y.
3. Results and Analysis
3.1. Correlation Analysis between Chlorophyll Content and Spectra of Differential Scale
It could be found that the correlation coefficient curve became more and more smooth and the correlation had been improved with the increase of the differential window scale from the chart of correlation coefficient between chlorophyll content and differential spectra under different differential window scales (Figure 1). When the differential window scale exceeded 10, the correlation coefficient of water absorption peak increased gradually.
Figure 1. Correlation curves between chlorophyll content of apple leaves and the first derivative spectral reflectance at different scales of differential windows.
Two sensitive wavelengths and two maximum values of the absolute value of correlation coefficient were chosen under different scales of differential window (Table 2). When the scales of differential window were within 1st to 5th, the best result was at the 4th differential window scale, the maximum absolute value of the correlation coefficient was 0.7231 and 0.7573 (at 526 nm and 692 nm). When the scales of differential window were within 6th to 10th, the best result was at the 7th differential window. The maximum absolute value of the correlation coefficient was 0.7512 and 0.7544 (at 526 nm and 691 nm). When the scales of differential window were within 11th to 15th, the best result was at the13th differential window scales. The maximum absolute value of the correlation coefficient was 0.7678 and 0.7567 (at 526 nm and 685 nm). When the scales of differential window were within 16th to 20th, the best result was at the 17th differential window. The maximum absolute value of the correlation coefficient was 0.7493 and 0.7550 (at 522 nm and 683 nm). When the scales of differential window were within 21th to 25th, the best result was at the 22th differential window. The maximum absolute value of the correlation coefficient was 0.7601 and 0.7637 (at 526 nm and 628 nm). When the scales of differential window were within 26th to 30th, the best result was at the 30th differential window scales. The maximum absolute value of the correlation coefficient was 0.7601 and 0.7637 (at 526 nm and 585 nm).
3.2. Structure of Hyperspectral Parameters
To eliminate the occasionality of a single sensitive wavelength, a and b were set for the two selected sensitive wavelength of every different scale of differential window. Absolute value (Table 3) of correlation coefficient was obtained after correlation analysis chlorophyll content with the data that processed by six kinds of methods (addition, subtraction, multiply, divide and normalization). When the differential window scales were the 4th, 7th, 13th, 17th, 22th and 30th, the correlation coefficient increased with the processing of multiplication. When
Table 2. Correlation description between chlorophyll contents of apple leaves and the first derivative spectral reflectance at different scales of differential window scales.
the differential window scales were 4th, 7th, 13th and 17th, the correlation coefficient increased with the pro- cessing of addition. When the differential window scales were 22th and 30th, the correlation coefficient increased with the processing of subtraction. The threshold for screening spectral parameters was set at 0.76. The higher absolute value of the correlation coefficient, the better effect would be, otherwise the closer the better. Eventually, when the different scale of differential window was 4th, the correlation coefficients of sensitive parameter FD526*FD692 and FD526+FD692 reached 0.7691 and 0.7710 respectively, when the different scale of differential window was 7th, the correlation coefficients of sensitive parameter FD526+FD691 and FD526*FD691 reached 0.7636 and 0.7662 respectively. When the different scale of differential window was 13th, the correlation coefficients of sensitive parameter FD526+FD685 and FD526*FD685 reached 0.7678 and 0.7717 respectively. When the different scale of differential window was 17th, the correlation coefficients of sensitive parameter FD526+FD681 and FD526*FD681 reached 0.7645 and 0.7690 respectively. When the different scale of differential window was 22th, the correlation coefficients of sensitive parameter FD526+FD628 and FD526* FD628 reached 0.7826 and 0.7806 respectively. When the different scale of differential window was 30th, the correlation coefficients of sensitive parameter FD526+FD585 and FD526*FD585 reached 0.7725 and 0.7729 respectively.
3.3. Establishment of Estimation Model
3.3.1. Partial Least Squares Model
PLS models were established based on the best sensitive parameters corresponding to different scale of differential window of 4th, 7th, 13th, 17th, 22th and 30th, respectively. The best model was selected according to the principle of maximum determination coefficient (R2). The results were shown in Table 4.
Table 4 showed that the R2 of PLS estimation models under different derivative windows increased at first and decreased afterward, with the increase of differential window scale. While the differential window scale was at the 13th, the R2 of PLS model which based on FD526+FD685 and FD526*FD692 were the largest, reached 0.7978. Therefore, the PLS model was more suitable for the estimation of chlorophyll content in apple leaves
Table 3. Correlation of the spectral parameters with chlorophyll contents.
Note a, b for the two selected sensitive wavelength of each different scale of differential window.
Table 4. PLS models of estimating chlorophyll at differential window scale.
than that of differential window scale of the 4th, 7th, 17th, 22th and 30th.
3.3.2. Stepwise Regression Model
SR models were established based on the best sensitive parameters corresponding to different scale of differential window of the 4th, 7th, 13th, 17th, 22th and 30th, respectively. The best model was selected according to the principle of maximum R2. When building models, variables were repeatedly introduced or removed until no significant variables could be removed and introduced. The results were shown in Table 5.
Table 5 showed that the R2 of SR estimation models under different derivative windows increased at first and decreased afterward, with the increase of differential window scale, which was consistent with the trend of PLS R2. While the differential window scale was at the 13th, the R2 of SR model which based on FD526+FD685 and FD526*FD685 was the largest, reached 0.7958. The SR model was more suitable for the estimation of chlorophyll content in apple leaves than that of differential window scale of the 4th, 7th, 17th, 22th and 30th, which was consistent with PLS model. When the differential window scale was at the 13th, the estimation effect of the model was better than that of the other differential window scales.
3.4. Model Validation
When the differential window scale was at the 13th, the absolute coefficient R2 of the model had greater value. The 20 validation samples were brought into the PLS and SR models, y = 4.919 − 383.9x1 ? 288,744.5x2 and y = 4.746 − 259.0*x1 ? 382,188.4*x2, which were established when differential window scale was at the 13th. Figure 2 was obtained by fitting estimate values with the measured values.
Table 5. SR models of estimating chlorophyll contents at differential window scale.
Figure 2. Chlorophyll content measured values and estimated values 1:1 scatter diagram at differential window scale 13th (left: SR model, right: PLS model).
In the SR regression model, R2 was higher than that in the PLS regression model of 0.0015, RMSE was lower than that of the PLS regression model of 0.0007, RE was lower than that of the PLS regression model of 0.03. SR regression model was better than that of PLS to estimate the chlorophyll content of apple leaves at differential window scale 13th.
4. Conclusions and Discussion
Differential treatment was a common method of spectral processing. Differential processing could eliminate the effect of linear and quadric form background noise on the spectrum. From previous studies on chlorophyll content, the differential scale window used in the transformation of the actual spectral data was 2 [9] [11] [16] . There was no research on the different differential scale window of spectral data transformation and the selection of the best differential scale. In this study, the first differential transformation from 1 to 30 window scales was performed on the actual spectral data respectively. Correlation analyses were done between apple leaf chlorophyll content and first differential data. With the increase of differential window scale, the correlation coefficient curves of the first order differential value of the actual spectrum and the chlorophyll content of apple leaves gradually became smooth and the R2 of estimation model under different derivative window scales decreased after initial increase. The differential of the large window scales had a certain effect of eliminating noise on the spectrum. First differential transformation of 1 to 30 window scales was studied in this research, the higher differential window scales was not studied and discussed. It needs to be examined in later study.
The established estimation model provided the best results when the derivative window was at the 13th. Testing the PLS model and the SR model established under differential window 13th found that the R2 of the SR model was higher than that of the PLS model. The RMSE and RE% of the SR model were lower than that of the PLS model, which showed that SR model was more suitable to estimate chlorophyll content.
Acknowledgements
This paper was supported by the National Nature Science Foundation of China (41271369), Shandong Province Natural Science Fund (ZR2012DM007), Youth Science and Technology Innovation Fund of Shandong Agricultural University (23731), the National Nature Science Foundation of China (41301482) and Agriculture Big Data Project of Shandong Agricultural University (75016).
Cite this paper
ZhaoyingHan,XicunZhu,ZhuoyuanWang,GengxingZhao,LingWang, (2015) Estimating Chlorophyll Content of Apple Leaves Based on Different Scales in Differential Window. Agricultural Sciences,06,1106-1114. doi: 10.4236/as.2015.69106
References
- 1. Li, R.H., Guo, P.G., Michael, B., Stefania, G. and Salvatore, C. (2006) Evaluation of Chlorophyll Content and Fluorescence Parameters as Indicators of Drought Tolerance in Barley. Agricultural Sciences in China, 10, 751-757.
http://dx.doi.org/10.1016/S1671-2927(06)60120-X - 2. Zlatev, Z., Berova, M., Stoeva, N. and Vassilev, A. (2003) Use of Physiological Parameters as Stress Indicators. Journal of Environmental Protection and Ecology, 4, 841-849.
- 3. Yi, Q.X., Huang J.F., Wang X.Z. and Qian, Y. (2007) Hyperspectral Remote Sensing Estimation Models for Chlorophyll Concentration in Corn. Bulletin of Science and Technology, 23, 83-87. (In Chinese)
- 4. Daughtry, C.S.T., Walthall, C.L., Kim, M.S., de Colstount, E.B. and McMurtrey III, J.E. (2000) Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sensing of Environment, 74, 229-239.
http://dx.doi.org/10.1016/S0034-4257(00)00113-9 - 5. Feng, W., Yao, X., Tian, Y.C., Cao, W.X. and Zhu, Y. (2008) Monitoring Leaf Pigment Status with Hyperspectral Remote Sensing in Wheat. Australian Journal of Agricultural Research, 59, 748-760.
http://dx.doi.org/10.1071/AR07282 - 6. Hansen, P.M. and Schjoerring, J.K. (2003) Reflectance Measurement of Canopy Biomass and Nitrogen Status in Wheat Crops Using Normalized Difference Vegetation Indices and Partial Least Squares Regression. Remote Sensing of Environment, 86, 542-553.
http://dx.doi.org/10.1016/S0034-4257(03)00131-7 - 7. Chen, Y.J., Yan, G.J., Lv, L., Zhang, K. and Li, K. (2012) Hyperspectral Reflectance Model to Estimate Chlorophyll Content in Soybean Leaves. Journal of Beijing Normal University (Natural Science), 1, 60-65. (In Chinese)
- 8. Song, K.S., Zhang, B., Wang, C.M. Liu, H.J. and Duan, H.T. (2006) Inverse Model for Estimating Soybean Chlorophyll Concentration Using In-Situ Collected Canopy Hyperspectraldata. Transactions of the CSAE, 22, 16-21. (In Chinese)
- 9. Yuan, J., Wang, D.W., Huang, C.Y., Qi, Y.Q., Chen, Y., Ma, Q.J. and Wang, H.R. ( 2007) Estimating Chlorophyll Density of Cotton Canopy in North of Xinjiang by Using Hyperspectral Date. Agricultural Research in the Arid Areas, 25, 89-93. (In Chinese)
- 10. Wang, D.W., Li, S.K., Tian, Q.J., Huang, C.Y., Cao, L.P., Xiao, C.H., Ma, Y.Q. and Yang, X.J. (2003) Estimating of Main Cultivation Physiology Parameters of Cotton by Using Hyperspectral Remote Sensing. Scientia Agricultura Sinica, 36, 770-774. (In Chinese)
- 11. Huang, C.Y., Wang, D.W., Yan, J., Zhang, H.X., Cao, L.P. and Cheng, C. (2007) Monitoring of Cotton Canopy Chlorophyll Density and Leaf Nitrogen Accumulation Status by Using Hyperspectral Data. Acta Agronomica Sinica, 33, 931-936. (In Chinese)
- 12. Wang, D.W., Huang, C.Y., Zhang, W., Ma, Q.J. and Zhao, P.J. (2008) Relationships Analysis between Cotton Chlorophyll Content, Chlorophyll Density and Hyperspectral Data. Cotton Science, 36, 368-371. (In Chinese)
- 13. Yang, J., Tian, Y.C., Yao, X., Cao, W.X., Zhang, Y.C. and Zhu, Y. (2009) Hyperspectral Estimation Model for Chlorophyll Concentrations in Top Leaves of Rice. Acta Ecologica Sinica, 29, 6561-6571. (In Chinese)
- 14. Chen, S.Y., Tian, Q.J. and Shi, R.H. (2005) Study on Simulation of Rice Leaf’s Chlorophyll Concentration via the Spectrum. Remote Sensing Information, 6, 12-16. (In Chinese)
- 15. Zhu, X.C., Zhao, G.X., Wang, R.Y., Dong, F., Wang, L. and Lei, T. (2010) Hyperspectral Characteristics of Apple Leaves and Their Pigment Contents Monitoring. Scientia Agricultura Sinica, 43, 1189-1197. (In Chinese)
- 16. Li, M.X., Zhang, L.S., Li, B.Z., Zhang, H.Y. and Guo, W. (2010) Relationship between Spectral Reflectance Feature and Their Chlorophyll Concentrations and SPAD Value of Apple Leaves. Journal of Northwest Forestry University, 25, 35-39. (In Chinese)
- 17. Liang, S., Zhao, G.X. and Zhu, X.C. (2012) Hyperspectral Estimation Models of Chlorophyll Content in Apple Leave. Spectroscopy and Spectral Analysis, 32, 1367-1370. (In Chinese)
- 18. Fang, X.Y., Zhu, X.C., Wang, L. and Zhao, G.X. (2013) Hyperspectral Monitoring of the Canopy Chlorophyll Content at Apple Tree Prosperous Fruit Stage. Scientia Agricultura Sinica, 46, 3504-3513. (In Chinese)
- 19. Pan, B., Zhao, G.X., Zhu, X.C., Liu, H.T., Liang, S. and Tian, D.D. (2013) Estimation of Chlorophyll Content in Apple Tree Canopy Based on Hyperspectral Parameters. Spectroscopy and Spectral Analysis, 33, 2203-2206. (In Chinese)
- 20. Zhang, Q.L., Chen, W.H., Zhang, Y.H., Guo, X.C., Zhu, W.D. and Xu, H.M. (2011) Estimation Models of Chlorophyll Contents in Leaves of Acacia Confusa Based on the Red Edge Position. Journal of Subtropical Resources and Environment, 6, 9-17. (In Chinese)
- 21. Lu, X. and Peng, H.C. (2015) Predicting Cherry Leaf Chlorophyll Concentrations Based on Foliar Reflectance Spectra Variables. Indian Society of Remote Sensing, 43, 109-120.
http://dx.doi.org/10.1007/s12524-014-0397-1
NOTES

*Corresponding author.




