Journal of Applied Mathematics and Physics
Vol.2 No.7(2014), Article
ID:47219,7
pages
DOI:10.4236/jamp.2014.27076
Analytical Solutions of Fukui-Ishibashi (FI) Model and Quick-Start (QS) Model
Shinji Kukida, Jun Tanimoto, Naoki Ikegaya, Aya Hagishimaors
Interdisciplinary Graduate School of Engineering Sciences, Kyushu University, Kasuga, Japan
Email: kukida.shinji@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 May 2014; revised 7 June 2014; accepted 15 June 2014
ABSTRACT
Through straightforward deduction procedure, we explicitly show analytical solutions for both Fukui-Ishibashi (FI) model and Quick-Start (QS) model, which are fundamental deterministic Cellular Automaton (CA), applied to traffic flow.
Keywords:Cellular Automaton, Analytical Solutions

1. Introduction
For recent years, simulation study on traffic flow has been attracted much attention of physicists. Among wide variety of approaches, Cellular Automaton (CA), where vehicles are treated as discrete self-drive particles in an entirely discrete spatiotemporal system, are most heavily used because of its flexibility as well as robustness to apply various practical problems.
There have been proposed many traffic CA models so far. For example, Rule-184 [1] , which was originally presented by Wolfram as a part of 256 elementary CA archetypes for general discussion, has been regarded as the simplest traffic model. Fukui-Ishibashi (FI) model [2] extended vehicle’s speed v more variable;
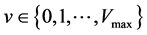 instead of
instead of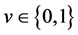 . Nagel-Schreckenberg (NS) model [3] , which has been most heavily applied as a fundamental template model by many studies, considers random braking effect on the basis of FI model. Quick-start (QS) model [4] takes account of driver’s anticipation effect. Slow-to-start (SlS) model [5] can consider inertia effect of vehicles. Base on NS model, Stochastic Nishinari-Fukui-Schadshneider (S-NFS) model [6] takes account of all those effects; random braking, quick-start as well as slow-to-start. Revised S-NFS model [7] improves random braking effect in order to reproduce synchronized flow depicted in Kerner’s three phase theory [8] . Asymmetric Simple Exclusion Process (ASEP) [9] and Zero Range Process (ZRP) [10] are simpler CA models, thus have been used by some theoretical studies.
. Nagel-Schreckenberg (NS) model [3] , which has been most heavily applied as a fundamental template model by many studies, considers random braking effect on the basis of FI model. Quick-start (QS) model [4] takes account of driver’s anticipation effect. Slow-to-start (SlS) model [5] can consider inertia effect of vehicles. Base on NS model, Stochastic Nishinari-Fukui-Schadshneider (S-NFS) model [6] takes account of all those effects; random braking, quick-start as well as slow-to-start. Revised S-NFS model [7] improves random braking effect in order to reproduce synchronized flow depicted in Kerner’s three phase theory [8] . Asymmetric Simple Exclusion Process (ASEP) [9] and Zero Range Process (ZRP) [10] are simpler CA models, thus have been used by some theoretical studies.
By previous works, analytical solutions of Rule-184, ASEP and ZRP have been derived, since flux—density relation can be fixed deterministically [11] [12] . Although both FI model and QS model never contain stochastic elements, analytical solutions for those two have not been known ever. This paper reports the result of it, which we are successfully able to deduce this time. .
2. Analytical Solution of FI Model
The update rule of FI model is as follows;
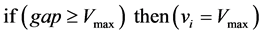 ,
,
 where
where 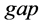 means the number of unoccupied sites in front of vehicle
means the number of unoccupied sites in front of vehicle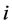 ,
, 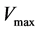 means the maximum velocity and
means the maximum velocity and 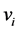 means the velocity of vehicle
means the velocity of vehicle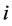 . It is obvious from Figure 1 that the critical density, making traffic flux maximum, is
. It is obvious from Figure 1 that the critical density, making traffic flux maximum, is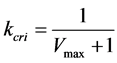 .Thus, the maximum flux is drawn by
.Thus, the maximum flux is drawn by .
.
Let us prove that the fundamental diagrams by FI model can be described as an asymmetrical tent-type polygonal line functions as below.
Proposition 1 When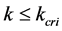 , it is trivial that the relation between density and flux must be a linear function originated from
, it is trivial that the relation between density and flux must be a linear function originated from
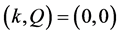 with slope
with slope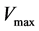 .
.
When , let us evaluate the relation between density and flux as follows. Figure 2 shows an example of flow state when
, let us evaluate the relation between density and flux as follows. Figure 2 shows an example of flow state when . Schematic implication and definition of average velocity, we know;
. Schematic implication and definition of average velocity, we know;

and it is also trivial;
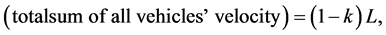
where L is system length. Hence,
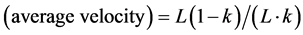
Therefore, flux 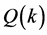 is;
is;
 which explicitly implies a linear function of
which explicitly implies a linear function of . This negative slope line obviously crosses both critical state and complete jam state;
. This negative slope line obviously crosses both critical state and complete jam state;  and
and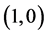 .
.
(QED)
According to Proposition 1, the fundamental diagram can be described as an asymmetric tent-type function, consisting of two liner functions. The above-deduced critical density and maximum flux is the vertex of this asymmetric tent-type function.
As the next step, we should discuss whether the function consisting of two linear lines can be expressed by a single expression Proposition 2 What we expect is that the function consisting of two linear lines can be expressed by a single expression;
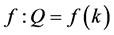 (Figure 3(a)).Shifting the function in the direction of
(Figure 3(a)).Shifting the function in the direction of 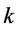 by
by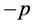 , we obtain
, we obtain 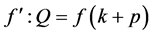
(Figure 3(b)).
Meanwhile, two equations to touch at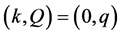 ;
;  and
and  , shown in Figure 3(b) can be expressed as below;
, shown in Figure 3(b) can be expressed as below;
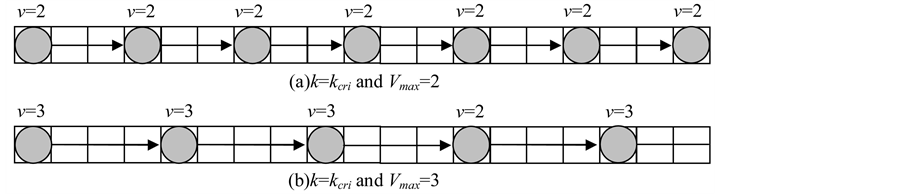
Figure 1. Flow states explaining for FI model.
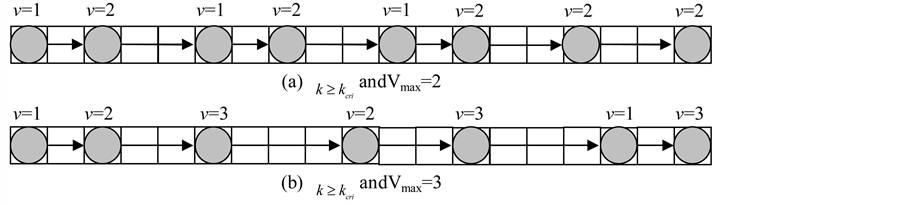
Figure 2. Flow states explaining for FI model in case if .
.
 (a) (b)
(a) (b)
Figure 3. Asymmetric tent-type function.
 . (1)
. (1)
 . (2)
. (2)
The expression of  is determined because it must be symmetric against
is determined because it must be symmetric against 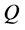 axis. By superposing those two liner functions, we obtain the asymmetric tent-type functionas below;
axis. By superposing those two liner functions, we obtain the asymmetric tent-type functionas below;
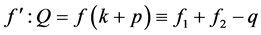 By substituting Equations (1) & (2), we obtain:
By substituting Equations (1) & (2), we obtain:
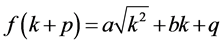 . (3)
. (3)
When the branch of square root is taken into consideration, it is as follows;
 then,
then,
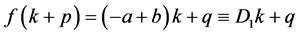 , (4)
, (4)
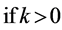 then,
then,
 . (5)
. (5)
(QED)
We know; 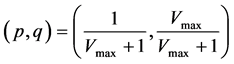 and
and .
.
By substituting above conditions into Equations (4) & (5), we get;
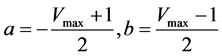 . (6)
. (6)
By substituting these into Equation (2), we obtain the following.
 . (7)
. (7)
As consequence,  is;
is;
 .
.
Namely; we obtain;
 (8)
(8)
By rearranging, analytical solution of FI model can be derived as follows;
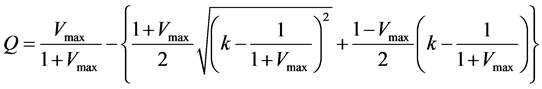 , (9)
, (9)
where 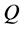 means the flux and
means the flux and 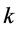 means density, respectively.
means density, respectively.
Figure 4 shows the fundamental diagrams by Equation (10) when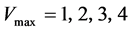 .
.
3. Analytical Solution of QS Model
The update rule of QS model is as follows;
If there is an empty site in forward S-sites then the focal vehicle moves.
Where S means the number of sites that a vehicle foresees for quick-start. It is obvious from Figure 5 that the critical density is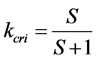 . Thus, the maximum flux is drawn by
. Thus, the maximum flux is drawn by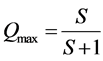 , because
, because . Like FI model, Let us prove that the fundamental diagrams by QS model can be described as an asymmetrical tent-type poly-gonal line functions as below.
. Like FI model, Let us prove that the fundamental diagrams by QS model can be described as an asymmetrical tent-type poly-gonal line functions as below.
Proposition 3 When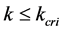 , it is trivial that the relation between density and flux must be a linear function originated from
, it is trivial that the relation between density and flux must be a linear function originated from
 with slope
with slope .
.
When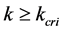 , let us evaluate the relation between density and flux as follows. Figure 6 shows an example of flow state when
, let us evaluate the relation between density and flux as follows. Figure 6 shows an example of flow state when . Schematic implication and definition of average velocity, we know;
. Schematic implication and definition of average velocity, we know;

Observing Figure 6, we notice that vehicles staying in S sites behind each empty site can move. Thus;
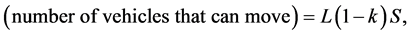
and;
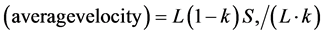
Therefore, flux  is;
is;
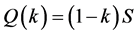 which explicitly implies a linear function of
which explicitly implies a linear function of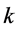 . This negative slope line obviously crosses both critical state and
. This negative slope line obviously crosses both critical state and

Figure 4. The fundamental diagram by Equation (9).
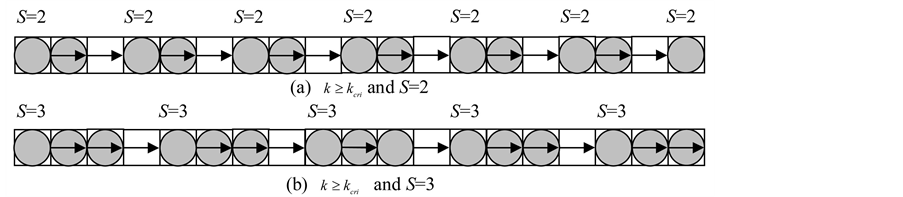
Figure 5. Flow states explaining for QS.
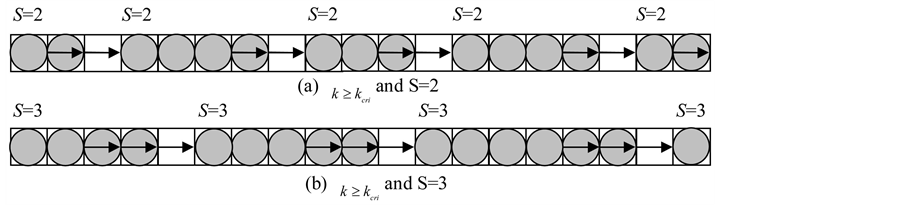
Figure 6. Flow states explaining for QS model l in case if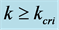 .
.
complete jam state; 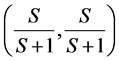 and
and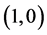 .
.
(QED)
Proposition 3 enables us to draw that the fundamental diagram can be described as an asymmetric tent-type function, consisting of two liner functions. The above-deduced critical density and maximum flux is the vertex of this asymmetric tent-type function.
Like the case of FI model, as the next step for the discussion, we should note how Proposition 2 leads that the function consisting of two linear lines can be expressed by a single expression Namely, we know;  and
and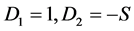 .
.
By substituting above conditions into Equations (4) & (5), we get;
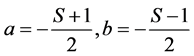 (10)
(10)
By substituting these into Equation (2), we obtain the following.
 (11)
(11)
Therefore,  is;
is;

Figure 7. The fundamental diagram by Equation (13).
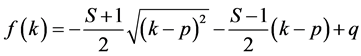 .
.
Finally, we get;
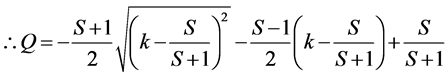 (12)
(12)
By rearranging, analytical solution of QS model is derived as follows;
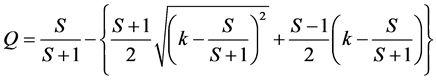 (13)
(13)
Figure 7 shows the fundamental diagrams by Equation (13) when .
.
4. Conclusions
We explicitly reported analytical solutions fort FI model and QS model.
Although the two are important models for depicting basic traffic features, analytical solutions for those two have not been known ever.
Helped by the fact that FI model and QS model never contain stochastic elements, our process to deduce was simple and straightforward.
Acknowledgements
This study was partially supported by a Grant-in-Aid for Scientific Research by the Japan Society for the Promotion of Science, awarded to Prof. Tanimoto (#25560165), Tateishi Science and Technology Foundation. We would like to express our gratitude to these funding sources.
References
- Wolfram, S. (1986) Theory and Applications of Cellular Automata. World Scientific, Singapore.
- Fukui, M. and Ishibashi, Y. (1996) Traffic Flow in 1D Cellular Automaton Model including Cars Moving with High Speed. Journal of the Physical Society of Japan, 65, 1868-1870. http://dx.doi.org/10.1143/JPSJ.65.1868
- Nagel, K. and Schreckenberg, M. (1992) A Cellular Automaton Model for Freeway Traffic. Journal de Physique I, 2, 2221. http://dx.doi.org/10.1051/jp1:1992277
- Barlovic, R., Santen, L., Schadschneider, A. and Schreckenberg, M. (1998) Metastable State in Cellular Automata for Traffic Flow. European Physical Journal B, 5, 793-800. http://dx.doi.org/10.1007/s100510050504
- Nishinari, K. and Takahashi, D. (2000) Multi-Value Cellular Automaton Model for Freeway Traffic. Journal of Physics A, 33, 7709. http://dx.doi.org/10.1088/0305-4470/33/43/304
- Sakai, S., Nishinari, K. and Iida, S. (2006) A New Stochastic Cellular Automaton Model on Traffic Flow and Its Jamming Phase Transition. Journal of Physics A: Mathematical and General, 39, 15327. http://dx.doi.org/10.1088/0305-4470/39/50/002
- Kokubo, S., Tanimoto, J. and Hagishima, A. (2011) A New Cellular Automata Model Including a Decelerating Damping Effect to Reproduce Kerner’s Three-Phase Theory. Physica A: Statistical Mechanics and Its Applications, 390, 561-568. http://dx.doi.org/10.1016/j.physa.2010.10.027
- Kerner, B.S. and Klenov, S.L. (2009) Phase Transitions in Traffic Flow on Multilane Roads. Physical Review E, 80, Article ID: 056101. http://dx.doi.org/10.1103/PhysRevE.80.056101
- Derrida, B., Evans, M.R., Hakim, V. and Pasquier, V. (1993) Exact Solution of a1D Asymmetric Exclusion Model Using a Matrix Formulation. Journal of Physics A: Mathematical and General, 26, 1493. http://dx.doi.org/10.1088/0305-4470/26/7/011
- O’Loan, O.J., Evans, M.R. and Cates, M.E. (1998) Jamming Transition in a Homogeneous One-Dimensional Systems: The Bus Route Model. Physical Review E, 58, 1404. http://dx.doi.org/10.1103/PhysRevE.58.1404
- Schadschneider, A. and Schreckenberg, M. (1993) Cellular Automaton Models and Traffic Flow, Journal of Physics A: Mathematical and General, 26, L679. http://dx.doi.org/10.1088/0305-4470/26/15/011
- Klauck, K. and Shadshneider, A. (1999) On the Ubiquity of Matrix-Product States in One-Dimensional Stochastic Processes with Boundary Interactions. Physica A, 271, 102-117. http://dx.doi.org/10.1016/S0378-4371(99)00176-4

