Paper Menu >>
Journal Menu >>
 J. Biomedical Science and Engineering, 2010, 3, 677-683 JBiSE doi:10.4236/jbise.2010.37092 Published Online July 2010 (http://www.SciRP.org/journal/jbise/). Published Online July 2010 in SciRes. http://www.scirp.org/journal/jbise A pilot study of a novel pulsatile flow generator using large collapsible bladder Ponangi Udaya Prashant1, Nagaraj Balasubramanya2 1Institute G-5, Sneha Sindhu Apartments, Kavalabyrasandra, Bangalore; 2Department of Civil Engineering, M.S. Ramaiah Engineering College, Bangalore, India. Email: udayaprashant_p@yahoo.co.in; jhrumbaa@gmail.com Received 30 April 2010; revised 21 May 2010; accepted 22 May 2010. ABSTRACT Background: There are different experimental mod- els avialable for generating pulsatile flow in labora- tory and study their heamodynamic effects on blood vessels. We aim to produce a novel pulsatile flow gen- erator utilizing a large collapsible rubber bladder and the phenomenon of fluid structure interactions occurring in a specially designed flexible tube ar- rangement. Mehtods: Water enters from a reservoir above into a large collapsible bladder made of rubber which opens into ‘U’ shaped tube made of flexible material and held by non rigid structures. As liquid starts flowing the distal end of collapsible bladder collapses under the negative atmospheric pressure generated inside closing the mouth of ‘U’ shaped tube and produces pulsatile flow. Resuts: The frequency of pulsations, pressure fluctuations and velocity profile resemble that of in vivo blood flow. As the flow en- tering into collapsible bladder increases the fre- quency of pulsatile flow decreases and also when height of the collapsible bladder from the ground was changed. The whole cycle of alternate collapse/expan- sion of collapsible bladder with generation of pulsa- tile flow continue indefinitely as long as there is enough water in reservoir and vertical gradient to sustain the flow. Conclusions: The pulsatile flow so produced has many of the characteristics of physio- logical blood flow and can be used to study mecha- nisms of various cardiovascular diseases in labora- tory. Keywords: Collapsible Tubes; Buckling; Pulsatile Flow Generator; Unsteady Flow; Fluid Structure Interactions 1. INTRODUCTION Cardiovascular diseases are major causes of death throu- ghout the world, yet the mechanisms of these diseases, especially atherosclerosis is poorly understood. The most important aspect of the development and progression of cardiovascular diseases is the role of pulsatile flow in hemodynamics of cardiovascular diseases like athero- sclerosis [1,2]. Pulsatile flow induces complex shear stress on walls of vessels and is basis for many athero- sclerotic diseases like aneurysms and stenotic lesions [3]. A number of attempts have previously been made to simulate pulsatile human arterial flow [4-7]. Hopmann and Liu described a pump that uses an elas- tic chamber squeezed by a cam, with pressure-actuated check valves [4]. The use of a gear pump controlled by a closed-loop servosystem was reported by Issartier et al. [4,7]. Kiyose et al. have described a mechanical piston pump system for simulating peripheral arterial flow [4]. Petersen described a system using two gear pumps, one to generate forward flow and the other to generate re- verse flow [5]. A microcomputer regulated a pneumatic control valve so that the total flow at any instant could be controlled. Errikson et al. used a microcomputer con- trols a motor which in turn drives a piston pump to gen- erate the flow [6]. However, the system appears to lack the flexibility to generate different waveforms. Many of the existing pulsatile flow generators are complicated, consume significant power and require computers to function [4-7]. They are also expensive and none of them are based on principle of flow limitation occurring in collapsible tubes. Many interesting phe- nomena are observed like flow limitation and the pro- pensity to develop large amplitude self-excited oscilla- tions during study of flows in collapsible tubes [8]. Flow induce collapse is very common in many phy- siological situations like regulation of blood vessel cali- ber, generation of murmurs, snoring sounds, wheezing in airways, micturation etc [9]. The collapsible tubes buck- les and collapses at the distal most point of tube as the internal pressure is least between entry and exit end due to viscous pressure drop [10]. Buckled vessels are very flexible and even small changes in fluid pressure can induce large changes of their cross-sectional area [11]. 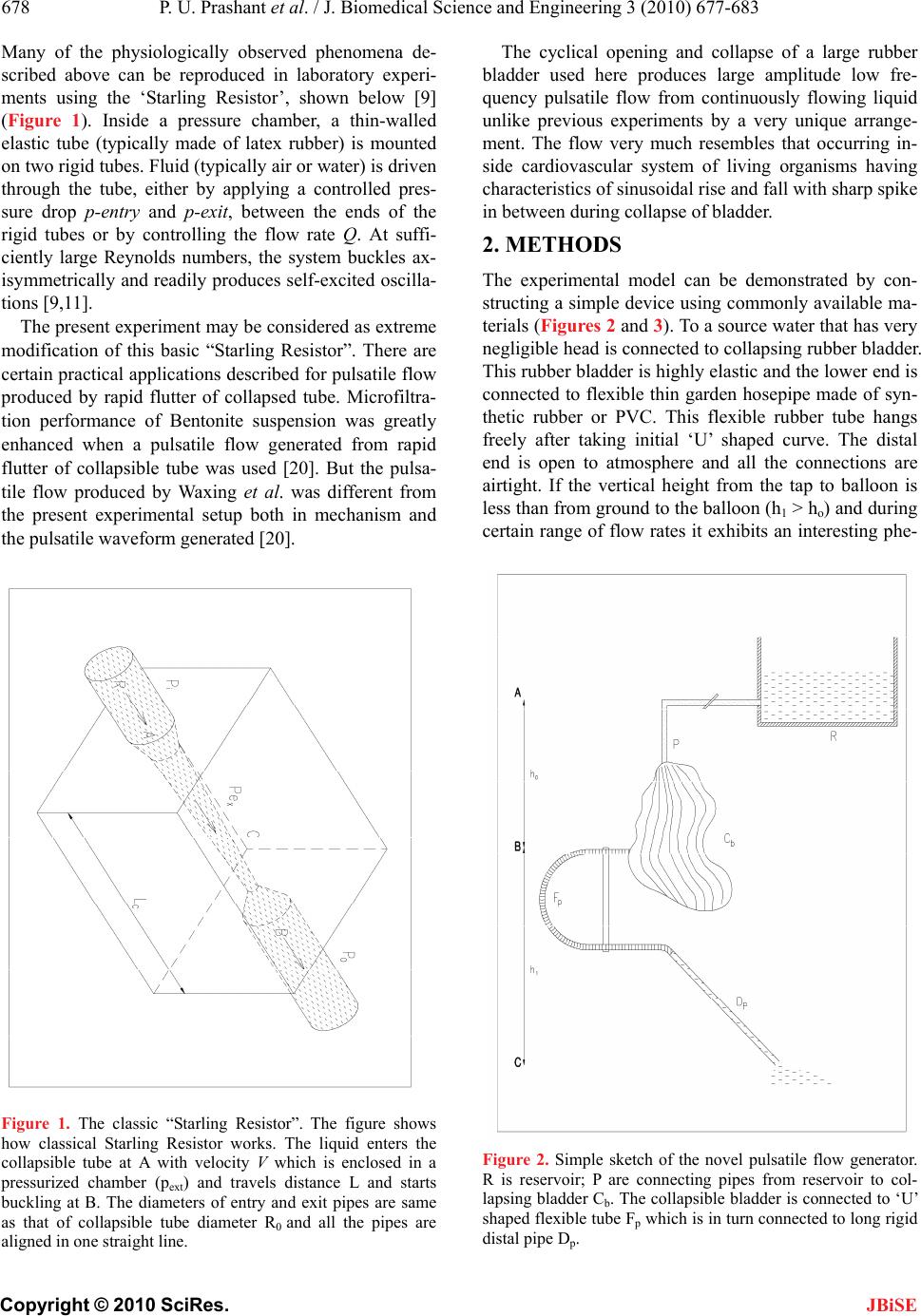 P. U. Prashant et al. / J. Biomedical Science and Engineering 3 (2010) 677-683 Copyright © 2010 SciRes. JBiSE 678 Many of the physiologically observed phenomena de- scribed above can be reproduced in laboratory experi- ments using the ‘Starling Resistor’, shown below [9] (Figure 1). Inside a pressure chamber, a thin-walled elastic tube (typically made of latex rubber) is mounted on two rigid tubes. Fluid (typically air or water) is driven through the tube, either by applying a controlled pres- sure drop p-entry and p-exit, between the ends of the rigid tubes or by controlling the flow rate Q. At suffi- ciently large Reynolds numbers, the system buckles ax- isymmetrically and readily produces self-excited oscilla- tions [9,11]. The present experiment may be considered as extreme modification of this basic “Starling Resistor”. There are certain practical applications described for pulsatile flow produced by rapid flutter of collapsed tube. Microfiltra- tion performance of Bentonite suspension was greatly enhanced when a pulsatile flow generated from rapid flutter of collapsible tube was used [20]. But the pulsa- tile flow produced by Waxing et al. was different from the present experimental setup both in mechanism and the pulsatile waveform generated [20]. Figure 1. The classic “Starling Resistor”. The figure shows how classical Starling Resistor works. The liquid enters the collapsible tube at A with velocity V which is enclosed in a pressurized chamber (pext) and travels distance L and starts buckling at B. The diameters of entry and exit pipes are same as that of collapsible tube diameter R0 and all the pipes are aligned in one straight line. The cyclical opening and collapse of a large rubber bladder used here produces large amplitude low fre- quency pulsatile flow from continuously flowing liquid unlike previous experiments by a very unique arrange- ment. The flow very much resembles that occurring in- side cardiovascular system of living organisms having characteristics of sinusoidal rise and fall with sharp spike in between during collapse of bladder. 2. METHODS The experimental model can be demonstrated by con- structing a simple device using commonly available ma- terials (Figures 2 and 3). To a source water that has very negligible head is connected to collapsing rubber bladder. This rubber bladder is highly elastic and the lower end is connected to flexible thin garden hosepipe made of syn- thetic rubber or PVC. This flexible rubber tube hangs freely after taking initial ‘U’ shaped curve. The distal end is open to atmosphere and all the connections are airtight. If the vertical height from the tap to balloon is less than from ground to the balloon (h1 > ho) and during certain range of flow rates it exhibits an interesting phe- Figure 2. Simple sketch of the novel pulsatile flow generator. R is reservoir; P are connecting pipes from reservoir to col- lapsing bladder Cb. The collapsible bladder is connected to ‘U’ shaped flexible tube Fp which is in turn connected to long rigid distal pipe Dp. 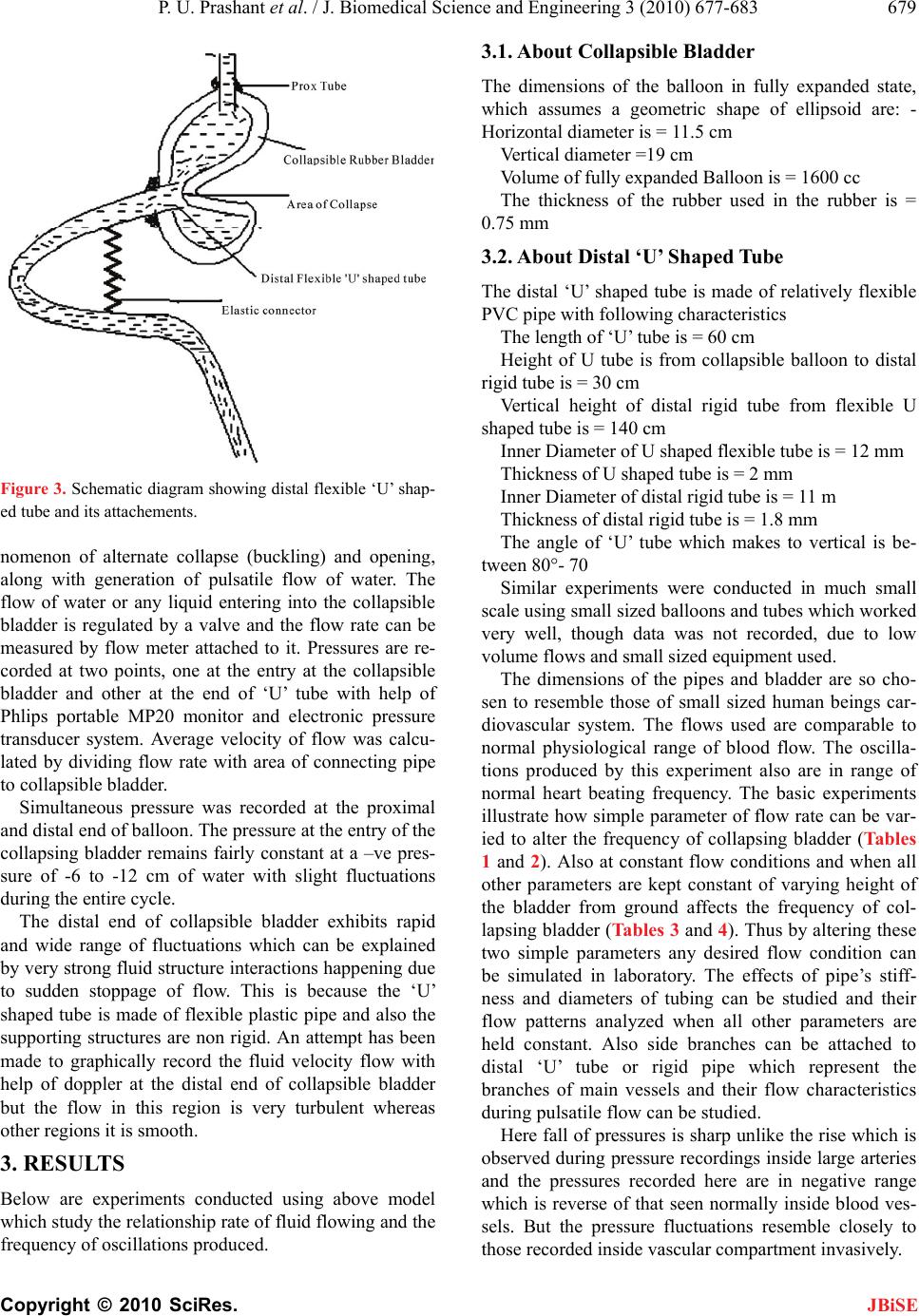 P. U. Prashant et al. / J. Biomedical Science and Engineering 3 (2010) 677-683 Copyright © 2010 SciRes. JBiSE 679 Figure 3. Schematic diagram showing distal flexible ‘U’ shap- ed tube and its attachements. nomenon of alternate collapse (buckling) and opening, along with generation of pulsatile flow of water. The flow of water or any liquid entering into the collapsible bladder is regulated by a valve and the flow rate can be measured by flow meter attached to it. Pressures are re- corded at two points, one at the entry at the collapsible bladder and other at the end of ‘U’ tube with help of Phlips portable MP20 monitor and electronic pressure transducer system. Average velocity of flow was calcu- lated by dividing flow rate with area of connecting pipe to collapsible bladder. Simultaneous pressure was recorded at the proximal and distal end of balloon. The pressure at the entry of the collapsing bladder remains fairly constant at a –ve pres- sure of -6 to -12 cm of water with slight fluctuations during the entire cycle. The distal end of collapsible bladder exhibits rapid and wide range of fluctuations which can be explained by very strong fluid structure interactions happening due to sudden stoppage of flow. This is because the ‘U’ shaped tube is made of flexible plastic pipe and also the supporting structures are non rigid. An attempt has been made to graphically record the fluid velocity flow with help of doppler at the distal end of collapsible bladder but the flow in this region is very turbulent whereas other regions it is smooth. 3. RESULTS Below are experiments conducted using above model which study the relationship rate of fluid flowing and the frequency of oscillations produced. 3.1. About Collapsible Bladder The dimensions of the balloon in fully expanded state, which assumes a geometric shape of ellipsoid are: - Horizontal diameter is = 11.5 cm Vertical diameter =19 cm Volume of fully expanded Balloon is = 1600 cc The thickness of the rubber used in the rubber is = 0.75 mm 3.2. About Distal ‘U’ Shaped Tube The distal ‘U’ shaped tube is made of relatively flexible PVC pipe with following characteristics The length of ‘U’ tube is = 60 cm Height of U tube is from collapsible balloon to distal rigid tube is = 30 cm Vertical height of distal rigid tube from flexible U shaped tube is = 140 cm Inner Diameter of U shaped flexible tube is = 12 mm Thickness of U shaped tube is = 2 mm Inner Diameter of distal rigid tube is = 11 m Thickness of distal rigid tube is = 1.8 mm The angle of ‘U’ tube which makes to vertical is be- tween 80°- 70 Similar experiments were conducted in much small scale using small sized balloons and tubes which worked very well, though data was not recorded, due to low volume flows and small sized equipment used. The dimensions of the pipes and bladder are so cho- sen to resemble those of small sized human beings car- diovascular system. The flows used are comparable to normal physiological range of blood flow. The oscilla- tions produced by this experiment also are in range of normal heart beating frequency. The basic experiments illustrate how simple parameter of flow rate can be var- ied to alter the frequency of collapsing bladder (Tables 1 and 2). Also at constant flow conditions and when all other parameters are kept constant of varying height of the bladder from ground affects the frequency of col- lapsing bladder (Tables 3 and 4). Thus by altering these two simple parameters any desired flow condition can be simulated in laboratory. The effects of pipe’s stiff- ness and diameters of tubing can be studied and their flow patterns analyzed when all other parameters are held constant. Also side branches can be attached to distal ‘U’ tube or rigid pipe which represent the branches of main vessels and their flow characteristics during pulsatile flow can be studied. Here fall of pressures is sharp unlike the rise which is observed during pressure recordings inside large arteries and the pressures recorded here are in negative range which is reverse of that seen normally inside blood ves- sels. But the pressure fluctuations resemble closely to those recorded inside vascular compartment invasively. 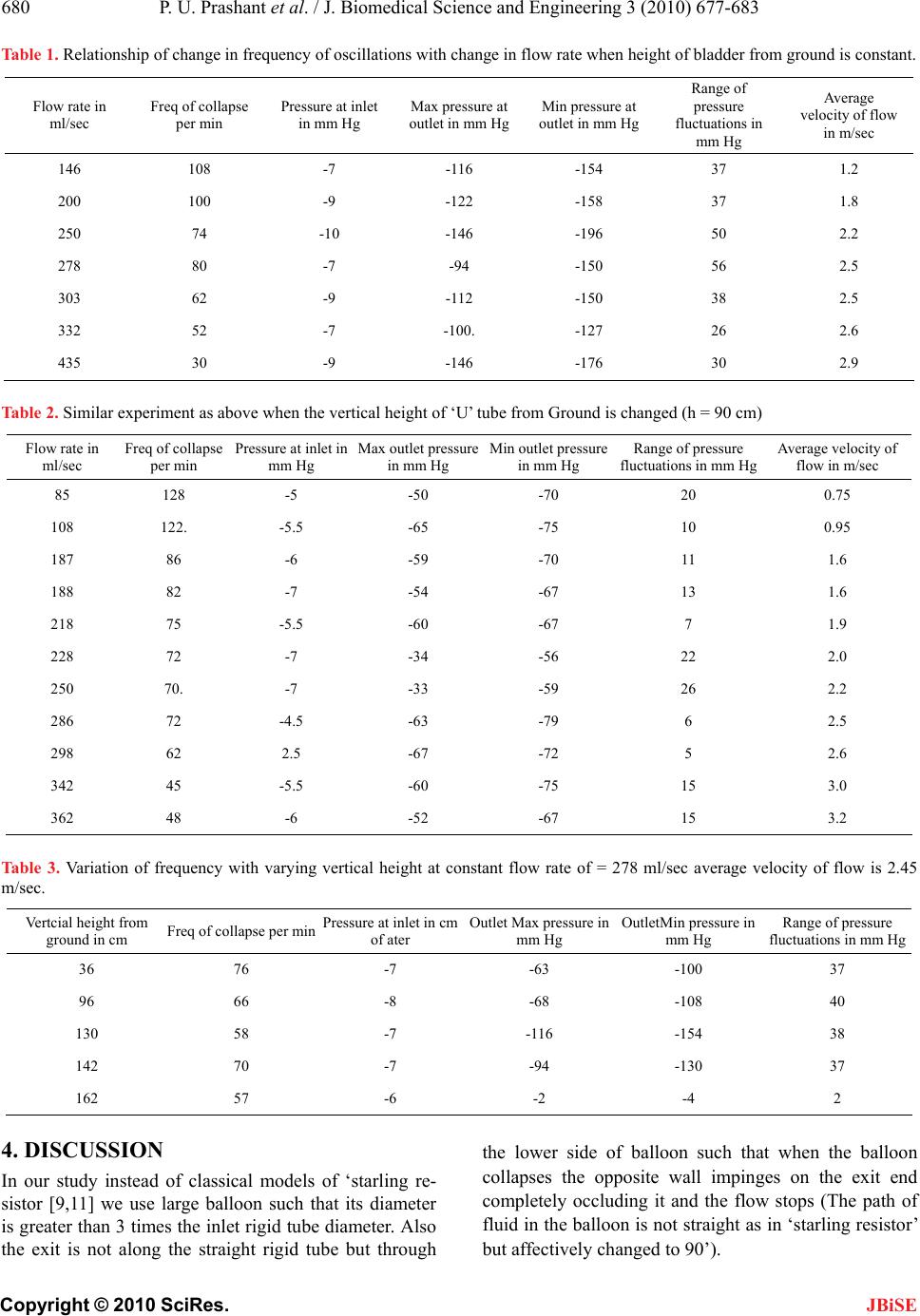 P. U. Prashant et al. / J. Biomedical Science and Engineering 3 (2010) 677-683 Copyright © 2010 SciRes. JBiSE 680 Table 1. Relationship of change in frequency of oscillations with change in flow rate when height of bladder from ground is constant. Flow rate in ml/sec Freq of collapse per min Pressure at inlet in mm Hg Max pressure at outlet in mm Hg Min pressure at outlet in mm Hg Range of pressure fluctuations in mm Hg Average velocity of flow in m/sec 146 108 -7 -116 -154 37 1.2 200 100 -9 -122 -158 37 1.8 250 74 -10 -146 -196 50 2.2 278 80 -7 -94 -150 56 2.5 303 62 -9 -112 -150 38 2.5 332 52 -7 -100. -127 26 2.6 435 30 -9 -146 -176 30 2.9 Table 2. Similar experiment as above when the vertical height of ‘U’ tube from Ground is changed (h = 90 cm) Flow rate in ml/sec Freq of collapse per min Pressure at inlet in mm Hg Max outlet pressure in mm Hg Min outlet pressure in mm Hg Range of pressure fluctuations in mm Hg Average velocity of flow in m/sec 85 128 -5 -50 -70 20 0.75 108 122. -5.5 -65 -75 10 0.95 187 86 -6 -59 -70 11 1.6 188 82 -7 -54 -67 13 1.6 218 75 -5.5 -60 -67 7 1.9 228 72 -7 -34 -56 22 2.0 250 70. -7 -33 -59 26 2.2 286 72 -4.5 -63 -79 6 2.5 298 62 2.5 -67 -72 5 2.6 342 45 -5.5 -60 -75 15 3.0 362 48 -6 -52 -67 15 3.2 Table 3. Variation of frequency with varying vertical height at constant flow rate of = 278 ml/sec average velocity of flow is 2.45 m/sec. Vertcial height from ground in cm Freq of collapse per min Pressure at inlet in cm of ater Outlet Max pressure in mm Hg OutletMin pressure in mm Hg Range of pressure fluctuations in mm Hg 36 76 -7 -63 -100 37 96 66 -8 -68 -108 40 130 58 -7 -116 -154 38 142 70 -7 -94 -130 37 162 57 -6 -2 -4 2 4. DISCUSSION In our study instead of classical models of ‘starling re- sistor [9,11] we use large balloon such that its diameter is greater than 3 times the inlet rigid tube diameter. Also the exit is not along the straight rigid tube but through the lower side of balloon such that when the balloon collapses the opposite wall impinges on the exit end completely occluding it and the flow stops (The path of fluid in the balloon is not straight as in ‘starling resistor’ but affectively changed to 90’). 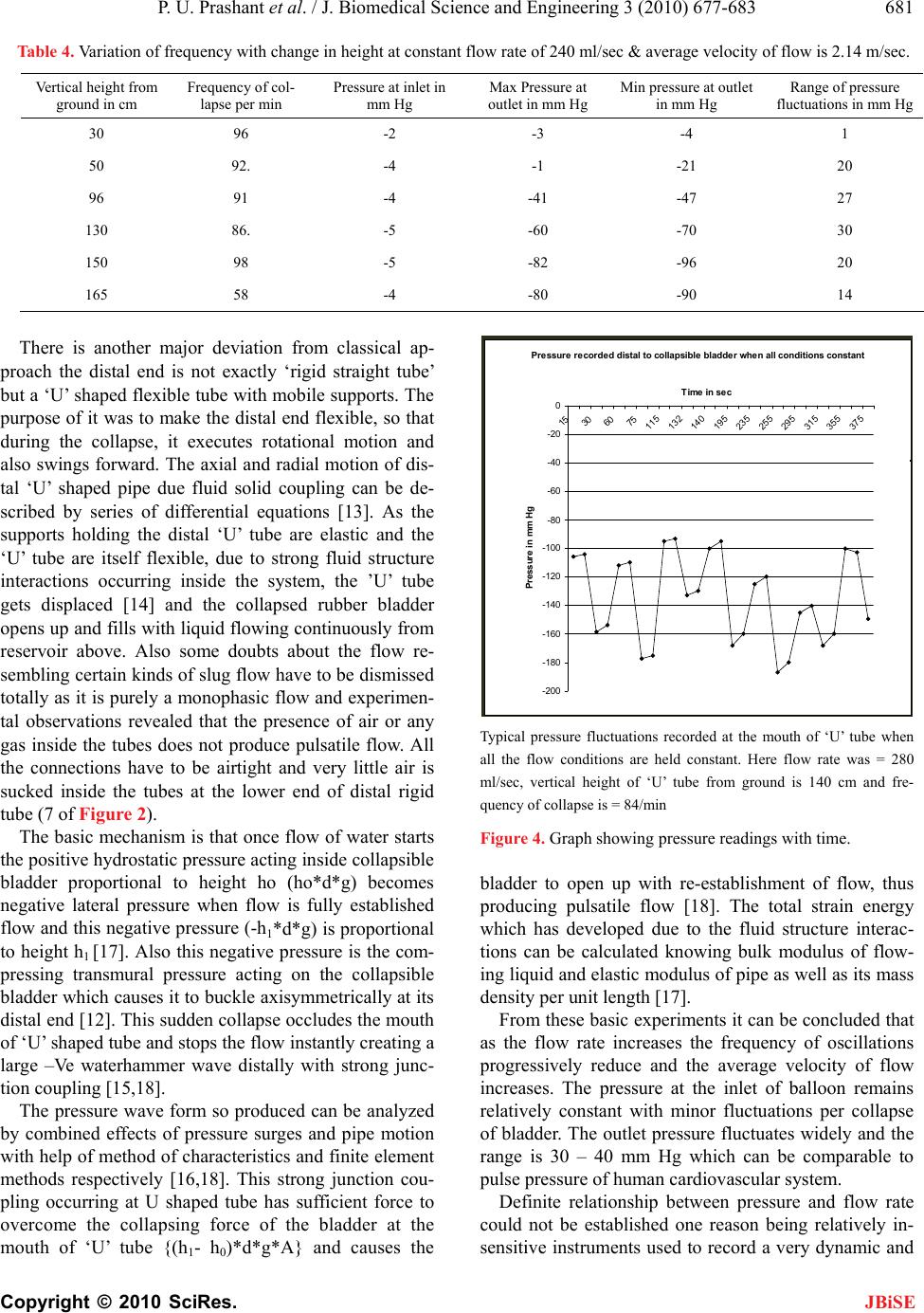 P. U. Prashant et al. / J. Biomedical Science and Engineering 3 (2010) 677-683 Copyright © 2010 SciRes. JBiSE 681 Table 4. Variation of frequency with change in height at constant flow rate of 240 ml/sec & average velocity of flow is 2.14 m/sec. Vertical height from ground in cm Frequency of col- lapse per min Pressure at inlet in mm Hg Max Pressure at outlet in mm Hg Min pressure at outlet in mm Hg Range of pressure fluctuations in mm Hg 30 96 -2 -3 -4 1 50 92. -4 -1 -21 20 96 91 -4 -41 -47 27 130 86. -5 -60 -70 30 150 98 -5 -82 -96 20 165 58 -4 -80 -90 14 There is another major deviation from classical ap- proach the distal end is not exactly ‘rigid straight tube’ but a ‘U’ shaped flexible tube with mobile supports. The purpose of it was to make the distal end flexible, so that during the collapse, it executes rotational motion and also swings forward. The axial and radial motion of dis- tal ‘U’ shaped pipe due fluid solid coupling can be de- scribed by series of differential equations [13]. As the supports holding the distal ‘U’ tube are elastic and the ‘U’ tube are itself flexible, due to strong fluid structure interactions occurring inside the system, the ’U’ tube gets displaced [14] and the collapsed rubber bladder opens up and fills with liquid flowing continuously from reservoir above. Also some doubts about the flow re- sembling certain kinds of slug flow have to be dismissed totally as it is purely a monophasic flow and experimen- tal observations revealed that the presence of air or any gas inside the tubes does not produce pulsatile flow. All the connections have to be airtight and very little air is sucked inside the tubes at the lower end of distal rigid tube (7 of Figure 2). The basic mechanism is that once flow of water starts the positive hydrostatic pressure acting inside collapsible bladder proportional to height ho (ho*d*g) becomes negative lateral pressure when flow is fully established flow and this negative pressure (-h1*d*g) is proportional to height h1 [17]. Also this negative pressure is the com- pressing transmural pressure acting on the collapsible bladder which causes it to buckle axisymmetrically at its distal end [12]. This sudden collapse occludes the mouth of ‘U’ shaped tube and stops the flow instantly creating a large –Ve waterhammer wave distally with strong junc- tion coupling [15,18]. The pressure wave form so produced can be analyzed by combined effects of pressure surges and pipe motion with help of method of characteristics and finite element methods respectively [16,18]. This strong junction cou- pling occurring at U shaped tube has sufficient force to overcome the collapsing force of the bladder at the mouth of ‘U’ tube {(h1- h0)*d*g*A} and causes the Pressure recorded distal to collapsible bladder when all conditions constant -200 -180 -160 -140 -120 -100 -80 -60 -40 -20 0 15 30 60 75 115 13 2 140 195 23 5 255 295 315 355 375 Time in sec Pressure in mm Hg Typical pressure fluctuations recorded at the mouth of ‘U’ tube when all the flow conditions are held constant. Here flow rate was = 280 ml/sec, vertical height of ‘U’ tube from ground is 140 cm and fre- quency of collapse is = 84/min Figure 4. Graph showing pressure readings with time. bladder to open up with re-establishment of flow, thus producing pulsatile flow [18]. The total strain energy which has developed due to the fluid structure interac- tions can be calculated knowing bulk modulus of flow- ing liquid and elastic modulus of pipe as well as its mass density per unit length [17]. From these basic experiments it can be concluded that as the flow rate increases the frequency of oscillations progressively reduce and the average velocity of flow increases. The pressure at the inlet of balloon remains relatively constant with minor fluctuations per collapse of bladder. The outlet pressure fluctuates widely and the range is 30 – 40 mm Hg which can be comparable to pulse pressure of human cardiovascular system. Definite relationship between pressure and flow rate could not be established one reason being relatively in- sensitive instruments used to record a very dynamic and  P. U. Prashant et al. / J. Biomedical Science and Engineering 3 (2010) 677-683 Copyright © 2010 SciRes. JBiSE 682 unstable pressure tracing. The minimum flow where it functions is where the flow inside the pipe work be- comes closed channel laminar flow [17]. That means the whole of pipe area is in contact with flowing water. At flow rates below this it is open channel flow. Also the velocity of flow is 0.5 -2 m/sec which is very low. At flow velocity > 3 m/sec or at higher Rey- nolds numbers the efficiency markedly falls and little higher flow velocity it doesn’t behave as pulsatile bal- loon but it simply expands and remains in that position and water starts flowing passively. When diameter of U and distal pipe is increased the lower and upper flow rate limit where these pulsations are observed both are in- creased and also simultaneously the range at which op- erates efficiently are increased correspondingly. Yannick et al. performed in a specially designed mo- ckup simulating the heart’s behavior (the Dual Activa- tion Simulator) to understand pulsatile flow inside heart like chambers in terms of mechanical behavior to under- stand cardiovascular diseases in laboratory without re- sorting to animal models or patients [19]. The gear pumps used by Issartier et al., Petersen et al., etc produce cavitation and damage to suspended parti- cles [4-5] whereas the present model the occurrence of cavitation is very less and can be easily prevented by altering flow conditions. There is also no damage to blood particles as it does not involve rotating metal gears. Peristaltic pumps which were developed later to pre- vent particle damage of gear pumps suffer the drawback of production of only limited subset of waveforms even if they are computer controlled and the systems lack flexibility to operate under wide flow conditions [4,6,7]. Also generating continuous flow from peristaltic pumps is difficult. The present model operates under wide range of flow conditions which can be produced by simply opening the inflow valve or raising the height of col- lapsible bladder from ground. Besides pulsatile flow, continuous can be easily produced simply by halting the oscillations of ‘U’ shaped tube and no further additional arrangement is required. Microcomputer controlled piston pumps are very complicated, difficult to set up and cumbersome to oper- ate [4-7]. The present apparatus offers an easier solution of producing pulsatile flow in laboratory by using read- ily available cost effective materials and can save lot of expenses and power. The collapse of collapsible bladder resembles some- what superficially of “beating heart” and waveforms produced are very close to invivo flow including sudden surges of pressures seen during valve closure. The pulsa- tile flow so produced can be studied for progression of diseases like atherosclerosis, effects of vessel wall stiff- ness and other properties for development of vascular diseases like hypertension and atherosclerosis. Initial preliminary studies the apparatus works even when glycerol water having viscosity similar to blood are used as flowing liquid instead of water. However this is a pilot study and needs to be validated by further re- search and all the variables which affect the flow have to be studied more exhaustively with better instrumentation and advanced mathematical approach, before real useful conclusions drawn. 5. CONCLUSIONS A novel and cost-effective pulsatile flow generator can be constructed using a large collapsible bladder con- nected to a flexible ‘U’ shaped tubing system and the pulsatile flow so produced can be used as simulation model for studying in vivo blood flow. 6. AUTHOR’S CONTRIBUTIONS PUP developed the experimental setup from beginning, conducted the experiments and drafted the manuscript. NBS provided technical support for conducting experi- ments in MSRIT lab and suggested the utility of using it as simulation model for cardiovascular system. 7. ACKNOWLEDGEMENTS I thank MSRIT institute for providing me laboratory support for my research especially Dept of Civil engineering and the Principal of MSRIT. REFERENCES [1] Afshin, A.-B., Mohammad, T.-S., Nasser, F., et al. (2008) A new system to analyze pulsatile flow characteristics in elastic tubes for hemodynamic applications. American Journal of Applied Sciences, 5(12), 1730-1736. [2] Chatzizisis, Y.S. and Giannoglou, G.D. (2006) Pulsatile flow: A critical modulator of the natural history of ath- erosclerosis. Electronic Publication, 67(2), 338-340. [3] Finol, E.A. and Amon, C.H. (2001) Blood flow in ab- dominal aortic aneurysms: Pulsatile flow hemodynamics. Journal of Biomechanical Engineering, 123(5), 474-484. [4] Law, Y.F., Cobbold, R.S.C., et al. (1987) Computer-con- trolled pulsatile pump system for physiological flow si- mulation. Medical & Biological Engineering & Comput- ing, 25(5), 590-595. [5] Petersen, J.N. (1984) Digitally controlled system for re- producing blood flow waveforms in vitro. Medical and Biological Engineering and Computing, 22(3), 277-280. [6] Eriksson, A., Persson, H.W. and Lindstrom, K. (2000) A computer-controlled arbitrary flow wave form generator for physiological studies. Review of Scientific Instru- ments, 71(1), 235-242. [7] Holdswoth, D.W., Rickey, D.W., et al. (1991) “Com- puter-controlled positive pump for physiological flow  P. U. Prashant et al. / J. Biomedical Science and Engineering 3 (2010) 677-683 Copyright © 2010 SciRes. JBiSE 683 simulation,” Medical & Biological Engineering & Com- puting, 29(4), 565-570. [8] Kamm, R.D. and Shapiro, A.H. (1979) Unsteady flow in a collapsible tube subjected to external pressure or body forces, Journal of Fluid Mechanics, 95(1), 1-78. [9] Heil, M. and Jensen, O.E. (2003) Flows in deformable tubes and channels -- Theoretical models and biological applications. Chapter 2 of: flow in collapsible tubes and past other highly compliant boundaries. Pedley, T.J. and Carpenter, P.W., Eds., Kluwer, Dordrecht, Netherlands Heil, 15-50. [10] Heil, M. (1996) The stability of cylindrical shells con- veying viscous flow. Journal of Fluids and Structures, 10(2), 173-196. [11] Heil, M. and Pedley, T.J. (1996) Large post-buckling deformations of cylindrical shells conveying viscous flow. Journal of Fluids and Structures, 10(6), 565-599. [12] Heil, M. (1998) Stokes flow in an elastic tube -- A large- displacement fluid-structure interaction problem. The In- ternational Journal for Numerical Methods in Fluids, 28(2), 243-265. [13] Tijsseling, A. (2007) Water hammer with fluid-structure interaction in thick-walled pipes. Computers and Struc- tures, 85(11-14), 844-851. [14] Heinsbroek, A.G.T.J. and Tijsseling, A.S. (1994) The influence of support rigidity on waterhammer pressures and pipe stresses. Proceedings of the Second Interna- tional Conference on Water Pipeline System and BHR Group, Edinburgh, 17-30. [15] Wiggert, D.C. and Tijsseling, A. S. (2001) Fluid tran- sients and fluid-structure interaction in flexible liquid filled piping. ASME, 455-481. [16] Tijsseling, A.S. and Heinsbroek. A.G.T.J. (1999) The influence of bend motion on waterhammer pressures and pipe stresses. Proceedings of the 3rd ASME & JSME Joint Fluids Engineering Conference, Symposium S-290 Water Hammer (Editor JCP Liou), San Francisco, July 1999, ASME-FED, 248, Paper FEDSM99-6907. [17] Kumar, D.S. (2010) Fluid mechanics and fluid power engineering. S. K. Kataria & Sons Publishers and Dis- tributors, New Delhi, Chapter 9. [18] Ahmad A. and Ali R.K. (2008) Investigation of the junc- tion coupling due to various types of the discrete points in a piping system. The 12th International Conference of International Association for Computer Methods and Advances in Geomechanics (IACMAG), Goa, India. [19] Knapp, Y., Bertrand, E. and Mouret, F. (2003) 2D-PIV measurements of the pulsatile flow in a left heart simu- lator. Proceedings of PSFVIP-4, Chamonix, F4082. [20] Wang, W.X. and Christopher D.B. (2007) Effects of col- lapsible-tube-induced pulsation vigour on membrane fil- tration performance. Journal of Membrane Science, 288 (1-2), 298-306. |

