 Creative Education 2012. Vol.3, No.4, 540-556 Published Online August 2012 in SciRes (http://www.SciRP.org/journal/ce) http://dx.doi.org/10.4236/ce.2012.34082 Copyright © 2012 SciRes. 540 How to Introduce the Basis of Algorithmics? Thanks to the Enumeration and Composition of All Riffle Shuffles from an N Card Deck Used in MathMagic Pierrot Schott Art et Recherche NUMérique (ARNUM), Ecole Supérieure d’Informatique, d’Electronique et d’Automatisme (ESIEA), Paris, France Email: schott@esiea.fr, pierrot.schott@laposte.net, magie.carte@laposte.net, arnum@esiea-recherche.eu Received April 17th, 2012; revised May 22nd, 2012; accepted May 30th, 2012 Why use magic for teaching combinatory, algorithms and finally informatics basis as tables, control structure, loops and recursive function? Magicians know that once the surprise has worn off, the audience will seek to understand how the trick works. The aim of every teacher is to interest their students, and a magic trick will lead them to ask “how?” and “why?” and “how can I create one myself?” In this article we consider a project I presented in 2009, the subject of which was “How many riffle shuffles does exist from an n card deck? Find the composition of each possible riffle shuffle”. The aim of the paper is not only to describe the project scope, the students’ theoretical studies, their approach to this problem and their computer realizations, but also to give ideas for a course or project using pedagogy. That is why only remarkable students’ realizations are shown. In order to complete the given project, the students must answer three steps: the first one is to answer to the following question: “how can I find all possible riffle shuffles with few cards?” (for example 3, 4 or 5 cards) the second one (to go further) is to answer to the following question “how can I generalize this solution through an algorithm?” the last one (to obtain the results!) is to program the algorithm with a recursive and a non-recursive solution). Each step of the Mat- lab™ solution code is associated with an informatics basis. Whatever the student’s professional ambitions, they will be able to see the impact that originality and creativity have when combined with an interest in one’s work. That’s why, two ameliorations of the “basic” algorithm are proposed and a study of the gain thanks to these ameliorations is done. The students know how to “perform” a magic trick for their family and friends thanks to the use of riffle shuffle in Gilbreath’s principles, a trick that they will be able to ex- plain and so enjoy a certain amount of success with. Sharing a mathematical/informatics demonstration is not easy and the fact that they do so means that they will have worked on and understood and are capable of explaining this knowledge. Isn’t this the aim of all teaching? Keywords: Higher Education; Engineer; Educational Method; Informatics; Algorithm Introduction I am fascinated by magic (or rather, conjuring) and for many years I have used this way of teaching, both in my physics classes and as higher education teacher trainer. In this paper I present all the notions, a brief history of magic and finally the researchers who have used this art to teach and/ or to research. The aim of the magician is to hide the principles he uses (us- ing maths, physics, psychology, sleight of hand, etc.) by dis- guising the trick so that the audience has no way of discovering how it is done; thus allowing the magic to remain. The teacher can do exactly the opposite: unraveling a magic trick to highlight the principles used! A Brief Histor y of Ma gi c From the beginning of time people have feared what they don’t understand, and sought logical explanations for inexpli- cable phenomena. To begin with, they considered them to be the work of magic, then the work of the gods, then the work of God himself. The church discouraged the spread of the con- jurer’s art as it preferred not to have rational explanations for what was considered supernatural. The first magic tricks were performed in the Middle Ages by clowns and con-men who would entertain passers-by by getting them to bet on the position of a ball hidden in one of three up- turned goblets, the bet being usually lost. This trick is known nowadays by the name “cups and balls” (Mayol, 2000). The first book considered to be about modern magic (or should we say, “conjuring”) was written and printed in the 16th Century, and was about magic with ropes (Ammar, 1998). It wasn’t until the end of the 19th Century that the word magic took on its present-day meaning when the famous magician Houdini, fa- ther of modern magic, made it the art it is today. Since then, a good number of principles have been invented and improved on by magicians and gamblers (Erdnase, 1902), especially for bets with card tricks. Since the 1980s, the secrets that were once passed on from master to apprentice are now universally available through the use of video cassettes and modern communication technology, and magic has become a big business.  P. SCHOTT Card Magi c a s the Vector of Res earch and Tea ching From 1886 until 1896, Poincaré occupied the chair of “prob- ability Calculus” in the Paris University “La Sorbonne”. He wrote a work named “probability calculus” (Poincare, 1912; Sheynin, 1991) which was printed for the first time in 1896. In the second edition, he brings very fundamental new reflections on the groups and the hypercomplex systems and on the ergodic theory. He is brought to these innovations by the study of the card shuffling and liquid mixing. The problems with the card shuffling and liquid diffusion studied by Poincaré are applica- tion cases of the ergodic theory, which is at the center of the probability leveling phenomenon: if the deck was shuffled for a long time, all the possible permutations have the same prob- ability. Both principles of Gilbreath (Gilbreath, 1958; Gilbreath, 1966; Gilbreath, 1989) are fascinating principles, allowing one to do extraordinary card tricks! Some Mathematicians, such as M. Gardner (Magid, 2005; Gardner, 1958; Gardner, 2005), P. Diaconis (Diaconis, 1998; Diaconis, 2003; Assaf, 2009) or C. Mulcahy (Mulcahy, 2003; Mulcahy, 2004; Mulcahy, 2007), and some computer special- ists, such as G. Huet (Huet, 1991)—one of the creators of the COQ language which allows automatic mathematical proofs to be made—studied this principle (and they are not the only ones). We shall not present this principle here but it is necessary to know that it is based on a card shuffle commonly used on both sides of the Atlantic Ocean: the American riffle shuffle. Summary The subject was given for the 4th semester students in a higher education school in France (named “Grandes écoles d’ingénieurs”) as a Multi Disciplinary Project (MDP) described in (Schott, 2010). The students had to solve and illustrate the following problem: “How many riffle shuffles does exist from an n card deck? Find the composition of each possible riffle shuffle.” A theoretical solution of the number of riffle shuffles is given by D. Aldous and P. Diaconis (Aldous, 1986). However, the composition was not given. “A first mathematical and algorith- mically study is given in french by A. Lachal (Lachal, 2012). I introduce here firstly many algorithmic ameliorations and the use of data files and secondly a pedagogic point of view by giving, through the article construction, an possible approach for teaching an high level informatics language By giving this project, I would like the students to: Find and understand the paper in which a solution part is written; Understand the whole problem and determine the way that the human being can solve it; Transliterate this “human solution” into a real algorithm; Write the algorithm using an informatics language; I choose Matlab™; Discover all of the basis of the sequential language (data format, table, loop, recursively, etc.); Discover a fascinating area and improve their creativity. The Aim of the Paper: To Not Only Show the Result of a High Education Project, But Also Give Ideas for a Course or U sing Project Pedagogy The description of the higher education in France, and the scopes and the educational objectives of the MDP are described in (Schott, 2010). I do not want to describe the given subject, the composition of the student group, my motivations, my expectations and the realization of the students. I prefer to write the “true” solution of the problem in order to give some ideas for an example in an algorithmic course or for a course using project pedagogy. However, the order and the name of titles in this paper could be the course structure. In fact, I introduce step by step all of essentials programming basis in the following order: Modeling the problem, Solving the problem thanks a analytics solution, Finding algorithms, Programming the algorithms by: Introducing the data types, o Introducing the data types, o Programming with the “for” and “while” loops, o Using the branch instruction as “if” … “then” … “else”, o Writing results in files, o Recursively programming, o Changing a recursive function by a simple ‘while’ loop. Results analysis versus computing time. Number and Composition of All of the Riffle Shuffles from a 2 Card Deck, 3 Card Deck and 4 Card Deck (From the Problem to an Algorithm: Step 1) If we take an n card deck, how can we find the composition? It is humanly “impossible” if the number of cards is greater than 7 because the number of different riffle shuffles is: n Mn2 n (1) This relation is proved in Appendix A. In order to find a general algorithm, we have to understand the way of solving the problem with a deck of only a few cards. Mathematical Notations We introduce three following notations: MT(n): the number of possible riffle shuffles, M(n): the number of different possible riffle shuffles, Mi(p,q): the number of possible riffle shuffles between a p card deck and a q card deck (the insertion of the first card of the p card deck is under the ith card of the q card deck) with p + q = n. Each card will be represented by the quantity where i is the initial position of the card in the deck and j is the position of this card after j shuffles. This will be written more simply by Ci. j i C Definition of Riffle Shuffle Let an n card deck be cut into two portions, called subdecks. Each subdeck is riffled with the hands, and the cards of each subdeck become entangled, as presented in Figure 1. Number and Composition of All Possible Riffle Shuffles of a 2 Card Deck Let us take a 2 card deck in this order: C1-C2. There is only one way possible to cut this deck into two subdecks as pre- Copyright © 2012 SciRes. 541  P. SCHOTT sented in Figure 2. There are two different possible riffle shuffles, presented in Figure 3. In summary, there are only 2 riffle shuffles from a 2 card deck and Equation (1) is verified. So the number of riffle shuffles MT(2) is : 2 T 22 02 and 2222 MM M (2) Number and Composition of All Possible Riffle Shuffles of a 3 Card Deck Let us take a 3 card deck in this order: C1-C2-C3. There are only two ways possible to cut this deck into two subdecks as presented in Figure 4. So, the number of all riffle shuffles MT(3) is worth: T0 0 2 T0 p1 32,11, 3p,3p MM M MM 2 (3) For each of the configurations presented in Figure 4, there Figure 1. Example of a cut for an n card deck and then a riffle shuffle. Figure 2. All possible cuts of a 2 card deck. Figure 3. All possible riffle shuffles of a 2 card deck. Figure 4. All possible cuts of a 3 card deck. are several possible shuffles, which are presented in Figure 5. In summary, there are 2 possible cuts and 6 riffle shuffles (of which 5 are different) from a 3 card deck and the Equation (1) is verified. The number of riffle shuffles between a 1 card subdeck and a 2 card subdeck, M0(1,2), is the same as the number of shuffles between a 2 card subdeck and a 1 card subdeck, M0(2,1)! 00 1, 232,1MM (4) Thanks to Equations (3) and (4), the number of riffle shuf- fles-MT(3)-comes easily: T0 0 32,11,26 MM M (5) The number of different riffle shuffles M(3) is worth: 3 T 3315 and 5233 MM M (6) Number and Composition of all Possible Riffle Shuffle of a 4 Card Deck Let us take a 4 card deck in this order: C1-C2-C3-C4. Only three ways are possible to cut this deck into two subdeck as presented in Figure 6. So, the number of all riffle shuffles MT(4) is worth: T0 00 3 T0 p1 43,12,21, 4p,4p MM MM MM 3 (7) For each of three configurations presented in Figure 6, there are several possible shuffles, which are presented in Figures 7 and 9. For the first cut—noted (a), and the third cut—noted (c), all of possible riffle shuffle are presented in Figure 7. For each configuration (a) and (c), a one card deck is shuf- fled with a 3 card deck: 00 3,11, 34 MM (8) Figure 5. All possible riffle shuffles of a 3 card deck. Figure 6. All possible cuts of a 4 card deck. Copyright © 2012 SciRes. 542  P. SCHOTT For the (b) configuration, the first card (here C1) is put away. Thus the new configuration is so: one subdeck with one card (C2) and the second unchanged subdeck (C3-C4). This configu- ration is well known and the riffle shuffles are presented in Figure 8. Three riffle shuffles are obtained. The C1 card is shuffled in these 3 shuffled subdecks. What is essential to note is that the C1 card must be inserted over the C2 card. All of the possible riffle shuffles so obtained are presented in Figure 9. We thus have found the value of M0(2,2). Mathematically, it becomes: 0123 3 0k k1 2, 21,31,31, 3 2, 21,3 MMMM MM (9) Thanks to Figure 9, we can notice that: 12 3 1,33; 1,32; 1,31MM M (10) So, the value of M0(2,2) is worth: 02, 23216M (11) Figure 7. All possible riffle shuffles of a 4 card deck [cut (a) and (c)]. Figure 8. All possible riffle shuffles between (C1-C2) and (C3-C4). Figure 9. All possible riffle shuffles of a 4 card deck [configuration (b)]. Figure 10. All possible riffle shuffles of a 4 card deck. Thanks to the Equations (7), (8) and (11), MT(4) can easily be calculated: T0 00 41,32,21,3 14 MM MM (12) Figure 10 summarises the whole process to calculate MT(4). In summary, there are 3 possible cuts and 14 riffle shuffles (of which 12 are different) from a 4 card deck and the Equation (1) is verified. 4 T 44212 and 12244 MM M (13) Number and Composition of All of Riffle Shuffles of an N Card Deck (From the Problem to an Algorithm: Step 2) Four points are presented in order to find the number and composition of all riffle shuffles of an n card deck: All possible cuts of an n card deck: relation between MT(n) and [M0(i,j)]i+j=n; Main program algorithm; All possible riffle shuffles between a p card subdeck and a q card subdeck M0(p,q) ; The obtained riffle shuffle from a 1 card subdeck and a q card deck: M0(1,q) and Mi(1,q). For each point, the human approach and its transliteration into an algorithm are given. The informatics bases are given in the next section because I would like to describe first the algo- rithm, and then the programming solution! All Possible Cuts from an N Card Deck: Relation between MT(n) and [M0(i,j)]i+j=n I present, firstly, all possible cuts of an n card deck, secondly the mathematics formulation with the [M0(i,j)]i+j=n, and finally the main program algorithm. Decomposition “By Hand” and Mathematics Formulation Let us take an n card deck in this order: C1-C2- ··· -Ci- ··· -CN. Only (N − 1) ways are possible to cut this deck in two subdecks as presented in Figure 11. Mathematically, in order to calculate all of the possible riffle shuffles, it is necessary: Firstly, to find all possible cuts of the n card deck, so (n − 1) possibilities, as presented in Figure 12; Secondly, to calculate the number of possible riffle shuffles [M0(i,j)]i+j=n. Copyright © 2012 SciRes. 543  P. SCHOTT Thus Equation (14) generalizes Equation (3) [resp. (7)] found where n = 3 [resp. n = 4]: n-1 T0 p1 np,n MMp (14) Figure 11. All possible cuts of an n card deck. Figure 12. All possible cuts of an n card deck. Let us remark a coarse relation: the number of possible riffle shuffles between a p card deck and a q card deck is the same as the ones between a q card deck and a p card deck: 00 ,q q,pMM (15) So the number of terms in the sum of Equation (14) can be divided by 2. Lastly, Equation (16) generalizes Equation (4) [resp. (8)] found where n = 3 [resp. n = 4] and Equation (15) too: ii ,q q,pMM (16) Main Program Algorithm Thanks to the proposed decomposition by Equation (14), the main program algorithm comes quite naturally, as presented in Figure 13. Every rectangle in the “loop” requires of course an algorithm much more detailed in order to program all of the software. The Matlab™ main program is called “tous_melanges_ americains” (translated as “all_riffle_shuffles” in English). It is given in Appendix B. Figure 13. Main program algorithm called “tous_melanges_americains”. Copyright © 2012 SciRes. 544  P. SCHOTT Copyright © 2012 SciRes. 545 All Possible Riffle Shuffles between a p Card Subdeck and a q Card Subdeck M0(p,q) By using Equation (20), the following equation is obtained: To determine the number and the composition of all possible riffle shuffles [MT(n)], (n − 1)*M0(p,n − p) must be deter- mined. To determine them, thanks to the study with a few cards, we have to follows this strategy, described in Figure 15. 1) If the p card subdeck contains: More than one card, the top card is put away and the new subdeck-which contains (p − 1) cards-must be shuffled with the q card subdeck, as presented in Figure 14; Only a single card (say Cp), this card is shuffled in the q card subdeck, as presented in Figure 18. 2) All the calculated riffle shuffles must be now shuffled with the card Cp-1. All calculated riffle shuffles must be now be shuffled with the card Cp-2 and so on, as presented in Figure 19. The Enumeration Representation of All Riffle Shuffles between a p Car d De ck and a q Card Deck M0(p,q) Thanks to a Tree All riffle shuffles between a p card deck and a q card deck thanks to a tree are presented in Figure 16. The aim is to cal- culate the tree’s number having the value (q + 1) at the step p (and not before), then having the value (q), then (q − 1), etc. associated to the riffle shuffle number M0(1,i)]0≤i≤q. The first iteration of the given algorithm in Figure 16 in or- der to calculate M0(p,q): q1 0k k1 ,qp 1,q1 MM (17) q1 00 k1 ,qp1,q1 k MM (18) In order to program this decomposition, both choices are possible: 1) To calculate step by step (vertically), as presented in Fig- ure 17, for which the Matlab™ code is given in Matlab pro- gram 6 in Appendix B; 2) To calculate step by step (horizontally—the branches are calculated one after another) as presented in Figure 23 for which the Matlab™ code is given in Matlab program 5 in Ap- pendix B. Whatever the chosen algorithm, we need to obtain the num- ber and the composition of all riffle shuffles between a 1 card deck and a q card deck. The Obtained Riffle Shuffle from a 1 Card Subdeck and a q Card Deck: M 0(1,q) The operating mode used in order to calculate M0(1,q) is presented in Figure 18. All riffle shuffles between a 1 card deck and a q card deck is (q + 1). It generalizes Equation (4) (resp. (8)) found where n = 1 + q = 3 (resp. n = 4): 01, qq1M (19) The Obtained Riffle Shuffle from a 1 Card Subdeck and a q Card Deck over the ith Card Subdeck: M0(1,q) The operating mode used in order to calculate Mi(1,q) is presented in Figure 19. Let us note that all cards must be in- Figure 14. Decomposition of the p card subdeck in order to shuffle with a q card subdeck. Figure 15. Algorithm to calculate and determine all of the compositions of possible riffle shuffles between a p card subdeck and a q card subdeck.  P. SCHOTT Figure 16. All riffle shuffles between a p card deck and a q card deck enumeration thanks to a tree. Figure 17. Algorithm of the function which calculates all riffle shuffles between a p card deck with a q card deck M0(p,q). Figure 18. Modus operandi to find all riffle shuffles between a 1 card deck and a q card deck enumeration and decomposition. Mq(p,q). Figure 19. Modus operandi to find all riffle shuffles between a 1 card deck and a q card deck enumeration and decomposition. Mi(1,q) = M0(1,i−1) . serted over card Ci. All riffle shuffles between a 1 card deck and a q card deck over the ith position is worth (i). It generalizes Equation (10) found where n = 4: i0 1, q1, i1 MM (20) Copyright © 2012 SciRes. 546  P. SCHOTT Thanks to a similar approach, the number of riffle shuffles between a p card deck and a q card deck, when the first inserted card in the q card deck must be over the position 1 is: 1 ,qp1M (21) We can define last equation where q = 0 ··· which is physi- cally impossible! 0 ,0 1 M (22) From the Algorithm to a Matlab Program The algorithms are found and it is necessary to program them. Thanks to each algorithm shown, one new notion is introduced: The tables: card deck representation; The “FOR” loop: to generate all of the possible cuts; The “IF THEN ELSE” control: to generate all of the possible riffle shuffles between a 1 card deck and a q card deck [Mi (p,q)] with the first insertion at the ith card of the q card deck; The “WHILE” loop: to generate all of the possible riffle shuffles between a p card deck and a q card deck [M0(p,q)], The recursive function (vs “WHILE” loop): to generate all of the possible riffle shuffles between a p card deck and a q card deck [M0(p,q)]. Card Deck Representation: Introduction to the Table To represent the card deck, we shall allocate a value to each single card of the n card deck: Card value between 1 and 52; Card value between 101 and 113, 201 and 213, 301 and 313 and finally 401 and 413 (the hundred value represents the card family. The value between 1 and 13 represents the card value in the growing order from Ace to King)... Thus, whatever the choice, a bijection between each single card of the deck and a number is done. A new bicycle card deck is presented in Figure 20. This new bicycle card deck in the informatics program is presented in Figure 21 with the card representation between 1 and 52. This new bicycle card deck in the informatics program is presented in Table 1 with the card representation with hundred numbers. The corresponding Matlab program is shown below. n =52; Pi(1:13)=101:113; Pi(14:26)=Pi(1:13)+100; Pi(27:40)=313:-1::301; Pi(1:13)= Pi(27:40)+100; Matlab™ program 1. Generation of the card deck. To Generate All of the Possible Cuts: The “FOR” Loop The algorithm of all possible cuts generation is presented in Figure 22. The associated Matlab™ program, using the “for” Figure 20. A new bicycle card deck. Figure 21. A new bicycle card deck informatics representation with card num- bered between 1 and 52. loop, is given too. n = 52; Pi = 1:n; for i = 1:n-1 P1 = Pi(1:i) P2 = Pi(i+1:n); end Matlab program 2. Matlab™ program: Generation of all possible cuts of an n card deck: example of the “for” loop. To Generate all of the Possible Riffle Shuffles between an 1 Card Deck and a q Card Deck [Mi(p,q)] with the First Insertion at the ith Card of the q Card Deck: The “IF THEN ELSE” Control The algorithm of all possible riffle shuffles (between a 1 card deck and q card deck) generation has been presented in Figures 18 and 19. The associated sanitized Matlab™ program is given using the “if then else” control sequence. function [M,place_carte] = melange_1_dans_n(i,c1,P2) n2 = length(P2) ; if (i <= 0) fin = n2 + 1 ; elseif (i > n2+1) fin = n2 + 1 ; else fin = i ; end for k = 1:fin … end Matlab™ program 3. Bowdlerized Matlab™ program: generation of all possible riffle shuf- fles between a 1 card deck and a q card deck. To Generate All of the Possible Riffle Shuffles between a p Card Deck and a q Card Deck [M0(p,q)]: The “WHILE” Loop The algorithm of all possible riffle shuffles (between a p card Table 1. Used Abbreviations for the cards values. Card Value Ace of Heart 2 of Heart … King of Heart Ace of Club … King of Club King of Diamond … Ace of diamond King of Spade … Ace of Spade Informatics representation 101 102 … 113 201 … 213 313 … 301 413 … 401 Copyright © 2012 SciRes. 547  P. SCHOTT deck and q card deck) generation has been presented in Figure 17. The associated sanitized Matlab™ program is given using the “while” loop (and the “for’ loop”). function [M,place_carte] = melange_p_dans_n_non_recursif(P1,P2) n1 = length(P1) ; n2 = length(P2) ; nb_cartes_restantes = n1 ; while (nb_cartes_restantes > 0) … tab = size(Mi) ; nb_ligne_Mi = tab(1) ; for i=1:nb_ligne_Mi [Mii,place_carte_ii,nb_appel,nb_insertion_carte] =melange_1_dans_n(place_carte_i(i),carte_dessus,Mi(i,:)) ; … end nb_cartes_restantes = nb_cartes_restantes - 1 ; end Matlab™ program 3. Bowdlerized Matlab™ program: Generation of all possible riffle shuf- fle between a pa card deck and a q card deck (non recursive function): example of the “while” loop. Figure 22. Algorithm: generation of all possible cuts of an n card deck: example of the “for” loop. To Generate All of the Possible Riffle Shuffles between a p Card Deck and a q Card Deck [M0(p,q)]: The Recursive Function (vs “WHILE” Loop) The algorithm of all possible riffle shuffles (between a p card deck and q card deck) generation has been presented in Figure 17. It can be programmed in two different ways; with a “while” loop or with a recursive function presented in Figure 23. Indeed, at the end of the decomposition presented in Figure 15, only a single card is shuffled in a k card deck! Thus, the program is called as many times as possible until arriving to shuffle a 1 card deck with a q card deck, giving (q + 1) shuffles and quitting the program automatically. The second card is shuffled with each of (q + 1) shuffles and so on thanks to the recursivity! The associated Matlab™ program is given in Appendix B in Matlab™ program 5. Computing Time Comparison between the Recursive Module and the WHILE Loop Module All the simulations were carried out with the help of a com- puter COMPAQ “Presario CQ62”. The main characteristics are Figure 23. Algorithm of the function which calculates all riffle shuffles between a p card deck with a q card deck M0(p,q): recursive version. Copyright © 2012 SciRes. 548  P. SCHOTT the following: the processor is a 2.2 GHz AMD with a random access memory of 2 Go. Every computing time under a second was voluntarily inter- preted as zero (for the application it’s practically a real time answer). Over 20 cards, the computer has not enough memory. That’s why Figure 24 shows the computing time when the recursive module is used (full red line) and when the WHILE loop module is used (dotted blue line). We notice that the difference between the 2 curves is not sig- nificant to be able to conclude that one method is faster than the other! Improvement of the Initial Algorithm We present alternately 2 improvements of the initial recur- sive algorithm. The first one uses a not yet used parity property whereas the second one is only purely algorithmic by using files—which allows us to introduce the notion of file in an unusual way. Use of the Problem Symmetries Let us use the break-down shown in Figure 11. It is easy to verify that shuffle a 1 card deck into a (q − 1) card deck is simi- lar to shuffling a (q − 1) card deck into a 1 card deck, which can be mathematically written by: 0 1, qq1q,1MM 0 s are necessary to e two decks are switched before, as pre- se the higher the number of cards, the more these gains decrease— (23) However if no improvement is added to the current algo- rithm, only one call to the recursive module is necessary to calculate M0(1,q). At the same time, (q − 1) call calculate M0(q,1), as presented in Figure 25. In order to determine M0(p,q) the initial algorithm is still used but if p > q, th nted in Figure 26. The gains are not significant. In Figure 27, let us note that Figure 24. Computing time comparison between the recursive module (full red line) and the iterative module using the while loop (dotted blue line). Figure 25. All possible cuts of an n card deck and initial algorithm presentation using the recursive module for each cut. Copyright © 2012 SciRes. 549  P. SCHOTT Figure 26. All possible cuts of an n card deck and initial algorithm presentation using the recursive module and all problem symmetries for each cut. Figure 27. Computing time comparison between the initial algorithm using the ule (full red line) versus the implementation of the prob- e the saved calls (thanks to the problem n fact shuffling a 1 ffling a 2 card deck as to recursive mod lem symmetries simplifications (dotted blue line) and relative differ- ence (black dashed line). which is normal becaus symmetries properties) become small relative to the total calls. So we have to find other ideas to improve significantly and durably the computing time. Use of Files: Presentation of the Idea During the use of the initial algorithm for a 3 card deck— described in Figure 4—we noticed that the algorithm does the same thing twice to obtain the same result! I card deck into a 2 card deck is similar to shu into a 1 card deck. During the use of the initial algorithm for a 4 card deck— described in Figure 6—we notice that the algorithm does the same thing twice to obtain the same result (shuffling 3 cards into 1). Furthermore, during the initial algorithm process— described in Figure 8—we notice that at the end a 2 cards decks must be shuffled into a 1 card deck—which is already evaluated thanks to the riffle shuffle count for a 3 card deck! These considerations are summarized in Figure 28. So, it’s very sensible to use the previous riffle shuffle results. So, all riffle shuffle results of a p card deck into a q card deck must be saved in files. Moreover, at any time, the program h know which shuffle results are already saved: we use a spe- cific file whose content is similar to the one presented in the Table 2. As we want to reuse the previous results, they must be inde- pendent of the card order of the chosen initial deck. That is why we decide to save the results with the agreements presented in Figure 21. It is necessary to create two “small” modules thanks to them the program can transform the real deck into a (1 to p) numbered deck and its reciprocity so allowing to generate the riffle shuffle obtained with the chosen deck. Copyright © 2012 SciRes. 550 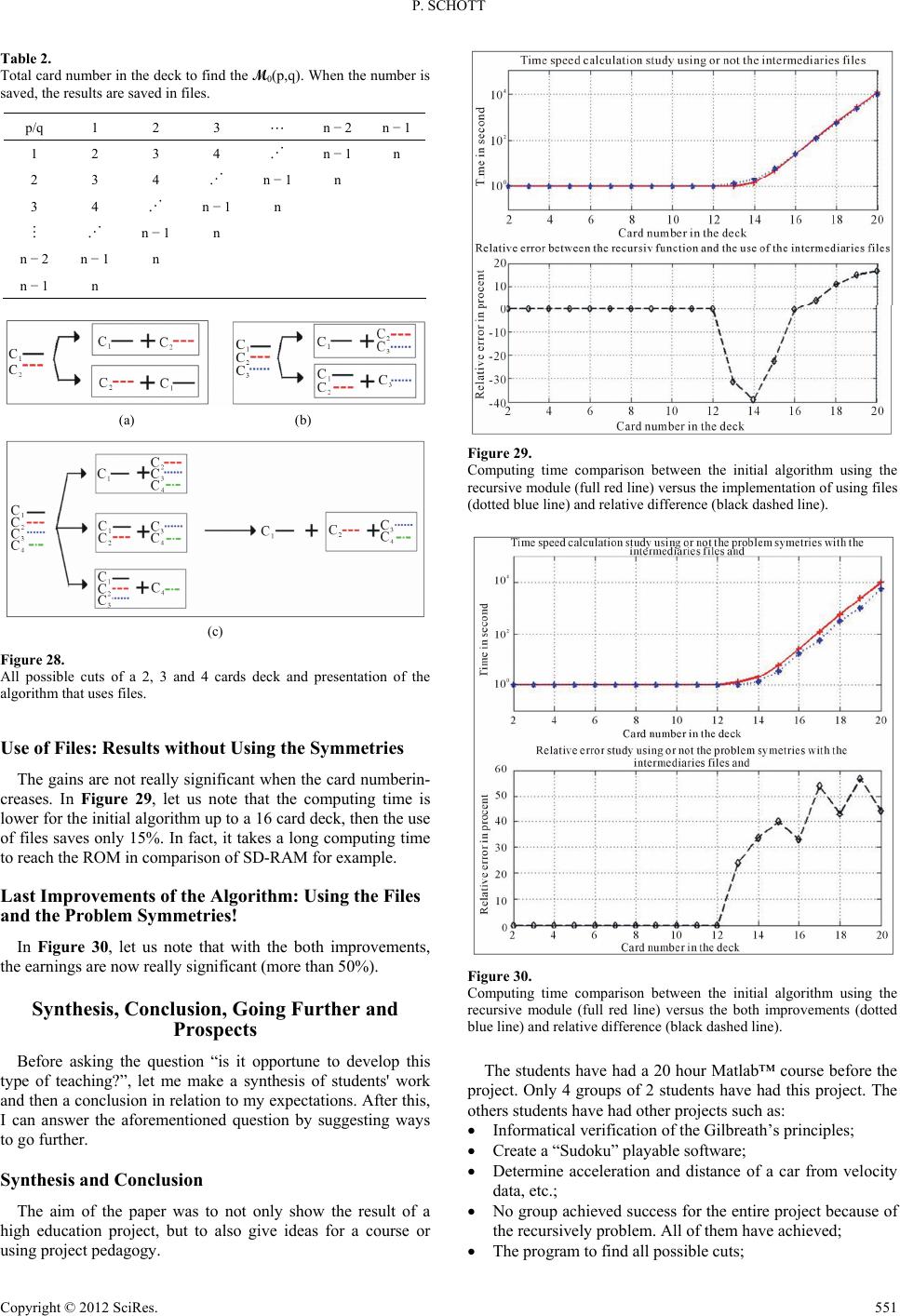 P. SCHOTT Table 2. Total card number in the deck to find the M0(p,q). When the number is saved, the results are saved in files. 1 2 3 p/q n − 2 n − 1 1 2 3 4 n − 1 n 2 3 4 n − 1 n n n n n n n 3 4 − 1 − 1 n − 2 − 1n − 1 n (a) (b) (c) Figure 28. All possible cuts of a 2, 3 and 4 cards deck and presentation of the algorithm that uses files. ally significant when the card numberin- reases. In Figure 29, let us note that the computing time is se e to nts, this type rk and , I can answer the aforemn by suggesting ways to project, but to also give ideas for a course or using project pedagogy. Use of Files: Results without Using the Symmetries The gains are not re c lower for the initial algorithm up to a 16 card deck, then the u of files saves only 15%. In fact, it takes a long computing tim reach the ROM in comparison of SD-RAM for example. Last Improvements of the Algorithm: Using the Files and the Problem Symmetries! In Figure 30, let us note that with the both improveme the earnings are now really significant (more than 50%). Synthesis, Conclusion, Going Further and Prospects Before asking the question “is it opportune to develop of teaching?”, let me make a synthesis of students' wo then a conclusion in relation to my expectations. After this entioned questio go further. Synthesis and Conclusion The aim of the paper was to not only show the result of a high education Figure 29. Computing time comparison between the initial algorithm using the recursive module (full red line) versus the implementation of using files (dotted blue line) and relative difference (black dashed line). Figure 30. Computing time comparison between the initial algorithm using the recursive module (full red line) versus the both improvements (dotted blue line) and relative difference (black dashed line). ciples; se of The students have had a 20 hour Matlab™ course before the project. Only 4 groups of 2 students have had this project. The others students have had other projects such as: Informatical verification of the Gilbreath’s prin Create a “Sudoku” playable software; Determine acceleration and distance of a car from velocity data, etc.; No group achieved success for the entire project becau ave achieved; the recursively problem. All of them h The program to find all possible cuts; Copyright © 2012 SciRes. 551  P. SCHOTT The program to shuffle one card in a q card deck; The program to find many riffle shuffles—but not all! In- e first , then a card number th re- m or a 2p card deck; for example answer this OUT Faro must have done ’ to position ‘k’ in the card primary school to higher education (Schott, 20 the “week of the science” with pr deed in order to determine ONE possible riffle shuffle, the program determines randomly a card number of th card deck P1 to go in the final shuffle of the second deck P2 to go in the final shuffle, and so on. It is very interesting to note that one of the groups made a Human Machine Interface under Matlab™, which was not ex- pected (!), presented in Figure 31 (Xuereb, 2010). They have discovered many things that exceeded my expectations… I have shown to the students the application of magic tricks anks to Gilbreath’s principles, and these students have to work with students groups who have undertaken the Gilbreath’s project in order to demonstrate Gilbreath’s principles using informatics. This is why, in my project management, I inded them repeatedly that the project was primarily scientific, but also applicable to the magic. This is why I think that this method is efficient and practica- ble. Going Further and Prospects This kind of project could be continued by these ideas: Find mathematical demonstrations of Gilbreath’s principles. Find relations f question: “Whose suit of IN and to move a card from position ‘j deck?” The answer is given by (Lachal, 2010), but it must be very interesting to give a new project in order that the students dis- cover and prove this property. This leads me to think about adapting this to all mathematics teaching, from 09) is to use magic as an investigation method to lead stu- dents to understand the mathematics principles and to come to fond of maths. I participate in imary and college classes; the results are promising. (a) (b) (c) (d) Figure 31. Card deck representation with real cards—final card deck after 7 riffle shuffles—thanks to the Matlab™ GUI interface. (a) Initial 52 new card deck; (b) 2 subdeck (cut at the 26th card); (c) Choice of shuffle num bers; (d) Initial card deck after 7 riffle shuffles. In the past, I h students a first magic to discover the optics principles (Schott, s of subjects tudents to be a trick. It is for this reason that I de- UX, the head of ARNUM, Peter WILSON who corrected the English. A special mentiocal colleague of mi - ad proposed to two groups of project using 2010). The results were different: one group having focused on the realization of the magic trick, the other one on the physical principles. That is why I continued to propose these kind and after a more formal follow-up, the results improved. One group even suggested to me a different (magic) subject which I reformatted to fit the P.E.S imperatives. However, the magic/science parallel must be perfect and not felt by the s velop at present approaches which seem to me much more adapted than the magic: An informatics project: using origami for teaching the C language; An electronics project: creation of a robot playing several musical “home made” instruments in order to allow them discover the principles of waves propagation, the program- ming of an embarked system, etc. The most important thing for me remains to use my passion for the magic as a teaching vector which also weaves a human bond between the professor and the student. Acknowledgements This paper could not have been written without the encour- agements of Bernard SCHOTT, my father, the invaluable help of Anne SERRIE, my mother, Claire LERO n for Ph. Quost, a mathemati ne: thanks for your invaluable help! REFERENCES Aldous, D., & Diaconis, P. (1986). Shuffling cards and stopping times. The American Mathematical M onthly, 93, 333-348. doi:10.2307/2323590 Ammar, M. (1998). The complete cups & balls. Tahoma, MA: L&L Publishing. Assaf, S., Soundararajan9). Riffle shuffles of a , K., & Diaconis, P. (200 deck with repeated cards. 21st International Conference on Formal Power Series and Algebraic Combinatorics, Hagenberg, 20-24 July 2009, 89-102. Diaconis, P., Graham, R. L., & Kantor, W. M. (1983). The mathematics of perfect shuffles. Advances in Applied Mathematics, 4, 175-196. doi:10.1016/0196-8858(83)90009-X Diaconis, P. (1998). From shuffling cards to walking around the build- ing. An introduction to markov chain theory. Proceedings of the In- ternational Congr e s s of Mathematicians, 1, 187-204. Diaconis, P. (2003). Mathematical developments from the analysis of riffle-shuffling. In A. Fuanou, & M. Liebeck, (Eds.), Groups combi- natorics and geometr y (pp.73-97). Hackensack, NJ: World Scientific. G H q Proof Assistant. Proceedings of Erdnase, S. W. (1902). The expert at the card table. Mineola, NY: Dover Publication. ardner, M. (1958). Mathematics, magic and mystery. Mineola, NY: Dover Publication. Gardner, M. (2005). Martin Gardner’s mathematical games: The entire collection of his scientific American columns. Washington DC: Mathe- matical Association of America. Gilbreath, N. L. (1958). Magnetic colors. The Linking Ring, 3, 60. Gilbreath, N. L. (1966). Second Gilbreath principle. Linking Ring, June 1966. ilbreath, N. L. (1989G). Magic for an audience. Series of 3 Articles in Genii, 52. uet, G. (1991). The Gilbreath trick: A case study in axiomatisation and proof development in the Co Copyright © 2012 SciRes. 552  P. SCHOTT Copyright © 2012 SciRes. 553 Second Workshop on L o g i c a l Frameworks, Edinburgh, May 1991. doi:10.1017/CBO9780511569807 achal, A.L, & Schott, P. (2012). Cartomagie: Principes de Gilbreath (I). M. Notices. Washington DC: American Mathematical M Mive card trick. Maths Horizon, 10. Society, 11. ety, 14. P és. Paris: Gauthier-Villars. ucation. Proceedings of ICERI2009 Conference, Sclic group and its properties n, 1, 27-40. X 2010). Le mélange américain. Quadrature, 85, 24-35. agid, A. (2005) Society. ayol, H. (2000). La magie des cordes maestro. Gassaway, WV: HBM Production. ulcahy, C. (2003). Fitch Cheney’s f Mulcahy, C. (2004). Top 5 reasons to like mathematical card tricks. American Mathematical Mulcahy, C. (2007). An ESPeriment with Cards. American Mathema- tical Soci oincaré, H. (1912). Calcul des probabilit Schott, P. (2009). The use of magic in mathematics: From primary school to higher ed Madrid, 16-18 November 2009, 58-70. Schott, P. (2010). The use of magic in optics in higher education. Crea- tive Education, 1, 11-17. chott, P. (2011). How to introduce the cy representation with Matlab? Thanks to Magic using the perfect Faro shuffle. Creative Educatio Sheynin, O. B. (1991). H. Poincaré’s work on probability. Archive for History of Exact Sciences, 42. uereb, C., Clement, O., & Haddad, D. ( Projet IRI 5, Paris: ESME Sudria.  P. SCHOTT Appendix A: Mathematical Demonstration: ‘‘How Many Different Riffle Shuffles Exist for an N Card Deck MT(n)?’’ We propose the enumeration demonstration riffle shuffles between a p card deck and a q card deck M0(p,q). Then the demonstration of MT(n) is done. Calculation of M0(p,q) Thanks to the study for n = 2, 3 and 4, we think that the com- binatorial must be used. Let us define n C: p n n! C !n p! (24) Indeed, we have the following properties: qp 00q (p,q)(q,p) et CC MM q p 1 (25) Finally, Equation (19) can be written with combinatory as follows: q1 0 (1,q)q1C M (26) Then, this equation can be extrapolated and demonstrated by recurrence. Recurrence Hyp othesis The recurrence equation is: q 0p ,qC M (27) Verification of Recurrence Hypothesis q Is Fixed and p Varies p = 1, the hypothesis is verified thanks to Equation (26), p = 2, M0(2,q) must be calculated. Using the proposed al- gorithm, we have: 1) Firstly, the last card is put away; 2) Secondly, the number and the composition of all riffle shuffles between a 1 card deck and a q card deck M0(1,q) is worth: (q + 1); 3) Lastly the card that was put away is shuffled with the (q + 1) obtained shuffles. So: 00 (1,q )(1,q ) i0 i0 i0 1,q 11,q 1iMM MM (28) 0(1,q) i i0 (1,q 1)1 23qq 1M M (29) 0(1,q) i i0 q1q2 1,q 12 M M (30) Other hand, is calculated and worth: 2q 2 C 2q 2 q2! q1q2 C2! q22 !2 (31) By equalizing the Equations (30) and (31), the recurrence hy- pothesis is verified for p = 2. The Recurrence Hypothesis Is Considered as True Until a Given p for a Constant Value q We suppose that Equation (27) is true. Then Equation (18) becomes: q1 q 00 k0 (p,q)p 1,q1 kC MM p (32) Recurrence Hypothesis Demonstration for “p + 1” with the q Constant Value Let us calculate M0(p + 1,q). Thanks to Equation (18), we obtain: q1 00 k1 1,qp,q 1k MM q1 q q-kp q 1-k 0p k0 k0 p1,qCC Mp 1 The telescopic sum is well known: n in kk i0 CC Thus: 1q 0 p1,qC Mp 1 p (33) which concludes the demonstration by recurrence. Calculus of MT(n) Let us take Equation (14) using Equation (27): n1 n T p1 nC M (34) Appendix B: Informatics Matlab Programs No representations are given here of the Matlab™ programs. To test the entire software, you have to: Save the given programs in 4 files. Be careful, the name of the file must be the same as the function name; Enter “tous_melanges_americains” in the Matlab command window. Main Program: “tous_melanges_americains.m” The Matlab™ program and the header of the main program (Table B1) “tous_mealnges_americains” are given below: clear all close all clc n=4 ; Pi=1:n; choix_algo = 1; for i = 1:n-1 P1=Pi(1:i) P2=Pi(i+1:n) ; if (choix_algo ==1) [Mi,place_carte] = melange_p_dans_n(P1,P2); else [Mi,place_carte] = melange_p_dans_n_non_recursif(P1,P2) end if (i==1) M=Mi; else M=[M;Mi]; end clear P1 clear P2 end Matlab™ program 4. Main program: “tous_melanges_americains”. Copyright © 2012 SciRes. 554  P. SCHOTT Table B1. Header of the Matlab™ program “tous_melanges_americains.m”. Synopsis The program generates all possible cuts with n cards and for each cut, all riffle shuffles are calculated and generated. Input None Output None n Choix_algo =1 if recursif; 0 Pi, P1, P2 Card deck Local M,Mi Shuffles Matrix (one horizontal line = one shuffle) To Generate All of the Possible Riffle Shuffles between a p Card Deck and a q Card Deck [M0(p,q)]: The Recursive Function “melange_p_dans_n.m” The Matlab™ program and the header of the main program (Table B2) “melange_p_dans_n” are given below: function [M,place_carte] = melange_p_dans_n(P1,P2) n1 = length(P1); n2 = length(P2); if (n1 == 1) [M,place_carte] = melange_1_dans_n(0,P1(1,1),P2) ; else carte_dessus = P1(1) ; P1reste = P1(1,2:n1) ; [Mi,place_carte_p_dans_n] = melange_p_dans_n(P1reste,P2) ; tab = size(Mi) ; nb_ligne_Mi = tab(1) ; for i=1:nb_ligne_Mi [Mii,place_carte_i] = melange_1_dans_n(place_carte_p_dans_n(i),carte_dessus,Mi(i,:)) ; if (i == 1) M=Mii ; place_carte = place_carte_i ; else M=vertcat(M,Mii) ; place_carte = horzcat(place_carte,place_carte_i) end clear Mii ; clear place_carte_i end end Matlab™ program 5. Recursive function: “melange_p_dans_n”. Table B2. Header of the Matlab™ program “mealnge_p_dans_n.m”. Synopsis The program generates all possible riffle shuffles between P1 and P2. Input P1, P2 Card deck (the first card in the table is the upper one!) place_carte Table of the last inserted card position in the shuffle. Output M Shuffles Matrix (one horizontal line = one shuffle). n1,n2 Card number of deck XXXi Intermediare variable XXX carte_dessus The put away card of P1 Local Nb_ligne_Mi Shuffles number of Mi To Generate All of the Possible Riffle Shuffles between a p Card Deck and a q Card Deck [M0(p,q)]: The “WHILE” Loop Function ”melange_p_dans_n_nr.m” Only the Matlab™ program of the non-recursive “melange_ p_dans_n_non_recursif” is given below. The header is the same as the function header “melange_p_dans_n” (Table B3): function [M,place_carte] = melange_p_dans_n_non_recursif(P1,P2) n1 = length(P1); n2 = length(P2); nb_cartes_restantes = n1 ; nb_tour_while = 0 ; while (nb_cartes_restantes > 0) nb_tour_while = nb_tour_while + 1 ; clear M ; clear place_carte ; if (nb_tour_while == 1) [M,place_carte] = melange_1_dans_n(0,P1(1,n1),P2); else carte_dessus = P1(1,n1-nb_tour_while+1); tab = size(Mi); nb_ligne_Mi = tab(1); for i=1:nb_ligne_Mi [Mii,place_carte_ii] =melange_1_dans_n(place_carte_i(i),carte_dessus,Mi(i,:)); if (i == 1) M=Mii; place_carte = place_carte_ii; else M=vertcat(M,Mii); place_carte = horzcat(place_carte,place_carte_ii); end clear Mii clear place_carte_ii end end Mi = M ; place_carte_i = place_carte ; nb_cartes_restantes = nb_cartes_restantes - 1 ; end Matlab™ program 6. Recursive function: “melange_p_dans_n_non_recursif”. Table B3. Header of the Matlab™ program “mealnge_1_dans_n.m”. Synopsis The program generates all possible riffle shuffles between the card c1 and P2 under the ith card of P2. P2 Card deck (the first card in the table is the upper one!). i Position limit in P2 for the inserted card c1. Input c1 Inserted card in P2. place_carte Table of the last inserted card position in the shuffle. Output M Shuffles Matrix (one horizontal line = one shuffle). Local n2 Card number of deck fin Last possible position for the insertion of c1. Copyright © 2012 SciRes. 555  P. SCHOTT Copyright © 2012 SciRes. 556 To Generate All of the Possible Riffle Shuffles between an 1 Card Deck and a q Card Deck [M0(1,q)]: The “if-then-else” and “FOR” Loop: “melange_1_dans_n.m” function [M,place_carte] = melange_1_dans_n(i,c1,P2) n2 = length(P2) ; if (i == 0) fin = n2 + 1; elseif (i > n2+1) fin = n2 + 1; else fin = i; end s for k=1:fin place_carte(k) = k ; if (k==1) M(k,1) = c1; M(k,2:n2+1) = P2(1,:); elseif (k==n2+1) M(k,1:n2) = P2(1,:) ; M(k,n2+1) = c1 ; else M(k,1:k-1) = P2(1,1:k-1) ; M(k,k) = c1 ; M(k,k+1:n2+1) = P2(1,k:n2) ; end end end Matlab™ program 7. Function “melange_1_dans_n”.
|