Engineering, 2010, 2, 432-437
doi:10.4236/eng.2010.26056 Published Online June 2010 (http://www.SciRP.org/journal/eng)
A Note on the Effect of Negative Poisson’s Ratio on the
Deformation of a Poroelastic Half-Space by Surface Loads
Sunita Rani1, Raman Kumar1, Sarva Jit Singh2
1Department of Mathematics, Guru Jambheshwar University of Science and Technology, Hisar, India
2 Honorary Scientist, Indian National Science Academy, New Delhi, India
Received January 8, 2010; revised March 4, 2010; accepted March 9, 2010
Abstract
The aim of this note is to study the effect of negative Poisson’s ratio on the quasi-static deformation of a
poroelastic half-space with anisotropic permeability and compressible fluid and solid constituents by surface
loads. Two particular cases considered are: two-dimensional normal strip loading and axisymmetric normal
disc loading. It is found that a negative Poisson’s ratio makes the Mandel-Cryer effect more prominent. It
also results in an increase in the magnitude of the surface settlement.
Keywords: Anisotropic Permeability, Auxetic Material, Negative Poisson’s Ratio, Poroelastic Half-Space,
Quasi-Static Deformation, Surface Loading
1. Introduction
A homogeneous, isotropic, poroelastic medium can be
characterized by four constitutive parameters. Let these
parameters be: the shear modulus (G), the drained Pois-
son’s ratio (
 ), the undrained Poisson’s ratio ( 
u) and the
Biot-Willis coefficient (
 ), with –1    
u  0.5. For
highly compressible pore fluid
 = 
u and for incom-
pressible fluid and solid constituents

u = 0.5. Materials
with negative Poisson’s ratio were unknown until Lakes
[1] showed that such materials can be artificially created.
In a series of papers, Lakes and his coworkers have in-
vestigated interesting properties of materials with nega-
tive Poisson’s ratio. Negative Poisson’s ratio materials
are also called auxetic materials or auxetics [2]. Yang
et al. [3] presented a review on auxetic materials.
The dynamic behaviour of auxetic materials has been
studied by many investigators. The effect of negative
Poisson’s ratio on several dynamic problems of elasticity
was studied by Lipsett & Beltzer [4]. Chen & Lakes [5]
examined possible use of auxetic materials for viscoelas-
tic damping applications. Freedman [6] studied the effect
of negative Poisson’s ratio on Lamb modes in a free
plate. Chen & Lakes [7] compared the dynamic wave
dispersion and loss properties of conventional and auxetic
polymeric cellular materials. Scarpa et al. [8] claim an
overall superiority regarding damping and acoustic pro-
perties of auxetic polyurethane foams as compared to the
original conventional foam. They suggest possible use of
auxetic foams in the field of antivibration pads and
gloves. Auxetic materials also offer very good sound and
vibration absorption and could have many applications in
aerospace and defence areas.
Ting & Barnett [9] derived simple necessary and suf-
ficient conditions on elastic compliances to identify if
any given anisotropic material of cubic or hexagonal
symmetry is completely auxetic or nonauxetic. Stability
of an elastic material with negative stiffness and negative
Poisson’s ratio has been discussed by Shang & Lakes
[10]. In a recent paper, Kocer et al. [11] investigated the
properties of a layered composite, with alternating layers
of materials with negative and positive Poisson’s ratio.
They observed an increase in the resistance to mechani-
cal deformation above the average value of the two con-
stituent materials. Therefore, it might be possible to fab-
ricate materials, with a designed microstructure, using
both conventional and auxetic materials, for specific en-
gineering applications. Possible applications of auxetic
materials are based on their superior toughness, shear
resistance, indentation resistance and fracture toughness.
Motivation for the present study was provided by Ku-
rashige et al. [12]. Foams with negative Poisson’s ratio
are being considered as possible future advanced materi-
als for a variety of applications. Further, poroelastic ma-
terials have interesting properties due to coupling be-
tween elastic skeletel deformation and pore fluid diffu-
sion. It is, therefore, useful to study the response of foam
to sudden loading if it possesses a negative Poisson’s

S. RANI ET AL.433
ratio and is saturated with a fluid.
Kurashige et al. [12] studied four Mandel and Cryer
problems for fluid-saturated auxetic foams, assuming the
displacement field as irrotational. Sawaguchi and Kura-
shige [13] studied the transient response of a poroelastic
circular cylinder subjected to axial compression with a
constant strain rate. They showed that if the Poisson’s
ratio of the cylinder is negative, the surface of the cylin-
der extends in the tangential direction immediately after
loading but stops extending after a while. Thereafter, the
surface of the cylinder experiences tangential contraction.
The purpose of the present note is to study numerically
the effect of negative Poisson’s ratio on the diffusion of
the pore pressure and time-settlement of a poroelastic
half-space with anisotropic permeability and compressi-
ble fluid and solid constituents by two-dimensional strip
loading or axisymmetric disc loading. For this purpose,
we use the analytical expressions for the pore pressure
and the vertical displacement derived recently by Singh
et al. [14,15] and calculate these quantities by numerical
integration.
2. Theory
2.1. Normal Strip Loading
Consider a strip –L  x  L of infinite length in the
y-direction on the surface of a permeable poroelastic
half-space z  0. Let a normal load

0 per unit length
acting in the positive z-direction be uniformly distributed
over the strip. Then the Laplace transform of the pore
fluid pressure at any point of the half-space is given by
Singh et al. [14]
0
0
=
() sin
()cos








—
—
-mz -kz
u
p
ννsσk+m kL
eekx d
πηΩ kL k

(1)
where
s = Laplace transform variable
1-2
=2(1- )
ν
ηα
ν
12
2 1
33
cs
mk
cc




c1 = hydraulic diffusivity in the horizontal direction
c3 = hydraulic diffusivity in the vertical direction
 = s ( 
u –
 ) (k – m) – sa (1 – 
u) (k + m)
sa = s + (c1 – c3) k2. (2)
We are assuming the half-space to be poroelastic with
anisotropic permeability and compressible fluid and solid
constituents. In the particular case of isotropic perme-
ability, c1 = c3. For incompressible fluid and solid con-
stituents,
 = 1, 
u = 0.5.
On taking the limit s  , we get the pore pressure
for the undrained state (fast loading, short-term behav-
iour). In this case, the integral appearing in (1) can be
evaluated analytically, yielding
1 0
222
() 2
tan
(12 )
u
u
Lz
pLzxL








. (3)
In (3) it is assumed that z > 0, x2 + z2  L. However, if
x2 + z2 < L2, we must add  to tan–1 ( ) term appearing in
(3).
2.2. Normal Disc Loading
Suppose a total normal load Q0 is uniformly applied in
the positive z-direction over a circular surface area (z = 0,
r  a) of a radius with its centre at the origin. If the sur-
face (z = 0) of the half-space is permeable, the Laplace
transform of the pore fluid pressure given by Singh et al.
[15] is
0
01
0
=
() ()()() .








-mz -kz u
p
ν-νsQ m+k
e-e JkrJkadk
πaηΩ
(4)
The vertical (down) displacement in the Laplace trans-
form domain is
  
0
0
() 1
-1
2








-mz -kz u
uau
w=
Qν-νms e-e sν-ν+s -ν
πaGk -m


×-1-1- 





-kz -kz
ua
m+k
m+k zeννse
k

01
1
×.
J
kr Jkadk
Ω (5)
On taking the limit s and evaluating the integrals
we get the pore pressure and the vertical displacement
for the undrained state in the form

 

+1
2
0
222
=0
=
2-1
1- 4+
2n 1
n









u
n
n
u
n
p
ν-νQa
πaην rz
2+1 22
×
+




n
z
P
zr


, (6)


+1
2
22
=0
=-1
4+
2n 1
n



 








n
n
0
u
n
Qza
wπaG arz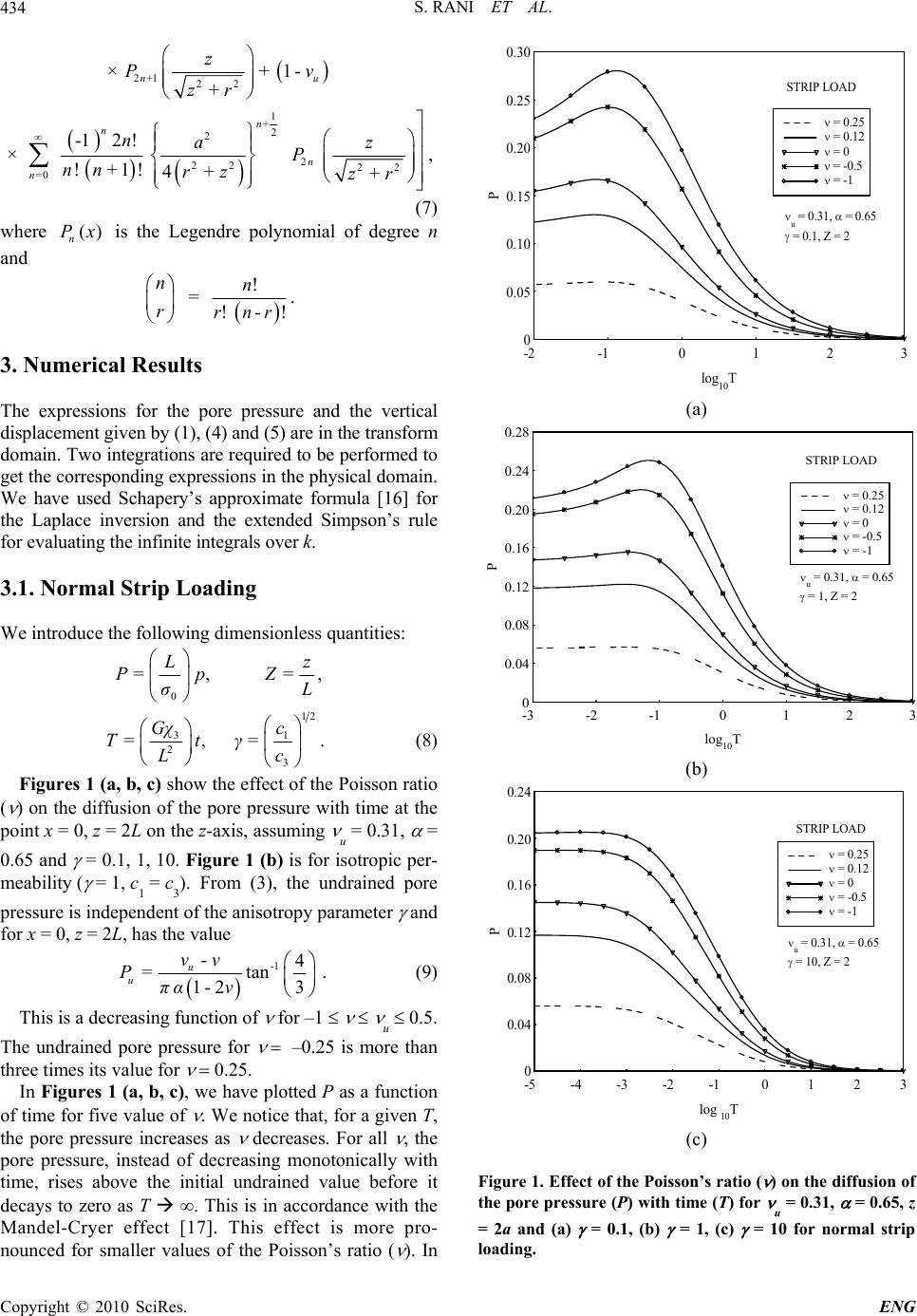

S. RANI ET AL. 434

2+1 22
×+
+




nu
z
Pν
zr
1-



1
+2
2
2
22 22
=0
-12 !
×!+1!
4+ +










 
 

n
n
n
n
naz
P
nn rz zr
,
(7)
where is the Legendre polynomial of degree n
and
()
n
Px



n
r =

!
!-
n
rnr!
.
3. Numerical Results
The expressions for the pore pressure and the vertical
displacement given by (1), (4) and (5) are in the transform
domain. Two integrations are required to be performed to
get the corresponding expressions in the physical domain.
We have used Schapery’s approximate formula [16] for
the Laplace inversion and the extended Simpson’s rule
for evaluating the infinite integrals over k.
3.1. Normal Strip Loading
We introduce the following dimensionless quantities:
0
=, =



Lz
PpZ
σL,
12
31
2
3
=,=. (8)

 

 
Gχc
Ttγc
L
Figures 1 (a, b, c) show the effect of the Poisson ratio
(  ) on the diffusion of the pore pressure with time at the
point x = 0, z = 2L on the z-axis, assuming

u = 0.31,
 =
0.65 and  = 0.1, 1, 10. Figure 1 (b) is for isotropic per-
meability (  = 1, c1 = c3). From (3), the undrained pore
pressure is independent of the anisotropy parameter  and
for x = 0, z = 2L, has the value

-1 4
=tan
1-23



u
u
ν-ν
Pπα ν.
(9)
This is a decreasing function of
 for –1    
u  0.5.
The undrained pore pressure for   –0.25 is more than
three times its value for
 0.25.
In Figures 1 (a, b, c), we have plotted P as a function
of time for five value of
 . We notice that, for a given T,
the pore pressure increases as
 decreases. For all  , the
pore pressure, instead of decreasing monotonically with
time, rises above the initial undrained value before it
decays to zero as T  . This is in accordance with the
Mandel-Cryer effect [17]. This effect is more pro-
nounced for smaller values of the Poisson’s ratio (
 ). In
0
0.05
0.10
0.15
0.20
0.25
0.30
-2 -10 1 2 3
 = 0.25
 = 0.12
 = 0
 = -0.5
 = -1
STRIP LOAD

u
= 0.31,  = 0.65
 = 0.1, Z = 2
log10T
P
(a)
0
0.04
0.08
0.12
0.16
0.20
0.24
0.28
-3 -2 -1 0 1 2 3
 = 0.25
 = 0.12
 = 0
 = -0.5
 = -1

u
= 0.31,  = 0.65
 = 1, Z = 2
STRIP LOAD
log
10
T
P
(b)
0
0.04
0.08
0.12
0.16
0.20
0.24
-5 -4 -3-2 -1 0 1 2 3
 = 0.25
 = 0.12
 = 0
 = -0.5
 = -1

u
= 0.31,  = 0.65
 = 10, Z = 2
STRIP LOAD
log 10T
P
(c)
Figure 1. Effect of the Poisson’s ratio (  ) on the diffusion of
the pore pressure (P) with time (T) for 
u = 0.31,
 = 0.65, z
= 2a and (a)  = 0.1, (b)  = 1, (c)  = 10 for normal strip
loading.

S. RANI ET AL.435
particular, the Mandel-Cryer effect is much more promi-
nent for a poroelastic half-space with a negative Pois-
son’s ratio (
 ) than for a poroelastic half-space with a
positive
 .
Figures 2 (a, b, c) show the depth profile of the pore
0
2
4
6
8
10
00.09 0.18 0.27 0.36 0.4
5
 = 0.25
 = 0.12
 = 0
 = -0.5
 = -1

u
= 0.31,  = 0.65
 = 0.1, T = 0.1
STRIP LOAD
Z
P
(a)
0
2
4
6
8
10
00.09 0.18 0.27 0.36 0.45
 = 0.25
 = 0.12
 = 0
 = -0.5
 = -1
u = 0.31,  = 0.65
 = 1, T = 0.1
STRIP LOAD
Z
P
(b)
0
2
4
6
8
10
00.03 0.06 0.09 0.12 0.15
 = 0.25
 = 0.12
 = 0
 = -0.5
 = -1
u = 0.31,  = 0.65
 = 10, T = 0.1
STRIP LOAD
Z
P
(c)
Figure 2. Effect of the Poisson’s ratio on the depth profile of
the pore pressure at T = 0.1 for 
u = 0.31,
 = 0.65 and (a) 
= 0.1, (b)
 = 1, (c)  = 10 for normal strip loading.
pressure for 
u = 0.31,
 = 0.65, T = 0.1 and  = 0.1, 1,
10 for five values of  . The pore pressure is zero at the
surface, attains a maximum at a depth depending upon

and T and then tends to zero as Z  ∞. Here again, we
notice that, at all depths, the pore pressure increases as 
decreases.
3.2. Normal Disc Loading
We introduce the following dimensionless quantities:
2
00
=,= ,
 
 
 
πaπaG z
PpWwZ
QQ
=
a
12
31
2
3
=
χGc
T=t γc
a

 

 
,. (10)
Figures 3 (a, b, c) show the time-settlement at the
centre of the disc load (r = 0, z = 0) for

u = 0.31,
 =
0.65,  = 0.1, 1, 10 for five values of  = –1, –0.5, 0, 0.12,
0.25. For t > 0, as
 decreases, the surface settlement
increases. In particular, the surface settlement for a half-
space with a negative Poisson’s ratio (  ) is much more
than for a half-space with a positive
 . The undrained
surface settlement is independent of the Poisson’s ratio
 .
Figures 4 (a, b, c) display the influence of the Pois-
son’s ratio (
 ) on the diffusion of the pore pressure with
time at the point r = 0, z = 2a on the axis of symmetry for
three values of the anisotropy parameter  = 0.1, 1, 10.
From (6), the undrained pore pressure at the point r = 0, z
= 2a is
Pu =



21
0
21
1
1
12 4



















n
n
u
n
n
n


=




24 5
12
u



 (11)
which is a decreasing function of  for –1    
u  0.5.
The pore pressure vanishes in the drained state (slow
loading, long-term behaviour). As in the case of normal
strip loading, we notice that the pore pressure increases
as the Poisson’s ratio decreases. The effect of a decrease
in  is to enhance the Mandel-Cryer effect. In particular,
in a poroelastic half-space with a negative Poisson’s ratio
(  ), this effect is much more prominent than for a poroe-
lastic half-space with a positive  .
4. Conclusions
For almost all common materials the Poisson’s ratio is
positive. However, in 1987, R. S. Lakes showed that
materials possessing negative Poisson’s ratio can be arti-
ficially created. We have studied the effect of negative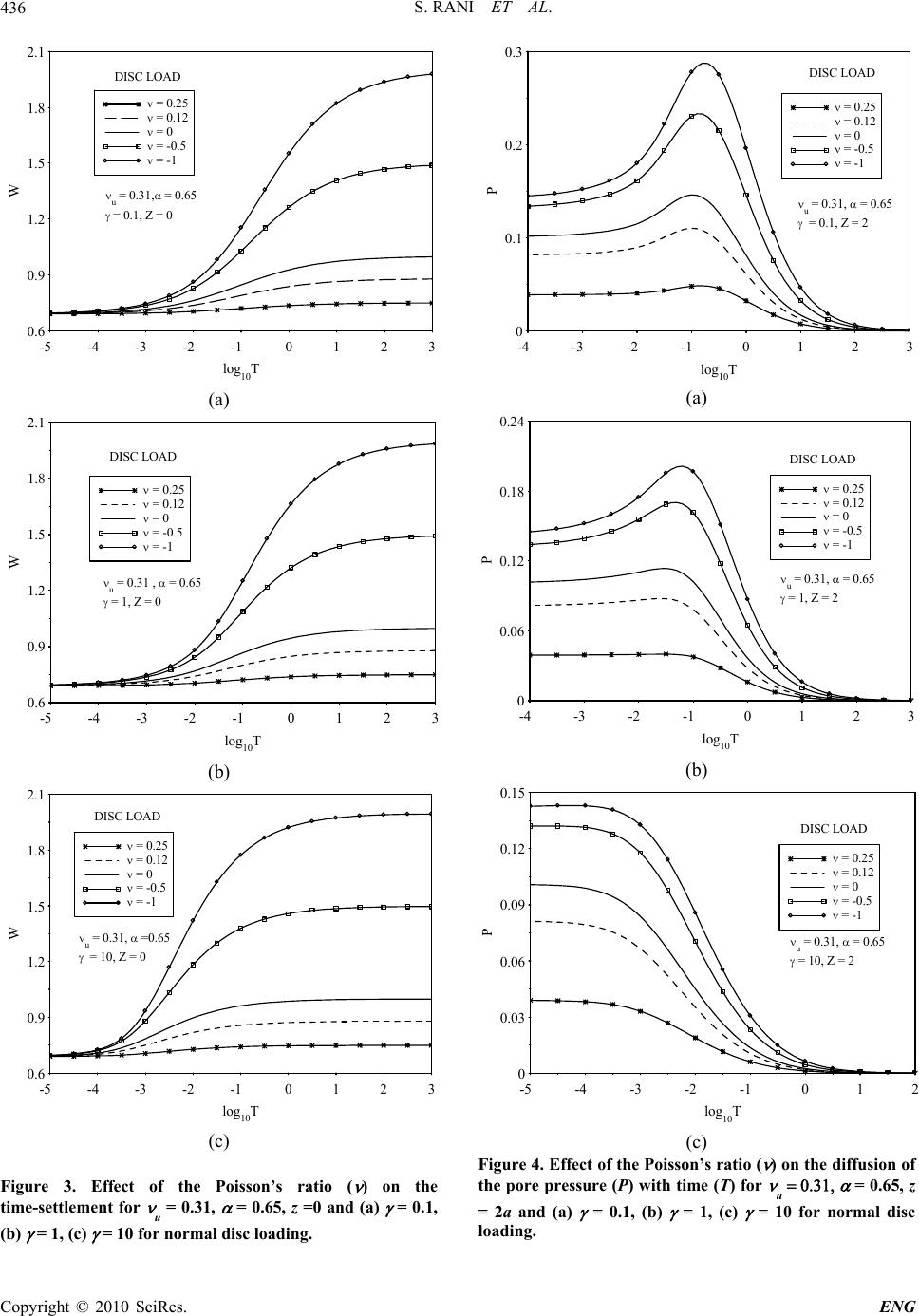

S. RANI ET AL. 436
0.6
0.9
1.2
1.5
1.8
2.1
-5 -4 -3 -2 -10123
 = 0.25
 = 0.12
 = 0
 = -0.5
 = -1
DISC LOAD

u
= 0.31,  = 0.65
 = 0.1, Z = 0
log
10
T
W
(a)
0.6
0.9
1.2
1.5
1.8
2.1
-5 -4-3 -2-10123
 = 0.25
 = 0.12
 = 0
 = -0.5
 = -1
DISC LOAD

u
= 0.31 ,  = 0.65
 = 1, Z = 0
log
10
T
W
(b)
0.6
0.9
1.2
1.5
1.8
2.1
-5 -4 -3 -2 -1 0 12 3
 = 0.25
 = 0.12
 = 0
 = -0.5
 = -1
DISC LOAD

u
= 0.31,  =0.65
 = 10, Z = 0
log
10
T
W
(c)
Figure 3. Effect of the Poisson’s ratio (  ) on the
time-settlement for 
u = 0.31,
 = 0.65, z =0 and (a)  = 0.1,
(b)
 = 1, (c)  = 10 for normal disc loading.
0
0.1
0.2
0.3
-4 -3 -2 -10 1 2 3
 = 0.25
 = 0.12
 = 0
 = -0.5
 = -1
DISC LOAD

u
= 0.31,  = 0.65
 = 0.1, Z = 2
log
10
T
P
(a)
0
0.06
0.12
0.18
0.24
-4 -3 -2 -1 0 1 2 3
 = 0.25
 = 0.12
 = 0
 = -0.5
 = -1
DISC LOAD

u
= 0.31,  = 0.65
 = 1, Z = 2
log
10
T
P
(b)
0
0.03
0.06
0.09
0.12
0.15
-5 -4 -3-2-10 1 2
 = 0.25
 = 0.12
 = 0
 = -0.5
 = -1
DISC LOAD

u
= 0.31,  = 0.65
 = 10, Z = 2
log
10
T
P
(c)
Figure 4. Effect of the Poisson’s ratio (  ) on the diffusion of
the pore pressure (P) with time (T) for

u
   = 0.65, z
= 2a and (a)  = 0.1, (b)  = 1, (c)  = 10 for normal disc
loading.

S. RANI ET AL. 437
Poisson’s ratio on the consolidation of a poroelastic
half-space by the surface loads. It has been observed that
in case of negative Poisson’s ratio, Mandel-Cryer effect
is more pronounced. It also results in an increase in the
magnitude of the surface settlement.
5. Acknowledgements
SJS thanks the Indian National Science Academy for
financial support.
6
. References
[1] R. S. Lakes, “Foam Structures with a Negative Poisson’s
Ratio,” Science, Vol. 235, No. 27, 1987, pp. 1038-1040.
[2] B. D. Caddock and K. E. Evans, “Microporous Materials
with Negative Poisson’s Ratios: I. Microstructure and
Mechanical Properties,” Journal of Physics D: Applied
Physics, Vol. 22, No. 12, 1989, pp. 1877-1882.
[3] W. Yang, Z.-M. Li, W. Shi, B.-H. Xie and M.-B. Yang,
“Review on Auxetic Materials,” Journal of Materials
Science, Vol. 39, No. 10, 2004, pp. 3269-3279.
[4] A. W. Lipsett and A. I. Beltzer, “Reexamination of Dy-
namic Problems of Elasticity for Negative Poisson’s Ra-
tio,” The Journal of the Acoustical Society of America,
Vol. 84, No. 6, 1988, pp. 2179-2186.
[5] C. P. Chen and R. S. Lakes, “Dynamic Wave Dispersion
and Loss Properties of Conventional and Negative Pois-
son’s Ratio Polymeric Cellular Materials,” Cellular Poly-
mers, Vol. 8, No. 5, 1989, pp. 343-359.
[6] A. Freedman, “The Variation, with the Poisson’s Ratio,
of Lamb Modes in a Free Plate, I, General Spectra,”
Journal of Sound and Vibration, Vol. 137, No. 2, 1990,
pp. 209-230.
[7] C. P. Chen and R. S. Lakes, “Micromechanical Analysis
of Dynamic Behavior of Conventional and Negative Pois-
son’s Ratio Foams,” Journal of Engineering Materials
and Technology, Vol. 118, 1996, pp. 285-288.
[8] F. Scarpa, L. G. Ciffo and J. R. Yates, “Dynamic Proper-
ties of High Structural Integrity Auxetic Open Cell
Foam,” Smart Materials and Structures, Vol. 13, No. 1,
2004, pp. 49-56.
[9] T. C. T. Ting and D. M. Barnett, “Negative Poisson’s
Ratios in Anisotropic Linear Elastic Media,” Journal of
Applied Mechanics, Vol. 72, No. 6, 2005, pp. 929-931.
[10] X. Shang and R. S. Lakes, “Stability of Elastic Material
with Negative Stiffness and Negative Poisson’s Ratio,”
Physica Status Solidi B, Vol. 244, No. 3, 2007, pp.
1008-1026.
[11] C. Kocer, D. R. McKenzie and M. M. Bilek, “Elastic
Properties of a Material Composed of Alternating Layers
of Negative and Positive Poisson’s Ratio,” Materials
Science and Engineering: A, Vol. 505, No. 1-2, 2009, pp.
111-115.
[12] M. Kurashige, M. Sato and K. Imai, “Mandel and Cryer
Problems of Fluid-Saturated Foams with Negative Pois-
son’s Ratio,” Acta Mechanica, Vol. 175, No. 1-4, 2005,
pp. 25-43.
[13] H. Sawaguchi and M. Kurashige, “Constant Strain-Rate
Compression Test of a Fluid-Saturated Poroelastic Sam-
ple with Positive or Negative Poisson’s Ratio,” Acta
Mechanica, Vol. 179, No. 3-4, 2005, pp. 145-156.
[14] S. J. Singh, S. Rani and R. Kumar, “Quasi-Static Defor-
mation of a Poroelastic Half-Space with Anisotropic Per-
meability by Two-Dimensional Surface Loads,” Geo-
physical Journal International, Vol. 170, No. 3, 2007, pp.
1311-1327.
[15] S. J. Singh, R. Kumar and S. Rani, “Consolidation of a
Poroelastic Half-Space with Anisotropic Permeability and
Compressible Constituents by Axisymmetric Surface Load-
ing,” Journal of Earth System Science, Vol. 118, No. 5,
2009, pp. 563-574.
[16] R. A. Schapery, “Approximate Methods of Transform
Inversion for Viscoelastic Stress Analysis,” Proceedings
4th US National Congress on Applied Mechanics, Berkely,
USA, 1962, pp. 1075-1085.
[17] C. W. Cryer, “A Comparison of the Three-Dimensional
Consolidation Theories of Biot and Terzaghi,” The Quar-
terly Journal of Mechanics and Applied Mathematics,
Vol. 16, No. 4, 1963, pp. 401-412.