Journal of Minerals & Materials Characterization & Engineering, Vol. 11, No.3, pp.321-333, 2012
jmmce.org Printed in the USA. All rights reserved
321
Interlaminar Fracture Toughness and Low-V el oc ity Impac t R esi st an ce of
Woven Glass Epoxy Composite L amin ates of EP3 Grade
N. Rajesh Mathivanan*1, J. Jerald 2
1Department of Mechanical Engg., P. E. S. Institute of Technology, Bangalo r e - 85, India
2Dept. of Production Engg., N ational Institute of Technology, Tiruchirappalli - 15, India
*Corresponding Author: [e-mail]
ABSTRACT
This work presents the delamination resistance of woven glass fibre reinforced polymers
(GFRP) and its influence on GFRP’s resistance to point impact. Two different types of
laminates were fabricated by hand lay-up technique; (i) woven glass fibre epoxy matrix
laminates and (ii) woven glass fibre epoxy matrix laminates with 3% graphite particulate
fillers. End Notch Flexure (ENF) test was adopted for the measurement of delamination
resistance. The two GFRPs laminates show similar mode II delamination resistance. At
impact velocities between 2.215 and 4.429 m/sec, the GFRP developed a smaller damage size
than the graphite-based GFRP laminates, indicating higher impact toughness. Difference of
the impact resistance between the two GFRPs is mainly on the impact damage size
developed. The total energy absorbed during the impact remains the same, which is
independent of mode II delamination resistance of the GFRP. The history of relevant dynamic
and energetic quantities, both to synthesize the dependency of the energy parameters and
force threshold values on the impact velocity are discussed.
Keywor d s: Polymer matrix composite; Fibre; Laminates; Impact toughness.
1. INTRODUCTIO N
There has been a growing interest in the use of composite materials in structural applications
like automotive, marine, aircraft and space structures because of their high specific tensile
and compressive strengths, good fatigue and corrosion resistance properties. However, the
response of composite structures can be greatly affected by the presence of failure modes
such as delaminations, matrix cracks and fibre fracture, which are typical failures of
laminated composite materials [1]. Studies on the impact response of composite materials and
structures can be found in review papers [2–3]. The presence and growth of delamination in

322 N. Rajesh Mathivanan, J Jerald Vol.11, No.3
laminates significantly reduces the compressive load-carrying capacity of a structure and
causes initiation of catastrophic failure [4]. Therefore, it is very important to consider
delamination failure when designing composite structures. Even though fibre fracture is the
ultimate failure mode, the damage would initiate in the form of matrix cracking/lamina
splitting and would lead to delamination. Damage-free composites are necessary for their
effective use [5].
Impact damage is generally not considered to be a threat in metal structures because, owing
to the ductile nature of the m at erial , l ar ge am ou nt s o f ener gy may be absor bed. At yield st res s
the material may flow for very large strains (up to 20%) at constant yield before work
hardening. In contrast, composites can fail in a wide variety of modes and contain barely
visi ble im pact dam age ( BVID) whi ch nev erthel ess sever ely r educes the s tru ctural i nte grit y of
the component. Most composites are brittle and so can only absorb energy in elastic
deformation and through damage mechanisms, and not b y plastic deformat ion. Effect of low-
velocit y impact response on woven glass fibre epox y matrix composite laminates at different
velocities on various thicknesses is presented in the earlier work [6]. Zhang and Richardson
[7] revealed that there was a significant reduction in flexural properties due to the impact-
induced damage and that the residual flexural strength is more susceptible to damage than
residual modulus. Choi et al., [8] suggested that both the opening mode (mode I) and the in-
plane shear mode (mode II) are involved in the delamination of the laminates under impact is
initiated by matrix cracking. Razi and Kobayashi [9] analyzed the energy required for the
delamination growth in mode II using a simplified line-loading condition with (0/90/0) fibre
layup to suppress initiation of bending cracks. On the other hand, Sun and Manoharan [10],
using (90/0/90) fibre reinforcement, investigated the delamination growth in mode I.
Compston et al. [11] indicated that there was no significant effect of loading rate or matrix
toughness on GIIC. However, they concluded that failure is interface controlled, whereby
unstable fracture is initiated after a similarl y short period of crack growth in each composite,
and before an increase in GIIC as a result of increased matrix toughness becomes apparent.
Under the same impact conditions, Jar et al. [12-13] reported that variation of the matrix
toughness did not affect the total energy absorbed during the impact, only causing difference
in the damage size development. Therefore, the impact toughness is deemed to vary with the
matrix toughness only if the impact toughness is defined as the energy absorbed per unit
damage area. This, however, requires a tremendous effort to quantify the damage size in the
test coupons.
In this paper, the delamination resistance and impact resistance of the woven GFRP of EP3
grade and graphite-based GFRP laminates were characterized using static mode II
delamination tests and drop-weight impact tests. The results elucidate the role of
delamination resistance on the GFRP’s impact behaviour.
2. EXPERIMENTAL PRO CEDURE
2.1. Materials and Specimen Fabrication

Vol.11, No .3 Interlaminar fracture toughness and low-velocity 323
Two different types of laminates were fabricated; (i) woven glass fi b re epoxy matrix
laminates of EP3 Grade and (ii) woven glass fibr e epoxy matrix laminates with 3% graphite
particulate fillers. The laminates were fabricated by dry hand la y-up technique at Reinforced
Plastics Industries, Bangalore. Hand lay-up technique was chosen as it was ideally suited to
manufacture low volume with minimum tooling cost. Fabrication p rocess involves four basic
steps: lay-up, wetting/impregnation, consolidation, and solidification. E-glass plain weave
roving fabric, which is compatible to epoxy resin, is used as the reinforcement. Araldite LY
556 epoxy resin with HY 951 grade room temperature curing hardener with diluent DY 021
(all supplied by Hindustan Ciba Geigy) mix was employed for the matrix material. Graphite
powder is a fine black powder that can be mixed with epoxy resin to produce low friction
exterior surfaces, commonly used on boat bottoms, rudders and centerboards. Graphite
powders were dispersed into araldite LY 556 epoxy resin with a novel and si mple setup. The
resin consisting of 3% graphite powders were agitated at 400 rpm, to ensure proper mixing.
Composite laminates were form ed by pla cin g su cc ess iv e layers of th e fi b re and resin mixture.
Each fabric layer was wetted with resin mixture using a squeezing plate for proper
impregnation. The squeezing plates were used to remove excess resin and air, which results
in compaction of the plies. During lay-up, each ply is impregnated with an epoxy resin
mixture with graphite particulate filler. The purpose of this step is to make sure that the resin
flows entirely around all fibres. Consolidation is a very important step in obtaining a good
quality part. During this step, intimate contact between each layer of the lamina is formed,
which ensures that all the entrapped. Vacuum [550 Hg/mm²] was applied through vacuum
valve at one corner of th e s ystem, which helps in air evacuation, to draw out the air between
the plies. The system is allowed for ambient cure along with vacuum pressure. The bagged
part was then placed in an oven and cured under the specified time, temperature and pressure.
The final step is solidification, which may take up to 120 min for thermosets. In thermoset
resins, usually the higher the cure temperature, the faster is the cross-linking process. The
temperature was maintained at 80°C for the first 2 hrs and then 120°C for another 2 hrs and
later allowed to cool at room temperature.
2.2. Mechanical Tests
2.2.1. Tensile test
Tensile specimens 250 mm long and 2 mm thick with a gauge length of 50 mm and width of
25 mm were prepared and the end tabs fixed to the specimens. Tensile tests were performed
on a FIE servo-hydraulic universal testing machine at a crosshead rate of 5 mm/min which
corresponds to a strain rate of 0.2% per second. The strains were recorded with strain gauge s.
At least three tests w ere carried out fo r ea ch cas e. Fig. 1 shows the geometr y of the sp ecimen
and Fig. 2 shows the specimen before and after tensile testing.

324 N. Rajesh Mathivanan, J Jerald Vol.11, No.3
Figure 1 Dimensions of tensile test specimen
Figure 2 Tensile test specimens before and after tensile testing
2.2.2 End Notch Flexure (ENF) test
Several test methods are widely used to quantify the delamination resistance, among which
End Notch Flexure (ENF) test is being adopted as an international standard for the
measurement of mode II delamination resistance. The 3-point bending is the common mode
used to induce fracture, b ut yet acc ept ed as a st andard [ 14] . Never th eles s, the 3-point bending
test on specimens with an end-notched defect, kn own as end notch flex ure test, has b een used
by many researchers to assess composites’ mode II delamination resistance. FIE universal
testing machine was used for the ENF tests, with a crosshead speed of 5 mm/min. At least
three specimens were tested for each condition to ensure reproducibility of the results. The
sample did not break into two fragments, demonstrating a true composite ‘‘pseudo-plastic’’
behaviour. Fig. 3 shows the specimen mounted on FIE UTM and Fig. 4 shows the schematic
sketch for the set-up and the specimen dimensions used for the ENF test [15],
Figure 3 Experimental set-up with data acquisition system
.

Vol.11, No .3 Interlaminar fracture toughness and low-velocity 325
Figure 4 Schematic diagrams of the set-up for ENF test
The mode II ENF test provides the critical strain energy release rate (GIIC) based on the
modified beam theory method [16]:
32
22
16
9
EhB
Pa
GIIC =
(1)
3
3
4BCh
L
E=
(2)
where ‘‘a’’ is the crack length in m, P the force in N, B the specimen width in , L half the
span length in m, h half the specimen thickness in m, and 1/C the initial slope of the load-
displacement plot in N/m. The GIIC values obtained from each ENF specimen are calculated
from the first nonlinear point on the force-displacement curve using eq. (1-2). It should be
noted that some stable crack growth has occurred in ENF test of graphite-based GFRP, after
the force reached the maximum point, followed by unstable crack growth that caused
significant drop of the force. For the ENF test of the GFRP, on the other hand, unstable crack
growth occurred immediately after the force reached the maximum point.
2.2.3 Low-velocity impact testing.
The falling weight impact test is employed for low-velocit y ranges and is used to investi gate
the impact behavior under lower acceleration. This type of impact tests helps to understand
the behavior of materials when they are subjected to impact loads. The tests were performed
using an instrumented falling weight testing machine with no energy storage device: the
maximum impact energy is limited by the adjustable falling height (up to a maximum of
about 1500 mm) and the fix ed mass, 10 kg, of the impactor. This gives up to a peak of about
150 J of energy with an impact velocit y of 6.25 m/s completely supplied by the gravitational
field. The impactor mass together with the height of drop determines the energy of impact.
Wit h an increase in m ass and height the potential energy of the dart will increase and thus on
releasing the tool holding assembly the potential energy is converted to kinetic energy. The
dart material used was steel.
In accordance with ASTM D 3029 standard, a batch of square (150 mm side; 2 mm thick)
specimens was clamped on a fixture with a slot (sq 100 mm). The dart had a hemispherical
B (~ 20 mm)
2h
(~ 6 mm)
2L (~ 10 0 mm)
a0 (~ 25 mm)
P

326 N. Rajesh Mathivanan, J Jerald Vol.11, No.3
head of 10 mm diameter; the piezoelectric load cell is placed at the other extremity of the
calibrated cylindrical rod that constitutes the dart, at which the pushing mass was connected.
Fig. 5 shows the specimen clamping apparatus, specifically designed in order to assure the
constancy of the clamping force, through the pre-loading of four helical springs. A fixed
impactor mass of 15.69 N with the dart was released from varying heights; 0.25, 0.5 and 1 m
were considered. The vertical guides of the impact tower were lubricated frequently to
minimize any friction generated during the descent of the impactor.
Figure 5 Specimen clamping apparatus
3. RESULTS AND DISCUSSION
From the tensile test results (Table 1), it can be concluded that the tensile strength of
graphite-based GFRP laminate are higher than that of woven GFRP laminate (by 11%). The
inclusion of graphite particulate fillers in epox y resin increases the tensile modulus and hence
the stiffness. A typical stress–strain plot for both the specimens is presented in Fig. 6. The
specimen was separated into two parts during loading at a strain as indicated by point A. The
failure was observed at the gauge section. The strain corresponding to point A was 0.18 and
0.16 for woven GFRP and graphite-based GFRP laminates, respectively. It is interesting to
note that the laminate perform in a similar fashion whereby their behavior is almost linear
before reaching the peak load. On the other hand, beyond that peak points of the load–
displacement curves majority of the laminate experienced large displacements before
fracture, which proved that these woven laminates are able to absorb large amounts of energy
before fracture. The results have revealed that inclusion of graphite particulate filler directly
affects the distribution of load between the fibres and the matrix.
From the ENF test results the GIIC values suggest that the two GFRP are nearl y identical for
the mode II delamination resistance. The force-deflection curves from the ENF tests, as
shown in Fig. 7, are nearly identical between the two GFRP up to the point of 1100 N, after
which the graphite-based GFRP showed a gradual force drop, while the GFRP showed some
increase of the force before a gradual force drop, but less significant force drop. This is an
indication of a much more stable crack growth in the GFRP. However, calculation of the GIIC
only used data up to the point of the maxi mum force. Therefore, GIIC values i n tabl e 1 do not

Vol.11, No .3 Interlaminar fracture toughness and low-velocity 327
reflect such different fracture behavior.
Figure 6 Stress strain diagrams of woven GFRP and graphite-based woven GFRP laminates
Figure 7 Typical force-deflection curves from the ENF specimens
Table 1: Summary of tensile and ENF test results
Propert ies Woven
GFRP Graphite-based woven GFRP laminate
Density (g/cc) 1.936 1.656
CSA (mm
2
) 69.75 54.47
Tensile load (kN) 19.86 17.22
Tensile strength (MPa) 284.73 316.26
ENF test results
Peak load (kN) 1.28 1.10
Displ acement at peak load (mm) 4.71 3.56
Breaking load (kN) 0.645 0.56
GIIC values (J/m2) 2743.67 2026.27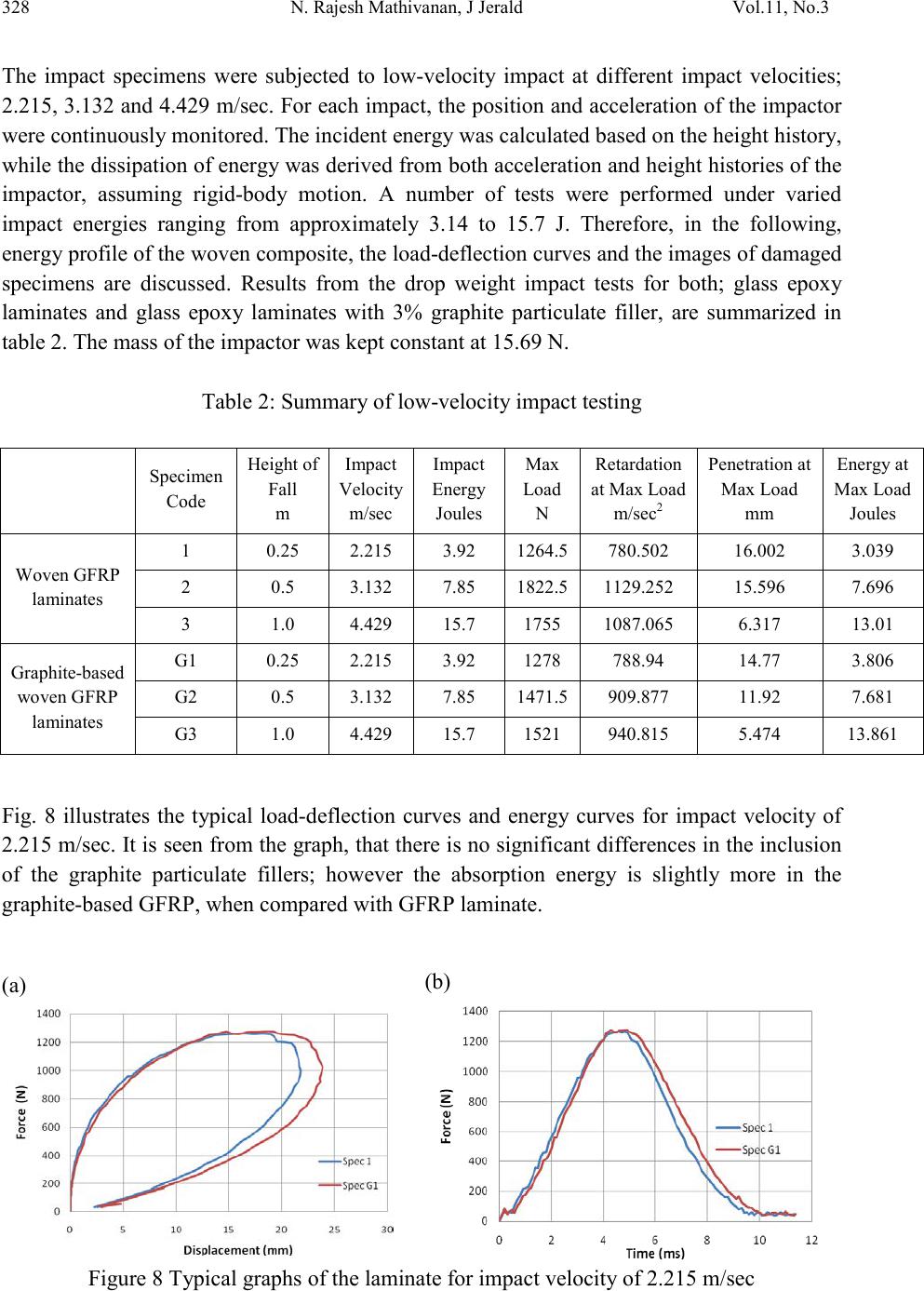

328 N. Rajesh Mathivanan, J Jerald Vol.11, No.3
The impact specimens were subjected to low-velocity impact at different impact velocities;
2.215, 3.132 and 4.429 m/sec. For each impact, the position and acc eleration o f the impactor
were continuously monitored. The incident energy was calculated based on the height history,
while the dissipation of energy was derived from both acceleration and height histories of the
impactor, assuming rigid-body motion. A number of tests were performed under varied
impact energies ranging from approximately 3.14 to 15.7 J. Therefore, in the following,
energy profile of the woven composite, the load-deflection curves and the images of damaged
specimens are discussed. Results from the drop weight impact tests for both; glass epoxy
laminates and glass epoxy laminates with 3% graphite particulate filler, are summarized in
table 2. The mass of the impactor was kept constant at 15.69 N.
Table 2: Summary of low-velocity impact testing
Specimen
Code
Height of
Fall
m
Impact
Velocity
m/sec
Impact
Energy
Jo ules
Max
Load
N
Retardation
at Max Load
m/sec2
Penetratio n at
Max Load
mm
Energy at
Max Load
Jo ules
Wo ven GFR P
laminates
1 0.25 2.215 3.92 1264.5 780.502 16.002 3.039
2 0.5 3.132 7.85 1822.5 1129.252 15.596 7.696
3 1.0 4.429 15.7 1755 1087.065 6.317 13.01
Graphite-based
wove n GFRP
laminates
G1 0.25 2.215 3.92 1278 788.94 14.77 3.806
G2 0.5 3.132 7.85 1471.5 909.877 11.92 7.681
G3 1.0 4.429 15.7 1521 940.815 5.474 13.861
Fig. 8 illustrates the typical load-deflection curves and energy curves for impact velocity of
2.215 m/sec. It is seen from the graph, that there i s no significant differences in the inclusion
of the graphite particulate fillers; however the absorption energy is slightly more in the
graphite-based GFRP , when compared with GFRP laminate.
(a)
(b)
Figure 8 Typical graphs of the laminate for impact velocity of 2.215 m/sec

Vol.11, No .3 Interlaminar fracture toughness and low-velocity 329
Energy profile and damage process impact energy (Ei) and absorbed energy (Ea) are two
main parameters that can be used to assess damage process in composite structures after an
impact event. Ei can be defined as the kinetic energy of the impactor right before contact-
impact takes place while Ea is termed as the amount of energy absorbed by the composite
specimen at the end of an impact event. Absorbed energy can be calculated from force-
displacement (F–d) curves.
The for ce versus displac ement graph (Fi g. 8a) shows a closed loop. The area under the curve
is the absorbed energy that is progressively transferred from the dart to the plate, when the
saturation of the load carrying capacity of the plate is reached. For specimens having
rebounding, i.e. closed type curves, the absorbed energy can also be calculated from the
initial kinetic energy minus the rebound kinetic energy using the initial and rebound
velocities.
(a)
(b)
Figure 9 Typical graphs of the laminate for impact velocity of 3.132 m/sec
Similarly, Fig. 9 illustrates the typical load-deflection curves and energy curves for impact
velocity of 3.132 m/sec. As the energ y absorbed by the specimen was not too high, a r ebound
occurred. For GFRP laminate, the force history (Fig. 10a) shows two thresholds: the first one
is at about 500 N, where the curve sharply changes its look and a deviation is visible, the
second one is at about 1600 N, where the curve sharply drops down and then takes again to
grow but with a slope lower than the previous one. Whereas for the graphite-based GFRP
laminates, the force history also shows two thresholds: the first one is at about 500 N, sim ilar
to glass epoxy laminate, whereas the second one is at about 1150 N. The first threshold can
be interpreted as the indication of the first material damage. The second threshold occurs at
the first lamina failure. It is seen that the absorption energy is more in the GFR P, when
compared with graphite-based GFRP laminate.
The force versus displacement graph does not show a closed loop, but terminates at a
displacement of about 4mm when the dart st ops. The area under the curve is the deformation
energ y th at i s i ni t ial l y pr o gres si vely trans ferred fr om th e dart to t he p l at e a nd th en giv en back
from the plate to the rebounding dart, the area included inside the loop refers to the energy
absorbed during the impact. The energ y appears to grow further; this i s due to the friction of

330 N. Rajesh Mathivanan, J Jerald Vol.11, No.3
the edges of the perforation hole against the lateral surface of the dart. In Fig. 9b, it is well
visible that, after perforation, the force remains nearly constant and the energy grows with a
constant slope.
Open type F–d curves have a horizontal section at the very end, post-perforation frictional
section. In order to identify the true energy absorption due to damage formation in the
specimens, the post-perforation frictional sections need to be removed from the curves. For
this purpose, the ending part of the descending section of the F–d curve may be extended to
the displacement axis.
Fig. 10 illustrates the t ypical l oad-deflecti on curves and ener gy curves for impact velocit y o f
4.429 m/sec. The force versus displacement graph (Fig. 10a) shows an open loop. The area
under the curve is the deformation energy that is progressively transferred from the dart to the
plate, when the saturation of the load carrying capacity of the plate is reached, perforation
takes place. At this instant the maximum energy absorbed by the material damage
mechanisms is read. All curves in force -time graphs contain some load oscillation in the
initial period, which is most clearly shown in Fig. 10(b) at the impact velocity of 4.429 m/sec.
(a)
(b)
Figure 10 Typical graphs of the laminate for impact velocity of 4.429 m/sec
At impact velocity of 2.215 and 3.132 m/sec, the two GFRP showed significantly different
force-deflection curves. For GFRP specimens 1 and 2, a non-recoverable slope change
occurred at a load level around 1.2-1.8 kN. A similar change in slope is also visible in
graphite-based GFRP specimens G1 and G1, but at a lower load level of around 1.2–1.4 kN.
The non-recoverable change of slope in the load-deflection curves has been suggested by
Hirai et al. [17] to represent the incipient damage under impact. They also found the load for
the incipient damage to be independent of the impact energy level, and believed that this is a
consequence of matrix cracking near the back surface of the specimen. The same point, but
on the load-time curve, was identified by Davallo et al. [18] who suggested that the point
represents the on-set of delamination, initiated from the matrix cracking.
Specim ens hav e been examin ed aft er t he i mp act t est wi th th e aim of es t ablis hi ng a correl ati on
between the test conditions and the plate damage. For comparison, images of the damaged
specimens are given in Fig. 11. Damage extent at both front (impacted) and back side of the

Vol.11, No .3 Interlaminar fracture toughness and low-velocity 331
specimens are given. Inspection of the post impact specimens at the speed of 2.215 m/sec
suggests that little damage, apart from indentation, is visible in GFRP, as shown in specimen
1. The load oscillation below 1200 N is b elieved to be a perturbation of the GFRP’s response
to impact, not representing the incipient impact damage.
For a low energy level (falling height of 0.5 m, impact velocity 3.132 m/s), this fibre layout
shows good impact resistance characteristics: almost all the energy is released back to the
rebounding dart. The maximum energy is reached at about 7.696 J. Specimen 3 exhibited
complete perforations when compared with specimen 2. The post impact examination reveals
that the specimen number 2 and 3 do not offer significant support under impact loading
conditions. At impact velocity of 4.429 m/sec, there is clearly a catastrophic failure of
laminates. The major difference between the two GFRP is their impact damage size. Under
the same impact condition, the damage size in the graphite-based GFRP is much larger than
that in the GFRP. Failure modes of the laminates were evaluated through visual inspection. It
is evident that clearly two types of failure modes were identified viz., crack initiation and
perforation of the laminate.
Impact
velocit y Front Back
2.215 m/sec
Specimen 1
Specimen
G1
3.132 m/sec
Specimen 2
Specimen
G2

332 N. Rajesh Mathivanan, J Jerald Vol.11, No.3
4.429 m/sec
Figure 11 Post-perforation images of damaged specimens
4. CONCLUSIO NS
The influence of loading rate and matrix toughness on the mode II interlaminar fracture
toughness has been investigated in GFRP and graphite-based GFRP laminates. End notch
flexure specimens were tested at crosshead displacement rate at 5 mm/min. Low-velocity
impact tests were conducted at different impact velocities; 2.215, 3.132 and 4.429 m/sec.
• The results show a consistent trend between the mode II delamination resistance and the
critical force for the incipient impact damage.
• Difference of the impact resistance between the two GFRP, however, is mainly on the
impact damage size developed.
• The total energy absorbed during the impact remains the same.
• The test results suggest that, based on the criterion of the energy absorption at maximum
load during the impact, the two GFRP have similar impact resistance.
• However, if the criterion also considers the damage area generated during the impact, that
is, using the energy absorbed per unit damage area as the criterion, the GFRP is much
tougher than graphite-based GFRP.
• The results also suggest that despite the difference of the crack growth behaviour in the
ENF specimens, the two GFRP show very similar GIIC values.
REFERENCES
[1] Abrate S. Impact on laminated composite materials. Appl Mech Rev 1991;44(4):155–89.
[2] Cantwell WJ, Morton J. Impact resistance of composite materials – a r eview. Composites
Part A 1991;22:347–62.
[3] Richardson MOW, Wisheart MJ. Review of low-velocity impact properties of composite
materials. Composites Part A 1996;27:1123–31.
[4] Laksimi A, Benzeggah ML, Jing G, Hecini M, Roelandt J M. Mode I Interlaminar fracture
of symmetrical cross-ply composites. Compos Sci Technol 1991;41:147–64.
[5] Naik NK et al. Damage in woven–fabric composites subjected to low-velocity impact.
Compos Sci Technol 2000;60:731–44.

Vol.11, No .3 Interlaminar fracture toughness and low-velocity 333
[6] Rajesh Mathivanan N, Jerald J. Experimental investigation of low-velocity impact
characteristics of woven glass fib re epoxy matrix composite laminates of EP3 grade.
Mater Design 2010;31(9):4553-60.
[7] Zhang ZY, Richardson MOW. Low velocity impact induced damage evaluation and its
effect on the residual flexural properties of pultruded GRP composites. Compos Struct
2007;81:195–201.
[8] Choi HY, Chang F-K. A model for predicting damage in graphite/epoxy laminated
composites resulting from low velocity point impact. J Compos Mater 1992;26:2134–69.
[9] Razi H, Kobayashi AS. Delamination in cross-pl y laminated composite subjected to low-
velocity impact. AIAA Journal 1993;31(8):1498–502.
[10] Sun CT, Manoharan MG. Growth of delamination cracks due to bending in a
[905/05/905] laminate. Compos Sci Technol 1989;34:365–77.
[11] Compston P, J ar P-YB, Burchill PJ, Takahashi K. The effect of matrix toughness and
loading rate on the mode II interlaminar fracture toughness of glass-fibre/vinyl-ester
composites. Compos Sci Technol 2001;61:321–33.
[12] Jar P-YB, Gros XE, Takahashi K, Kawabata K, Murai J, Shinagawa Y. Evaluation of
delamination resistance of glass fibre reinforced pol ymers under impact loading. J Adv
Mater 2000;32(3):35–45
[13] Kuboki T, Jar P-YB, For est TW. Influence of interlaminar fracture toughness on impact
resistance of glass fibre reinforced polymers. Compos Sci Technol 2003;63:943–53.
[14] Davies P, Sims GD, Blackman BRK, Brunner AJ, Kageyama K, Hojo M, et al.
Comparison of test configuration for determination of mode II interlaminar fracture
toughness results from international collaborative test programme. Plast Rub Compos
1999;28(9):432–7.
[15] Protocols for interlaminar fracture testing of composites. Delft (The Netherlands):
European Structural Integrity Society (ESIS); 1993
[16] Carlsson LA, Gillespie JW. Mode II interlaminar fracture of composites. In: Friedrich
K, editor. Application of fracture mechanics to composite materials. Amsterdam:
Elsevier; 1989;113–57.
[17] Hirai Y, Hamada H, Kim J-K. Impact response of woven glass fabric composites—I.
Effect of fibre surface treatment. Compos Sci Technol 1998;58:91–104.
[18] Davallo M, Clemens ML, Taylor H, Wilkinson AN. Low energy impact behaviour of
polyester-glass composites formed by resin transfer moulding. Plast Rub Compos Proc
Appl 1998;27(8):384–91.