Journal of Minerals & Materials Characterization & Engineering, Vol. 10, No.15, pp.1473-1485, 2011
jmmce.org Printed in the USA. All rights reserved
1473
Simulation of Torque during Rod Rolling of HC SS316 at Low Strain Rate
Using “Phantom-Roll” Method
P. O. Aiyedun
1
*, O. S. Igbudu
2
, B.O. Bolaji
1
1
Department of Mechanical Engineering, University of Agriculture,
P.M.B. 2240, Abeokuta, Nigeria.
2
Department of Mechanical Engineering, Ambrose Alli University, Ekpoma, Nigeria
*Corresponding Author: [e-mail]
ABSTRACT
Rolling torque for a seventeen passes, 125 x 125 mm HC SS316 billets rolled to a 16 mm
diameter rod have been simulated. Torque calculations based on pressure exerted by the
metal on the rolls and the area of contact during longitudinal rolling were obtained using the
temperature values derived using the “Phantom Roll” method. Investigations were carried
out for four different starting mean rolling temperatures between 988
0
C and 1191
0
C and at
four different strain rates of 0.4s
-1
, 0.8s
-1
, 1.2 s
-1
and 1.6s
-1
. Results obtained showed that for
all cases, rolling in grooved rolls required higher torque compared to rolling in flat rolls. In
general, it was observed that torque value increased as starting temperature decreases and
for each set of starting temperatures, the torque value increases with temperature. In all
cases, the torque values for grooved rolls were higher than those for flat rolls. This was due
to the higher frictional effect, occasioned by the larger contact area between roll and stock.
Results obtained also revealed an inverse relationship between strain rate and torque.
Keywords: simulation, rod rolling, grooved, phantom roll method, torque.
1. INTRODUCTION
Rolling is a direct compressive type of deformation in which applied compressive stress
induces two compressive stresses, which are on mutually perpendicular planes. It is one of the
most important metal working processes [1]. Forging and extrusion also fall under this type of
deformation process. Rolling is used to reduce the thickness of the work-piece [2]. It could be
carried out either cold or hot. Cold rolling is carried out at temperature below the
recrystallization temperature of the metal, while hot rolling is carried out at temperature
above the recrystallization temperature.

1474 P. O. Aiyedun, O. S. Igbudu, B.O. Bolaji Vol.10, No.15
Cold rolling increases the dislocation density and alters the shape, but not the average size of
the metal grain. The process generally increases the strength and decreases the ductility of the
metal. On the other hand, hot rolling significantly alters the microstructure of the metal such
as homogeneity of texture, the size and shape of grains and the concentration of point and line
defects (dislocations).
Two methods of rolling are distinguished-flat rolling and form rolling. Flat rolling is a
process in which a work-piece of constant thickness enters a set of rolls and exit as a product
with different constant thickness using flat rolls. Form rolling or shape rolling is a rolling
method for products such as I-beam, channels, railroad tracts and large diameter pipes and
rods using grooved rolls [3]. For rod rolling, which is the focus of this work, grooved rolls are
used.
Warm working is deformation carried out at any temperature and strain rate that some amount
of strain hardening is always evident [4, 5] or the simultaneous occurrence of deformation and
recovery process whereby metals are deformed in their plastic condition by successive passes
carried out at temperature above recrystallisation using a rolling mill [6]. The simultaneous
deformation and recrystallisation, apart from saving of energy, also results in considerable
speeding-up of the process. Rod rolling as a hot working process is the basis of this work
using HC SS316 at low strain rates. In general, rolling is a more economical method of
deformation than forging if metal is required in long lengths of uniform cross-section [1].
The “phantom roll” concept assumes that the temperature in the surface layer of the slab and
in the surface region of the roll are parabolic thus satisfying the heat transfer balance and the
heat transfer balance between the slab and the roll. The ratio of surface temperature change of
slab and roll is obtained as a function of the thermal properties and the initial surface
temperature of the slab and the roll and the instantaneous slab surface temperature [3].
Computer simulation models which predict temperature, load, torque and micro structural
changes are very powerful tools as it would be difficult, if not impossible, to obtain these
parameters from a few surface measurements. The knowledge of accurate temperature makes
it possible to evaluate torque during rolling and micro structural changes [7].
A lot of computer simulation models have been reported in the past in flat rolling, mainly for
load calculations to design mills at the maximum energy consumption. Kawai
[7]
developed a
computer simulation model, which predicts temperature and micro structural changes for rod
rolling of mild steel and medium carbon steel.
Oseghale [8] in his work expanded the ‘phantom roll’ method to take care of load and torque
calculations by neglecting the effect of roll flattening or deformation in the near surface
region of the rolls. He also, in addition to the assumptions made by Kawai, assumed that a
two dimensional deformation of metal (carbon manganese steel) during reduction.

Vol.10, No.15 Simulation of Torque 1475
Aiyedun [9] in his work made a comparison between the theoretical load and torque to that
obtained experimentally using HC SS316 steel slab at low reduction and low strain rate (0.08-
1.5s
-1
) by hot rolling the steel at different temperature using the modified Leduc’s programme
which uses the Sim’s sticking friction approach. He observed that there was excessive load
and torque in comparison with values obtained by normal rolling practice at low strain rates
and low reduction for flat rolling. The difference was observed to be influenced by
temperature, micro structural changes, precipitation strengthening and composition. The
precipitation strengthening was more pronounced at low strain rates [10].
In this work, attempt has been made to roll-up all above three discussed models into one so
as to simplify and integrate the various features linking them together for the evaluation of
torque during rod rolling of HC SS316 at low strain rates using phantom roll method. A
continuous rolling mill was used in view of the shortcomings of a two-high mill.
2. MATHEMATICAL MODEL
2.1 Rolling Torque
The mathematical model used for the simulation is presented below:
The rolling torque, in N-m is
T = 2ϕPR (1)
where, ϕ = coefficient of lever arm; P = load, N; and R = undeformed roll radius, m.
P = A
p
K
w
(2)
where, A
p
, = projected area, m
2
; K
w,
= mean roll pressure, calculated under actual rolling
conditions, N/m
2
.
A
p
= b
m
L (3)
(
)
2
1
bb
b
o
m
+
= (4)
where, L = projected contact length, m; b
m
= mean stock width, m; b
o
= breadth before entry,
m; b
1
= breadth after exit, m.
2.2 Yield Strength of the Roll Stock
K′
w
can be used instead of K
w
in Eq. (2), where K′
w
= standard rolling deformation resistance
of rolled stock when only reduction (R), Temperature (T) and the ratio of exit height (h
1
) to
roll diameter (d) are variables. An analytical expression was derived which approximates very
closely to the Siebel’s graphical function:
K′
w
= f(R, T, h
1
/d)
K′
w
= Kexpα (5)
where, α = f(R, T, h
1
/d)
α = m a n y (6)
(mathematical specification for m, a, n and y are given below)
K = yield strength of the rolled stock at a temperature of 1000
o
C, N/m
2

1476 P. O. Aiyedun, O. S. Igbudu, B.O. Bolaji Vol.10, No.15
For conditions different from the predicted standard one, a number of correction factors are
introduced and Eq. (5) becomes
[9]
:
K
w
= (Kexpα)a
1
a
2
a
3
a
4
a
5
(7)
Where a
1
, a
2
, a
3
, a
4
and a
5
are defined as follows:
a
1
: is the coefficient of rolling speed
a
2
: is the effect of the outer zones for rolling of flats in free spread conditions
a
3
: is the effect of form factor. It is assumed 1 for rolling in grooved rolls.
a
4
: is effect of roll material. This refers to the type of material that is being rolled.
a
5
: is effect of chemical composition of rolled stock; for carbon steel it is function of h
1
/d,
KEM and Temperature, T, where
77.4
Cr3.0MnC2.4
KEM +++ = (8)
where, C, Mn and Cr are percentage contents of Carbon, Magnesium and Chromium
respectively.
For the steel (HC SS316) employed, the parameters in equations (5), (6) and (7) can be
obtained as illustrated below:
Mathematical specification for Eq. (5)
C
SIGMA
B
K+= (9)
where
SIGMA = 100h
1
/d (10)
B = 3 + 0.350R (11)
C = 10 + 0.025R (12)
Mathematical specification for Eq. (6)
( ) 517.012.0SIGMA
797.1
−×
=m (13)
(
)
1000
1000 T
a− =
(14)
For SIGMA ≥ 1.2,
n = 1 (15)
For 1.2 > SIGMA > 0.6,
)270SIGMA300sin(
200
65.035.0
200 −





−++= TT
n
(16)
For Sigma ≤ 0.6,
3.0
1000 −=
T
n (17)
For T < 1000,
( )
100
1000
5.243
900
2SIGMA8.1
458
1100
5.1
−
−
+− 




−
=
T
T
T
y
(18)
For 1000 ≤ T ≤ 1100,

Vol.10, No.15 Simulation of Torque 1477
y = 1 (19)
For T > 1100,
( )
100
1100
3.127
1200
40.4
5.4 26
1000
6.1
T
T
SIGMA
T
y
−
−
+− 




−
=
(20)
Mathematical specification for Eq. (7)
The expressions for coefficients a
1
, a
2
, a
3
, a
4
and a
5
are as given below
For v/d ≥ 1.5,
a
1
= 1 + THETA × ln(1 – TAU) (21)
where
34.2
200
800
023.0142.0THETA 




−
+=T (22)
TAU = 1.5 – v/d (23)
For v/d ≤ 1.5,
a
1
= 1 – THETA.TAU – 0.257(TAU)
3
+ 0.0547(TAU)
5
(24)
For L/h
m
≥ 1
a
2
= 1 (25)
For L/h
m
< 1
a
2
= (L/h
m
)
-0.4
(26)
Coefficient a
3
, form factor, we have
for A ≤ 0
a
3
= 0.797 – RHO (27)
where,
3
100
60
RHO 




−
=R (28)
R = 100r (percentage reduction, %); r = (h
o
– h
1
)/h
1
(fractional reduction).
for 0 < A < 1
a
3
= 0.797 – RHO + 0.247A (29)
where,
A = ln(DELTA) (30)
DELTA = b
o
/h
o
(31)
for A = 1
a
3
= 1.037 – RHO + 0.007A (32)
for A ≥ 1
a
3
= 1 (33)
For coefficient a
4
(roll surface hardness and structure), we have,
HSC = Roll Surface Hardness Shore Number
= 0.006; Steel and Steel Base
= 0.001; Nodular Pealithic Cast Iron
= 0.002; Nodular Marthenistic Cast Iron
a
4
= 1.05(HSC – 40) (0.001R + KSC) (34)
Coefficient a
5
(grade of rolled steel)

1478 P. O. Aiyedun, O. S. Igbudu, B.O. Bolaji Vol.10, No.15
for Sigma ≤ 14
( ) SIGMAln335.01OMEGA
220
1200
1
5
−
−
+= T a (35)
where,
( )
2
KEM21
OMEGA
17
−−
= (36)
for Sigma ≤ 14
( )








−
+=
91.2
5
SIGMA
251
OMEGA
220
1200
1T a
(37)
2.3 Evaluation of Contact Area (A
p
) Between the Rolled Material and the Rolls
The mean width of the rolled strip over zone of deformation (b
m
) is determined using Eq. (3).
However, if the edge of the rolled strip over the zone of deformation is approximated not by a
circle but by an arc of a parabola then, Eq. (38) is used.
(
)
oom
bbbb ++=
1
3
2
(38)
The quantity L in Eq. (2) is found from the relation given below if the angle of contact is
known.
hrACL ∆== (39)
For rolling in non-rectangular section rolls, and taking ∆h equal to the mean linear reduction
over the width of the section, that is,
1
1
b
Q
b
Q
h
o
o
−=∆ (40)
for a Rhombus Rolled from Rhombus,
∆h = (0.55 to 0.56) (h
o
– h
1
) (41)
for Oval Rolled from a Square,
∆h = h
o
– 0.7h
1
(for shallow oval) (42)
∆h = h
o
– 0.85h
1
(for round oval) (43)
for a Square Rolled from an Oval,
∆h = (0.65 to 0.7)h
o
- (0.55 to 0.6)h
1
(44)
for a Circle Rolled from an Oval,
∆h = 0.85h
o
– 0.79h
1
(45)
where, h
o
= depth of cross-section of strip before the pass, m; and h
1
= depth of cross-section
of strip after the pass, m.
2.4 Evaluation of Zener-Hollomon Parameter (Z)
The Zener-Hollomon parameter (Z) is given as [11]:








=TR
Q
Z
g
.
exp ε (46)
where Q = activation energy, kJ/kg; R
g
= gas constant, kJ/kg.K; and
ε
= strain rate, s
-1
.

Vol.10, No.15 Simulation of Torque 1479
The strain rate is obtained using Eq. (47)
[3]
:








==∫
L
d
E
0
)(ln
1
ln εεεε
(47)
the approximate mean rolling strain rate
ε
is given by Eq. (48)
[3]
:
45.0
2
1
25.0
21
ln
08.1























∆








∆
=h
h
hh
h
hR
V
ε (48)
2.5 Calculation of Graph Equations
Torque (T
r
) =C log
10
Z + D (49)
where C and D are constants which were obtained from curve fitting of torque versus log
10
Z.
2.6 Simulation of the Model
In the simulation of the model, conditions and input data similar to those Aiyedun et al. [12]
were assumed for this work. A 125 × 125 mm
2
stainless steel (HCSS 316) square billet was
used as the starting material for rolling to a 16 mm diameter rod using 17 sequential passes at
low strain rates, the following assumptions made were:
 Roll cooling systems were neglected;
 Air cooling condition was taken to be the same as in the laboratory although a lower
cooling rate is probable due to the obstruction of the radiation by the trough between
stands;
 The roll radii for flat and grooved roll were taken to be 140 mm and 254 mm respectively;
 One dimensional heat flow within the material and heat flows from the center to the
surface;
 The value of the activation energy (Q) of deformation for HC SS 316 was taken to be
460kJ/kg,
[9]
;
 Heat gain due to deformation is equally distributed to each element and for every time
interval during rolling;
 Heat loss is caused by radiation and convection during air-cooling and by conduction
during rolling; and
 A ‘phantom roll’ method was used.
The ‘phantom roll’ method makes it possible to save the computer calculation in the roll by
assuming a parabolic temperature distribution
[3, 8]
.
3. RESULTS DISCUSSION
The simulation was carried out starting with four different mean temperatures of 988
0
C, 1094
0
C, 1095
0
C and 1191
0
C and starting strain rates of 0.4 s
-1
, 0.8 s
-1
, 1.2 s
-1
and 1.6 s
-1
,
respectively for seventeen sequential passes in a continuous rolling mill. The input data were
based on those of Aiyedun et al. [12]. Figs. 1 to 4 show the plots of torque against
temperature for both flat rolls and grooved rolls for strain rates of 0.4 s
-1
and 1.6 s
-1
, the points
were fitted with curves for all starting temperatures.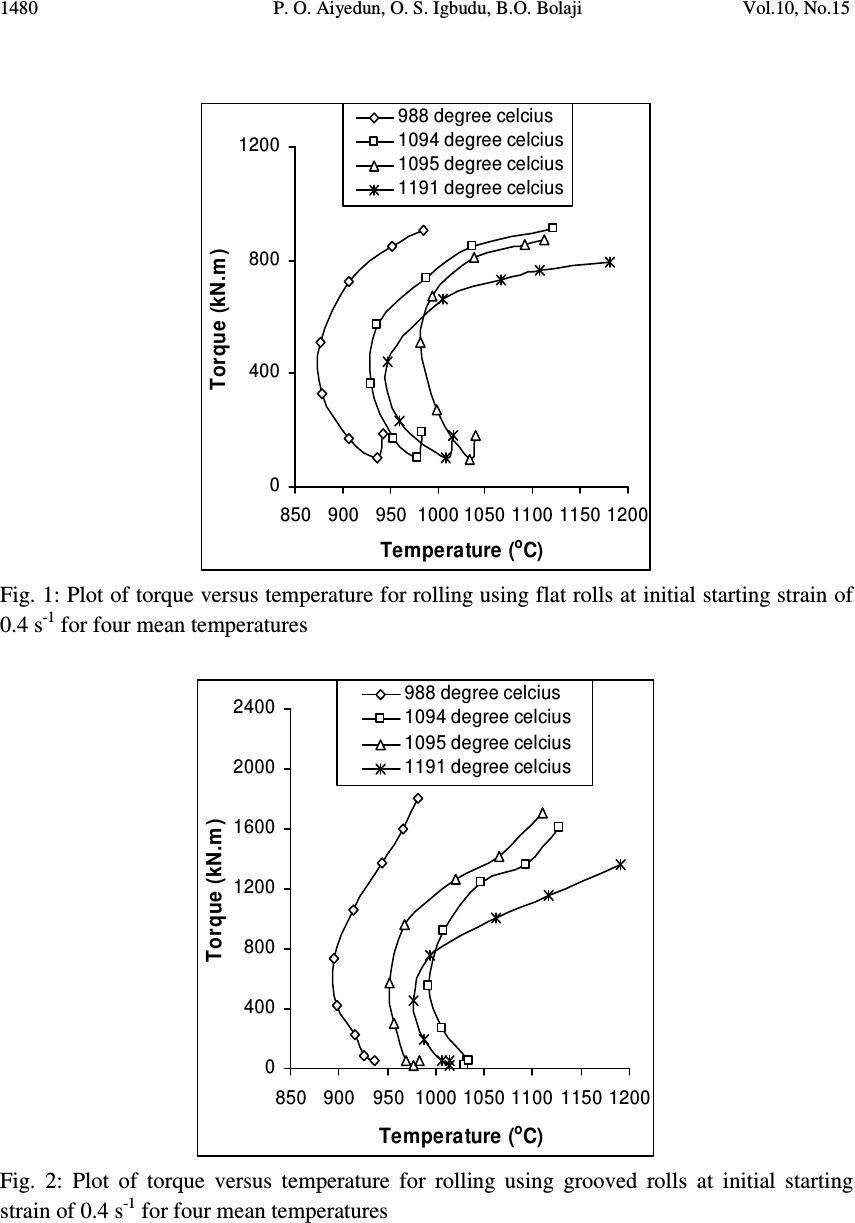

1480 P. O. Aiyedun, O. S. Igbudu, B.O. Bolaji Vol.10, No.15
0
400
800
1200
85090095010001050 1100 1150 1200
Temperature (
o
C)
Torque (kN.m)
988 degree celcius
1094 degree celcius
1095 degree celcius
1191 degree celcius
Fig. 1: Plot of torque versus temperature for rolling using flat rolls at initial starting strain of
0.4 s
-1
for four mean temperatures
0
400
800
1200
1600
2000
2400
8509009501000 1050 11001150 1200
Temperature (
o
C)
Torque (kN.m)
988 degree celcius
1094 degree celcius
1095 degree celcius
1191 degree celcius
Fig. 2: Plot of torque versus temperature for rolling using grooved rolls at initial starting
strain of 0.4 s
-1
for four mean temperatures

Vol.10, No.15 Simulation of Torque 1481
0
400
800
1200
85090095010001050 11001150 1200
Temperature (oC)
Torque (kN.m)
988 degree celcius
1094 degree celcius
1095 degree celcius
1191 degree celcius
Fig. 3: Plot of torque versus temperature for rolling using flat rolls at initial starting strain of
1.6 s
-1
for four mean temperatures
0
400
800
12 00
16 00
85090095010001050 11001150 1200
Temperature (oC)
Torque (kN.m)
988 degree celcius
1094 degree celcius
1095 degree celcius
1191 degree celcius
Fig. 4: Plot of torque versus temperature for rolling using grooved rolls at initial starting
strain of 1.6 s
-1
for four mean temperatures
As shown in these figures, it was observed that for grooved rolls, torque values were larger
than for flat rolls; this translates into more power dissipation with grooved rolls. The higher
values encountered are possibly due to the following reasons:

1482 P. O. Aiyedun, O. S. Igbudu, B.O. Bolaji Vol.10, No.15
 For rolling in grooved rolls, the area of contact between roll and stock increases towards
exit and not constant as in flat rolls. Since torque is a function of contact area, this could
account for the difference.
 Friction effect due to the side wall of grooved rolls is greater because of the greater
contact area.
The plot of torque against temperature, hyperbolic curves were obtained both for flat and
grooved rolling (Figs. 1 to 4). Towards the end of rolling, the increase in temperature did not
produce a corresponding increase in torque thus explaining the conic shape of the curves.
Further investigation of the combined effects of temperature and strain rate on torque was
carried out by calculating the Zener-Hollomon parameter (Z), which combined these effects.
Plots of torque against log
10
(Z) are shown in Figs. 5 and 6 for strain rates of 0.8 and 1.6 s
-1
,
respectively. Points were fitted with straight lines for both flat and grooved rolls. An inverse
relationship exists between log
10
(Z) and torque.
A peculiar variation was observed for the highest temperature (1191
o
C). This trend was
general for the various strain rates and rolls (Figs. 5 and 6).
0
4 0 0
8 0 0
120 0
160 0
200 0
18 2022 2426 28
Log
10
(Z)
Torque (kN.m)
Flat rolls at 1095 degree celcius
Grooved rolls at 1095 degree celcius
Flat rolls at 1191 degree celcius
Grooved rolls at 1191 degree celcius
Fig. 5: Plot of torque versus log
10
(Z) for seventeen passes for starting temperatures of 1095
and 1191
0
C, and strain of 0.8s
-1
using flat and grooved rolls

Vol.10, No.15 Simulation of Torque 1483
0
4 0 0
8 0 0
120 0
160 0
18 20 2224 26 28
Log
10
(Z)
Torque (kN.m)
Flat rolls at 1095 degree celcius
Grooved rolls at 1095 degree celcius
Flat rolls at 1191 degree celcius
Grooved rolls at 1191 degree celcius
Fig. 6: Plot of torque versus log
10
(Z) for seventeen passes for starting temperatures of 1095
and 1191
0
C, and strain of 1.6s
-1
using flat and grooved rolls
This abnormal behaviour could be that recrystallization and hence recovery never fully taking
place during rolling at this temperature thereby resulting in strain localization.
The plot of torque against strain rate for flat roll at various rolling temperatures is shown in
Fig. 7.
0
200
400
600
800
1000
020 406080
Strain (s
-1
)
Torque (kN.m)
988 degree celcius
1094 degree celcius
1095 degree celcius
1191 degree celcius
Fig. 7: Plot of torque versus strain rate for rolling in flat rolls at starting temperatures of 988,
1094, 1095 and 1191
0
C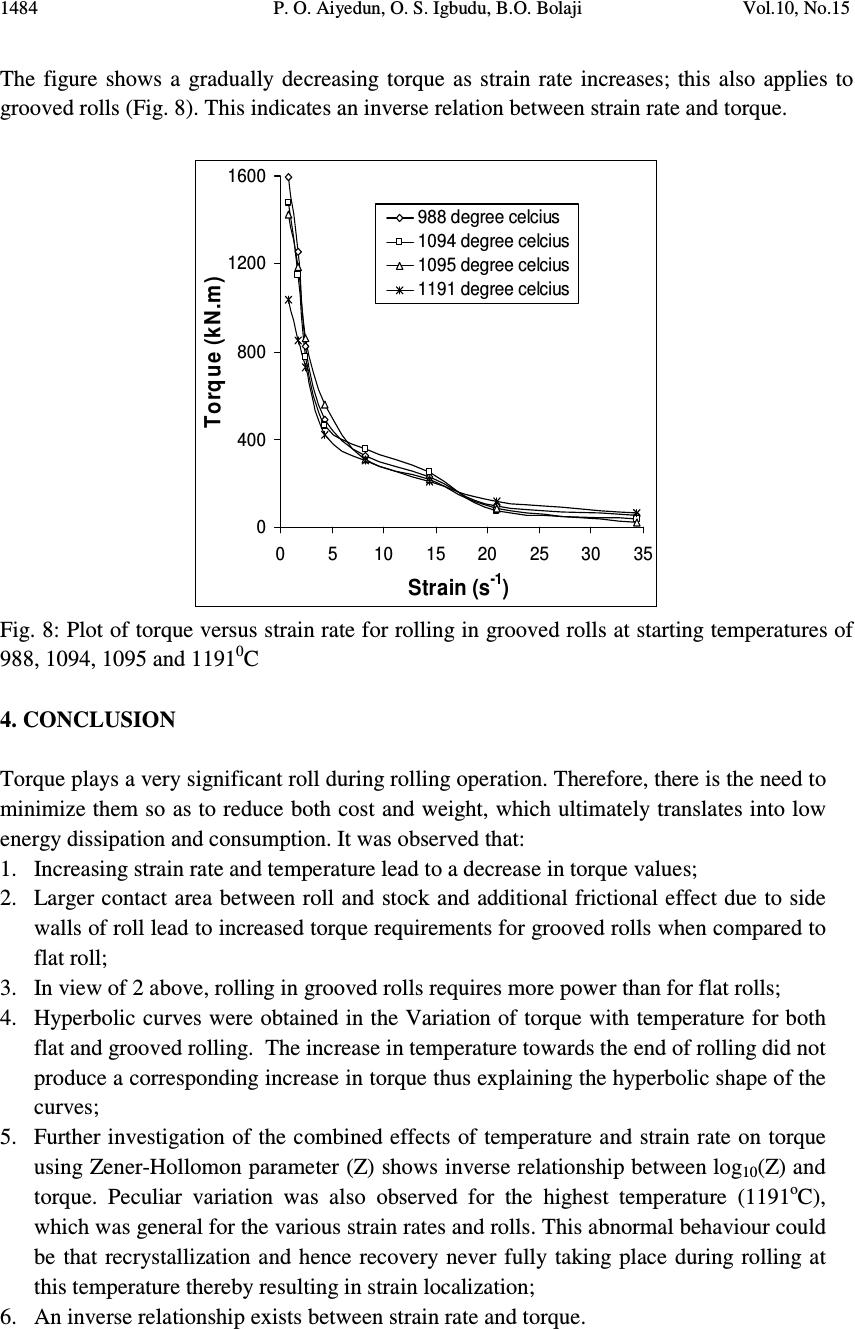

1484 P. O. Aiyedun, O. S. Igbudu, B.O. Bolaji Vol.10, No.15
The figure shows a gradually decreasing torque as strain rate increases; this also applies to
grooved rolls (Fig. 8). This indicates an inverse relation between strain rate and torque.
0
400
800
1200
1600
0510 1520 2530 35
Strain (s
-1
)
Torque (kN.m)
988 degree celcius
1094 degree celcius
1095 degree celcius
1191 degree celcius
Fig. 8: Plot of torque versus strain rate for rolling in grooved rolls at starting temperatures of
988, 1094, 1095 and 1191
0
C
4. CONCLUSION
Torque plays a very significant roll during rolling operation. Therefore, there is the need to
minimize them so as to reduce both cost and weight, which ultimately translates into low
energy dissipation and consumption. It was observed that:
1. Increasing strain rate and temperature lead to a decrease in torque values;
2. Larger contact area between roll and stock and additional frictional effect due to side
walls of roll lead to increased torque requirements for grooved rolls when compared to
flat roll;
3. In view of 2 above, rolling in grooved rolls requires more power than for flat rolls;
4. Hyperbolic curves were obtained in the Variation of torque with temperature for both
flat and grooved rolling. The increase in temperature towards the end of rolling did not
produce a corresponding increase in torque thus explaining the hyperbolic shape of the
curves;
5. Further investigation of the combined effects of temperature and strain rate on torque
using Zener-Hollomon parameter (Z) shows inverse relationship between log
10
(Z) and
torque. Peculiar variation was also observed for the highest temperature (1191
o
C),
which was general for the various strain rates and rolls. This abnormal behaviour could
be that recrystallization and hence recovery never fully taking place during rolling at
this temperature thereby resulting in strain localization;
6. An inverse relationship exists between strain rate and torque.

Vol.10, No.15 Simulation of Torque 1485
REFERENCES
[1] A.G. Antonio and R.V. Renato, The Effect of Finishing Temperature and Cooling Rate on
the Microstructure and Mechanical Properties of As-Hot Rolled Dual Phase Steel,
Antonio Augusto Gorni, 1996, Home page, http://www.Geocities.com.
[2] P.J. Schaffer, A. Sexana, D.S. Antolovich, T.H. Sanders and B.S. Warner, Science and
Design of Engineering Materials, 2nd ed., McGraw-Hill Company Inc., New York, 1999.
[3] P.O. Aiyedun, O.S. Igbudu and B.O. Bolaji, Simulation of Load during Rod Rolling of
HCSS316 at Low Strain Rate, Proceedings of 2nd International Conference on
Engineering Research and Development: Innovation, April 15-17, 2008 (Nigeria),
University of Benin, Benin City, Nigeria, 2008, p 422-430.
[4] S. Venkadesan, P. Sivaprasad, S. Venugopal and V. Seetharaman, Tensile Deformation
Behaviour of Warm-Rolled Type 316 Austenitic Stainless Steel, Journal of Mechanical
Working Technology, 12, 1986, p 351-354.
[5] E.C. Rollason, Metallurgy for Engineers 4th ed., Edward Anorld, New York, 1992.
[6] H. Qamark, G.W. Buckley and M. Lewis, Computer Programmed Speed Roll-Torque
Data Calculation, Journal of Iron and Steel International, 53, 1980, p 29-37.
[7] R. Kawai, “Simulation of Rod Rolling of Carbon-Manganese Steel,” M.Phil. Thesis,
University of Sheffield, UK, 1985.
[8] L.E. Oseghale, “Simulation of Load and Torque During Rod Rolling Using the
‘Phanthom Roll’ Method,” M.Sc. Thesis, Univesity of Ibadan, Nigeria, 1998.
[9] P.O. Aiyedun, “A study of loads and torque for light reduction in hot flat rolling at low
strain rates,” Ph.D. Thesis, University of Sheffield, UK, 1984.
[10] R.W.K. Honey-Combe, The Plastic Deformation of Metals, 2nd ed., Anorld, New York,
1983.
[11] O.J. Alamu and M.O. Durowoju, Evaluation of Zener-Hollomon parameter variation
with pass reduction in hot steel rolling, International Journal of Environmental Issues, 1,
2003, p 148-159.
[12] P.O. Aiyedun, L.E. Oseghale and O.J. Alamu, Simulation of Load Bearing Rod Rolling
of Carbon-Manganese Steel Using the “Phantom Roll” Method, Pacific Journal of
Science and Technology, 10, 2009, p 4-14.