Journal of Modern Physics
Vol.06 No.13(2015), Article ID:60738,8 pages
10.4236/jmp.2015.613198
Establishment of New Solution for Complex Systems in Multidisciplinary Science Based on Feedback System Analysis Method and Proven by Simulator
Deok-Soo Cha
Eho Technology Co., Busan, South Korea
Email: chdsoo@hotmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 August 2015; accepted 26 October 2015; published 29 October 2015
ABSTRACT
This paper establishes a very important scientific solution to science of complexity for physicists, and presents a multidisciplinary involved physics and engineering. The innovative solution for complex systems presented here is verified on the basis of principles in engineering such as feedback-system analysis using the classical control theory. This paper proposes that a complex system is a closed-loop system with a negative feedback element and is a solvable problem. A complex system can be analyzed using the system analysis theory in control engineering, and its behavior can be realized using a specially designed simulator.
Keywords:
Complex Systems, Feedback System, System Simulator, System Modeling, Multidisciplinary

1. Introduction
This paper establishes a very important scientific solution about complexity, which will be of interest to physicists and may be considered a significant innovation in modern sciences. Complex systems have not yet been solved and are considered a difficult subject in different fields of science. Some of the prevalent examples include the black hole, sun magnetic field, nuclear theory, super conductor, plasma, climate change, turbulence, and complex systems. It is the consensus regarding a single universal definition of complex systems does not yet exist, and the key problems of complex systems are the difficulties in formal modeling and simulations.
However, this paper reports a multidisciplinary (hyper linked Wilipedia) study involving physics and engineering. It presents a very innovative solution for complex systems that is successfully verified on the basis of engineering principle such as feedback-system analysis in classical control theory. Furthermore, a new electrotype complex system simulator, shown in Figure 1, which can demonstrate the dynamically behavior of complex systems in real time, is presented here. It is very useful equipment for scientists without knowledge about feedback-system analysis method in classical control theory, including college students. The electronic components of this system are constructed based on the mathematical solutions presented in this paper.
This paper establishes a new solution that already released in other document [1] [2] . It presents a multidisciplinary study combined complex systems theory and classical control theory, as shown in Appendix I. Therefore, the editor and readers should be familiar with physics and engineering, including (automatic) control theory. Unfortunately, an unexpected and serious problem was encountered: I had not found a physicist possible to understand the questionnaire on control theory in Appendix I; therefore, most physicists were outsiders in the classical control theory, in same case, as most engineers were outsides in complex systems theory or chaos theory in physics, this is not their mistake to each other; because they did not formally studied these topics in school. Nevertheless, most physicists did not acknowledge the truth themselves; therefore, they cannot review and evaluate. However, this should not be a problem in the current context. I believe the problem is an invisible border between physics and engineering. Then, I propose to the journal editor a requirement for establishment.
Requirement: This is an important consideration for the editor or reader: if unfamiliar with control engineering, readers skip Sect 2 and try to perform a simulation directly using the simulator shown above and watching the simulation video clip (hyper linked) in YouTube.
Summary: The solution is validated and I believe that the results are convincing; if the readers have any questions, I recommend discussing with control engineers at first. This paper establishes that many systems in nature are closed-loop systems with feedback characteristics. In traditional physics, a complex system is deal with a black box. However, in this study, the complex system is not a black box but a feedback system, as shown in Figure 2. Its behavior can be analyzed in real time by the proposed electronic complex system simulator.
2. Theoretical Background
2.1. Modeling Mechanisms of Complex Systems in Science
1) What is a system in science?
According to Wikipedia, (Refer to “Wikipedia: Academic use” in Wikipedia), a system is a set of interacting or interdependent components forming an integrated whole, as shown Figure 3 and Table 1.
Most scientists believe that complex systems are chaotic and cannot be solved; hence, they are considered as a
Figure 1. Electro-type complex system simulator: The simulator is an invention (patented) and unique device, the design of which is described in detail in Appendix II. The equipment can be simulated under all kinds of conditions by its adjustable controller. It is portable and ultra-small, thus allowing experiments to be performed anywhere at any time. In addition, it would distribute the devices to scientists and personnel in the education field and its cost is less than $100.
Figure 2. The mechanism of a complex system.
Figure 3. A system in nature. Fields involved in the study of the general properties of systems include systems science, systems theory, systems modeling, systems engineering, cybernetics, dynamical systems, thermodynamics, complex systems, system analysis and design, and systems ar- chitecture.
Table 1. Types of systems. Systems can be classified into two groups: artificial or man-made systems and natural systems. Artificial systems are engineering systems that can be controlled by humans, e.g., control systems and computer systems. In contrast, natural systems cannot be controlled artificially.
mysterious problem. In this paper, I analyze three complex systems using my model.
2) Modeling thermodynamic systems in physics
All complex systems in science have feedback characteristics that involve the law of the conservation of energy, which is a law of thermodynamics. One such system is shown in Figure 4.
The entropy of solar energy tends to move toward only the low-temperature side through G(s). The time-se- ries function for S, the entropy of heat, is given by
 (1)
(1)
Accordingly, G(s) in Figure 4, is Equation (1) is transformed as
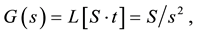 (2)
(2)
where s is the Laplace operator.
The side Y(s) in Figure 4, which is at a low temperature, tends to pull heat energy from the side U(s), which is at a high temperature. As the heat moves from U(s) to Y(s), there is a delay of time T because heat does not move instantaneously. The other side, there is another entropy as a factor in here; it is an “attraction power” with
Figure 4. Model for the law of conservation of energy.
negative characteristics; the entropy of the attraction power restricts the overall energy overflow. However, the system shown in Figure 4 is when, after some time, the output Y(s) equals the input U(s) and the heat energy stops moving. Therefore, the total input energy and the total output energy are equal and there is only a delay of time T (energy conservation). Therefore, the solar heat that flows to Earth moves to the polar regions where it is emitted back into space so that the overall temperature of the Earth remains constant (a balanced state). Thus, it can be concluded that this thermodynamic system is a closed-loop system with feedback, as shown in Figure 4.
3) Modeling the stock market system as a complex system
The stock market is a representative complex system. It has the same inner mechanisms as the feedback system shown in Figure 4. If the price of a stock on the previous day is higher than the current price, the stock market is under pressure to lower the price by reducing the current transaction volume and decreasing the current stock price; this system is shown in Figure 4. This property prevents “runaway” stock prices through negative feedback. This can be explained by the economic theory of the “law of supply and demand”. Because supply and demand are related and the volume of supply provides negative feedback to prevent runaway stock prices, the market remains balanced. Thus, it can be concluded that the stock market is a feedback system, as shown in Figure 4.
4) Modeling ecological systems
Ecological systems are similar to the system shown in Figure 4. One example is the deer that inhabit the grassland. The deer require food for energy, which is needed for propagation. If there are no predators and the amount of food, Q(t), is constant, the deer population N(t) continues to increase over time, as shown in Figure 5. If the population increases, the amount of food per deer, Q(t)/N(t), decreases gradually (even after allowing for natural decrease in food), as shown in Figure 5, and the deer ultimately are driven into a struggle for survival.
In the struggle for survival, the fertility rate decreases, thus affecting population growth. Therefore, the increase of the deer population is restrained and the number of deer converges to a fixed value, as shown by the flowchart in Figure 6, which shows the negative feedback characteristics of the system. The output of the ecosystem―the deer population N(t)―causes a reduction in the amount of available food, Q(t), i.e., Q(t), which is the input element, determines the population volume N(t). The output N(t) provides negative feedback by reducing the input Q(t) and is expressed as
 (3)
(3)
Therefore, the ecosystem is a feedback system similar to that shown in Figure 4.
2.2. Mathematical Method for Analyzing the Basic System [3]
1) Overview of the classical control theory
Unfortunately, most physicists are not familiar with the classical control theory, which is the fundamental theoretical background of a basic system. However, the theory is not discussed in this paper. For a discussion of
Figure 5. The dynamics of an ecosystem.
Figure 6. An ecosystem flowchart.
the basic model of a feedback system between the input U(s) and output Y(s) in real time and its general mathematical solution (Figure 7), refer to the textbook [3] or Wikipedia.
2) Description of the mathematical solution
In Figure 7, U(s) and Y(s) are functions defined using the Laplace operator s, where U(s) is the input element, i.e., the amount of material, and Y(s) is the output element, i.e., the production volume. For example, the entropy of the production process is given by K(t), a time-series function representing the production volume per hour. Therefore, K(t) is equivalent to S(t) defined by Equation (1), and G(s) is transformed from entropy G(t) defined by Equation (2). The general equation for H(s) is  (variable A&B is constant) and H(s) must be greater than 1. If H(s) is zero, the system is an open-loop system. Substituting these functions into the equation
(variable A&B is constant) and H(s) must be greater than 1. If H(s) is zero, the system is an open-loop system. Substituting these functions into the equation
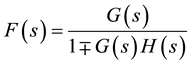
yields
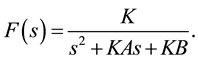 (4)
(4)
If A = 0, B = 1, then . The response of the unit step function u(t) for this equation is a pe-
. The response of the unit step function u(t) for this equation is a pe-
riodic function of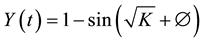 , as determined by MATLAB (The MathWorks Co., Natick, MA,
, as determined by MATLAB (The MathWorks Co., Natick, MA,
USA). The program is generally applicable to mathematical solutions using the Laplace transform of a system problem.
3. Experiment
3.1. Overview of the Electrotype Complex Systems Simulator
This paper presents a simulator based on the schematic in Figure 7 for physicists without knowledge of feedback analysis theory. The simulator is described in Appendix II and shown in Figure A1. It is possible to demonstrate the behavior of complex systems electrically in real time. Moreover, the device is portable and ultra-small, thus allowing experiments to be performed by anyone anywhere and at any time. The device comprises electronic components assembled according to a mathematical solution. A simulation video (hyper linked YouTube) file is opened separately, and I recommend watching the video. In the demonstration experiment, the simulation was performed in two steps. First, the simulator was provided to input function as a constant value; unit-step function u(t) from the source level controller; then the output is displayed in Figure 8. Second, the simulator was provided to input function as a variable value; random function x(t); the output is displayed in Figure 9.
3.2. Review Based on Simulation Results [4]
In reference [4] and Wikipedia, the representative behavior of complex systems is described in terms of chaotic, fractal, self-organization, and butterfly-effect etc. For instance, in the Figure 8, for the first step, the input value as the unit step function u(t), represented by the lower blue curve, is displayed by the upper yellow curve in Figure 8; the output equation is 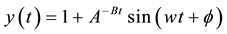 [3] . We can understand the behavior of complex systems through Figure 8, overlapping irregularity (chaotic) and regularity (fractal), periodic (self-organization), initial phenomenon (butterfly-effect). However, the displayed output cannot be analyzed any further the results in Figure 8.
[3] . We can understand the behavior of complex systems through Figure 8, overlapping irregularity (chaotic) and regularity (fractal), periodic (self-organization), initial phenomenon (butterfly-effect). However, the displayed output cannot be analyzed any further the results in Figure 8.
For the more detail described again, Figure 8 shows the behavior of a complex system: 1) The initial phenomenon of a rapid increase corresponds to the butterfly effect, a characteristic of a complex system; 2) the periodic
Figure 7. The basic model of a closed-loop system with negative feedback H(s).
Figure 8. The result of the response of a unit step function.
Figure 9. Simulation results of stock price.
sine wave form shows regularity; 3) the decrease in the sine wave form with convergence shows self-organi- zation; and 4) there is irregularity at the output because the input and output are not identical and overlap. Furthermore, it appears that regardless of the circumstances, the output y(t) never exhibits runaway or overflow. In addition, the complex system cannot be completely controlled externally. In step two, the input value as variable random function x(t), shown by the blue curve in Figure 9; the output y(t), displayed as the yellow curve in Figure 9, shows the characteristics of a complex system. The output shown in Figure 9 was overlapped chaotic, fractal, self-organization and butter-fly effect. For more details, refer to [4] .
4. Results
This paper provides a new solution for complex systems and demonstrates that this system is not a black box. A complex system in nature is a closed-loop system with negative feedback characteristics and conserves energy. It can be analyzed using systems analysis of classical control theory, which is well known in engineering. The characteristics of a complex system were verified using a simulator. It was found that the complex system is a feedback system with an internal structure, as shown in Figure 2. The transfer function of a complex system is given by Equation (4). However, I hope that scientists become more involved in the study of control theory in the future. In the meantime, I look forward to applying the simulator in different fields of science.
5. Conclusion
This paper suggests that a complex system is a natural closed-loop system with a feedback, discloses its internal structure, and proposes a simulator that implements the same characteristics. After verification of the findings presented in this paper, they have the potential to be used in many studies.
Cite this paper
Deok-SooCha, (2015) Establishment of New Solution for Complex Systems in Multidisciplinary Sci-ence Based on Feedback System Analysis Method and Proven by Simulator. Journal of Modern Physics,06,1927-1934. doi: 10.4236/jmp.2015.613198
References
- 1. Cha, D. (2012) What Is the System in Electrical System? KIEE in Korea.
- 2. Cha, D. (2015) International Journal of Mulitidisciplinary Science and Engineering, 6.
- 3. Benjamin, K. (2003) Automatic Control Systems. John Wiley & Sons. Ltd., New York.
- 4. John, C. (1995) Complexification: Explaining a Paradoxical World through the Science of Surprise. Harper Collins Publishers Ltd., New York.
Appendix I
Questionnaire about automatic control engineering: (solutions and basic equation) the figure below shows a block diagram and transfer function that can be used to analyze a feedback system, whether the solution is known or not.
Appendix II: The Electro-Type System Simulator [1] [2]
This paper introduces a system simulator based on Figure 7. However, it is possible to demonstrate the behavior of complex systems electrically and the experiments can be performed anywhere by anyone at any time. The device comprises electronic components assembled according to a mathematical solution, and it is portable and ultra-small.
Overview of the system simulator: The simulator, the design of which is shown in Figure 8, was assembled with electronic devices
The electronics circuit is illustrated in Figure A1; it comprises three operational amplifier circuits. The transfer function for the electronic circuit is
which is equivalent to Equation (4). In addition, various system characteristics can be implemented by adjusting the resistance R and capacitance C in the circuit. The simulation process, shown in Figure A2, is as follows: [input ⇨ {simulator} ⇨ output]. Then, we can measure the output in real time, and the experiment can be performed by anyone.
Figure A1. A circuit diagram of the system simulator and basic system.
Figure A2. Preparation for demonstration.















