Received 6 July 2015; accepted 24 August 2015; published 27 August 2015

ABSTRACT

We investigate the effect of the Majorana Fermions which are formed at the boundary of a p-wave superconductor. When the Majorana overlapping energy is finite we construct the scattering matrix S by mapping the Majorana zero mode to Fermions for which coherent states are defined and a path integral is obtained. The path integral is used to compute the scattering matrix in terms of the electrons in the leads. This method is suitable for computing the conductivity. We investigate a chiral Majorana Hamiltonian and show that in the absence of vortices the conductivity vanishes. We compute the conductivity for p wave superconductor coupled to two metallic leads, and we show that when the overlapping energy between the two Majorana fermions is finite, the Andreev Crossed reflection conductance is finite.

Keywords:

Andreev, Majorana

1. Introduction

At the surface of a topological insulator electrons carry a Berry phase of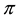; in the presence of an attractive interactions superconductivity is induced. For a low-level doping we obtain a p-wave topological superconductor. Majorana fermions appear on the surface of a topological insulator in a region where the chemical potential 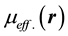changes sign. We consider the effect of the Majorana modes on the p-wave superconductor [1] -[4] . When two metallic leads are attached to the superconductor, the Majorana fermion induces resonant Andreev reflection [5] or crossed Majorana Andreev reflection. With increasing doping, a regular superconductor is ex-

pected with the Andreev conductance of the order of 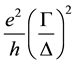(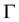is the tunneling width and 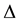is the su-

perconducting gap), which is much smaller than the Andreev conductance carried by the Majorana fermions. The phenomena of Andreev reflection and crossed Andreev reflection can be understood from the general properties of the scattering S [5] -[11] . The scattering matrix S is computed using the continuity equations and the unitarity properties. For finite Majorana energies, it is difficult to obtain the scattering matrix S. For such cases it is

preferable to represent the scattering matrix S as a Dyson series 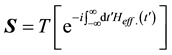[12] , expressed in terms

of the leads Hamiltonian. This is obtained by integrating the Majorana fermions. This approach has the advantage of taking account the renormalization effect for the tunneling matrix element. Experimentally the tunneling for the differential conductance is in disagreement with the quantized values [13] . The purpose of this paper is

to introduce the scattering matrix S as a Dyson series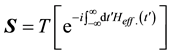. Using the scattering matrix we

will compute the differential conductance for different cases considered in the literature. The plan of the paper is as follows. In Section 2, we formulate the problem in terms of the leads and the fermionic representation of the Majorana fermions. In Section 3, we consider a superconducting island deposited on the surface of a three-dimensional topological insulator. The area outside the superconductor is gaped by a ferromagnetic material. We demonstrate that in the absence of vortices the conductivity between the metallic leads vanishes. In Section 4, we consider two Majorana fermions coupled to two leads and compute the Andreev crossed reflection for the p-wave superconductor. Section 5 is devoted to conclusions.

2. Majorana Fermions for a P-Wave Superconductor

We consider a p-wave superconductor described by the 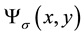the Bogoliubov-de Genes fermion operator. At the boundary between the superconductor and the metallic leads Majorana zero modes are formed (the chemical potential changes sign). The Bogoliubov-de Genes operator contains also the zero modes given by the operator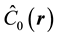. The coupling of the p-wave superconductor to the two leads is given by,

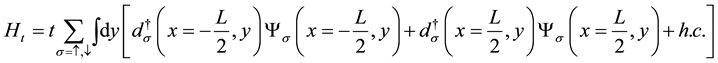(1)

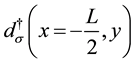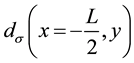, are the fermions in the left lead and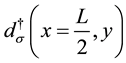, repre-

sent the fermions in the right lead.

I the presence of the Majorana fermions we replace the Bogoliubov-de Genes operator 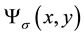by the zero mode part.

For an even number of Majorana fermions, we replace the zero mode by the representation:

(2)

The spinors are given by and

(3)

The two component spinors are localized at the positions and. We introduce the fermion operators and,. The transformation between the two representation is given by:

, ,.

The overlap between different Majorana fermions will introduce the energy for the Majorana Hamiltonian:. This allows to obtain the Majorana action,

(4)

The action in Equation (4) allows for the construction of the integral for the Majorana fermions which will be used for computing the conductivity. For an odd number of Majorama Fermions we will have for the

Majorana an unpaired Fermionic, we can choose for or.

3. A Chiral Majorana Fermion Coupled to Two Leads

We consider a grounded superconducting island of radius R deposited on the surface of a three dimensional topological insulator. The area outside the superconductor is gaped by a ferromagnetic material. We will attach the superconducting island to two leads at (left lead) and (right lead). We will show that in the absence of vortices the left lead is effectively not coupled to the right lead and therefore the conductance vanish.

3.1. No Vortex in the Superconductor

The Hamiltonian at the interface is described by a chiral Majorana Hamiltonian.

(5)

We replace the Majorana fermion by regular fermions and,

and expand the fermion in angular momentum states:. The Majorana Hamiltonian takes the Bogoliubov-de Genes form:

(6)

The Bogoliubov-de Genes eigenvalues for the Hamiltonian in Equation (6) are: and.

The eigenspinors are, (for the zero eigenvalue) and (for the non zero eigenvalues).

(7)

The tunneling Hamiltonian is given by

(8)

We substitute the eigenspinor, and and find:

(9)

The Hamiltonian in Equation (9) is independent from. The integration of the Majorana fermions in Equations (7)-(10) will give a scattering matrix. We find that the scattering matrix depends only on the right

lead! The left lead which couples to will not appear in the scattering

matrix! As a result the cross-Andreev conductance will vanish.

3.2. A Vortex inside the Superconductor

When a vortex is added to the case considered in case given in 3.1 we need to add the impurity Hamiltonian:

(10)

is the Majorana vortex which couple with the strength to the chiral Majorana fermion. Due to this coupling the two leads will be coupled and the cross-Andreev conductance will be finite. The exact result of the Andreev conductance will depend on the details of the coupling.

4. A Pair of Two Majorana Fermions Coupled to Two Leads

We consider a grounded p-wave topological superconductor attached to two leads. Close to the leads due to the boundary condition the p-wave superconductor has to Majorana modes. We will compute the Crossed Andreev Reflection a process where an incoming electron from lead 1 is turned into an outgoing hole in lead 2. In this case a single electron at each lead is tunneling into superconductor to form a Cooper pair. We consider

two half vortices localized in the superconductor at and.

For this case, we have for the zero modes,

(11)

where and are the two Majorana operators. We attach the two leads at and, and due to the non-locality of the spinors, the Majorana fermions couples to the

fermions in the two leads. We consider a situation where the two Majorana fermions overlap with energy. Using the energy we construct the Hamiltonian. The tunneling Hamiltonian between the leads and the Majorana fermions is given by the Hamiltonian:

(12)

, are the fermions in the left lead and, are

the fermions in the right lead. describes the overlapping between the two Majorana Fermions (two independent half vortices). The two vortices are localized at positions R₁, R₂ and their wave functions are non-orthogonal.

We replace the two Majorana Fermions with a single fermion, and. The

tunneling Hamiltonian is given in terms of leads operators and V form:

(13)

The operators and V are expressed in terms of the one dimensional leads:

(14)

The action for this case is given by:

(15)

Using the Grassman integration [14] (see Equation (1.191) in Nakahara) for the Majorana Fermions, we obtain the effective Hamiltonian for the leads:

(16)

For the electrons in the leads, we use the right (R) and left (L) movers representation. and are the electrons in the left lead (1) and and are the eletrons in the right lead (1).

(17)

We apply on the left lead a voltage, and on the right lead a voltage. As a result, we obtain for each lead, two Green’s functions. For the left lead (1) we have (right mover) and (left mover).

(18)

Similarly, for the right (2) lead we have

(19)

is the step function which is zero for and one for). The current in the leads is given by:

. v is then electron velocity in both leads,

is the current density in the left (1) lead, and is the current density in the right lead (2) [15] . In order to compute the current, we will compute the Green’s functions. The Green’s function will be computed perturbatively using the effective coupling to the leads given in Equation (16). is represented in terms of one dimensional fermions given in Equation (17) we have for each lead and fermions. The perturbation theory is controlled by the coupling constant g². We will compute

perturbatively the Green’s function, (left leads) and, (right leads) (the index 1 and 2 represent the leads and L and R represents the left and right

fermions). This Green’s function contains the contributions of the particles-holes, particles-particles, and holes-holes in the same and opposite leads. From the Green’s function we extract the self energies for each lead and each mover, , and,. We find, to order, the self energies:

(20)

where is the band with, is a damping factor which is induced at high momenta, and is the Majorana energy. The imaginary part of the self energy obeys and the real part of the self energy obeys. The Green’s funtions are given in terms of the self energies:

(21)

The real part of the self energy is used to compute the wave function renormalization function.

(22)

The tunneling current at the left leads will be given by (which replaces the expression for zero voltage) in terms of the renormalized Green’s function.

(23)

We will use to evaluate the differential conductance for the Crossed Andreev

reflection. Due to the nonlinearity of the effective action, we will use the scaling equations [12] [15] -[18]

for the coupling constant g². The scaling of g² determines the width. We find the Renormalization Group

equation for the width, with. The solution as a function of

is given by:

(24)

This solution will be used in Equation (23), where is replaced by. Substituting gives us

the result for the differential conductance,

(25)

We find that for a pair of vortices the Andreev crossed reflectioion obeys. Figure 1 shows the differential v conductivity for the Andreev crossed reflection as a function of the voltage difference

between the two leads. We observe that in the limit the maximum value for the conductance is obtained. This result follows from the scaling equation for the width given in Equation (24).

Comparing the diferential conductivity with the experiments [13] one observes that the perfect quantization is

not achieved this suggest the possibility that the width is controlled by additional operators causing not to flow to zero when.

5. Conclusion

In this paper we have introduced a new method for computing the conductance in the presence of the Majorana Fermions. We map the problem of Majorana fermions to regular fermions for which a path integral and the Berry phase are obtained. This allows us to integrate out the Majorana fermions and allows us to obtain the

scattering matrix S as a Dyson series. Using this method we have computed the differential

conductance for different cases, Achiral Majorana fermion coupled to leads with and without an additional vortex and studied the Andreev crossed reflection for a pair of Majorana coupled to two leads. We have computed

the differential v conductivity for the Andreev crossed reflection as a function of the voltage difference

between the two leads. We observe that in the limit the conductance reaches the maximum value.

Cite this paper

DavidSchmeltzer, (2015) The Andreev Crossed Reflection—A Majorana Path Integral Approach. Journal of Modern Physics,06,1371-1379. doi: 10.4236/jmp.2015.69142

References