Journal of Modern Physics
Vol.4 No.6(2013), Article ID:33466,5 pages DOI:10.4236/jmp.2013.46117
Stability of Triangular Points of the Generalized Photogravitational Robes Restricted Three-Body Problem
Department of Statistics and Mathematical Sciences, Kwara State University, Malete-Ilorin, Nigeria
Email: raz11ng@yahoo.com
Copyright © 2013 Abdul Razaq Abdul Raheem. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 5, 2013; revised April 15, 2013; accepted May 13, 2013
Keywords: Stability; Triangular Points; Robes Problem; Density Parameter
ABSTRACT
The linear stability of the triangular points was studied for the Robes restricted three-body problem when the bigger primary (rigid shell) is oblate spheroid and the second primary is radiating. The critical mass obtained depends on the oblateness of the rigid shell and radiation of the second primary as well as the density parameter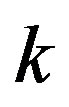 . The stability of the triangular points depends largely on the values of
. The stability of the triangular points depends largely on the values of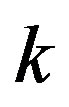 . The destabilizing tendencies of the oblateness and radiation factors were enhanced when
. The destabilizing tendencies of the oblateness and radiation factors were enhanced when 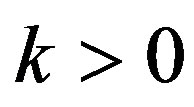 and weakened for
and weakened for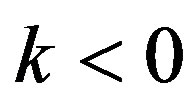 .
.
1. Introduction
Robe [1] introduced a new kind of restricted three-body problem that incorporates the effect of buoyancy force. One of the primaries 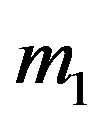 is a rigid shell of mass filled with homogeneous incompressible fluid of density
is a rigid shell of mass filled with homogeneous incompressible fluid of density . The second primary
. The second primary 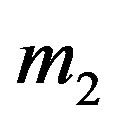 is a point mass located outside the shell. The third body
is a point mass located outside the shell. The third body 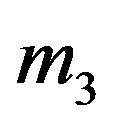 is the particle of negligible mass of density
is the particle of negligible mass of density 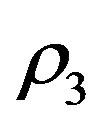 which moves inside the shell under the influences of the gravitational attraction of the primaries and the buoyancy force of the fluid of density
which moves inside the shell under the influences of the gravitational attraction of the primaries and the buoyancy force of the fluid of density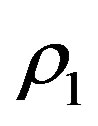 . Robe studied the motion of the infinitesimal mass when
. Robe studied the motion of the infinitesimal mass when 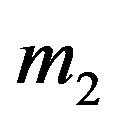 describes both circular and elliptic orbits. He obtained the equilibrium points and showed that, for the circular case, the equilibrium point is linearly stable when
describes both circular and elliptic orbits. He obtained the equilibrium points and showed that, for the circular case, the equilibrium point is linearly stable when 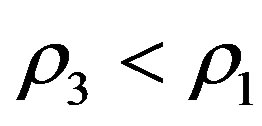 and unstable when
and unstable when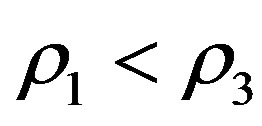 .
.
Robes model may be useful for studying the small oscillations of the earth’s inner core by taking into consideration the moon’s attraction. The model is also applicable to the study of the motion of the artificial satellite under the influence of the earth’s attraction.
Robes problem has been modified to define a new problem (Shrivastava and Garain [2], Plastino and Plastino [3], Giordano, Plastino and Plastino [4], Hallan and Rana [5] and Hallan and Mangang [6]).
In our model we consider a rigid shell which is oblate spheroid and the second primary which radiates to study the effect of oblateness of the first primary and radiation of the second primary on the stability of the triangular equilibrium points of the Robes restricted three-body problem.
The paper consists of four sections. Section one establishes the relevant equations of motion that incorporates the effect of buoyancy force using some basic assumptions. In the second section we obtained the equilibrium points. Section three deals with the variational equations of motion of the problem and solutions of the resulting characteristic equation obtained. In section four, we obtained the critical mass of the mass parameter. This is followed by the conclusion on the findings.
2. Equations of Motion
Let the mass of the rigid shell be 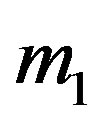 and the point mass be
and the point mass be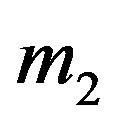 . Let the density of the incompressible fluid inside the shell be
. Let the density of the incompressible fluid inside the shell be 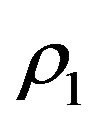 and that of the infinitesimal mass be
and that of the infinitesimal mass be 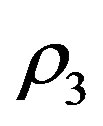 and it’s mass
and it’s mass . Let
. Let  denote the oblateness coefficient of the first primary such that
denote the oblateness coefficient of the first primary such that 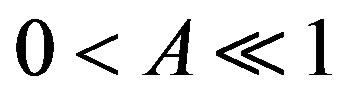 and
and 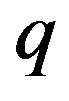 the radiation force of the second primary which given by
the radiation force of the second primary which given by 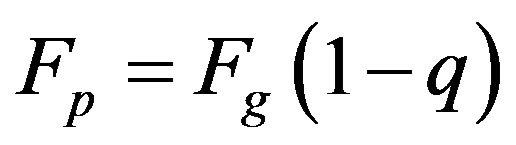 such that
such that .
.
Let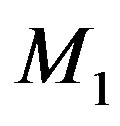 ,
, 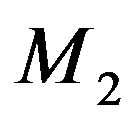 and
and 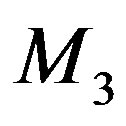 be the centers of
be the centers of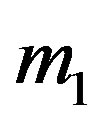 ,
,  and
and 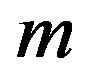 respectively such that
respectively such that 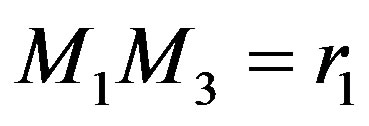 and
and 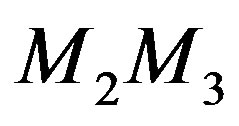
 . Let G be the gravitational constant and
. Let G be the gravitational constant and 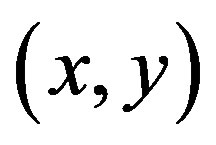 the coordinates of the infinitesimal mass
the coordinates of the infinitesimal mass . Let the line joining
. Let the line joining 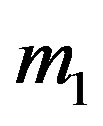 and
and 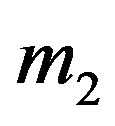 be the
be the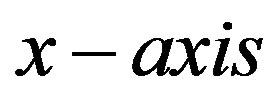 . Then the total potential acting on
. Then the total potential acting on 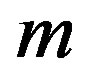 is
is
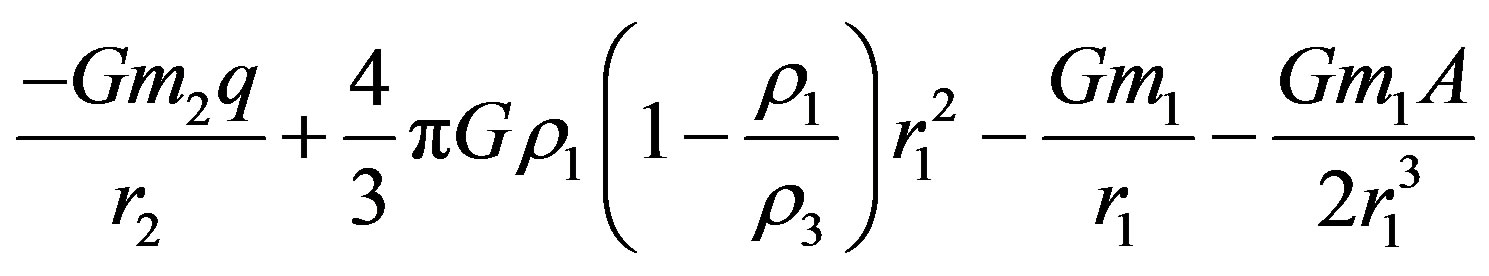 (1)
(1)
where
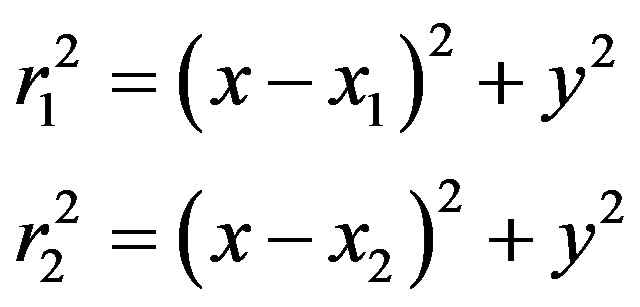 (2)
(2)
Let the coordinates of 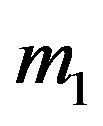 and
and 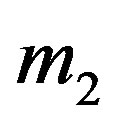 be
be 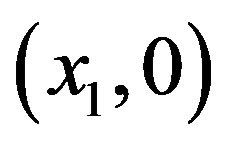 and
and 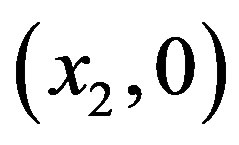 respectively. In the dimensionless rotational coordinate system we choose the unit of mass to be the sum of the masses of the primaries (
respectively. In the dimensionless rotational coordinate system we choose the unit of mass to be the sum of the masses of the primaries (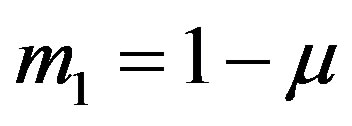 and
and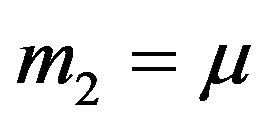 ). We take the unit of length equal to the distance between the primaries and is chosen such that
). We take the unit of length equal to the distance between the primaries and is chosen such that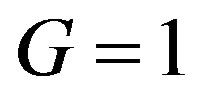 .
.
The equations of motion of the infinitesimal body are (AbdulRaheem and Singh, [7]),
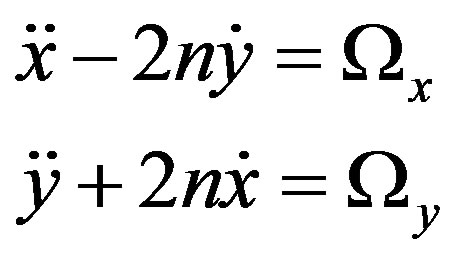 (3)
(3)
where
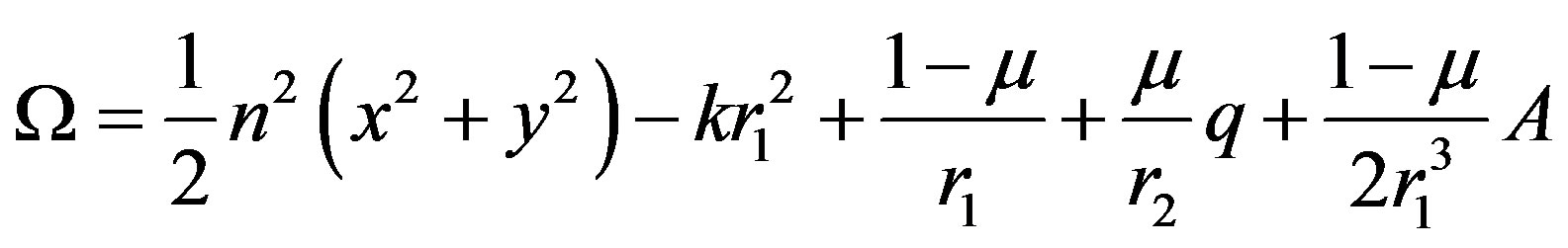 (4)
(4)
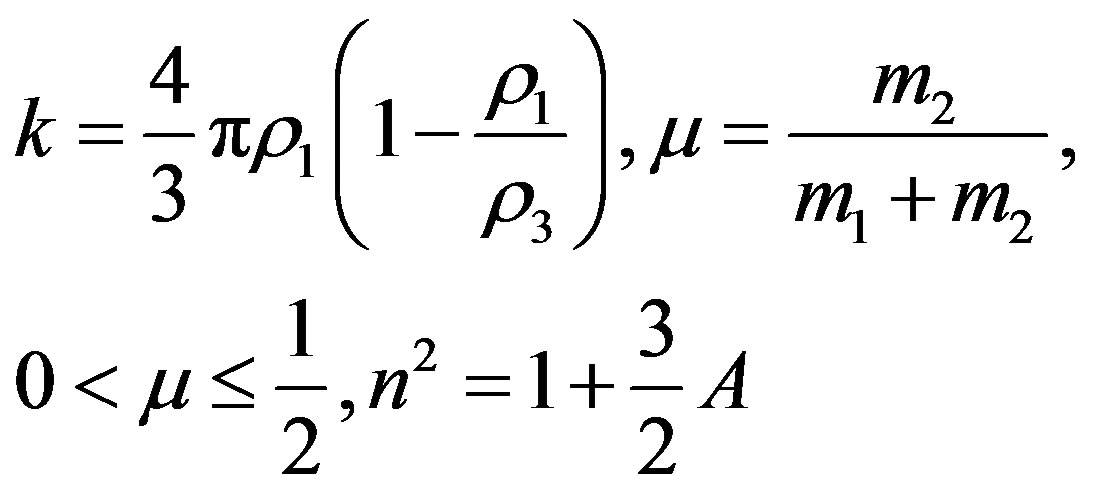
 (5)
(5)
3. Equilibrium Points
Equilibrium points exist when
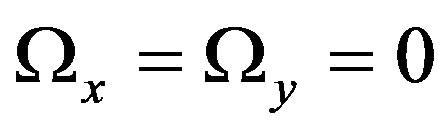 (6)
(6)
For 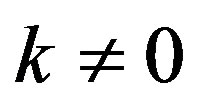 we have
we have
 (7)
(7)
 . (8)
. (8)
Triangular Points
The triangular points are given by the equations
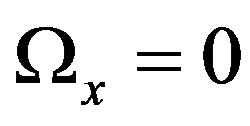 ,
, 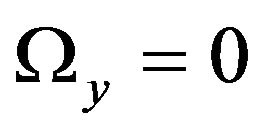 ,
, .
.
That is
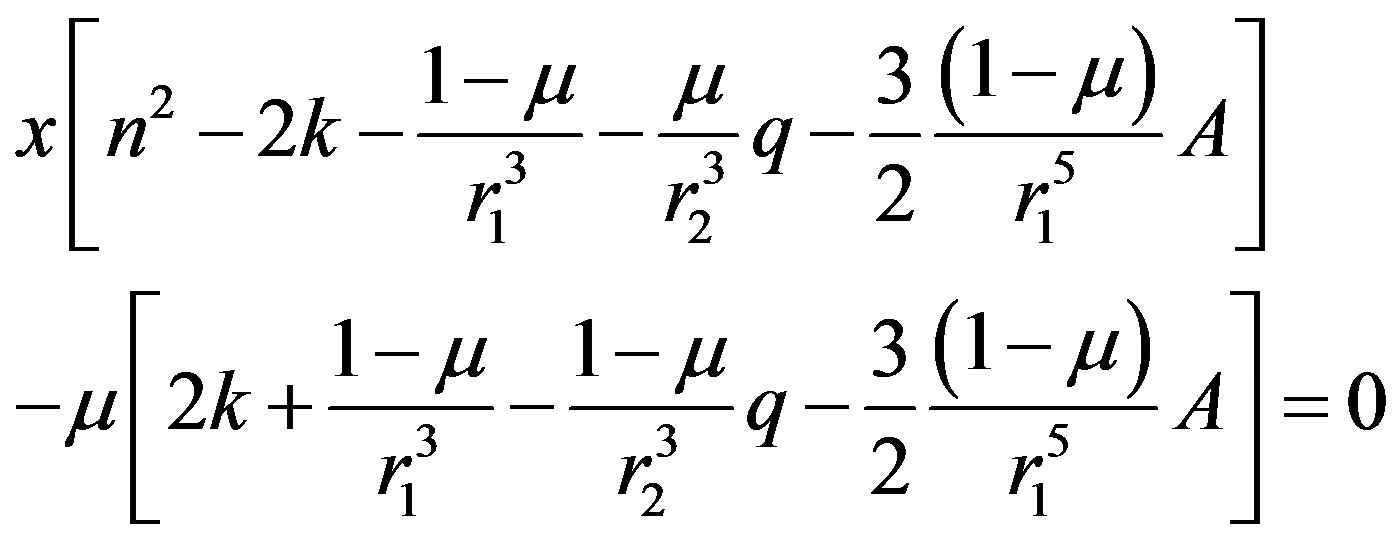 (9)
(9)
and
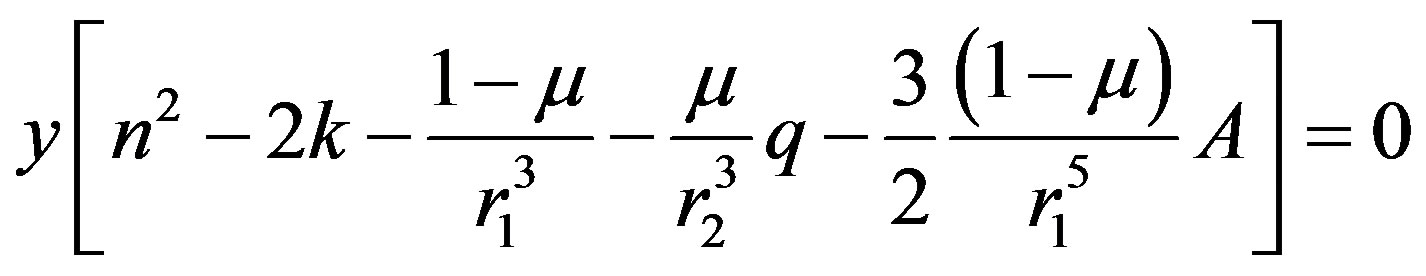 . (10)
. (10)
Equations (9) and (10) give
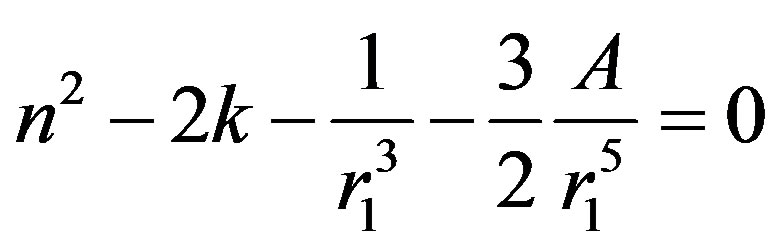 (11)
(11)
 (12)
(12)
Knowing  and
and 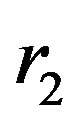 from Equations (11) and (12) the exact coordinates of the triangular points are obtained by using Equation (5) for
from Equations (11) and (12) the exact coordinates of the triangular points are obtained by using Equation (5) for 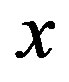 and
and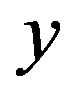 .
.
Thus
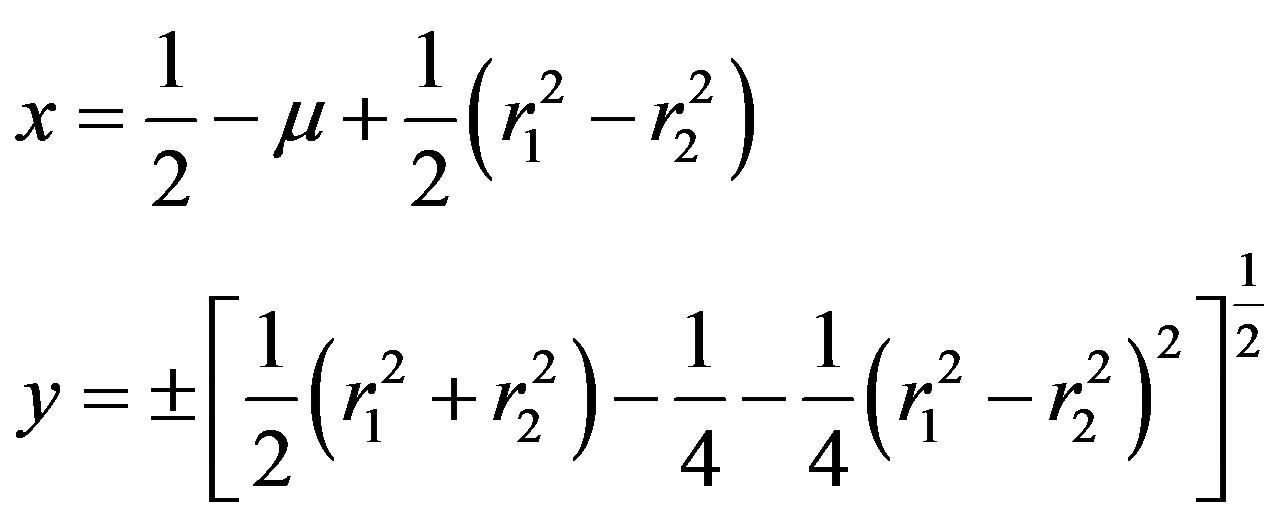 (13)
(13)
When the bigger primary is not oblate, the smaller primary is not radiating and 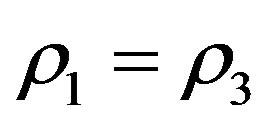
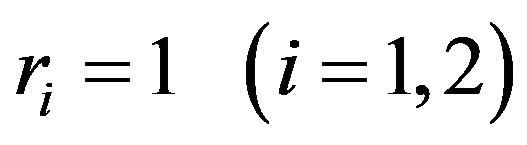 . (14)
. (14)
We assume the solutions of equations (11) and (12) are
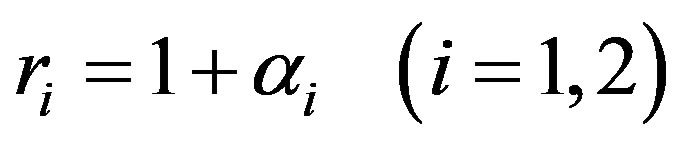 (15)
(15)
where 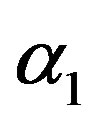 and
and 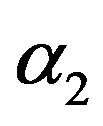 are very small perturbations. Using Equations (11) and (12) and restricting ourselves to linear terms in
are very small perturbations. Using Equations (11) and (12) and restricting ourselves to linear terms in ,
, 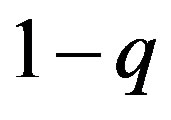 and
and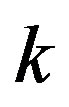 , we obtain
, we obtain
 (16)
(16)
The coordinates 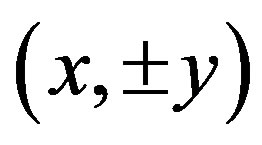 obtained in Equation (16) are the triangular points and are denoted by
obtained in Equation (16) are the triangular points and are denoted by 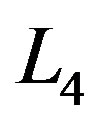 and
and .
.
4. Stability of Triangular Points
Putting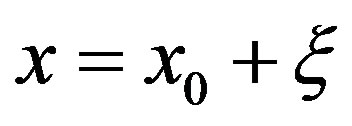 ,
, 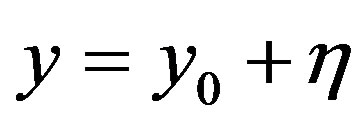 in Equation (3), in order to study the motion near the triangular points
in Equation (3), in order to study the motion near the triangular points  and
and , we obtain the variational equations of motion as
, we obtain the variational equations of motion as
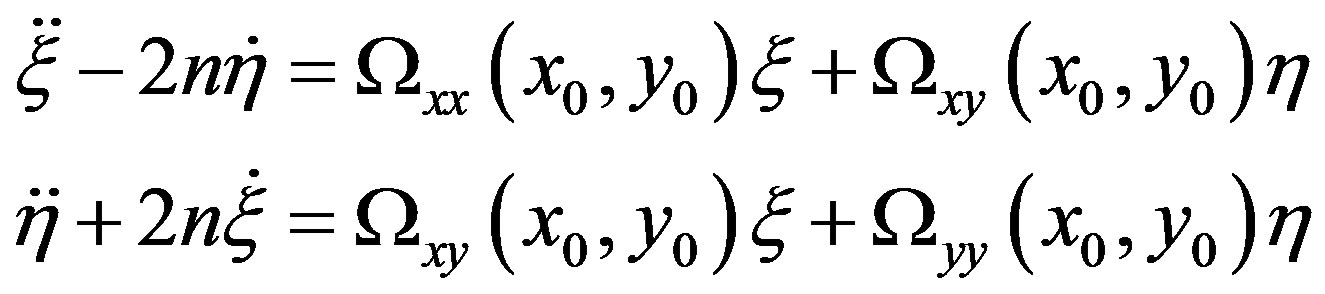 (17)
(17)
The characteristic equation is
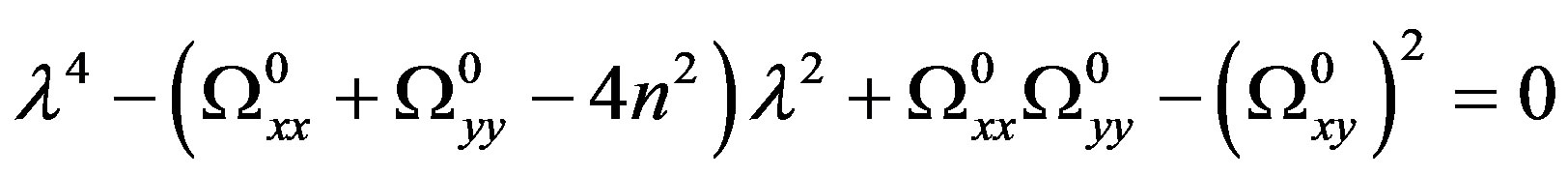 (18)
(18)
where the superscript 0 indicates that the partial derivatives are evaluated at the triangular points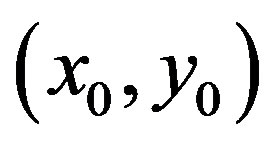 , and are given by
, and are given by
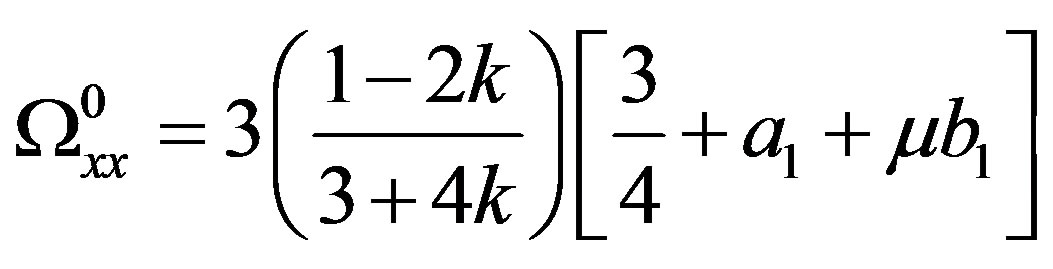
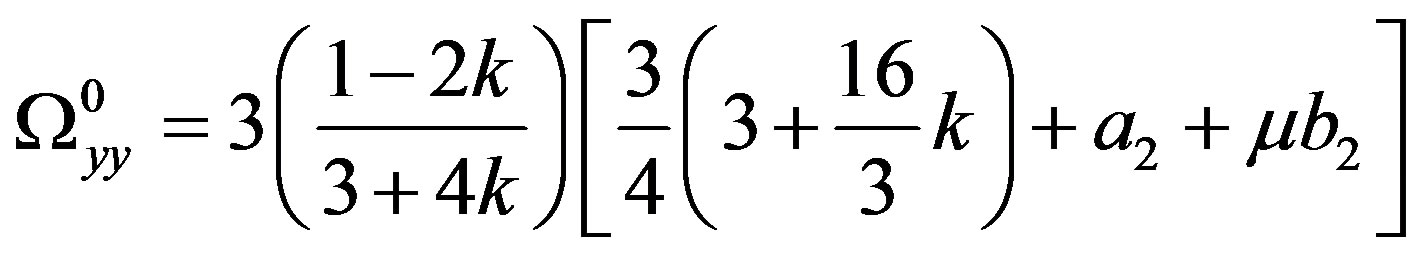
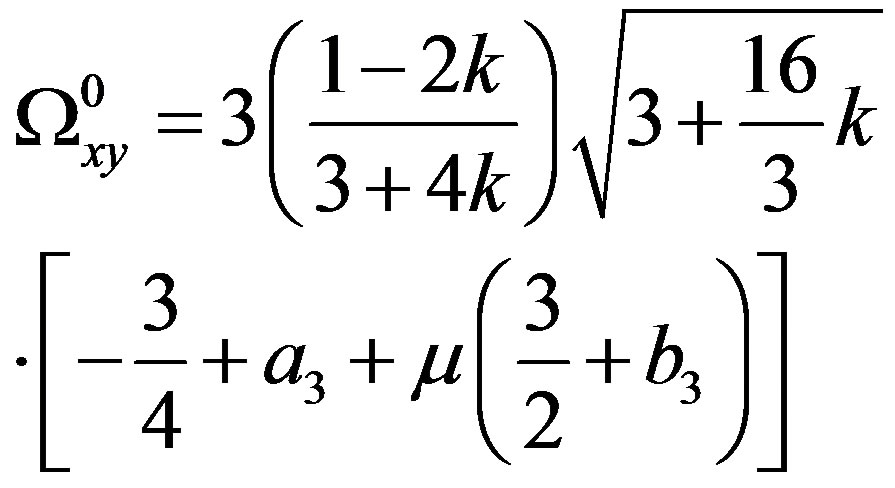
where
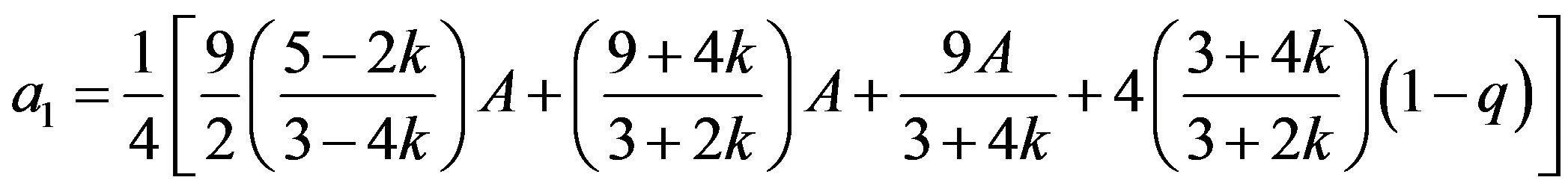
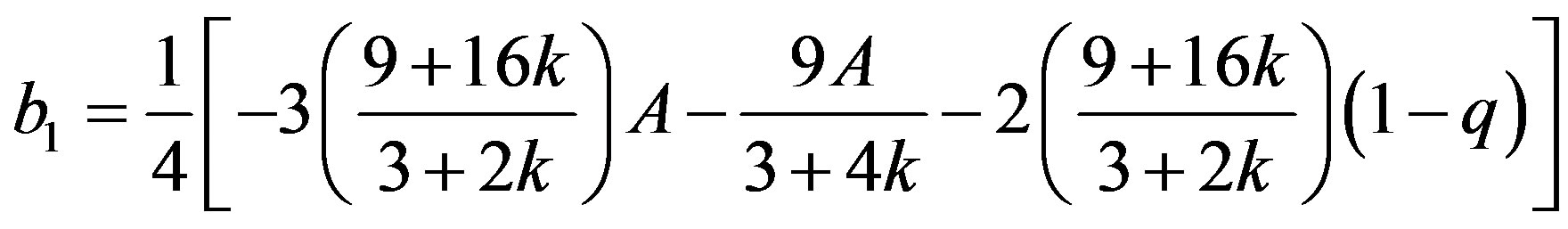
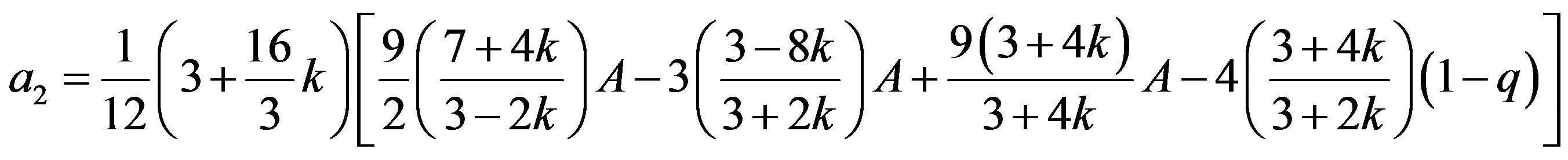
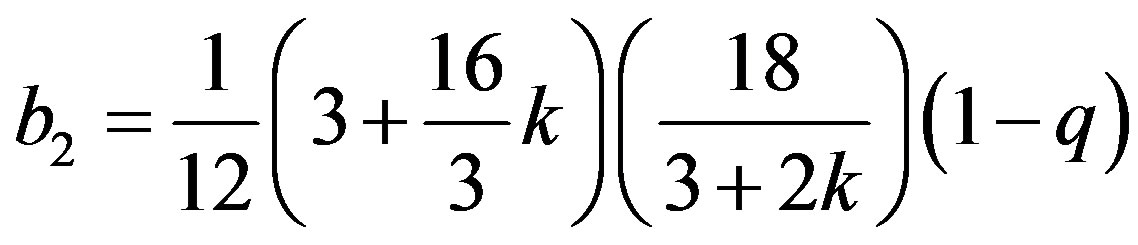
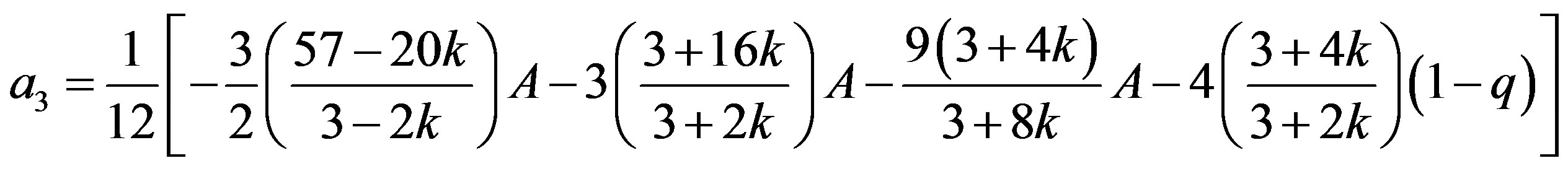
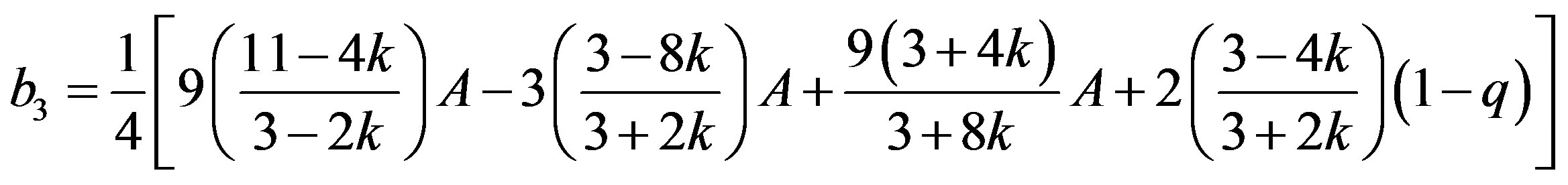 (19)
(19)
Each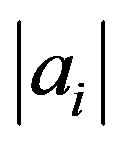 ,
, 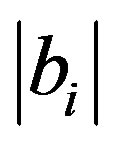 is very small.
is very small.
The characteristic equation becomes
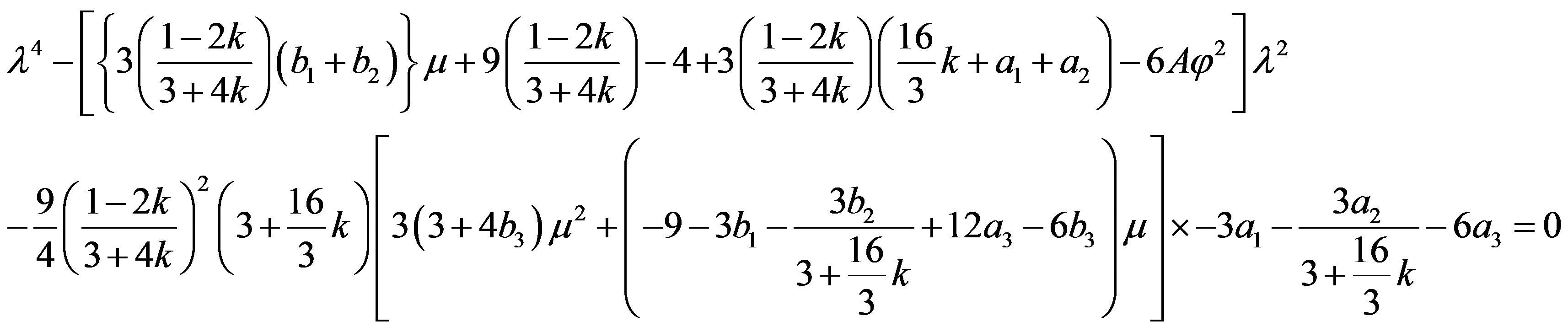
Its roots are

We observe that the roots are functions of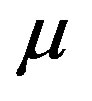 ,
, 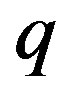 ,
,  ,
, 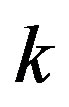 and they depends upon the nature of the discriminant
and they depends upon the nature of the discriminant  and is given by
and is given by
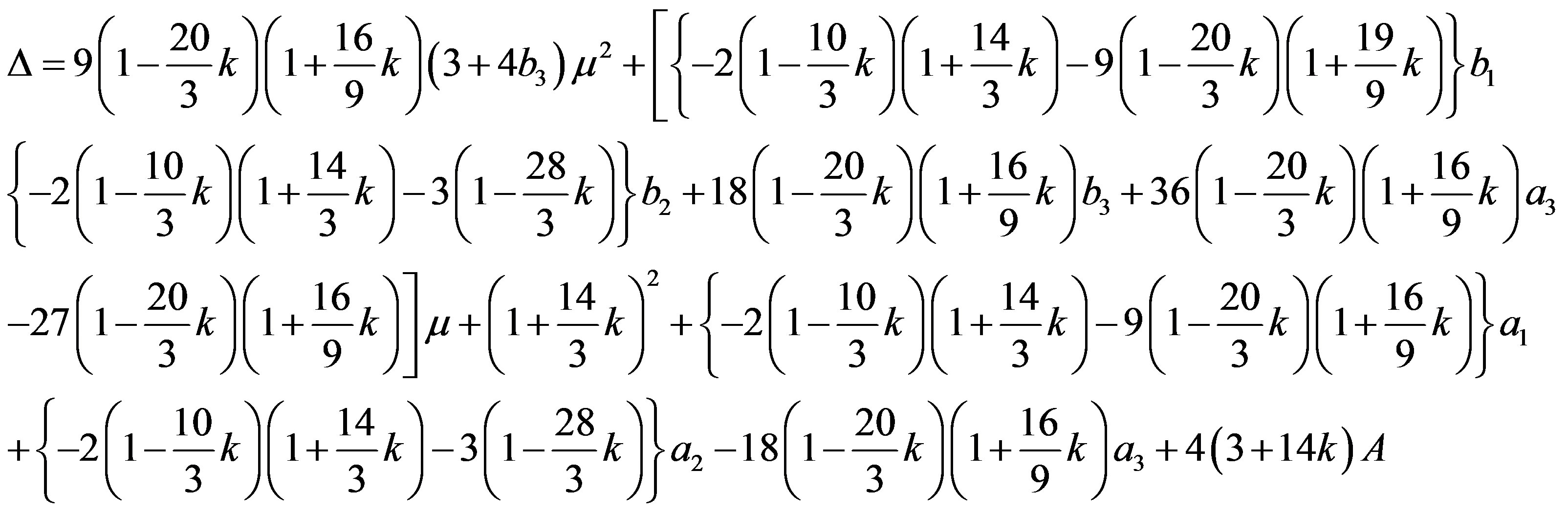 . (20)
. (20)
Three cases can be discussed for :
:
1) When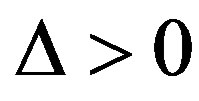 , we have that the roots are negative showing that the triangular points are linearly stable.
, we have that the roots are negative showing that the triangular points are linearly stable.
2) When , we have that the real parts of two of the four roots are positive and equal, showing that the triangular points are unstable.
, we have that the real parts of two of the four roots are positive and equal, showing that the triangular points are unstable.
3) When , we have that the double roots give secular terms, showing that the triangular points are unstable.
, we have that the double roots give secular terms, showing that the triangular points are unstable.
5. Critical Mass
The solution of the equation 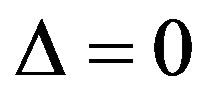 gives the critical mass value
gives the critical mass value 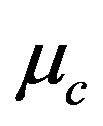 of the mass parameter. That is
of the mass parameter. That is
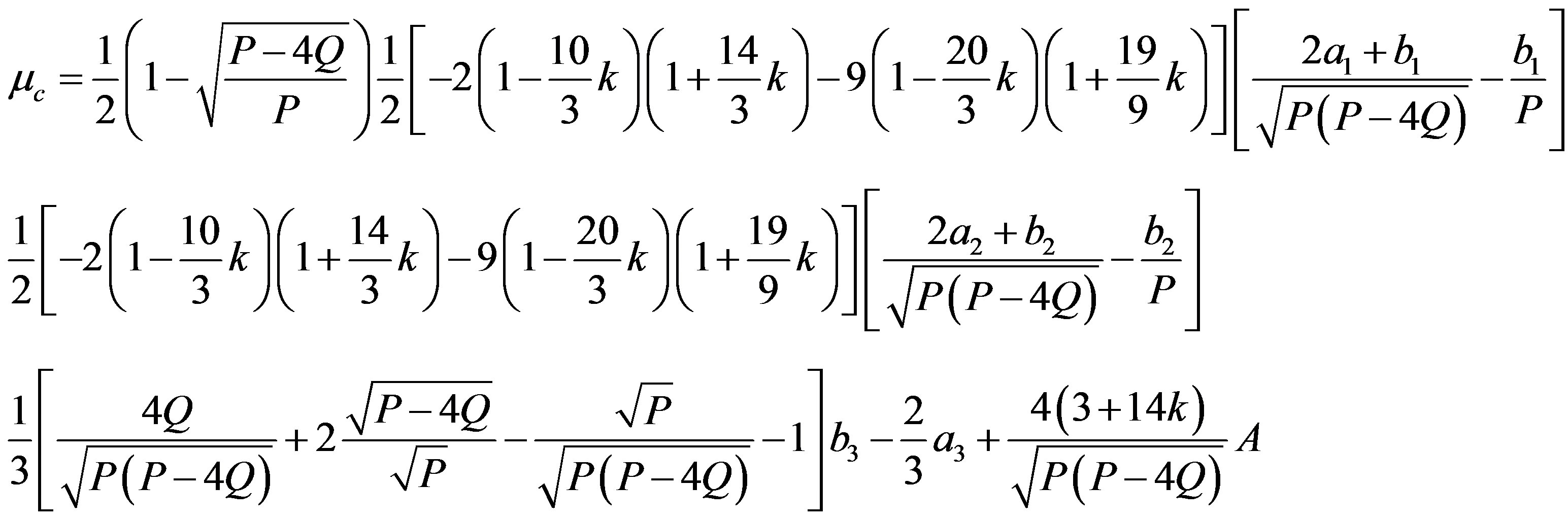 (21)
(21)
where 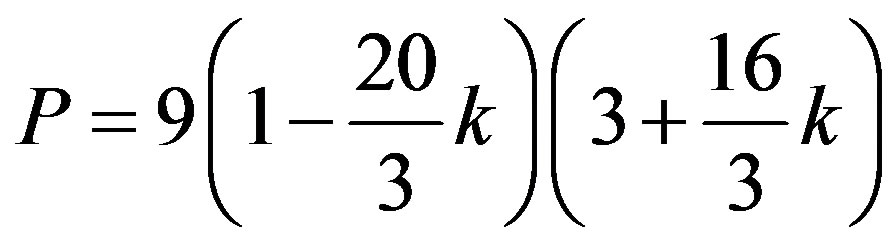 and
and
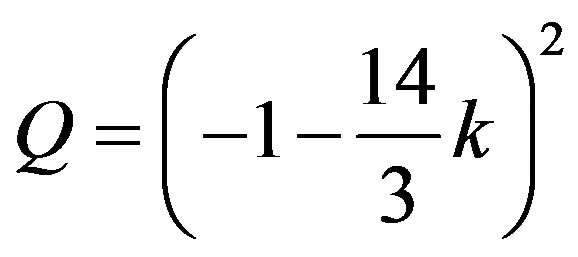 . Restricting ourselves to linear terms in
. Restricting ourselves to linear terms in
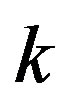 ,
, 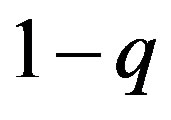 and
and , and neglecting the product
, and neglecting the product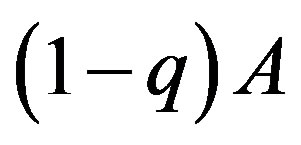 , we find that
, we find that
 (22)
(22)
where
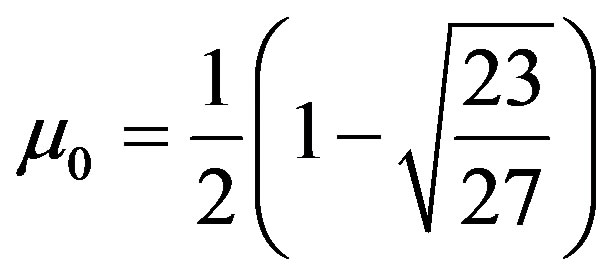
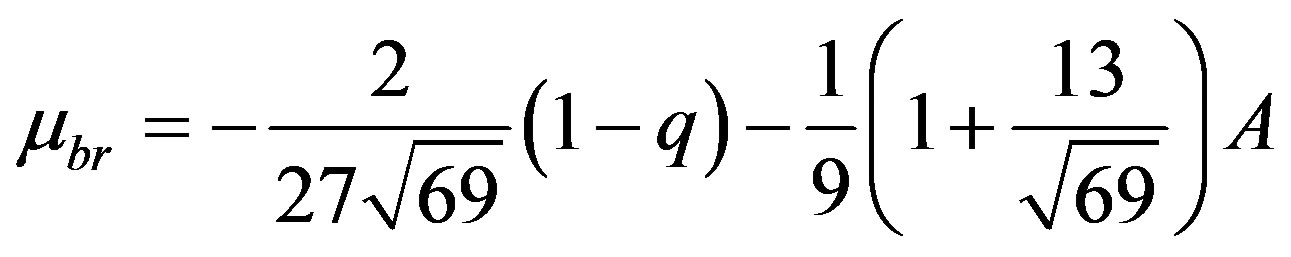
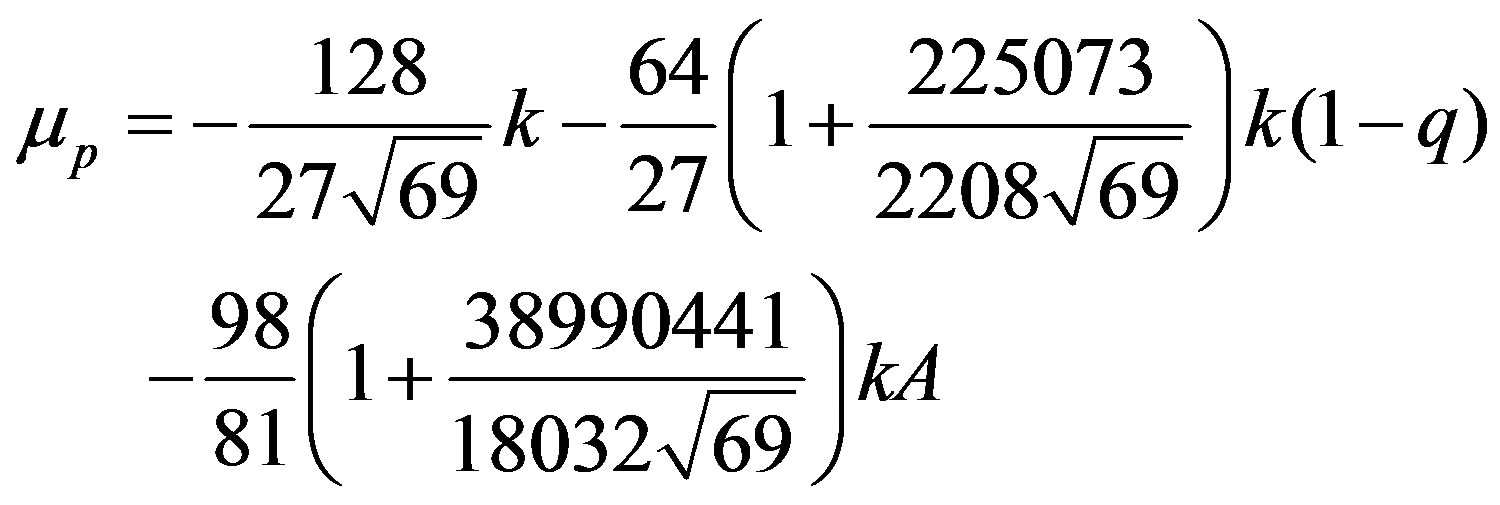
Equation (22) gives the critical mass value 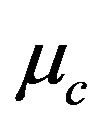 of the mass parameter. It reflects the effect of the oblateness of the first primary (rigid mass) and the radiation of the second primary on the critical mass of the Robes restricted three-body problem, indicating a destabilizing effect on the triangular equilibrium points.
of the mass parameter. It reflects the effect of the oblateness of the first primary (rigid mass) and the radiation of the second primary on the critical mass of the Robes restricted three-body problem, indicating a destabilizing effect on the triangular equilibrium points.
The destabilizing tendencies of both the oblateness and radiating factors are further enhanced when 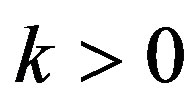
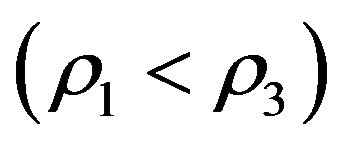 and weakened when
and weakened when 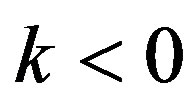
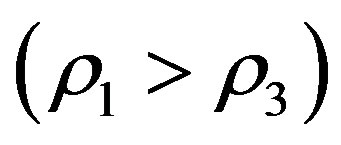 .
.
When  we confirm the result of Abdul Raheem and Singh (2006) for
we confirm the result of Abdul Raheem and Singh (2006) for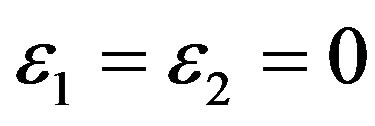 ,
, 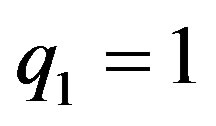 and
and .
.
When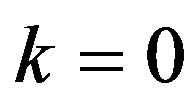 ,
, 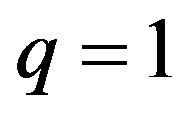 and
and 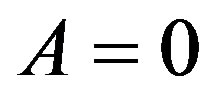 we obtain the critical mass value of the classical restricted three-body problem.
we obtain the critical mass value of the classical restricted three-body problem.
6. Conclusions
The effect of oblateness of the first primary (rigid shell) and radiation of the second primary on the stability of the triangular equilibrium points of the Robes restricted three-body problem was studied. The value of the critical mass value obtained depends on the oblateness coefficient of the rigid shell, radiation factor of the second primary and the density of the fluid and that of the infinitesimal mass in the shell.
It was observed that the oblateness and radiation factors have destabilizing tendencies on the triangular equilibrium points. These destabilizing tendencies are further enhanced or weakened, depending on whether the density of the fluid in the shell is less than that of the infinitesimal mass or the density of the infinitesimal mass is less than that of the fluid.
REFERENCES
- H. A. G. Robe, Celestial Mechanics, Vol. 16, 1977, pp. 345-351. doi:10.1007/BF01232659
- A. K. Shrivastava and D. Garain, Celestial Mechanics and Dynamical Astronomy, Vol. 51, 1991, pp. 67-73. doi:10.1007/BF02426670
- A. R. Plastino and A. Plastino, Celestial Mechanics and Dynamical Astronomy, Vol. 61, 1995, 197-206. doi:10.1007/BF00048515
- C. M. Giordano, A. R. Plastino and A. Plastino, Celestial Mechanics and Dynamical Astronomy, Vol. 66, 1997, pp. 229-242. doi:10.1007/BF00054966
- P. P. Hallan and N. Rana, Indian Journal of Pure and Applied Mathematics, Vol. 35, 2004, pp. 401-413.
- P. P. Hallan and K. B. Mangang, Planetary and Space Science, Vol. 55, 2007, pp. 512-516. doi:10.1016/j.pss.2006.10.002
- A. AbdulRaheem and J. Singh, Astronomical Journal, Vol. 131, 2006, pp. 1880-1885. doi:10.1086/499300

