Journal of Modern Physics
Vol.3 No.8(2012), Article ID:21676,6 pages DOI:10.4236/jmp.2012.38107
Semileptonic Decay of Bc Meson into S Wave Charmonium in a QCD Potential Model with Coulombic Part as Perturbation
1Department of Physics, Arya Vidyapeeth College, Guwahati, India
2Department of Physics, Gauhati University, Guwahati, India
Email: kkingkar@gmail.com
Received May 2, 2012; revised May 31, 2012; accepted June 16, 2012
Keywords: Dalgarno Method; Isgur-Wise Function; Form Factors; Decay Width
ABSTRACT
We present the semileptonic decay of Bc meson in a QCD potential model with the coulombic part of the Cornell potential 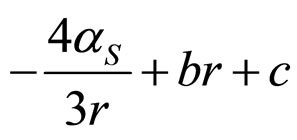 as perturbation. Computing the slope and curvature of Isgur-Wise function in this approach, we study the pseudoscalar and vector form factors for the transition of Bc meson to its S wave charmonium
as perturbation. Computing the slope and curvature of Isgur-Wise function in this approach, we study the pseudoscalar and vector form factors for the transition of Bc meson to its S wave charmonium  states. Numerical estimates of widths for the transitions of
states. Numerical estimates of widths for the transitions of 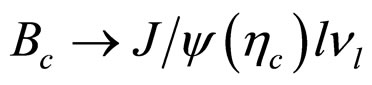 are presented.
are presented.
1. Introduction
The investigation of weak decays of mesons composed of a heavy quark and antiquark gives a very important insight in the heavy quark dynamics. The exclusive semileptonic decay processes of heavy mesons generated a great excitement not only in extracting the most accurate values of Cabbibo-Kobayashi Maskawa (CKM) matrix elements but also in testing diverse theoretical approaches to describe the internal structure of hadrons. The great virtue of semileptonic decay processes is that the effects of the strong interaction can be separated from the effects of the weak interaction into a set of Lorentzinvariant form factors, i.e., the essential informations of the strongly interacting quark/gluon structure inside hadrons. Thus, the theoretical problem associated with analyzing semileptonic decay processes is essentially that of calculating the weak form factors.
The decay properties of the Bc meson are of special interest, since it is the only heavy meson consisting of two heavy quarks with different flavor. This difference of quark flavors forbids annihilation into gluons. As a result, the excited Bc meson states lying below the BD meson threshold undergo pionic or radiative transitions to the pseudoscalar ground state which is considerably more stable than corresponding charmonium or bottomonium states and decays only weakly. The CDF Collaboration reported the discovery of the Bc ground state in 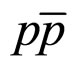 collisions already more than ten years ago [1]. However, up till recently its mass was known with a very large error. Now it is measured with a good precision in the decay channel
collisions already more than ten years ago [1]. However, up till recently its mass was known with a very large error. Now it is measured with a good precision in the decay channel . More experimental data on masses and decays of the Bc mesons are expected to come in near future from the Tevatron at Fermilab and the Large Hadron Collider (LHC) at CERN. The estimates of the Bc decay rates indicate that the c quark transitions give the dominant contribution while the b quark transitions and weak annihilation contribute less. However, from the experimental point of view the Bc decays to charmonium are easier to identify. Indeed, CDF and D0 observed the Bc meson and measured its mass analyzing its semileptonic and nonleptonic decays
. More experimental data on masses and decays of the Bc mesons are expected to come in near future from the Tevatron at Fermilab and the Large Hadron Collider (LHC) at CERN. The estimates of the Bc decay rates indicate that the c quark transitions give the dominant contribution while the b quark transitions and weak annihilation contribute less. However, from the experimental point of view the Bc decays to charmonium are easier to identify. Indeed, CDF and D0 observed the Bc meson and measured its mass analyzing its semileptonic and nonleptonic decays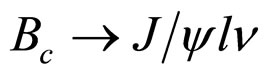 .
.
There are many theoretical approaches to the calculation of exclusive Bc semileptonic decay modes. Some of them are: QCD sum rules [2-4], the relativistic quark model [5-7] based on an effective Lagrangian describing the coupling of hadrons to their constituent quarks, the quasipotential approach to the relativistic quark model [8-10], the instantaneous nonrelativistic approach to the Bethe-Salpeter (BS) equation [11], the relativistic quark model based on the BS equation [12,13], the QCD relativistic potential model [14], the relativistic quark-meson model [15], the nonrelativistic quark model [16], the covariant light-front quark model [17], and the constituent quark model [18-21] using BSW (Bauer, Stech, and Wirbel) model [22] and ISGW (Isgur, Scora, Grinstein, and Wise) model [23]. The purpose of this paper is to extend a QCD potential model [24] with coulombic part as perturbation to calculate the hadronic form factors and decay widths for the exclusive semileptonic decay of Bc meson.
Recently, we have reported the slope and curvature of I-W function for D and B mesons with the coulombic part of the potential as the perturbation in two particular renormalisation schemes  and V scheme [24]. Instead of using a particular renormalisation schemes, here in this manuscript we use the strong coupling constant as a scale dependent parameter and compute the slope and curvature of I-W function for Bc meson with a different set of mass input parameters than that of reference [24]. We then use the I-W function to study the form factors and decay rates of Bc meson into its S wave charmonium
and V scheme [24]. Instead of using a particular renormalisation schemes, here in this manuscript we use the strong coupling constant as a scale dependent parameter and compute the slope and curvature of I-W function for Bc meson with a different set of mass input parameters than that of reference [24]. We then use the I-W function to study the form factors and decay rates of Bc meson into its S wave charmonium 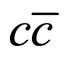 states within the framework of the potential model.
states within the framework of the potential model.
The rest of the paper is organised as follows: Section 2 contains the formalism with its subsections containing the model wavefunction, Masses, hadronic form factors and decay widths. In Section 3 we place our results and conclusions.
2. Formalism
2.1. The Wavefunction
The wavefunction computed by Dalgarno method [25,26] with coulombic part 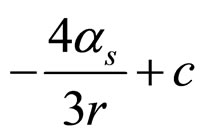 of the potential as perturbation and linear part
of the potential as perturbation and linear part 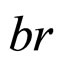 as parent has been reported in reference [24] and the alternate approach of choosing the linear part as perturbation has been reported earlier [27,28]. For the calculations on the hadronic matrix elements, only the long-distance behaviours of the wavefunctions are important or dominant, so that taking the Coulomb piece as a perturbation becomes legitimate. The wavefunction with linear part as parent becomes an Airy function, which in fact is a diverging function. So in this manuscript we consider the wave function upto the order
as parent has been reported in reference [24] and the alternate approach of choosing the linear part as perturbation has been reported earlier [27,28]. For the calculations on the hadronic matrix elements, only the long-distance behaviours of the wavefunctions are important or dominant, so that taking the Coulomb piece as a perturbation becomes legitimate. The wavefunction with linear part as parent becomes an Airy function, which in fact is a diverging function. So in this manuscript we consider the wave function upto the order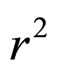 . For completeness we summarise the main equations in this section.
. For completeness we summarise the main equations in this section.
The total wave function corrected upto first order with normalisation is [24]
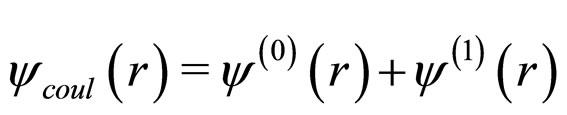 (1)
(1)
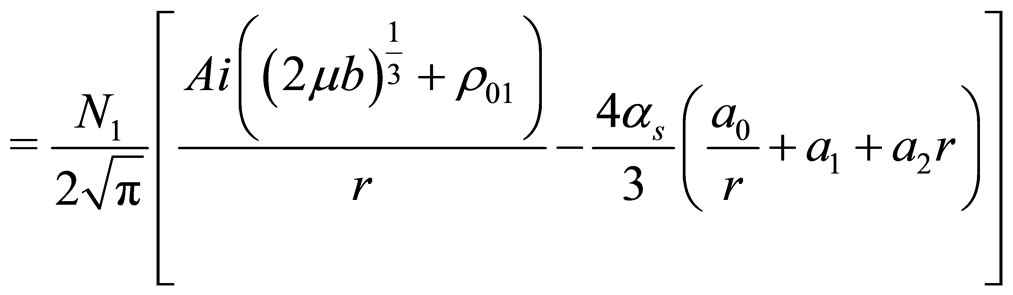 (2)
(2)
where 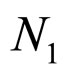 is the normalisation constant for the total wave function
is the normalisation constant for the total wave function  with subscript “coul” means coulombic potential as perturbation.
with subscript “coul” means coulombic potential as perturbation.
Where  are given as [29,30]:
are given as [29,30]:
 (3)
(3)
 (4)
(4)
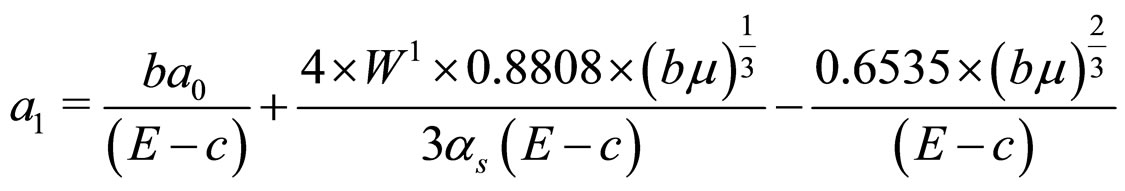 (5)
(5)
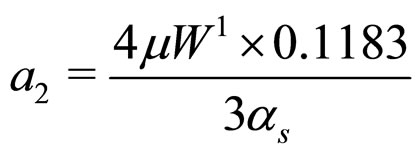 (6)
(6)
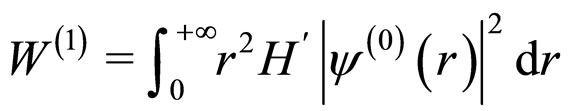 (7)
(7)
and
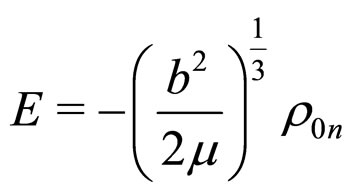 (8)
(8)
here b and c are the model input parameters as is used in our previous works [24,27,28]. “n” is the principal quantum no. (n = 1 for ground state),  is the reduced mass of mesons and
is the reduced mass of mesons and 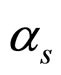 is the strong running coupling constant.
is the strong running coupling constant.
2.2. Pseudoscalar and Vector Form Factors
In the case of the final 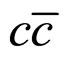 states corresponds to the
states corresponds to the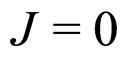 ,
, 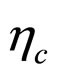 states, as the matrix element of any axial current
states, as the matrix element of any axial current 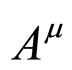 between the two pseudoscalar mesons vanishes, only vector current
between the two pseudoscalar mesons vanishes, only vector current 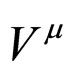 contributes. Unlike in the case of electromagnetic current of the charged pions, here the vector current
contributes. Unlike in the case of electromagnetic current of the charged pions, here the vector current  is not conserved as
is not conserved as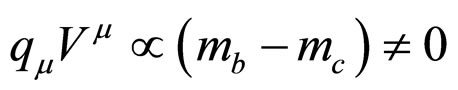 . So the matrix element of the hadronic current,
. So the matrix element of the hadronic current, 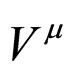 between the two
between the two 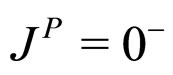 mesons is expressed in terms of two form factors
mesons is expressed in terms of two form factors 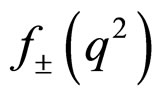 as
as
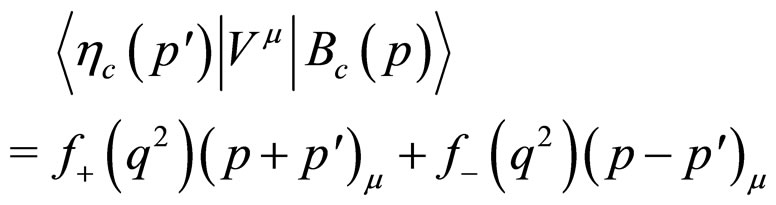 (9)
(9)
where 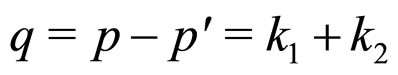 is the four momentum transfer and
is the four momentum transfer and 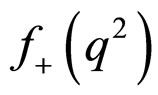 and
and 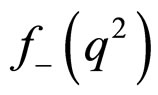 are the dimensionless weak transition form factors corresponds to
are the dimensionless weak transition form factors corresponds to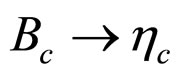 , which are functions of the invariant
, which are functions of the invariant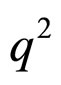 . Here
. Here 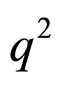 varies within the range
varies within the range
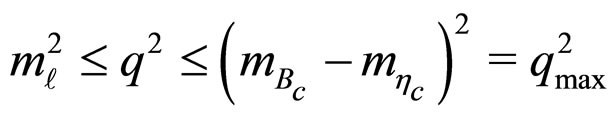 .
.
The transition between the pseudoscalar Bc and the vector  mesons depends on four independant form factors as,
mesons depends on four independant form factors as,
 (10)
(10)

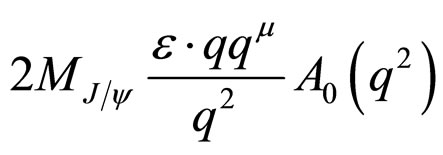 (11)
(11)
In the present study we treat Bc system similar to D 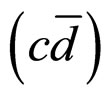 system as the ratio of the constituent quark masses in the Bc meson is very close to that of D meson. So we extend the HQET of the
system as the ratio of the constituent quark masses in the Bc meson is very close to that of D meson. So we extend the HQET of the 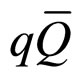 system for the study of Bc meson also. And on the basis of HQET, the most general form of the transition discussed by Equations (9) and (10) can be expressed as [31],
system for the study of Bc meson also. And on the basis of HQET, the most general form of the transition discussed by Equations (9) and (10) can be expressed as [31],
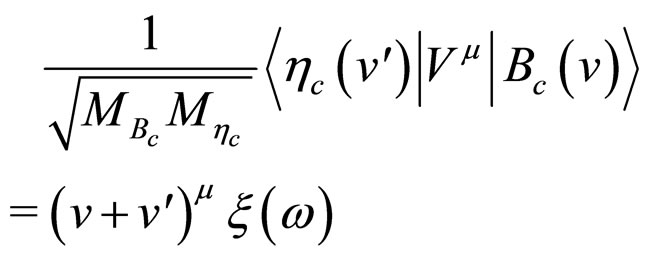 (12)
(12)
 (13)
(13)
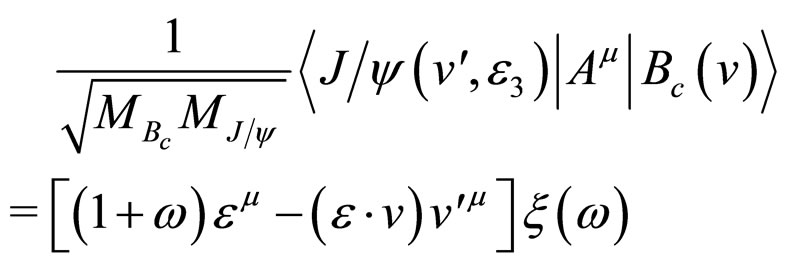 (14)
(14)
where 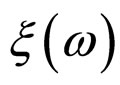 is the Isgur-Wise function. For small, nonzero recoil, it is conventional to write the Isgur-Wise function as [32]:
is the Isgur-Wise function. For small, nonzero recoil, it is conventional to write the Isgur-Wise function as [32]:
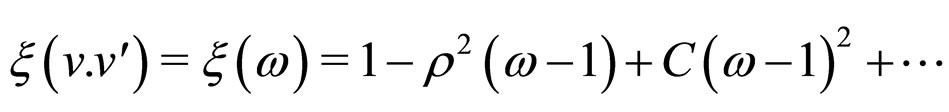 (15)
(15)
where  is given by,
is given by,
 (16)
(16)
The quantity 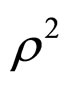 is the slope of I-W function at
is the slope of I-W function at 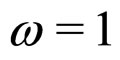 and known as charge radius:
and known as charge radius:
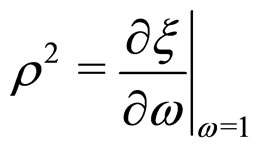 (17)
(17)
The second order derivative is the curvature of the I-W function known as convexity parameter:
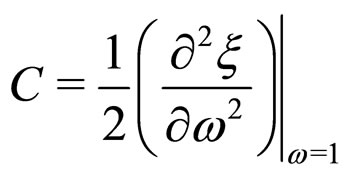 (18)
(18)
For the heavy-light flavor mesons the I-W function can also be written as [27,33]:
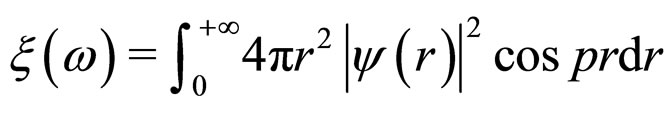 (19)
(19)
where
 (20)
(20)
In Equation (1), the strong coupling constant connected to the potential is a function of the momentum as
 (21)
(21)
where  is the number of flavour and
is the number of flavour and 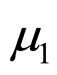 is the renormlistion scale related to the constituent quark mass and
is the renormlistion scale related to the constituent quark mass and  is the QCD scale which is taken as 0.150 GeV by fixing
is the QCD scale which is taken as 0.150 GeV by fixing 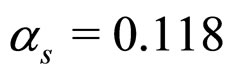 at the Z boson mass (91 GeV). We use the most common renormalisation scale as
at the Z boson mass (91 GeV). We use the most common renormalisation scale as
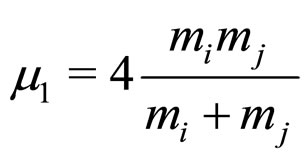
with 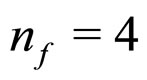 [34] and then evaluate
[34] and then evaluate . For numerical calculation, we use the model input parameters as,
. For numerical calculation, we use the model input parameters as, 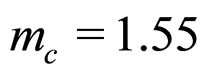 GeV and
GeV and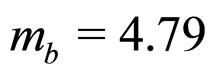 .
.
Using Equations (1), (15) and (19), we compute the slope and curvature of I-W function as
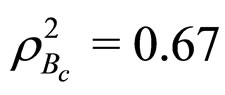 and
and 
Consequently, the form factors 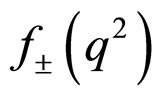 correspond to the
correspond to the 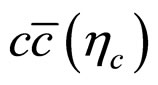 final state are related to the Isgur-Wise function as [31]
final state are related to the Isgur-Wise function as [31]
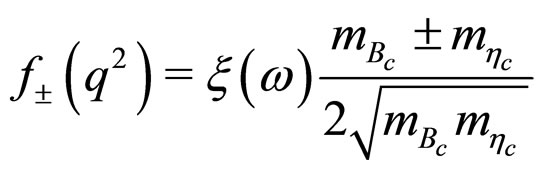 (22)
(22)
and those related to the 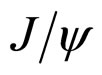 as the final hadronic state are given by
as the final hadronic state are given by
 (23)
(23)
It is evident from Equation (23) that at 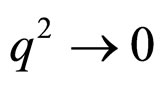
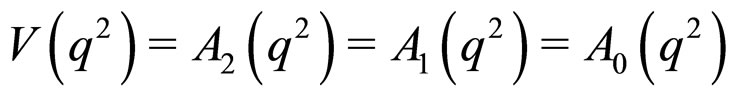 (24)
(24)
Thus knowing the masses and Isgur-Wise function of the transition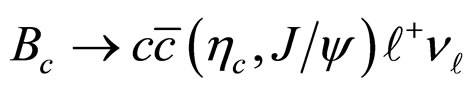 , we will be able to compute respective form factors correspond to
, we will be able to compute respective form factors correspond to 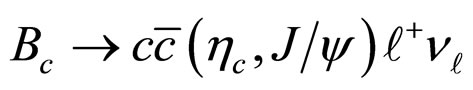 transitions.
transitions.
It should be noted that by virtue of transversality of the lepton current 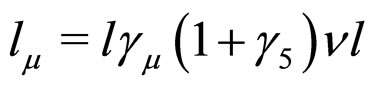 in the limit
in the limit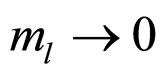 , the probabilities of semileptonic decays into
, the probabilities of semileptonic decays into 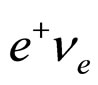 and
and 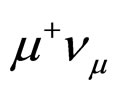 are independent of
are independent of . Thus, in calculation of these particular decay modes of Bc meson this form factor can be consistently neglected [3].
. Thus, in calculation of these particular decay modes of Bc meson this form factor can be consistently neglected [3].
The differential semileptonic decay rates can be expressed in terms of these form factors by
1) 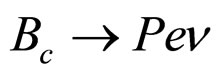 decay (
decay (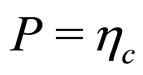 )
)
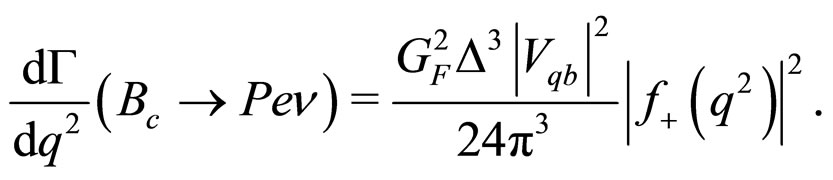 (25)
(25)
2) 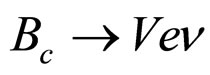 decay (
decay (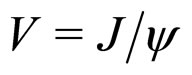 ) The decays rate in transversally and longitudinally polarized vector mesons are defined by [35]
) The decays rate in transversally and longitudinally polarized vector mesons are defined by [35]
 (26)
(26)
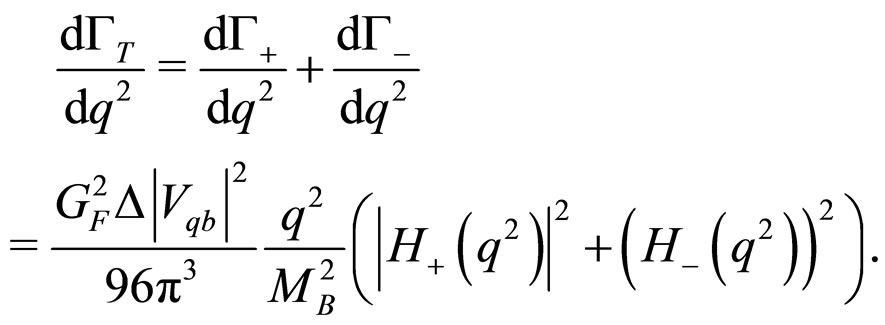 (27)
(27)
where helicity amplitudes are given by the following expressions
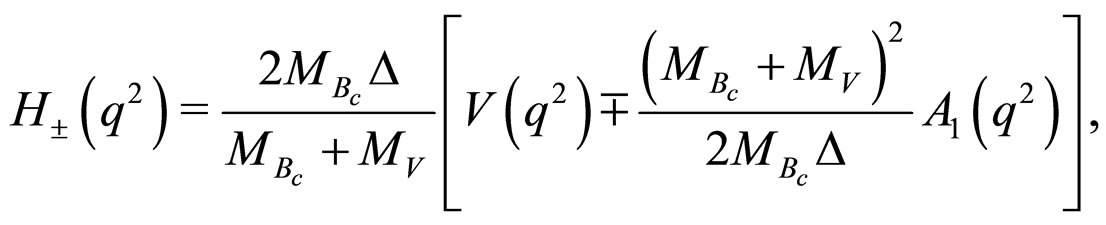 (28)
(28)
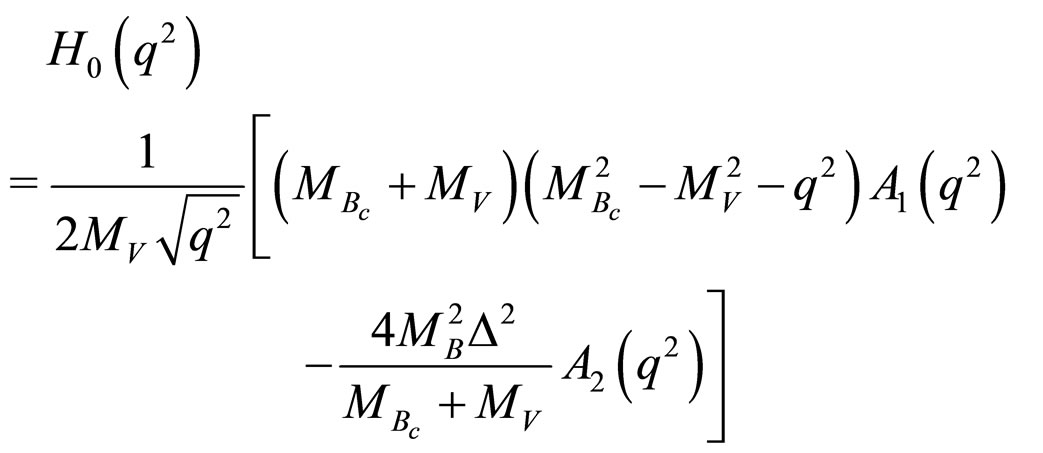 (29)
(29)
Thus the total decay rate is given by
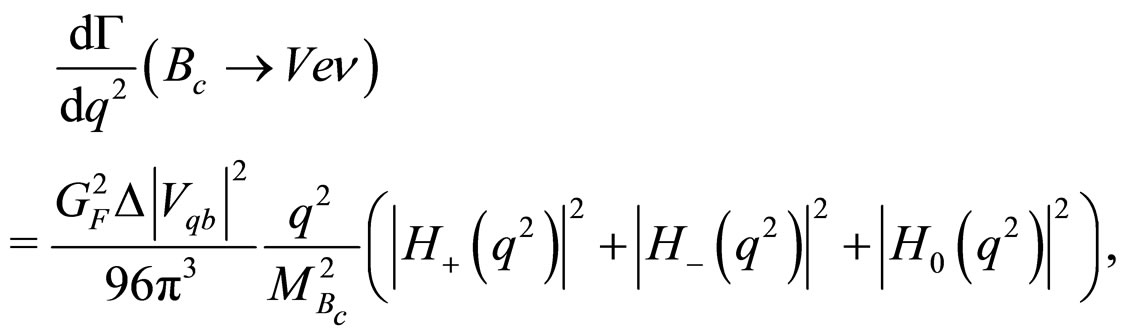 (30)
(30)
where 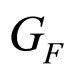 is the Fermi constant,
is the Fermi constant, 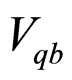 is CKM matrix element (
is CKM matrix element (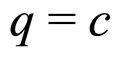 ),
),
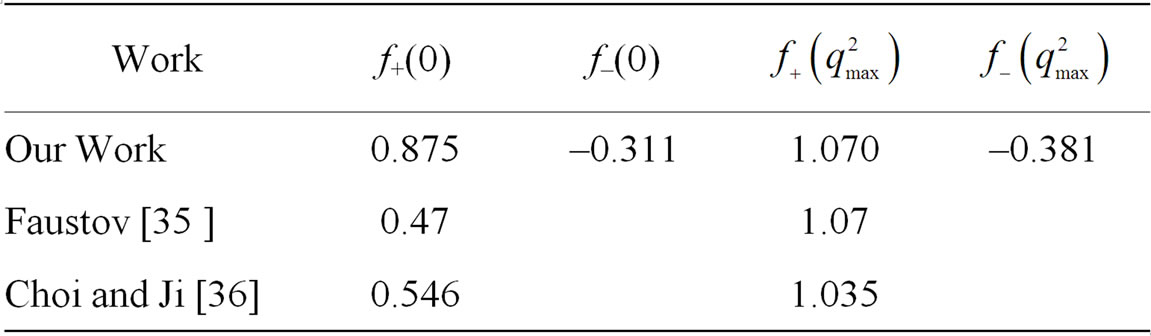
Table 1. Form factors for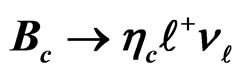 .
.
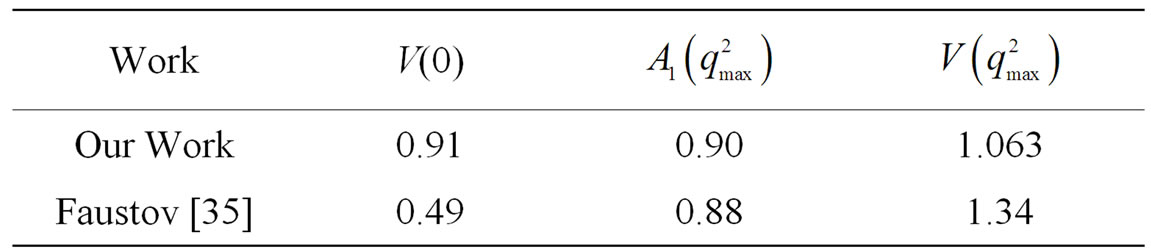
Table 2. Form factors for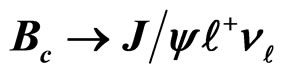 .
.

Table 3. Decay width for 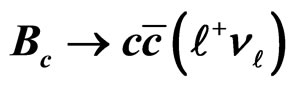 in
in .
.
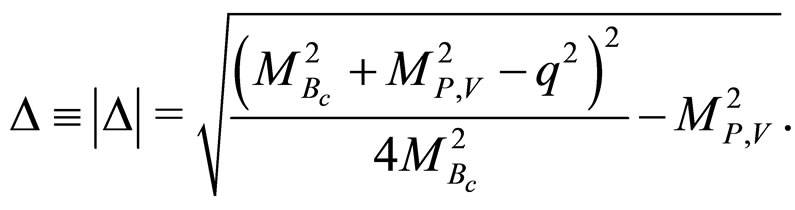
Integration over 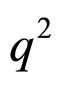 of these formulas gives the total rate of the corresponding semileptonic decay. The computed results for the form factors and the total decay rate is shown in Tables 1-3 respectively and compared with the other theoretical values.
of these formulas gives the total rate of the corresponding semileptonic decay. The computed results for the form factors and the total decay rate is shown in Tables 1-3 respectively and compared with the other theoretical values.
3. Results and Discussion
In this paper, we have computed the slope and curvature of Isgur-Wise function for Bc meson, considering the coulombic part of the cornell potential as perturbation and compute the different formfactors. We summarise and comment the result in the present work as follows.
1) We relate the form factors to the Isgur-Wise function in equations [22,23] which are based on the heavy flavour symmetry and is broken in the case of mesons containing two heavy quarks [39]. Spin symmetry breaking effects can occur when the c-quarks recoil momentum is larger than mc. However we expects that the equations are applicable to other kinematic point since the recoil momentum  state is small (
state is small ( ) due to its heavy mass [40]. We nave computed the hadronic form factors of Bc meson using HQET in analogy to D meson system and are compared with other available results which are shown in Tables 1 and 2.
) due to its heavy mass [40]. We nave computed the hadronic form factors of Bc meson using HQET in analogy to D meson system and are compared with other available results which are shown in Tables 1 and 2.
2) The values of  and C are found to be smaller than the other theoretical values for D and B mesons. The reason is presumably due to the truncating of higher terms in the Airy function (which is an infinite series).
and C are found to be smaller than the other theoretical values for D and B mesons. The reason is presumably due to the truncating of higher terms in the Airy function (which is an infinite series).
3) Numerical solution of Schrodinger equation with the specific potential also gives more accurate result than the present one. However, such approach appears to lack of physical insight into the problem unlike the relatively crude potential model approach pursued here.
4) The computed decay width for 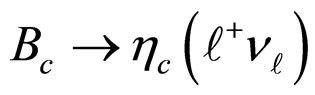 in this approach is found to be in good agreement with other theoretical results but the corresponding one for
in this approach is found to be in good agreement with other theoretical results but the corresponding one for 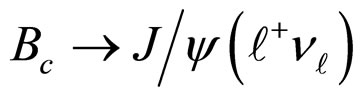 overshoots the other results and is shown in table 3. The branching ratio obtained for this semileptonic transition becomes
overshoots the other results and is shown in table 3. The branching ratio obtained for this semileptonic transition becomes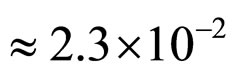 . This value is larger than the inclusive branching ratio reported in the PDG 2011 [41]
. This value is larger than the inclusive branching ratio reported in the PDG 2011 [41] 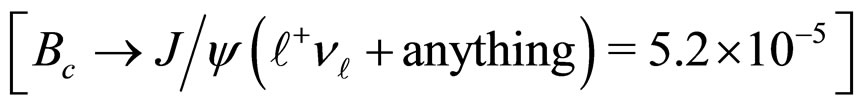 , which in principle includes the exclusive channel under consideration.
, which in principle includes the exclusive channel under consideration.
REFERENCES
- F. Abe, et al., “Observation of Bc Mesons in pp Collisions at
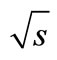 = 1.8 TeV,” Physical Review D, Vol. 58, No. 11, 1998, Article ID: 112004. doi:10.1103/PhysRevD.58.112004
= 1.8 TeV,” Physical Review D, Vol. 58, No. 11, 1998, Article ID: 112004. doi:10.1103/PhysRevD.58.112004 - I. P. Gouz, V. V. Kiselev, A. K. Likhoded, V. I. Romanovsky and O. P. Yushchenko, “Prospects for the Bc studies at LHCb,” Physics of Atomic Nuclei, Vol. 67, No. 8, 2004, pp. 1559-1570. doi:10.1134/1.1788046
- V. V. Kiselev, A. E. Kovalsky and A. K. Likhoded, “Bc Decays and Lifetime in QCD Sum Rules,” Nuclear Physics B, Vol. 585, No. 1, 2000, pp. 353-382.
- T. Huang and F. Zuo, “Semileptonic Bc Decays and Charmonium Distribution Amplitude,” The European Physical Journal C, Vol. 51, No. 4, 2007, pp. 833-839. doi:10.1140/epjc/s10052-007-0333-4
- M. A. Ivanov, J. G. Körner and P. Santorelli, “Semileptonic Decays of the Bc Meson,” Physical Review D, Vol. 63, No. 7, 2001, Article ID: 074010. doi:10.1103/PhysRevD.63.074010
- M. A. Ivanov, J. G Körner and P. Santorelli, “Semileptonic Decays of Bc Mesons into Charmonium States in a Relativistic Quark Model,” Physical Review D, Vol. 71, No. 9, 2005, Article ID: 094006. doi:10.1103/PhysRevD.71.094006
- M. A. Ivanov, J. G Körner and P. Santorelli, “Exclusive Semileptonic and Nonleptonic Decays of the Bc Meson,” Physical Review D, Vol. 73, No. 5, 2006, Article ID: 054024. doi:10.1103/PhysRevD.73.054024
- D. Ebert, R. N. Faustov and V. O. Galkin, “Properties of Heavy Quarkonia and Bc Mesons in the Relativistic Quark Model,” Physical Review D, Vol. 67, No. 1, 2003, Article ID: 014027. doi:10.1103/PhysRevD.67.014027
- D. Ebert, R. N. Faustov and V. O. Galkin, “Weak Decays of the Bc Meson to Charmonium and D Mesons in the Relativistic Quark Model,” Physical Review D, Vol. 68, No. 9, 2003, Article ID: 094020. doi:10.1103/PhysRevD.68.094020
- D. Ebert, R. N. Faustov and V. O. Galkin, “Weak Decays of the Bc Meson to Bs and B Mesonsin the Relativistic Quark Model,” The European Physical Journal C, Vol. 32, No. 1, 2003, pp. 29-43. doi:10.1140/epjc/s2003-01347-5
- C. H. Chang and Y. Q. Chen, “Decays of the Bc Meson,” Physical Review D, Vol. 49, No. 7, 1994, pp. 3399-3411. doi:10.1103/PhysRevD.49.3399
- J. F. Liu and K. T. Chao, “1/mQ Corrections to Form Factors and Extraction of |Vcb|,” Physical Review D, Vol. 56, No. 7, 1997, pp. 4133-4151. doi:10.1103/PhysRevD.56.4146
- A. Abd El-Hady, J. H. Munoz and J. P. Vary, “Semileptonic and Nonleptonic Bc Decays,” Physical Review D, Vol. 62, No. 1, 2000, Article ID: 014019. doi:10.1103/PhysRevD.62.014019
- P. Colangelo and F. De Fazio, “Using Heavy Quark Spin Symmetry in Semileptonic Bc Decays,” Physical Review D, Vol. 61, No. 3, 2000, Article ID: 034012. doi:10.1103/PhysRevD.61.034012
- M. A. Nobes and R. M. Woloshyn, “Decays of the Bc Meson in a Relativistic Quark-Meson Model,” Journal of Physics G, Vol. 26, No. 7, 2000, p. 1079. doi:10.1088/0954-3899/26/7/308
- E. Hernndez, J. Nieves and J. M. Verde-Velasco, “Study of Exclusive Semileptonic and Nonleptonic Decays of
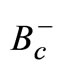 in a Nonrelativistic Quark Model,” Physical Review D, Vol. 74, No. 7, 2006, Article ID: 074008. doi:10.1103/PhysRevD.74.074008
in a Nonrelativistic Quark Model,” Physical Review D, Vol. 74, No. 7, 2006, Article ID: 074008. doi:10.1103/PhysRevD.74.074008 - W. Wang, et al., “Covarient Light Front Approach for Bc transition form factors,” Physical Review D, Vol. 79, No. 5, 2006, Article ID: 054012.
- M. Lusignoli and M. Masetti, “Bc Decays,” Physics and Astronomy, Vol. 51, No. 4, 1991, pp. 549-555. doi:10.1007/BF01565579
- D. Du and Z. Wang, “Predictions of the Standard Model for
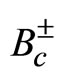 Weak Decays,” Physical Review D, Vol. 39, No. 5, 1989, pp. 1342-1348. doi:10.1103/PhysRevD.39.1342
Weak Decays,” Physical Review D, Vol. 39, No. 5, 1989, pp. 1342-1348. doi:10.1103/PhysRevD.39.1342 - R. Dhir, N. Sharma, and R.C. Verma, “Flavor Dependence of Bc Meson form Factors and Bc → PP Decays,” Journal of Physics G, Vol. 35, No. 8, 2008, Article ID: 085002. doi:10.1088/0954-3899/35/8/085002
- S. Godfrey, “Spectroscopy of Bc Mesons in the Relativized Quark Model,” Physical Review D, Vol. 70, No. 5, 2004, Article ID: 054017. doi:10.1103/PhysRevD.70.054017
- M. Wirbel, B. Stech and M. Bauer, “Exclusive Semileptonic Decays of Heavy Mesons,” Zeitschrift für Physik C Particles and Fields, Vol. 29, No. 4, 1985, pp. 637-642. doi:10.1007/BF01560299
- N. Isgur, D. Scora, B. Grinstein, and M. B. Wise, “Semileptonic B and D Decays in the Quark Model,” Physical Review D, Vol. 39, No. 3, 1989, pp. 799-818. doi:10.1103/PhysRevD.3 9.799
- B. J. Hajarika, K. K. Pathak and D. K. Choudhury, “Isgur-Wise Function in a QCD Potential Model with Coulombic Potential as Perturbation,” Modern Physics Letters A, Vol. 26, No. 21, 2011, p. 1547. doi:10.1142/S0217732311036000
- D. K. Choudhury, P. Das, D. D. Goswami and J. K. Sarma, “Static and Dynamic Properties of Pseudoscalar Mesons,” Pramana Journal of Physics, Vol. 44, No. 4, 1995, pp. 519-534.
- A. K. Ghatak and S. Lokanathan, “Quantum Mechanics,” McGraw Hill, New York, 1997.
- D. K. Choudhury and N. S. Bordoloi, “The Isgur-Wise Function in a QCD Inspired Quark Model,” International Journal of Modern Physics A, Vol. 15, No. 23, 2000, p. 3667. doi:10.1142/S0217751X00002743
- D. K. Choudhury and N. S. Bordoloi, “The Isgur-Wise Function in an Improved QCD Inspired Quark Model,” Modern Physics Letters A, Vol. 24, No. 6, 2009, p. 443. doi:10.1142/S0217732309028308
- I. J. R. Aitchison and J. J. Dudek, “Variationally Improved Perturbation Theory and the Potential −α/r + βr,” European Journal of Physics, Vol. 23, No. 6, 2002, p. 605. doi:10.1088/0143-0807/23/6/302
- Abramowitz and Stegun, “Handbook of Mathematical Functions,” 1964, Dover Publications.
- H. K. Quang and X. Y. Pham, “Elementary Particles and Their Interaction,” Springer, 1998.
- N. Isgur and M. B. Wise, “Weak Decays of Heavy Mesons in the Static Quark Approximation,” Physics Letters B, Vol. 232, No. 1, 1989, pp. 113-117. doi:10.1016/0370-2693(89)90566-2
- F. E. Close and A. Wambach, “Quark Model Form Factors for Heavy-Quark Effective Theory,” Nuclear Physics B, Vol. 412, No. 1-2, 1994, pp. 169-180. doi:10.1016/0550-3213(94)90498-7
- S. Deoghuria and S. Chakrabarty, “Can the Colour Hyperfine Interaction Explain 1P1 Data?” Journal of Physics G: Nuclear and Particle Physics, Vol. 15, No. 8, 1989, p. 1213.
- D. Ebert, R. N. Faustov and V. O. Galkin, “Weak Decay of Bc meson,” 2004.
- H.-M. Choi and C.-R. Ji, “Nonleptonic Two-Body Decays of the Bc Meson in the Light-Front Quark Model and the QCD Factorization Approach,” Physics Review D, Vol. 80, No. 11, 2009, Article ID: 114003. doi:10.1103/PhysRevD.80.114003
- V. V. Kiselev, A. K. Likhoded and A. I. Onishchenko, “Semileptonic Bc-Meson Decays in Sum Rules of QCD and NRQCD,” Nuclear Physics B, Vol. 569, No. 1-3, 2000, pp. 473-504. doi:10.1016/S0550-3213(99)00505-2
- M. A. Sanchis-Lozano, “Weak Decays of Doubly Heavy Hadrons,” Nuclear Physics B, Vol. 440, No. 1-2, 1995, pp. 251-275. doi:10.1016/0550-3213(95)00064-Y
- E. Jenkins, M. Luke, A. V. Manohar and M. J. Savage, “Semileptonic Bc Decay and Heavy Quark Spin Symmetry,” Nuclear Physics B, Vol. 390 No. 2, 1993, pp. 463- 473. doi:10.1016/0550-3213(93)90464-Z
- M.-T. Choi and J. K. Kim, “Determination of |Vcb| from the Polarization of Vector Meson in the Semileptonic Decay of B and Bc Meson,” Nuclear Physics B, Vol. 419, No. 1-4, 1998, pp. 377-380. doi:10.1016/S0370-2693(97)01480-9
- K. Nakamura, et al., “Review of Particle Physics,” Journal of Physics G: Nuclear and Particle Physics, Vol. 37, No. 7A, 2010, Article ID: 075021. doi:10.1088/0954-3899/37/7A/075021

