Journal of Modern Physics
Vol.2 No.9(2011), Article ID:7151,6 pages DOI:10.4236/jmp.2011.29130
Single Adatom Adsorption and Diffusion on Fe Surfaces
1Department of Civil Engineering, Luoyang Institute of Science and Technology, Luoyang, China
2Department of Mathematics and Physics, Luoyang Institute of Science and Technology, Luoyang, China
3School of Physics and Engineering, Key Laboratory of Material Physics of Ministry of Education, Zhengzhou University, Zhengzhou, China
E-mail: *cqw@lit.edu.cn
Received December 25, 2010; revised March 22, 2011; accepted April 8, 2011
Keywords: EAM Potential, Molecular Dynamics, Diffusion, Nudged Elastic Band (NEB) Method, Iron, Adsorption
ABSTRACT
Using Embedded-atom-method (EAM) potential, we have performed in detail molecular dynamics studies on a Fe adatom adsorption and diffusion dynamics on three low miller index surfaces, Fe (110), Fe (001), and Fe (111). Our results present that adatom adsorption energies and diffusion barriers on these surfaces have similar monotonic trend: adsorption energies, Ea(110) < Ea(001) < Ea(111), diffusion barriers, Ed(110) < Ed(001) < Ed(111). On the Fe (110) surface, adatom simple jump is the main diffusion mechanism with relatively low energy barrier; nevertheless, adatoms exchange with surface atoms play a dominant role in surface diffusion on the Fe (001).
1. Introduction
Understanding the processes of nucleation and growth on a substrate surface is of importance for growing highquality thin film materials. The diffusion energetics and dynamics of atomic adsorbates on a substrate play an important role in crystal growth, thin film formation, reactivity, catalysis and other surface processes. On the atomic scale, investigating the diffusion behaviors of single adatom on the surface, aids our understanding of the mechanism of these surface processes. These issues are of great interest for scientific reasons and technological applications. These problems have been intensively studied experimentally and theoretically.
Atom diffusion on body-centered cubic (BCC) metal surfaces has not been studied as extensively as facecentered cubic (FCC) metal surfaces (for a review see [1,2]). Atom diffusion on the BCC Fe [3-7], W [8], Mo [9,10] surfaces was studied experimentally using the STM, the reflection high-energy electron diffraction (RHEED), ion scattering, spin polarized low energy electron microscope (SPLEEM) and low energy electron diffraction (LEED) techniques, but the dominant diffusion mechanism could not be identified. Theoretically, using First Principles [11], Molecular Dynamics [12-15] and Monte Carlo (MC) [16,17], it has been investigated intensively [18].
Iron is a very common metal for application. Abundant work has been done on atom diffusion on the Fe surfaces for comparison. STM observation at the temperature range of 20˚C - 250˚C has been reported that the activation energy of a Fe atom diffusion on Fe (001) surface yields 0.45 eV [3]. Using EAM potential, H. Chamati [12] et al. carried out molecular dynamics studies on Fe self-diffusion on Fe (001) and gave adatom diagonal-exchange diffusion mechanism. In [15], they investigated a vacancy diffusing on the Fe (100) surface by Molecular Dynamics technique. However, little work has been done about adatom diffusion on Fe (110) and Fe (111) surfaces. Finite temperature molecular dynamics simulations are very helpful to study adatom diffusion, as they allow tracking the adatom on the surface. Moreover, it is convenient to find low energy diffusion path and new diffusion mechanism.
In this paper, using EAM potential [12] of iron, molecular dynamics studies have been carried out on a Fe adatom diffusion on three low index surfaces, Fe (110), Fe (001), Fe (111). Due to different structural stability of these three surfaces, it is well known that the Fe (110) surface is more stable than the Fe (100) surface, and the Fe (111) surface is the most unstable surface [12]. We have found that adatoms diffusion mechanism is diverse extremely by our molecular dynamics simulations. On the compact Fe (110) surface, adatoms diffuse rapidly by simple hopping mechanism. However, on the Fe (001) and Fe (111) surface, it is difficult to diffuse by simple hopping of adatoms. Adatoms exchange with substrate surface atoms is a frequent occurrence on the Fe (001) surface.
2. Methods
Our simulations were performed by using Embeddedatom-method (EAM) potential for BCC Fe [12,19]. Although the potential is semi-empirical, it can give reasonable results about the bulk Fe and Fe (001) surface [12,15], such as elastic constants, phonon dispersion curves, vacancy and atom diffusion.
Our modeling calculations were performed by using twenty 400-atom (total 8000 Fe atoms) layers as a substrate eliminating sufficiently small size effect, with periodic boundary conditions in the two directions parallel to the surface. Fe atoms in upper eighteen layers of the slab with a 20 Å vacuum to eliminate the interaction between its two surfaces are free to relax in the three directions. Nevertheless, Fe atoms of the lowest two of the slab are fixed to the BCC positions. To control the system temperature to be isothermal, the velocity scale constant temperature scheme was applied. For the numerical integration, the Verlet algorithm was employed in our calculations at the constant temperature, constant pressure (NPT ensemble), with a time step of 2 fs. In order to determine the lattice constant at each simulated temperature controlled by the Andersen method [20], used for properly constructing the simulation box. The NEB method [21] has been used to compute the energy barriers of low energy diffusion paths.
3. Results and Discussions
3.1. An Adatom Adsorption on Fe Surfaces
As listed in Table 1, adsorption energies at different high symmetrical sites on three Fe low miller surfaces have been computed by using molecular dynamics relaxation technique, given by
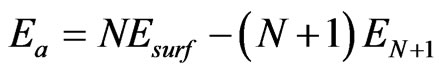 , (1)
, (1)
where ,
,  and
and  represent the adsorption energy, average atom energy of the N atoms slab, and average atom energy of the slab and an adatom, respectively.
represent the adsorption energy, average atom energy of the N atoms slab, and average atom energy of the slab and an adatom, respectively.
Adatom adsorption energies at different adsorbed sites
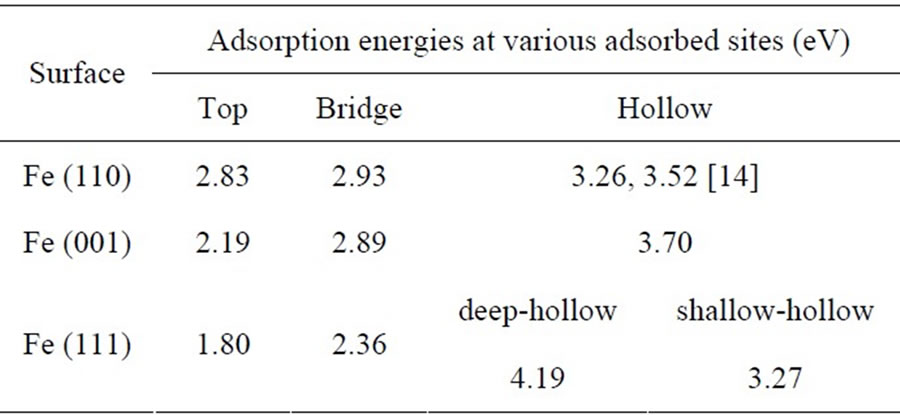
Table 1. Adatom adsorption energies at different adsorbed sites on three Fe low miller surfaces, Fe (110), Fe (001) and Fe (111) were calculated by molecular dynamics with the EAM method.
on three Fe low miller surfaces, Fe (110), Fe (001) and Fe (111) were calculated by combining molecular dynamics with the EAM method. Calculation results have been shown in Table 1. From Table 1, we have discovered two valuable conclusions. Firstly, for all of the three low miller surfaces of BCC Fe, the adatom adsorbed at hollow site is the most stable, with higher adsorption energy values of 3.26, 3.70 and 4.19 eV for Fe (110), Fe (100) and Fe (111) surfaces, respectively. Other top and bridge sites are unstable adsorption sites. Adatoms adsorbed at these sites diffuse easily into neighbor hollow sites. Secondly, we have found that adsorption energies of the most stable adsorption positions (hollow sites) on the three surfaces increase in turn, Ea(110) < Ea(001) < Ea(111). They have the similar trend with surface structural stabilities for three low index surfaces of iron. The Fe (110) surface with the most compact surface atom structure has the minimal surface energy. However, the Fe (111) surface with the minimal surface atom density among the three low index surfaces has the maximal surface energy.
As shown in the Figure 1, we have presented schematic diagrams of an adatom adsorbed in the hollow site for Fe (110) (a), Fe (001) (b), Fe (111) (c) (d). For Fe (001) and Fe (110) surfaces, hollow sites have fourfold symmetry, whereas, threefold symmetry for Fe (111) surface. It is worth notice that, for Fe (111) surface, there are two (deepand shallow-) hollow sites. An adatom adsorbed in the deep-hollow site (as Figure 1(d)) is more stable and has higher adsorption energy (4.19 eV) than the shallow-hollow site (as Figure 1(c)). In the Figure 1, Arrows represent crystallographic directions. Interatomic separations (Å) within the first layer have been shown. Due to the adatom adsorption, surface atoms around it restructure to achieve the lowest energy. For the Fe (110) and Fe (001) surfaces, the four surface atoms around the adatom are all away from it. The first nearest-neighbor (1NN) distances increase, from 2.492 to 2.507 Å for Fe (110) and from 2.878 to 3.012 Å for Fe (001) surface, respectively. The adatom adsorbed on the Fe (110) apart
 (a)
(a)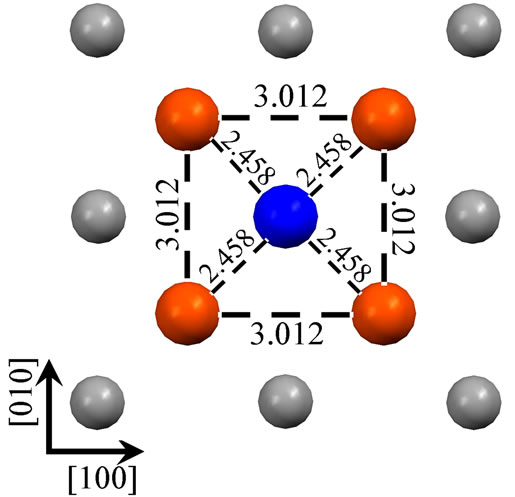 (b)
(b)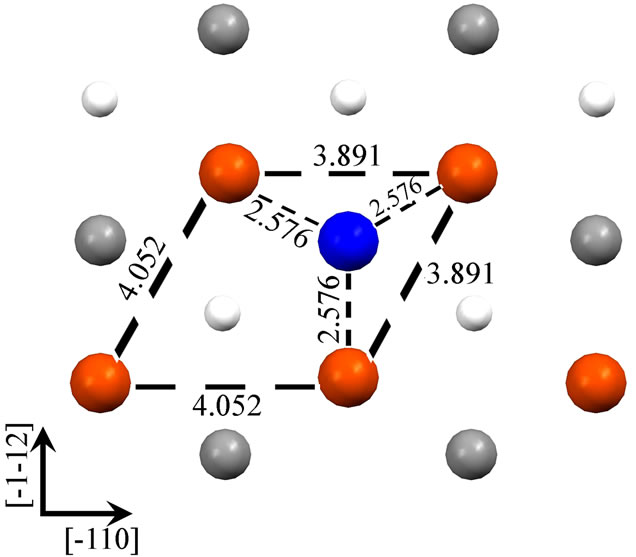 (c)
(c)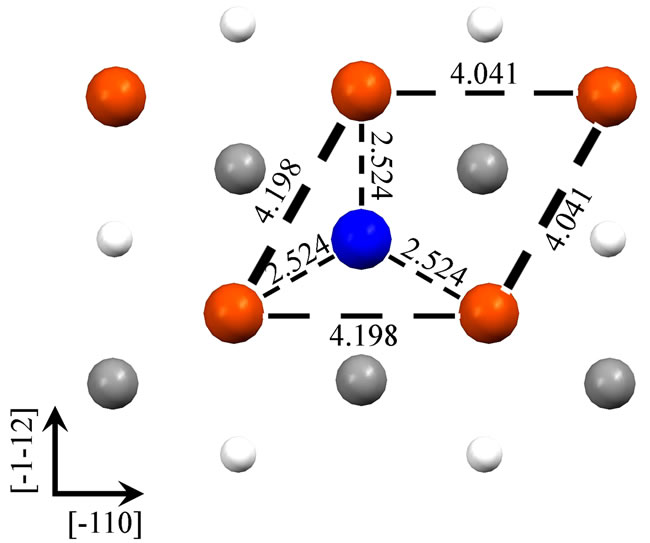 (d)
(d)
Figure 1. Four Fe adatom stable hollow adsorbed configurations on Fe (110) (a), Fe (001) (b), Fe (111) (c) (d). Figure (c) and (d) represent shallow-hollow and deep-hollow site, respectively. Blue, red, black and small white circles represent the adatom, first, second and third layer substrate atoms respectively. The following figures are presented in the same way. Arabic numerals in the figure represent interatomic separations (Å). Arrows represent crystallographic directions.
from the surface 1.771 Å is higher than the distance between the adatom adsorbed on the Fe (001) and the surface, 1.240 Å. More relaxation for the Fe (001) surface when the adatom adsorbed on it results in lower energy with more adsorption energy than the Fe (110) surface. For the Fe (111) surface, there are two adsorption (deepand shallow-) hollow sites. The three surface atoms around the adatom adsorbed on the shallow-hollow site are close to not apart from it. This leads to decreasing the surface 1NN distance from 4.070 to 3.891 Å. It is not the case for the adatom adsorbed on the deep-hollow site. The three surface atoms around the adatom adsorbed on the deep-hollow site are apart from it. It leads to increasing the surface 1NN distance from 4.070 to 4.198 Å. From Figures 1(c) and (d), we can find that the distance between the adatom adsorbed on the deep-hollow site and the nearest surface atoms is closer than that between the adatom adsorbed on the shallow-hollow site and its nearest surface atoms, 2.524 and 2.576 Å, respectively. For the distance between the adatom and the surface, it is shorter for the deep-hollow than shallow-hollow site, 0.739 and 1.297 Å, respectively. Similarly to the Fe (001) surface, more relaxation for the deep-shallow site when the adatom adsorbed on it results in lower energy with more adsorption energy than the shallow-hollow site.
3.2. An Adatom Diffusion on Fe Surfaces
To study adatom diffusion behaviors on Fe surfaces, we put one adatom on the free surface of a constructed slab and calculated the static energy barrier by the NEB method [21]: choose and change a certain freedom according to the diffusion path, then at each fixed increment of this freedom, all the other freedoms of the active atoms are fully relaxed. Firstly, we have calculated one adatom diffusion energy barrier in various high-symmetry directions chosen according to the Fe surface structure. Next, in order to find the low energy path of adatoms diffusion, we performed molecular dynamics simulations in the temperature range of 200 - 1000 K. And then the energy barrier of the low energy path, compared with the former energy barriers, was computed by the NEB method.
In Table 2, we have listed the diffusion energy barriers in various high-symmetry directions and low energy path, the values in references [12,14], and the corresponding experimental values [3,4]. We noted firstly that our results are consistent well with the reported values.

Table 2. Adatom diffusion energy barriers in various highsymmetry directions and low energy path on Fe (110), Fe (001) and Fe (111) surface have been computed by molecular dynamics with the EAM and NEB method. For comparison, the available values in references have been listed as well.
Secondly, we find that the barriers of the low energy path on the three surfaces have similar trend with surface energies and adatom adsorption energies, that is, the energy barrier of the adatom diffusion the Fe (110) surface has the lowest value, but the energy barrier of the adatom diffusion on the Fe (111) face has the maximal value. For the Fe (110) surface, its rhombus surface atom structure has four-fold symmetry. The energy barriers of adatom diffusion along two diagonal directions of the rhombus, [001] and [–110], have the same values 0.44 eV. Because of the maximum surface atom density of Fe (110) surface, it has the lowest surface energy. Surface atoms along [–111] have the most compact atom density. Adatoms adsorbed on this surface should diffuse relatively easily along the most compact direction. We have performed molecular dynamics simulations in the range of temperature 200 - 1000 K and discovered that the adatom diffusion along this direction happens frequently. The diffusion energy barrier along [–111] direction has been computed by NEB method, 0.24 eV. It is consistent well with the result 0.30 reported by D Chen [14]. For the Fe (001) surface, its surface atom structure is isotropic. The energy barriers of monomer diffusion along the two high symmetry directions, [100] and [010], have the same values 0.81 eV. It is less than the result that H. Chamati has reported 0.84 eV [12]. It is difficult relatively that single adatom diffuses by adatom hopping mechanism along the diagonal [110] direction with the energy barrier 1.47 eV. However, adatoms exchange with the surface atoms can occur in the process of adatoms diffusion on a substrate. We have calculated the energy barrier of diagonal exchange mechanism 0.49 eV, which is consistent well with the experimental value 0.45 eV [3,4] measured by STM and RHEED. Because of high surface energy and adatom adsorption energy of the Fe (111) surface with three-fold symmetry surface atom structure, single adatom transfers relatively difficultly on this surface. Energy barriers of a single adatom diffusion on the Fe (111) surface along two surface directions, [–1–12] and [–110], are very high, 2.40 and 1.11 eV, respectively.
In the Figure 2, low energy path of Fe adatom diffusion on the Fe (110) surface has been shown. This surface with the maximal atomic density is the most closely packed surface. The energetically stable configuration for a single Fe adatom on this surface is located in the fourfold position (Figure 2(a)). The diffusion mechanism of a monomer is known to be performed by the translation from the stable site to the adjacent nearest-neighbor site, and occur by atomic hopping along the most compact direction, i.e. along [–111] or [–11–1] crystallographic orientation. The potential energy transformation during the process of the Fe monomer diffusion along the [–111] direction on the Fe (110) surface is shown in the Figure 2. From Figure 2 we can find that Fe monomer diffusion energy barrier on Fe (110) surface is very low, only 0.24 eV, which is consistent well with the result that Chen [14] et al. reported, 0.30 eV. In our calculations, only a saddle point position (Figure 2(b)) has been discovered, that is different from that Chen [14] et al. have reported that existed two saddle point during the process of the monomer diffusion on the Fe (110) surface. The physical origins of this difference maybe lie in the difference of the used potentials.
Single Fe monomer diffusion mechanism on the Fe (001) surface is very different from the Fe (110) surface. Diagonal exchange with a surface atom along the [110] direction happens frequently. In the diffusion process, the monomer at a fourfold hollow site (Figure 3(a)) replaces a surface atom (Figure 3(b)) along the diagonal [110] direction and then the later moves to the adjacent fourfold hollow site (Figure 3(c)) from the Fe (001) surface. The energy barrier of the diagonal exchange mechanism is 0.49 eV which is consistent well with the results that reported experimentally with STM and RHEED measurement [3,4], 0.45 eV.

Figure 2. Single Fe adatom low energy diffusion path along [–111] direction on the Fe (110) surface: simple jump mechanism.
Because of higher surface energy of Fe (111) surface, little work has been done about Fe monomer diffusion on this surface. On the contrary, single vacancy self-diffusion in Fe (111) surface has been studied by using the modified analytical embedded-atom method (MAEAM) [13]. As far as we know, molecular dynamics simulation has been performed firstly on adatom diffusion on this surface in this paper. Low energy diffusion path on Fe (111) surface has been presented in the Figure 4. In this figure, the blue bold circle represents Fe adatom and the other circles represent surface atoms. It is obvious that the energy curve of self-diffusion along this path is symmetric. However, the saddle point position in the diffusing process is located at the bridge adsorption site (Figure 4(b)). In this diffusing process, the diffusing atom moves from the deep-hollow site to the shallow-hollow site (Figure 4(c)) across the saddle point by
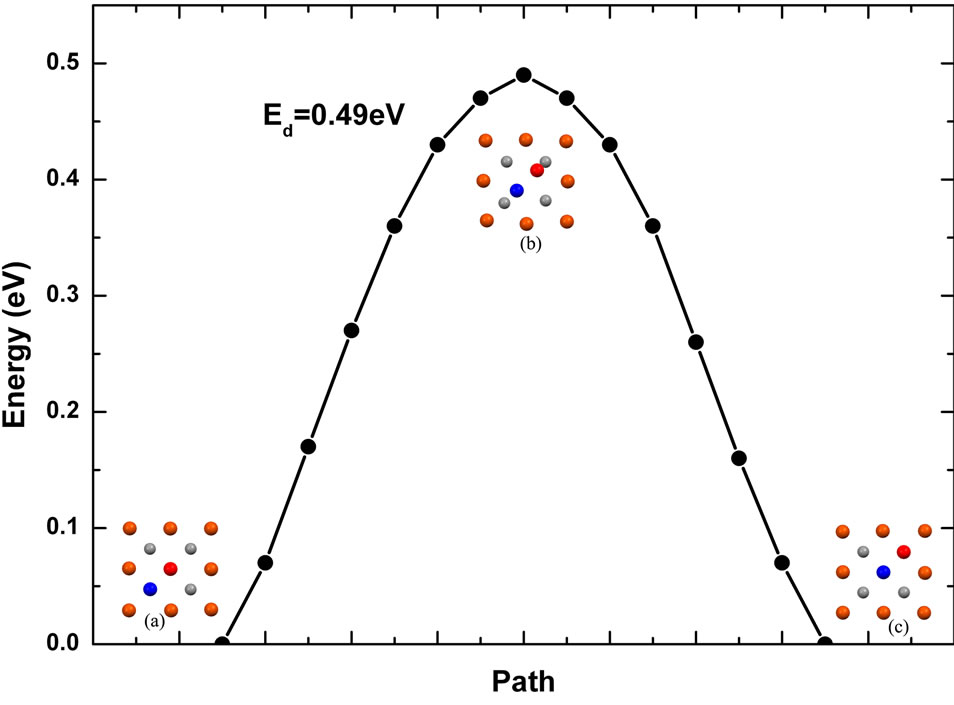
Figure 3. Single Fe adatom low energy diffusion path along [110] direction on the Fe (001) surface: diagonal exchange mechanism. Blue circles represent adatoms. The red circle in the insert map (a) is the surface atom.
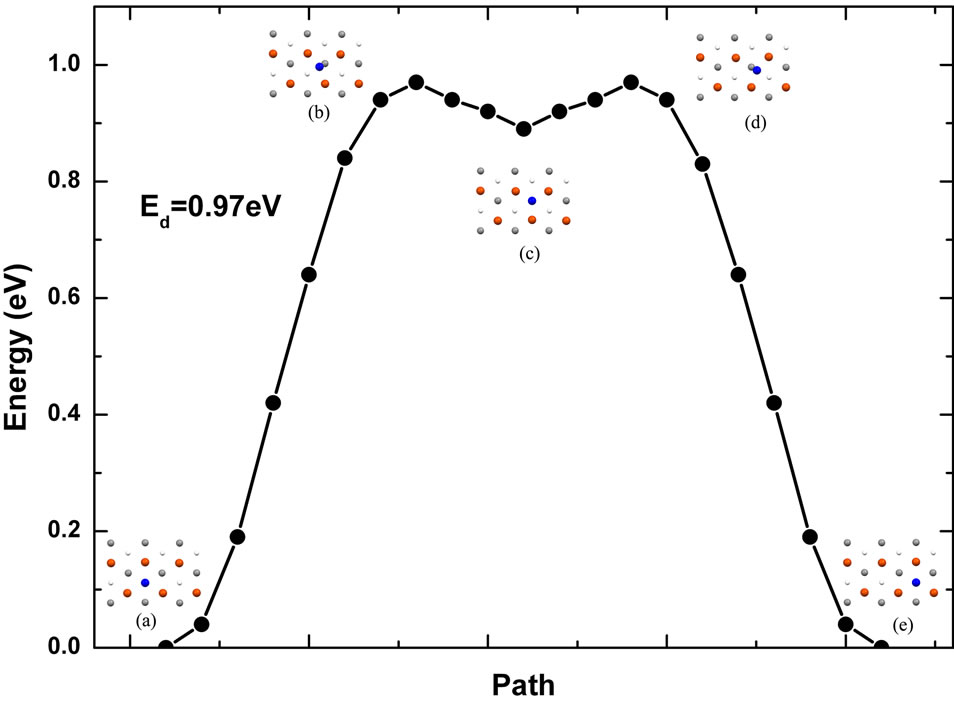
Figure 4. Single Fe adatom low energy diffusion path on the Fe (111) surface.
overcoming 0.97 eV energy barrier. The adatom diffuses from the deep-hollow site to the shallow-hollow site with a 0.08 eV energy barrier.
4. Conclusions
Single Fe adatom adsorption and diffusion properties on Fe (110), Fe (001), and Fe (111) surfaces have been studied by using molecular dynamics simulations. Adsorption energies and diffusion activation energy barriers of the adsorbed atom on these three low index surfaces have been calculated with Embedded-atom-method potential.
It is presented that adatom adsorption energies and diffusion energy barriers increase in turn according to the three surfaces, Ea(110) < Ea(001) < Ea(111), Ed(110) < Ed(001) < Ed(111). Because of the maximal surface energy of Fe (111) which is most unstable, it is more inclined to adsorb adatoms to reduce system energy. Therefore the energy barrier on Fe (111) surface has the highest value for the maximal adsorption energy on this surface. Our results present as well that adatom simple hopping is the main diffusion mechanism on the Fe (110) surface; nevertheless, adatoms exchange with surface atoms play a dominant role in surface diffusion on the Fe (001).
5. Acknowledgements
The authors acknowledge the financial support from the NSF of China (Grant Nos. 60876014), and the NSF of Henan province (Grant No. 072300410180, 092300410131). The project is also sponsored by program for science & technology innovation talents in universities of Henan province (Grant No. 2008HASTIT029).
REFERENCES
- H. Brune, “Microscopic View of Epitaxial Metal Growth: Nucleation and Aggregation,” Surface Science Reports, Vol. 31, No. 4-6, 1998, pp. 125-229. doi:10.1016/S0167-5729(99)80001-6
- G. Antczak and G. Ehrlich, “Jump Processes in Surface Diffusion,” Surface Science Reports, Vol. 62, No. 2, 2007, pp. 39-61. doi:10.1016/j.surfrep.2006.12.001
- J. A. Stroscio, D. T. Pierce and R. A. Dragoset, “Homoepitaxial Growth of Iron and a Real Space View of Reflection-High-Energy-Electron Diffraction,” Physical Review Letters, Vol. 70, No. 23, 1993, pp. 3615-3618. doi:10.1103/PhysRevLett.70.3615
- J. A. Stroscio and D. T. Pierce, “Scaling of Diffusion-Mediated Island Growth in Iron-on-Iron Homoepitaxy,” Physical Review B, Vol. 49, No. 12, 1994, pp. 8522-8525. doi:10.1103/PhysRevB.49.8522
- P. J. Feibelman, “Scanning Tunneling Microscopy: Energetics from Statistical Analysis,” Physical Review B, Vol. 52, No. 16, 1995, pp. 12444-12446. doi:10.1103/PhysRevB.52.12444
- R. Pfandzelter, T. Igel and H. Winter, “Real-Time Study of Nucleation, Growth, and Ripening during Fe/Fe (100) Homoepitaxy Using Ion Scattering,” Physical Review B, Vol. 62, No. 4, 2000, pp. R2299-R2302. doi:10.1103/PhysRevB.62.R2299
- F. Dulot, B. Kierren and D. Malterre, “Determination of Kinetic Parameters in Layer-By-Layer Growth from RHEED Profile Analysis,” Thin Solid Films, Vol. 423, No. 1, 2003, pp. 64-69. doi:10.1016/S0040-6090(02)00990-2
- R. Zdyb, A. Pavlovska, M. Jałochowski and E. Bauer, “Self-Organized Fe Nanostructures on W (110),” Surface Science, Vol. 600, No. 8, 2006, pp. 1586-1591. doi:10.1016/j.susc.2005.11.041
- P.-O. Jubert, O. Fruchart and C. Meyer, “Nucleation and Surface Diffusion in Pulsed Laser Deposition of Fe on Mo (110),” Surface Science, Vol. 522, No. 1-3, 2003, pp. 8-16. doi:10.1016/S0039-6028(02)02413-5
- I. V. Shvets, S. Murphy and V. Kalinin, “Nanowedge Island Formation on Mo (110),” Surface Science, Vol. 601, No. 15, 2007, pp. 3169-3178. doi:10.1016/j.susc.2007.05.013
- D. SpiŠák and J. Hafner, “Diffusion Mechanisms for Iron on Tungsten,” Surface Science, Vol. 584, No. 1, 2005, pp. 55-61.
- H. Chamati, N. I. Papanicolaou, Y. Mishin and D. A. Papaconstantopoulos, “Embedded-Atom Potential for Fe and Its Application to Self-Diffusion on Fe (100),” Surface Science, Vol. 600, No. 9, 2006, pp. 1793-1803.
- Y. N. Wen, J. M. Zhang and K. W. Xu, “Atomistic Simulation of the Self-Diffusion in Fe (111) Surface,” Surface Science, Vol. 253, No. 21, 2007, pp. 8620-8625. doi:10.1016/j.apsusc.2007.04.060
- D. Chen, W. Y. Hu, J. Y. Yang and L. X. Sun, “The Dynamic Diffusion Behaviors of 2D Small Fe Clusters on a Fe(110) Surface,” Journal of Physics: Condensed Matter, Vol. 19, No. 44, 2007, pp. 446009: 1-8.
- N. I. Papanicolaou and H. Chamati, “Diffusion of a Vacancy on Fe (100): A Molecular-Dynamics Study,” Computational Materials Science, Vol. 44, No. 4, 2009, pp. 1366-1370. doi:10.1016/j.commatsci.2008.09.006
- J G. Amar and F. Family, “Critical Cluster Size: Island Morphology and Size Distribution in Submonolayer Epitaxial Growth,” Physical Review Letters, Vol. 74, No. 11, 1995, pp. 2066-2069. doi:10.1103/PhysRevLett.74.2066
- C. Ratsch, P. Šmilauer, A. Zangwill and D. D. Vvedensky, “Submonolayer Epitaxy without a Critical Nucleus,” Surface Science, Vol. 329, No. 1-2, 1995, pp. L599-L604. doi:10.1016/0039-6028(95)00353-3
- O. Fruchart, P. O. Jubert1, M. Eleoui, F. Cheynis, B. Borca, P. David, V. Santonacci, A. Liénard, M. Hasegawa and C. Meyer, “Growth Modes of Fe(110) Revisited: A Contribution of Self-Assembly to Magnetic Materials,” Journal of Physics: Condensed Matter, Vol. 19, No. 5, 2007, pp. 053001: 1-43.
- M. S. Daw and M. I. Baskes, “Embedded-Atom Method: Derivation and Application to Impurities, Surfaces, and Other Defects in Metals,” Physical Review B, Vol. 29, No. 12, 1984, pp: 6443-6453. doi:10.1103/PhysRevB.29.6443
- H. C. Andersen, “Molecular Dynamics Simulations at Constant Pressure and/or Temperature,” Journal of Chemical Physics, Vol. 72, No. 4, 1980, pp. 2384-2393. doi:10.1063/1.439486
- G. Mills and H. Jónsson, “Quantum and Thermal Effects in H2 Dissociative Adsorption: Evaluation of Free Energy Barriers in Multidimensional Quantum Systems,” Physical Review Letters, Vol. 72, No.7, 1994, pp. 1124- 1127. doi:10.1103/PhysRevLett.72.1124

