Received 17 June 2015; accepted 24 July 2015; published 27 July 2015

ABSTRACT

We consider a similarity kinematic of a deltoid by studying locally the scalar curvature for the corresponding two dimensional kinematic surfaces in the Euclidean space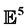. We prove that there is no two dimensional kinematic surfaces with scalar curvature K is non-zero constant. We describe the equations that govern such the surfaces.

Keywords:

Kinematic Surface, Similarity Kinematic Motion, Scalar Curvature, Cycloid Curves

1. Introduction

The last name of tricuspid is deltoid. The deltoid has no real discoverer because of its relation to the cycloid. The deltoid is a special case of a cycloid, and it is also called a three-cusped hypocycloid or a tricuspid. It was named the deltoid because of its resemblance to the Greek letter Delta. Despite this, Leonhard Euler was the first to claim credit for investigating the deltoid in 1754. Though, Jakob Steiner was the first to actually study the deltoid in depth in 1856. From this, the deltoid is often known as Steiner’s Hypocycloid.

To understand the deltoid, aka the tricuspid hypocycloid, we must first look to the hypocycloid, A hypocy- cloid is the trace of a point on a small circle drawn inside of a large circle, the small circle rolls along inside the circumference of the larger circle, and the trace of a point in the small circle will form the shape of the hypocy- cloid, The ratio of the radius of the inner circle to that of the outer circle 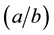is what makes each Hypocy-

cloid unique, curved are an engineering point replace the circumference of a circle with a radius of a roll within a radius 3a, Where a is the radius of the large fixed circle and b is the radius of the small rolling circle [1] .

From the view of differential geometry, deltoid is a geometric curve with non vanishing constant curvature K [2] . Similarity kinematic transformation in the n-dimensional an Euclidean space 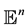is an affine transfor- mation whose linear part is composed by an orthogonal transformation and a homothetical transformation [3] - [7] . Such similarity kinematic transformation maps points according to the rule

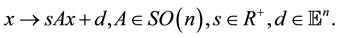(1)

The number s is called the scaling factor. Similarity kinematic motion is defined if the parameters of (1), including s, are given as functions of a time parameter t. Then a smooth one-parameter similarity kinematic motion moves a point x via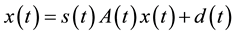. The kinematic corresponding to this transformation group is called equiform kinematic. See [8] [9] . Consider hypersurfaces in space forms generated by one- parameter family of spheres and having constant curvature [10] -[13] .

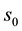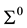In this work, we consider the similarity kinematic motion of the deltoid. Let and 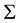be two copies of Euclidean space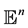. Under a one-parameter similarity kinematic motion of moving space 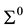with respect to fixed space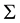, we consider which is moved according similarity kinematic motion. The point paths of the deltoid generate a kinematic surface X, containing the position of the starting tricuspid. At any moment, the infinitesimal transformations of the motion will map the points of the deltoid 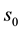into the velocity vectors whose end points will form an affine image of 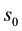that will be, in general, a deltoid in the moving space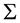. Both curves are planar and therefore, they span a subspace W of, with. This is the reason why we restrict our considerations to dimension.

2. Locally Representation of the Motion

In two copies, of Euclidean 5-space, we consider a unit deltoid in the -plane of with its centered at the origin and represented by

Under a one-parameter similarity kinematic motion of in the moving space with respect to fixed space. The position of a point at “time” t may be represented in the fixed system as

(2)

where describes the position of the origin of at the time t,

, is an orthogonal matrix and provides the scaling factor of the moving system. For varying t and fixed, gives a parametric representation of the path (or trajectory) of. Moreover, we assume that all involved functions are of class. Using the Taylor’s expansion up to the first order, the representation of the kinematic surface is

where denotes the differentiation with respect to t.

As similarity kinematic motion has an invariant point, we can assume without loss of generality that the moving frame and the fixed frame coincide at the zero position. Then we have

Thus

where, is a skew-symmetric matrix. In this paper all values of and their derivatives are computed at and for simplicity, we write and instead of and respectively. In these frames, the representation of is given by

or in the equivalent form

(3)

For any fixed t in the above expression (3), we generally get a deltoid with its centered at the point subject to the following condition

(4)

3. Scalar Curvature of Two-Dimensional Kinematic Surfaces

In this section we compute the scalar curvature of the two-dimensional kinematic surface. The tangent vectors to the parametric curves of are

A straightforward computation leads to the coefficients of the first fundamental form defined by, ,:

Under the conditions (5) a computation yields

(5)

where

(6)

The scalar curvature of is defined by

where be the Christoffel symbols of the second kind are

where, are indices that take the value 1 or 2 and is the inverse matrix of see [14] . Although the explicit computation of the scalar curvature can be obtained, for example, by using the Mathematica programme, its expression is some cumbersome. However, the key in our proofs lies that one can write as

(7)

The assumption of the constancy of the scalar curvature implies that (7) converts into

(8)

Equation (8) means that if we write it as a linear combination of the functions namely,

, the corresponding coefficients must vanish.

4. Kinematic Surfaces with K = 0

In this section we assume that on the surface. From (7), we have

Then the work consists in the explicit computations of the coefficients and.

We distinguish different cases that fill all possible cases. The coefficients are trivially zero and the coefficient is

We have two possibilities.

1) If. From expression (6), we have which yields to a contradiction.

2) If. Then most coefficients are trivially zero and the coefficients and are

If, we have or. Then if we have all coefficients are trivially zero. Now if , from expression (6), we have for. We then conclude:

Theorem 4.1 Let be a two dimensional kinematic surfaces obtained by similarity kinematic motion of deltoid s₀ and given by (3) under condition (4). Assume. Then on the surface if and one of the following conditions are satisfies

1),

2).

In particular, if, the deltoid generating the two dimensional kinematic surfaces are coaxial.

5. Kinematic Surfaces with K ¹ 0

Assume in this section that the scalar curvature of the kinematic surfaces given in (3) is a non- zero constant. The identity (8) writes then as

(9)

Following the same scheme as in the case studied in Section 4, we begin to compute the coefficients and. Let us put.

The coefficient is

We have to two possibilities:

1) If. The coefficient and are

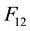
It follows that and or. If and, then coefficient is

Then implies that which give a contradiction. Now if, then the coefficient is. Then leads to which gives a contradiction also.

2). If. Then the coefficient is

Then implies that contradiction. As conclusion of the above reasoning, we conclude:

Theorem 5.1 There are not two dimensional kinematic surfaces obtained by similarity kinematic motion of a deltoid and given by (3) under condition(4) whose scalar curvature is a non-zero constant.

6. Examples of Two Dimensional Kinematic Surfaces with Vanishing Scalar Curvature

In this section, we construct two examples of a kinematic surface with constant scalar curvature. The first example corresponds with the case. In the second example, we assume.

Example 1 Case.

Consider the following orthogonal matrix.

(10)

We assume that the factor and. Here we have, , for, , and, for. Then Theorem 4.1 says us that the corresponding surface has. In Figure 1, we display a piece of of Example 1 in axonometric viewpoint. For this, the unit vectors and are mapped onto the vectors and respectively (5). Then

and

Example 2 Case. Let now the orthogonal matrix

(11)

We assume and. Then

.

Theorem 4.1 says that. In Figure 2, we display a piece of of Example 2 in axonometric viewpoint. For this, the unit vectors and are mapped onto the vectors and respectively (5). Then

and

7. A Local Isometry between Two Dimensional Surfaces

In this section, we shall study the existence of a local isometry between a two dimensional surface in represented by in (3) with constant scalar curvature and a two dimensional surface in Euclidean three-space. For more details see [6] [15] .

Now, we construct a two dimensional surface in locally isometric determined by (3). Where and defined in the same domain U such that and in U. Then the map is a local isometry.

For this, we assume that the initial deltoid is the same that in. Then writes as

(12)

The computation of the first fundamental form of leads to

(13)

And

(14)

As in the case studied, we have assumed that the original two axis of the deltoid are orthogonal. This means. On the other hand, the first fundamental form of was calculated in (5). From X and, we have equations on the trigonometric functions and.

The identities imply

, , ,

and, , , ,.

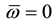
Thus

Then. We impose that the scalar curvature k is constant. We know that Or when In particular , or. We conclude:

Theorem 7.1 Consider a two dimensional kinematic surface in given by the parametrization in (3) under condition (4) and with constant scalar curvature. Let be a two dimensional kinematic surface in defined by (12). If the following equations hold:

Then both surfaces and are locally isometric. The Gaussian curvature of the surface in Euclidean space must vanish.

Cite this paper

E. M.Solouma,M. M.Wageeda,Y. Gh.Gouda,M.Bary, (2015) Studying Scalar Curvature of Two Dimensional Kinematic Surfaces Obtained by Using Similarity Kinematic of a Deltoid. Applied Mathematics,06,1353-1361. doi: 10.4236/am.2015.68128

References