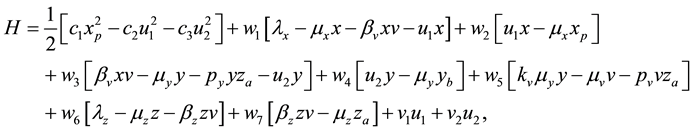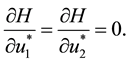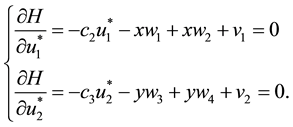Applied Mathematics
Vol.06 No.06(2015), Article ID:57139,15 pages
10.4236/am.2015.66102
An Optimal Control Approach to HIV Immunology
Edilson F. Arruda1, Claudia M. Dias2, Camila V. de Magalhães3, Dayse H. Pastore3, Roberto C. A. Thomé3, Hyun Mo Yang4
1Instituto Alberto Luiz Coimbra de Pós Graduação e Pesquisa de Engenharia, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brazil
2Instituto Multidisciplinar, Universidade Federal Rural do Rio de Janeiro, Nova Iguaçu, Brazil
3Departamento de Matemática, Centro Federal de Educação Tecnológica Celso Suckow da Fonseca, Rio de Janeiro, Brazil
4Departamento de Matemática Aplicada, Universidade Estadual de Campinas, Campinas, Brazil
Email: efarruda@po.coppe.ufrj.br, mazzaclaudia@gmail.com, milamagal@yahoo.com.br, dpastore@cefet-rj.br, rthome@cefet-rj.br, hyunyang@ime.unicamp.br
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 May 2015; accepted 12 June 2015; published 15 June 2015
ABSTRACT
This paper introduces a mathematical model which describes the dynamics of the spread of HIV in the human body. This model is comprised of a system of ordinary differential equations that involve susceptible cells, infected cells, HIV, immune cells and immune active cells. The distinguishing feature in the proposed model with respect to other models in the literature is that it takes into account cells that represent two distinct mechanisms of the immune system in the defense against HIV: the non-HIV-activated cells and the HIV-activated cells. With a view at minimizing the side effects of a treatment that employs a drug combination designed to attack the HIV at various stages of its life cycle, we introduce control variables that represent the infected patient’s medication. The optimal control rule that prescribes the medication for a given time period is obtained by means of Pontryagin’s Maximum Principle.
Keywords:
HIV, Mathematical Modelling, Optimal Control, Pontryagin’s Maximum Principle

1. Introduction
Belonging to the family of retroviruses, the Human Immunodeficiency Virus (HIV) is responsible for AIDS. HIV infection results in a chronic, progressive disease that can lead to the destruction of the immune system. The disease is characterized by a high rate of viral replication, which results in the emergence of more virulent variants. HIV infection is currently characterized by the count of CD4+ T cells, by the amount of viral particles in the blood (viral load) and also by the clinical symptoms. Not all patients develop every stage of the disease, and the time elapsed between the infection and the manifestation of different clinical symptoms is highly variable, even though the causes of such a variation remain partly unknown.
To reproduce, HIV joins the membrane of the T4 cell, which is vital to the immune response. The virus releases its RNA and an enzyme, which produces the DNA of the virus. Then, the DNA of the virus enters the nucleus and joins to the DNA of the cell, taking full control. The result of this union is the pro-viral DNA, that produces the messenger RNA, which contains the genetic code of the virus. The messenger RNA then reaches the cytoplasm and produces virions, which leave the host cell as newly formed HIV’s. Thus, when joined to a T4 cell, a single virus produces many potential threats to other cells.
By making quantification possible and unfolding non-trivial equilibrium points, the analysis of viral load in HIV infection has facilitated the management of the disease. It turns out that an exponential decrease in viral levels in plasma can be attained by the reverse transcriptase inhibitors and protease that are included in Anti- retroviral Therapy (ART) [1] [2] .
When HIV viruses invade the human body, they attack the CD4+ T cells in their way. When attacked, these auxiliary cells signal the presence of an invader to other immune cells (CD8+ T cells). The CD8+ T cells then respond to this signal and become Cytotoxic T Lymphocytes (CTL) by attempting to destroy the infected cells [3] - [6] . This process, which is not exploited in typical HIV models, plays an important role in the proposed approach. Indeed, a novel feature of the present work is the introduction of a variable to represent the CD8+ T cells. Such a variable is extremely important to the model, since it enables the decision maker to evaluate the interaction between the CD8+ T cells, CTL and the other variables in the model, such as the virus load.
This work proposes a simple mathematical model to describe the dynamics of the HIV taking into account the immune response. The proposed model introduces changes to several existing models in the literature [7] - [10] . As mentioned above, one such change is the introduction of a new variable to provide a more detailed des- cription of the defense of the immune system. This variable represents the number of unactivated CD8+ T defense cells, which can become activated (i.e. HIV-specific, or CTL) after being warned by some CD4+ T cell. In contrast to the formulation proposed by [4] , which accounts for the activated cells but does not model the activation mechanism, the proposed model keeps track of both the unactivated CD8+ T cells and the activated cells, thus taking into account the dynamics of the activation process.
Even though ART has produced undisputed advances in the treatment of HIV infection, it has been argued that the inhibitors that comprise ART may cause adverse effects; see for example [11] - [13] . Hence, one can argue that a compromise should be reached between the benefits obtained from ART and the adverse effects that it may cause. The ideal treatment should keep the benefits to a maximum degree while also minimizing the adverse effects. It is the development of such a treatment that we address in this paper, making use of the optimal control theory framework. We propose a dynamic model to represent the dynamics of the HIV infection, which takes into account the effects of the ART therapy and introduces control parameters that determine the intensity of the medication. An optimal control problem is then proposed to determine the optimal medication levels in such a way to maximize the benefits of the therapy, while keeping the medication to a minimum efficient level. The side effects assessment is another novelty of the paper, which also strives to provide insights into the effects in the optimal treatment by changing the parameters of the optimal control problem. In order to achieve our goal and minimize the side effects, optimal control theory is applied to the HIV infection model encompassing drug treatments. That, on the other hand, produces a problem whose solution is numerically obtained by standard algorithms, such as the gradient descent method; for more details on these algorithms we refer to [14] . The gradient algorithm makes use of both the solution to the system’s dynamics under a given control sequence, i.e., the medication levels for the complete treatment, and the solution of the co-state equations under the same medication, to generate an improved control sequence, and so on, until convergence is attained. The solutions to both the system’s dynamics and the co-state equations are obtained by means of finite diffe- rence algorithms.
This work is organized as follows. Section 2 introduces the model, while Section 3 derives the trivial equi- librium point and analyzes the stability of the model. Section 4 introduces the optimal control problem, which derives the optimal medication levels. In Section 5, numerical experiments are proposed to illustrate the proposed approach and shed light into the behavior of the controlled system. Finally, Section 6 concludes the paper.
2. Model Formulation
Let x represent the susceptible cells, i.e. the cells that can be infected with HIV, and define y as the cells that are already infected. In addition, assume that v represents the free viruses in the body, z denotes the defense cells (CD8+ T and B) and  corresponds to the activated defense cells, i.e., cytotoxic T cells and plasma (activated CD8+ T and B cells). In the proposed model, the interaction of these variables is represented by the following set of differential equations:
corresponds to the activated defense cells, i.e., cytotoxic T cells and plasma (activated CD8+ T and B cells). In the proposed model, the interaction of these variables is represented by the following set of differential equations:
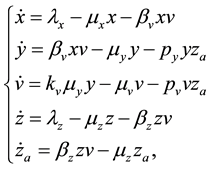 (1)
(1)
with initial conditions: 
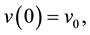
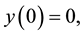

The parameters in the above equations are described in Table 3. Note that uninfected cells x are produced at a constant rate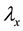 , and decay at rate
, and decay at rate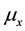 . In addition, these cells are infected by the free viruses at rate
. In addition, these cells are infected by the free viruses at rate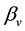 . As for the infected cells y, they are produced from the interaction of their uninfected counterparts and the viruses, at rate
. As for the infected cells y, they are produced from the interaction of their uninfected counterparts and the viruses, at rate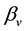 , decay at rate
, decay at rate 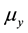 and are eliminated by the activated defense cells at rate
and are eliminated by the activated defense cells at rate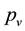 . Free viruses v are generated from infected cells at rate
. Free viruses v are generated from infected cells at rate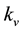 , decay at rate
, decay at rate  and are eliminated by means of the activated defense cells
and are eliminated by means of the activated defense cells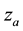 , at rate
, at rate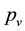
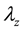
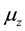
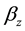

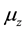
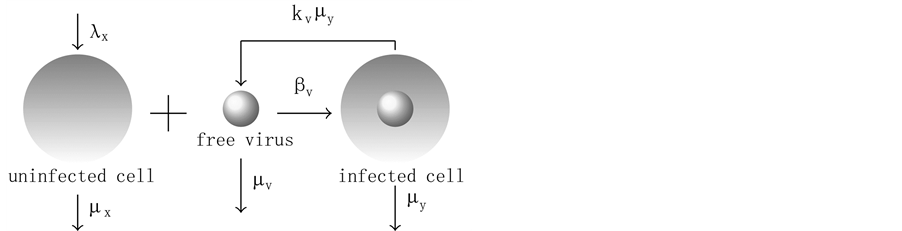
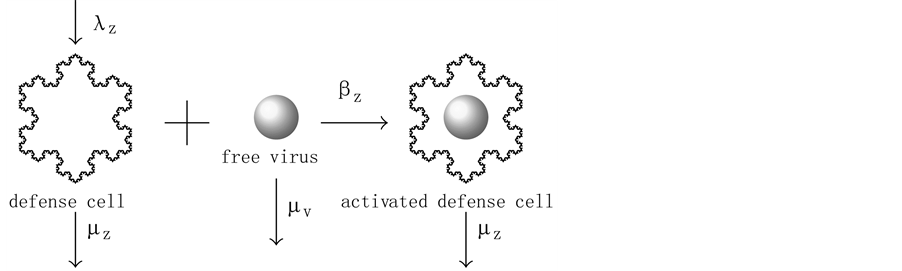
The virus replication mechanism is depicted in Figure 1. Observe that free viruses (v) and uninfected cells (x, CD4+ T) produce infected cells (y) that, in turn, produce new free viruses. Figure 2 illustrates the activation of the defense cells (z, CD8+ T). Note that they are activated in the presence of free viruses.
In the model, one can notice the introduction of two variables z and 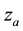
It is worth point out that, in the proposed model, the immune CTL cells are activated directly by the free viruses. In contrast, some previous works in the literature assume they are activated by infected cells, healthy cells and also CTL cells [15] . Observe that this is a simplification of the proposed model, which takes advantage of the fact that all elements that act to activate the immune CTL cells are mediated directly or indirectly by the virus. This hypothesis in our model simplifies the complex phenomena of activation and inactivation of the immune system by cytokines and dendritic cells (antigen presenting cells) [15] . Such a simplification is very useful in the optimal control formulation, which results in a larger and more complex set of equations.
Figure 1. Virus replication.
Figure 2. CD8+ T response.
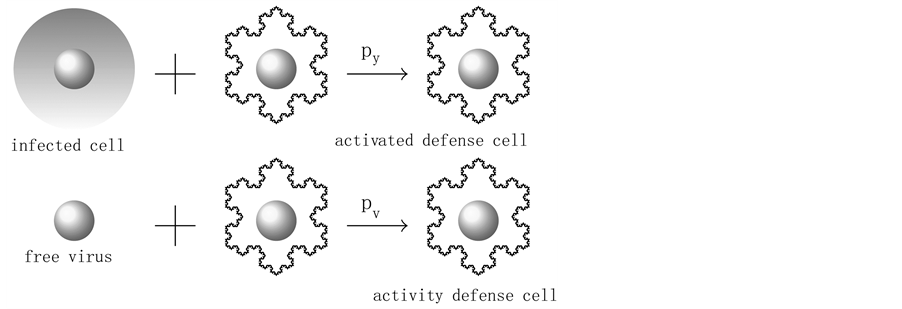
Figure 3. CTL response.
3. Equilibrium Points and Stability
3.1. Trivial Equilibrium Point
For a non-HIV-infected person, 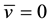
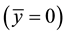
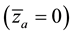

3.2. Stability of Trivial Equilibrium Point
By Hartman-Grobman’s theorem [16] , one can say that an equilibrium point is stable if the sign of the real part of the eigenvalues of the Jacobian matrix, evaluated at this point, is negative. Making use of this theorem, it is possible to show that if the basic reproduction number of the virus 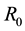
The Jacobian matrix of the system (1), 
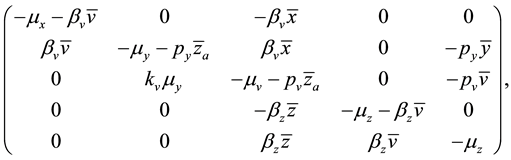
evaluated at values corresponding to the equilibrium points.
The Jacobian matrix evaluated at the point of trivial equilibrium (2) is given by:
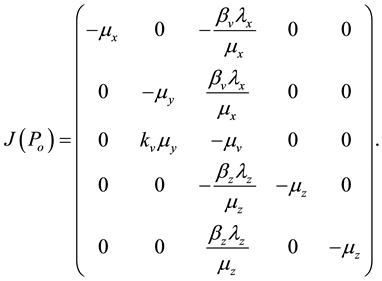
The eigenvalues of the matrix 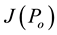
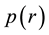

It can be noted that 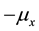
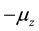
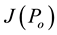
i.e.,
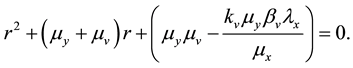
Applying Routh-Hurwitz criterion [17] , one can see that the system is stable if the last term in Equation (6) is positive. Hence, the system is stable if
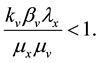
Lets assume that one virus infects one person. During its average survival time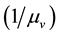
countering and infecting one target cell 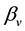
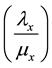
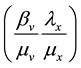
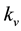

viruses produced by one virus infecting a cell in a completely susceptible population of CD4+ T cells.
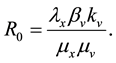
So, if 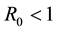
3.3. Non-Trivial Equilibrium Points
Equating to zero all the differential equations given in (1), one comes up to the following general formulation for the equilibrium points of the dynamical system:
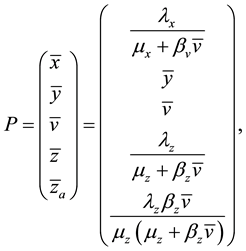
where:
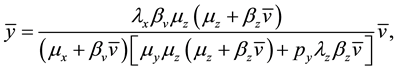
or
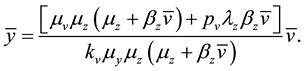
It is possible to observe that when 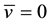
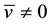
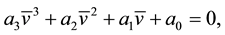
where the coefficients are:

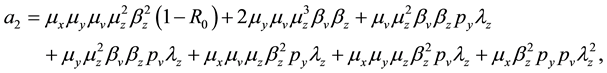
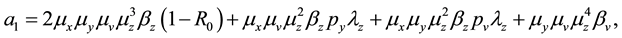

The coefficients of Equation (12) are positive when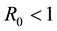
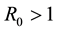
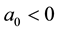


4. Optimal Control Formulation
In order to study the effect of treating HIV infection with the use of a cocktail of drugs, we introduce two control variables (
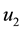
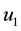
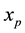
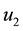
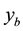
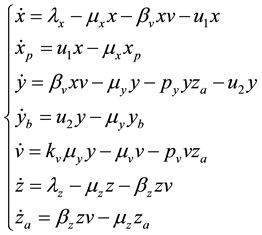
The initial conditions were obtained by running the uncontrolled model from Equation (1) for a period of 365 days. Note that the second and fourth equations are decoupled.
We point out that 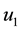
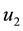
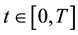
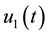
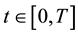

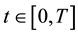
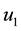

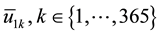

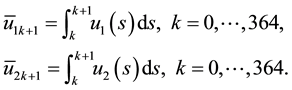
Alternatively, doctors could prescribe average values of the sequences 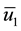
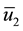
Observe that, if the dosages 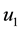
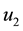
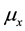
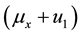
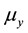
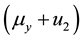


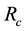
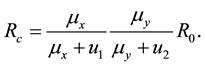
Note that the terms multiplying 
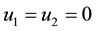
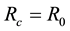
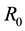
In the remainder of this paper, we analyze the system’s dynamics with 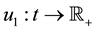

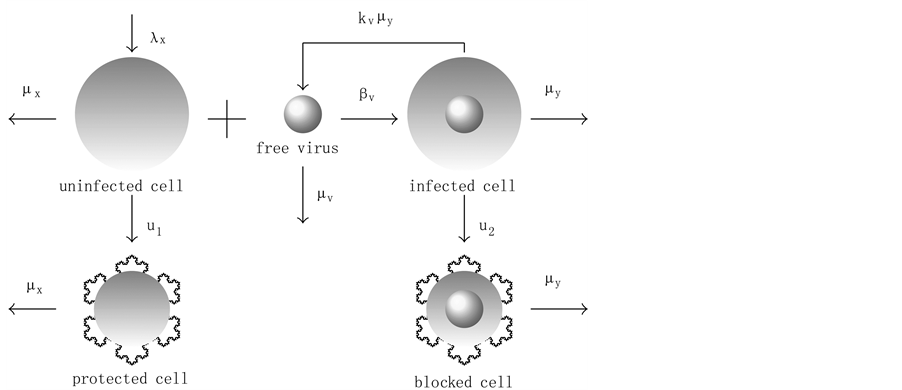
It is worth reinforcing that, in relation to typical HIV models that simulate the production rates and infect- ability of the virus, the proposed model includes two new variables in the dynamics: protected uninfected cells 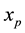

The introduction of the new variables, namely protected uninfected cells 
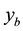
Observing the model we note that the defense cells CD8+ T (z) produce the activated cells CTL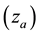
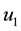


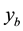
4.1. Objective Function
System (17) is now optimized with respect to control parameters 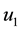
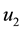
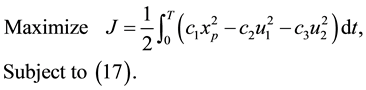
In the expression above, 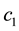
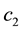
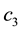
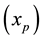
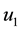

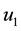
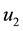
4.2. The Hamiltonian
To find the optimal control variables 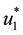
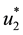
Table 1. New variables after control.
Figure 4. Virus replication with antiretroviral therapies.
principle [14] [18] [19] , and derive the Hamiltonian of our optimal control problem, which is given by:
where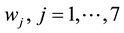
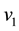
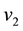
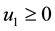
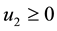
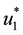

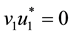
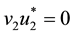

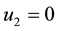
1) Considering the set:
It follows from Pontryagin’s maximum principle that the optimal control variables 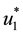
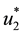
Then,
Thus, isolating 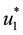
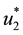
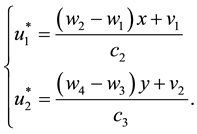
As in this case we necessarily have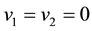
2) Considering the set:
It follows from Equation (21), that
Since, by definition, 
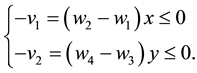
Therefore, to ensure that 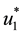
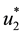
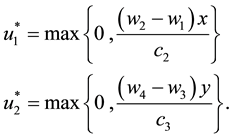
Hence, the optimal control for Problem (20) is characterized by (25).
4.3. The Co-State Equations
The necessary conditions of the Pontryagin’s maximum principle [14] also establish that the adjoint variables satisfy:

Finally, we analyze the conditions of transversality. In our case, there is no terminal value for the state variables. Therefore, the transversal conditions to the adjoint variables are given by
Observe that the optimal control values in (25) depend directly on the co-state variables and, through these variables, on the dynamics described in (17). Hence, they cannot be analytically determined. Consequently, to solve Problem (20), one searches for optimal control values 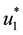
5. Numerical Results
For the numerical simulations we have used the dataset described in Table 2 and Table 3, which was also studied in [8] [9] [20] . For this data set, the reproduction number 
5.1. The Uncontrolled System
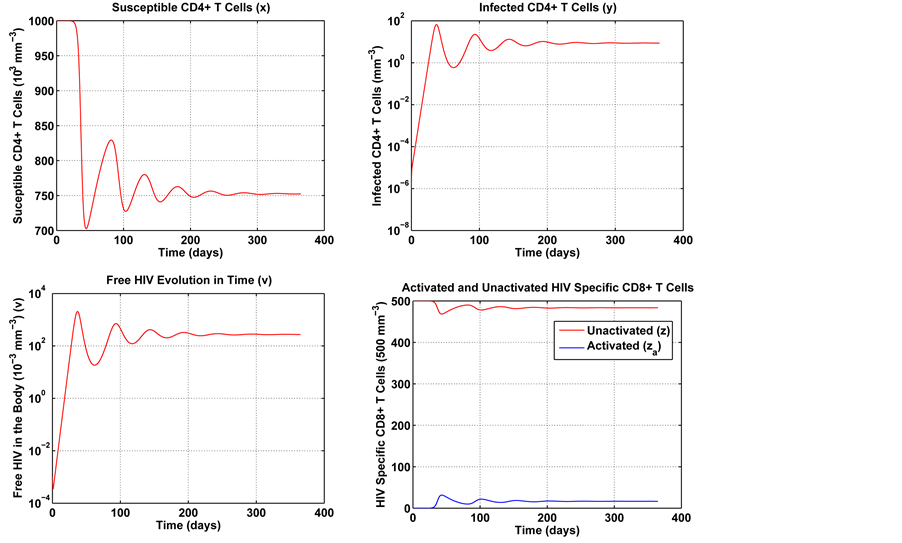
Figure 5 conveys a numerical simulation of the uncontrolled model in Equation (1), solved by means of the Finite Difference Method, for a one year period. Note that the solution represents the typical behavior of the immune system in the presence of HIV [9] [21] - [23] . The system rapidly approaches the non-trivial equilibrium point.
In Figure 5, one can see a steep increase in the number of viruses and infected cells in the first month. In contrast, the number of susceptible cells presents a substantial decrease over the same period. In the subsequent
Table 2. Initial conditions.
Table 3. Parameters.
Figure 5. Numerical experiment without control.
periods, these variables stabilize and gradually approach a non-trivial equilibrium point. As previously men- tioned, the proposed model describes the typical behavior of the immune system in the presence of HIV. The difference is that it also allows a separate analysis of the activated defense cells. In Figure 5, one can notice a migration of immune cells into the compartment of activated defense cells. We believe that this could lead, over the years, to the saturation of the immune system. Furthermore, the results seem to suggest a trend for a regular non-trivial dynamical system balance.
5.2. Adding Medication: The Optimal Control Problem
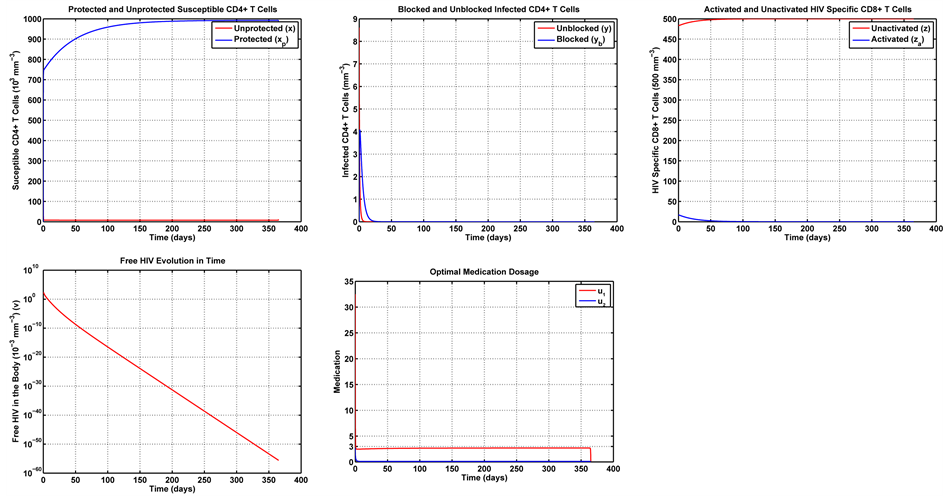
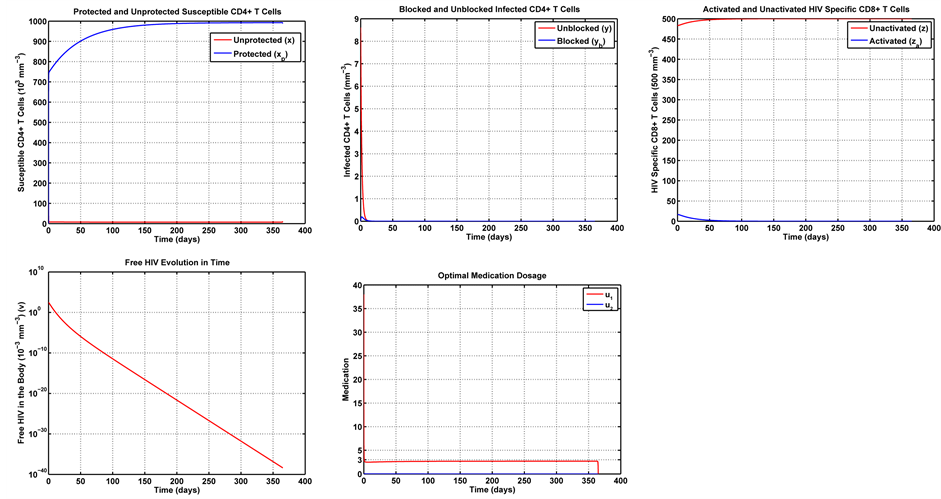
The optimal control problem in Equation (20) was solved for a one year treatment period. The initial condition for the state variables was obtained by running the uncontrolled system in Equation (1) for a one year period. The last value of each variable (after 365 days) was taken as the initial value for the same variable in the controlled problem. In this work, we first consider Case 1, with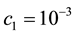
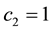
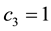
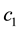
Note in Figure 6 that the first week of treatment causes a substantial decrease in the unprotected (susceptible) CD4+ T cells, with an increase in the number of protected cells. That is because the treatment makes most of these cells become protected cells. Note that, since the medication efficiently fights the infection, the number of HIV-specific CD8+ T cells can be reduced with respect to the uncontrolled dynamics in Figure 5. That leaves the imune system free to combat other infections. With regards to the infected cells, blocked and unblocked, they rapidly vanish. Note that the unblocked cells vanish more rapidly than their blocked counterparts. Note also that the number of remaining viruses rapidly decays to zero, its trivial equilibrium point. It is also noteworthy that the optimal dosage of the transcriptase inhibitor 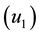

5.3. Sensitivity Analysis
In this section we examine the effects of the parameters of the optimal control problem in Equation (20). We vary the parameters 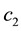
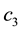
Figure 6. Optimal trajectories for Case 1: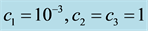
objective is to verify the implications of different compromises between immune response and side effects into the medication levels as time elapses.
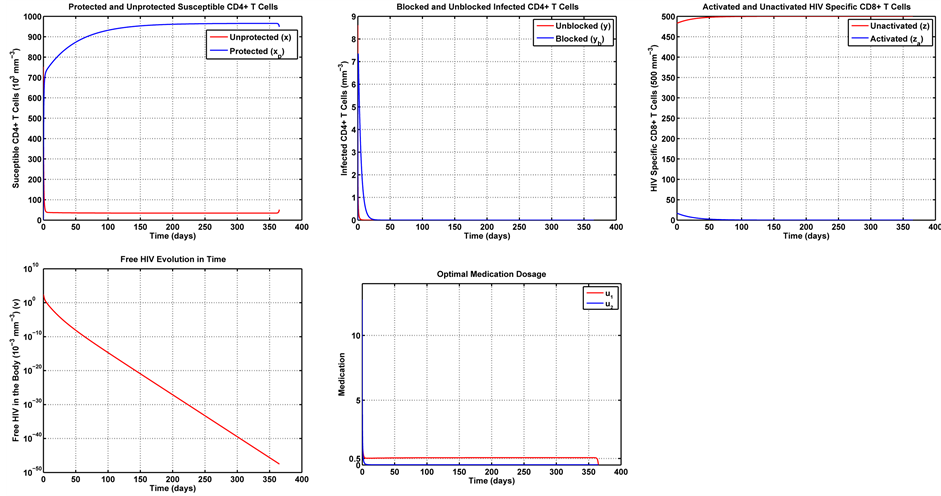
In Case 2, we examine the influence of parameter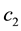
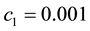
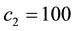
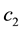
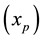
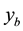
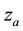
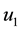
In Case 3 we make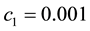
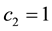
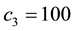

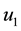
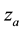

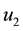

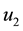
In Case 4 we make 


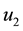
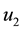
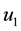
6. Concluding Remarks
This paper introduces a novel model of HIV dynamics. In contrast to typical HIV dynamics models, the pro- posed model explicitly describes the protected CD4+ T cells and the HIV-specific CD8+ T cells. That allows us to explicitly understand and quantify these effects, thus providing a better understanding of the system’s dynamics.
The dynamics of the proposed model can be influenced by the use of Anti-retroviral Therapy (ART), which has produced significant advances in the treatment of HIV infection. Such a therapy, however, is associated to side effects, which should be avoided whenever possible. To take account of the side effects and produce a desirable compromise between treatment effectiveness and side effects, we propose an optimal control approach
Figure 7. Optimal trajectories for Case 2: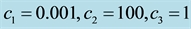
Figure 8. Optimal trajectories for Case 3: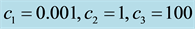
Figure 9. Optimal trajectories for Case 4: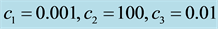
which prescribes an optimal treatment aimed at maximizing the benefits of the treatment, while also minimizing the side effects. The optimal control problem is solved by means of Pontryagin’s maximum principle and the optimal medication levels are numerically found by a standard gradient algorithm.
The proposed optimal control formulation is analyzed in the light of selected numerical examples, which provide insight into the behavior of the system under different compromises between medication effectiveness and side effects. We evaluate the sensitivity of the method with respect to the parameters in the optimal control functional by means of a series of examples, which shed light on the optimal trajectories of the variables with respect to different compromises between efficiency and side-effects. We analyze four different cases with distinct levels of side effect introduced by drugs 

Acknowledgements
The authors would like to thank FAPESP (Projeto temático Fapesp, 09/15098-0), and the Carlos Chagas Filho Foundation for Research Support of the State of Rio de Janeiro, FAPERJ, for supporting the research by means of grants APQ1 E-26/111.940/2012, E-26/110.379/2014 and E-26/110.087/2014. This work was partially sup- ported by the Coordination for the Improvement of Higher Education Personnel of Brazil―CAPES, under grant No. BEX2025/14-0, and by the National Council for Scientific and Technological Development―CNPq, under grant No.302716/2011-4.
References
- Eisele, E. and Siliciano, R. (2012) Redefining the Viral Reservoirs That Prevent HIV-1 Eradication. Immunity, 37, 377- 388. http://dx.doi.org/10.1016/j.immuni.2012.08.010
- Finzi, D., Blankson, J., Siliciano, J., Margolick, J., Chadwick, K., Pierson, T., Smith, K., Lisziewicz, J., Lori, F., Flexner, C., Quinn, T., Chaisson, R., Rosenberg, E., Walker, B., Gange, S., Gallant, J. and Siliciano, R. (1999) Latent Infection of CD4+ T Cells Provides a Mechanism for Lifelong Persistence of HIV-1, Even in Patients on Effective Combination Therapy. Nature Medicine, 5, 512-517. http://dx.doi.org/10.1038/8394
- Balamurali, M., Petravic, J., Loh, L., Alcantara, S., Kent, S.J. and Davenport, M.P. (2010) Does Cytolysis by CD8+ T Cells Drive Immune Escape in HIV Infection? The Journal of Immunology, 185, 5093-5101. http://dx.doi.org/10.4049/jimmunol.1002204
- Nowak, M. and Bangham, C. (1996) Population Dynamics of Immune Responses to Persistent Viruses. Science, 272, 74-79. http://dx.doi.org/10.1126/science.272.5258.74
- Perelson, A. (2002) Modelling Viral and Immune System Dynamics. Nature Reviews Immunology, 2, 28-36. http://dx.doi.org/10.1038/nri700
- Siewe, B., Wallace, J., Rygielski, S., Stapleton, J.T., Martin, J., Deeks, S.G. and Landay, A. (2014) Regulatory B Cells Inhibit Cytotoxic t Lymphocyte (CTL) Activity and Elimination of Infected CD4 T Cells after in Vitro Reactivation of HIV Latent Reservoirs. PLoS ONE, 9, e92934. http://dx.doi.org/10.1371/journal.pone.0092934
- Grégio, J., Caetano, M. and Yoneyama, T. (2009) State Estimation and Optimal Long Period Clinical Treatment of HIV Seropositive Patients. Anais da Academia Brasileira de Ciências, 81, 3-12. http://dx.doi.org/10.1590/S0001-37652009000100002
- Nowak, M. and May, R. (2000) Virus Dynamics: Mathematical Principles of Immunology and Virology. Oxford University Press, Oxford.
- Perelson, A. and Nelson, P. (1999) Mathematical Analysis of HIV-1 Dynamics in Vivo. SIAM Review, 41, 3-44. http://dx.doi.org/10.1137/S0036144598335107
- Perelson, A. and Ribeiro, R. (2013) Modeling the Within-Host Dynamics of HIV Infection. BMC Biology, 11, 96. http://dx.doi.org/10.1186/1741-7007-11-96
- Daugas, E. and Rougier, J. (2005) HAART-Related Nephropathies in HIV-Infected Patients. Kidney International, 67, 393-403. http://dx.doi.org/10.1111/j.1523-1755.2005.67096.x
- Sreenivasan, S. and Dasegowda, V. (2010) Adverse Effects after HAART Initiation in Resource-Limited Settings: A Prospective Study from Mysore, India. The Journal of Infection in Developing Countries, 4, 750-753. http://dx.doi.org/10.3855/jidc.934
- Torres, R. and Lewis, W. (2014) Aging and HIV/AIDS: Pathogenetic Role of Therapeutic Side Effects. Laboratory Investigation, 94, 120-128. http://dx.doi.org/10.1038/labinvest.2013.142
- Kirk, D. (1970) Optimal Control Theory: An Introduction. Prentice-Hall, Englewood Cliff.
- Adkinson Jr., N.F., Bochner, B.S., Busse, W.W., Holgate, S.T., Lemanske, R.F. and Simons, F.E. (2003) Middleton’s Allergy―Principles and Practice. Vol. 1, Mosby, Philadelphia.
- Kreysig, E. (1978) Introductory Functional Analysis with Applications. Wiley, New York.
- Dorf, R.C. and Bishop, R.H. (2001) Modern Control Systems. 9th Edition, Prentice Hall, Upper Saddle River.
- Lewis, F. and Syrmos, V. (1995) Optimal Control. John Wiley and Sons, New York.
- Pontryagin, L., Boltyanskij, V., GamKrelidze, R. and Mishchenko, E. (1961) The Mathematical Theory of Optimal Processes. Interscience Publishers, New York.
- Mclean, A. (2013) Infectious Disease Modeling. In: Kanki, P. and Grmes, D.J., Eds., Infectious Diseases, Springer, New York, 99-115. http://dx.doi.org/10.1007/978-1-4614-5719-0_5
- Chun, T., Carruth, L., Finzi, D., Shen, X., Digiuseppe, J., Taylor, H., Hermankova, M., Chadwick, K., Margolick, J., Kuo, Y., Brookmeyer, R., Zeiger, M., Barditch-Crovo, P. and Siliciano, R. (1997) Quantification of Latent Tissue Reservoirs and Total Body Viral Load in HIV-1 Infection. Nature, 387, 183-188. http://dx.doi.org/10.1038/387183a0
- Ho, P., Neumann, A., Perelson, A., Chew, W., Leonardo, J. and Markowitz, M. (1995) Rapid Turnover of Plasma Virions and CD4 Lymphocytes in HIV-1 Infection. Nature, 373, 123-126. http://dx.doi.org/10.1038/373123a0
- Lafeuillade, A., Poggi, C., Profizi, N., Tamalet, C. and Costes, O. (1996) Human Immunodeficiency Virus Type 1 in Lymph Nodes Compared with Plasma. Journal of Infectious Diseases, 174, 404-407. http://dx.doi.org/10.1093/infdis/174.2.404