Applied Mathematics
Vol.05 No.19(2014), Article ID:51323,20 pages
10.4236/am.2014.519297
The False Problem of the Maintenance of Sex (Review of the Original Approach)
Jose Maria Mancebo Quintana
Freelance Researcher, Arenas de San Pedro, Spain
Email: chemamancebo@yahoo.es
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 September 2014; revised 10 October 2014; accepted 28 October 2014
ABSTRACT
We analyze here the keys of the original approach about the twofold cost: the return to the asexuality starting with a mutant female, with the same reproductive capacity than a sexual one, and with double genetic-reproductive success. We propose a new approach in which 1) all individuals in a population have regulatory mechanisms of reproductive mode, and when such change occurs, it happens in all its population at the same time; 2) after a change of reproductive mode in the population there can be variations in average offspring per female, according to the environmental quality; and 3) the genetic-reproductive success of the males and its unequal paternity success are accounted for. Results: The most advantageous reproductive strategy depends on the demographic situation of the population and the degree of the unequal paternity success of males. For harem values observed in nature and in populations with moderate growth rate, stable or decreasing population, the sexual strategy is advantageous. If the population growth rate is high, the asexual strategy is advantageous. In species subject to high demographic fluctuations the best strategy depends on the ability to predict the time of occurrence of the population bottleneck: if predictable, the best strategy is the alternation of generations, if not, permanent parthenogenesis.
Keywords:
Strategy, Reproduction, Offspring, Harem, Success

1. The Double Cost of the Sexual Strategy
The fact that sexual reproduction is used by the vast majority of eukaryotic species could be considered strong evidence that it is a very effective reproductive method. However, this would not appear to be so due to the high costs involved, including the time and energy needed to find a partner and mate, the extra length of meiosis, the possibility of contracting sexually-transmitted diseases, added to the fact that randomly mixing your own genes with those of another individual is a seemingly risky method of producing offspring. The most significant costs involve the sexual production of offspring, known as the twofold cost of sex demonstrated by John Maynard Smith ([1] [2] , p. 3) and George Williams ( [3] , p. 8) in the 70s: asexual lineages can primarily reproduce at twice the rate of sexual; and asexual females transmit twice as many genes to each offspring compared to females that reproduce sexually [1] - [6] (reviewed in [7] [8] ) (Figure 1). Theoretically, transitions to asexuality in sexual species should lead to a rapid displacement of all sexual ancestors. A large number of theories have been proposed to explain why sexual reproduction prevails in most animal taxa [2] [3] [5] [9] - [12] , but the question has still to receive a satisfactory answer [13] - [16] .
The key aspects of the original approach to the twofold cost are as follows: 1) in a sexual species with an equal number of males and females, a mutation occurs that causes a female to produce only parthenogenetic females ( [2] , p. 3); 2) the number of offspring of a mutant female is the same as for the sexual female ( [2] , p. 3); and 3) the asexual mother has twice the genetic representation in the next generation as the sexual female, because in sexual reproduction the male contributes half of the alleles to the offspring ( [3] , p. 8).
1.1. Mutation as a Mechanism for Returning to Asexuality
Is it correct to assume that sexuality may appear by mutation in a single individual? We know that asexuality is the ancestral strategy in the history of life on earth, that sex appeared in unicellular eukaryotes associated to some advantage of syngamy (e.g. [17] ) and, with the appearance of multicellular beings, isogamic sex gave way to anisogamic sex, also due to some associated advantage (e.g. [18] ). It therefore seems unlikely that asexuality―a throwback to the past―can offer any advantage to current organisms with sexual reproduction. If this is indeed the case―and given that asexuality is the ancestral condition―it seems logical that the return to asexuality should occur in a facultative manner by silencing or activating certain genes, perhaps in response to certain signs of change in the environment. In fact nowadays, species with an alternation of generations continually change their reproductive mode in response to control systems, rather than depending on the fortuitous occurrence of a mutation. It is, therefore, not surprising that many authors believe these species provide an ideal opportunity for testing hypotheses on the maintenance of sex [19] .
Once we have rejected the mutational approach as a mechanism for reverting to asexuality, we should now ask ourselves whether reproductive change occurs simultaneously in a population. In the case of a parthenogenetic population reaching its maximum, and facing a habitat with limited resources, the benefits of switching to sexual reproduction, whatever they are, will only be possible if all asexual females produce sexual offspring. Otherwise, evidently, the only females a male could fecundate would be his sisters. If, however, the environmental conditions indicate that asexual reproduction is more advantageous, the population growth rate of the lineage that persists in using sexual reproduction will be half that of the rest of the population. As we can see, the benefits and costs conferred on an individual by each alternative will depend on the choice of the rest of the
Figure 1. Traditional scheme used to show the twofold cost of sex. While a parthenogenetic female transmits all her genes to her offspring (left), a sexual female transmits only 50% on average (right). Furthermore an asexual population grows at twice the rate of the sexual, because in the latter the males do not contribute to producing offspring.
population. Therefore, the choice of the best reproductive strategy is an example of an Evolutionarily Stable Strategy (ESS) [20] [21] .
A correct approach to calculating sexual and asexual reproductive success should therefore consider that all individuals in a population should have mechanisms regulating their reproductive strategy, and that when this change occurs, it does so in the whole population at the same time.
1.2. Changes in the Number of Offspring Due to the Change in the Reproductive Strategy
Obviously the number of offspring is a key factor for determining the most effective reproductive strategy, as mentioned by Williams himself in his original proposal: “Unless something causes a difference in the numbers of offspring...” ([3] , p. 8). However, an approach in which changes in reproductive strategy occur in unison in the entire population can have drastic effects on the average offspring per female.
In nature, resources are limited in most situations and most of the time, resulting in a direct relationship between density and number of offspring (e.g. [22] ). The relationship between rich habitats and fertility can be seen on both large and small scales: on a large scale, from the fact that in widespread species of both birds and mammals, the largest clutch sizes and litters occur at high latitudes (e.g. [23] ); and on a small scale, in the relationship between clutch size in birds and the abundance of their prey (e.g. [24] ). Density dependence is seen, for example, in bird studies over long periods of time, where clutch size decreases in years with a high density of couples in breeding periods (e.g. [24] ). In the case of populations in balance, the average number of offspring per female in an asexual population is one individual, whereas in a sexual population the average is two. Therefore the average offspring per female in a population in balance that changes its mode of reproduction is reduced by half when changing from sexual to asexual reproduction, or doubled for the reverse. Upon completion of the change in reproductive strategy, the average offspring once again stabilizes―at one in asexual and at two in sexual populations (Figure 2). In nature there is no possibility of checking this phenomenon as we describe it, but we can conduct studies in asexual and sexual lineages within the same species or taxa that are very close phylogenetically and have different types of reproduction, and compare the number of offspring per female in each case. The following two studies conducted with Daphnia pulex are particularly relevant. In the study by Wolinska & Lively [25] the optimal reproductive strategy depends on the field conditions in which experiments were developed, with the asexual strategy being better in rich habitats (“at the beginning of the season, when resource competition is low”), and the sexual strategy in poor habitats (“when conditions deteriorate as the population approaches carrying capacity”). In the study by Innes et al. [26] the fecundity of the sexual female was 75% higher than the asexual female in high-density conditions.
Would the same be true in virgin habitats? Obviously not, because in habitats with unlimited resources individuals do not compete for them, and all females―regardless of their density―will have the highest fertility for their species. We should therefore see the same fertility in sexual and asexual females in experiments with unlimited resources. This is the case, for instance, in experiments with the scolytid insect Ips acuminatus [27] , stick insects [28] , the fish genus Poecilia [29] and freshwater snails [30] . These works confirm our prediction that sexual and asexual fecundity are similar in benign demographic conditions; however, they do not discriminate whether a species has the same or different fecundity in adverse conditions, and are merely presented as demonstrations of the existence of the twofold cost of sex.
A correct approach to calculating sexual and asexual reproductive success should thus consider the effect of environmental quality on average offspring per female after a change of reproductive strategy in the population.
1.3. The “Genetic” Success of the Methods of Reproduction
According to G. Williams, an asexual mother has twice the genetic representation of the sexual in the generation of offspring, as in this case half the alleles are provided by the male ([3] , p. 8). This is true, yet ultimately, all the male’s alleles come from a female. For species that have practiced sexual reproduction for eons, this may involve going far back in time, but not for species with alternation of generations. In these species, an asexual female―the last of the period of asexual reproduction―produces sons and daughters that are genetically equal to her. She obviously trusts that producing males will ensure some genetic-reproductive―and not merely reproductive―success (as in the case of their daughters). Therefore in any population with sexual females, there are males with the capacity to transmit alleles, half of which have been received from other females (from their
Figure 2. Variations in average female offspring due to changes in reproductive strategy. The diagram shows, for populations in balance, the composition and size of different populations over time (histograms) and the average offspring per female (lower charts). (a) Sexual population, in which every female has an average of two descendants per generation; (b) Asexual population, with an average of one descendant per individual; (c) An asexual population changing to sexual, in which the average descendants goes from one individual to two in the first sexual generation; (d) Sexual population changing to asexual, with a reduction by half in the average offspring per female in the first asexual generation. We assume that the reproductive strategy is facultative and that the change in strategy would therefore occur in unison throughout the whole population (triggered by changes in the environment).
mothers). It can be deduced from this that the genetic-reproductive success (the ability to transmit alleles to the next generation) of a sexual female is obtained by the sum of the alleles transmitted through her sons and daughters: through her daughters in the first generation and through her sons in the second. This fact complicates the calculation of reproductive success, as the first generation of females is counted as the first generation for the mother, but the second generation for the father.
It is also the case that the paternity success of males is highly unequal from some individuals to others. This phenomenon has been known since the works of Angus Bateman in 1948 [31] , and since then has generated a large body of literature. In recent years studies have been published showing that, contrary to prevailing opinion, competition among females for access to males and selection by males are both more common than previously thought [32] . According to Hadany and Baker [33] , “If males have differential mating success, then the amount of progeny fathered by a successful male offspring can more than compensate for the twofold cost” (Figure 3). However, these authors do not estimate the reproductive success of the dominant male, but the effect of unequal success on the deleterious mutation load.
Using the terminology of Williams ([3] , p. 8), it can be said that in sexual populations there is a successful male in each generation that (in his territory) greatly multiplies an Am allele (on average in half the females he fecundates). Therefore the size of the harem appears to be a key factor determining which strategy is more advantageous for a female.
A correct approach to calculating sexual and asexual reproductive success should therefore consider male reproductive success (genetic) and unequal paternity success.
Figure 3. Scheme of sexual reproduction including the fecundation capacity of males and their unequal fecundation success. It is evident that the number of offspring generated by a successful male can vastly outweigh the twofold cost of sex.
2. Model and Results of the Comparative Analysis of Reproductive Success of Sexual and Parthenogenetic Strategies
2.1. Approach
The incorporation of the above points to the comparative analysis of reproductive strategies should contribute to developing a model that will allow us to predict the conditions in which one or the other reproductive strategy would be more advantageous, without the problems of the original approach. The model 1) should consider the ability to transmit genes from males, so it needs to cover at least two generations (the reproductive success of a sexual female through her sons is embodied in the grandchildren they can give her). 2) The first generation cannot be sexual, as the male’s fecundation involves a phenomenon we want to relegate, for the definition of sexual strategy, to the second generation. 3) Nor will the third generation be sexual, as the males in this generation materialize their reproductive success in the following generation, i.e., the fourth. 4) The model must also take into account the unequal paternity success of males. 5) Furthermore, the number of offspring per female depends to a greater or lesser degree on the density of females in the previous generation based on the quality of the environment. Finally, 6) the changes in reproductive mode occur in unison throughout the population.
We propose a scheme based on species with alternation of generations (sexual and asexual) as the ideal experimental system for testing hypotheses on the maintenance of sex [19] . In the transition to sexuality, one parthenogenetic female produces sexual males and females without the help of a male; returning to parthenogenesis, males and females of the sexual generation have offspring exclusively comprising females. We will therefore compare the reproductive success of two females through three generations, one with an asexual-sexual-asexual strategy (Figure 4, left), and the other completely asexual (Figure 4, right). (Obviously, in the case of the lineage with sexual generation, we assume that males fertilize females to whom they are unrelated.) Here we understand reproductive success as the capacity to multiply a marked allele Am existing in the founder females. The number of descendants (d) in the first generation is equal for both strategies, with the only obvious exception that sexual offspring is composed equally by females and males. In the second generation of the sexual lineage, however, half the offspring are female, and so their average offspring (d') may be different from the asexual lineage.
2.2. Variations in Average Offspring per Female
The relationship between female density in an area and the number of descendants per female in the next generation is evident in populations in balance, in which the average number of descendants per female in an asexual population is one individual, whereas the average in a sexual population is two. Therefore a change in reproductive strategy will mean the average offspring per female is reduced by half when the change is from sexual to
Figure 4. Approach comparing sexual and asexual strategies that resolves all errors or failures of the original approach to the twofold cost of sex. We compare the reproductive success of two females through three generations, one with an asexual- sexual-asexual strategy and the other completely asexual. Here we understand reproductive success as the capacity to multiply a marked allele Am existing in the founder females. The number of descendants per female (d and d') depends on the number of females of the previous generation and on the environmental richness (further explanation is given in the text).
asexual, or doubled, if reversed (Figure 2). On the other hand, in an environment where resources are not limiting there is no competition for them, and all females regardless of their number will present the maximum fertility for their species.
2.3. Parameters
Our model includes the following parameters:
・ d (of descendants): the average number of descendants per individual. By descendants we understand the sons and daughters who reach adulthood in the next generation. This therefore corresponds to k・S or number-of-eggs-laid-by-a-female × probability-of-survival-per-egg according to the terminology of Maynard Smith ([2] , p. 3). When it is necessary to distinguish two parameters, one for the average sexual offspring of a female and the other for the asexual one, we use ds and dp respectively.
・ h (of harem): the average number of females fertilized by the dominant male in the group. We followed the simplest model: i.e., there is only one dominant male for every h male, and that he alone fertilizes h females (always assuming a 50:50 sex ratio). If females have an average of d descendants, the dominant male will have hd descendants, half males and half females. The remaining males, h − 1, do not have offspring. We assume that the size of the harem is intrinsic to each species and independent of environmental conditions. (The model could be improved by incorporating a mathematical curve that describes the distribution of fertilizations of h females among the h males.)
・ ht: the threshold harem; the harem size for which both reproductive strategies have the same reproductive success.
Our model does not take into account the contribution of males in the production of offspring, as this makes the approach simpler and addresses the maintenance of sex in its most difficult version. The maintenance of sex becomes an issue when the reproductive success of the sexual female is less than the asexual female, and the contribution of the males to the breeding tips the balance toward sexuality.
Here we show the model in its discrete form, with only two demographic environments: one in a poor medium (population in balance) and another in a rich medium (population growing rapidly with average offspring per female close to the maximum for the species). This was chosen as it is simpler and sufficiently effective. In Appendix the model is developed on a continuous basis throughout the full range of environmental qualities.
2.4. Calculation of Reproductive Success in Reproductive Strategies
The reproductive success of both strategies according to our model is calculated by means of the following scheme (Figure 5), corresponding to the approach explained in Section 2.1:
The population that follows the sexual strategy faces two changes in reproductive strategy. As we have shown in the previous section (Section 2.2. Variations in average offspring per female), average female offspring in the first generation does not change, but now the offspring will consist of 50% males and females. Thus a female will have 0.5d females and 0.5d males in G1. Of these latter we only count one, which will be dominant among h males. All of them―the females and the dominant male―will inherit a hypothetical marked allele. This second sexual generation may already undergo variation in the average offspring per female depending on habitat quality. In poor habitats the average offspring is doubled, while in rich habitats it remains unchanged and close to the maximum offspring per female. In this generation each daughter has only a 50% probability of inheriting the marked allele. The reproductive success of the sexual strategy is obtained by multiplying the offspring of each generation by the probability of the transmission of the marked allele, adding the results of the female and dominant male genealogical lineages (although we know the number of descendants of a couple are either from the female or the male, which is the same amount). Therefore:
Reproductive success―sexual female = 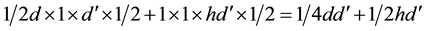 (1)
(1)
In poor habitats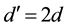 , so that Equation (1) is as follows:
, so that Equation (1) is as follows:
Reproductive success―sexual female in poor environments = 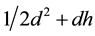 (2)
(2)
While in rich habitats , so that Equation (1) becomes:
, so that Equation (1) becomes:
Reproductive success―sexual female in rich environments = 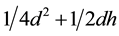 (3)
(3)
Figure 5. Scheme for calculating the reproductive success of two parthenogenetic females following two different strategies (Figure 4) over three generations. The first has an asexual-sexual-asexual strategy, and the second is entirely asexual. We assume that the reproductive strategy is facultative and changes in unison throughout the population. The number of descendants per female depends on the environmental conditions and the strategy of the previous generation (see Section 2.2). Here we understand reproductive success as the capacity to multiply a marked allele Am existing in the founder females.
The population that follows the asexual strategy maintains the same average female offspring generation after generation (Figure 2), so
Reproductive success―parthenogenetic female =  (4)
(4)
To calculate the size of the harem that equates the two strategies (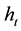 or threshold harem) we equalize the equations for each type of reproduction. In demographic conditions and for those species in which the average size of the dominant male’s real harem is lower than the calculated
or threshold harem) we equalize the equations for each type of reproduction. In demographic conditions and for those species in which the average size of the dominant male’s real harem is lower than the calculated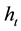 , parthenogenesis will be advantageous and would therefore lead to a paradox (the real problem of the maintenance of sex). If instead we obtain a value of
, parthenogenesis will be advantageous and would therefore lead to a paradox (the real problem of the maintenance of sex). If instead we obtain a value of 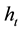 that is matched or exceeded by the majority of the species, sexuality should be the norm.
that is matched or exceeded by the majority of the species, sexuality should be the norm.
2.5. Results
Case 1. Poor habitats (average offspring per female far from the maximum offspring of the species).
To calculate  we equate Equation (2) and Equation (4):
we equate Equation (2) and Equation (4):

Isolating

The harem size that produces equal sexual and asexual reproductive success is only half the average offspring of the species. For the specific case of sexual populations in balance, in which d = 2, the harem needed consists of one individual: i.e., monogamy equals the reproductive success of the asexual strategy. If there were―and we know there is―unequal paternity success, the sexual strategy would have greater reproductive success. This result explains why the vast majority of higher organisms use the sexual strategy.
Case 2. Rich habitats (average offspring per female almost attains or is at the maximum for the species).
To calculate 
Isolating

The harem size that produces equal sexual and asexual reproductive success is 1.5 times the maximum offspring of the species. A population growing at its maximum growth rate would therefore have a high threshold harem, higher in any case than the real average harem. This result would explain why asexual strategy is advantageous in virgin habitats.
2.6. Solution for the Full Range of Habitat Qualities
The calculation of the threshold harem for the full range of habitat qualities is more complicated and is shown in Appendix (Continuous Calculation of Reproductive Success). It is based on the relationship habitat quality/ offspring per female in the shape of a saturation curve, logical relationship and with sufficient empirical sup- port.
The formula deduced in Appendix is as follows:

where 
We can now calculate a table of values taken by 


It can be seen that in populations in balance with sexual reproduction―where d = 2―the threshold harem is practically one individual: i.e., monogamy equals the reproductive success of the asexual strategy. Conversely, in rapidly-growing populations the threshold harem is very high and may exceed the real harem of the species, thus making the asexual strategy advantageous.
Table 1. Threshold harem necessary for equal reproductive success in sexual and parthenogenetic strategies, depending on the maximum offspring of the species (M) and the average female offspring (d); this last parameter depends on habitat quality.
3. Verifying the Correspondence of the Model with Observations in Nature
3.1. Prevalence of the Sexual Strategy
Sexual reproduction is used at least occasionally by the vast majority of eukaryotes. Among the known animal species, only ~0.1% is considered completely asexual [34] . According to our results, the sexual strategy is advantageous in poor habitats (=populations in balance) if the average harem of the dominant male is higher than half the average female offspring. The average offspring per female is d = 2 in populations with a demographic balance, thus the threshold harem is only one female, as seen above. In a recent paper, Michael J. Wade and Stephen M. Shuster [35] collected 26 published papers on harem size in 20 species, including crustaceans, insects, amphibians, reptiles, birds and mammals, with values ranging from a minimum of 1.4 (approximately) in humans up to 6.75 in the African lion (Panthera leo). In these species, and provided the population is close to the balanced situation, the sexual strategy is more efficient than the asexual.
3.2. Cyclical Parthenogenesis
There are few experimental systems that allow tests of short- and long-term hypotheses on the maintenance of sex. Among these, organisms such as aphids that are capable of both sexual and asexual reproduction are of special interest because they allow a direct assessment of the costs and benefits of sex versus asex [19] . Like other sexual organisms, aphids theoretically have at least a twofold reproductive disadvantage over asexuals every annual cycle [36] [37] . The cost of sex in aphids increases greatly in excess of the standard twofold cost because several asexual generations are produced for each sexual generation [37] . The paradox of sex (the prevalence of cyclical over obligate parthenogenesis) thus seems to be even more marked in aphids than in most other organisms [19] .
The typical aphid reproductive mode indeed involves a succession of usually numerous parthenogenetic generations, followed by a single sexual one within the annual life cycle [19] [38] . This reproductive system is also known as cyclical parthenogenesis in animals, and is found in other invertebrates such as cynipid wasps, midges, water fleas (Daphnia) and a wide range of trematodes [39] . The asexual phase of aphids occurs during the growing season (spring and summer) and up to 20 asexual generations can be produced if climatic conditions are favorable. The annual population curve (see e.g. [40] ) clearly shows a period of exponential population growth, coinciding with the period of abundance of resources caused by the opening of buds and the longitudinal growth of new branches, followed by a halt and a sharp decline in population in late summer, when there is practically no food in the plants on which these populations feed (Figure 6). According to our results, during the exponential
Figure 6. Typical annual curve of the aphid population with exponential growth in spring and summer, and final collapse (continuous black line). Data are fictitious and similar to those shown in the work of F. J. Hills [40] . The population growth rate, assuming that a generation lasts a month, is shown by the dashed black line. The resulting threshold harem, calculated using Equation (12) and assuming a maximum offspring of the species M = 10, is shown by the dashed gray line. For a species with an average harem of three females, the best reproductive strategy is shown in the lower bar.
growth phase the asexual strategy will be advantageous if the dominant male’s harem is less than 1.5 times the average offspring of a female; this offspring is equal to the rate of population growth in the case of asexual populations. An asexual population growing at a rate of 5 or 10 per generation would have a threshold harem of 7.5 and 15, respectively, which would be unlikely (but verifiable). In late summer, however, the average asexual female offspring becomes 1 (in the case that the population remains stable) or lower (if the population decreases), and as the threshold harem is only half the average offspring, it therefore reaches low and feasible values (one in the stable population, 0.5 in a population that decreases by half per generation). The best strategy is therefore the alternation of generations (Figure 6).
A particularly interesting question relating to the alternation of generations is the predictability of disturbance or of periods of shortage of resources. It should be recalled that, following our model, the reproductive success of a female with an asexual-sexual-asexual strategy (like aphids) is achieved in the last generation, after the male’s unequal fecundation. Furthermore, the last asexual generation prior to the change involves a high rate of population growth; otherwise it would not be asexual. Therefore the change from the asexual to the sexual reproduction mode will only succeed if a female can somehow foresee that the number of her descendants will decrease enough to make the sexual strategy advantageous. In the case of aphids, it is the lack of resources in late summer that imposes a reduction in offspring, apparently triggered by changes in the photoperiod [41] . In Chara canescens (Charales, Charophyceae), a species with sexual and parthenogenetic forms, the sexual forms appear in habitats with a very short growing season and which dry out annually [42] , so that here also the sexual strategy is associated to a periodic and predictable disturbance. If, however, a population regularly faces unpredictable disturbances, after which the habitat again becomes available for the survivors, the best strategy will be permanent parthenogenesis. This may be an explanation for geographical parthenogenesis, as discussed in the following section.
3.3. Geographical Parthenogenesis
Clonally reproducing all-female lineages of plants and animals are often more frequent at higher altitudes, in anthropogenically disturbed environments, at the margins of a species range, on islands versus the mainland, and in successional versus climax communities [5] [43] -[45] . A number of hypotheses have been proposed to explain geographical parthenogenesis (according to [46] ): all-female reproduction provides superior colonizing ability and reproductive assurance [47] [48] ; biotic uncertainty favors genotypically diverse sexuals in species-packed central environments [43] [49] ; destabilizing hybridization favors displacement of parthenogens from the sexual range [44] [50] ; heterozygosity assurance due to cloning favors asexual lineages in subdivided metapopulations [51] [52] ; and so forth.
According to our results, asexuality could be observed more frequently in the mentioned environments if conditions were to allow a high rate of population growth. This can happen in two ways: either because the environment is virgin, such as on the edge of a species’ range, and perhaps at high altitudes; or because the population suffers periodic (but random) disturbances that drastically reduce their size, as occurs at high altitudes, in habitats disturbed by man, on islands and in successional communities. We have included the condition of randomness in the occurrence of disturbances, because if they were in any way predictable by the population, the sexual strategy would be advantageous in the last (or later) generations before and during the population bottleneck, as we have seen in the previous section.
3.4. Sympatric Coexistence of Sexual and Asexual Populations
A particularly interesting case for testing hypotheses about the maintenance of sex is found in aphid species with sexual and asexual populations coexisting in a sympatric way. Perhaps the most widely studied is the pea aphid (Acyrthosiphon pisum), a species in which the mode of reproduction is likely to be adaptative [53] . According to A. Frantz et al. [53] , the investment level in the sexual phase (i.e. the proportion of sexual lineages and the proportion of sexual morphs produced) was higher among host populations originating from annual crops than among the host populations from perennial crops. The fields of annual crops are completely harvested in summer and therefore represent periodically destroyed habitats. Aphid populations living on these crops are subjected to frequent bottlenecks. Conversely, the relatively high temporal stability on perennial crops, cultivated over several years, would allow the maintenance of asexual lineages.
The only explanation for this phenomenon to date is based on one of the genetic advantages indicated for sexual reproduction: the capacity to rapidly combine favorable mutations, which provides sexual lineages with better adaptability to changing environments [54] [55] . According to our results, however, sexual strategy is advantageous when a population approaches or reaches the equilibrium population, and more so in the case of lower growth rates (as in a population bottleneck), such as in populations of pea aphid living in annual crop fields. The asexual strategy could be permanently advantageous if the unequal paternity success is low or―more likely―new virgin environments continuously appear to colonize, such as perennial crops.
4. Discussion
4.1. What Is the Twofold Cost of Sex?
What is the twofold cost of sex? It is the result of a comparative analysis of a quantitative type of reproductive success of two reproductive strategies: anisogamous sex and parthenogenesis. The result of this analysis should be that sexual strategy is advantageous, since we know that evolutionary history begins with asexual reproduction, which gave way to isogamous sex and finally to anisogamous sex in multicellular organisms. However, the result of the original authors’ approach is, as we know, that anisogamous sex has a cost. Since the publication of these results, many authors have unsuccessfully attempted to find the advantages of sex that would offset the twofold cost. In our opinion, two strategies should have been initiated simultaneously after the publication of the problem of the twofold cost. The first and most obvious would be to study the advantages of anisogamy versus isogamy in multicellular beings (because we know that sex is mostly isogamous in single-celled organisms). Not only do we know the evolutionary advantage of anisogamy, but also the amount of this advantage. Unfortunately, the hypotheses as to the origin of anisogamy are scarce and the most widely accepted of these ( [18] ) has important basic failures [56] . The second strategy is to reshape the approach to the twofold cost: Is it correct to assume that the return to asexuality can be initiated in a single individual and that it requires a mutational origin? Would we obtain the same result if the entire population simultaneously changed its reproduction mode? If the number of descendants is a key factor in the approach, can we deduce some variation in average offspring after a change of reproductive mode in a population? Does habitat quality, through its relationship with average off- spring, have an impact on the advantages of one or another reproductive strategy? And with regard to genetic advantages, why is the male’s fecundation success not taken into account?
With these questions in mind, we have designed an alternative approach. We are confident that other comparative approaches or schemes can be designed, but we believe they will be more mathematically complex and less elegant than our own. The starting and end points are the same for both reproductive strategies: they both begin with the offspring produced by a parthenogenetic female, and end in a generation also composed exclusively of parthenogenetic females. The calculation of reproductive success simply counts the number of copies that have, in the last generation, a hypothetical marked allele carried by each of the founder females. We cannot conceive of a more elegant, simple and powerful approach.
4.2. Variation in the Number of Descendants Due to the Change in Reproduction Mode
4.2.1. Justification
The variation in the number of descendants due to the change in the mode of reproduction in a population has been overlooked so far in all works on the twofold cost of sex. During the review process of this work by other authors we have found this phenomenon to be difficult to understand. For some it may therefore require more justification than has been given hitherto.
Let us suppose there is no such effect, and that reproductive strategies have no influence on the average offspring per female. We will consider the change in reproductive strategy in a population in balance, where births and deaths are offset so the population size remains stable, and where the population is also isolated (so we can dispense with immigration and emigration in the population growth formula).
a) We start with an asexual population. What is the average offspring per female? One, without a doubt, as we know the population remains stable in number. At one point the population becomes sexual: A parthenogenetic female produces either a sexual female or a male, with a 50% probability in each case. In this second―sexual― generation, each female again has a single descendant. Now, however, as the males do not have offspring, the population is halved in each generation until it disappears. From the point of view of population ecology this is absurd: If it is the environment that limits the size of the population, why is the population now halved in each generation? Does fertility not increase or mortality decline to ensure the population remains stable?
b) Now let us suppose that the initial population is sexual. The average female offspring in this case will be two. The transformation into asexual occurs: each sexual female produces two asexual females. The entire population is already formed by asexual females. As each female still has two descendants on average, the population progressively doubles. As in the previous case, this is absurd from the point of view of population ecology: If it is the environment that limits the size of the population, why has the population now been able to double and grow exponentially? Should fertility not be reduced or mortality increased to ensure the population remains in balance?
We emphasize that the variation in offspring after the reproductive mode change is all that counts for the purposes of reproductive strategies, regardless of whether it is caused by variations in fertility or mortality during development. This can be demonstrated with a different example: the case of a semelparous species with external fertilization and without paternal or maternal care. Males and females come together to mate at the end of their life. They die after spawning and egg fertilization. If, for a male, the fight for females means a cost equal to that of a female to reproduce, this effect ends once the dominant males have fertilized eggs. From there on the eggs themselves face the struggle to reach adulthood. In a stable environment with limited resources, the number of eggs reaching adulthood does not depend on its initial number, but on the capacity of the habitat. This number can be expected to be approximately the same as in the previous generation. If the clutch (counting all individuals) is exceptionally large, there will be a high mortality during development. If it is small, there will be low mortality. The point is that in poor habitats―and generally in habitats where populations are saturated―fertility and mortality during development are related, so the population size remains stable. Regarding the number of descendants: if the population is sexual, each female will have two descendants; if the population is asexual, each female will have one descendant; if the reproductive strategy changes, the offspring per female varies.
4.2.2. Empirical Support
There is an extensive body of literature on the changes in fertility of females in sexual and asexual natural populations. These studies are conducted with asexual and sexual lineages within the same species or with taxa that are phylogenetically very close, and different types of reproduction. The first studies―on varieties derived from parthenogenetic forms with compulsory cyclical parthenogenesis―are more reliable [44] [57] [58] . Table 2 shows the value of the sexual-offspring/asexual-offspring 
As we can see, most of the results yield values of 

Table 2. Numerical relationship between the number of descendants of females in sexual and parthenogenetic populations (in different species or groups of related species).
1Some works analyze the size of the litter or the clutch while others analyze the number of descendants (d in our denotation).
Among those that do, some have been conducted in rich habitats with or without minimal population growth constraints. Similar fertility in sexual and asexual forms was obtained in these cases, as expected if observing the maximum offspring. This occurs for example in the work of Loyning [27] with Ips acuminatus, in which one or two females colonized pine logs, and thus had minimal or no competition for resources (40 eggs/female on average); in the study on stick insects by Morgan-Richards [28] , in which the females are kept alone or with a male for six weeks and the number of eggs laid ranges between 44 and 112; in the study by Schlupp et al. [29] with Poecilia, fed ad libitum in the first experiment and with food supplements in the second; and in the study by Jokela et al. [30] , in which the asexual population is multiplied by 11. These studies confirm our prediction that sexual and asexual fecundity are similar in benign demographic conditions. They obviously do not discriminate whether a species has the same or different fertility in adverse conditions, but are presented merely as demonstrations of the twofold cost of sex.
Much more interesting for our purposes are the works that include benign and adverse conditions. Of particular relevance are the following two studies on Daphnia pulex, as they highlight the different fertility rates in poor habitats and similar rates in rich ones. In the study by Wolinska & Lively [25] , although asexual females have higher fertility than sexual females, asexual specimens were excluded in competition experiments with food shortages. In the study by Innes et al. [26] , similarly fertility was obtained 

4.3. Unequal Paternity Success
The idea that differential male mating success or harsher selection on males in general may have something to dowith the maintenance of sex is not new, and dates back at least to Trivers [74] [75] . Trivers, however, suggested that sex provided an immediate benefit: females chose males who would give them daughters that were twice as fit as they would obtain if they had mated randomly. If deleterious mutations are the chief source of additive genetic variance in fitness then this idea is untenable, as it requires mutation rates 20 - 100 times higher than those observed in nature [76] . Other studies have focused on males and their role in the reduction of mutational load in sexual populations [77] - [80] . Other authors have suggested that differential mating success in males would lead to improved adaptation to a changing environment [81] -[83] .
5. Conclusions
A correct approach for the calculation of sexual and asexual reproductive success must consider 1) that all individuals in a population have mechanisms regulating their reproductive mode and, when the change occurs, it occurs in unison throughout the population; 2) the effect of environmental quality on average offspring per female after a change of reproductive mode in the population; and 3) the genetic-reproductive success of males and their unequal paternity success.
The results of this approach are:
1) The size of the dominant male harem and the offspring per female are shown to be key variables to determine which reproductive strategy is advantageous. Given that the offspring per female depends on environmental conditions, through the availability of resources for reproduction, the key variables would be the harem and habitat quality. (Although sensu stricto, the harem would be a constant for each species, not a variable.)
2) In populations with a moderate growth rate and a stable or declining population, the sexual strategy is advantageous (the threshold harem is half the average offspring of a female). For the specific case of populations in balance, monogamy equals the reproductive success of asexual reproduction.
3) In populations with a high population growth rate, the asexual strategy becomes advantageous (the threshold harem is 1.5 times the average offspring of a female).
4) In species subject to high demographic fluctuations, the best strategy depends on the ability to predict the time of occurrence of the population bottleneck: if predictable, the best strategy is the alternation of generations, if not, permanent parthenogenesis.
Our approach and mathematical scheme could be improved or extended in several aspects: 1) by incorporating the average and variance of the male fertilizing success; 2) by adding a parameter related to the contribution of males in the production of offspring; and 3) by adding parameters and geographical or territorial effects (dispersion of offspring, reducing the resources available for females for reproduction according to the local density of females, etc.).
Acknowledgements
The author is extremely grateful to Juan Carranza Almansa (University of Extremadura) for his critical discussion of the work, to Santiago Mancebo for his critical analysis of the approach, to Joseph Yusta for his help in translation, Ana Romero for her revision of the translation and to Prudence Brooke-Turner for her professional review of the writing style and the translation into English.
Cite this paper
Jose MariaMancebo Quintana, (2014) The False Problem of the Maintenance of Sex (Review of the Original Approach). Applied Mathematics,05,3135-3155. doi: 10.4236/am.2014.519297
References
- 1. Smith, J.M. (1971) The Origin and Maintenance of Sex. In: Williams, G.C., Ed., Group Selection, Aldine-Atherton, Chicago, 163-175.
- 2. Smith, J.M. (1978) The Evolution of Sex. Cambridge University Press, Oxford.
- 3. Williams, G.C. (1975) Sex and Evolution. Princeton University Press, Princeton.
- 4. Smith, J.M. (1971) What Use Is Sex? Journal of Theoretical Biology, 30, 319-335.
http://dx.doi.org/10.1016/0022-5193(71)90058-0 - 5. Bell, G. (1982) The Masterpiece of Nature: The Evolution and Genetics of Sexuality. University of California Press, Berkeley.
- 6. Otto, S.P. and Lenormand, T. (2002) Resolving the Paradox of Sex and Recombination. Nature Reviews Genetics, 3, 252-261.
http://dx.doi.org/10.1038/nrg761 - 7. Lehtonen, J., Jennions, M.D. and Kokko, H. (2012) The Many Costs of Sex. Trends in Ecology and Evolution, 27, 172-178.
http://dx.doi.org/10.1016/j.tree.2011.09.016 - 8. Otto, S.P. (2009) The Evolutionary Enigma of Sex. The American Naturalist, 174, S1-S14.
http://dx.doi.org/10.1086/599084 - 9. Muller, H.J. (1964) The Relation of Recombination to Mutational Advance. Mutation Research/Fundamental and Molecular Mechanisms of Mutagenesis, 1, 2-9.
http://dx.doi.org/10.1016/0027-5107(64)90047-8 - 10. Hamilton, W.D., Axelrod, R. and Tanese, R. (1990) Sexual Reproduction as an Adaptation to Resist Parasites (a Review). Proceedings of the National Academy of Sciences of the United States of America, 87, 3566-3573.
http://dx.doi.org/10.1073/pnas.87.9.3566 - 11. Kondrashov, A.S. (1993) Classification of Hypotheses on the Advantage of Amphimixis. Journal of Heredity, 84, 372-387.
- 12. Otto, S.P. and Gerstein, A.C. (2006) Why Have Sex? The Population Genetics of Sex and Recombination. Biochemical Society Transactions, 43, 519-522.
- 13. Birky, C.W. (1996) Heterozygosity, Heteromorphy, and Phylogenetic Tress in Asexual Eukaryotes. Genetics, 144, 427-437.
- 14. Barton, N.H. and Charlesworth, B. (1998) Why Sex and Recombination? Science, 281, 1986-1990.
http://dx.doi.org/10.1126/science.281.5385.1986 - 15. Vrijenhoek, R.C. (1998) Clonal Organisms and the Benefits of Sex. In: Advances in Molecular Ecology, IOS Press, Amsterdam, 151-172.
- 16. Birky, C.W., Wolf, C., Maughan, H., Herbertson, L. and Henry, E. (2005) Speciation and Selection without Sex. Hydrobiologia, 546, 29-45.
http://dx.doi.org/10.1007/s10750-005-4097-2 - 17. Quintana, J.M.M. and Quintana, S.M. (2012) A Short-Term Advantage for Syngamy in the Origin of Eukaryotic Sex: Effects of Cell Fusion on Cell Cycle Duration and Other Effects Related to the Duration of the Cell Cycle—Relationship between Cell Growth Curve and the Optimal Size of the Species, and Circadian Cell Cycle in Photosynthetic Unicellular Organisms. International Journal of Evolutionary Biology, 2012, Article ID: 746825.
- 18. Parker, G.A., Baker, R.R. and Smith, V.G.F. (1972) The Origin and Evolution of Gamete Dimorphism and the Male-Female Phenomenon. Journal of Theoretical Biology, 36, 529-553.
http://dx.doi.org/10.1016/0022-5193(72)90007-0 - 19. Simon, J.C., Rispe, C. and Sunnucks, P. (2002) Ecology and Evolution of Sex in Aphids. Trends in Ecology & Evolution, 17, 34-39.
http://dx.doi.org/10.1016/S0169-5347(01)02331-X - 20. Smith, J.M. (1972) Game Theory and the Evolution of Fighting. In: On Evolution, Edinburgh University Press, Edinburgh.
- 21. Smith, J.M. and Price, G. (1973) The Logic of Animal Conflict. Nature, 246, 15-18.
http://dx.doi.org/10.1038/246015a0 - 22. Lack, D. (1954) The Natural Regulation of Animal Numbers. Clarendon Press, Oxford.
- 23. Cody, M. (1966) A General Theory of Clutch Size. Evolution, 20, 174-184.
http://dx.doi.org/10.2307/2406571 - 24. Perrins, C. (1965) Population Fluctuations and Clutch Size in the Great Tit, Parus major L. Journal of Animal Ecology, 34, 601-647.
http://dx.doi.org/10.2307/2453 - 25. Wolinska, J. and Lively, C.M. (2008) The Cost of Males in Daphnia pulex. Oikos, 117, 1637-1646.
http://dx.doi.org/10.1111/j.1600-0706.2008.16760.x - 26. Innes, D.J., Fox, C.J. and Winsor, G.L. (2000) Avoiding the Cost of Males in Obligately Asexual Daphnia pulex (Leydig). Proceedings of the Royal Society B: Biological Sciences, 267, 991-997.
http://dx.doi.org/10.1098/rspb.2000.1101 - 27. Loyning, M.K. (2000) Reproductive Performance of Clonal and Sexual Bark Beetles (Coleoptera: Scolytidae) in the Field. Journal of Evolutionary Biology, 13, 743-748.
http://dx.doi.org/10.1046/j.1420-9101.2000.00227.x - 28. Morgan-Richards, M., Trewick, S.A. and Stringer, I.A.N. (2010) Geographic Parthenogenesis and the Common Tea-Tree Stick Insect of New Zealand. Molecular Ecology, 19, 1227-1238.
http://dx.doi.org/10.1111/j.1365-294X.2010.04542.x - 29. Schlupp, I., Taebel-Hellwig, A. and Tobler, M. (2010) Equal Fecundity in Asexual and Sexual Mollies (Poecilia). Environmental Biology of Fishes, 88, 201-206.
http://dx.doi.org/10.1007/s10641-010-9630-0 - 30. Jokela, J., Lively, C.M., Dybdahl, M.F. and Fox, J.A. (1997) Evidence for a Cost of Sex in the Freshwater Snail Potamopyrgus antipodarum. Ecology, 78, 452-460.
http://dx.doi.org/10.1890/0012-9658(1997)078[0452:EFACOS]2.0.CO;2 - 31. Bateman, A.J. (1948) Intra-Sexual Selection in Drosophila. Heredity, 2, 349-368.
http://dx.doi.org/10.1038/hdy.1948.21 - 32. Clutton-Brock, T. (2007) Sexual Selection in Males and Females. Science, 318, 1882-1885.
http://dx.doi.org/10.1126/science.1133311 - 33. Hadany, L. and Beker, T. (2007) Sexual Selection and the Evolution of Obligatory Sex. BMC Evolutionary Biology, 7, 245.
http://dx.doi.org/10.1186/1471-2148-7-245 - 34. Vrijenhoek, R.C. (1998) Animal Clones and Diversity. BioScience, 48, 617-628.
http://dx.doi.org/10.2307/1313421 - 35. Wade, M.J. and Shuster, S.M. (2004) Sexual Selection: Harem Size and the Variance in Male Reproductive Success. The American Naturalist, 164, E83-E89.
http://dx.doi.org/10.1086/424531 - 36. Bulmer, M. (1982) Cyclical Parthenogenesis and the Cost of Sex. Journal of Theoretical Biology, 94, 197-207.
http://dx.doi.org/10.1016/0022-5193(82)90341-1 - 37. Rispe, C. and Pierre, J. (1998) Coexistence between Cyclical Parthenogens, Obligate Parthenogens, and Intermediates in a Fluctuating Environment. Journal of Theoretical Biology, 195, 97-110.
http://dx.doi.org/10.1006/jtbi.1998.0784 - 38. Moran, N. (1992) The Evolution of Aphid Life Cycles. Annual Review of Entomology, 37, 321-348.
http://dx.doi.org/10.1146/annurev.en.37.010192.001541 - 39. De Meester, L., Gomez, A. and Simon, J. (2004) Evolutionary and Ecological Genetics of Cyclical Parthenogens. In: Evolution: From Molecules to Ecosystems, Oxford University Press, Oxford.
- 40. Hills, F.J. (1982) Sugarbeet Pest Management: Aphid-Borne Viruses. University of California, Oakland.
- 41. Marcovitch, S. (1924) The Migration of the Aphididae and the Appearance of the Sexual Forms as Affected by the Relative Length of Daily Light Exposure. Journal of Agricultural Research, 27, 513-522.
- 42. Schaible, R., Bergmann, I. and Schubert, H. (2009) A Survey of Sexually Reproducing Female and Male Populations of Chara canescens (Charophyta) in the National Park Neusiedler See-Seewinkel. Cryptogamie, Algologie, 30, 279-294.
- 43. Glesener, R.R. and Tilman, D. (1978) Sexuality and the Components of Environmental Uncertainty: Clues from Geographic Parthenogenesis in Terrestrial Animals. The American Naturalist, 112, 659-673.
http://dx.doi.org/10.1086/283308 - 44. Lynch, M. (1984) Destabilizing Hybridization, General-Purpose Genotypes and Geographic Parthenogenesis. The Quarterly Review of Biology, 59, 257-288.
http://dx.doi.org/10.1086/413902 - 45. Parker, E.D.J. (2002) Geographic Parthenogenesis in Terrestrial Invertebrates: Generalist or Specialist Clones? In: Progress in Asexual Propagation and Reproductive Strategies, Oxford-IBH, Oxford, 93-114.
- 46. Vrijenhoek, R.C. and Parker Jr., E.D. (2009) Geographical Parthenogenesis: General Purpose Genotypes and Frozen Niche Variation. In: Lost Sex. The Evolutionary Biology of Parthenogenesis, Springer, Berlin, 99-131.
- 47. Baker, H.G. (1965) Characteristics and Modes of Origin of Weeds. In: Genetics of Colonizing Species, Academic Press, New York, 147-172.
- 48. Tomlinson, J. (1966) The Advantage of Hermaphroditism and Parthenogenesis. Journal of Theoretical Biology, 11, 54-58.
http://dx.doi.org/10.1016/0022-5193(66)90038-5 - 49. Hamilton, W., Henderson, P. and Moran, N. (1981) Fluctuation of Environmental and Coevolved Antagonist Polymorphism as Factors in the Maintenance of Sex. In: Natural Selection and Social Behavior, Chiron Press, New York, 363-381.
- 50. Paulissen, M.A., Walker, J.M. and Cordes, J.E. (1988) Ecology of Syntopic Clones of the Parthenogenetic Whiptail Lizard, Cnemidophorus laredoensis. Journal of Herpetology, 22, 331-342.
http://dx.doi.org/10.2307/1564157 - 51. Vrijenhoek, R.C. (1985) Animal Population Genetics and Disturbance: The Effects of Local Extinctions and Recolonizations on Heterozygosity and Fitness. In: The Ecology of Natural Disturbance and Patch Dynamics, Academic Press, New York, 265-285.
- 52. Haag, C.R. and Ebert, D. (2004) A New Hypothesis to Explain Geographic Parthenogenesis. Annales Zoologici Fennici, 41, 539-544.
- 53. Frantz, A., Plantegenest, M. and Simon, J.C. (2006) Temporal Habitat Variability and the Maintenance of Sex in Host Populations of the Pea Aphid. Proceedings of the Royal Society B: Biological Sciences, 22, 2887-2891.
http://dx.doi.org/10.1098/rspb.2006.3665 - 54. Kondrashov, A.S. (1988) Deleterious Mutations and the Evolution of Sexual Reproduction. Nature, 336, 435-440.
http://dx.doi.org/10.1038/336435a0 - 55. Hadany, L. and Becker, T. (2003) On the Evolutionary Advantage of Fitness-Associated Recombination. Genetics, 165, 2167-2179.
- 56. Randerson, J.P. and Hurst, L.D. (2001) The Uncertain Evolution of the Sexes. Ecology & Evolution, 16, 571-579.
http://dx.doi.org/10.1016/S0169-5347(01)02270-4 - 57. Cullum, A.J. (1997) Comparisons of Physiological Performance in Sexual and Asexual Whiptail Lizards (Genus Cnemidophorus): Implications for the Role of Heterozygosity. The American Naturalist, 150, 24-47.
http://dx.doi.org/10.1086/286055 - 58. Mee, J.A. and Rowe, L. (2006) A Comparison of Parasite Loads on Asexual and Sexual Phoxinus (Pisces: Cyprinidae). Canadian Journal of Zoology, 84, 808-816.
http://dx.doi.org/10.1139/z06-064 - 59. Stelzer, C.P. (2011) The Cost of Sex and Competition between Cyclical and Obligate Parthenogenetic Rotifers. The American Naturalist, 177, E43-E53.
http://dx.doi.org/10.1086/657685 - 60. Weeks, S.C. (1995) Comparisons of Life-History Traits between Clonal and Sexual Fish (Poeciliopsis: Poeciliidae) Raised in Monoculture and Mixed Treatments. Evolutionary Ecology, 9, 258-274.
http://dx.doi.org/10.1007/BF01237772 - 61. Crummett, L.T. and Wayne, M.L. (2009) Comparing Fecundity in Parthenogenetic versus Sexual Populations of the Freshwater Snail Campeloma limum: Is There a Two-Fold Cost of Sex? Invertebrate Biology, 128, 1-8.
http://dx.doi.org/10.1111/j.1744-7410.2008.00150.x - 62. Congdon, J.D., Vitt, L.J. and Hadley, N.F. (1978) Parental Investment: Comparative Reproductive Energetics in Bisexual and Unisexual Lizards Genus Cnemidophorus. The American Naturalist, 112, 509-521.
http://dx.doi.org/10.1086/283293 - 63. Scheiner, S.M. and Yampolsk, L.Y. (1998) The Evolution of Daphnia pulex in a Temporally Varying Environment. Genetical Research, 72, 25-37.
http://dx.doi.org/10.1017/S0016672398003322 - 64. Roth, L.M. (1974) Reproductive Potential of Bisexual Pycnoscelus indicus and Clones of Its Parthenogenetic Relative Pycnoscelus surinamensis. Annals of the Entomological Society of America, 67, 215-223.
- 65. Lamb, R.Y. and Willey, R.B. (1979) Are Parthenogenetic and Related Bisexual Insects Equal in Fertility? Evolution, 33, 774-775.
http://dx.doi.org/10.2307/2407801 - 66. Kramer, M.G. and Templeton, A.R. (2001) Life-History Changes That Accompany the Transition from Sexual to Parthenogenetic Reproduction in Drosophila mercatorum. Evolution, 55, 748-761.
http://dx.doi.org/10.1554/0014-3820(2001)055[0748:LHCTAT]2.0.CO;2 - 67. Kearney, M. and Shine, R. (2005) Lower Fecundity in Parthenogenetic Geckos than Sexual Relatives in the Australian Arid Zone. Journal of Evolutionary Biology, 18, 609-618.
http://dx.doi.org/10.1111/j.1420-9101.2004.00866.x - 68. Uzzel, T.M. (1964) Relations of the Diploid and Triploid Species of the Ambystoma jeffersonianum Complex (Amphibia, Caudata). Copeia, 1964, 257-300.
http://dx.doi.org/10.2307/1441023 - 69. Weinzierl, R.P., Schmidt, P. and Michiels, N.K. (1999) High Fecundity and Low Fertility in Parthenogenetic Planarians. Invertebrate Biology, 118, 87-94.
http://dx.doi.org/10.2307/3227051 - 70. Lynch, M. (1989) The Distribution of Life-History Variation in the Daphnia pulex Complex. Evolution, 43, 1724-1736.
http://dx.doi.org/10.2307/2409388 - 71. Domes, K., Scheu, S. and Maraun, M. (2007) Resources and Sex: Soil Re-Colonization by Sexual and Parthenogenetic Oribatid Mites. Pedobiologia, 51, 1-11.
http://dx.doi.org/10.1016/j.pedobi.2006.11.001 - 72. Enghoff, H. (1976) Parthenogenesis and Bisexuality in the Millipede Nemasoma varicorne C.L. Kock, 1847 (Diplopoda: Blaniulidae). Morphological, Ecological, and Biogeographical Aspects. Videnskabelige Meddelelser Dansk Naturhistorisk Forening, 139, 21-59.
- 73. Corley, L.S. and Moore, A.J. (1999) Fitness of Alternative Modes of Reproduction: Developmental Constraints and the Evolutionary Maintenance of Sex. Proceedings of the Royal Society of London: Biological Sciences, 266, 471-176.
- 74. Trivers, R.L. (1972) Parental Investment and Sexual Selection. In: Campbell, B., Ed., Sexual Selection and the Descent of Man, Aldine Press, Chicago, 136-179.
- 75. Trivers, R.L. (1976) Sexual Selection and Resource-Accruing Abilities in Anolis garmani. Evolution, 30, 253-269.
http://dx.doi.org/10.2307/2407700 - 76. Siller, S. (2001) Sexual Selection and the Maintenance of Sex. Nature, 411, 689-692.
http://dx.doi.org/10.1038/35079578 - 77. Atmar, W. (1991) On the Role of Males. Animal Behaviour, 41, 195-205.
http://dx.doi.org/10.1016/S0003-3472(05)80471-3 - 78. Koeslag, P.D. and Koeslag, J.H. (1994) Koinophilia Stabilizes Bi-Gender Sexual Reproduction against Asexual in an Unchanging Environment. Journal of Theoretical Biology, 166, 251-260.
http://dx.doi.org/10.1006/jtbi.1994.1023 - 79. Kodric-Brown, A. and Brown, J.H. (1987) Anisogamy, Sexual Selection, and the Evolution and Maintenance of Sex. Evolutionary Ecology, 1, 95-105.
http://dx.doi.org/10.1007/BF02067393 - 80. Manning, J.T. (1984) Males and the Advantage of Sex. Journal of Theoretical Biology, 108, 215-220.
http://dx.doi.org/10.1016/S0022-5193(84)80067-3 - 81. Lorch, P.D., Proulx, S., Rowe, L. and Day, T. (2003) Condition-Dependent Sexual Selection Can Accelerate Adaptation. Evolutionary Ecology Research, 6, 867-881.
- 82. Proulx, S.R. (2002) Niche Shifts and Expansion Due to Sexual Selection. Evolutionary Ecology Research, 3, 351-369.
- 83. Whitlock, M.C. (2000) Fixation of New Alleles and the Extinction of Small Populations: Drift Load, Beneficial Alleles, and Sexual Selection. Evolution, 54, 1855-1861.
http://dx.doi.org/10.1111/j.0014-3820.2000.tb01232.x - 84. Marshall, S.M. and Orr, A.P. (1955) The Biology of a Marinc Copepod, Calanus finmarchicus (Gunnerus), Oliver and Boyd.
- 85. Comita, G.W. and Comita, J.J. (1966) Egg Production in Tigriopus brevicornis. In: Some Contemporary Studies in Marine Science, Allen and Unwin, 171-185.
- 86. Lack, D. (1947) The Significance of Clutch-Size. Ibis, 89, 302-352.
http://dx.doi.org/10.1111/j.1474-919X.1947.tb04155.x - 87. Lack, D. (1948) The Significance of Clutch-Size. Part III. Some Interspecific Comparisons. Ibis, 90, 25-45.
http://dx.doi.org/10.1111/j.1474-919X.1948.tb01399.x - 88. Klomp, H. (1970) The Determinatio of Clutch-Size in Birds. A Review. Ardea, 58, 1-124.
- 89. Bengtson, S.A. (1971) Variations in Clutch-Size in Ducks in Relation to the Food Supply. Ibis, 113, 523-526.
http://dx.doi.org/10.1111/j.1474-919X.1971.tb05190.x - 90. Högstedt, G. (1981) Effect of Additional Food on Reproductive Success in the Magpie (Pica pica). Journal of Animal Ecology, 50, 219-229.
http://dx.doi.org/10.2307/4041 - 91. Arcese, P. and Smitht, J.N.M. (1988) Effects of Population Density and Supplemental Food on Reproduction in Song Sparrows. Journal of Animal Ecology, 57, 119-136.
http://dx.doi.org/10.2307/4768 - 92. Zanette, L., Clinchy, M. and Smith, J.N.M. (2006) Food and Predators Affect Egg Production in Song Sparrows. Ecology, 87, 2459-2467.
http://dx.doi.org/10.1890/0012-9658(2006)87[2459:FAPAEP]2.0.CO;2 - 93. Tannerfeldt, M. and Angerbjörn, A. (1998) Fluctuating Resources and the Evolution of Litter Size in the Arctic Fox. Oikos, 545-559, 83.
- 94. Karels, T.J., Byrom, A.E., Boonstra, R. and Krebs, C.J. (2000) The Interactive Effects of Food and Predators on Reproduction and Overwinter Survival of Arctic Ground Squirrels. Journal of Animal Ecology, 69, 235-247.
http://dx.doi.org/10.1046/j.1365-2656.2000.00387.x - 95. Teixeira, P.F., Kaminski, S.M., Avila, T.R., Cardozo, A.P., Bersano, J.G.F. and Bianchini, A. (2010) Diet Influence on Egg Production of the Copepod Acartia tonsa (Dana, 1896). Anais da Academia Brasileira de Ciências, 82, 333-339.
- 96. Glazier, D.S. (1992) Effects of Food, Genotype, and Maternal Size and Age on Offspring Investment in Daphnia magna. Ecology, 73, 910-926.
http://dx.doi.org/10.2307/1940168 - 97. Checkley Jr., D.M. (1980) The Egg Production of a Marine Planktonic Copepod in Relation to Its Food Supply: Laboratory Studies. Limnology and Oceanography, 25, 430-446.
http://dx.doi.org/10.4319/lo.1980.25.3.0430
Appendix. Continuous Calculation of Reproductive Success
In the main text of this paper we have calculated the sexual and asexual reproductive success in two very different demographic environments: in poor environments and with a population in balance, on the one hand; and virgin habitats or habitats without limitations, with the population growing at the maximum rate of fecundity of the species, on the other. Here we show the continuous calculation across the entire spectrum of environmental qualities.
To do so, we must first elucidate the shape of the curve for habitat quality/offspring per female. Habitat quality, understood as the amount of resources and energy available to females for reproduction, is directly related to fecundity (e.g. [24] ). However, beyond a certain resource level, the fecundity of the females will reach a maximum that is intrinsic to the species, due to the maximum number of ovules, pregnancy or litters a female can have throughout her life. The resulting habitat quality/fecundity curve will be a typical saturation curve, similar to the known saturation-type kinetic model (Figure A1). Indeed, there is a vast literature to support the direct relationship between resources and fecundity, as expected in the lowest range of habitat quality: in copepods [83] [85] , in birds (clutch size) [86] - [92] , in mammals such as the arctic fox [93] and the arctic squirrel [94] . Furthermore, the saturation curve in the relation between habitat quality/fecundity has been observed in copepod crustaceans [95] , in Daphnia [96] and Paracalanus parvus [97] (the latter two also crustaceans).
Fecundity therefore relates to habitat quality through a saturation curve. Is this also true of the probability of survival of offspring or litter? We have not found any literature on the subject, but logically the answer should be yes. The quality/descendants curve will be the result of the product of two functions, quality/fecundity and quality/survival, which is also a saturation curve.
The resulting curve is defined by three parameters, which are added to our mathematical model:
・ 
・ 
・ 



Therefore, we define:

The equations of the average number of descendants of a female, for the second generation after a change of reproductive mode, will be:
For the transition from sexual to asexual reproduction:
Figure A1. Relation between environmental quality, sensu lato, understood as the set of all variables that influence the growth rate of the population, and the number of descendants per female, which follows the saturation curve described in Equation (7), defined using only two variables: the maximum number of descendants of the species (M) and a constant of reproduction (c), which is the value of q for which d is 1/2 of M (M = 20 and c = 5 in this figure).

For the transition from asexual to sexual reproduction:

As in the calculation of the scheme of reproductive success, d' is the average number of descendants after the change from sexual to asexual reproduction, and is calculated by Equation (9)
Now, isolating q in Equation (7):
We do the same in Equation (9):
Equating the two resulting expressions and isolating

This first result serves to demonstrate that the average offspring per female is duplicated in a population after the change from sexual to asexual reproduction in poor environments, while remaining unchanged in rich ones (as we have assumed in the discrete calculation method) . We do this by verifying that when 







To calculate the threshold harem, for all environments, we proceed as follows:
Equalizing Equation (1) and Equation (4):
Isolating

Substituting 

Figure A2. In poor environments, where the curve q/d is practically a straight line, changes in reproductive strategy have a noticeable effect on the average offspring per female in the generation in which the change occurs. Here M = 20 and c = 5 (as in Figure A1).
Figure A3. In rich or virgin environments the curve q/d is almost asymptotic with the maximum offspring (M), so that changes in the reproductive strategy hardly influence the average offspring per female in the generation in which the change occurs. Here M = 20 and c = 5 (as in Figure A1).















