Applied Mathematics
Vol.5 No.1(2014), Article ID:42087,9 pages DOI:10.4236/am.2014.51021
Oscillatory Behavior of a Network Epidemic SIS Model with Nonlinear Infectivity
College of Science, Mathematics and Technology, Alabama State University, Montgomery, USA
Email: cfeng@alasu.edu
Received August 5, 2013; revised September 5, 2013; accepted September 13, 2013
ABSTRACT
In this paper, an epidemic SIS model with nonlinear infectivity on heterogeneous networks and time delays is investigated. The oscillatory behavior of the solutions is studied. Two sufficient conditions are provided to guarantee the oscillatory behavior for the solutions. Some computer simulations are demonstrated.
Keywords:Epidemic SIS Network Model; Delay; Oscillation
1. Introduction
The classical susceptible-infected-susceptible (SIS) model is a system consisting of three differential equations. For example, if the host population 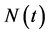 is divided into susceptibles,
is divided into susceptibles,  , and infectives,
, and infectives,  , Zhou proposed the following model [1]:
, Zhou proposed the following model [1]:
 (1)
(1)
where A is the constant recruitment rate, 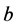 is the fertility of susceptibles,
is the fertility of susceptibles, 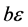 is the infectives,
is the infectives, 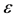 is the fertility reduction factor due to infection,
is the fertility reduction factor due to infection, 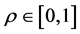 is the probability of newborns of infectives which are susceptible,
is the probability of newborns of infectives which are susceptible,  is the probability of vertical transmission from a mother to her newborn baby before, during, or just after birth, d
is the probability of vertical transmission from a mother to her newborn baby before, during, or just after birth, d ![]() is the natural death rate,
is the natural death rate, 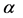 is the disease-related death rate, and
is the disease-related death rate, and 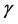 is the recovery rate. Zhou studied the global asymptotic stabilities of the equilibrium described in the model (1). Several authors have investigated the dynamical behavior of various models similar to system (1) [2-6]. Hethcote et al. discussed a predator-prey model with infected prey [7]. Sinha et al. studied a predator-prey system with infected prey in polluted environment [8]. Those epidemic models are based on uniform mixing population. However, in practice, it seems that each individual has limited contact with those they can pass disease which leads to a new theory that the ensemble of all such individuals forms a complex network. A particular class of infections such as computer viruses also spread naturally in networks. Using the new network models to compute the epidemic dynamics has been shown in the effects of network structure on disease spreading [9-16]. Recently, Zhu et al. proposed a new epidemic SIS network model with nonlinear infectivity as follows [15]:
is the recovery rate. Zhou studied the global asymptotic stabilities of the equilibrium described in the model (1). Several authors have investigated the dynamical behavior of various models similar to system (1) [2-6]. Hethcote et al. discussed a predator-prey model with infected prey [7]. Sinha et al. studied a predator-prey system with infected prey in polluted environment [8]. Those epidemic models are based on uniform mixing population. However, in practice, it seems that each individual has limited contact with those they can pass disease which leads to a new theory that the ensemble of all such individuals forms a complex network. A particular class of infections such as computer viruses also spread naturally in networks. Using the new network models to compute the epidemic dynamics has been shown in the effects of network structure on disease spreading [9-16]. Recently, Zhu et al. proposed a new epidemic SIS network model with nonlinear infectivity as follows [15]:
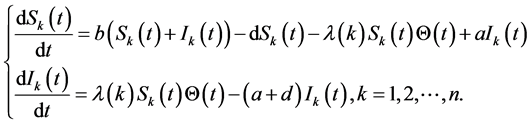 (2)
(2)
where 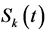 and
and 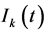 represent the relative densities of the susceptible and infected nodes,
represent the relative densities of the susceptible and infected nodes,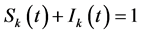 ;
; 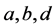 represent the recovery rate, birth rate and death rate respectively;
represent the recovery rate, birth rate and death rate respectively;  is the correlated infection rate; and
is the correlated infection rate; and
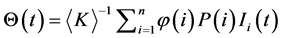 (3)
(3)
where  denotes the mean degree value,
denotes the mean degree value, 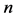 is the largest degree number,
is the largest degree number, 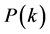 is the probability that a node has k
is the probability that a node has k ![]() edges,
edges,  represents the occupied edges which can transmit the disease and
represents the occupied edges which can transmit the disease and  can be consisted as a force of infection [15]. Based on death rate which is equal to birth rate, then Model (2) changes to the following simple form:
can be consisted as a force of infection [15]. Based on death rate which is equal to birth rate, then Model (2) changes to the following simple form:
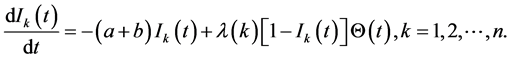 (4)
(4)
The global attractivity of the model (4) is studied mathematically by the authors. However, the recovery rate, birth rate may have different values in each edge. Also the incubation period 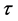 for infected term needs to be considered.
for infected term needs to be considered.
Therefore, in this paper, we investigate the oscillatory behavior of the following elementary extension of Model (4) with time delay:
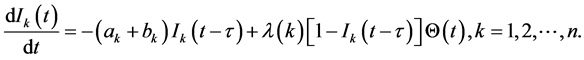 (5)
(5)
The oscillatory behavior of the solution for System (5) means that the disease is still limited spreading.
2. Main Results
Based on a practical consideration, we assume that the initial condition for System (4) as follows:
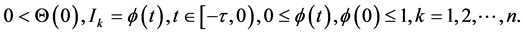 (6)
(6)
Definition 1. The solution  of System (5) is called oscillation about the equilibrium
of System (5) is called oscillation about the equilibrium  if there exists a sequence
if there exists a sequence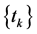 ,
, 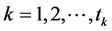 tends to infinity as
tends to infinity as 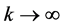 such that
such that 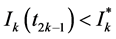 and
and  If there exists at least one component of the solution
If there exists at least one component of the solution 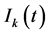 is non-oscillating, then we say that the solution is partly oscillation.
is non-oscillating, then we say that the solution is partly oscillation.
Lemma 1. The solutions  of System (5) with initial condition (6) are nonnegative and bounded.
of System (5) with initial condition (6) are nonnegative and bounded.
Proof. It is known that time delay can induce the instability of the solutions of the system. It does not change a bounded solution to unbounded solution. Therefore, we only need to prove that the bounded solution for the following system:
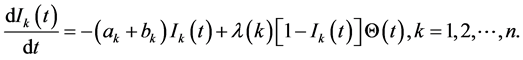 (7)
(7)
Since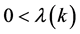 ,
, 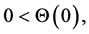 according to the definition of
according to the definition of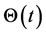 , we can easily see that
, we can easily see that  for any
for any  Then we have
Then we have
 (8)
(8)
Therefore,
 (9)
(9)
On the other hand,
 (10)
(10)
We get
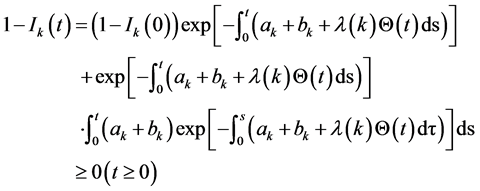 (11)
(11)
So, for any  Based on the initial condition (6), we have that
Based on the initial condition (6), we have that 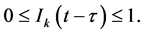
Lemma 2. Assume that the initial condition (6) and the following condition are satisfied:
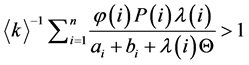 . (12)
. (12)
Then there exists a unique positive equilibrium point of System (5).
Proof. The proof is similar to Theorem 2.2 [15]. Indeed, the equilibrium point of (5) is the solution of the following algebraic equation:
 (13)
(13)
From (13) we get
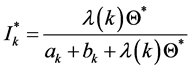 (14)
(14)
Substituting (14) into (3) we have
 (15)
(15)
Since 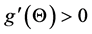 and
and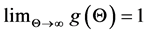 , the equation
, the equation 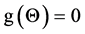 has a unique non-trivial solution
has a unique non-trivial solution 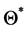 if the assumption is satisfied. The proof is completed.
if the assumption is satisfied. The proof is completed.
Note that 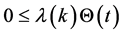 and
and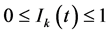 . From (5) we have
. From (5) we have
 (16)
(16)
where 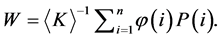 Thus, the instability of the trivial solution for the following system (17) and (18) implies the instability of the equilibrium point of System (5).
Thus, the instability of the trivial solution for the following system (17) and (18) implies the instability of the equilibrium point of System (5).
 (17)
(17)
 (18)
(18)
We can rewrite System (17) as a matrix form
 (19)
(19)
where 
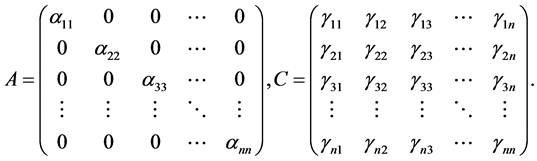
In which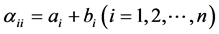 ,
, 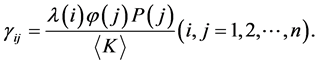
Theorem 1. Assume that the initial condition (6) holds and there exists a unique positive equilibrium point of System (5). Let 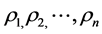 denote the eigenvalues of the matrix
denote the eigenvalues of the matrix 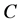 of the System (19). Suppose that there exists some
of the System (19). Suppose that there exists some  that satisfies
that satisfies
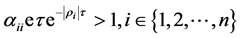 (20)
(20)
Then there exists an oscillatory or partly oscillatory solution of System (5).
Proof. We shall prove that the trivial solution of (19) is unstable. Suppose this is not the case, then there exists an 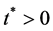 such that the trivial solution is convergent for
such that the trivial solution is convergent for  Since
Since 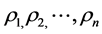 are eigenvalues of the matrix
are eigenvalues of the matrix  we have immediately that
we have immediately that

or
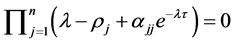 (21)
(21)
Consider the characteristic equation for some 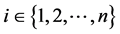
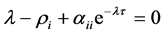 (22)
(22)
If the trivial solution of (20) is convergent for 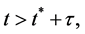 then
then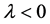 . From (22) and noting that
. From (22) and noting that 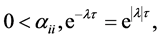 we get
we get
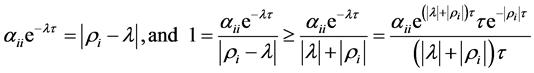 (23)
(23)
From (23) this yields 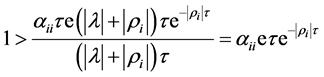 by the formula
by the formula , which contradicts the condition (20). Similarly, from (18) we can get
, which contradicts the condition (20). Similarly, from (18) we can get
 (24)
(24)
(24) is also a contradiction with (20). Thus the trivial solutions of Systems (17) and (18) are unstable, implying that the unique positive equilibrium point of System (5) is unstable. Namely, System (5) generates an oscillatory or partly oscillatory solution.
Theorem 2. Assume that the initial condition (6) holds and there exists a unique positive equilibrium point of System (5). Suppose that the following inequality holds
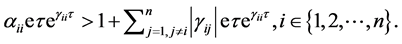 (25)
(25)
Then there exists an oscillatory solution of System (5).
Proof. The characteristic equation corresponding (19) is the following:
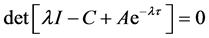
If the trivial solution of (19) is convergent for 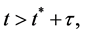 then there exists an eigenvalue say
then there exists an eigenvalue say 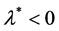 that satisfies
that satisfies
 (26)
(26)
By Gershgorin’s theorem [17] 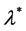 satisfies
satisfies 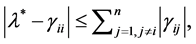 or
or
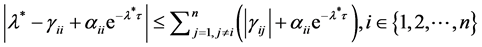 (27)
(27)
From (27), and note that 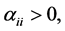 we have
we have
 (28)
(28)
We get
 (29)
(29)
Both sides divided by 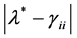 in (29) we get
in (29) we get
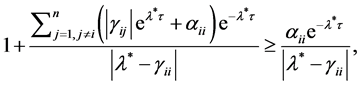 (30)
(30)
Noting that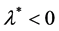 , then
, then 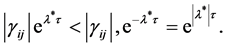 And again using the formula
And again using the formula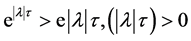 , this leads to
, this leads to
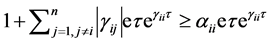 (31)
(31)
But (31) contradicts our assumption (25). Thus the trivial solution of System (19) is unstable. Similarly, one can show that the trivial solution of System (18) is also unstable under the condition (25). The instability of the trivial solutions of Systems (18) and (19) implies the instability of the unique positive equilibrium point of System (5). Therefore, System (5) generates an oscillatory or partly oscillatory solution.
3. Simulation Results
In Figure 1, we discuss the case that the largest degree number n is three in System (5), let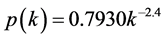 so
so 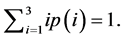 We first select
We first select 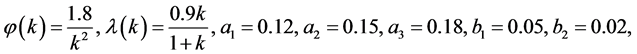
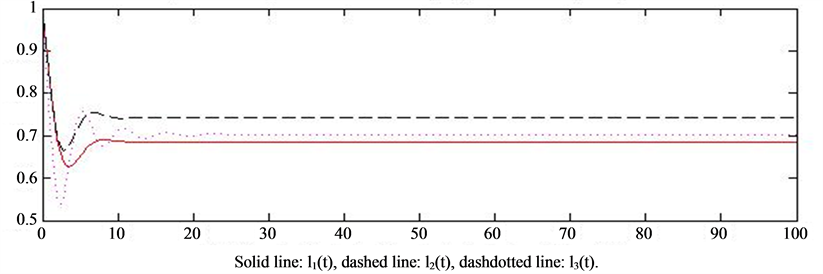
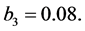 We see that the solutions of the system are convergent when delay
We see that the solutions of the system are convergent when delay  (see Figure 1(a)). However, setting delay
(see Figure 1(a)). However, setting delay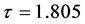 , partial oscillation of the solution occurs (Figure 1(b)). Then we take
, partial oscillation of the solution occurs (Figure 1(b)). Then we take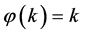 ,
,
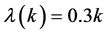 . The matrix
. The matrix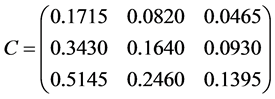 . The eigenvalues of matrix C are
. The eigenvalues of matrix C are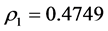 ,
,
 and
and  We select
We select  Let
Let 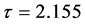 and 2.165 respectively, each component of the solution is oscillatory (Figure 1(c) and Figure 1(d)). It seems that the amplitude the more the larger of
and 2.165 respectively, each component of the solution is oscillatory (Figure 1(c) and Figure 1(d)). It seems that the amplitude the more the larger of 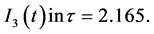 In this case, we have
In this case, we have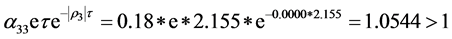 . Based on Theorem 1, the equilibrium point is unstable. There exists an oscillatory solution.
. Based on Theorem 1, the equilibrium point is unstable. There exists an oscillatory solution.
 (a)
(a)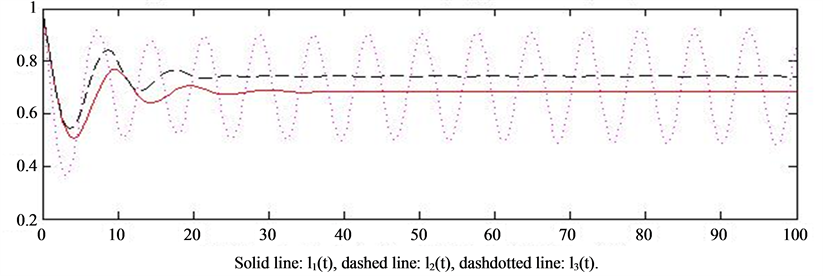 (b)
(b)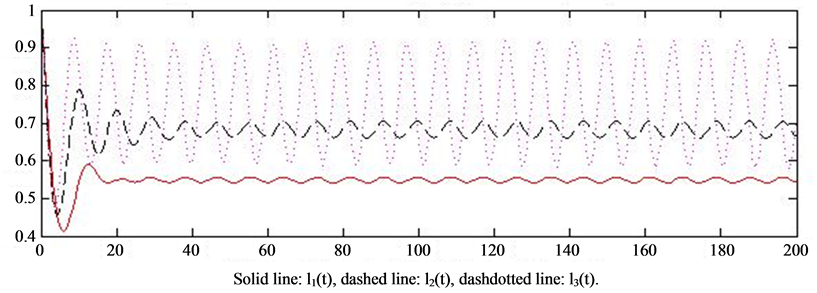 (c)
(c) (d)
(d)
Figure 1. (a) Convergence of the solution, P(k) = 0.7903k−2.4, delay 1.205; (b) Partial oscillation of the solution, P(k) = 0.7903k−2.4, delay 1.805; (c) Oscillation of the solution P(k) = 0.7903k−2.4, delay 2.155; (d) Oscillation of the solution P(k) = 0.7903k−2.4, delay 2.165.
In Figure 2, we discuss the case that the largest degree number n is four in System (5), setting
 , thus
, thus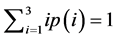 , we first select
, we first select , Thus the matrix
, Thus the matrix

The eigenvalues of matrix C are 
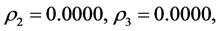 and
and . Take
. Take 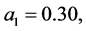
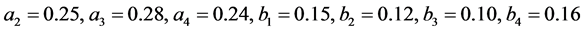 . Select
. Select 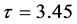 we have
we have 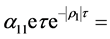
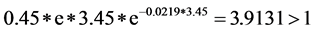 . Based on Theorem 1, the trivial solution is oscillatory (see Figure 2(b)). However, when
. Based on Theorem 1, the trivial solution is oscillatory (see Figure 2(b)). However, when  we see that the trivial solution is still convergent (Figure 2(a)). This implies that delay induced oscillation. Also oscillation appeared when delay reached a certain extent.
we see that the trivial solution is still convergent (Figure 2(a)). This implies that delay induced oscillation. Also oscillation appeared when delay reached a certain extent.
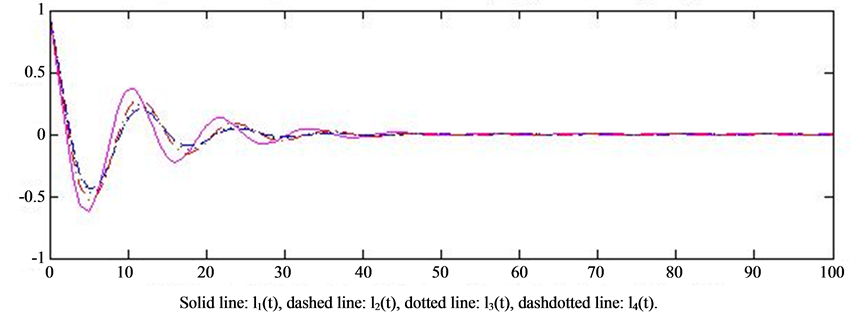
In Figure 3, we take

We see that there are two components of the solution that are convergent when delay equals to 0.612, while they are oscillatory as delay equals to 0.615.
 (a)
(a)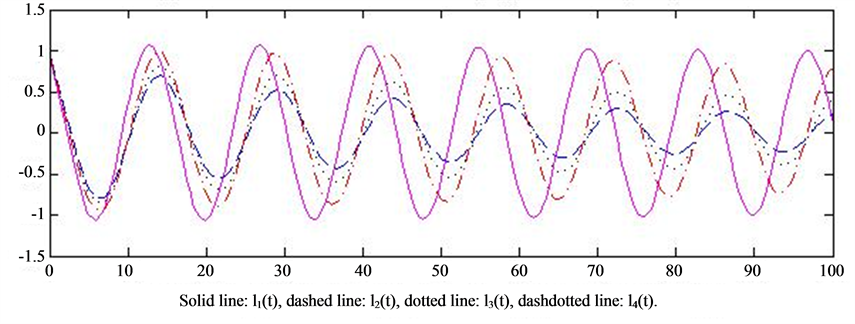 (b)
(b)
Figure 2. (a) Convergence of the trivial solution, P(k) = 0.7209k−2.1, delay 2.5; (b) Oscillation of the trivial solution P(k) = 0.7209k−2.1, delay 3.45.
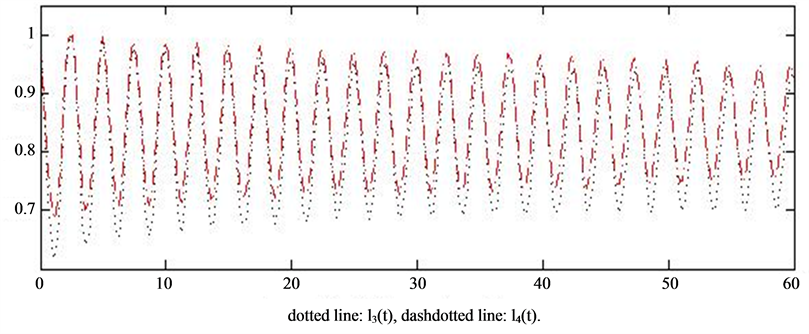 (a)
(a)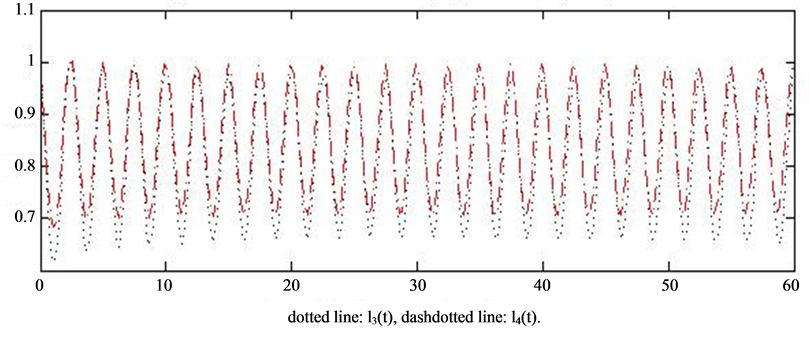 (b)
(b)
Figure 3. (a) Convergence of the solutions, P(k) = 0.7209k−2.1, delay 0.612. (b) Oscillation of the solutions, P(k) = 0.7209k−2.1, delay 0.615.
4. Conclusion
This paper discusses an epidemic SIS model with time delays. The oscillatory behavior of the solutions about the equilibrium point is studied. Two sufficient conditions are provided to guarantee the oscillatory behavior for the solutions. The computer simulation suggests time delay induced oscillation or partial oscillation. However, why the time delay will lead to a partial oscillation, this is a very interesting open problem. From Figure 3, what is the time delay critical value between oscillation and non-oscillation for this system is another open problem.
REFERENCES
- J. S. Zhou, “An SIS Disease Transmission Model with Recruitment-Birth-Death Demographics,” Mathematical and Computer Modelling, Vol. 21, No. 11, 1995, pp. l-11. http://dx.doi.org/10.1016/0895-7177(95)00074-C
- Y. N. Xiao and L. S. Chen, “Analysis of a SIS Epidemic Model with Stage Structure and a delay,” Communications in Nonlinear Science and Numerical Simulation, Vol. 6, No. 1, 2001, pp. 35-39. http://dx.doi.org/10.1016/S1007-5704(01)90026-7
- M. Safan and F. A. Rihan, “Mathematical Analysis of an SIS Model with Imperfect Vaccination and Backward Bifurcation,” Mathematics and Computers in Simulation, 2011, in Press.
- Y. N. Xiao and S. Y. Tang, “Dynamics of Infection with Nonlinear Incidence in a Simple Vaccination Model,” Nonlinear Analysis: RWA, Vol. 11, No. 5, 2010, pp. 4154-4163.
- Y. F. Li and J. G. Cui, “The Effect of Constant and Pulse Vaccination on SIS Epidemic Models Incorporating Media Coverage,” Communications in Nonlinear Science and Numerical Simulation, Vol. 14, No. 5, 2009, pp. 2353-2365. http://dx.doi.org/10.1016/j.cnsns.2008.06.024
- C. F. Wu and P. X. Weng, “Stability Analysis of a Stage Structured SIS Model with General Incidence Rate,” Nonlinear Analysis: RWA, Vol. 11, No. 3, 2010, pp. 1826-1834.
- H. W. Hethcote, W. D. Wang, L. T. Han and Z. E. Ma, “A Predator-Prey Model with Infected Prey,” Theoretical Population Biology, Vol. 66, No. 3, 2004, pp. 259-268. http://dx.doi.org/10.1016/j.tpb.2004.06.010
- S. Sinha, O. P. Misra and J. Dhar, “Modelling a Predator-Prey System with Infected Prey in Polluted Environment,” Applied Mathematical Modelling, Vol. 34, No. 7, 2010, pp. 1861-1872. http://dx.doi.org/10.1016/j.apm.2009.10.003
- R. P. Satorras and A. Vespignani, “Epidemic Spreading in Scale-Free Networks,” Physical Review Letters, Vol. 86, No. 3, 2001, p. 3200. http://dx.doi.org/10.1103/PhysRevLett.86.3200
- R. P. Satorras and A. Vespignani, “Epidemic Dynamics and Endemic Statesin Complex Networks,” Physical Review E, Vol. 63, No. 6, 2001, Article ID: 066117. http://dx.doi.org/10.1103/PhysRevE.63.066117
- Y. Moreno, R. Pastor-Satorras and A. Vespignani, “Epidemic Outbreaks Incomplex Heterogeneous Networks,” European Journal of Physics, Vol. 26, No. 4, 2002, pp. 521-529. http://dx.doi.org/10.1140/epjb/e20020122
- M. Boguna, R. Pastor-Satorras and A. Vespignani, “Absence of Epidemicthreshold in Scale-Free Networks with Degree Correlations,” Physical Review Letters, Vol. 90, No. 2, 2003, Article ID: 028701. http://dx.doi.org/10.1103/physrevlett.90.028701
- H. J. Shi, Z. S. Duan and G. R. Chen, “An SIS Model with Infective medium on Complex Networks,” Physica A, Vol. 387, No. 8-9, 2008, pp. 2133-2144. Http://Dx.Doi.Org/10.1016/J.Physa.2007.11.048
- H. F. Zhang and X. C. Fu, “Spreading of Epidemicson Scale-Free Networks with Nonlinear Infectivity,” Nonlinear Analysis: TMA, Vol. 70, No. 9, 2009, pp. 3273-3278. http://dx.doi.org/10.1016/j.na.2008.04.031
- G. H. Zhu, X. C. Fu and G. R. Chen, “Global Attractivity of a Network-Based Epidemic SIS Model with Nonlinear Infectivity,” Communications in Nonlinear Science and Numerical Simulation, Vol. 17, No. 6, 2012, pp. 2588-2594. http://dx.doi.org/10.1016/j.cnsns.2011.08.039
- A. d’Onofrio, “A Note on the Global Behavior of the Network-Based SIS Epidemic Model,” Nonlinear Analysis: RWA, Vol. 9, No. 4, 2008, pp. 1567-1572.
- R. C. Horn and C. R. Johnson, “Matrix Analysis,” Cambridge University Press, Cambridge, 1985. http://dx.doi.org/10.1017/CBO9780511810817

