Applied Mathematics
Vol.5 No.8(2014), Article ID:45898,7 pages DOI:10.4236/am.2014.58123
A Sobel-TV Based Hybrid Model for Robust Image Denoising
Jihui Tu1, Bin Yang2
1Electronics & Information School of Yangtze University, Jingzhou, China
2Electronic Information Engineering School of HEBI College of Vocation and Technology, Henan, China
Email: green666@126.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 10 March 2014; revised 10 April 2014; accepted 17 April 2014
ABSTRACT
The traditional Total-Variation algorithm has a good result to de-noise for noise image of small scale details, but it easily losses the details for the image with rich texture and tiny boundary. In order to solve this problem, this paper proposes a Sobel-TV model algorithm for image denoising. It uses TV model to de-noise and uses Sobel algorithm to control smoothness of image, which not only efficiently removes image noise but also simultaneously retail information, such as edge and texture. The experiments demonstrate that the proposed algorithm is simple, practical and generates better SNR, which is an important value to preprocess image.
Keywords:TV Model, Sobel Algorithm, Sobel-TV Model, Image Denoising

1. Introduction
The actual image is inevitably disturbed by various noises while it may be introduced by the image formation process, image recording, image transmission, etc. So image denoising is a key component in image processing. The problem aims to remove noises and preserve edges and small scale structures such as textures, which is to enhance signal to noise ratio and improve image quality. Nowadays researchers have proposed many methods to solve this problem of image denoising, such as median filtering methods, smooth filtering methods, total variation (TV) [1] [2] diffusion methods, etc. Filtering methods tend to blur an image but edges in the image are not well preserved. Though TV De-noising method, [3] [4] can remove image noise and preserve image edges characteristics. This method will retain salt and pepper noise point as the edge of the image, which cannot remove salt and pepper noise [5] -[7] . In this paper, we propose a Sobel-TV model algorithm for image denoising. The algorithm distills the image edge through using Sobel algorithm, then uses TV algorithm to remove image noise according to image edge information. The algorithm not only suppresses image noise, but also maintains the image edge and texture information.
2. Sobel-TV Model
The TV (total variation) method makes the image restoration problem transformed into a functional extremum problem through introducing the energy function, which is widely used in image denoising. The image denoising may be mathematically modeled as
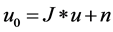 (1)
(1)
where 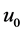 is the noise image, u is the original image, n is noise, J is the Gaussian convolution operator. Set
is the noise image, u is the original image, n is noise, J is the Gaussian convolution operator. Set 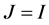 (Unit matrix), and assuming that the image noise is Gaussian noise that the mean value
(Unit matrix), and assuming that the image noise is Gaussian noise that the mean value 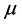 is a zero and the variance is
is a zero and the variance is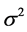 , hence (1) simplifying gives:
, hence (1) simplifying gives:
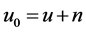 (2)
(2)
The image denosiing TV model to recover nosied image 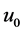 to original image u is
to original image u is
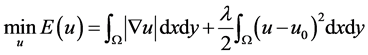 (3)
(3)
In (3), 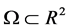
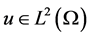 , and have Lipschitz continuous boundary;
, and have Lipschitz continuous boundary; 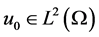 is the observation image with noise;
is the observation image with noise; 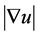 is the mode of the image gradient; the first one of the right of equation, called regex, is TV norm of image u, which relies on the edge of the image. Regular in the TV model has played a very important role, it allows that the image has non-continuous part, but does not allows that the image has oscillations part, so it can remove the noise of the image. The second of the right of equation is approximation term, which controls the different of the image u and the observation image
is the mode of the image gradient; the first one of the right of equation, called regex, is TV norm of image u, which relies on the edge of the image. Regular in the TV model has played a very important role, it allows that the image has non-continuous part, but does not allows that the image has oscillations part, so it can remove the noise of the image. The second of the right of equation is approximation term, which controls the different of the image u and the observation image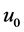 ,
, 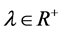 is the scale parameter, which plays a balancing role in the regularization and approximation term. Euler-Lagrange equation in the discrete-time domain is:
is the scale parameter, which plays a balancing role in the regularization and approximation term. Euler-Lagrange equation in the discrete-time domain is:
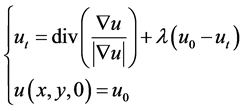 (4)
(4)
In (4), 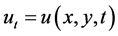 ,
, 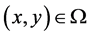 ,
, 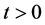 ,
, 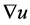 is the gradient of image u.
is the gradient of image u.
The TV model is a piecewise continuous function in the bounded variation space, hence, the model has good removal effect for the repeating patterns of small-scale details and noise, but it is likely to cause loss of detail for he rich texture image.
In (4) above, fidelity approximation 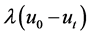 keeps the original image features and reduces image distortion effect, diffusion term
keeps the original image features and reduces image distortion effect, diffusion term 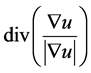 remove noise of the image. When diffusion term removes noise of the image, it also make the whole image smooth, which losses the small feature in the image and blurres image. To solve the problem above, in (4) introduce a guide function
remove noise of the image. When diffusion term removes noise of the image, it also make the whole image smooth, which losses the small feature in the image and blurres image. To solve the problem above, in (4) introduce a guide function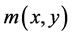 , and its improved form as follows:
, and its improved form as follows:
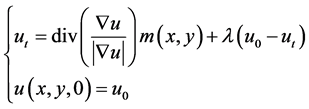 (5)
(5)
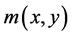 has the feature as follows: the value of
has the feature as follows: the value of 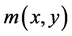 is the smaller in the larger gray value of the place; the value of
is the smaller in the larger gray value of the place; the value of 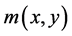 is the bigger in the slower gray value of the place. Therefore, the function
is the bigger in the slower gray value of the place. Therefore, the function 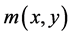 can selectively denoise or smooth image according to the gray-scale value changing in the each part of the image. From above, the function
can selectively denoise or smooth image according to the gray-scale value changing in the each part of the image. From above, the function 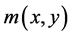 is expressed as follows:
is expressed as follows:
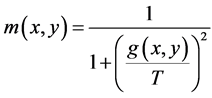 (6)
(6)
In (6), 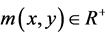 and
and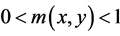 ;
; 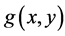 is the edge detection value in the coordinate point
is the edge detection value in the coordinate point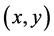 ; T is a preset threshold and its value may be changed according the demand of image processing,
; T is a preset threshold and its value may be changed according the demand of image processing, 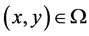 ,
,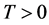 .
.
Through edge detection, 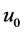 can be transformed into
can be transformed into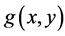 . The math model of edge detection have first order differential operators and second order differential operators. Because the second-order differential operator computation is very complexity, we choice first-order differential operators, which is more flexibility. Firstorder differential operators that use to detect image edge have two popular methods: prewitt operator and sobel operator. The prewitt operator is very sensitive to noise and remove image noise, but it maintains worse edges in the image than sobel operator. Sobel operator weights the impact of the image pixel location, which can reduce the degree of edge blur, so it has better effect.
. The math model of edge detection have first order differential operators and second order differential operators. Because the second-order differential operator computation is very complexity, we choice first-order differential operators, which is more flexibility. Firstorder differential operators that use to detect image edge have two popular methods: prewitt operator and sobel operator. The prewitt operator is very sensitive to noise and remove image noise, but it maintains worse edges in the image than sobel operator. Sobel operator weights the impact of the image pixel location, which can reduce the degree of edge blur, so it has better effect.
For digital image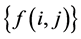 , the discrete form of the Sobel operator is defined as follows:
, the discrete form of the Sobel operator is defined as follows:
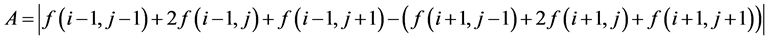 (7)
(7)
In (7), A is vertical direction edge detection.
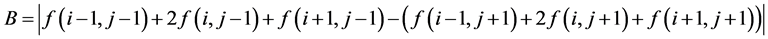 (8)
(8)
In (8), B is horizontal direction edge detection.
From (7) and (8) above, we have
 (9)
(9)
Or
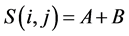 (10)
(10)
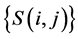 is the image after the Sobel operator detects edge.
is the image after the Sobel operator detects edge.
Figure 1 displays sobel operator template.
3. Algorithm Implementation
Sobel-TV algorithm for image denoising is firstly using sobel operator to detect image edges, then using TV to remove image noise according to the image edge information. The specific algorithm is as follows:
Step 1. Choose Sobel operator to detect original image 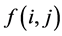 edge, we have
edge, we have
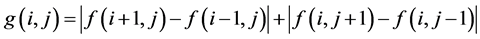 (11)
(11)
Step 2. Using (12), remove image noise according to the image edge information.
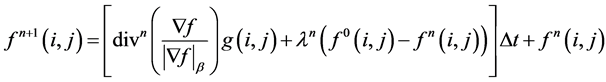 (12)
(12)
where 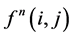 is the result of n iterations,
is the result of n iterations, 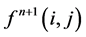 is the result of
is the result of 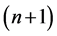 iterations.
iterations.  is the time step length.
is the time step length. 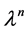 is the parameter of the regular. In order to avoid the expression
is the parameter of the regular. In order to avoid the expression 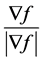 is not zero, we have introduced the parameter
is not zero, we have introduced the parameter 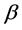 by defining
by defining
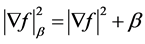 (13)
(13)
According to divergence, it arrives as follows.
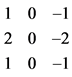 (a)
(a)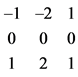 (b)
(b)
Figure 1. Sobel operator template. (a) Vertical direction; (b) Horizontal direction.
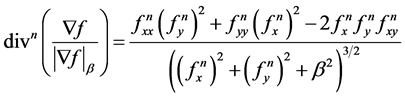 (14)
(14)
where fx the first derivatives in the x direction; fy the first derivatives in the y direction; fxx the second derivatives in the x direction fyy the second derivatives in the y direction; fxy the second derivatives for fx on y. The boundary conditions is:
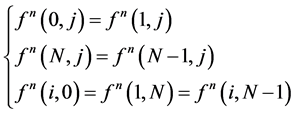 (15)
(15)
The scale parameter formula is as follows:
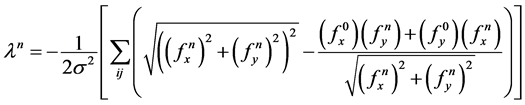 (16)
(16)
In this paper, the parameter is set as follows:
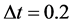 ;
;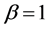 ;
;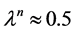 .
.
4. Numerical Experiments
We performed experiments on several images including the well-known Lean, Cameraman, Peppers and Barbara to show the performance of our proposed model. All numerical experiments were performed on 64-bit Windows 7 on a desktop with an Intel CPU at 3.0 GHz and 4 GB memory. In order to estimate the performance of different methods, we use Signal to Noise Ratio (SNR) as the image quality measure that is defined as,
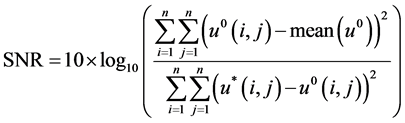 (17)
(17)
where u0 is the original image, u* is the mean intensity value of u, and u is the restored image. We also adopt the structure similarity index measure (SSIM) to measure the similarity between two images, which is defined as
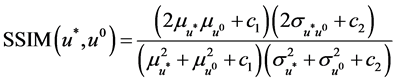
where 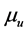 is the average of u0,
is the average of u0, 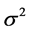 is the variance of u0,
is the variance of u0, 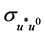 is the covariance of u* and u0 and c1 c2 are two constants to avoid instability.
is the covariance of u* and u0 and c1 c2 are two constants to avoid instability.
4.1. Parameter Values [8] [9]
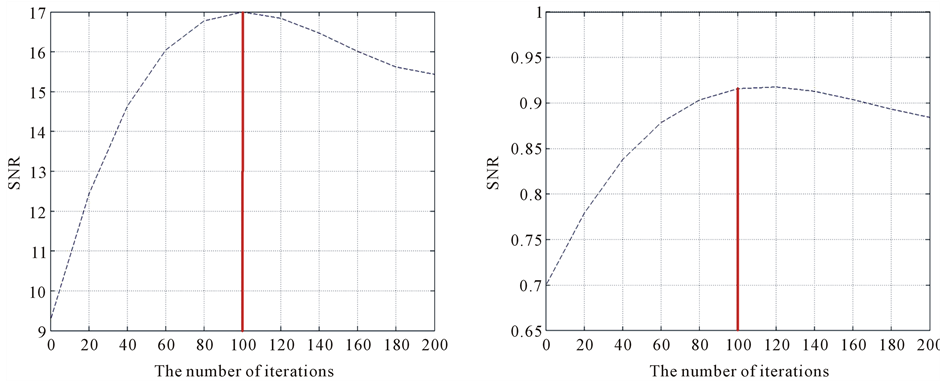
Figure 2(a) and Figure 2(b) show the relationship between SNR or SSIM and the number of iterations. The results show that the SNR and SSIM is the maximum value when the number of iterations is 100. Therefore, the number of iterations in (12) chooses 100.
4.2. Results of Comparison
In this subsection, we tested the algorithm on four different images. The noisy images are shown in Figure 3(b), Figure 4(b), Figure 5(b) and Figure 6(b). The result using mean filter and median filter algorithm are shown in Figure 3(c), Figure 3(d), Figure 4(c), Figure 4(d), Figure 5(c), Figure 5(d) and Figure 6(c), Figure 6(d). The result using the Sobel-TV algorithm are shown in Figure 3(e), Figure 4(e), Figure 5(e) and Figure 6(e). The
 (a) (b)
(a) (b)
Figure 2. (a) The relationship between SNR and the number of iterations; (b) The relationship between SSIM and the number of iterations.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e)
Figure 3. The contract of de-noising for three methods to image Cameraman. (a) Original image; (b) Noisy image; (c) Denoising image by mean filter; (d) De-noising image by median filter; (e) De-noising image by Sobel-TV.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e)
Figure 4. The contract of de-noising for three methods to image Lena. (a) Original image; (b) Noisy image; (c) De-noising image by mean filter; (d) De-noising image by median filter; (e) De-noising image by Sobel-TV.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e)
Figure 5. The contract of de-noising for three methods to image Barbara. (a) Original image; (b) Noisy image; (c) De-noising image by mean filter; (d) De-noising image by median filter; (e) De-noising image by Sobel-TV.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d) (e)
(e)
Figure 6. The contract of de-noising for three methods to image Peppers. (a) Original image; (b) Noisy image; (c) Denoising image by mean filter; (d) De-noising image by median filter; (e) De-noising image by Sobel-TV.
Table 1. Comparison of the SNR values.
Table 2. Comparison of the SSIM values.
testing results demonstrate that the Sobel-TV algorithm for de-noising image is better than the other algorithm. In Table 1 and Table 2, we list the SNR and SSIM values for mean filter, median filter and Sobel-TV. The best SNR and SSIM value for Sobel-TV are obtained. From Figures 3-6 and the numerical results in the Table 1, Table 2 it is evident that the proposed method is effective in both removing image noise and maintaining retail information.
5. Conclusion
In this paper, we have proposed Sobel-TV models that use Sobel-TV to remove the noise for digital images. The proposed algorithm is firstly using sobel operator to detect image edges, then using TV to remove image noise according to the image edge information, which not only removes noise but also preserves the image contours and texture detail information. We have also presented some promising evidence for our methods on a real world dataset. The result of experiment shows that the proposed algorithm is validating the efficacy.
References
- Rudin, L.I., Osher, S. and Fatemi, E. (1992) Nonlinear Total Variation Noise Removal Algorithms. Physica D, 60, 259-268. http://dx.doi.org/10.1016/0167-2789(92)90242-F
- Aubert, G. and Vese, L. (1997) A Variantal Method in Image Recovery. SIAM Journal of Numerical Analysis, 34, 1948-1979. http://dx.doi.org/10.1137/S003614299529230X
- Chen, L.-X., Song, G.X., Ding, X.-H. and Wang X.-D. (2009) Improved Total Variation Algorithms to Remove Noise. Acta Photonica Sinica, 38, 1000-1004.
- Combettes, P.L. and Pesquet, J.-C. (2004) Image Restoration Subject to a Total Variation Constraint. IEEE Transactions on Image Processing, 13, 1213-1222. http://dx.doi.org/10.1109/TIP.2004.832922
- Vese, L.A. and Oshers, J. (2003) Modeling Textures with Total Variation Minimization and Oscillating Patterns in Image Processing. Journal of Scientific Computing, 19, 553-572. http://dx.doi.org/10.1023/A:1025384832106
- Bonettini, S. and Ruggiero, V. (2012) On the Convergence of Primal-Dual Hybrid Gradient Algorithms for Total Variation Image Restoration. Journal of Mathematical Imaging and Vision, 44, 236-253.
- Zhang, Y.D. and Wu, L.N. (2012) A Robust Hybrid Restarted Simulated Annealing Particle Swarm Optimization Technique. Advances in Computer Science and Its Applications, 1, 5-8.
- Lysaker, M. and Tai, X.-C. (2006) Iterative Image Restoration Combining Total Variation Minimization and a Second-Order Functional. International Journal of Computer Vision, 66, 5-18. http://dx.doi.org/10.1007/s11263-005-3219-7
- Michailovich, O.V. (2011) An Iterative Shrinkage Approach to Total-Variation Image Restoration. IEEE Transactions on Image Processing, 20, 1281-1299. http://dx.doi.org/10.1109/TIP.2010.2090532


