Applied Mathematics
Vol.3 No.10A(2012), Article ID:24124,6 pages DOI:10.4236/am.2012.330197
Using of Particle Swarm for Performance Optimization of Helicopter Rotor Blades
Dipartimento di Ingegneria Meccanica e Aerospaziale, Politecnico di Torino, Corso Duca degli Abruzzi, Torino, Italy
Email: giorgio.guglieri@polito.it
Received July 7, 2012; revised August 7, 2012; accepted August 15, 2012
Keywords: Helicopter Flight Mechanics; Nature Inspired Meta-Heuristic Algorithms; Optimal Design Methods
ABSTRACT
As part of a research activity at Politecnico di Torino, aiming to develop multi-disciplinary design procedures implementing nature inspired meta-heuristic algorithms, a performance design optimization procedure for helicopter rotors has been developed and tested. The procedure optimizes the aerodynamic performance of blades by selecting the point of taper initiation, the root chord, the taper ratio, and the maximum twist which minimize horsepower for different flight regimes. Satisfactory aerodynamic performance is defined by the requirements which must hold for any flight condition: the required power must be minimized, both the section drag divergence Mach number on the advancing side of the rotor disc and the maximum section lift coefficient on the retreating side of the rotor disc must be avoided and, even more important, the rotor must be trimmed. The procedure uses a comprehensive mathematical model to estimate the trim states of the helicopter and the optimization algorithm consists of a repulsive particle swarm optimization program. A comparison with an evolutionary micro-genetic algorithm is also presented.
1. Introduction
The successful design of a helicopter relies on multidisciplinary optimization, perhaps to a greater extent than for any other aerospace vehicle [1,2]. From the extensive literature review presented in Ref. [2], it can be outlined that these optimization problems may involve 1) computationally expensive aeroelastic or finite element analysis, 2) presence of local minima, and 3) presence of numerical noise and convergence difficulties. Therefore, the availability of robust and computationally light optimization procedures becomes relevant for rotorcraft optimal design.
An example of rotorcraft optimization is the design of the main rotor system, which requires a merging of several disciplines, such as aerodynamics, dynamics, structures, and acoustics. An even broader integration may be required when handling qualities considerations are brought into the design [1]. As a matter of fact, one of the primary goals for main rotor design is to improve the aerodynamic performance of rotor blades in both hover and forward flight by optimally selecting certain blade design parameters such as twist, chord distribution, taper, sweep, and airfoil sections. The rotor blade aerodynamic design process is also made complex by conflicting performance requirements between hover and forward flight. An example for this type of design process is given in Ref. [3].
The purpose of the present paper is to develop and test a performance design optimization procedure (eventually also applicable to a multi-disciplinary design approach) by accounting for nature inspired meta-heuristic algorithms, exploring the ability of these methods to overcome some of the limitations of conventional gradient based optimization algorithms (including a straightforward software implementation). The procedure aims to optimize the aerodynamic performance of helicopter rotor blades by selecting the point of taper initiation, root chord, taper ratio, and maximum twist which minimize horsepower for different flight regimes. Satisfactory aerodynamic performance is defined by the requirements which must hold for any flight condition: The required power must be minimized, the section drag divergence Mach number on the advancing side of the rotor disc as well as the maximum section lift coefficient on the retreating side of the rotor disc must be avoided and the rotor must be trimmed. The procedure uses a comprehensive mathematical model to estimate the trim states of the helicopter and the optimization algorithm consists of a repulsive particle swarm optimization program. The performance of this solver is compared with an alternative optimizer based on an evolutionary micro-genetic algorithm.
2. The Optimization Algorithm
Optimization, that is finding minimum or maximum of a single-valued function, is required in many practical applications. If the problem is convex (it has only one minimum or maximum point), the local minimum (maximum) is also a global minimum (maximum). However, this is not always the case. One may have to optimize a function that has many local optima (and sometimes several global optima as well). Programs that work very well in optimizing convex functions very often perform poorly when the problem has multiple local minima or maxima. They are often caught or trapped in the local minima/maxima.
The main types of search methods are considered in Ref. [4]: Calculus-based, enumerative and random. Calculus-based methods are local, i.e. the optimal conditions they search are the best in a neighborhood of the current point. They depend upon both the existence of derivatives and the continuity of the function to be maximized. This last point is a severe limitation in terms of robustness for several engineering applications. Enumerative methods seek the optimal solution by computing the objective function in every point of the search space. This makes the enumerative algorithms substantially inefficient and time consuming when applied to large domains of possible solutions. Random search and meta-heuristic algorithms constitute an alternative strategy that can bypass the limitations of the previous methods. A complete review and the state-of-the-art of nature-inspired metaheuristic algorithms for global optimization is given in Ref. [5], including Particle Swarm Optimization (PSO) algorithms.
PSO may have some similarities with Genetic Algorithms (GA) but it is much simpler as it does not use mutation and crossover operators. Instead, it uses the real number randomness (no encoding/decoding of the parameters is required) and the global communication among the swarm particles. Various studies show that PSO algorithms can outperform genetic algorithms and other conventional solvers for solving many optimization problems [5].
The particle swarm optimization algorithm belongs to the category of swarm intelligence techniques. The swarm intelligence concepts are inspired by the social behavior of flocking animals such as swarms of birds, ants and fish school. PSO was first developed and introduced as a stochastic optimization algorithm by Eberhart and Kennedy [6]. The approach can be viewed as a distributed behavioral algorithm that performs a multidimensional search. PSO has been found to be useful in a wide variety of optimization tasks. Due to its natural ability to converge faster, PSO algorithm is also used to solve multi-objective optimization problems. PSO is a population based algorithm that exploits a population of individuals to probe promising regions of the search space. The individual behavior is affected either by the best local or best global individual. The performance of each individual is measured using fitness function similar to evolutionary algorithms. The population is referred as a swarm and individuals are called particles. The particles move in a multidimensional search space with adaptable velocity. In PSO, the particles remember the best position in the past and the best position ever attained by the particles. This property helps the particles to search the multidimensional space faster.
The particle swarm method has many variants. The Repulsive Particle Swarm (RPS) method of optimization, one of such variants, is particularly effective in finding out the global optimum in very complex search spaces (although it may be slower on certain types of optimization problems). The traditional RPS gives little scope of local search to the particles. They are guided by their past experience and the communication received from the others in the swarm. The traditional RPS method was modified and extensively tested in Ref. [7] by endowing stronger (wider) local search ability to each particle. This solver (Fortran library) was adopted for the present application.
3. The Mathematical Model
The mathematical model [8] is a nonlinear blade-element type representation of a single rotor helicopter with rigid fuselage (see Figure 1).
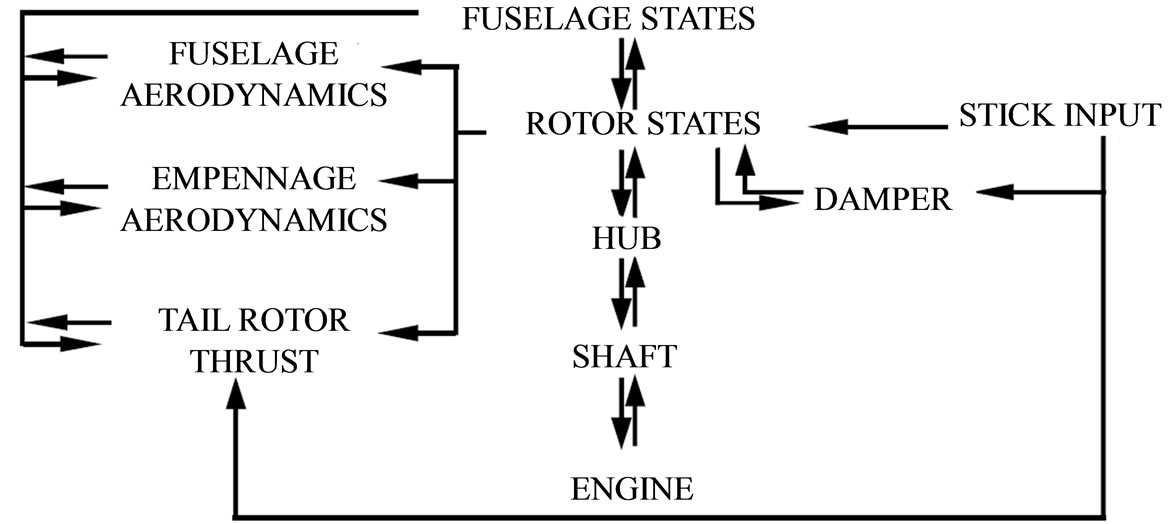
Figure 1. The mathematical model (helicopter dynamics).
The main rotor blades are individually modeled as rigid bodies and the coupled flap-lag dynamics is included. The equations of motion of the rotor are formulated and solved in a rotating coordinate system. No small angle assumption is invoked for aerodynamic angles of rotor and fuselage. The profile aerodynamic loads are calculated using two-dimensional blade element theory corrected for blade twist. A NACA0012 symmetric airfoil is considered for blade design and the lift/drag coefficients are given as a function of local angle of attack and Mach number [9]. The reactions generated by the lag dampers are linear functions of the axial velocity of the damper itself (damping ratio is 0.348). The aerodynamics of fuselage and stabilizers is modeled using coefficients derived from wind tunnel data interpolated for varying angles of attack and sideslip. A three-state dynamic inflow model [10] is used for the main rotor.
The rigid body motion of the aircraft is modeled using six nonlinear force and moment equations and three kinematic relations:
1) Force equilibrium along body axes:
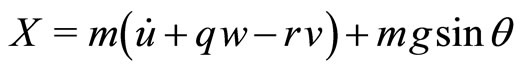
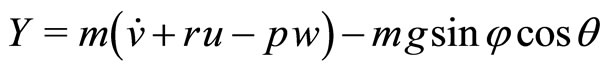
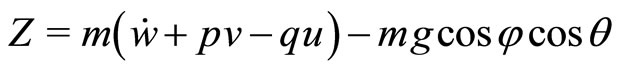
2) Moment equilibrium about body axes:
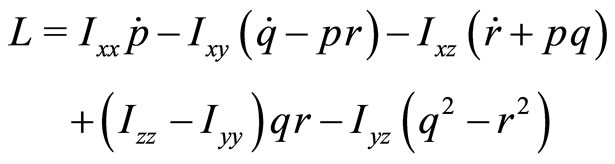
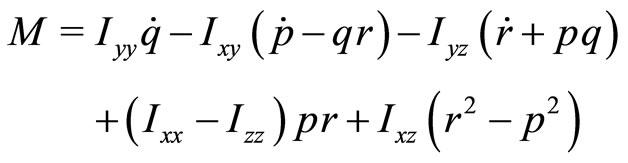
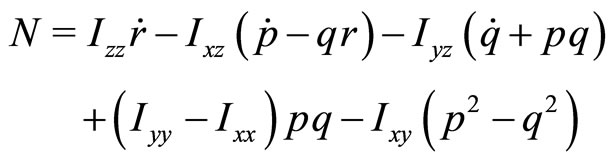
3) Relationships between aircraft angular rates and Euler angles:
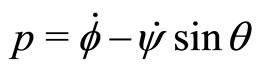
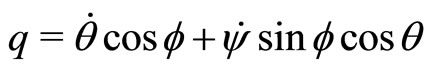
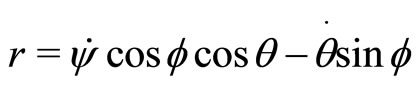
The heading rate 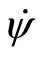 is assumed to be constant for trim analysis only (coordinated turn with null lateral load factor):
is assumed to be constant for trim analysis only (coordinated turn with null lateral load factor):
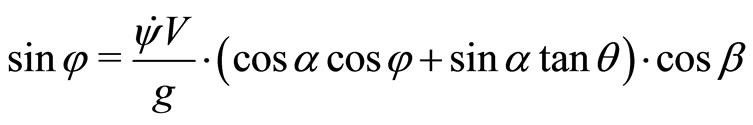 (1)
(1)
The climb angle γ is related to fuselage attitudes and aerodynamic angles for trim computation:
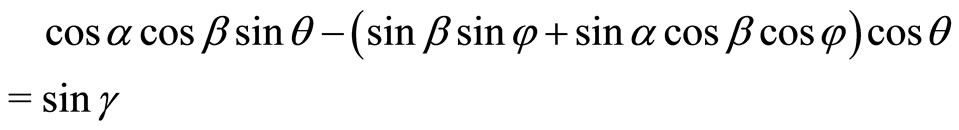 (2)
(2)
The forces (X, Y, Z) and the moments (L, M, N) depend on the blade motion and provide the main source of coupling between the rotor and the fuselage. They also contain contributions from fuselage, tail rotor and other aerodynamic surfaces. The most important feature of the set of equations of motion for the fuselage used in the present study is that the fuselage states need not to be small quantities; thus, all the kinematic nonlinearities associated with the motion of the fuselage are retained.
The trim procedure is the same as in Ref. [11]. Thus, the rotor equations of motion are transformed into a system of nonlinear algebraic equations using the Galerkin method (10 eqns.). These residuals are estimated considering 240 azimuth positions for the blade, dividing the lifting surface into 200 segments (spanwise discretization). The algebraic equations enforcing force and moment equilibrium (9 eqns.), the additional kinematic equations (2 eqns.) that must be satisfied in forward flight (or in a turn), and the momentum inflow equations for both main and tail rotor (3 + 1 eqns.) are added to the rotor equations, and the combined system (25 eqns.) is solved simultaneously. The solution yields the harmonics of a Fourier series expansion of the rotor degrees of freedom, the pitch control settings, trim attitudes and rates of the entire helicopter, and main and tail rotor inflow.
Flight without sideslip is arbitrarily assumed for μ ≤ 0.1, while roll attitude is set to zero for higher airspeed.
The propulsion system is not included in the trim process. This implies two assumptions. The first is that the engine can generate a sufficient torque in any flight condition. The second is that the small fluctuations of rotor speed associated with the lag dynamics of the rotor do not affect the engine torque.
4. Discussion of Results
The helicopter adopted for the present analysis is a single rotor helicopter (Table 1) with articulated flap and lag hinges. The reference blades are rectangular (untapered planform). The flight condition corresponds to sea level flight in standard atmosphere and, more specifically, for the nominal rotor design 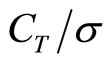 = 0.055 in hover.
= 0.055 in hover.
The parameters of the particle swarm optimization program were set selecting the population size N = 30 individuals, the number of randomly chosen neighbors NN = 15 individuals, the number of iterations ITRN = 250, enabling random chaotic perturbation of individuals, this last feature helping to jump out of local minima.
The fitness function 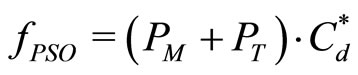 to be
to be
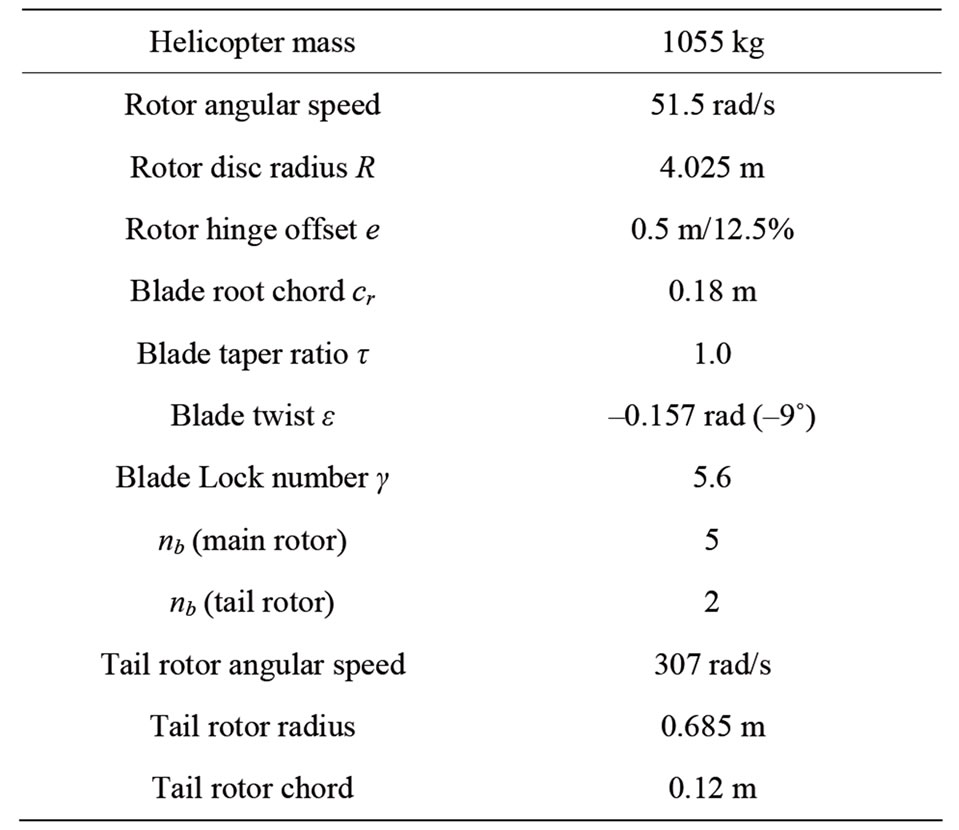
Table 1. The helicopter configuration.
minimized is the sum of main rotor and tail rotor power multiplied by the parameter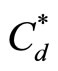 , i.e. the maximum profile drag coefficient along the blade for each of the azimuth coordinates outside of the reverse flow region. This multiplier helps to address the convergence to a blade design without drag divergence on the advancing side of the rotor disc limiting the maximum section lift coefficient on the retreating side of the rotor disc. As a general comment, the representation of airfoil aerodynamics (drag and lift coefficients) may change the fitness function
, i.e. the maximum profile drag coefficient along the blade for each of the azimuth coordinates outside of the reverse flow region. This multiplier helps to address the convergence to a blade design without drag divergence on the advancing side of the rotor disc limiting the maximum section lift coefficient on the retreating side of the rotor disc. As a general comment, the representation of airfoil aerodynamics (drag and lift coefficients) may change the fitness function 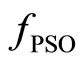 in a way to introduce multiple minima. This case was not explored in the present analysis, even if the full nonlinearity of 2D airfoil aerodynamics was retained [9]. The robustness of the repulsive PSO algorithm to trapping in local minima was already demonstrated in Ref. [7]. A penalty function for untrimmed flight conditions (based on the size of the numerical residual) is also introduced, preventing the convergence towards unrealistic blade designs.
in a way to introduce multiple minima. This case was not explored in the present analysis, even if the full nonlinearity of 2D airfoil aerodynamics was retained [9]. The robustness of the repulsive PSO algorithm to trapping in local minima was already demonstrated in Ref. [7]. A penalty function for untrimmed flight conditions (based on the size of the numerical residual) is also introduced, preventing the convergence towards unrealistic blade designs.
The procedure aims to optimize the aerodynamic performance of the helicopter rotor blades by selecting the point of taper initiation (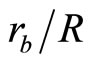 = 0.25/1), the root chord (cr = 0.175/0.225 m), the taper ratio (τ = 0.25/1), and the maximum twist angle (ε = −0.25/0 rad) which minimize the fitness function for different flight regimes (μ = 0.0/0.1/0.2).
= 0.25/1), the root chord (cr = 0.175/0.225 m), the taper ratio (τ = 0.25/1), and the maximum twist angle (ε = −0.25/0 rad) which minimize the fitness function for different flight regimes (μ = 0.0/0.1/0.2).
The design parameters of the blade were also optimized with a search strategy based on a genetic algorithm (GA). The genetic solver adopted for the design of the rotor is a Fortran version of the driver described by D. Carroll in Refs [12,13], widely tested in Refs [14,15]. The micro-GA operating mode was adopted combined with uniform crossover (the probability for a crossover occurring at each chromosome position was fixed to 0.5). The code was set for a maximum micro population size of 5 individuals, 48 bits per individual and 4 parameters (i.e. 12 binary bits per parameter and 212 possible solutions per parameter). Niching and elitism were activated, creep mutation was disabled and one child per pair of parents was considered. The fitness function to be maximized was adapted as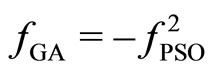 . In any case, the coincidence of minimum for
. In any case, the coincidence of minimum for 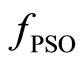 and maximum for
and maximum for 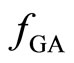 was verified numerically.
was verified numerically.
The output of the optimization process is presented in Table 2. The results for μ ≥ 0.1 show that the solvers aim to select a very slender design falling outside of the allowable design range. The most significant result is found for μ = 0.0, i.e. for the dimensioning flight condition for which maximum power output is required (hovering flight). The PSO algorithm provides a very accurate estimation of the optimal design measured for reference with an enumerative approach (marked as FCN in Table 2). The convergence of PSO to the solution is in any case slower if compared with that shown by the GA solver (as usually observed for RPS algorithms). On the other side, the GA solver provides the solution with some inaccuracy induced by the binary encoding of the variables.
The impact of inaccuracy on the estimation of the optimal design is evaluated in terms of required horsepower (see Table 3).
The planform design of the optimal blade is presented in Figure 2. The lower and higher allowed boundaries for the optimization process are also shown. As expected, the optimization procedure addresses the design towards slender blades as a mean for increasing aerodynamic efficiency of the lifting surface.
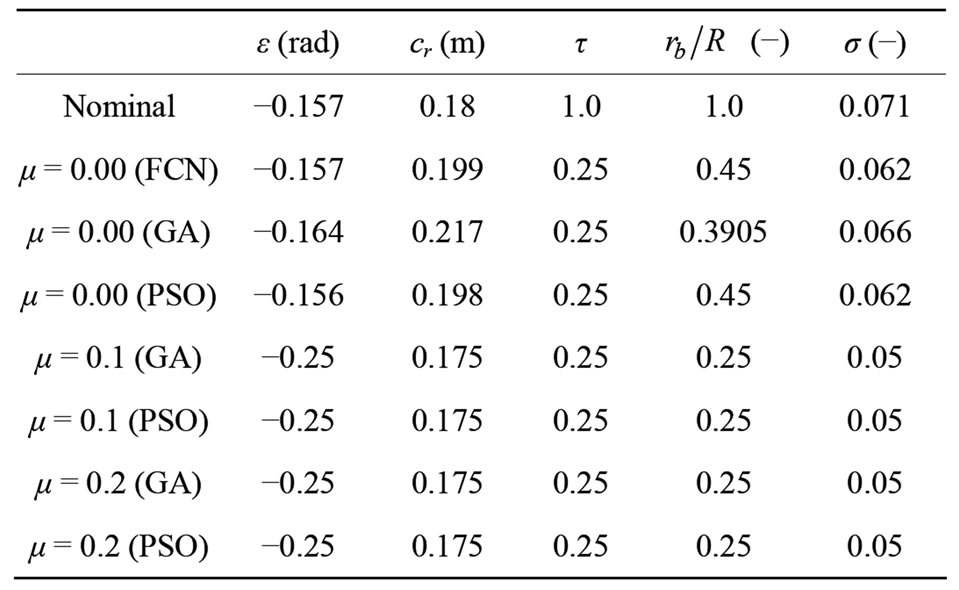
Table 2. The output of optimization process (design parameters).
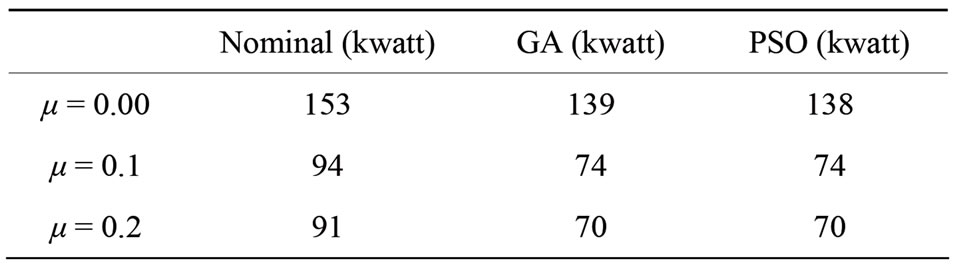
Table 3. The output of optimization process (main and tail rotor power).
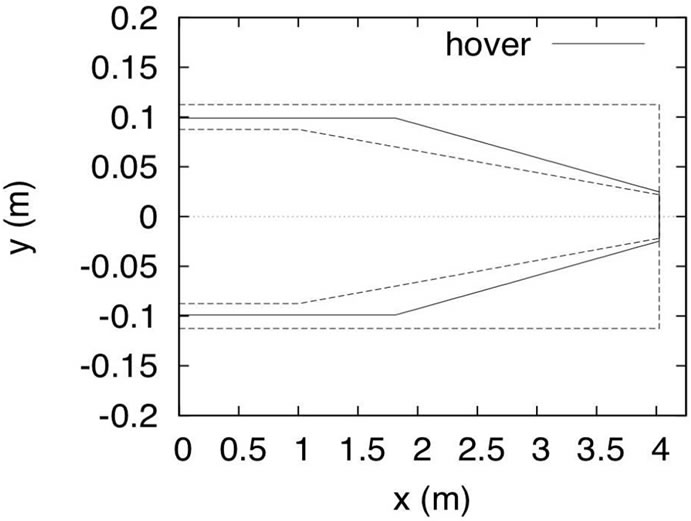
Figure 2. The optimal blade design (hover – μ = 0).
The effect of the design parameters on the minimum of the fitness function 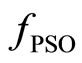 in hovering flight (μ = 0) is shown in Figure 3. The plots show that minimal changes of the size of the root chord cr and the position of the taper initiation point rb (for constant blade twist ε and taper τ) induce a relevant shift of the minimum i.e. minimal inaccuracies in the estimation of these design variables may compromise the accurate estimation of the optimal solution, as observed with the results obtained with the GA solver for the same advance ratio.
in hovering flight (μ = 0) is shown in Figure 3. The plots show that minimal changes of the size of the root chord cr and the position of the taper initiation point rb (for constant blade twist ε and taper τ) induce a relevant shift of the minimum i.e. minimal inaccuracies in the estimation of these design variables may compromise the accurate estimation of the optimal solution, as observed with the results obtained with the GA solver for the same advance ratio.
Even if this study aimed to design an optimal blade with minimum horsepower requirements in hover, it is relevant to verify how the blade performs in forward flight at several advance ratios. Figure 4 shows a plot of the horsepower required versus advance ratio for the blade design obtained from the particle swarm optimization process compared with the nominal design. As shown in the figure, the optimized blade requires less horsepower than the reference blade over the flight speed range shown (advance ratios of 0.0 to 0.325). The primary reason for this is that the optimized blade has less solidity σ than the reference blade. The reference rectangular blade is designed for wider flight requirements (higher CT and advance ratios) than those chosen in this analysis, including maneuvering flight.
5. Concluding Remarks
The present paper shows a numerical procedure to optimize the aerodynamic performance of helicopter rotor blades by selecting the point of taper initiation, root chord, taper ratio, and maximum twist which minimize horsepower for different flight regimes. The procedure uses a comprehensive mathematical model to estimate the trim states of the helicopter and the optimization algorithm consists of a repulsive particle swarm optimization program developed in Ref. [7]. A comparison with an evolutionary micro-genetic algorithm [12,13] is also presented. The results show that the PSO algorithm is slower but very accurate, matching the optimal design with negligible error. Differently, the GA solver converges quite fast to the solution, failing to be as accurate
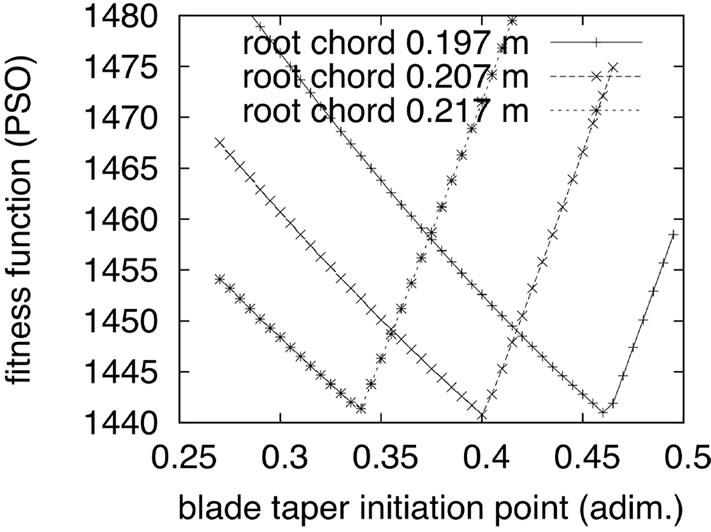
Figure 3: The impact of design parameters on the global minimum of the fitness function (hover – μ = 0 – ε = –0.157 rad – τ = 0.25).
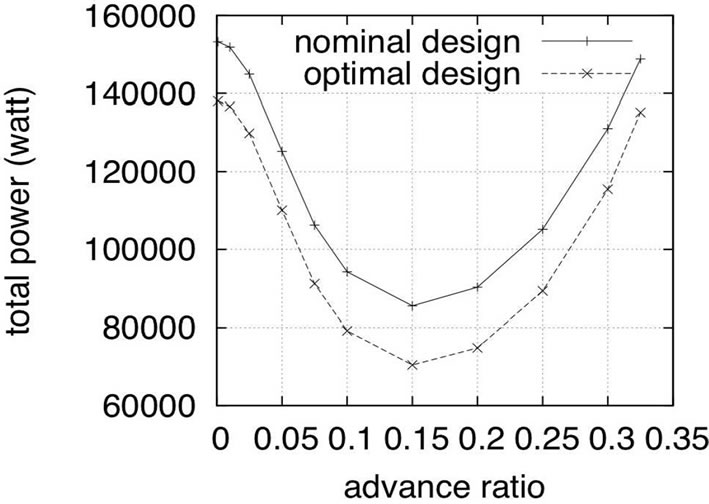
Figure 4. The nominal and the optimal blade design (total power).
as the particle swarm optimizer. This result is promising in order to extend the use of this optimization procedure to critical multi-disciplinary design problems that are sensitive to fractional changes of the design variables, in which the design may be compromised by these inaccuracies (blade aeroelastic design). As an additional comment, a remarkable advantage of PSO (and specifically RPS) is the straightforward implementation, requiring a minimum programming effort.
REFERENCES
- R. Celi, “Recent Applications of Design Optimization to Rotorcraft—A Survey,” American Helicopter Society 55th Annual Forum, Montreal, 25-27 May 1999.
- R. Ganguli, “Survey of Recent Developments in Rotorcraft Design Optimization,” Journal of Aircraft, Vol. 41, No. 3, 2004, pp. 493-510. doi:10.2514/1.58
- J. L. Walsh, “Performance Optimization of Helicopter Rotor Blades,” NASA Langley Research Center, Hampton, USA, 1991.
- D. E. Goldberg, “Genetic Algorithm in Search, Optimization and Machine Learning,” Addison-Wesley, Reading, 1989.
- X.-S. Yang, “Nature-Inspired Meta-Heuristic Algorithms: Second Edition,” Luniver Press, Frome, 2010.
- R. C. Eberhart and J. Kennedy, “Particle Swarm Optimization,” Proceedings of the 4th IEEE International Conference on Neural Networks, Piscataway, 27 November-1 December 1995, pp. 1942-1948.
- S. K. Mishra, “Global Optimization by Particle Swarm Method: A Fortran Program,” 2007. http://mpra.ub.uni-muenchen.de/874
- G. Guglieri and R. Celi, “On Some Aspects of Helicopter Flight Dynamics in Steady Turns,” Journal of Guidance, Control and Dynamics, Vol. 21, No. 3, 1998, pp. 383-390. doi:10.2514/2.4270
- T. S. Beddoes, “Representation of Airfoil Behaviour,” Vertica, Vol. 7, No. 2, 1983, pp. 183-197.
- D. A. Peters and N. Haquang, “Dynamic Inflow for Practical Applications,” Journal of the American Helicopter Society, Vol. 33, No. 4, 1988, pp. 64-68. doi:10.4050/JAHS.33.64
- R. Celi, “Hingeless Rotor Dynamics in Coordinated Turns,” Journal of the American Helicopter Society, Vol. 36, No. 4, 1991, pp. 39-47. doi:10.4050/JAHS.36.39
- D. L. Carrol, “Chemical Laser Modeling with Genetic Algorithms,” AIAA Journal, Vol. 34, No. 2, 1996, pp. 338- 346. doi:10.2514/3.13069
- D. L. Carroll, “Genetic Algorithms and Optimizing Chemical Oxygen-Iodine Lasers,” Developments in Theoretical and Applied Mechanics, Vol. 18, 1996, pp. 411-424.
- R. Fantinutto, G. Guglieri and F. Quagliotti, “Flight Control System Design and Optimisation with a Genetic Algorithm,” Aerospace Science and Technology, Vol. 9, No. 1, 2005, pp. 73-80. doi:10.1016/j.ast.2004.09.003
- G. Guglieri, B. Pralio and F. Quagliotti, “Flight Control System Design for a Micro Aerial Vehicle,” Aircraft Engineering and Aerospace Technology, Vol. 78, No. 2, 2006, pp. 87-97. doi:10.1108/17488840610653397
Nomenclature
cr: Blade root chord (m)
ct: Blade tip chord (m)
CT: Thrust coefficient e: Hinge offset (m)
f: Fitness function
FCN: Function
g: Acceleration due to gravity (m/s)
GA: Genetic Algorithm
Iii: Aircraft moment of inertia (kg·m2)
Iij: Aircraft product of inertia (kg·m2)
m: Helicopter mass (kg)
nb: Number of blades
p, q, r: Angular velocities (body axes) (rad/s)
PM: Main rotor power (watt)
PT: Tail rotor power (watt)
PSO: Particle Swarm Optimization
R: Rotor disc radius (m)
RPS: Repulsive Particle Swarm
rb: Point of taper initiation (m)
u, v, w: Velocity components (body axes) (m/s)
V: Airspeed (m/s)
α: Angle of attack (rad)
β: Angle of sideslip (rad)
ε: Blade twist (rad)
γ: Blade Lock number
μ: Advance ratio
ϕ, θ, ψ: Fuselage Euler angles (rad)
σ: Main rotor solidity
τ: Blade taper ratio 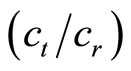
(·): Time derivative (s–1)

