Applied Mathematics
Vol.3 No.6(2012), Article ID:20357,20 pages DOI:10.4236/am.2012.36096
Image Mathematics—Mathematical Intervening Principle Based on “Yin Yang Wu Xing” Theory in Traditional Chinese Mathematics (I)
1School of Finance and Statistics, East China Normal University, Shanghai, China
2The College English Teaching and Researching Department, Xinxiang University, Xinxiang, China
Email: ysh_zhang@163.com, yszhang@stat.ecnu.edu.cn
Received March 26, 2012; revised May 2, 2012; accepted May 9, 2012
Keywords: Image Mathematics; “Yin Yang Wu Xing” Theory; Steady Multilateral Systems; Opposite Non-Compatibility Relations; Intervention Rule; Self-Protection Rule; Mathematical Side Effects; Mathematical Intervention Resistance Problem
ABSTRACT
By using mathematical reasoning, this paper demonstrates the mathematical intervening principle: “Virtual disease is to fill his mother but real disease is to rush down his son” (虚则补其母, 实则泄其子) and “Strong inhibition of the same time, support the weak” (抑强扶弱) based on “Yin Yang Wu Xing” Theory in image mathematics of Traditional Chinese Mathematics (TCMath). We defined generalized relations and generalized reasoning, introduced the concept of steady multilateral systems with two non-compatibility relations, and discussed its energy properties. Later based on the intervention principle in image mathematics of TCMath and treated the research object of the image mathematics as a steady multilateral system, it has been proved that the mathematical intervening principle is true. The kernel of this paper is the existence and reasoning of the non-compatibility relations in steady multilateral systems, and it accords with the oriental thinking model.
1. Main Differences between Traditional Chinese Mathematics and Western Mathematics
In Western Mathematics (mathematics; Greek: μ α θ η μ α τ ι κ), the word comes from the ancient Greek in the west of the μ θ η μ α (mathēma), its have learning, studying, science, and another relatively narrow meaning and technical sense-“mathematics study”, even in its neck comes in. The adjective μ α θ η μ α τ ι κ (mathē- matikos), meaning and learning about or for the hard, also can be used to index of learning. In English on the function of the plural form of, and in French surface mathematiques plural form, can be back to Latin neutral plural mathematica, due to the Greek plural τ α μ α θ η μ α τ ι κ (tamathēmatika), the Greek by Aristotle brought refers to “all things several” concept. (Latin: Mathemetica) original intention is number and count of the technology.
According to the understanding of the now in Western mathematics, mathematics is the real world number relationship and the form of the space science. Say simply, is the study of the form and number of science. The start of the study is always from the Axiomatic system. Any Axiomatic system of form and number comes from the observations. Because of the demand on life and labor, and even the most original nationality, also know simple count, and the fingers or physical count development to use digital count. Basic mathematics knowledge and use always individual and community essential to life. The basic concept of the refining is as early as in ancient Egypt, Mesopotamia, and in ancient India of ancient mathematical text and see in considerable. Since then, its development will continue to have a modest progress, and the 16th century until the Renaissance, because of the new scientific and found interactions and the generated mathematical innovation leads to the knowledge of the acceleration, until today.
Mathematics is used in different areas of the world, including science, engineering, medicine and economics, etc. The application of mathematics in these fields are usually called applied mathematics, sometimes also stir up new mathematical discovery, and led to the development of new subject. Mathematician also study didn’t any application value of pure mathematics, even if the application is found in often after.
The Boolean school, founded in the 1930s in France by Boolean, thinks: mathematics, at least pure mathematics, is the study of the theory of abstract structure. Structure, it is the initial concept and the deduction system of Axiom. Boolean school also thinks that, there are three basic kinds of abstract structure: algebraic structure (group, ring, the domain...), sequence structure (partial order, all the sequence...), the topological structure (neighborhood, limit, connectivity, dimension...). Mathematics is a kind of transformation, an abstract model, and a sign system, the real world converted into mathematical model, using mathematical language describe them later, after operation, the results can back, explained in the real world specific scientific.
There is a basic logic that the human is everything, they can be observed to establish an Axiom system, make nature operations according to the Axiom system by human assumption. But in the traditional Chinese philosophy, always think that humans are the small, they can not establish a set of rules, let nature operation in accordance with the running rules of the human assumption. In front to nature, human’s only doing things is its behavior request, with its development with nature.
In other words, the western mathematics thinks the mathematical object of study is a simple system, which can be observed to establish an Axiom system, and then logical analysis. It is because a simple system can be assumed. But the image mathematics of the traditional Chinese mathematics thinks the mathematical object of study is a complex system, human can’t do specific research object hypothesis, humans can only be clear, for general object of study (model-free), what kind of logic structure analysis can reach the humans to understand the research object of certain relations. It is because a complex system cannot be assumed.
Simple said: the western mathematics deals directly with the research object through the directly observed, but the image mathematics of the traditional Chinese mathematics researches object through the relationship between indirect processing analysis.
In fact, Western mathematics late nineteenth century was introduced into China, initially, “mathematics” to be directly translated as “arithmetic (算术)”, and then said “arithmetic learn (算学)”, and then they changed to “mathematics (数学)” words. But the ancient Chinese for this concept, in 3000 years ago, has been officially use the word “Gua (卦)” as the form, the “Xiang (象)” as the number. In the Yi-Jing (“易经”), this “mathematics (数学)” concept is defined as “Image Mathematics (象数学)”. It is part of the Traditional Chinese Mathematics (TCMath). This article mainly concerns image mathematical content in TCMath, so also said the image mathematics as TCMath. Image mathematics generally contains hexagrams (“Gua (卦)”) and images (“Xiang (象)”) two content. The hexagrams (“Gua (卦)”) is only the hexagrams mathematical symbols, which there is not the size since the size of number is about the definition of human beings. In general, the research object in the complex system is independent of human definition. The image (“Xiang (象)”) is the study way or the calculation method for some mathematical indexes in order to know the objective existence of the fixed a state. The way or the calculation method for some mathematical indexes is independent of the complex system and only is Human’s some methods of operation in order to study the relationship of the complex system.
The ancients speak of “mathematics” in Chinese is a word as the way for running (intervening and controlling) a complex system through the analysis of the use of hexagrams (“Gua (卦)”) and images (“Xiang (象)”). This and what we now understand the mathematical completely different things. In other words, in the image mathematics of Traditional Chinese Mathematics (TCMath), both intervening and controlling of an engineering are believed to as a complex system. It is because to run an engineering is difficult and complex in which there are the loving relation, the killing relation and the equivalent relation among many Axiom systems. The loving and killing relations are non-compatibility relations, which can compose the whole energy of the system greater than or less than the sum of each part energy of the system, respectively, rarely equal conditions. Mathematics means managing or controlling or intervening for the complex system through the analysis of the use of hexagrams (“Gua (卦)”) and images (“Xiang (象)”), and so on. Pursue the goal is the harmonious sustainable of the complex system in order to compose the complex system not outward expansion development. Generally speaking, the assumption involved the behavior of people is not needed since the system is complex.
But, in Western mathematics, mathematics means first through the observation to establish one Axiom system, then performing mathematical inference from the Axiom system. Both obtaining and inference of reasoning are believed to as a simple system, because all the conclusions and definition of are compatible with the Axiom system. Compared with Axiom system speaking, there are true and false. Major mathematical analysis method is to judge true or false from simple assumptions or simple model. It is because to obtain the true and false relationship of one Axiom system is easy and simple in which there is only a compatibility relation or a generalized equivalent relation under one Axiom system assumption. The compatibility relation or generalized equivalent relation can compose the whole energy of the system equal to the sum of each part energy of the system. Thus to obtain or to analyze under one Axiom system assumption can compose the simple system outward expansion development. Therefore, pursue the goal is for obtaining or analyzing in order to compose the simple system outward expansion development. Generally speaking, the various hypothetical models involves the behavior of people. This phenomenon in the image mathematics of TCMath is not allowed since a complex system cannot be supposed. Both true and false cannot be judged if the Axiom system has not been assumed.
Western mathematics using simple assumptions or simple models treats directly mathematical complex system from Microscopic point of view, always destroy the original mathematical complex system’s balance, and has none beneficial to mathematical complex system’s immunity. Western mathematical intervention method can produce imbalance of mathematical complex system, having strong side effects. Excessively using methods of mathematical intervention for a complex system can easily paralysis the mathematical complex system’s immunity, which the debate of mathematical schools under different from Axiom systems is a product of Western mathematics since there are a number of Axiom systems in nature which are different to the people of faith. Using the method of mathematical intervention for a complex system too little can easily produce the mathematical intervention resistance problem.
The image mathematics of TCMath studies the world from the Macroscopic point of view, and its target is in order to maintain the original balance of mathematical complex system and in order to enhance the mathematiccal complex system’s immunity. The image mathematics believes that each mathematical intervention has onethird of badness. She never encourage government to use mathematical intervention in long term. The ideal way is Wu Wei Er Wu Bu Wu (无为而无不为)—by doing nothing, everything is done. The image mathematics has over 5000-year history. It has almost none side effects or mathematical intervention resistance problem.
After long period of practicing, our ancient mathematical scientists use “Yin Yang Wu Xing” Theory extensively in the image mathematics to explain the origin of mathematical complex system, the law of mathematiccal complex system, mathematical changes, mathematiccal diagnosis, mathematical prevention, mathematical self-protection and mathematical intervening. It has become an important part of the image mathematics. “Yin Yang Wu Xing” Theory has a strong influence to the formation and development of traditional Chinese mathematical theory. As is known to all, China in recent decades, economy and related mathematical work have made great strides in development. Its reason is difficult to say the introduction of western mathematics, the fact that the Chinese traditional culture is in all kinds of mathematical decision plays a role. Her many mathematical intervening methods come from the traditional Chinese medicine since both human body and mathematical research objects of image mathematics are all complex systems. But, many Chinese and foreign schoolars still have some questions on the reasoning of image mathematics, such as Traditional Chinese Medicine which is due to image mathematics. In this article, we will start to the western world for presentation of image mathematics introduced some mathematical and logic analysis concept.
Zhang’s theories, multilateral matrix theory [1] and multilateral system theory [2-19], have given a new and strong mathematical reasoning method from macro (Global) analysis to micro (Local) analysis. He and his colleagues have made some mathematical models and methods of reasoning [20-35], which make the mathematical reasoning of image mathematics possible based on “Yin Yang Wu Xing” Theory [36-38]. This paper will use steady multilateral systems to demonstrate the intervening principle of image mathematics: “Real (mathematical) disease is to rush down his son but virtual (mathematical) disease is to fill his mother” and “Strong inhibition of the same time, support the weak”.
The article proceeds as follows. Section 2 contains basic concepts and main theorems of steady multilateral systems while the intervening principle of image mathematics is demonstrated in Section 3. Some discussions in image mathematics are given in Section 4 and conclusions are drawn in Section 5.
2. Basic Concept of Steady Multilateral Systems
In the real world, we are enlightened from some concepts and phenomena such as “biosphere”, “food chain”, “ecological balance” etc. With research and practice, by using the theory of multilateral matrices [1] and analyzing the conditions of symmetry [20-24] and orthogonality [25-35] what a stable complex system must satisfy, in particular, with analyzing the basic conditions what a stable working procedure of good product quality must satisfy [10,29], we are inspired and find some rules and methods, then present the logic model of analyzing stability of complex systems-steady multilateral systems [2-19]. There are a number of essential reasoning methods based on the stable logic analysis model, such as “transition reasoning”, “atavism reasoning”, “genetic reasoning” etc. We start and still use concepts and notations in papers [3-6].
2.1. Generalized Relations and Reasoning
Let V be a non-empty set and  . The non-empty subset
. The non-empty subset 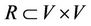 is called a relation of V. Image mathematics mainly researches general relation rules for general V rather than for special V. So the general V cannot be supposed. We can only do matter is to research the structure of the set of relations
is called a relation of V. Image mathematics mainly researches general relation rules for general V rather than for special V. So the general V cannot be supposed. We can only do matter is to research the structure of the set of relations .
.
For any relation set , we can define both an inverse relationship of
, we can define both an inverse relationship of  and a relation multiplication between
and a relation multiplication between  and
and  as follows:
as follows:
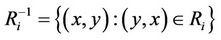
and  there is at least a
there is at least a  such that
such that 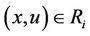 and
and .
.
The relation 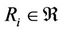 is called reasonable if
is called reasonable if . A generalized reasoning of general V is defined as for
. A generalized reasoning of general V is defined as for 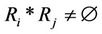 there is a relation
there is a relation 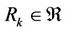 such that
such that 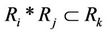 .
.
The generalized reasoning satisfies the associative law of reasoning, i.e.,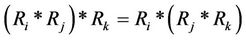 . This is the basic requirement of reasoning in TCMath. But there are a lot of reasoning forms which do not satisfy the associative law of reasoning in Western Science. For example, in true and false binary of proposition logic, the associative law does not hold on its reasoning because
. This is the basic requirement of reasoning in TCMath. But there are a lot of reasoning forms which do not satisfy the associative law of reasoning in Western Science. For example, in true and false binary of proposition logic, the associative law does not hold on its reasoning because
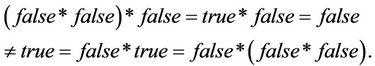
2.2. Equivalence Relations
Let V be a non empty set and  be its a relation. We call it an equivalence relation, denoted by ~, if the following three conditions are all true:
be its a relation. We call it an equivalence relation, denoted by ~, if the following three conditions are all true:
1) Reflexive:  for all
for all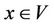 , i.e.,
, i.e.,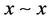 ;
;
2) Symmetric: if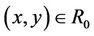 , then
, then , i.e., if
, i.e., if , then
, then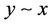 ;
;
3) Conveyable (Transitivity): if ,
,  , then
, then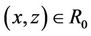 , i.e., if
, i.e., if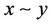 ,
, 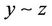 , then
, then 
Furthermore, the relation R is called a compatibility relation if there is a non-empty subset 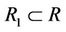 such that
such that  satisfies at least one of the conditions above. And the relation R is called a non-compatibility relation if there doesn’t exist any non-empty subset
satisfies at least one of the conditions above. And the relation R is called a non-compatibility relation if there doesn’t exist any non-empty subset  such that
such that  satisfies any one of the conditions above. Any one of compatibility relations can be expanded into an equivalent relation to some extent [2].
satisfies any one of the conditions above. Any one of compatibility relations can be expanded into an equivalent relation to some extent [2].
Western Science only considers the reasoning under one Axiom system such that only compatibility relation reasoning is researched. However there are many Axiom systems in Nature. Traditional Chinese Science mainly researches the reasoning among many Axiom systems in Nature. Of course, she also considers the reasoning under one Axiom system but she only expands the reasoning as the equivalence relation reasoning.
2.3. Two Kinds of Opposite Non-Compatibility Relations
Equivalence relations, even compatibility relations, can not portray the structure of the complex systems clearly. In the following, we consider two non-compatibility relations.
In image mathematics, any Axiom system is not considered, but should first consider to use a logic system. Believe that the rules of Heaven and the behavior of Human can follow the same logic system (天人合一). This logic system is equivalent to a group of computation. The method is to abide by the selected logic system to the research object classification, without considering the specific content of the research object, namely classification taking images (比类取象). Analysis of the relationship between research object, make relationships with computational reasoning comply with the selected logic system operation. And then in considering the research object of the specific content of the conditions, according to the logic of the selected system operation to solve specific problems. In mathematics, the method of classification taking images is explained in the following Definition 2.1.
Definition 2.1. Suppose that there exists a finite group  of order m where g0 is identity. Let V be a none empty set satisfying that
of order m where g0 is identity. Let V be a none empty set satisfying that 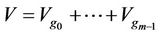 where the notation means that
where the notation means that ,
, 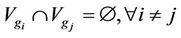 (the following the same).
(the following the same).
In image mathematics, the  is first called a factor image of group element
is first called a factor image of group element  for any j, and
for any j, and  is called a factor space (all “Gua (卦)”). We do not consider the factor size (class variables) and only consider it as mathematical symbols (“Gua (卦)”), such as, 0 or 1, because the size is defined by a human behavior for V, but we have no assumption of V.
is called a factor space (all “Gua (卦)”). We do not consider the factor size (class variables) and only consider it as mathematical symbols (“Gua (卦)”), such as, 0 or 1, because the size is defined by a human behavior for V, but we have no assumption of V.
A mathematical index of the unknown multivariate function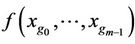 ,
, 
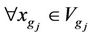 is called a function image of V. All mathematical indexes of the unknown multivariate function f compose of the formation of a new set, namely image space
is called a function image of V. All mathematical indexes of the unknown multivariate function f compose of the formation of a new set, namely image space
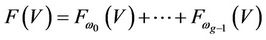
where  is also a finite group of order g. The
is also a finite group of order g. The 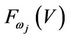 is also called an Axiom system for any j if
is also called an Axiom system for any j if 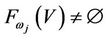 because any Axiom system is the assumption of
because any Axiom system is the assumption of
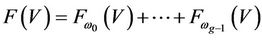
(or, equivalent, V) in which there is only the compatibility relations, i.e., pursuing the same mathematics index
 . We do not consider the special multivariate function f (i.e., special function image) and only consider the calculation way of the general mathematical indexes of f from the factor space
. We do not consider the special multivariate function f (i.e., special function image) and only consider the calculation way of the general mathematical indexes of f from the factor space 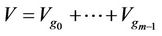 in order to know some causal relations, because we have no assumption of f. But the size of the data image should be considered if we study specific issues by the general rules of data images.
in order to know some causal relations, because we have no assumption of f. But the size of the data image should be considered if we study specific issues by the general rules of data images.
Say simply, a study of the hexagrams (“Gua (卦)”) in image mathematics is to learn the generalized properties of the inputs  of any multivariate function f for the given factor space
of any multivariate function f for the given factor space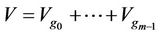 , such as there are non-size, non-order relation, orthogonal relations and symmetrical relations, and so on. A study of the image (“Xiang (象)”) in image mathematics is to learn the generalized properties of all outputs f for the image space
, such as there are non-size, non-order relation, orthogonal relations and symmetrical relations, and so on. A study of the image (“Xiang (象)”) in image mathematics is to learn the generalized properties of all outputs f for the image space , such as there are size specific meaning, a sequence of relationship, killing relations, loving relations, equivalent relations, and so on.
, such as there are size specific meaning, a sequence of relationship, killing relations, loving relations, equivalent relations, and so on.
Without loss of generality, we put the function image space 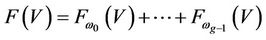 and the factor image space
and the factor image space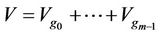 , still keep for V because of no assumption of V. In order to study the generalized relations and generalized reasoning, image mathematics researches the following relations.
, still keep for V because of no assumption of V. In order to study the generalized relations and generalized reasoning, image mathematics researches the following relations.
Denoted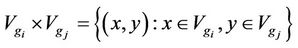 , where the note × is the usual Cartesian product or cross join. Define relations
, where the note × is the usual Cartesian product or cross join. Define relations

where 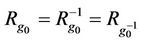 is called an equivalence relation of V if g0 is identity; denoted by ~;
is called an equivalence relation of V if g0 is identity; denoted by ~; 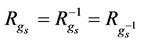 is called a symmetrical relation of V if
is called a symmetrical relation of V if ,
, ; denoted by
; denoted by  or
or ;
; 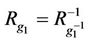 is called a neighboring relation of V if
is called a neighboring relation of V if ; denoted by
; denoted by 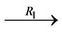 or
or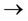 ;
;  is called an alternate (or atavism) relation of V if
is called an alternate (or atavism) relation of V if ,
, 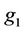 ,
,  ,
,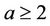 ; denoted by
; denoted by 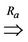 or
or . #
. #
In this case, the equivalence relations and symmetrical relations are compatibility relations but both neighboring relations and alternate relations are non-compatibility relations. For the given relation set , these relations
, these relations  are all reasoning relations since the relation
are all reasoning relations since the relation  if
if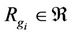 .
.
The equivalence relation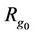 , symmetrical relations
, symmetrical relations , neighboring relation
, neighboring relation 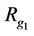 and alternate relations
and alternate relations  are all the possible relations for the method of classification taking images. In this paper, we mainly consider the equivalence relation
are all the possible relations for the method of classification taking images. In this paper, we mainly consider the equivalence relation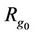 , neighboring relation
, neighboring relation  and alternate relations
and alternate relations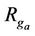 .
.
There is an unique generalized reasoning between the two kinds of opposite non-compatibility relations for case m = 5. For example, let V be a none empty set, there are two kinds of opposite relations: the neighboring relation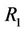 , denoted ® and the alternate (or atavism) relation
, denoted ® and the alternate (or atavism) relation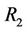 , denoted
, denoted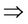 . The logic reasoning architecture [2-19] of “Yin Yang Wu Xing” Theory in Ancient China is equivalent to the following reasoning:
. The logic reasoning architecture [2-19] of “Yin Yang Wu Xing” Theory in Ancient China is equivalent to the following reasoning:
1) If x ® y, y ® z, then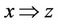 ; i.e., if
; i.e., if ,
,  , then
, then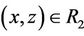 ; or,
; or,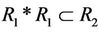 ;
; 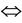 if x ® y,
if x ® y,  , then y ® z; i.e., if
, then y ® z; i.e., if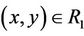 ,
,  , then
, then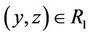 ; or,
; or, ;
; 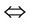 if
if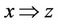 , y ® z, then x ® y; i.e., if
, y ® z, then x ® y; i.e., if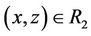 ,
, 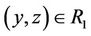 , then
, then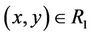 ; or,
; or,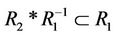 .
.
2) If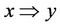 ,
, 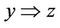 then z ® x; i.e., if
then z ® x; i.e., if ,
, 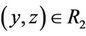 , then
, then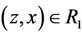 ; or,
; or,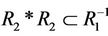 ;
;  if z ® x,
if z ® x,  , then
, then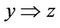 ; i.e., if
; i.e., if ,
, 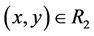 then
then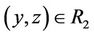 ; or,
; or,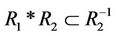 ;
; 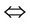 if
if , z ® x then
, z ® x then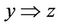 ; i.e., if
; i.e., if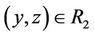 ,
, 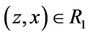 , then
, then ; or,
; or,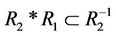 .
.
Let 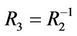 and
and . Then above reasoning is equivalent to the calculating as follows:
. Then above reasoning is equivalent to the calculating as follows:

where the 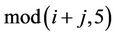 is the addition of module 5.
is the addition of module 5.
Two kinds of opposite relations can not be exist separately. Such reasoning can be expressed in Figure 1. The first triangle reasoning is known as a jumping-transition reasoning, while the second triangle reasoning is known as an atavism reasoning. Reasoning method is a triangle on both sides decided to any third side. Both neighboring relations and alternate relations are not compatibility relations, of course, none equivalence relations, called non-compatibility relations.
2.4. Genetic Reasoning
Let V be a none empty set with the equivalent relation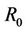 , the neighboring relation
, the neighboring relation 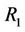 and the alternate relations
and the alternate relations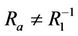 ,
, . Then a genetic reasoning is defined as follows:
. Then a genetic reasoning is defined as follows:
1) If x ~ y, y ® z, then x ® z; i.e., if ,
,  , then
, then ; or,
; or,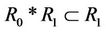 ;
;
2) If x ~ y, 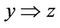 , then
, then ; i.e., if
; i.e., if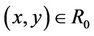 ,
, 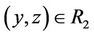 , then
, then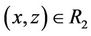 ; or,
; or, ;
;
3) If x ® y, y ~ z, then x ® z; i.e., if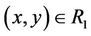 ,
,  , then
, then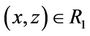 ; or,
; or, ;
;
4) If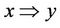 , y ~ z, then
, y ~ z, then ; i.e., if
; i.e., if ,
, 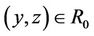 , then
, then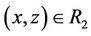 ; or,
; or, .
.
The genetic reasoning is equivalent to that
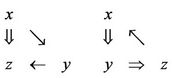
Figure 1. Triangle reasoning.

since ,
,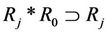 . The genetic reasoning is equivalent to that there is a group
. The genetic reasoning is equivalent to that there is a group  with the operation * such that V can be cut into
with the operation * such that V can be cut into 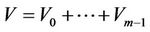 where Vi may be an empty set and the corresponding relations of reasoning can be written as the forms as follows
where Vi may be an empty set and the corresponding relations of reasoning can be written as the forms as follows
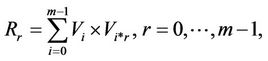
satisfying .
.
2.5. Steady Multilateral Systems
For a none empty set V and its a relation set 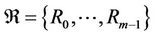 , the form
, the form 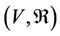 (or simply, V) is called a multilateral system [2-19], if
(or simply, V) is called a multilateral system [2-19], if  satisfies the following properties:
satisfies the following properties:
1) 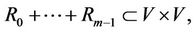 i.e.
i.e.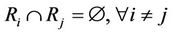 .
.
2) 
3) The relation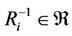 if
if .
.
4) For , there is a relation
, there is a relation 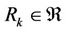 such that
such that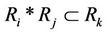 .
.
The 4) is called the reasoning, the 1) the uniqueness of reasoning, the 2) the hereditary of reasoning (or genetic reasoning) and the 3) the equivalent property of reasoning of both relations 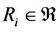 and
and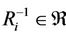 , i.e., the reasoning of
, i.e., the reasoning of  is equivalent to the reasoning of
is equivalent to the reasoning of . In this case, the two-relation set
. In this case, the two-relation set  is a lateral relation of
is a lateral relation of . The
. The  is called an equivalence relation. The multilateral system
is called an equivalence relation. The multilateral system  can be written as
can be written as . Furthermore, the V and
. Furthermore, the V and  are called the state space and relation set considered of
are called the state space and relation set considered of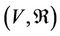 , respectively. For a multilateral system
, respectively. For a multilateral system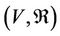 , it is called complete (or, perfect) if “
, it is called complete (or, perfect) if “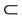 ” changes into “=”. And it is called complex if there exists at least a non-compatibility relation
” changes into “=”. And it is called complex if there exists at least a non-compatibility relation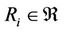 . In this case, the multilateral system is also called a logic analysis model of complex systems.
. In this case, the multilateral system is also called a logic analysis model of complex systems.
Let 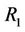 be a non-compatibility relation. A complex multilateral system
be a non-compatibility relation. A complex multilateral system
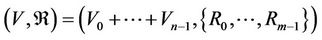
is said as a steady multilateral system (or, a stable multilateral system) if there exists a number n such that  where
where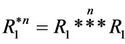 . The condition is equivalent to there is a the chain
. The condition is equivalent to there is a the chain 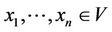 such that
such that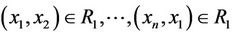 , or
, or . The steady multilateral system is equivalent to the complete multilateral system. The stability definition given above, for a relatively stable system, is most essential. If there is not the chain or circle, then there will be some elements without causes or some elements without results in a system. Thus, this system is to be in the state of finding its results or causes, i.e., this system will fall into an unstable state, and there is not any stability to say.
. The steady multilateral system is equivalent to the complete multilateral system. The stability definition given above, for a relatively stable system, is most essential. If there is not the chain or circle, then there will be some elements without causes or some elements without results in a system. Thus, this system is to be in the state of finding its results or causes, i.e., this system will fall into an unstable state, and there is not any stability to say.
Theorem 2.1. The system  is a multilateral system if and only if there exists a finite group
is a multilateral system if and only if there exists a finite group
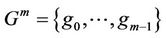 of order m where g0 is identity such that the relation set
of order m where g0 is identity such that the relation set 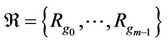 satisfying
satisfying 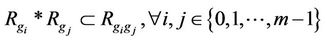 .
.
In this case, the multilateral system 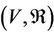 can be written as
can be written as 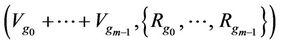 satisfying
satisfying 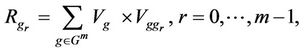 where
where  may be an empty set.
may be an empty set.
Theorem 2.2. If the multilateral system
 is a steady multilateral system, then
is a steady multilateral system, then  and
and 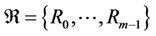 is a finite group of order m about the relation multiplication
is a finite group of order m about the relation multiplication 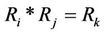 where
where  must be a non empty set.
must be a non empty set.
Definition 2.2. Suppose that a multilateral system 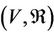 can be written as
can be written as 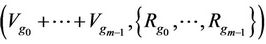 satisfying
satisfying 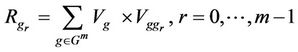 and
and  .
.
The group 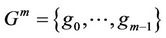 of order m where g0 is identity is called the representation group of the multilateral system
of order m where g0 is identity is called the representation group of the multilateral system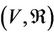 . The representing function of
. The representing function of 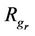 is defined as follows
is defined as follows
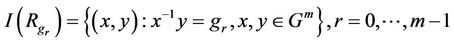 .
.
Let multilateral systems  be with two representation groups
be with two representation groups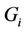 ,
,  , respectively. Both multilateral systems
, respectively. Both multilateral systems 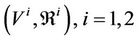 are called isomorphic if the two representation groups
are called isomorphic if the two representation groups ,
,  are isomorphic.
are isomorphic.
Theorems 2.1 and 2.2 and Definitions 2.1 and 2.2 are key concepts in multilateral system theory because they show the classification taking images as the basic method. In the following, introduce two basic models to illustrate the method.
Theorem 2.3 Suppose that 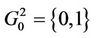 with multiplication table
with multiplication table

i.e., the multiplication of  is the addition of module 2. In other words,
is the addition of module 2. In other words,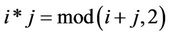 .
.
And assume that 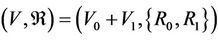 satisfying
satisfying

 .
.
Then 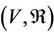 is a steady multilateral system with one equivalent relation
is a steady multilateral system with one equivalent relation  and one symmetrical relation
and one symmetrical relation  which is a simple system since there is not any noncompatibility relation. In other words, the relations
which is a simple system since there is not any noncompatibility relation. In other words, the relations ’s are the simple forms as follows:
’s are the simple forms as follows:
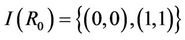 ,
, 
where (i, j) is corresponding to .
.
It will be proved that the steady multilateral system in Theorem 2.3 is the reasoning model of “Tao” (道) in TCMath if there are two energy functions  and
and  satisfying
satisfying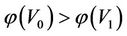 , called Dao model, denoted by
, called Dao model, denoted by .
.
Theorem 2.4. For each element x in a steady multilateral system V with two non-compatibility relations, there exist five equivalence classes below:

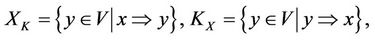

which the five equivalence classes have relations in Figure 2.
It can be proved that the steady multilateral system in Theorem 2.4 is the reasoning model of “Yin Yang Wu Xing” in TCMath if there are five energy functions (Defined in Section 3) 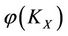
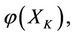
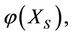
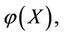 and
and 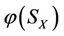 satisfying
satisfying  called Wu-Xing model, denoted by
called Wu-Xing model, denoted by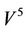 .
.
By Definition 2.2, the Wu-Xing model 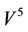 can be written as follows:
can be written as follows:
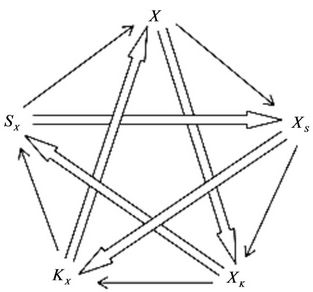
Figure 2. The method of finding Wu-Xing.
Define ,
, 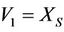 ,
, 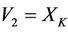 ,
,  ,
,  , corresponding to wood, fire, soil, metal, water, and assume
, corresponding to wood, fire, soil, metal, water, and assume  and
and  satisfying
satisfying
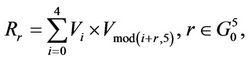
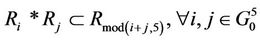
i.e., the relation multiplication of 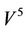 is isomorphic to the addition of module 5. Then
is isomorphic to the addition of module 5. Then  is a steady multilateral system with one equivalent relation
is a steady multilateral system with one equivalent relation 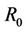 and two non-compatibility relations
and two non-compatibility relations  and
and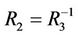 .
.
These Theorems can been found in [1-6,11-16]. Figure in Theorem 2.4 is the Figure of “Yin Yang Wu Xing” Theory in Ancient China. The steady multilateral system V with two non-compatibility relations is equivalent to the logic architecture of reasoning model of “Yin Yang Wu Xing” Theory in Ancient China. What describes the general method of complex systems can be used in mathematical complex system.
3. Relationship Analysis of Steady Multilateral Systems
3.1. Energy of a Multilateral System
Energy concept is an important concept in Physics. Now, we introduce this concept to the multilateral systems (or image mathematics) and use these concepts to deal with the multilateral system diseases (mathematical index too bad or too good ).In mathematics, a multilateral system is said to have Energy (or Dynamic) if there is a none negative function 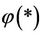 which makes every subsystem meaningful of the multilateral system.
which makes every subsystem meaningful of the multilateral system.
For two subsystems Vi and Vj of multilateral system V, denote  (or
(or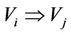 , or
, or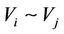 , or
, or ) means
) means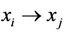 ,
, 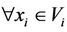 ,
, 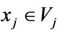 (or
(or ,
, 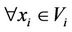 ,
, 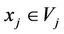 , or
, or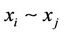 ,
, 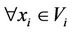 ,
,  , or
, or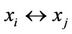 ,
,  ,
,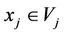 ).
).
For subsystems Vi and Vj where ,
, . Let
. Let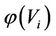 ,
, 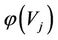 and
and 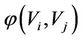 be the energy function of Vi, the energy function of Vj and the total energy of both Vi and Vj, respectively.
be the energy function of Vi, the energy function of Vj and the total energy of both Vi and Vj, respectively.
For an equivalence relation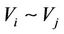 , if
, if 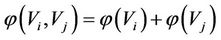 (the normal state of the energy of
(the normal state of the energy of ), then the neighboring relation
), then the neighboring relation  is called that Vi likes Vj which means that Vi is similar to Vj. In this case, the Vi is also called the brother of Vj while the Vj is also called the brother of Vi. In the causal model, the Vi is called the similar family member of Vj while the Vj is also called the similar family member of Vi. There are not any causal relation considered between Vi and Vj.
is called that Vi likes Vj which means that Vi is similar to Vj. In this case, the Vi is also called the brother of Vj while the Vj is also called the brother of Vi. In the causal model, the Vi is called the similar family member of Vj while the Vj is also called the similar family member of Vi. There are not any causal relation considered between Vi and Vj.
For a symmetrical relation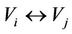 , if
, if 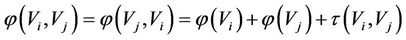
(the normal state of the energy of ) where the
) where the  is an interaction of
is an interaction of 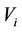 and
and 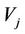 satisfying
satisfying  , then the symmetrical relation
, then the symmetrical relation 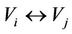 is called that Vi is corresponding to Vj which means that Vi is positively (or non-negatively) corresponding to Vj if
is called that Vi is corresponding to Vj which means that Vi is positively (or non-negatively) corresponding to Vj if  (or
(or ) and that Vi is negatively corresponding to Vj if
) and that Vi is negatively corresponding to Vj if . In this case, the Vi is also called the counterpart of Vj while the Vj is also called the counterpart of Vi. In the causal model, the Vi is called the reciprocal causation of Vj while the Vj is also called the reciprocal causation of Vi. There is a reciprocal causation relation considered between Vi and Vj.
. In this case, the Vi is also called the counterpart of Vj while the Vj is also called the counterpart of Vi. In the causal model, the Vi is called the reciprocal causation of Vj while the Vj is also called the reciprocal causation of Vi. There is a reciprocal causation relation considered between Vi and Vj.
For an neighboring relation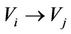 , if
, if 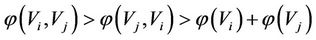
(the normal state of the energy of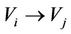 ), then the neighboring relation
), then the neighboring relation  is called that Vi bears (or loves) Vj [or that Vj is born by (or is loved by) Vj] which means that Vi is beneficial on Vj each other. In this case, the Vi is called the mother of Vj while the Vj is called the son of Vi. In the causal model, the Vi is called the beneficial cause of Vj while the Vj is called the beneficial effect of Vi.
is called that Vi bears (or loves) Vj [or that Vj is born by (or is loved by) Vj] which means that Vi is beneficial on Vj each other. In this case, the Vi is called the mother of Vj while the Vj is called the son of Vi. In the causal model, the Vi is called the beneficial cause of Vj while the Vj is called the beneficial effect of Vi.
For an alternate relation , if
, if 
(the normal state of the energy of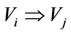 ), then the alternate relation
), then the alternate relation 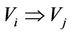 is called as that Vi kills (or hates) Vj [or that Vj is killed by (or is hated by) Vi] which means that Vi is harmful on Vj each other. In this case, the Vi is called the bane of Vj while the Vj is called the prisoner of Vi. In the causal model, the Vi is called the harmful cause of Vj while the Vj is called the harmful effect of Vi.
is called as that Vi kills (or hates) Vj [or that Vj is killed by (or is hated by) Vi] which means that Vi is harmful on Vj each other. In this case, the Vi is called the bane of Vj while the Vj is called the prisoner of Vi. In the causal model, the Vi is called the harmful cause of Vj while the Vj is called the harmful effect of Vi.
In the future, if not otherwise stated, any equivalence relation is the liking relation, any symmetrical relation is the reciprocal causation relation, any neighboring relation is the born relation (or the loving relation), and any alternate relation is the killing relation.
Suppose V is a steady multilateral system having energy, then V in the multilateral system during normal operation, its energy function for any subsystem of the multilateral system has an average (or expected value in Statistics), this state is called normal when the energy function is nearly to the average. Normal state is the better state.
That a subsystem of a multilateral system is not running properly (or, abnormal), is that the energy deviation from the average of the subsystems is too large (or too big), the high (mathematical real disease or economic overheating or real disease) or the low (mathematical virtual disease or economic downturn or virtual disease). Both mathematical real disease and mathematical virtual disease are all diseases of mathematical complex systems.
In a subsystem of a multilateral system being not running properly, if this sub-system through the energy of external forces increase or decrease, making them return to the average (or expected value), this method is called intervention (or making a mathematical treatment) to the multilateral system.
The purpose of intervention is to make the multilateral system return to normal state. The method of intervention is to increase or decrease the energy of a subsystem.
What kind of intervening should follow the principle to treat it? For example, Western economics emphasizes direct intervening, but the indirect intervening of oriental economics is required. In mathematics, which is more reasonable?
Based on this idea, many issues are worth further discussion. For example, if an economic intervening has been done to an economic society, what situation will happen?
3.2. Intervention Rule of a Multilateral System
For a steady multilateral system V with two non-compatibility relations, suppose that there is an external force (or an intervening force) on the subsystem X of V which makes it the energy 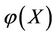 change increment
change increment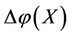 , then the energies
, then the energies 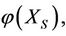

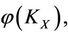
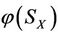 of other subsystems XS, XK, KX, SX (defined in Theorem 2.4) of V will be changed by the increments
of other subsystems XS, XK, KX, SX (defined in Theorem 2.4) of V will be changed by the increments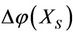 ,
, 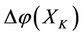 ,
,  and
and , respectively.
, respectively.
It is said that the multilateral system has the capability of intervention reaction if the multilateral system has capability to response the intervention force.
If a subsystem X of multilateral system is intervened, then the energies of the subsystems XS and SX which have neighboring relations to X will change in the same direction of the force outside on X. We call them beneficiaries. But the energies of the subsystems XK and KX which have alternate relations to X will change in the opposite direction of the force outside on X. We call them victims.
In general, there is an essential principle of intervenetion: any beneficial subsystem of X changes in the same direction of X, and any harmful subsystem of X changes in the opposite direction of X. The size of the energy changed is equal, but the direction opposite.
Intervention Rule: In the case of virtual disease or economic downturn, the intervening method of intervention is to increase the energy. If the intervening has been done on X, the energy increment (or, increase degree)  of the son XS of X is greater than the energy increment
of the son XS of X is greater than the energy increment 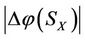 of the mother SX of X, i.e., the best beneficiary is the son XS of X. But the energy decrease degree
of the mother SX of X, i.e., the best beneficiary is the son XS of X. But the energy decrease degree  of the prisoner XK of X is greater than the energy decrease degree
of the prisoner XK of X is greater than the energy decrease degree 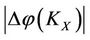 of the bane of X, i.e., the worst victim is the prisoner XK of X.
of the bane of X, i.e., the worst victim is the prisoner XK of X.
In the case of real disease or economic overheating, the intervening method of intervention is to decrease the energy. If the intervening has been done on X, the energy decrease degree  of the mother SX of X is greater than the energy decrease degree
of the mother SX of X is greater than the energy decrease degree 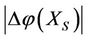 of the son of X, i.e., the best beneficiary is the mother SX of X. But the energy increment
of the son of X, i.e., the best beneficiary is the mother SX of X. But the energy increment 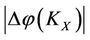 of the bane KX of X is greater than the energy increment
of the bane KX of X is greater than the energy increment 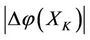 of the prisoner XK of X, i.e., the worst victim is the bane KX of X.
of the prisoner XK of X, i.e., the worst victim is the bane KX of X.
In mathematics, the changing laws are as follows.
1) If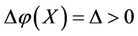 , then
, then ,
, 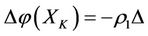 ,
, 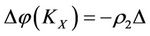 ,
,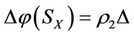 ;
;
2) If , then
, then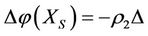 ,
,  ,
,  ,
,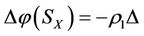 ;
;
where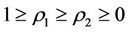 . Both
. Both  and
and  are called intervention reaction coefficients, which are used to represent the capability of intervention reaction. The larger
are called intervention reaction coefficients, which are used to represent the capability of intervention reaction. The larger 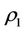 and
and , the better the capability of intervention reaction. The state
, the better the capability of intervention reaction. The state  is the best state but the state
is the best state but the state 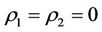 is the worst state.
is the worst state.
This intervention rule is similar to force and reaction in Physics. In other words, if a subsystem of multilateral system V has been intervened, then the energy of subsystem which has neighboring relation changes in the same direction of the force, and the energy of subsystem which has alternate relation changes in the opposite direction of the force. The size of the energy changed is equal, but the direction opposite.
In general,  and
and 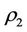 are decreasing functions of the intervention force Δ since the intervention force
are decreasing functions of the intervention force Δ since the intervention force  is easily to transfer all if Δ is small but the intervention force is not easily to transfer all if Δ is large. The energy function of complex system, the stronger the more you use. In order to magnify
is easily to transfer all if Δ is small but the intervention force is not easily to transfer all if Δ is large. The energy function of complex system, the stronger the more you use. In order to magnify 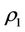 and
and , should set up a mathematical complex system of the intervention reaction system, and often use it.
, should set up a mathematical complex system of the intervention reaction system, and often use it.
Mathematical intervening resistance problem is that such a question, beginning more appropriate mathematiccal intervening method, but is no longer valid after a period. It is because the capability of intervention reaction is bad, i.e., the intervention reaction coefficients 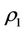 and
and  is too small. In the state
is too small. In the state , any mathematical intervening resistance problem is non-existence but in the state
, any mathematical intervening resistance problem is non-existence but in the state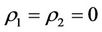 , mathematical intervening resistance problem is always existence. At this point, the paper advocates the essential principle of intervening to avoid mathematical intervening resistance problems.
, mathematical intervening resistance problem is always existence. At this point, the paper advocates the essential principle of intervening to avoid mathematical intervening resistance problems.
3.3. Self-Protection Rule of a Multilateral System
If there is an intervening force on the subsystem X of a steady multilateral system V which makes the energy  changed by increment
changed by increment  such that the energies
such that the energies 
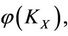
 of other subsystems XS, XK, KX, SX (defined in Theorem 2.4) of V will be changed by the increments
of other subsystems XS, XK, KX, SX (defined in Theorem 2.4) of V will be changed by the increments ,
, 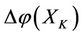 ,
, 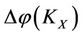 ,
, 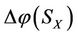 , respectively, then can the multilateral system V has capability to protect the worst victim to restore?
, respectively, then can the multilateral system V has capability to protect the worst victim to restore?
It is said that the steady multilateral system has the capability of self-protection if the multilateral system has capability to protect the worst victim to restore. The capability of self-protection of the steady multilateral system is said to be better if the multilateral system has capability to protect all victims to restore.
In general, there is an essential principle of self-protection: any harmful subsystem of X should be protected by using the same intervention force but any beneficial subsystem of X should not.
Self-protection Rule: In the case of virtual disease or economic downturn, the intervening method of intervention is to increase the energy. If the intervening has been done on X by the increment , the worst victim is the prisoner XK of X which has the increment
, the worst victim is the prisoner XK of X which has the increment . Thus the intervening principle of self-protection is to restore the prisoner XK of X and the restoring method of self-protection is to increase the energy
. Thus the intervening principle of self-protection is to restore the prisoner XK of X and the restoring method of self-protection is to increase the energy  of the prisoner XK of X by using the intervention force on X according to the intervention rule. In general, the increase degree is
of the prisoner XK of X by using the intervention force on X according to the intervention rule. In general, the increase degree is 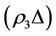 where
where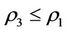 .
.
In the case of real disease or economic overheating, the intervening method of intervention is to decrease the energy. If the intervening has been done on X by the increment , the worst victim is the bane KX of X which has the increment
, the worst victim is the bane KX of X which has the increment . Thus the intervening principle of self-protection is to restore the bane KX of X and the restoring method of self-protection is to decrease the energy
. Thus the intervening principle of self-protection is to restore the bane KX of X and the restoring method of self-protection is to decrease the energy 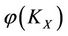 of the bane KX of X by using the same intervention force on X according to the intervention rule. In general, the decrease degree is
of the bane KX of X by using the same intervention force on X according to the intervention rule. In general, the decrease degree is  where
where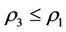 .
.
In mathematics, the following self-protection laws hold.
1) If , then the energy of subsystem XK will decrease the increment
, then the energy of subsystem XK will decrease the increment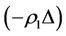 , which is the worst victim. So the capability of self-protection increases the energy of subsystem XK by increment
, which is the worst victim. So the capability of self-protection increases the energy of subsystem XK by increment 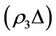 where
where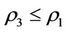 , in order to restore the worst victim by according to the intervention rule.
, in order to restore the worst victim by according to the intervention rule.
2) If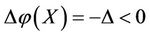 , then the energy of subsystem KX will increase the increment
, then the energy of subsystem KX will increase the increment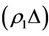 , which is the worst victim. So the capability of self-protection decreases the energy of subsystem KX by increment
, which is the worst victim. So the capability of self-protection decreases the energy of subsystem KX by increment  where
where , in order to restore the worst victim by according to the intervention rule.
, in order to restore the worst victim by according to the intervention rule.
In general, 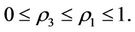 The
The 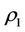 is the intervenetion reaction coefficient. The
is the intervenetion reaction coefficient. The  is called an self-protection coefficient, which is used to represent the capability of self-protection. The larger
is called an self-protection coefficient, which is used to represent the capability of self-protection. The larger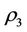 , the better the capability of self-protection. The state
, the better the capability of self-protection. The state  is the best state but the state
is the best state but the state 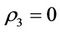 is the worst state of self-protection. According to the general economy of the protection principle,
is the worst state of self-protection. According to the general economy of the protection principle, 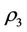 should be not greater than
should be not greater than  since the purpose of protection is to restore the victims and not reward the victims.
since the purpose of protection is to restore the victims and not reward the victims.
The self-protection rule can be explained as: the general principle of self-protection subsystem is that the most affected is protected firstly, the protection method and intervention force are in the same way.
In general, 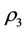 is also a decreasing function of the intervention force Δ since the worst victim is easily to restore all if Δ is small but the worst victim is not easily to restore all if Δ is large. The energy function of complex system, the stronger the more you use. In order to magnify
is also a decreasing function of the intervention force Δ since the worst victim is easily to restore all if Δ is small but the worst victim is not easily to restore all if Δ is large. The energy function of complex system, the stronger the more you use. In order to magnify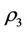 , should set up an economic society of the selfprotection system, and often use it.
, should set up an economic society of the selfprotection system, and often use it.
Theorem 3.1. Suppose that a steady multilateral system V which has energy function  and capabilities of intervention reaction and self-protection is with intervention reaction coefficients
and capabilities of intervention reaction and self-protection is with intervention reaction coefficients  and
and , and with self-protection coefficient
, and with self-protection coefficient . If the capability of self-protection wants to restore both subsystems XK and KX, then the following statements are true.
. If the capability of self-protection wants to restore both subsystems XK and KX, then the following statements are true.
1) In the case of virtual disease, the treatment method is to increase the energy. If an intervention force on the subsystem X of steady multilateral system V is implemented such that its energy  has been changed by increment
has been changed by increment , then all five subsystems will be changed finally by the increments as follows:
, then all five subsystems will be changed finally by the increments as follows:
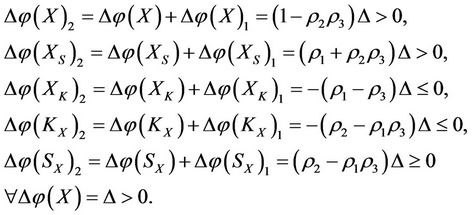 (1)
(1)
2) In the case of real disease, the treatment method is to increase the energy. If an intervention force on the subsystem X of steady multilateral system V is implemented such that its energy  has been changed by increment
has been changed by increment , then all five subsystems will be changed by the increments as follows:
, then all five subsystems will be changed by the increments as follows:
 (2)
(2)
where the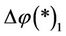 ’s and
’s and ’s are the increments under the capability of self-protection.
’s are the increments under the capability of self-protection.
Corollary 3.1. Suppose that a steady multilateral system V which has energy function  and capabilities of intervention reaction and self-protection is with intervention reaction coefficients
and capabilities of intervention reaction and self-protection is with intervention reaction coefficients 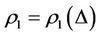 and
and , and with self-protection coefficient
, and with self-protection coefficient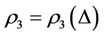 . Then the capability of self-protection can make both subsystems XK and KX to be restored at the same time, i.e., the capability of self-protection is better, if and only if
. Then the capability of self-protection can make both subsystems XK and KX to be restored at the same time, i.e., the capability of self-protection is better, if and only if 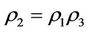 and
and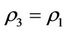 .
.
Side effects of mathematical intervening problems were the question: in the mathematical intervening process, destroyed the normal balance of non-fall ill subsystem or non-intervention subsystem. By Theorem 3.1 and Corollary 3.1, it can be seen that if the capability of self-protection of the steady multilateral system is better, i.e., the multilateral system has capability to protect all the victims to restore, then a necessary and sufficient condition is  and
and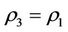 . General for a complex system of mathematical complex system, the condition
. General for a complex system of mathematical complex system, the condition 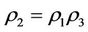 is easy to meet since it can restore two subsystems by Theorem 3.1, the condition
is easy to meet since it can restore two subsystems by Theorem 3.1, the condition  is difficult to meet it only can restore one subsystem by Theorem 3.1. At this point, the paper advocates the principle to avoid any side effects of intervening.
is difficult to meet it only can restore one subsystem by Theorem 3.1. At this point, the paper advocates the principle to avoid any side effects of intervening.
3.4. Mathematical Reasoning of Intervening Principle by Using the Neighboring Relations of Steady Multilateral Systems
Intervening principle by using the neighboring relations of steady multilateral systems is “Virtual disease or mathematical virtual disease is to fill his mother but mathematical real disease is to rush down his son”. In order to show the rationality of the intervening principle, it is needed to prove the following theorems.
Theorem 3.2. Suppose that a steady multilateral system V which has energy function and capabilities of intervention reaction and self-protection is with intervention reaction coefficients 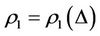 and
and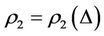 , and with self-protection coefficient
, and with self-protection coefficient 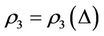 satisfying
satisfying 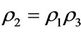 and
and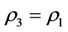 . Then the following statements are true.
. Then the following statements are true.
In the case of virtual disease, if an intervention force on the subsystem X of steady multilateral system V is implemented such that its energy 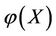 increases the increment
increases the increment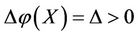 , then the subsystems SX, XK and KX can be restored at the same time, but the subsystems X and XS will increase their energies by the increments
, then the subsystems SX, XK and KX can be restored at the same time, but the subsystems X and XS will increase their energies by the increments
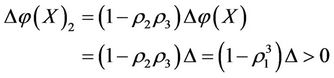
and

respectively.
On the other hand, in the case of real disease, if an intervention force on the subsystem X of steady multilateral system V is implemented such that its energy 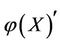 decreases, i.e., by the increment
decreases, i.e., by the increment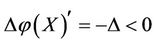 , the subsystems XS, XK and KX can also be restored at the same time, and the subsystems X and XS will decrease their energies, i.e., by the increments
, the subsystems XS, XK and KX can also be restored at the same time, and the subsystems X and XS will decrease their energies, i.e., by the increments

and

respectively.
Theorem 3.3. For a steady multilateral system V which has energy function  and capabilities of interveneing reaction and self-protection, assume intervention reaction coefficients are
and capabilities of interveneing reaction and self-protection, assume intervention reaction coefficients are 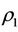 and
and , and let the selfprotection coefficientbe
, and let the selfprotection coefficientbe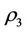 , which satisfy
, which satisfy ,
, 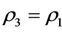 and
and 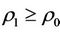 where
where 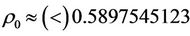 (the following the same) is the solution of
(the following the same) is the solution of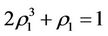 . Then the following statements are true.
. Then the following statements are true.
1) If an intervention force on the subsystem X of steady multilateral system V is implemented such that its energy 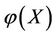 has been changed by increment
has been changed by increment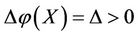 , then the final increment
, then the final increment  of the energy
of the energy 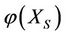 of the subsystem XS changed is greater than or equal to the final increment
of the subsystem XS changed is greater than or equal to the final increment  of the energy
of the energy  of the subsystem X changed based on the capability of self-protection.
of the subsystem X changed based on the capability of self-protection.
2) If an intervention force on the subsystem X of steady multilateral system V is implemented such that its energy  has been changed by increment
has been changed by increment , then the final increment
, then the final increment  of the energy
of the energy 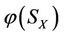 of the subsystem SX changed is less than or equal to the final increment
of the subsystem SX changed is less than or equal to the final increment 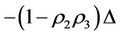 of the energy
of the energy 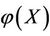 of the subsystem X changed based on the capability of self-protection.
of the subsystem X changed based on the capability of self-protection.
Corollary 3.2. For a steady multilateral system V which has energy function  and capabilities of intervening reaction and self-protection, assume intervention reaction coefficients are
and capabilities of intervening reaction and self-protection, assume intervention reaction coefficients are 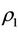 and
and , and let the self-protection coefficient be
, and let the self-protection coefficient be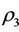 , which satisfy
, which satisfy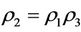 ,
,  and
and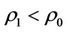 . Then the following statements are true.
. Then the following statements are true.
1) In the case of virtual disease, if an intervention force on the subsystem X of steady multilateral system V is implemented such that its energy  has been changed by increment
has been changed by increment , then the final increment
, then the final increment 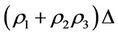 of the energy
of the energy  of the subsystem XS changed is less than the final increment
of the subsystem XS changed is less than the final increment  of the energy
of the energy  of the subsystem X changed based on the capability of self-protection.
of the subsystem X changed based on the capability of self-protection.
2) In the case of real disease, if an intervention force on the subsystem X of steady multilateral system V is implemented such that its energy  has been changed by increment
has been changed by increment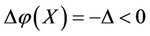 , then the final increment
, then the final increment 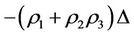 of the energy
of the energy 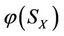 of the subsystem SX changed is greater than the final increment
of the subsystem SX changed is greater than the final increment 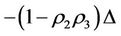 of the energy
of the energy  of the subsystem X changed based on the capability of self-protection. #
of the subsystem X changed based on the capability of self-protection. #
By Theorems 3.2 and 3.3 and Corollary 3.2, the intervention method of “Virtual disease or economic downturn is to fill his mother but real disease or economic overheating is to rush down his son” should be often used in case: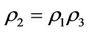 ,
,  and
and  since in this time,
since in this time,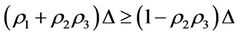 .
.
3.5. Mathematical Reasoning of Intervening Principle by Using the Alternate Relations of Steady Multilateral Systems
Intervening principle by using the alternate relations of steady multilateral systems is “Strong inhibition of the same time, support the weak”. In order to show the rationality of the intervening Principle, it is needed to prove the following theorems.
Theorem 3.4. Suppose that a steady multilateral system V which has energy function 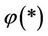 and capabilities of intervention reaction and self-protection is with intervention reaction coefficients
and capabilities of intervention reaction and self-protection is with intervention reaction coefficients 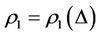 and
and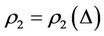 , and with self-protection coefficient
, and with self-protection coefficient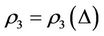 . Then the following statements are true.
. Then the following statements are true.
Assume there are two subsystems X and XK of V with an alternate relation such that X encounters virtual disease, and at the same time, XK befalls real disease. If an intervention force on the subsystem X of steady multilateral system V is implemented such that its energy  has been changed by increment
has been changed by increment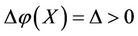 , and at the same time, another intervention force on the subsystem XK of steady multilateral system V is also implemented such that its energy
, and at the same time, another intervention force on the subsystem XK of steady multilateral system V is also implemented such that its energy 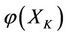 has been changed by increment
has been changed by increment , then all other subsystems: SX, KX and XS can be restored at the same time, and the subsystems X and XK will increase and decrease their energies by the same size but the direction opposite, i.e., by the increments
, then all other subsystems: SX, KX and XS can be restored at the same time, and the subsystems X and XK will increase and decrease their energies by the same size but the direction opposite, i.e., by the increments
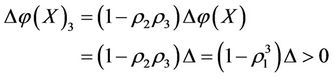
and
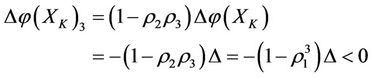
respectively.
Assume there are two subsystems X and KX of V with an alternate relation such that X encounters real disease, and at the same time, KX befalls virtual disease. If an intervention force on the subsystem X of steady multilateral system V is implemented such that its energy 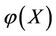 has been changed by increment
has been changed by increment , and at the same time, another intervention force on the subsystem KX of steady multilateral system V is also implemented such that its energy
, and at the same time, another intervention force on the subsystem KX of steady multilateral system V is also implemented such that its energy 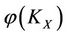 has been changed by increment
has been changed by increment , then all other subsystems: SX, XK and XS can be restored at the same time, and the subsystems X and KX will decrease and increase their energies by the same size but the direction opposite, i.e., by the increments
, then all other subsystems: SX, XK and XS can be restored at the same time, and the subsystems X and KX will decrease and increase their energies by the same size but the direction opposite, i.e., by the increments

and
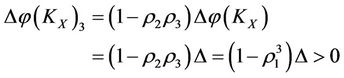
respectively.
By Theorems 3.3 and 3.4 and Corollary 3.2, the method of “Strong inhibition of the same time, support the weak” should be used in case: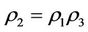 ,
, 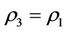 and
and  since
since .
.
4. Rationality of Intervening Principle of Traditional Chinese Mathematics and “Yin Yang Wu Xing” Theory
4.1. Chinese Traditional Mathematics and “Yin Yang Wu Xing” Theory
Ancient Chinese “Yin Yang Wu Xing” [38] Theory has been surviving for several thousands of years without dying out, proving it reasonable to some extent. If we regard ~ as the same category, the neighboring relation ® as beneficial, harmony, obedient, loving, etc. and the alternate relation  as harmful, conflict, ruinous, killing, etc., then the above defined stable logic analysis model is similar to the logic architecture of reasoning of “Yin Yang Wu Xing”. Both “Yin” and “Yang” mean that there are two opposite relations in the world: harmony or loving ® and conflict or killing
as harmful, conflict, ruinous, killing, etc., then the above defined stable logic analysis model is similar to the logic architecture of reasoning of “Yin Yang Wu Xing”. Both “Yin” and “Yang” mean that there are two opposite relations in the world: harmony or loving ® and conflict or killing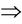 , as well as a general equivalent category ~. There is only one of three relations ~, ® and
, as well as a general equivalent category ~. There is only one of three relations ~, ® and 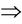 between every two objects. Everything X makes something (
between every two objects. Everything X makes something (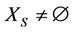 ), and is made by something (
), and is made by something (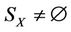 ); Everything restrains something (
); Everything restrains something ( ), and is restrained by something (
), and is restrained by something (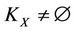 ); i.e., one thing overcomes another thing and one thing is overcome by another thing. The ever changing world V, following the relations: ~, ® and
); i.e., one thing overcomes another thing and one thing is overcome by another thing. The ever changing world V, following the relations: ~, ® and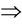 , must be divided into five categories by the equivalent relation ~, being called “Wu Xing”: wood (X), fire (XS), soil (XK), metal (KX), water (SX). The “Wu Xing” is to be “neighbor is friend”: wood (X) ® fire (XS) ® soil (XK) ® metal (KX) ® water (SX) ® wood (X), and “alternate is foe”: wood (X)
, must be divided into five categories by the equivalent relation ~, being called “Wu Xing”: wood (X), fire (XS), soil (XK), metal (KX), water (SX). The “Wu Xing” is to be “neighbor is friend”: wood (X) ® fire (XS) ® soil (XK) ® metal (KX) ® water (SX) ® wood (X), and “alternate is foe”: wood (X)  soil (XK)
soil (XK)  water (SX)
water (SX)  fire (XS)
fire (XS) 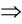 metal (KX)
metal (KX)  wood (X). In other words, the ever changing world must be divided into five categories:
wood (X). In other words, the ever changing world must be divided into five categories:
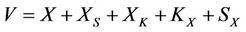
satisfying
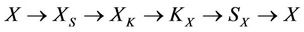
and
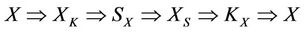
where elements in the same category are equivalent to one another. We can see, from this, the ancient Chinese “Yin Yang Wu Xing” theory is a reasonable logic analysis model to identify the stability and relationship of complex mathematical systems.
Image mathematics firstly uses the verifying relationship method of “Yin Yang Wu Xing” Theory to explain the relationship between mathematical complex system and environment. Secondly, based on “Yin Yang Wu Xing” Theory, the relations of development processes of mathematical complex system can be shown by the neighboring relation and alternate relation of five subsets. Then a normal mathematical complex system can be shown as a steady multilateral system in which there are the loving relation and the killing relation and the liking relation. The loving relation in image mathematics can be explained as the neighboring relation, called “Sheng (生)”. The killing relation in image mathematics can be explained as the alternate relation, called “Ke (克)”. The liking relation can be explained as the equivalent relation, called “Tong-Lei (同类)”. Constraints and conversion between five subsets are equivalent to the two kinds of triangle reasoning. So a normal mathematical complex system can be classified into five equivalence classes corresponding five mathematical indexes, respectively.
For example, in image mathematics, a mathematical complex system is similar to a human body. A mathematical index system of normal complex system following the “Yin Yang Wu Xing” Theory was classified into five equivalence classes as follows [29]:
Consider a complex system, its input  and output y can be written as
and output y can be written as
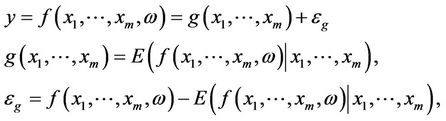 (2)
(2)
where not only all output functions
 ,
,  and
and 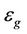 are not known, but also the input variables
are not known, but also the input variables  are not known. The problem is called model-free.
are not known. The problem is called model-free.
The inputs 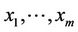 are called controllable if they are observed and controlled by human. So
are called controllable if they are observed and controlled by human. So
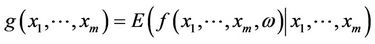
can be observed if the controllable inputs  can be choose.
can be choose.
The input 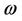 is called uncontrolled if it is not observed or controlled by human. So the freedom model error
is called uncontrolled if it is not observed or controlled by human. So the freedom model error

can not be assumed. But we can show the following properties:


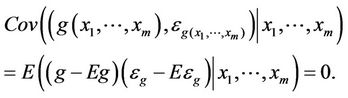
The condition is not hypothesis since they can be obtained if f makes the calculation meaningful, such as, if f is continuous.
In general, we can consider the inputs  as independent random variables with continuous distributions
as independent random variables with continuous distributions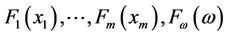 , respectively, since the inputs
, respectively, since the inputs  are controllable which can be selected independently by human under some similar conditions. If not independent, by factor analysis can select orthogonal factor. This operation of experiment under some similar conditions is equivalent to the uncontrolled input
are controllable which can be selected independently by human under some similar conditions. If not independent, by factor analysis can select orthogonal factor. This operation of experiment under some similar conditions is equivalent to the uncontrolled input  is independent of the controllable input
is independent of the controllable input  since
since  This operation of experiment that the inputs
This operation of experiment that the inputs  can be selected independently by human is equivalent to that the inputs
can be selected independently by human is equivalent to that the inputs  are independent random variables one another. For example, take
are independent random variables one another. For example, take 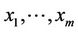 based on an orthogonal array since the orthogonality is equivalent to independence for discrete random variables and continuous random variables can be in a discrete random variable approximation [8].
based on an orthogonal array since the orthogonality is equivalent to independence for discrete random variables and continuous random variables can be in a discrete random variable approximation [8].
In this case, it is well known that the inputs

are independent random variables with the same continuous distribution  Assume
Assume

where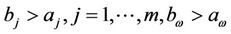 . Then the inputs
. Then the inputs  are independent random variables with continuous distributions
are independent random variables with continuous distributions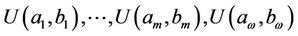 . In this case, the function
. In this case, the function

can replace f as a new system function since each of both h and f are all not known. Therefore, without loss of generality, we always consider 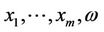 as independent random variables with continuous distributions
as independent random variables with continuous distributions
 .
.
On the other hand, the function f is considered as continuous, in order to ensure that condition expectations and partial derivative of existence and make the conventional mathematics method has significance.
To the complex system f, we need to decide an energy goal t, make y more close to target, the greater the function of the system. In general, the Target t is the maximum energy of y.
Image mathematics in TCMath considers the complex system stability problem, because the core problem of any complex system is stability. The stability can only through the fixed program to observe to do a test or experiment since the function f is not known. In general, the human wants to find a testing or experimental center  and testing or experimental tolerance
and testing or experimental tolerance 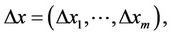
 for the observed function
for the observed function

under some similar conditions, such that 1) 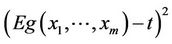

2) 
where the controllable inputs  are independent random variables and
are independent random variables and

In order to solve the stability problem, we get easily the following theorem [29]:
Theorem 4.1. Suppose that f is continuous and
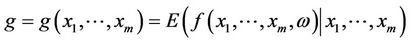 .
.
Then

where  #
#
1) In image mathematics, the index
 is called Distortion Degree. It belongs to the wood (X) subsystem of the complex system f since it cognizes the structure function g of the complex system f which is the beginning or birth stage of all things, just like in the Spring of a year. In mathematics,
is called Distortion Degree. It belongs to the wood (X) subsystem of the complex system f since it cognizes the structure function g of the complex system f which is the beginning or birth stage of all things, just like in the Spring of a year. In mathematics,
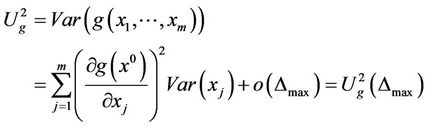
where  It is thought as the wood (X) image of generally complex system f since it is an objective constant independent of human observations, expressing birth, although the maximum and controllable experimental tolerance
It is thought as the wood (X) image of generally complex system f since it is an objective constant independent of human observations, expressing birth, although the maximum and controllable experimental tolerance 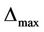 can be choose by human.
can be choose by human.
The index  can be taken as the energy function of the subsystem wood (X) since the smaller the distortion degree
can be taken as the energy function of the subsystem wood (X) since the smaller the distortion degree , the better the stability of the complex system f.
, the better the stability of the complex system f.
Although the distortion degree 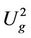 is unknown for freedom model speaking, it can be easily estimated by using orthogonal arrays
is unknown for freedom model speaking, it can be easily estimated by using orthogonal arrays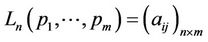 ,
,
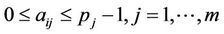 (see [29]). For example, take
(see [29]). For example, take

where
 then
then 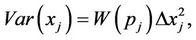 where
where
 .
.
And for the experiment data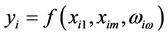 ,
,  , we have
, we have
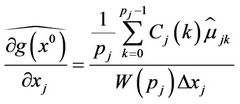 ,
,
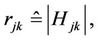

where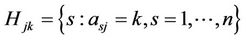 . Thus, we can obtained the estimation of the distortion degree
. Thus, we can obtained the estimation of the distortion degree 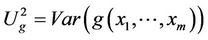 as
as
 .
.
The 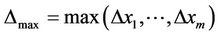 smaller, more exact estimate.
smaller, more exact estimate.
2) The index  is called Disturb Degree. It belongs to the fire (XS) subsystem of the complex system f since it controls the fluctuations of the complex system f which is the development and growth stage of all things, just like in the Summer of a year. In mathematics,
is called Disturb Degree. It belongs to the fire (XS) subsystem of the complex system f since it controls the fluctuations of the complex system f which is the development and growth stage of all things, just like in the Summer of a year. In mathematics,

where 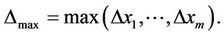 It is thought as the fire (XS) image of generally complex system f since it is also an objective constant independent of human observations, expressing growth, although the maximum and controllable experimental tolerance
It is thought as the fire (XS) image of generally complex system f since it is also an objective constant independent of human observations, expressing growth, although the maximum and controllable experimental tolerance 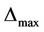 can be choose by human. The index
can be choose by human. The index 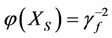 can be taken as the energy function of the subsystem fire (XS) since the smaller the disturb degree
can be taken as the energy function of the subsystem fire (XS) since the smaller the disturb degree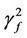 , the better the stability of the complex system f.
, the better the stability of the complex system f.
Although the disturb degree 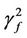 is unknown for freedom model speaking, it can be easily estimated by using experiment data
is unknown for freedom model speaking, it can be easily estimated by using experiment data  of orthogonal arrays (see [29]). For example, a good estimation of
of orthogonal arrays (see [29]). For example, a good estimation of 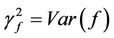 is the data standard variance
is the data standard variance
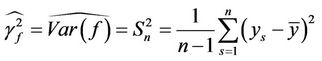 where
where .
.
3) The index  is called Information Decomposition Ratio (or Signal to Noise Ratio). It belongs to the soil (XK) subsystem of the complex system f since it makes the coordination of the center and fluctuation in the complex system f which is the continuous development and combined stage of all things, just like in the Long-Summer of a year. In mathematics,
is called Information Decomposition Ratio (or Signal to Noise Ratio). It belongs to the soil (XK) subsystem of the complex system f since it makes the coordination of the center and fluctuation in the complex system f which is the continuous development and combined stage of all things, just like in the Long-Summer of a year. In mathematics,
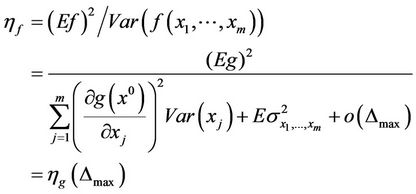
where 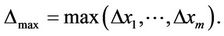 It is thought as the soil (XK) image of generally complex system f since it is an objective constant independent of human observations, expressing combined, although the maximum and controllable experimental tolerance
It is thought as the soil (XK) image of generally complex system f since it is an objective constant independent of human observations, expressing combined, although the maximum and controllable experimental tolerance 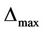 can be choose by human. The index
can be choose by human. The index  can be taken as the energy function of the subsystem soil (XK) since the bigger the information decomposition ratio
can be taken as the energy function of the subsystem soil (XK) since the bigger the information decomposition ratio , the better the stability of the complex system f.
, the better the stability of the complex system f.
Although the information decomposition ratio  is unknown for freedom model speaking, it can be easily estimated by using the experimental data
is unknown for freedom model speaking, it can be easily estimated by using the experimental data  of orthogonal arrays (see [29]). For example, a good estimation of
of orthogonal arrays (see [29]). For example, a good estimation of  is
is

Note: In data analysis situation, often taking  instead of
instead of . Limited to data observation point of view, they are in the statistical meaning equivalent, but the former is more advantageous to the statistical analysis.
. Limited to data observation point of view, they are in the statistical meaning equivalent, but the former is more advantageous to the statistical analysis.
4) The index 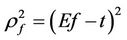 is called Deviation Degree. It belongs to the metal (KX) subsystem of the complex system f since it makes function characteristics (or data center and the expected goal deviation) in the complex system f which is the getting-results and accepted stage of all things, just like in the Autumn of a year. In mathematics,
is called Deviation Degree. It belongs to the metal (KX) subsystem of the complex system f since it makes function characteristics (or data center and the expected goal deviation) in the complex system f which is the getting-results and accepted stage of all things, just like in the Autumn of a year. In mathematics,
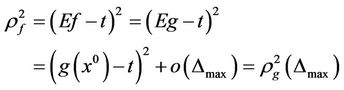
where 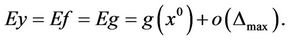 It is thought as the metal (KX) image of a generally complex system f since it is an objective constant independent of human observations expressing accepted, although the controllable inputs
It is thought as the metal (KX) image of a generally complex system f since it is an objective constant independent of human observations expressing accepted, although the controllable inputs 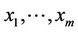 of the observed function
of the observed function

can be choose by human. The index 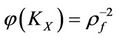 can be taken as the energy function of the subsystem metal (KX) since the smaller the deviation degree
can be taken as the energy function of the subsystem metal (KX) since the smaller the deviation degree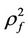 , the better the stability of the complex system f.
, the better the stability of the complex system f.
Although the deviation degree 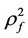 is unknown for freedom model speaking, it can be easily estimated by using the experimental data
is unknown for freedom model speaking, it can be easily estimated by using the experimental data  of orthogonal arrays (see [29]). For example, a good estimation of
of orthogonal arrays (see [29]). For example, a good estimation of 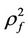 is
is
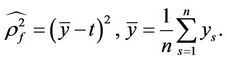
5) The index 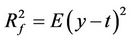 is called Risk Function (or Risk, or Loss Function). It belongs to the water (SX) subsystem of the complex system f since it makes the expected value of loss
is called Risk Function (or Risk, or Loss Function). It belongs to the water (SX) subsystem of the complex system f since it makes the expected value of loss 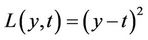 between each data y and the goal t in the complex system f which is the risk and hiding stage of all things, just like in the winter of a year. The best condition is
between each data y and the goal t in the complex system f which is the risk and hiding stage of all things, just like in the winter of a year. The best condition is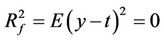 , but generally this is very hard to achieve, because right now all the data are equal to the target t and the system f is a simple system
, but generally this is very hard to achieve, because right now all the data are equal to the target t and the system f is a simple system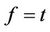 . In mathematics,
. In mathematics,

where 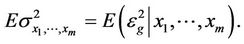 It is thought as the water (SX) image of generally complex system f since it is an objective constant independent of human observations, expressing hiding, although the observed function
It is thought as the water (SX) image of generally complex system f since it is an objective constant independent of human observations, expressing hiding, although the observed function

can be choose by human. The index 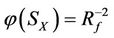 can be taken as the energy function of the subsystem water (SX) since the smaller the risk
can be taken as the energy function of the subsystem water (SX) since the smaller the risk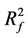 , the better the stability of the complex system f.
, the better the stability of the complex system f.
Although the risk 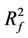 is unknown for freedom model speaking, it can be easily estimated by using the experimental data
is unknown for freedom model speaking, it can be easily estimated by using the experimental data 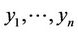 of orthogonal arrays (see [29]). For example, a good estimation of
of orthogonal arrays (see [29]). For example, a good estimation of  is
is
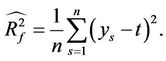
In image mathematics, each of the rows of orthogonal arrays is called one gua (卦) which is independent of the unknown system function f (model-free). The state space V of a multilateral system  based the unknown system function f is the set of mathematical indexes of the unknown system function f. By Theorem 2.4, the set V can be divided into five categories. Corresponding to every kind of five categories, each of mathematical indexes of the unknown system function f is called an image. Each of images must shows the complex system certain characteristics, such as, wood, fire, soil, metal, water.
based the unknown system function f is the set of mathematical indexes of the unknown system function f. By Theorem 2.4, the set V can be divided into five categories. Corresponding to every kind of five categories, each of mathematical indexes of the unknown system function f is called an image. Each of images must shows the complex system certain characteristics, such as, wood, fire, soil, metal, water.
For given each of the gua (卦) or each the rows of orthogonal arrays and for any unknown continuous system function f, it can be proved easily that each of true image mathematical indexes above can be obtained if the experiments or observations can be repeated (law of averages of great numbers). The way or calculation method of the image indexes is also independent of the unknown system function f (model-free).
In image mathematics, each of mathematical indexes represents an “Axiom system”, called a class. For each of classes, all theories and methods are in order to increase the energy of class or to make the corresponding mathematical index becomes to better. There are the loving and hating (or killing) relations among all images or mathematical indexes of classes. Generally speaking, close is love, alternate is hate.
In every category of internal, think that they are equivalent relationship, between each two of their elements there is a force of similar material accumulation of each other. It is because their pursuit of the goal is the same, i.e., follows the same “Axiom system”. It can increase the energy of the class if they accumulate together. All of nature material activity follows the principle of maximizing so energy. In general, the force of similar material accumulation of each other is smaller than the loving force or the killing force in a stable complex system. The stability of any complex system first needs to maintain the equilibrium of the killing force and the loving force. For a stable complex system, if the killing force is large, i.e.,  becomes larger, then the loving force is large and the force of similar material accumulation of each other is also large. They can make the complex system more stable. If the killing force is small, i.e.,
becomes larger, then the loving force is large and the force of similar material accumulation of each other is also large. They can make the complex system more stable. If the killing force is small, i.e.,  becomes smaller, then the loving force is small and the force of similar material accumulation of each other is also small. They can make the complex system becoming unstable.
becomes smaller, then the loving force is small and the force of similar material accumulation of each other is also small. They can make the complex system becoming unstable.
It has been shown in Theorems 2.1 - 2.4 that the classification of five subsets is quite possible based on the mathematical logic. As for the characteristics of the five subsets is rational or not, it is need more research work. It has been also shown in Theorems 3.1 - 3.4 that the logical basis of image mathematics is a steady multilateral system.
The vigor energy (or, Chi, Qi) of image mathematics means the energy function in a steady multilateral system.
There are two kinds of mathematical diseases in image mathematics: Mathematical real disease and mathematical virtual disease. They generally means the subsystem is abnormal, its energy is too high for mathematical real disease or too low for mathematical virtual disease.
The intervening method of image mathematics is to “xie Chi” which means to rush down the energy if a mathematical real disease is treated, or to “bu Chi” which means to fill the energy if a mathematical virtual disease is treated. Like intervening the subsystem, decrease when the energy is too high, increase when the energy is too low.
Both the capability of intervention reaction and the capability of self-protection of the multilateral system are equivalent to the Immunization of image mathematics. This capability is really existence for a mathematical complex system. Its target is to protect other mathematical subsystem while treating one mathematical subsystem. It is because if the capability is not existence, then . In this time, the energy of the system will be the sum of energy of each part. Thus the mathematical system will be a simple mathematical system which is not what we consider range.
. In this time, the energy of the system will be the sum of energy of each part. Thus the mathematical system will be a simple mathematical system which is not what we consider range.
4.2. Intervening Principle if Only One Subsystem of the Mathematical Complex System Falls Ill
If we always intervene the abnormal subsystem of the mathematical complex system directly, the intervention method always destroy the balance of the mathematical complex system because it is having strong side effects to the mother or the son of the subsystem which may be non-disease of mathematical subsystem or non-intervened subsystem by using Theorem 3.2. The intervening method also decrease the capability of intervention reaction because the method which don’t use the capability of intervention reaction makes the  and
and  near to 0. The state
near to 0. The state 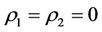 is the worst state of the mathematical complex system, namely mathematical intervenetion failure. On the way, the mathematical intervening resistance problem will be occurred since any mathematical intervening method is possible too little for some small
is the worst state of the mathematical complex system, namely mathematical intervenetion failure. On the way, the mathematical intervening resistance problem will be occurred since any mathematical intervening method is possible too little for some small 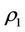 and
and .
.
But, by Corollary 3.2, it will even be better if we intervene subsystem X itself directly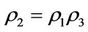 ,
,  and
and . In this case:
. In this case: . It can be explained that if a multilateral system which has a poor capability of intervention reaction, then it is better to intervene the subsystem itself directly than indirectly. But similar to above, the intervention method is always to destroy the balance of multilateral systems such that there is at least one of side effects occurred. And the intervention method also have harmful to the capability of intervention reaction making the mathematical interveneing resistance problem also occurred by Theorem 3.2. Therefore the intervention method directly can be used in case
. It can be explained that if a multilateral system which has a poor capability of intervention reaction, then it is better to intervene the subsystem itself directly than indirectly. But similar to above, the intervention method is always to destroy the balance of multilateral systems such that there is at least one of side effects occurred. And the intervention method also have harmful to the capability of intervention reaction making the mathematical interveneing resistance problem also occurred by Theorem 3.2. Therefore the intervention method directly can be used in case 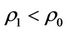 but should be used as little as possible.
but should be used as little as possible.
If we always intervene the abnormal subsystem of the mathematic complex system indirectly, the intervention method can be to maintain the balance of the mathematical complex system because it has not any side effects to all other subsystems which are not both the mathematical disease subsystem and the mathematical intervened subsystem by using Theorem 3.2. The intervening method also increase the capability of intervention reaction because the method of using the intervention reaction makes the 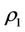 and
and  near to 1. The state
near to 1. The state  is the best state of the mathematical complex system. On the way, it is almost none mathematical intervening resistance problem since any mathematical intervening method is possible good for some large
is the best state of the mathematical complex system. On the way, it is almost none mathematical intervening resistance problem since any mathematical intervening method is possible good for some large 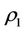 and
and .
.
For example, in China, many mathematical engineers generally only care about risk 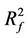 (or, income, water (SX)) and interfere
(or, income, water (SX)) and interfere 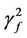 (or, disturb, fire (XS)) as two mathematical indexes which have the killing relations for a complicated engineering problem based on the freedom model (3). They frequently used method is: If only the risk
(or, disturb, fire (XS)) as two mathematical indexes which have the killing relations for a complicated engineering problem based on the freedom model (3). They frequently used method is: If only the risk 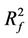 (i.e., water (SX) is not normal (or, the bigger, virtual disease), then they reduce deviation degree
(i.e., water (SX) is not normal (or, the bigger, virtual disease), then they reduce deviation degree  (i.e., increase the energy
(i.e., increase the energy 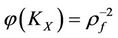 of metal (KX)) with linear optimization method since metal (KX) is the mother of water (SX); If only the interfere degree
of metal (KX)) with linear optimization method since metal (KX) is the mother of water (SX); If only the interfere degree 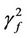 (i.e., fire (XS)) is not normal (or, the bigger, virtual disease), then they reduce distortion degree
(i.e., fire (XS)) is not normal (or, the bigger, virtual disease), then they reduce distortion degree 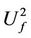 (i.e., increase the energy
(i.e., increase the energy 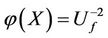 of wood (X)) of system function f with the method of adjusting stable center
of wood (X)) of system function f with the method of adjusting stable center 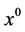 of the system function since wood (X) is the mother of fire (XS) (see [29]). The idea is precisely “Virtual disease is to fill his mother” if one subsystem of mathematical complex system falls virtual ill.
of the system function since wood (X) is the mother of fire (XS) (see [29]). The idea is precisely “Virtual disease is to fill his mother” if one subsystem of mathematical complex system falls virtual ill.
All in all, the mathematical complex system satisfies the intervention rule and the self-protection rule. It is said a healthy mathematical complex system when the intervention reaction coefficient  satisfies
satisfies . In logic and practice, it’s reasonable
. In logic and practice, it’s reasonable 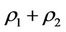 near to 1 if the input and output in a complex system is balanced, since a mathematical output subsystem is absolutely necessary social other subsystems of all consumption. In case:
near to 1 if the input and output in a complex system is balanced, since a mathematical output subsystem is absolutely necessary social other subsystems of all consumption. In case: , all the energy for intervening mathematical complex subsystem can transmit to other mathematical complex subsystems which have neighboring relations or alternate relations with the intervening mathematical complex subsystem. The condition
, all the energy for intervening mathematical complex subsystem can transmit to other mathematical complex subsystems which have neighboring relations or alternate relations with the intervening mathematical complex subsystem. The condition 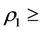
 can be satisfied when
can be satisfied when 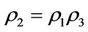 and
and 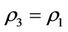 for a mathematical complex system since
for a mathematical complex system since  implies
implies  and
and
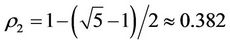 . If this assumptions is set upthen the intervening principle: “Real disease is to rush down his son and virtual disease is to fill his mother” based on “Yin Yang Wu Xing” Theory in image mathematics, is quite reasonable. But, in general, the ability of self-protection often is insufficient for an usual mathematical complex system, i.e.,
. If this assumptions is set upthen the intervening principle: “Real disease is to rush down his son and virtual disease is to fill his mother” based on “Yin Yang Wu Xing” Theory in image mathematics, is quite reasonable. But, in general, the ability of self-protection often is insufficient for an usual mathematical complex system, i.e.,  is small. A common standard is
is small. A common standard is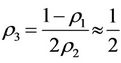 , i.e., there is a principle which all losses are bear in mathematical complex system. Thus the general condition often is
, i.e., there is a principle which all losses are bear in mathematical complex system. Thus the general condition often is 
 . Interestingly, they near to the golden numbers.
. Interestingly, they near to the golden numbers.
On the other hand, in image mathematics, mathematiccal real disease and mathematical virtual disease have their reasons. Mathematical real disease is caused by the born subsystem and mathematical virtual disease is caused by the bear subsystem. Although the reason can not be proved easily in mathematics or experiments, the intervening method under the assumption is quite equal to the intervening method in the intervention indirectly. It has also proved that the mathematical intervening princeple is true from the other side.
4.3. Intervening Principle If Only Two Subsystems with the Loving Relation of the Mathematical Complex System Encounter Sick
Suppose that the two subsystems X and XS of the mathematic complex system are abnormal (mathematical virtual disease or mathematical real disease). In the mathematical complex system of relations between two noncompatible with the constraints, by Theorem 3.2, only two situations may occur:
1) X encounters mathematical virtual disease, and at the same time, XS befalls mathematical virtual disease, i.e., the energy of X is too low and the energy of XS is also too low. It is because X bears XS. The mathematical virtual disease causal is X.
2) X encounters mathematical real disease, and at the same time, XS befalls mathematical real disease, i.e., the energy of X is too high and the energy of XS is also too high. It is because XS is born by X. The mathematical virtual disease causal is XS.
It can be shown by Theorem 3.3 that when intervenetion reaction and self-protection coefficients satisfy ,
, 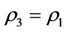 and
and , if one wants to treat the abnormal subsystems X and XS, then 1) For mathematical virtual disease, the one should intervene subsystem X directly by increasing its energy. It means “mathematical virtual disease is to fill his mother” because the mathematical virtual disease causal is X;
, if one wants to treat the abnormal subsystems X and XS, then 1) For mathematical virtual disease, the one should intervene subsystem X directly by increasing its energy. It means “mathematical virtual disease is to fill his mother” because the mathematical virtual disease causal is X;
2) For mathematical real disease, the one should intervene subsystem XS directly by decreasing its energy. It means “mathematical real disease is to rush down his son” because the mathematical real disease causal is XS.
For example, in China, many factories and enterprises generally only care about cost 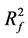 (or, risk, water (SX)) and quality
(or, risk, water (SX)) and quality  (or, deviation degree, metal (KX)) as two mathematical indexes which have the loving relation for a complicated economical problem based on the freedom model (3). They frequently used method is: If both cost and quality are all not normal (or, virtual diseases, i.e., high cost and poor quality), then they reduce deviation degree
(or, deviation degree, metal (KX)) as two mathematical indexes which have the loving relation for a complicated economical problem based on the freedom model (3). They frequently used method is: If both cost and quality are all not normal (or, virtual diseases, i.e., high cost and poor quality), then they reduce deviation degree  (i.e., improve quality, increase the energy
(i.e., improve quality, increase the energy 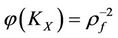 of metal (KX)) with linear optimization method since metal (KX) is the mother of water (SX) (see [29]). The idea is precisely “Virtual disease is to fill his mother” if one subsystem of mathematical complex system falls virtual ill.
of metal (KX)) with linear optimization method since metal (KX) is the mother of water (SX) (see [29]). The idea is precisely “Virtual disease is to fill his mother” if one subsystem of mathematical complex system falls virtual ill.
The intervention method can be to maintain the balance of the mathematical complex system because only two mathematical virtual disease subsystems are treated, by using Theorem 3.2, such that there is not any side effect for all other subsystems. And the intervention method can also be to enhance the capability of intervention reaction because the method of using intervention reaction makes the  and
and 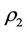 greater and near to 1. The state
greater and near to 1. The state 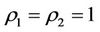 is the best state of the mathematical complex system. On the way, it almost have none mathematical intervening resistance problem since any mathematical intervening method is possible good for some large
is the best state of the mathematical complex system. On the way, it almost have none mathematical intervening resistance problem since any mathematical intervening method is possible good for some large  and
and .
.
4.4. Intervening Principle If Only Two Subsystems with the Killing Relation of the Mathematical Complex System Encounter Sick
Suppose that the subsystems X and XK of a mathematical complex system are abnormal (real disease or virtual disease). In the mathematical complex system of relations between two non-compatible with the constraints, only a situation may occur: X encounters mathematical virtual disease, and at the same time, XK befalls mathematical real disease, i.e., the energy of X is too low and the energy of XK is too high. The disease is serious because the XK has harmed the X by using the method of incest, i.e. damaged the king relation of X and XK.
It can be shown by Theorems 3.3 and 3.4 that when intervention reaction and self-protection coefficients satisfy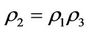 ,
, 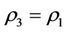 and
and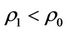 , if one wants to treat the abnormal subsystems X and XK, the one should intervene subsystem X directly by increasing its energy, and at the same, intervene subsystem XK directly by decreasing its energy. It means that “Strong inhibition of the same time, support the weak”.
, if one wants to treat the abnormal subsystems X and XK, the one should intervene subsystem X directly by increasing its energy, and at the same, intervene subsystem XK directly by decreasing its energy. It means that “Strong inhibition of the same time, support the weak”.
For example, in China, many sociologists generally only care about social and economic benefits  (or social benefits, water (SX)) and social equity extent
(or social benefits, water (SX)) and social equity extent  (or, information decomposition ratio, soil (XK)) with two mathematical killing indexes for a complicated social system based on the freedom model (3). If both social benefit
(or, information decomposition ratio, soil (XK)) with two mathematical killing indexes for a complicated social system based on the freedom model (3). If both social benefit 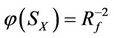 and social equity extent
and social equity extent  are not normal, often appear serious problem is that social benefit
are not normal, often appear serious problem is that social benefit  is too good (or,
is too good (or, 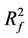 too low, real disease) but social equity extent
too low, real disease) but social equity extent 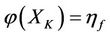 is too bad (or,
is too bad (or,  too low, i.e., virtual disease).The disease is serious because the XK has been harmed by the SX with the method of incest such that the soil (XK) cannot kill water (SX). For the serious disease, many mathematical sociologists of China now frequently used method is: to increase social equity extent
too low, i.e., virtual disease).The disease is serious because the XK has been harmed by the SX with the method of incest such that the soil (XK) cannot kill water (SX). For the serious disease, many mathematical sociologists of China now frequently used method is: to increase social equity extent 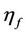 (or, to increase the information decomposition ratio
(or, to increase the information decomposition ratio  which is the energy of the soil (XK)) but to decrease social and economic benefits
which is the energy of the soil (XK)) but to decrease social and economic benefits  (i.e., to decrease the energy of water (SX)) at the same time since soil (XK) is the bane of water (SX). The idea is “Strong inhibition of the same time, support the weak” if XK falls virtual disease and at the same time, SX befalls real disease.
(i.e., to decrease the energy of water (SX)) at the same time since soil (XK) is the bane of water (SX). The idea is “Strong inhibition of the same time, support the weak” if XK falls virtual disease and at the same time, SX befalls real disease.
For another example, thirty years ago, China’s social coordination function 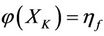 is very good, the complex system is rife with average socialist, but both social benefit
is very good, the complex system is rife with average socialist, but both social benefit  and social structure
and social structure 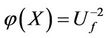 are all very poor. In addition, the mathematical complex system is not rich. In other words, both SX and X fall virtual diseases and at the same time, XK befalls real disease based on the freedom model (3). The disease is very serious because not only the wood (X) has been harmed by the soil (XK) with the method of incest such that wood (X) cannot kill soil (XK), but also there are 3 subsystems falling ill. Generally speaking, there are three or more than three of disease of the subsystem of a complex system, it is very difficult to cure. In order to cure the very serious disease, Deng Xiao-Ping’s taking method is to break the “iron bowl” and to develop the economy (to fill up the energies
are all very poor. In addition, the mathematical complex system is not rich. In other words, both SX and X fall virtual diseases and at the same time, XK befalls real disease based on the freedom model (3). The disease is very serious because not only the wood (X) has been harmed by the soil (XK) with the method of incest such that wood (X) cannot kill soil (XK), but also there are 3 subsystems falling ill. Generally speaking, there are three or more than three of disease of the subsystem of a complex system, it is very difficult to cure. In order to cure the very serious disease, Deng Xiao-Ping’s taking method is to break the “iron bowl” and to develop the economy (to fill up the energies  and
and 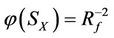 of both wood (X) and water (SX) at the same time, i.e., strengthen social structure and social benefit), and to allow a few people to get rich (to rush down the energy
of both wood (X) and water (SX) at the same time, i.e., strengthen social structure and social benefit), and to allow a few people to get rich (to rush down the energy  of soil (XK), abate the coordinated ability). The idea is, at the same time, to use both “Strong inhibition of the same time, support the weak” and “Virtual disease is to fill his mother”, if both SX and X fall virtual diseases and at the same time, XK befalls real disease.
of soil (XK), abate the coordinated ability). The idea is, at the same time, to use both “Strong inhibition of the same time, support the weak” and “Virtual disease is to fill his mother”, if both SX and X fall virtual diseases and at the same time, XK befalls real disease.
The intervention method can be to maintain the balance of mathematical complex system because only two mathematical virtual disease subsystems are treated, by using Theorems 3.2 and 3.4, such that there is none side effects for all other subsystems. And the intervention method can also be to enhance the capability of intervention reaction and self-protection because the method of using intervention reaction and self-protection makes the 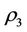 and
and 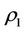 greater and near to 1. The state
greater and near to 1. The state  is the best state of the steady multilateral system. On the way, it almost have none mathematical intervening resistance problem since any mathematical intervening method is possible good for some large
is the best state of the steady multilateral system. On the way, it almost have none mathematical intervening resistance problem since any mathematical intervening method is possible good for some large 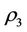 and
and .
.
5. Conclusions
This work shows how to treat the mathematical diseases (real or virtual) of a mathematical complex system in image mathematics and three methods are presented.
If only one subsystem falls ill, mainly the intervening method should be to intervene it indirectly for case: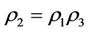 ,
,  and
and , according to the intervening principle of “Real disease is to rush down his son but virtual disease is to fill his mother”. The intervention method directly can be used in case
, according to the intervening principle of “Real disease is to rush down his son but virtual disease is to fill his mother”. The intervention method directly can be used in case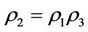 ,
, 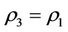 and
and  but should be used as little as possible.
but should be used as little as possible.
If two subsystems with the loving relation encounter sick, the intervening method should be intervene them directly according to the intervening principle of “Real disease is to rush down his son but virtual disease is to fill his mother”.
If two subsystems with the killing relation encounter sick, the intervening method should be intervene them directly also according to the intervening principle of “Strong inhibition of the same time, support the weak”.
Other properties, such as balanced, orderly nature of Wu-Xing, mathematical forecast, and so on, will be discussed in the next articles.
6. Acknowledgements
This article has been repeatedly invited as reports, such as Shanxi University, Xuchang College, and so on. The work was supported by Specialized Research Fund for the Doctoral Program of Higher Education of Ministry of Education of China (Grant No. 200802691021).
REFERENCES
- Y. S. Zhang, “Theory of Multilateral Matrices,” Chinese Stat. Press, Beijing, 1993.
- Y. S. Zhang, “Theory of Multilateral Systems,” 2007. http://www.mlmatrix.com
- Y. S. Zhang, “Mathematical Reasoning of Treatment Principle Based on ‘Yin Yang Wu Xing’ Theory in Traditional Chinese Medicine,” Chinese Medicine, Vol. 2, No. 1, 2011, pp. 6-15. doi:10.4236/cm.2011.21002
- Y. S. Zhang, “Mathematical Reasoning of Treatment Principle Based on ‘Yin Yang Wu Xing’ Theory in Traditional Chinese Medicine(II),” Chinese Medicine, Vol. 2, No. 4, 2011, pp. 158-170. doi:10.4236/cm.2011.24026
- Y. S. Zhang, “Mathematical Reasoning of Treatment Principle Based on the Stable Logic Analysis Model of Complex Systems,” Intelligent Control and Automation, Vol. 3, No. 1, 2012, pp. 6-15. doi:10.4236/ica.2012.31001
- Y. S. Zhang, “Mathematical Reasoning of Economic Intevening Principle Based on ‘Yin Yang Wu Xing’ Theory in Traditional Chinese Economic(I),” Modern Economics, Vol. 3, No. 2, 2012, pp.
- Y. S. Zhang, S. S. Mao, C. Z. Zhan and Z. G. Zheng, “Stable Structure of the Logic Model with Two Causal Effects,” Chinese Journal of Applied Probability and Statistics, Vol. 21, No. 4, 2005, pp. 366-374.
- C. Luo, X. D. Wang and Y. S. Zhang, “Orthogonality and Independence—New Thinking of Dealing with Complex Systems Series Three,” Journal of Shanghai Institute of Technology (Natural Science), Vol. 10, No. 4, 2010, pp. 271-277.
- C. Luo, X. P. Chen and Y. S. Zhang, “The Turning Point Analysis of Finance Time Series,” Chinese Journal of Applied Probability and Statistics, Vol. 26, No. 4, 2010, pp. 437-442.
- Y. S. Zhang, X. Q. Zhang and S. Y. Li, “SAS Language Guide and Application,” Shanxi People’s Press, Taiyuan, 2011.
- Y. S. Zhang and S. S. Mao, “The Origin and Development Philosophy Theory of Statistics,” Statistical Research, Vol. 12, 2004, pp. 52-59.
- N. Q. Feng, Y. H. Qiu, F. Wang, Y. S. Zhang and S. Q. Yin, “A Logic Analysis Model about Complex System’s Stability: Enlightenment from Nature,” Lecture Notes in Computer Science, Vol. 3644, 2005, pp. 828-838. doi:10.1007/11538059_86
- N. Q. Feng, Y. H. Qiu, Y. S. Zhang, F. Wang and Y. He, “A Intelligent Inference Model about Complex System’s Stability: Inspiration from Nature,” International Journal of Intelligent Technology, Vol. 1, 2005, pp. 1-6.
- N. Q. Feng, Y. H. Qiu, Y. S. Zhang, C. Z. Zhan and Z. G. Zheng, “A Logic Analysis Model of Stability of Complex System Based on Ecology,” Computer Science, Vol. 33, No. 7, 2006, pp. 213-216.
- C. Y. Pan, X. P. Chen, Y. S. Zhang and S. S. Mao, “Logical Model of Five-Element Theory in Chinese Traditional Medicine,” Journal of Chinese Modern Traditional Chinese Medicine, Vol. 4, No. 3, 2008, pp. 193- 196.
- X. P. Chen, W. J. Zhu, C. Y. Pan and Y. S. Zhang, “Multilateral System,” Journal of Systems Science, Vol. 17, No. 1, 2009, pp. 55-57.
- C. Luo and Y. S. Zhang, “Framework Definition and Partition Theorems Dealing with Complex Systems: One of the Series of New Thinking,” Journal of Shanghai Institute of Technology (Natural Science), Vol. 10, No. 2, 2010, pp. 109-114.
- C. Luo and Y. S. Zhang, “Framework and Orthogonal Arrays: The New Thinking of Dealing with Complex Systems Series Two,” Journal of Shanghai Institute of Technology (Natural Science), Vol. 10, No. 3, 2010, pp. 159-163.
- J. Y. Liao, J. J. Zhang and Y. S. Zhang, “Robust Parameter Design on Launching an Object to Goal,” Mathematics in Practice and Theory, Vol. 40, No. 24, 2010, pp. 126-132.
- Y. S. Zhang, S. Q. Pang, Z. M. Jiao and W. Z. Zhao, “Group Partition and Systems of Orthogonal Idempotents,” Linear Algebra and Its Applications, Vol. 278, No. 1-3, 1998, pp. 249-262. doi:10.1016/S0024-3795(97)10095-7
- J. L. Zhao and Y. S. Zhang, “The Characteristic Description of Idempotent Orthogonal Class System,” Advances in Matrix Theory and Its Applications, Proceedings of the 8th International Conference on Matrix and its applications, Taiyuan, Vol. 1, No. 1, 16-18 July 2008, pp. 445-448.
- X. P. Chen, C. Y. Pan and Y. S. Zhang, “Partitioning the Multivariate Function Space into Symmetrical Classes,” Mathematics in Practice and Theory, Vol. 39, No. 2, 2009, pp. 167-173.
- C. Y. Pan, X. P. Chen and Y. S. Zhang, “Construct Systems of Orthogonal Idempotents,” Journal of East China University (Natural Science), Vol. 141, No. 5, 2008, pp. 51-58.
- C. Y. Pan, H. N. Ma, X. P. Chen and Y. S. Zhang, “Proof Procedure of Some Theories in Statistical Analysis of Global Symmetry,” Journal of East China Normal University (Natural Science), Vol. 142, No. 5, 2009, pp. 127-137.
- X. Q. Zhang, Y. S. Zhang and S. S. Mao, “Statistical Analysis of 2-Level Orthogonal Satursted Designs: The Procedure of Searching Zero Effects,” Journal of East China Normal University (Natural Science), Vol. 24, No. 1, 2007, pp. 51-59.
- Y. S. Zhang, Y. Q. Lu and S. Q. Pang, “Orthogonal Arrays Obtained by Orthogonal Decomposition of Projection Matrices,” Statistica Sinica, Vol. 9, No. 2, 1999, pp. 595-604.
- Y. S. Zhang, S. Q. Pang and Y. P. Wang, “Orthogonal Arrays Obtained by Generalized Hadamard Product,” Discrete Mathematics, Vol. 238, No. 1-3, 2001, pp. 151- 170. doi:10.1016/S0012-365X(00)00421-0
- Y. S. Zhang, L. Duan, Y. Q. Lu and Z. G. Zheng, “Construction of Generalized Hadamard Matrices
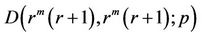 ,” Journal of Statistical Planning, Vol. 104, 2002, pp. 239-258. doi:10.1016/S0378-3758(01)00249-X
,” Journal of Statistical Planning, Vol. 104, 2002, pp. 239-258. doi:10.1016/S0378-3758(01)00249-X - Y. S. Zhang, “Data Analysis and Construction of Orthogonal Arrays,” East China Normal University, Shanghai, 2006.
- Y. S. Zhang, “Orthogonal Arrays Obtained by Repeating- Column Difference Matrices,” Discrete Mathematics, Vol. 307, No. 2, 2007, pp. 246-261. doi:10.1016/j.disc.2006.06.029
- X. D. Wang, Y. C. Tang, X. P. Chen and Y. S. Zhang, “Design of Experiment in Global Sensitivity Analysis Based on ANOVA High-Dimensional Model Representation,” Communications in Statistics—Simulation and Computation, Vol. 39, No. 6, 2010, pp. 1183-1195. doi:10.1080/03610918.2010.484122
- X. D. Wang, Y. C. Tang and Y. S. Zhang, “Orthogonal Arrays for the Estimation of Global Sensitivity Indices Based on ANOVA High-Dimensional Model Representation,” Communications in Statistics—Simulation and Computation, Vol. 40, No. 9, 2011, pp. 1324-1341. doi:10.1080/03610918.2011.575500
- J. T. Tian, Y. S. Zhang, Z. Q. Zhang, C. Y. Pan and Y. Y. Gan, “The Comparison and Application of Balanced Block Orthogonal Arrays and Orthogonal Arrays,” Journal of Mathematics in Practice and Theory, Vol. 39, No. 22, 2009, pp. 59-67.
- C. Luo and C. Y. Pan, “Method of Exhaustion to Search Orthogonal Balanced Block Designs,” Chinese Journal of Applied Probability and Statistics, Vol. 27, No. 1, 2011, pp. 1-13.
- Y. S. Zhang, W. G. Li, S. S. Mao and Z. G. Zheng, “Orthogonal Arrays Obtained by Generalized Difference Matrices with g Levels,” Science China Mathematics, Vol. 54, No. 1, 2011, pp. 133-143. doi:10.1007/s11425-010-4144-y
- Lao-tzu, “Tao Te Ching,” In: S. Mitchel, Transl., 2010. http://acc6.its.brooklyn.cuny.edu
- M.-J. Cheng, “Lao-Tzu, My Words Are Very Easy to Understand: Lectures on the Tao Teh Ching,” North Atlantic Books, Richmond, 1981.
- Research Center for Chinese and Foreign Celebrities and Developing Center of Chinese Culture Resources, “Chinese Philosophy Encyclopedia,” Shanghai People Press, Shanghai, 1994.

