Creative Education
Vol.10 No.06(2019), Article ID:93389,21 pages
10.4236/ce.2019.106099
The Assessment in Mathematics: Educational Process?*
Eliseo Ramírez Rincón
Researches Center, Faculty of Economics, Administrative and Accounting Sciences, Libre University, Bogotá, Colombia

Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 18, 2019; Accepted: June 27, 2019; Published: June 30, 2019
ABSTRACT
Evaluation as an educational process is fundamental and important, particularly of the teaching and learning process in the area of mathematics in which this research paper focuses, because although two different processes are closely related to each other and it is not possible to assess one of them without taking into account the other, because when assessing, for example, learning is necessary to evaluate the factors, contexts, emotions and other variables that affect to both, like the culture (interests, attitude, life project, values, and principles, teacher training, …), ICT and the quality.
Keywords:
Assessment Mathematics, Education Process, Equity-Quality, Education Policies

1. Introduction
What Is Meant by Assessment
The dictionary of the Spanish language RAE (2018) defines it as:
1) f. Action and effect of assessing.
2) f. School exam.
Given that the human being is eminently social, critical and curious, he constantly lives to make judgments about what he does, as well as about various aspects that interest him and that can benefit him and to another’s; in this sense assessment is a human activity (Zaragoza, 2003) , therefore, is an anthropological nature in which reality is relative insofar as it depends on who is observing or living this and, therefore, lacks objectivity and its neutrality is also relative (Santos, 2003) .
With the establishment of compulsory education in the 20th century, the assessment was also born, because it became necessary to classify students at different levels, according to Bravo and Fernández (2000) . This manner responds to the standardized and to the traditional assessment that affects only the students, is punitive because the mistake is sanctioned without considering it as part of the learning process, that is, as knowledge partial or unfinished learning, it is punctual, isolated and imposed by the teacher. Another important aspect of this type of assessment is that it focuses on learning by objectives that they privilege the memory recall and results as evidenced by the studies made by Tobón, Rial, Carretero, and García (2006) .
The assessment has also been conceived as a process that includes the following aspects: information about study, analysis of information, conclusions and decision-making Jorba and Sanmartí (1994) , according to Castillo and Cabrerizo (2003) as well as the above must be a value judgment regarding what you want to improve or modify.
It has also become evident that it is not possible to improve the quality of education without taking into account an assessment process, with authors as: (Black & William, 1998; Córdoba, 2006; Díaz-Barriga & Hernández, 2002; Crooks, 1988) because in addition, each country is interested in improving the quality of education; it must also guarantee a coherent and relevant assessment process, as well as the means to do so and institutional capacity with reliable plans that guarantee it (UNESCO, 2000) , without ignoring the difficulties and biases in evaluating the teacher by students, especially at the university level, as García (2000) said.
Assessment is closely linked to education, it is inherent to it because any educational process must also be assessed and in this sense it is worth rescuing what Rogers said about an educational process must be constituted in a social function and in a personal one, because they must be counselors so that a community transmits its legacy guaranteeing its own existence and development; that is to say that education must be considered as one of the fundamental objectives of a society (1989).
“In the last two decades, the Colombian education system has undergone a fundamental transformation”, OECD (2016, p. 15) . However, this article will present an analysis of assessment in one of the most complex areas of the educational process, such as mathematics, because serious difficulties remain latent in both learning and teaching, to the detriment of the constitutional principles of equity and quality, As will be demonstrated, the relationship between the educational process (changes and adjustments in government policies for education) and assessment in mathematics presents a different panorama, and given the social function Rogers speaks of, it is not equitable, nor is it of quality.
According to the above, we will present the problems that underlie the area of mathematics from the educational process and the standardized assessment, both national (Saber 9 and 11 tests, ICFES) and international (PISA test, OECD), the intention is not to make a comparison of any kind, but on the contrary to accept that they are different standardized and massive tests with differentiated processes and with particular and different interests, but because of their assessment quality they are powerful as measures of what is wanted.
On the other hand, there is a diversity of literature on diverse considerations of the educational process, but it is not in the author’s interest to delve deeper into any of them, but only to make evident the importance of an educational process in the processes of teaching and learning mathematics that, due to its complexity, must be integrative, inclusive, and broadly participatory. Among other reasons, because mathematics is taught at all levels (basic, middle and university) of Colombian education and because the latest reforms of the Saber tests have been aligned around generic mathematical knowledge (mathematics that any citizen should know) and not generic (mathematics for science and scientific knowledge).
2. Assessment in Colombia
The assessment, seen as the process by which are socially classified the traditional cultures, or as the process that generates the selection of social groups according with Ortiz and Buitrago (2017) are processes articulated with the assessment in Colombia. It is evident from the investigative work of these authors that historically in Colombia the assessment has had among its purposes the classification, they also say that: “The educational assessment came to the country with the first attempts by governments to create a public education that would contribute to integrating the national economy with the international economy” (page 147). In addition, the authors of this statement warn that this assessment has been favored by situations such as violence, marginalization and unequal development. In this sense, the evaluation and even more, education in Colombia responds to the interests of the international economic model and therefore the quality of it is measured with economic indicators and it is understood the desire of the governments of the last three or four decades to be part of the OCDE.
In Colombia, assessment gained interest with the creation of the ministry of National Education in 1928, when it was identified with this name, but it was not until the decade of the 1970s that it began as a process, with the standardization and conceptualization of school performance. For example, assessment in school mathematics as an evolutionary process of changes as educational policy in the last four decades, from which attention has focused on four fundamental axes; quality, pertinence, coverage, and efficiency have not generated significant changes in student learning, and on the contrary, difficulties and lags remain, despite good intentions, as evidenced by the results of external assessment, both the Saber tests and the PISA test (2006, 2009, 2012, 2015, 2018), this last without published results by OECD yet.
In Colombia, with the opening of the competencies in the Secondary Education (students of 16 - 18 years), the first large scale test is applied in the year 2000, to students of eleven grade of the average (school) of the whole country; as part of the changes in the processes of teaching and learning, from which the compulsory curriculum of the educational institutions of the Basic and Media so the M.E.N., to mitigate and strengthen these changes proposed as a standard document that is known as the Basic Standards of Competencies (MEN, 2003-2006a), but with conceptual differences with the Curricular Lineaments (MEN, 1998) which is an important document that emerged from the requirements of the General Education Law, also known as Law 115 of 1994 and that empowers from the constructivism, the achievements that in each level of the Basic and Average education had to reach the students (Knowledge, values, skills) that were measured (it assessed) from some indicators of achievement that evidenced a state reached in a certain process by competition (focused on know-how), which is closer to economic models than to educational ones.
The respective assessment was also changed, moving from indicators of achievement to performance measurement? “from management? From quality?”, which gave way to the measurement of quality and accreditation, improving the criteria for the classification of both students and institutions through the quality of education that arouse in Colombia, with the National Assessment System of Quality at the beginning of the 90s (20th century).
One of the profound differences between the Curricular Lineaments with the Basic Standards of Competencies was the abrupt change of an achievement by a process one of a Competence (focused on the know to do), which is closer to the economic models than the educational ones. The respective assessment was also changed, moving from indicators of achievement to performance measurement through indicators (MEN, 2013)
“of management? of quality?”, which gave way to the measurement of quality and accreditation, improving the criteria for the classification of both students and institutions, through the quality of education that arose in Colombia, with The National Assessment System off Quality at the beginning of the 90s (20th century).
In institutions of higher education, the process of standardized assessment, a large Scala, begins until 2003 the application of the test, ECAES (assessment of to large scale, that began with 27 programs), the which evolved, and it was necessary to adjust the curricula to this “style” of the national and international standardization both in the competencies as in the educational quality. In 2009, the ECAES test was called “Saber Pro”, when they are restructured as the large Scala tests and they begin to be compulsory for to obtain to undergraduate degree, with which the ICFES begins to deliver comparable results for all higher education too, as he had been doing with Basic and Middle Education with the other “Saber” tests. Since 2014, the ICFES is an independent entity ascribed to the M.E.N., which has contributed in the work that both have been developing around the national and international standards overassessment, with the order to improve the educational quality of the country, but that they cannot be evidenced in either the “Saber” tests or the PISA tests as will be presented in this paper according to previous studies by the OECD (2007) , ICFES ( 2007, 2013 , 2014) and the MEN (2010) .
In the century 21, the assessment focuses its attention on the quality of itself and from this perspective there is great interest both education policies, as in educational institutions, society, teachers and researchers because the focus is on the processes that can affect the education institutionality in general (administrators, teachers, researchers, students, parents and society) and not only about learning or teaching only, Castillo and Cabrerizo (2010) . It is also evident that this type of assessment standardized with international and globalized parameters is consequence of economic power interests that do not favor education from the cultural point of view, but use it for other purposes, for example, the standardized tests “SABER” and PISA that seek to investigate the national, regional and global factors that hinder the development of the competencies established by OECD for the s. XXI.
The assessment of the educational quality arises from the interest of the ministries of Education of the OECD member countries (1990) in the conference whose title was: An Education and training quality for all (Tiana, 1999) . The motivating interests for the quality of education correspond fundamentally to the economic changes whose impacts on a national and international level needing adjustments to respond to the social and economic differences experienced by people from countries such as Latin Americans in which there aren’t equity neither educational of quality, they are having and have had difficulties with a significantly high difference in comparison with the average of developed countries, Tiana (1996) . Another fundamental aspect regarding the assessment of educational quality corresponds to the one that broadens the interest and measurement on other referents; this is that not only worries about the teaching and learning processes only but also assesses teacher training, educational administration, educational institutions, educational policies and even the evaluation itself (Baartman, Prins, Kirshner, & Vleuten, 2007) .
It is also inferred that the standardized assessment leads to biases in the sense of ignoring the cultural and social contexts of the people who learn as well as the ones they teach because they are motivating superficial changes in the educative model, learning styles, teaching practices and content without deepening the relationships that must be established between cultural contexts, interests and relationships between the knowledge, for example, Pérez and Soto (2011) say that in addition to focusing education on an economic model, it skews the true interests of Education. On the other hand, Andina Corporation for Development (2007: p. 16) states that: “Social fragmentation hinders the implementation of the principles of democratic participation enshrined in the constitution”.
The standardized assessment in Colombia is done through the SABER tests, which as of 2014 second semester are aligned from the Basic Education (students between 7 and 15 years) to the middle school (students between 15 - 18 years) and are differentiated in three levels:
1) Basic; defined as the ability to identify, differentiate the rules and elements of use of each area. This level is composed of the grades from 1˚ to 9˚ (Basic Education) to those who undergo three national tests two primary Basic (3rd and 5th, students between 9 and 12 years) and one in Basic secondary (9˚, students 14 - 15 years), having as a fundamental objective to assess what the students of these courses know and what they know how to do with what they learn (framed as competences), these SABER tests are formative, because the institutions are forced from the results to propose and execute plans that improve the quality of Education.
2) Intermediate; defined as the ability to make inferences and deductions, as well as to use knowledge to give meaning to different situations and solve different types of problems, also known as SABER 11˚; designed for 11th grade students (16 - 18 years old), this test is done in secondary education and is a classificatory result, mandatory to enter higher education, it is not articulated with higher education beyond the generic competences they are evaluated in the SABER tests, neither is it articulated with the work options that require technical or technological competences (university education in technologies and/or technical careers), but rather in various occupations that do not require specific competences, this being a problem that has not been possible to settle through the educational policies that should be the priority interest of the state.
3) Superior; corresponds to the mandatory assessment that is made to all students who finish their respective undergraduate careers in the country’s universities, called SABER PRO. It serves among others to obtain important information for decision-making, accountability of higher education institutions and to classify nationally and internationally both programs and universities, likewise classifies students nationwide in percentiles according to performance levels (MEN, 2003; ICFES, 2013) .
Based on the above, it is important to mention that ICFES, as the governing body of the National System of Standardized Assessment of Education, in 2013 draw a document up entitled Alignment of the Saber 11˚ exam, through which changes are made to the state examinations (Saber 11˚ and Saber PRO) and three basic education tests (3˚, 5˚ and 9˚), the document further states that the tests are standardized, because the conditions of application and processing of the results are uniform and therefore all those assessed share the technical characteristics of the tests, in addition, there are both closed (four options) and open ended questions to interpret the answers of those evaluated.
Another aspect is the change in the definition of the notion of competence as: “a set knowledge, skills, attitudes, comprehensions and cognitive dispositions, metacognitives, socioafectives, communicatives and psychomotors appropriately related to each other to facilitate flexible, effective and meaningful performance of an activity or of certain types of tasks in relatively new and challenging contexts” (Vasco, 2003; mentioned in Alignment of the SABER 11˚ exam, 2013, p. 10), the document highlights generic competencies; their importance and need to develop them at the different levels of the educational system due to their longitudinal nature (complexity), while determining a transverse development (application) from all curricular areas. The document also clarifies that generic competencies “rather than possessing knowledge, it is knowing how to use it adequately and flexibly in new situations” (Torrado 2000, mentioned in Alignment of the SABER 11˚ exam, 2013, p. 13).
Among the changes contemplated in the Alignment of the SABER 11˚ exam, the current structure was changed until 2008 in which two groups were established; Common Core, which were tests presented by all students at all levels, such as Mathematics and Flexible Component, which contained four in-depth tests including mathematics and two interdisciplinary (environment, and Violence and Society).
Another referent of interest in the 2013 framework document is to openly accept the classification of Basic and Middle educational institutions (schools) into seven (7) performance categories: “greatly inferior, inferior, low, medium, high, superior or very superior” with which resources are allocated to municipalities according to the results of the schools and awards are given to outstanding schools. Why not give preferential help to schools weak in achievements? Not only economically, but it would be necessary to intervene in their infrastructure, technology, teacher training, pedagogy and assessment to address cases of low achievement institutions, because surely the institutions whose performance is precarious belong to very poor communities and therefore their basic needs are not covered, which makes them more vulnerable. This is corroborated of stretching or difference between the highest averages in the performance of the mathematics area and the lowest averages which have been increasing, deepening the deterioration of the principle of equity not only of gender, but also affect the poorest communities.
Another important aspect is to differentiate in Colombia the roles of the Ministry of Education (MEN), which particularly establishes education policies for the country1, of those referred to ICFES, which is particularly concerned with the Assessment of the Education System in the country. Unfortunately dictated by the government in power, which do not become permanent.
1Unfortunately dictated by the government in power, which do not become permanent.
Based on these differentiated roles, it has become evident in the country that ICFES has always been at the forefront, making proposals for improvement from the external and standardized assessment, but until 2013, distanced from the MEN, this distancing was reflected in a regrettable aspect for the teaching and learning processes because while of the MEN change from contents and objectives; to contents and processes, finally contents and competencies as political proposals framed in the interests of the international economy rather than in the educational interests of the cultures that make up the national territory and therefore almost to the force, whose changes instead of being motors of advance in the national economy from the educational development became bureaucratic obstacles, as for example, Decree 230 (2002, repealed in 2009), which established a 5% loss percentage for an educational institution of Basic and Middle School, but that the lack of pedagogy in the dissemination and scope of the decree deformed it in the understanding of what was known through its practice as “automatic promotion” and the disastrous consequences according to the assessment of ICFES and PISA test (2006, 2009, 2012 and 2015). Another negative aspect in the pedagogical practices of the teaching of mathematics had had in a large part that the institutions has been the excessive focus on finished contents.
In 2013, ICFES focuses the proposal on the official documents that are recognized and endorsed in Education, particularly in the Basic Standards of Competencies (MEN, 2006a) and the Curricular Guidelines (1998). Therefore, it establishes an alignment of its tests for all levels of Education basic, intermediate and university in the country, in accordance with the proposal of the MEN and they begin to be applied in all SABER tests together with the quantitative reasoning, from the second semester of 2014, but levels of performance in the tests are not proposed until 2016.
On the other hand, the quality of university education as a source of prestige is being discussed both nationally and internationally, because there are demands and pressures from society that focus attention on relevant learning and coherent with the needs of globalization, information technologies and no longer so much isolated programs focused on content (González, Gómez, Rodríguez, & Aguilera, 2009) . In this sense, for Cid, Pérez and Zabalza (2009) the quality of teaching is a complex process in which several and diverse elements interact, such as educational policies, available resources, cultural contexts, cultural and social needs, curricular organization, teacher training and experience, student training and motivation.
For García (2000) in the assessment of teaching there are inherent aspects of learning that do not depend on the teacher, but on the student, among them: the basic preparation to follow the chosen career, previous knowledge in a specific area, personal motivation, interest in study or personal effort in a knowledge.
The assessment, as a regulatory element in the provision of educational services, allows us to assess the progress and results of the process based on evidence that guarantees a pertinent, coherent and meaningful education for the student and the society in which he or she is located, and therefore cannot be isolated from educational policies, teacher training, the needs of society, globalization, technology and cultural contexts, among others.
The assessment should improve the quality of education, as well as serve educational establishments so that they can advance improvement processes based on the results obtained in the different types of existing assessment. The results of educational action in students are assessed through both internal and external classroom assessment (MEN, 2016) . “The complexity of assessment is closely related to teaching and learning, as well as to the elements that make them possible.”
2.1. Assessment in Mathematics vs. Educational Process
Diagram 1, presents some fundamental relationships between the evaluation of mathematics and an educational process. It is proposed in order to highlight the difficulties surrounding what Rogers described as the fact that an educational
Diagram 1. Complexity of education as a process. Source: own.
process must guarantee the benefit of a community and also of a personal nature; however, mathematical knowledge, being complex, generates situations that have not been taken into account in the educational processes that have been carried out in Colombia with the different proposals throughout the history reported and one of them corresponds to the little importance that has been given in practice to the principles of equity and quality.
School mathematics is a basic knowledge for a contemporary and globalized society, due to the diverse applications and uses, which range from being the most rigorous language of humanity with which science and technology communicate, to allowing any person to carry out activities that require some concepts of this knowledge, and therefore the importance that has been given both nationally and internationally, It is not enough to pretend that it is only a teaching problem, since it is demonstrated that there are cultural situations that also affect these processes such as nutrition, the diverse relationships between mathematical knowledge, the teacher, student, environment, technologies and contexts that mediate these relationships; But there are also educational policies that cannot be normative impositions, marked by international pressures, but must be consensuses based on regional and cultural needs that benefit development.
Since the birth of ICFES (1968) as the regulator of educational assessment in Colombia, the area of mathematics has been present and has undergone several changes during national history. Before 2000, the knowledge of the mathematics as area had a focus on declarative and procedural knowledge, problem solving, as well as numerical aptitudes and skills, however, in 2000 a reform was made in which the previous focus was changed to the assessment of competencies, since then changes and adjustments have been made in the assessment of the mathematics as area maintaining the focus of assessment of competencies (ICFES, 2013) . On the other hand, this assessment approach generates interest by the international assessment such as the made out by OECD with PISA tests, and the assessment process international in Colombia begins with the PISA tests in 2006.
In 2007, the design of the mathematics test was revised and some competences and components to be assessed were generated, such as the processes proper to mathematical activity and the mathematical knowledge present in the Basic Standards of Competences, although the document says it in an approximate manner (ICFES, 2007) . In accordance with the above, the following competencies were proposed: 1) Communication and representation; the ability to interpret and represent the same situation in different ways from mathematics. 2) Modeling, approaching and solving problems; the ability to formulate problems in mathematical language, to develop and use different strategies to solve them, as well as to define and justify the choice of methods and instruments. 3) Reasoning and argumentation; the ability to understand and justify strategies and procedures to achieve the solution of a given problem.
With respect to the components related to the above competencies were defined as: 1) Numerical and variational; it investigates the level of understanding of numbers, their properties and arithmetic operations, as well as the regularities and patterns present in a variational relationship that allow to identify and describe variables in phenomena of change and dependence. 2) Geometric and metric; it gives account of the characteristics of the basic geometric objects, of the relations between them, as well as of their transformations considering magnitudes and metric units. 3) Random; determines the understanding of the organization and interpretation of data and the formulation of inferences from arguments using central tendency and dispersion measures (ICFES, 2013: pp. 53-58) .
Among the changes in the assessment of the area of mathematics, in the SABER 11˚ Alignment document are the following: mathematical knowledge of a generic nature or quantitative reasoning (fundamental for a citizen of any profession or trade) and non-generic mathematical knowledge (general mathematics) are defined (ICFES, 2014) . Mathematical knowledge requires contexts, which for generics are: financial, scientific dissemination, social, occupational and for non-generics: mathematics, natural sciences, engineering and various scientific fields). Quantitative reasoning has been evaluated since the year 2000, however, from the new design of the test, emphasis is placed on the specific measurement of this reference from practical contexts that allow comparison with those reached in the SABER PRO test by students who are finishing their undergraduate studies (ICFES, 2013) .
Continuing with the external mathematics assessment carried out by the ICFES in the country through of the different SABER tests, which are composed of levels of performance that can be measured in this way:
2.1.1. Levels for Grade 9˚ in Math. (2006-20172)
1) Level A: a maximum of 5% of students assessed who do not meet the minimum achievement level are expected to remain at this level, with the minimum achievement level being “C”.
2No se toma el año 2018 porque la prueba SABER 9˚ no se aplicó en ese año y no se sabe si cambien de estructura.
2) Level C: It is expected that at least 20% of the students evaluated will be at this level, because they can solve routine problems in diverse contexts, making translations of diverse representations (symbolic, iconic, graphical) with arguments.
3) Level D: It is expected that at least 20% of the students evaluated will be able to solve non-routine problems, in which they must establish different relationships between variables and concepts involved.
4) Level E: It is expected that at least 55% of the students evaluated will be able to solve complex non-routine problems, for which they must find non-explicit relationships that allow them to establish strategies to solve them. These problems may involve different topics of mathematics that require a high level of conceptual understanding in mathematical knowledge (MEN, 2006b) .
2.1.2. Levels for Grade 11˚ in Math
In 2013 four performance levels were proposed for the 11th SABER test of mathematics, however, only until the second half of 2014 began to apply in the country, are they:
Level 1 (0 - 35 points): The student can read punctual information that relates to everyday situations, which may be presented in tables or graphs with explicit scale, grid or horizontal lines; however, he/she may have difficulties when comparing different sets of data, involving different variables or in the analysis of situations other than everyday situations.
Level 2 (36 - 50 points): In addition to the above, the student can make comparisons and establish relationships between data, as well as to extract local and global information directly, in personal or familiar contexts that involve graphs with explicit scale, grid or at least horizontal lines or other formats with little information.
Level 3 (51 - 70 points): In addition to the above, the student can select information, point out errors and make different transformations through simple arithmetic and algebraic manipulations; from which he can resolve situations that relate proportionality, conversion factors, areas and flat developments in work or occupational, mathematical or scientific contexts and community or social contexts.
Level 4 (71 - 100 points): In addition to the above, the student can solve problems and justify the truth value of propositions or statements made that need concepts of probability, algebraic properties, trigonometric relationships, and characteristics of real functions through fundamentally mathematical or abstract scientific contexts.
In Table 1. The results of the SABER tests are presented in the years in which Colombia also participated in the PISA test, to establish some generalities regarding performance, clarifying that comparisons will not be made, given that although they are massive standardized tests they have different guidelines, but there is interest in establishing the scopes of Colombia according to the performance of students in both tests.
Table 1. Assessment of mathematics, SABER tests 9˚.
Source: Own elaboration with data taken from MEN (2006b) , ICFES interactive (2019) .
From Table 1, it can be interpreted that in general more than 70% of 9th grade students are placed in the lower levels (insufficient and minimum), which is an indicator that despite the good intentions of the MEN and ICFES to improve from the proposals for change in the design and structure of the mathematics test, the results continue to be deficient.
In addition, the SABER 3˚, 5˚ and 9˚ tests were not performed in 2018. There is no official information from the Ministry of National Education on the matter, nor from ICFES, however, it is worrying because education has been treated for several decades with “warm water cloths”, with solutions that are of form, it is enough to know, for example, that according to the OECD (2018) Colombia is the country of the organization that assigns the lowest economic amount in education per student between 5 - 15 years and also because since 2006 that has participated in the PISA tests is among the last places, well below the performance levels of the average, without reaching levels 5 and 6; barely scratching level 4 with 2%.
Graph 1, presents a trend between the educational processes proposed at least four decades ago and the standardized assessment in national mathematics (ICFES) and international mathematics (PISA) from 2006 to 2015, considering data collected from the sources mentioned in this article in the basic (9th) and average (11th) for the ICFES and 15-year-old students for the PISA test.
Graph 1, presents the trend in the assessment of the area of mathematics as an educational process from an institutional point of reference, in which it is evident that the highest percentage of students (more than 73%) concentrated on the levels of insufficient and minimum, that the satisfactory level does not exceed 22%, and that the advanced level is less than 13%.
From this Graph 1, it can be said that the educational process or processes (according to the policies of the government in office) have not yielded the expected results and that, on the contrary, there is a stagnation generated in the concentration of 14- and 15-year-old students in the lowest levels of performance in the area.
Mathematics, language arts, natural sciences and English have become the flags of the different governments that present their policies on education to “improve” the educational process in the country and it has been demonstrated that if students have low performances in language they will also have them in mathematics and science, they correlate and this continues to be a great problem that seems to have not been solved.
Table 2, presents the average results of the 11˚ SABER test per semester, for which it is clarified that in semester I there are private schools and among them are rural schools, which are institutions with high socioeconomic levels, belonging to calendar B, and in semester II there are schools public and private from calendar A, normally they are institutions with low socioeconomic levels.
In general, the average results in Table 2, are at 50% of the total test score, which means that they show poor performance (performance levels 1 and 2) that when compared with the results obtained in SABER 9˚, are correlate and reflect that the difficulties and delays in the learning school mathematical knowledge are maintained, but also can reflect other causes that contribute with it, such as institutional, social, family, personal and above all educational policies. It is customary in the country to focus on teachers as the only ones responsible for the debacle, but in the educational dynamic, they are just one link that connects the institutionality (PEI) with the educational policies of each government and its culture, according to the environment of the school and mathematical knowledge.
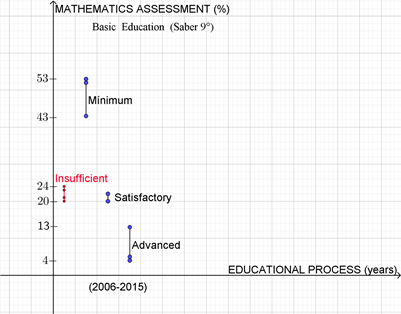
Graph 1. Saber 9˚ Assessment. Source: Geogebra 5.0 Classic, data taken from Table 1.
Table 2. Assessment of mathematics, SABER 11˚ test.
Source: Own elaboration with data taken from ICFES interactive (2019) . Weighted annual average.
The results of Table 2, also show the differences between the private schools of calendar B and those of the official and private sector of calendar A. In addition to the classification of the schools, there is also that of the students, because the stretching is notorious, which contributes to the imbalance of the principle of equity in social and cultural matters, because the rural sector presents difficulties that have not been properly attended to, both in the area of mathematics and in the area of science, and therefore the quality of education as a process is also deteriorated.
Similarly, Graph 2, is proposed for Saber 11, to review the historical behavior of the educational process versus the standardized assessment of the mathematics area for students who are finishing or have finished their high school studies. This is another gap that has not been bridged or resolved in the country’s education policies, given that the majority of students aged 16 - 18 who have completed their education at school do not have a clear idea what to do later, because approximately 60% of university education is private and very expensive, in addition to the university institutions of technical and technological careers, most are also private, they are not articulated with the school’s educational process and their cost is a factor that for some prevents access to this possibility. Another important reason is that the few public universities in the country have their own criteria for selecting students, such as, for example, high scores on the Saber 11 tests or exams of a high level of complexity that does not accommodate the majority; not in vain in the country 56% of students do not finish high school (grade 11).
Graph 2 shows that the average results per year are grouped between 45% and 50%, which is in any case lower than the latter value. It is in this sense that the educational process in mathematics that has been carried out for four decades in Colombia is questioned, because although it is true that changes have been made, it is also necessary to accept that the underlying problem remains and is resistant to these changes. And so, when evaluating it, is it still deficient?
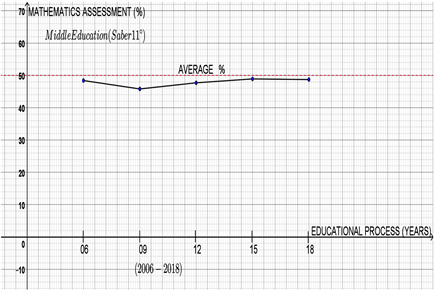
Graph 2. Saber 11˚ Assessment. Source: Geogebra 5.0 Classic, data taken from Table 2.
It should also be clarified that, until 2008, the test investigated the quality of secondary education and was oriented by competencies through a curricular structure with tests, including that of mathematics with in-depth study. As of 2009-2012, the SABER 11˚ tests are conformed and the tests that are make to the last semester students in the university, called ECAES are modified by the current SABER PRO, in them emphasis was made in the quantitative reasoning and its alignment is achieved with the SABER tests in general, through the mathematical contents that are called generic and correspond to the quantitative reasoning, the competences in the mathematics test are maintained: Communication and representation, modeling, problem solving, reasoning and argumentation (ICFES, 2013) .
Therefore, analyzing the international standardized mathematics test PISA, which is defined as a mathematical competence that measures in it the ability of a student to identify, reason and communicate through mathematical operations the solution of problems of the everyday life. The mathematical competence proposes some processes graduated in three levels of complexity, such as the 1) of reproduction, for which the common operations are fixed, the simple calculations and the solution of problems of the immediate or daily environment. 2) Those of connection, which require elaborated ideas and the establishment of mathematical procedures that account for mathematical models to solve situations, which are not considered ordinary or routine, but which can be developed in common scenarios or contexts. 3) Of reflection, which contemplate the solutions to complex problems, through more elaborated and better formed mathematical knowledge. In general, mathematical competence is expected for students to infer from a situation the mathematics they know (OECD, 2009: p. 12) .
The assessment should improve the quality of education, as well as serve educational establishments so that they can advance improvement processes based on the results obtained in the different types of existing assessment. The results of educational action in students are assessed through both internal and external classroom assessments (MEN, 2016) . “The complexity of assessment is closely related to teaching and learning, as well as to the elements that make them possible.”
The mathematical competence for PISA is defined as: The ability of a person to interpret, formulate and use mathematics in various contexts (social, every day, scientific and mathematical), which consider the type of mathematical reasoning and the conceptual know do, procedural, relation of facts and mathematical tools to describe, explain and predict situations specific to a phenomenon (OECD, 2013) .
Mathematical proficiency in PISA is assessed through 7 levels of performance, with 0 being the lowest performing and 6 the highest performing. The level zero determines that the students’ performance does not reach the basic levels proposed in level 1 for the area of mathematics. The performance levels proposed by PISA are from lower to higher complexity in the evaluation of student performance.
0) The basic performances proposed by the PISA test for the level are not achieved.
1) They answer questions in familiar contexts in which all the required information is present and all questions are clear and well defined. They are also able to identify information and carry out common procedures following direct instructions in explicit situations.
2) They interpret and recognize situations in contexts that require direct inferences. They can extract relevant information from a single source and use it in a single mode of representation. Use basic algorithms, procedures or conventions. They can reason directly and make literal interpretations of the results.
3) They perform procedures previously described, which may include sequential decisions. They select and apply simple strategies to solve a problem. They can interpret and use representations of different sources of information and reasoning directly from them. They can develop short communications from their interpretations, reasoning and results.
4) They work efficiently with explicit models in concrete and complex situations that may contain limitations or require assumptions. They select and integrate different symbolic representations that relate directly to the reality of the world. They use well developed skills and they can reason with flexibility in front of contexts. They construct and communicate explanations and arguments based on their interpretations, reflections and actions.
5) Develop and work with models to solve complex situations, identify constraints and specify assumptions. They select, compare and evaluate strategies to solve a complex problem related to a chosen model. They work strategically using broad thinking, cognitive skills for to reason about representations well related to symbolic and formal characterizations considering relevant knowledge. They can reflect on their actions, formulate and communicate their interpretations and their reasoning.
6) They conceptualize, generalize and use information based on their research, the modeling of complex situations of a problem. They link different sources of information, representation and relate them flexibly to each other. They achieve advanced mathematical thinking and reasoning. They apply their knowledge and understanding about it through symbolic and formal relationships, operations, and mathematical procedures. They formulate and communicate with precision their actions and reflections referring to their interpretations, discussions and results with pertinence and coherence (OECD, 2003, 2018) .
From the above, in Table 3, shows the percentages, according to performance levels, achieved by the students who have taken the PISA mathematics test in the country from 2006 to 2018.
From Table 3, and the 6 performance levels proposed by PISA to assess mathematical competence, the following is inferred: In spite of the fact that the number of students who have been participating by Colombia in the various mathematics tests proposed by PISA from 2006 to 2018 has increased, the backlog is maintained with respect to the OECD average and even with some countries
Table 3. Colombia’s performance in mathematics: PISA.
Source: Own elaboration with data taken from: National results report, Colombia in OECD (PISA, 2015: p. 29) ; MEN- ICFES, 2017 and OECD, 2018 .
in the region remains, but the most worrying thing is that at level zero there is a high percentage of students who do not reach the minimum level proposed by PISA, which can be explained and coincide with the results of the SABER tests (9th and 11th) with the growing gap that exists between the percentage of students who achieve better test scores with the percentage of them who have the lowest, which configures the detriment in equity over the right to a Quality Education and on the contrary consolidates the classification of the institutions and therefore of students with different quality of education.
Another striking aspect is that only 2% reach level 4, 0% reach higher levels 5 and 6, and only until 2015 was 34% reached between levels 2, 3 and 4, which determines that more than 66% are between levels 0 and 1. These results may have another type of analysis, but what is clear is that in terms of quality in education with international benchmarks such as that of the OECD from the economic point of view, they allow us to infer that there are important difficulties and that the complexity of the situation demands a judicious review not only from educational institutions, but also of educational policies because there is not and has not been a state policy in education but of the government, there is no continuity in the processes and there is a marked interest in recent governments to be part of the OECD not for education, because the evidence is clear, but for its importance in international economic policy.
In the following Graph 3, PISA results will be presented for assessment in mathematics.
In Graph 3, it can be observed that level 0, which has been viewed by the PISA organization as one in which students do not reach basic performance for level 1, has the highest percentage among the number of students who came to Colombia in the given period. It is also seen on a descending scale that, as the level becomes more complex, the percentage of students is lower, which shows that levels 5 and 6 are absent.
It is worrisome that in the area of mathematics the performances of students in general, both in the Saber and PISA tests, are very deficient and in this sense the assessment process presents the deficiencies of the teaching and learning processes, but it must also be clear that the educational process is also deficient;
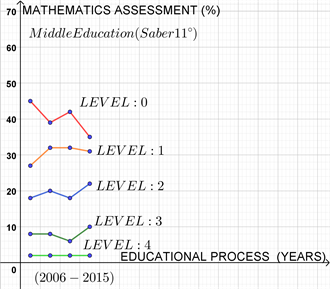
Graph 3. PISA Assessment. Source: Geogebra 5.0 Classic, data taken from Table 3.
as was said earlier in this writing that the educational process is complex and the main responsible for the results is the country’s educational system.
This can be articulated with the assertion made by OECD (2016) that the low performance of schools generates long-term consequences for both students and society, and that reducing the number of students with low achievements is a way to improve the quality of the education system and its equity, because in general students with low results come from families with socioeconomic disadvantages.
A question remains to be asked in Colombia, and when will education policy be a state policy? With a fair economic allocation, at least in line with the international average. If there are no processes in education, the results will continue to be the same. It is useless for there to be a Ministry of Education that generates policies of the current government and for there to be an education evaluation body such as ICFES if there are no solutions and basic proposals in the background that respond to the cultural and multiethnic needs of the country.
3. Conclusion
Although the PISA test assesses 15-year-old students from OECD member countries and others who have been invited to take the exam, without being affiliated to the organization, it should be noted that the mathematical competence establishes assessment criteria oriented from the particular economic framework of the global vision of the most powerful economies, but in any case without being specific in the processes of teaching and learning mathematical knowledge, from which allows particular inferences to be made, accepting the mathematics curriculum as a vision socially shared by the majority of countries on earth from which a common element is also shared in OECD in the assessment that is the contents guided (as a construction) by general processes that determine the so called mathematical competence and therefore it is a way of homogenizing a school knowledge such as mathematics.
The Saber tests are designed based on evidence-based research; however, the traditional curriculum continues to be empowered by the logic of content, at least in mathematics, which shows that framework documents such as the Basic Standards of Competencies and Curricular Guidelines have not been incorporated from the intention of the Saber tests.
Why, if institutions whose achievements are outstanding are awarded, those that are well below the average or the proposed performances are not attended with a methodology that studies both the basic conditions such as food, family, personal aspects, the technologies they have, the environment and the cultural needs required by them for their cultural and personal development?
In the analysis presented in this paper, it is clear that the responsibility for low performance in the area of mathematics does not only correspond to teaching and learning processes, but that there is more responsibility in the educational process, because it has not been continuous and also because each educational policy proposed by a government has generated changes that seem to favor more the economic model to the detriment of education.
If school mathematics has been proposed at all levels of Colombian education, is it enough just to propose knowledge differentiated into generic and non-generic? Is it enough to delegate greater responsibility to teachers?
Another important aspect to highlight is the way in which the different governments of Colombia in the last four decades have profiled their efforts not to improve processes and state policies that contribute to educational quality with social equity, but to belong to the OECD, at the cost of using education as a springboard and flag.
Conflicts of Interest
The author declares no conflicts of interest regarding the publication of this paper.
Cite this paper
Rincón, E. R. (2019). The Assessment in Mathematics: Educational Process? Creative Education, 10, 1317-1337. https://doi.org/10.4236/ce.2019.106099
References
- 1. Andina Corporation for Development (2007). Colombia. Decennial Plan of Education 2006-2015: Policy Notes. [Paper reference 1]
- 2. Baartman, L. K. J., Prins, F. J., Kirschner, P. A., & Vleuten, V. D. (2007). Determining the Quality of Competence Assessment Programs: A Self-Evaluation Procedure. Studies in Educational Evaluation, 33, 258-281. https://doi.org/10.1016/j.stueduc.2007.07.004 [Paper reference 1]
- 3. Black, P., & William, D. (1998). Assessment and Classroom Learning. Assessment in Education, 5, 7-74. https://doi.org/10.1080/0969595980050102 [Paper reference 1]
- 4. Bravo, A. A., & Fernández, del V. J. (2000). The Conventional Evaluation versus New Models of Authentic Evaluation. Psicothema, 12, 95-99. [Paper reference 1]
- 5. Castillo, A. S., & Cabrerizo, D. J. (2003). Educational Evaluation Practices. Madrid: Editorial Pearson. [Paper reference 1]
- 6. Castillo, A. S., & Cabrerizo, D. J. (2010). Educational Evaluation of Learning and Competencies. Madrid: Editorial Pearson. [Paper reference 1]
- 7. Cid, S. A., Pérez, A. A., & Zabalza, M. A. (2009). Declared Teaching Practices of the “Best Professors” of the University of Vigo. Relieve, 15, 1-29. http://www.uv.es/RELIEVE/v15n2/RELIEVEv15n2_7.htm [Paper reference 1]
- 8. Córdoba, F. (2006). The Evaluation of Students: An Open Discussion. Revista Iberoamericana de Education, 39, 1-9. [Paper reference 1]
- 9. Crooks, T. (1988). The Impact of Classroom Evaluation Practices on Students. Review of Educational Research, 58, 438-481. https://doi.org/10.3102/00346543058004438 [Paper reference 1]
- 10. Díaz-Barriga, F., & Hernández, G. (2002). Teaching Strategies for Meaningful Learning: A Constructivist Interpretation (2nd ed.). México: McGraw-Hill. [Paper reference 1]
- 11. García, J. M. (2000). What Extracurricular Factors or Biases Affect Teacher Assessment in Higher Education? Revista Mexicana de Investigación Educativa, 5, 303-325. [Paper reference 2]
- 12. González, F., Gómez, E., Rodríguez, M., & Aguilera, J. L. (2009). Prospective and Evaluation of the Teaching Practice of University Professors as an Exponent of Good Quality. Journal of the University and Knowledge Society, 6, 38-48. [Paper reference 1]
- 13. ICFES (2007). Proposal for a Conceptual Foundation in the Area of Mathematics. [Paper reference 2]
- 14. ICFES (2013). Sistema Nacional de Evaluación Estandarizada de la Educación: Alignment of the 11th SABER Exam. Bogotá. [Paper reference 6]
- 15. ICFES (2014). SABER 11 Exam Alignment: General Guidelines 2014, 2. Bogotá. [Paper reference 2]
- 16. ICFES (2017). National Results Report: Colombia in PISA 2015. [Paper reference 1]
- 17. ICFES (2019). http://www2.icfesinteractivo.gov.co/resultados.php [Paper reference 2]
- 18. Jorba, J., & Sanmartí, N. (1994). Systemic Networks. Teaching, Learning and Evaluating. A Continuous Evaluation Processes. Barcelona: Ministry of Education and Culture. [Paper reference 1]
- 19. MEN (2003). How to Understand the KNOW Tests and What Follows? Guide Series No. 2. [Paper reference 1]
- 20. MEN (2006a). Basic Standards of Proficiency in Language, Mathematics, Science, and Citizens: Guide to What Students Should Know and Know How to Do with What They Learn. Bogotá: Ministry of National Education. [Paper reference 1]
- 21. MEN (2006b). Changes in Assessment Policy, Altablero, (38), January-March. [Paper reference 2]
- 22. MEN (2010). Education Revolution 2002-2010: Actions and Lessons. Bogotá: Ministry of Education. [Paper reference 1]
- 23. MEN (2013). Presentation: Program for the Transformation of Educational Quality (pp. 1-25). [Paper reference 1]
- 24. MEN (2016). Assessment, Taken on January 4, 2019 from the MEN. https://www.mineducacion.gov.co/1759/w3-article-179264.html [Paper reference 2]
- 25. OECD (2003). Learners for Life. Student Approaches to Learning. Results from PISA 2000. Paris: OECD Publishing. https://doi.org/10.1787/9789264103917-en [Paper reference 1]
- 26. OECD (2007). PISA 2006: Science Competencies for Tomorrow’s World (Volume 1). Paris: OECD Publishing. [Paper reference 1]
- 27. OECD (2009). The OECD PISA Program: What It Is and What It Is for. https://www.oecd.org/pisa/39730818.pdf https://doi.org/10.1787/2c7c311d-en [Paper reference 1]
- 28. OECD (2013). PISA 2012 Results: What Students Know and Can Do (Volume I). [Paper reference 1]
- 29. OECD (2015). PISA 2015, Key Results. [Paper reference 1]
- 30. OECD (2016). Low-Performing Students: Why They Fall Behind and How to Help Them Succeed. http://www.oecd.org/edu/low-performing-students- 9789264250246-en.htm [Paper reference 2]
- 31. OECD (2018). “Colombia”, in Education at a Glance 2018: OECD Indicators. Paris: OECD Publishing. https://doi.org/10.1787/eag-2018-75-en [Paper reference 3]
- 32. Ortiz, J. G., & Buitrago, H. (2017). Assessment in the Colombian Educational Tradition. Social Classification Instrument. Revista Interamericana de Investigación, Educación y Pedagogía, 10, 145-172. https://doi.org/10.15332/s1657-107X.2017.0001.11 [Paper reference 1]
- 33. Pérez, A. I., & Soto, E. (2011). Lights and Shadows of PISA. Educational Meaning of External Assessments. Culture and Education. Journal of Theory, Research and Practice, 23, 171-182. https://doi.org/10.1174/113564011795944758 [Paper reference 1]
- 34. RAE (2018). The Dictionary of the Spanish Language . https://dle.rae.es/?id=H8JsfPe [Paper reference 1]
- 35. Santos, G. M. A. (2003). An Arrow on the Target. Assessment as Learning. Madrid: Editorial Narcea. [Paper reference 1]
- 36. Tiana, A. (1996). The Dilemmas of Quality and the Role of Assessment. Topics for Debate, 20, 46-51. [Paper reference 1]
- 37. Tiana, A. (1999). Assessment and Quality: Two Issues for Discussion. Essay on Public Policy in Education, 7, 25-46. [Paper reference 1]
- 38. Tobón, S., Rial, A., Carretero, M., & García, J. (2006). Competencies, Quality and Higher Education. Bogotá: Editorial Magisterio. [Paper reference 1]
- 39. UNESCO (2000). Education for All: Status and Trends 2000: Assessing Learning Achievement. [Paper reference 1]
- 40. Zaragoza, R. J. M. (2003). Attitudes of the Teachers of Obligatory Secondary School towards the Assessment of the Learning of the Students. Doctoral Thesis, Barcelona: Autonomous University of Barcelona. [Paper reference 1]
NOTES
*The assessment in mathematics: educational process.


