Received 30 December 2015; accepted 26 February 2016; published 29 February 2016

ABSTRACT

The present paper investigates the transient mixed convective boundary layer flow of an incompressible non-Newtonian quiescent nanofluid adjacent to a vertical stretching surface. The effects of the Brownian motion and thermophoresis are included for the nanofluid. Using appropriate non-similarity transformations the non-dimensional, coupled and highly non-linear system of equations is solved numerically using the efficient Keller-box implicit finite difference method for the whole transient from (initial state) to 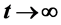(final steady-state flow). The box method is unconditionally stable. Numerical results for dimensionless velocity (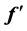), micro-rotation (g), temperature (q), nanoparticle volume fraction (f) at final steady state flow, skin friction function (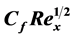), Nusselt number function () and Sherwood number function (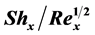) have been presented on various parameters inform of tables and graphs. The results indicate that as Nb and Nt increase, the Nusselt number decreases whereas Sherwood number increases at initial and early state time but decreases at the final steady state time. As the K increases, the friction factor decreases whereas surface mass transfer rate and the surface heat transfer rates slightly increase. The results reveal that there is a smooth transition of flow from unsteady state to the final steady state. A special case of our results is in good agreement with an earlier published work. The study has many practical applications such as extrusion of plastic sheets, paper production, glass blowing, metal spinning and drawing plastic films.

Keywords:

Nanofluid, Mixed Convection, Non-Newtonian Fluid, Brownian Motion, Keller?Box Numerical Method, Boundary Layers

1. Introduction

Mixed convection heat transfer problems in the boundary layer flows adjacent to the surface have many important applications in production and manufacturing processes. Some of the practical applications involve extrusion of plastic sheets, paper production, glass blowing, metal spinning and drawing plastic films.

The efficiencies of thermal devices and systems are related to heat transfer rates which in turn depend on the thermal conductivity of the working fluids. Despite considerable previous research and development efforts onheat transfer enhancement, the demand is growing for more efficient and robust heat transfer fluids with significantly higher thermal conductivities than traditional ones. Nanofluids are engineered by suspending nanoparticles with average sizes below 100 nm in traditional heat transfer fluids such as water, oil, and ethylene glycol. Many interesting properties of nanofluids have been reported in the past decades. The comprehensive references on nanofluids can be found in the recent book by [1] and in the review papers by [2] - [7] etc. They present the recent developments in the study of nanofluids, including the preparation methods, the evaluation methods for their stability, the ways to enhance their stability, the stability mechanisms, and their potential applications in heat transfer intensification, mass transfer enhancement, energy fields, mechanical fields, biomedical fields, and so forth.

An analytic study on the onset of convection in a horizontal layer of a porous medium with the Brinkman model and the Darcy model filled with a nanofluid was presented by [8] [9] . The flow and heat transfer characteristics on a moving plate in a nanofluid were investigated [10] . [11] studied the mixed Convection Flow of Non-Newtonian fluid from a Slotted Vertical Surface with Uniform Surface Heat Flux. [12] investigated theoretically the mixed convection in an axisymmetric stagnation flow of a non-Newtonian nanofluid on a vertical cylinder. [13] considered the unsteady free convective boundary layer flow of a nanofluid over a vertical cylinder. [14] studied the effect of Soret parameter on mixed convective flow along a vertical plate in a nanofluid under convective boundary conditions. A clear picture about the nanofluid boundary layer flows was still to emerge. [15] had been analyzed unsteady convective flow of a nanofluid over a stretching surface with variable transport properties and radiation effect in the presence of heat source. Very recently [16] , an unsteady flow, heat and mass transfer in a nanofluid over a stretching sheet was considered.

In recent years, the dynamics of micropolar fluids, originated from the theory of [17] [18] has been a popular area of search. Micropolar fluids are a special class of micromorphic fluids, in which the elements are allowed to undergo rigid rotations only without stretch. In thermo-micropolar fluid mechanics, the classical continuum and thermodynamics laws are extended with additional equations which account for the conservation of micro-iner- tia moments and the balance of first stress moments which arise due to the consideration of microstructure in a fluid. Hence, new kinematic variables (gyration tensor, micro inertia moment tensor), and concepts of body moments, stress moments and microstress are combined with classical continuum fluid dynamics theory. Thermo-micropolar fluids can accurately simulate liquids consisting of randomly oriented particles suspended in a viscous medium and offer an excellent framework to study advanced chemical engineering flow regimes. The theory may be applied to explain the flow of colloidal solutions, liquid crystals, fluids with additives, suspension solutions, blood flows, fluid with bar like elements, etc. An excellent early review about micropolar fluid mechanics is provided by [19] [20] . Thermal convection flows of micropolar fluids have been studied intensely by using numerical methodologies by [21] - [24] . [25] studied mixed convection micropolar boundary layers on a permeable sphere by Mangler transformation and potential outer flow velocity. [26] also studied mixed convection boundary layer flow about an isothermal sphere in micropolar fluid.

Moreover, combined heat and mass transfer problems over stretching surface is important in extrusion processes. The production of sheeting material arises in a number of industrial manufacturing processes and includes both metal and polymer sheets. The quality of the final product depends on the rate of heat transfer at the stretching surface. The boundary layer flow due to a stretching vertical surface in a quiescent viscous and incompressible fluid when the buoyancy forces are taken into account have been considered only with steady-state flow, but the flow and thermal fields may be unsteady due to either impulsive stretching of the surface or external stream and sudden changes in the surface temperature. In many other engineering applications, unsteadiness is an integral part of the problem. [27] studied the unsteady free convection flow over a continuous moving vertical surface in an ambient fluid, and [28] [29] investigated theoretically various stretching problems in micropolar fluids. Further, [30] [31] deal with the unsteady boundary layer flow due to impulsive starting from rest of a stretching sheet in a viscous fluid. [32] studied the coupled heat and mass transfer intransient flow by mixed convection past a vertical stretching sheet embedded in a fluid-saturated porous medium in the presence of a chemical reaction effect. [33] considered the flow and heat transfer over an unsteady shrinking sheet with suction in nanofluids.

Motivated by the above-mentioned investigations and applications, in this present paper the main objective is to investigate the unsteady mixed convective boundary layer flow of an incompressible non-Newtonian nanofluid over a stretching vertical surface in a quiescent viscous and incompressible fluid. The micropolar model is chosen for the non-Newtonian fluid since the spinning motion of the nanoparticles as they move along the stream-wise direction can be best described by the micropolar fluid model. The effects of the Brownian motion and thermophoresis are included for the nanofluid. The effects of the governing multi-physical parameters on heat and mass transfer characteristics are analyzed using a robust, implicit, well-tested finite difference method for the whole transient from 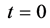(initial state) to 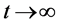(final steady-state flow). Such a study has to the authors’ knowledge thus far not appeared in the scientific literature.

2. Mathematical Model

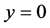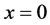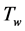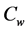Consider an unsteady, two dimensional, incompressible, combined convective boundary-layer flow of a micropolar nanofluid in the region driven by a plane surface located at with a fixed end at. The micropolar fluid model is selected to describe the motion of the solid nano particles. It is assumed the velocity components in x and y directions are u and v, respectively. We assume that and are the temperature and species (nanoparticle) concentration at the wall and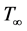, 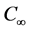are the temperature and species concentration far away from the sheet, respectively. The x-axis is taken along the stretching direction of the surface with the stretching rate where a > 0, and y-axis is perpendicular to it. When considering micro/nanoscale fluid flows several effects become increasingly important, which are typically excluded from the macroscale fluid flow. The non-Newtonian nanofluid model incorporates the effects of Brownian motion and thermophoresis. It is also assumed that all the fluid properties are constant except that of the influence of the density variation with temperature and the nanoparticles volume faction in the body force term (Boussinesq’s approximation). Figure 1 shows the schematic coordinate system and flow model.

Under the usual boundary layer approximation, the conservation equations for mass, momentum, energy and concentration can be shown to take the form:

Conservation of mass:

(1)

Conservation of linear momentum:

(2)

Conservation of angular momentum:

(3)

Conservation of energy:

(4)

Conservation of nanoparticle volume-fraction:

(5)

where, is the gyro-viscosity of micropolar fluid, j is the micro-in- ertia per unit, g is the acceleration due to gravity, is the fluid density, is the thermal conductivity, is the viscosity of the fluid, T and C are the temperature and concentration, is the density of the base fluid and is the density of the nanoparticles. and are the Brownian diffusion coefficient and the thermophoresis is diffusion coefficient, respectively, and are the heat capacity of the base fluid and the effective heat capacity of the nanoparticles material, respectively. is the thermal diffusivity.

The boundary conditions appropriate for the regime corresponding to Equations (1)-(5) are:

(6)

The above Equations (1) to (6) can be further non-dimensionalized using new variables:

, ,

(7)

where is the stream function defined in the usual way as and. Substituting (7) into Equations (1)-(6) and after some algebraic manipulation we arrive at the following transformed equations:

(8)

(9)

(10)

(11)

In the above equations, the primes denote the differentiation with respect to, the dimensionless radial coordinate, , , , are partial derivatives with respect to, the material parameter K is defined as. is the Prandtl number, is the Schmidt number, is the buoyancy ratio parameter, is the Brownian motion parameter, is the thermophoresis parameter, is the mixed convection parameter, is the local Grashof number, is the local Reynolds number. It may be noted that corresponds to the assisting flow (heated plate), corresponds to the opposing flow (cooled plate), and corresponds to the forced convection flow, respectively.

The corresponding boundary conditions are:

(12)

The engineering design quantities of physical interest include the skin-friction coefficient, Nusselt number and Sherwood number, which are given by:

(13)

(14)

(15)

3. Special Cases

To provide some means of interesting numerical calculations, we shall now obtain some special cases of the problem.

3.1. Initial State and the Early Unsteady Flow ()

For early unsteady flow, we have so Equations (8) to (11) reduce in the leading order approximation to

(16)

(17)

(18)

(19)

The corresponding boundary conditions are:

(20)

3.2. Final Steady State Flow ()

For this case Equations (8) to (11) takes the following forms:

(21)

(22)

(23)

(24)

subject to the boundary conditions (20).

4. Numerical Solution with Implicit Finite Difference Code

The Equations (8)-(11) governing the present problem under the boundary conditions (12) were solved numerically by the Keller-Box method described in the book by [34] which is an implicit finite difference scheme with unconditionally stable. This method, originally developed for low speed aerodynamic boundary layers by [35] has been employed in a diverse range of nonlinear magnetohydrodynamics and coupled heat transfer problems. Very few of these papers however have provided guidance for researchers as to customization of the Keller-box scheme to magnetohydrodynamic heat transfer problems. We therefore present a more detailed exposition here. Essentially 4 phases are central to the Keller Box Scheme. These are:

a) Reduction of the Nth order partial differential equation system to N 1st order equations

b) Finite difference discretization

c) Quasilinearization of Non-Linear Keller Algebraic Equations

d) Block-tridiagonal elimination of Linear Keller Algebraic Equations

A 2-dimensional computational grid is imposed on the x-η plane as sketched Figure 1(b). The stepping process is defined by:

(25a)

(25b)

where k_n and h_j denote the step distances in the x and h directions respectively. Denoting S as the value of any variable at station x_n, h_j, and the following central difference approximations are substituted for each reduced variable and their first order derivatives, viz:

(26a)

(26b)

(26c)

where k_n = streamwise stepping distance (x-mesh spacing) and h_j = spanwise stepping distance (h-mesh spacing) defined as follows:

(27a)

(27b)

Phase a) Reduction of the Nth order partial differential equation system to N 1st order equations

Equations (15) to (18) subject to the boundary conditions (19) are first written as a system of first-order equations. For this purpose, we introduce new dependent variables u(x,h), v(x,h), p(x,h), t(x,h) and m(x,h), and g(x,h), s = θ(x,h), z = φ(x,h) as the variables for temperature, concentration respectively. Therefore, we obtain the following nine first-order equations:

(28a)

(28b)

(28c)

(28d)

(28e)

(28f)

(28g)

(28h)

(26i)

where primes denote differentiation with respect to y. In terms of the dependent variables, the boundary conditions become:

(27)

Phase b) Finite difference discretization

The net rectangle considered in the x-hplane is shown in Figure 1(c), and the net points are denoted by:

(28a)

(28b)

where is the -spacing and is the -spacing. Here n and j are just sequence numbers that indicate the coordinate location. We approximate the quantities (f, u, v, g, p, s, t) at points of the net by, which we denote as net functions. We also employ the notion for points and quantities midway between net points and for any net function:

(29a, b)

(29c, d)

The derivatives in the x-direction are replaced by finite difference approximations. For any net function ( ), generally we have:

(30)

Further details of the solution procedure are documented in for example [36] , and omitted here for conservation of space. Effectively the complete linearized system is formulated as a block matrix system where each element in the coefficient matrix is a matrix itself. The numerical results are affected by the number of mesh points in both directions. Accurate results are produced by performing a mesh sensitivity analysis. After some trials in the y-direction a larger number of mesh points are selected whereas in the x-direction significantly less mesh points are utilized. y_max has been set at 10 and this defines an adequately large value at which the prescribed boundary conditions are satisfied. x_max is set at 1.0 for this flow domain. We have used 101 grid points in the ξ-direction and 501 grid points in the η-direction. The uniform step sizes 0.01 in ξ and 0.02 in η-directions respectively, are employed. To ensure grid independence a mesh sensitivity exercise has been performed. The convergence criterion has been set at 10⁻⁵ as the difference between the current and previous iterations for the desired accuracy.

5. Results and Discussion

A detailed parametric study has been performed for the influence of Material parameter (K), buoyancy parameter (λ), Brownian motion parameter (Nb), buoyancy ratio parameter (Nr), Thermophoretic parameter (Nt), Prandtl number (Pr), and Schmidt number (Sc) on dimensionless velocity (), micro-rotation (g), temperature

(q), nanoparticle volume fraction (f) at final steady state, skin friction function (), Nusselt number function () and Sherwood number function (). In order to assess the accuracy of the numerical

solution, we tabulated results for local Skin friction and Nusselt number for different values of λ and Pr when Nb = Nr = Nt = 0, K = 0, n = 0, Sc = 0.0 at the final steady state flow (ξ = 1). A comparison of the present results with literature data as reported by [28] suggests the present results are excellent coincide. Therefore, we believe that the comparison supports very well validity of the present results.

The viscous boundary layer flow develops slowly over the stretching surface and it becomes a fully developed flow after some time. The development of the boundary layer takes place in two stages. For small time (t = 1, i.e. 0 < ξ = 1), the flow is dominated by the viscous forces and the convective acceleration plays only a minor role in the flow development, the flow is unsteady. For large time (t → ∞, i.e. ξ = 1), the flow is dominated by the viscous forces and the convective acceleration, and the unsteady acceleration plays a minorrole in the flow development, the flow becomes steady. For the intermediate region, 1 < t < ∞, i.e. 0 < ξ < 1), there is a smooth transition from unsteady to steady flow or the transition from the unsteady to steady flow takes place without a singularity or flow instability (or formation of cells). All the obtained results furnished in Tables 1-6 for Skin friction, Nusselt and Sherwood coefficients values when final steady-state as well as unsteady flows and figures 2 to 8 for various flow distributions for different thermophysical parameters.

Results in parenthesis are reported by [28] .

Tables 2-6 present the values of Skin friction, Nusselt and Sherwood coefficients when final steady-state as well as unsteady cases for parametric values of variables governing the problem. Table shows that as material parameter (K) increases for n = 0 and 0.5, the Skin friction, Nusseltand nanoparticle Sherwood coefficients decreased. This can be utilized in applications where reduced friction and heat transfer may be attractive. Table 3 shows that as buoyancy parameter (λ) increases for n = 0 and 0.5, the friction factor and Sherwood number increase whereas heat transfer rate decreased. The value n = 0, N(x, 0) = 0, represents concentrated particle flows in which the particle density is sufficiently great that microelements close to the wall are unable to rotate. This case is also called strong interaction. The other case corresponding to n = 0.5 consequences in the vanishing of antisymmetric part of the stress tensor and represents weak concentration, so that the particle suspension is fine at the boundary because of the particle rotation is equal to fluid vorticity. When n = 1, we have flows which are representative of turbulent boundary layers. The case of n = 0.5 is considered in the present study. Form Table 3 clearly observed the friction values are higher for n = 0 than n = 0.5. Also Figure 4 depicts the same trend in the flow distributions.

Table 4 shows that the friction, heat and nanoparticle mass transfer rates for various values of K, Nt and Nb at early unsteady flow and final steady flow (ξ). As increase ξ, the friction and mass transfer rates increase whereas heat transfer rates decreased. The same trend is observed for the influence of thermophoresis parameter (Nt). Also the data interprets as increases in Brownian motion parameter (Nb), the friction and heat transfer rates are increased while nanoparticle mass transfer rates decreased.

Table 5 and Table 6 depicted the new results for small Pr = 0.7, Sc = 3 and large Pr = 100, Sc = 50 values. It can be seen that from Table 4 that when fixed Pr, increasing λ from a negative value to a positive value will increase friction rates, while increasing Pr leads to a decreasing of friction rates when λ > 0. The reverse tendency observed when λ < 0. All the friction values are coincide at a point where λ = 0, i.e. when buoyancy force is zero. This is due to uncoupling of Equations (21), (22) and (23) when λ = 0, in other words, the solutions to the flow field are not affected by the thermal field in which the buoyancy force is absent. Moreover, λ > 0 (assisting flow) produces an increase in the friction values, while λ< 0 (opposing flow) gives rise to a decrease in the local skin friction coefficient. This is because the fluid velocity increases when buoyancy force increases and hence increases the skin friction. The opposite trend occurs when buoyancy force decreases. Also, effects of λ on the locals k in friction coefficient are found to be more significant for fluids having large Prand Sc since the viscosity is greater than the fluids with small Pr and Sc. It is also observed that for particular values of Pr and Sc, the local Nusselt number is slightly increased as the buoyancy parameter λ is increased.

Figure 2 shows that the effect of material or vortex viscosity parameter K on dimensionless velocity, micro- rotation, temperature and nanoparticle volume fraction with n = 0.5 for final steady-state flow (ξ = 1). The figure represents as increases K, the velocity and micro-rotation increase whereas temperature and concentration decrease. So, the velocity boundary layer thickness increases with increasing values of K. For a particular value of K, the velocity decreases monotonically with η, and tends to zero at the outside of boundary layer. This property satisfies the boundary condition. Therefore, these figures hold the validity of the present results.

A variable relation between microrotation and the surface skin friction is appeared in the boundary condition, where n is constant and varies from 0 to 1. The distributions of fully developed velocity, micro-rotation, temperature and nanoparticle volume fraction within the boundary layer for final steady-state flow (ξ = 1) are shown in Figure 3. Figure 3 shows that as n increases, the velocity decrease but micro-rotation, temperature and nanoparticle volume fraction or concentration increase.

Figure 4 depicts the flow distributions of fully developed transient and final steady-state flow for Pr = 100 and λ = 1. The large value of Prandtl number correspond the thin boundary layer; it has the more significant ap-

plication in the particular region where we specified for heat enhancement. These figures show that the velocity profiles corresponding to increasing of ξ (0 < ξ < 1) to approach the steady profile corresponding to ξ = 1. It can be seen that all the profiles decreases monotonically with η, and become zero for away from the surface, which also holds the verification of boundary conditions. Again it is observed that the micro-rotation, temperature and concentration profiles decreased as increasing of ξ to reach steady flow.

Brownian motion is a random movement of nanoparticles and the motion occurs because of collisions with base fluid molecules. Brownian motion parameter (Nb) appears in Equations (10) and (11), Figure 5 depicts that velocity and temperature increases with increasing Nb. The reverse trend is observed for the concentration. Brownian motion increases with an increasing of temperature. Hence the heat transfer enhancement due to collision of high thermal energy with lower energy particles. The important mechanism thermophoresis is observed when a combination of particles is subjected to a temperature gradient force. The particles move in the direction of decreasing temperature. Thermophoresis parameter (Nt) appears in Equations (10) and (11) and it plays a physically powerful role in determining the diffusion of heat and nanoparticle concentration in the boundary layer. From Figure 6, we observed that the temperature and nanoparticle concentration increase as Nt increases, i.e. thermal and concentration boundary layer increased so that the system would be heated.

Figure 7 shows that as buoyancy parameter λ increases, the velocity and temperature decreased whereas micro-rotation and concentration increase. From Figure 8, the same trend is observed for Pr in the boundary layer. It is also observed that the heat transfer of the nanofluid decreases as the distance from the surface increases for small/large Pr until it reaches zero.

6. Conclusion

In this work, we have studied the problem of the unsteady mixed convection boundary layer flow of a non-Newtonian nanofluid over a stretching surface. Numerical results for surface heat transfer rate and mass transfer rate have been presented for parametric variations of the material parameters of the fluid, buoyancy parameter λ, Brownian motion parameter Nb, thermophoresis parameter Nt, Prandtl number and Schmidt number. The results indicate that as a result of the impulsive motion, the friction factor, heat transfer rate and mass trans-

fer rate have a larger values for small time (ξ ≈ 0) at the start of the motion and decrease monotonically and reach steady state at ξ = 1. There is a smooth transition from small time (at the start of the motion) to the large time (at steady state).

The results indicate that as Nt increases, the heat transfer rate (Nusselt number) decreases whereas mass transfer rate (Sherwood number) increases. As Nb increases, the surface mass transfer rate increases whereas the surface heat transfer rate decreases.

Cite this paper

Rama Subba ReddyGorla,BuddakkagariVasu,SadiaSiddiqa, (2016) Transient Combined Convective Heat Transfer over a Stretching Surface in a Non-Newtonian Nanofluid Using Buongiorno’s Model. Journal of Applied Mathematics and Physics,04,443-460. doi: 10.4236/jamp.2016.42050

References