Theoretical Economics Letters
Vol.05 No.02(2015), Article ID:56002,10 pages
10.4236/tel.2015.52039
Do the Indian Agricultural Commodities’ Prices Exhibit Non-Linear Mean Reversion? An Empirical Evidence
Aviral Kumar Tiwari, Mothkuri Aruna, Aruna Kumar Dash
IBS Hyderabad, IFHE University, Hyderabad, India
Email: aviral.eco@gmail.com, arunam@ibsindia.org, arundash06@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 March 2015; accepted 22 April 2015; published 28 April 2015
ABSTRACT
Indian economy’s inflation index often reflects double digit tendencies due to supply side short- ages caused by droughts, rise in the prices of crude oil in the international markets etc. These factors may be responsible for non-linear behaviour of inflation index. Against this backdrop, an attempt is made in this study to capture non-linear mean reversion of prices of 47 agricultural commodities of India. The study employs powerful non-linear unit root test so as to generate robust findings to infer valid policy implications. The results of the study indicate the presence of unit root with drift process for Food Grains, Cereals, Pulses, Fruits, Vegetables, Primary Articles, Ragi and Rice. And for rest of the commodities, it is observed that there is evidence of mean rever- sion and therefore, the impact would be only temporary in nature. Thus, the empirical inferences enable the policy makers to design appropriate short term and long term polices related to the prices of agricultural commodities.
Keywords:
Non-Linearity, Mean-Reversion, Prices of Agricultural Commodities, Inflation

1. Introduction
It is well known fact that country’s economic growth is closely associated with prevailing price level. Irrespective of the country’s status whether developed or developing or emerging economy, the policy makers concern is how to maintain price stability or how to achieve a desirable price level in the economy in general and agricultural commodity prices in particular. Thus, achieving a desirable range of inflation, which ensures efficient financial administration is a major challenge for the policy makers. Indian economy’s inflation index often reflects double digit tendencies due to supply side shortages caused by droughts, rise in the prices of crude oil in the international markets etc. Today the main concern of policy makers is to tackle the rising food inflation. Economic Survey of 2013-2014 reports that inflation showed signs of receding with average Wholesale Price Index (WPI) inflation falling to a three-year low of 5.98% during 2013-2014 compared to 7% and 9% over the previous two years. According to the survey, though Consumer Price Index (CPI) is more than WPI Index, it revealed the signs of moderation with CPI in terms of inflation declining from 10.21% from 2012-2013 to about 9.49% in 2013-2014. As far as food inflation is concerned, it remained persistently high during 2013-2014, reaching a peak of 11.95% in third quarter of 2013-2014.
The Indian economy which is exhibiting the features of emerging economy in terms of structural transformation from agricultural sector to service sector is associated with: rising income in rural areas particularly income groups benefited by the Mahatma Gandhi National Rural Employment Gurantee Act (MGNREGA) scheme, on one side and insufficient producer supply responses coupled with shocks from global food inflation on the other side as India integrates with the world.
The Economic Survey opines that high inflation, particularly food inflation is arising because of structural as well as seasonal factors and the commodity sub-groups that are associated with food inflation are: fruits and vegetables, egg, meat and fish. Further, Survey reports that inflation in Non-Food Manufactured Product (WPI core) is about 2.9% in 2013-2014, indicating that the underlying pressures of broad-based inflation have rather eased. The major cause for persistent inflation in India, in general and food inflation in particular, is due to changes in dietary habits and supply constraints.
There are numerous studies to capture seasonal trends, mean reversion, volatility in the area of economic and financial variables stock market, exchange rate, oil prices, output (measured by Industrial Index of Production, IIP), general inflation etc. However, literature in the area of agricultural commodities prices is scares. A recent study carried out by Gil-Alana & Tripathy [1] 1 employed fractional integration approach to examine the behaviour of the seven agricultural commodity prices in India. The results of the study indicated mean reversion in the prices of the five agricultural commodities such as Rice, Wheat, Maize, Bajra and Jowar. Further, the study documented that the general hypothesis of mean reversion was not rejected in case of Black gram and Arhar. However, the study did not consider structural breaks, role of volatility and hetroskedasticity, and non-linearity. In this study, an attempt is made to capture non-linear mean reversion of prices of 47 agricultural commodities in Indian context. This study employs powerful non-linear unit root tests so as to generate robust findings pertaining to mean reversion of agricultural commodities and to infer valid policy implications.
2. Data and Methodology
2.1. Data
All the agricultural commodity price data have been collected from the Central Statistical Organization (CSO). The data period is spanning from 2000:M1 to 2013:M1.
2.2. Methodology
Prior to empirical estimation, all the data have been seasonally adjusted through X-12 census method. For the purpose of the empirical estimation study, employs both the parametric and non-parametric tests to examine non-linear mean reversion of the prices of agricultural commodities under consideration together with testing of i.i.d. property, which is jointly refereed as random walk hypothesis.
2.2.1. Random Walk Hypothesis
To test random walk hypothesis, the study considers Rahman and Saadi’s [2] suggestion that the random walk hypothesis requires non-stationarity and serially uncorrelated increments. Thus random walk hypothesis is met in a series when it is non-stationarity and has serially uncorrelated increments. This necessitated testing of independent and identically distributed (i.i.d.) agricultural commodity prices. Therefore, the study employed test developed by Brock, Dechert, and Scheinkman [3] (henceforth BDS) and modified by Brock, Dechert, Scheinkman, and LeBaron [4] to test the i.i.d. characteristics of the agricultural commodity prices.
The BDS test is a nonparametric test with the null hypothesis that the series in question are i.i.d. against an unspecified alternative. The test is based on the concept of correlation integral, a measure of spatial correlation in 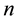 -dimensional space originally developed by Grassberger and Procaccia [5] .
-dimensional space originally developed by Grassberger and Procaccia [5] .
The specification of the model is:
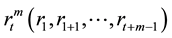
The correlation integral measures the number of 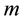 vectors within a distance of
vectors within a distance of 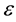 of one another. The correlation integral is defined as:
of one another. The correlation integral is defined as:
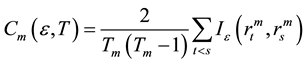
where the parameter 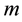 is the embedding dimension;
is the embedding dimension; 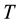 is the sample size;
is the sample size; 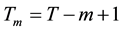 is the maximum number of overlapping vectors that can be formed with a sample size
is the maximum number of overlapping vectors that can be formed with a sample size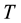 ; and
; and 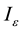 is an indicator function that is equal to one if
is an indicator function that is equal to one if 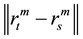 and equal to zero otherwise. A pair of vectors
and equal to zero otherwise. A pair of vectors 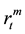 and
and 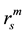 is said to be ε apart, if the maximum-norm
is said to be ε apart, if the maximum-norm  is greater or equal to ε. Under the null hypothesis of independently and identically distributed random variable,
is greater or equal to ε. Under the null hypothesis of independently and identically distributed random variable,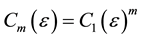 . Using this relation, the BDS test statistic can be represented as:
. Using this relation, the BDS test statistic can be represented as:
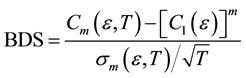
where 



2.2.2. Parametric Tests
The study employed Kapetanios, Shin, and Snell [6] non-linear unit root test which is the extended version of the DF and ADF unit root tests by allowing for nonlinear adjustment. This test is more appropriate because conventional univariate unit root tests such as the ADF test have comparatively low power to reject a false null hypothesis of unit roots (see for example, Campbell and Perron [7] ; Lothian and Taylor [8] [9] ) in the presence of breaks and non-linearity, and are sensitive to the choice of lag length (see for example, Cuddington and Liang [10] ).
KSS [6] proposed test is based on the following Exponential Smooth Transition Autoregressive (ESTAR) specification:

where 







The KSS [6] test directly focuses on the 


This is because 

To deal with this issue, KSS [6] reparameterize (1) by computing a first-order Taylor series approximation to specification (1) to obtain the auxiliary regression expressed by Equation (2):

Assuming a more general case where the errors in (2) are serially correlated, regression (2) is extended to

with the p augmentations, which are used to correct for serially correlated errors. The null hypothesis of nonstationarity to be tested with either Equation (2) or Equation (3) is H0: 



In this paper, the tNL statistics using regression (3) are estimated for de-meaned and de-trended data series and refer to them as tNL1 and tNL2, respectively. To utilize KSS [6] test the following steps are followed:
1) Regress each series on a constant or on both a constant and a time trend, respectively,
2) Save the residual obtained by regressing each series in step 1.
3) Estimate equation (3) using saved residuals in step 2.
4) Choose the appropriate lag length for step 3 to avoid problem of serial correlation.
Further, to select the lag length




2.2.3. Non-Parametric Tests
If some of the series in the data is not following normal distribution, non-parametric non linear unit root test need to be employed so as to capture non-linearity in mean reversion of prices series. For this purpose Breitung’s [12] nonparametric unit root test is employed. The test is based on the following specification:



where, 
The test involves following two steps:
1) Compute the partial sums
2) Calculate the following ratio
Under the unit root hypothesis, 







Null Hypothesis
H0: 
Alternative Hypothesis:
H1: 
3. Data Analysis and Findings
Initially the study is carried out to test whether prices of the agriculture commodities follow the normal distribution by using a battery of normality tests that includes Doornik-Hansen, Shapiro-Wilk, Lilliefors and Jarque- Bera test. The results (reported in Table 1) from all these tests of normality show that all price series of agricultural commodities have non-normal distribution. These findings indicate that all price series of agricultural commodities are non-linearly distributed.
The i.i.d property and the unit root hypothesis need to confirm to prove or disprove the random walk hypothesis. The i.i.d property is tested through the BDS test statistic. Results of BDS test statistic are also presented in Table 1. Results obtained from the BDS test statistic show that all price series of agricultural commodities have the i.i.d property.
Additionally, given the possibility that price series of agricultural commodities may indicate non-linearity, one need to detect it. To detect the nonlinear nature in the data series a battery of tests have been utilized. Employed nonlinearity tests include, White and Teraesvirta tests of neglected nonlinearities and Keenan and Tsay
Table 1. Results of normality analysis and BDS test.
Notes: Bold are not significant even at 10% level of significance. Source: Author’s calculation.
tests of nonlinearities. The null hypothesis of the White neural network test and Teraesvirta test is “the linearity in mean”. These tests use a Taylor series expansion of the activation function to arrive at a suitable test statistic. The null hypothesis of the Keenan test is that of “a linear model against a nonlinear specification”. The Tsay test explicitly tests for “quadratic serial dependence in the data”. It represents a more general form of the Keenan test. Nonlinear nature of the series may be identified if the null hypothesis is rejected by at least one test.
Results of non-linearity are presented in Table 2, which show the significant evidence of non-linearity for all commodities except Banana, Barley, Betelnut/Arecanut, Cabbage, Cardamom, Cashew Nut, Chillies (Dry), Coffee, Fish-Marine, Fruits, Fruits and Vegetables, Jowar, Masur, Pulses, Tea, Urad, and Wheat.
As the prices of some agriculture commodities such as Banana, Barley, Betelnut/Arecanut, Cabbage, Cardamom, Cashew Nut, Chillies (Dry), Coffee, Fish-Marine, Fruits, Fruits and Vegetables, Jowar, Masur, Pulses, Tea, Urad, and Wheat did not indicate significant evidence of nonlinearity, the study proceeded with two approaches namely linear and nonlinear unit root test. However, results of linear unit root tests―(such as ADF and PP) are presented only for those commodities which have not exhibited the nonlinear nature. Further, to have robust results from the linear unit root test analysis, wild-boots rapped approach is used and p-values with 10,000 replication are generated which are presented in Table 3. And to consider the non-linear nature of the price series of agricultural commodities, non-linear test of unit root test has been employed. Further, the robustness is tested through utilising a test which has stationarity as the null hypothesis and results of non-linear unit root, and linear
Table 2. Results of nonlinearity analysis.
Notes: P-value less than 0.1, and 0.05 shows the rejection of the null hypothesis at 10% and 5% level of significance, respectively. Source: Author’s calculation.
and non-linear stationarity tests are presented in Table 3.
To test the null hypothesis of unit root two non-linear unit root tests are employed-KSS [6] and Breitung’s nonparametric [12] and robustness of results obtained from the unit root analysis is tested through two nonlinear stationarity test proposed by Bierens and Guo [13] . All the tests are carried out with constant and trend model. Results from the KSS [6] test show that the null hypothesis of unit root is not rejected for Food Grains (Cereals + Pulses), Fruits, Vegetables, Primary Articles, Ragi and Rice even at 10% level of significance.
Bierens and Guo [13] test is employed so as to check the robustness of estimated results. The test assumes that series are zero-mean stationary process against the alternative that they are unit root with drift process. Breitung’s [12] test assumes that series is a unit root with drift process in the null and it is a trend stationary process in the alternative hypothesis. The Breitung’s [12] test rejects the null hypothesis of unit root against the alternative of trend stationary process for Banana, Brinjal, Cabbage, Garlic, Onion, Papaya, Potato, Sweet Potato, and Vegetables. However, Bierens and Guo [13] tests at 10% level of significance rejects the null hypothesis of zero-mean stationary process against the alternative hypothesis of unit root with drift process for Arhar, Bajra, Beef & Buffalo Meat, Betelnut/Arecanut, Black Pepper, Cardamom, Cashew Nut, Cereals, Chillies (Dry), Coffee, Condiments & Spices, Cummin, Egg, Eggs, Meat & Fish, Fish-Inland, Fish-Marine, Food Articles, Food Grains (Cereals + Pulses), Garlic, Ginger (Dry), Gram, Guava, Jowar, Maize, Milk, Moong, Okra (Lady Finger), Other Food Articles, Pork, Poultry Chicken, Primary Articles, Pulses, Ragi, Rice, Tapioca, Tea, Turmeric, Urad, Vegetables, and Wheat. The null hypothesis of unit root through the application of linear unit root tests (i.e., the PP test) is rejected only for Banana, Barley, Cabbage, Fruits and Fruits and Vegetables and for other commodities such as Betelnut/Arecanut, Cardamom, Cashew Nut, Chillies (Dry), Coffee, Fish-Marine, Jawar, Masur, Pulses, Tea, Urad, & Wheat the H0 is not rejected by PP test.
Table 3. Results of non-linear unit root and stationarity analysis.
Note: For Bierens-Guo trend stationarity tests critical values at 5% and 10% level of significance, respectively, are 12.706 and 6.314 and for Breitung’s nonparametric unit root test critical values at 5% and 10% level of significance, respectively, are 0.00343 and 0.00438. Bold are significant. Source: Author’s calculation.
4. Conclusion
Given the importance of inflation, in general and agricultural commodity prices in particular, this study attempted to find out the agricultural commodities whose prices have tendency to revert to mean (and specifically whose prices follow a random walk). In doing so, the study employed a battery of non-linear unit root tests and stationarity test. The study concludes that Food Grains (Cereals + Pulses), Fruits & Vegetables, Primary Articles, Ragi and Rice follow the unit root with drift process (at 10% level of significance) and rest of prices series of agricultural commodities exhibited the mean reversion behaviour. Though, there is evidence of unit root hypothesis supported by some more commodities but for those there is no robust evidence. This is because results change with the approach used to test the mean reversion behaviour of the price series of agricultural commodities. Therefore, it can be concluded that for the commodities exhibiting the unit root behaviour (such as, Food Grains (Cereals + Pulses), Fruits & Vegetables, Primary Articles, Ragi and Rice), policy decisions related to the fixing of maximum prices or ceiling pricing methods would give fruitful results. For rest of the commodities exhibiting the mean reversion behaviour any policy shock would have only temporary effect. Thus, the empirical results enable the policy makers to design their short term and long term policies related to the prices of agricultural commodities.
References
- Gil-Alana, L.A. and Tripathy, T. (2014) Mean Reversion in Agricultural Commodity Prices in India. International Advanced Economic Research, 20, 385-398.
- Rahman, A. and Samir, S. (2008) Random Walk and Breaking Trend in Financial Series: An Econometric Critique of Unit Root Tests. Review of Financial Economics, 17, 204-212. http://dx.doi.org/10.1016/j.rfe.2007.05.002
- Brock, W.A., Dechert, W.D. and Scheinkman, J.A. (1987) A Test for Independence Based on the Correlation Dimension, Department of Economics. University of Wisconsin at Madison, University of Houston, and University of Chicago.
- Brock, W.A., Scheinkman, J.A., Dechert, W.D. and LeBaron, B. (1996) A Test for Independence Based on the Correlation Dimension. Econometric Reviews, 15, 197-235. http://dx.doi.org/10.1080/07474939608800353
- Grassberger, P. and Procaccia, I. (1983) Measuring the Strangeness of Strange Attractors. Physica D (Nonlinear Phenomena), 9, 189-208.
- Kapetanios, G., Shin, Y. and Snell, A. (2003) Testing for a Unit Root in the Nonlinear STAR Framework. Journal of Econometrics, 112, 359-379. http://dx.doi.org/10.1016/S0304-4076(02)00202-6
- Campbell, J.Y. and Perron, P. (1991) Pitfalls and Opportunities: What Macroeconomists Should Know about Unit Roots. NBER Macroeconomics Annual, 6, 141-201. http://dx.doi.org/10.2307/3585053
- Lothian, J.R. and Taylor, M.P. (1996) Real Exchange Rate Behaviour: The Recent Float from the Perspective of the Past Two Centuries. Journal of Political Economy, 104, 488-509. http://dx.doi.org/10.1086/262031
- Lothian, J.R. and Taylor, M.P. (1997) Real Exchange Rate Behavior. Journal of International Money and Finance, 16, 945-954. http://dx.doi.org/10.1016/S0261-5606(97)00014-4
- Cuddington, J.T. and Hong, L. (2000) Purchasing Power Parity over Two Centuries? Journal of International Money and Finance, 19, 753-757. http://dx.doi.org/10.1016/S0261-5606(00)00029-2
- Hall, A.D. (1994) Testing for a Unit Root in Time Series with Pre-Test Data Based Model Selection. Journal of Business and Economic Statistics, 12, 461-470.
- Breitung, J. (2002) Nonparametric Tests for Unit Roots and Cointegration. Journal of Econometrics, 108, 343-363. http://dx.doi.org/10.1016/S0304-4076(01)00139-7
- Bierens, H.J. and Guo, S. (1993) Testing Stationarity and Trend Stationarity against the Unit Root Hypothesis. Econometric Reviews, 12, 1-32. http://dx.doi.org/10.1080/07474939308800252
- Ng, S. and Perron, P. (1995) Unit Root Tests in ARMA Models with Data Dependent Methods for the Selection of the Truncation Lag. Journal of the American Statistical Association, 90, 268-281. http://dx.doi.org/10.1080/01621459.1995.10476510
NOTES
1To the best of our knowledge this is only one study for Indian context in this regard.
2The “t-sig” approach has been shown to produce test statistics which have better properties in terms of size and power than information-based methods such as the Akaike Information Criterion or Schwartz Bayesian Criterion (see for example, Hall [11] , Ng and Perron, [14] ).
3We used conventional level of significance that is 5% level of significance as a benchmark and fixed kmax = 12.





