Theoretical Economics Letters
Vol. 2 No. 2 (2012) , Article ID: 19330 , 4 pages DOI:10.4236/tel.2012.22041
Revisiting the Effects of Economic Incentives on Motivation
Department of Economics and Finance, State University of New York, Plattsburgh, USA
Email: kpetr001@plattsburgh.edu
Received March 7, 2012; revised April 5, 2012; accepted April 10, 2012
Keywords: Incentives; Intrinsic Motivation; Non-Additive Probability
ABSTRACT
This paper presents a formal framework for modeling the effects of economic incentives on motivation. While economic models represent the utilities from monetary incentives and private benefits in an additive form, studies in psychology show that extrinsic and intrinsic motivation are non-additive and that there exists a continuum between the two. To accommodate for possible interaction effects, a non-additive probability model and evidence theory have been used in the principal-agent set-up. The model produces results consistent with prior evidence presented in social psychology studies.
1. Introduction
The interactions between economic incentives and intrinsic motivation have been widely documented in economics literature (see, for example, [1] and more recently [2] for surveys). Similarly, in social psychology, there is a vast amount of literature exploring the effect of rewards on intrinsic motivation ([3-5]). The main evidential claim presented is that, under certain conditions, monetary rewards decrease intrinsic motivation, and this may result in reduction of the activity or performance. This premise is based on the underlying assumption that every activity indeed has intrinsic motivation. Commonly accepted are two theoretical explanations: self-perception theory and cognitive evaluation theory [6]. The selfperception theory postulates that individuals do not have information about their own motives ([7,8]). Instead, they have to infer them from the circumstances under which the activity takes place. One representation of this idea is [9], who uses a simple informed-principal model to show how an agent, uncertain about his abilities, deduces his motives through the signaling mechanism. The agent interprets given reward as a signal of having low ability or as one of an unattractive task being proposed. In the absence of rewards he assigns the motives of performing to his intrinsic motivation. The cognitive evaluation theory [5] assumes that people have psychological needs for self-determination, competence and autonomy. It is the effect of rewards on these three elements that matters. When rewards are perceived as controlling, there is a negative effect on self-determination and autonomy. Hence, intrinsic motivation is undermined. Conversely, when rewards have an informational role (feedback, recognition etc.) they enhance intrinsic motivation by affecting the individual’s competence. The cognitive evaluation theory has more recently been generalized into the self-determination theory [10] which allows for a continuum between intrinsic and extrinsic motivation.
This paper offers a novel approach to model the effect of economic incentives on motivation as it is related to self-determination, autonomy and competence in cognitive evaluation theory by employing a subjective probability concept. To be able to use this set-up one more change must be made. Most economics studies represent the utilities from monetary incentives and private benefits in an additive form. In psychological literature extrinsic and intrinsic motivation are non-additive, but exhibit some form of interrelation and form a continuum ([5,10]). This paper will extend the formal set-up by employing a non-additive probability model, which allows the capturing of effects from interaction. At the same time this can be viewed more generally as an extension of the standard economic model of worker’s motivation.
2. Subjective Probability Model
Consider the following non-additive probability model1:
 (1)
(1)
where x is a vector of extrinsic rewards, y is a vector of intrinsic rewards,  is the probability level of total motivation (resulting from extrinsic and intrinsic factors),
is the probability level of total motivation (resulting from extrinsic and intrinsic factors), 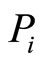 is the probability level of intrinsic motivation,
is the probability level of intrinsic motivation, 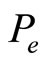 is the probability level of extrinsic motivation, and λ is a coefficient representing the degree of influence of the interaction between intrinsic and extrinsic rewards on the total motivation2. This model can be interpreted as follows: The total level of motivation
is the probability level of extrinsic motivation, and λ is a coefficient representing the degree of influence of the interaction between intrinsic and extrinsic rewards on the total motivation2. This model can be interpreted as follows: The total level of motivation  is affected either extrinsically
is affected either extrinsically 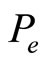 via some extrinsic reward x or intrinsically
via some extrinsic reward x or intrinsically 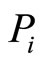 via some intrinsic reward y, or to some extent λ by the mutual interaction between x and y. Formally, this is a representation of the idea coming from psychology literature that extrinsic and intrinsic motivetion are non-additive, but exhibit some form of interacttion [10]. On the other hand, this can be viewed as an extension of the standard economic model of worker’s motivation which allows for a more comprehensive description of motivation, including the concept of intrinsic motivation. In the light of a principal-agent model, the following notations are used:
via some intrinsic reward y, or to some extent λ by the mutual interaction between x and y. Formally, this is a representation of the idea coming from psychology literature that extrinsic and intrinsic motivetion are non-additive, but exhibit some form of interacttion [10]. On the other hand, this can be viewed as an extension of the standard economic model of worker’s motivation which allows for a more comprehensive description of motivation, including the concept of intrinsic motivation. In the light of a principal-agent model, the following notations are used:
• The principal’s assessment of the total probability 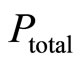 is
is . This is a subjective probability which represents how certain the principal (she) is about the agent’s motivation.
. This is a subjective probability which represents how certain the principal (she) is about the agent’s motivation.
• The agent (he) has his own assessment of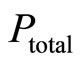 ,
, . It is assumed that
. It is assumed that . The case when
. The case when  is analyzed later on.
is analyzed later on. 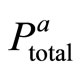 is also subjective and uncertain to some extent.
is also subjective and uncertain to some extent.
• The assumption is made that when the principal selects an extrinsic reward scheme  she is able to calculate
she is able to calculate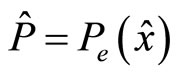 . The same concerns the agent, i.e. his probability level with respect to particular extrinsic reward scheme
. The same concerns the agent, i.e. his probability level with respect to particular extrinsic reward scheme 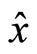 is
is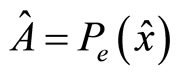 .
.
• The influence parameter λ is positive and λ ∈ [0, 1], where λ = 0 means that there is no interaction between extrinsic and intrinsic incentive schemes, but λ = 1 means strict interaction.
The principal forms 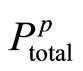 and selects a relative policy
and selects a relative policy , neither knowing the precise value of
, neither knowing the precise value of 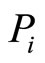 nor how this policy will affect
nor how this policy will affect . This paper discusses policy as opposed to a simple incentive scheme since y* as an element of this policy is not strictly defined. Choosing x* corresponds to the preparation of an incentive scheme in the standard principle-agent model. The new element here is how y* is taken into consideration to enable choice of the optimal x* regarding the agent’s real motivation. Note that when
. This paper discusses policy as opposed to a simple incentive scheme since y* as an element of this policy is not strictly defined. Choosing x* corresponds to the preparation of an incentive scheme in the standard principle-agent model. The new element here is how y* is taken into consideration to enable choice of the optimal x* regarding the agent’s real motivation. Note that when 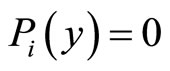 there is no intrinsic motivation; this results in
there is no intrinsic motivation; this results in
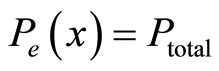 bringing the model back to the standard incentive model. The principal’s goal is to stimulate the agent’s initiative and intrinsic motivation through a proper combination of x* and a particular set-up of p which results in y*.
bringing the model back to the standard incentive model. The principal’s goal is to stimulate the agent’s initiative and intrinsic motivation through a proper combination of x* and a particular set-up of p which results in y*.
3. Aggregation of  and
and 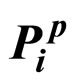
This section explores the uncertainty brought by introducing intrinsic motivation. For reasons that will be detailed later in this paper, a method to aggregate 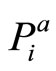 and
and 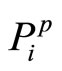 must be developed. Both
must be developed. Both  and
and  are overor underestimated. Wh le
are overor underestimated. Wh le  can be measured relative to its argument x* and any possible overor underestimation recovered, a similar measure cannot be achieved with respect to the pair
can be measured relative to its argument x* and any possible overor underestimation recovered, a similar measure cannot be achieved with respect to the pair 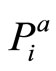 and
and . These two probabilities are dependent on the incentive scheme y* which is non-measurable. The uncertainty through
. These two probabilities are dependent on the incentive scheme y* which is non-measurable. The uncertainty through  and
and  is thus higher in comparison to
is thus higher in comparison to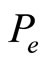 . They are more subjective. To derive an expression for the aggregation of
. They are more subjective. To derive an expression for the aggregation of 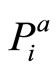 and
and 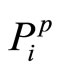 the evidence theory and the principle of maximum non-specificity ([11,12]) are used.
the evidence theory and the principle of maximum non-specificity ([11,12]) are used.
Let us consider a finite set of task-specific intrinsic motivators X. From this set, three subsets are of interest: the set A of intrinsic motivators which the principal considers as active with respect to incentive scheme y*; the set B of intrinsic motivators which the agent considers as active with respect to the incentive scheme y*, and the set 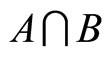 which is treated as an intersection between the active intrinsic motivators relative to the opinion of both the agent and the principal. In this sense a particular incentive scheme is optimal when
which is treated as an intersection between the active intrinsic motivators relative to the opinion of both the agent and the principal. In this sense a particular incentive scheme is optimal when . The subsets A and B are claimed for a particular y* to degrees
. The subsets A and B are claimed for a particular y* to degrees  and
and  respectively. Those degrees represent the total beliefs that put the attention on A and B. The aim now is to estimate the belief of
respectively. Those degrees represent the total beliefs that put the attention on A and B. The aim now is to estimate the belief of 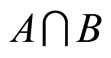 relative to the incentive scheme y* using the principle of maximum non-specificity. This principle is a safeguard that does not allow us to produce an answer that is more specific than warranted by the evidence, i.e.
relative to the incentive scheme y* using the principle of maximum non-specificity. This principle is a safeguard that does not allow us to produce an answer that is more specific than warranted by the evidence, i.e. 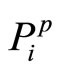 and
and . The use of the principle of maximum non-specificity leads, in this case, to the following optimization problem ([11,13]): determine the values of
. The use of the principle of maximum non-specificity leads, in this case, to the following optimization problem ([11,13]): determine the values of  and
and  for which the function:
for which the function:
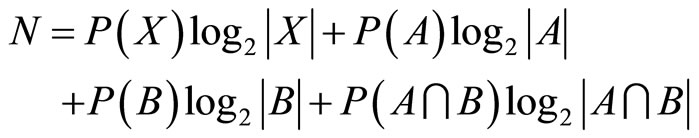 (2)
(2)
reaches its maximum when subjected to the following constraints:
 (3)
(3)
 (4)
(4)
 (5)
(5)
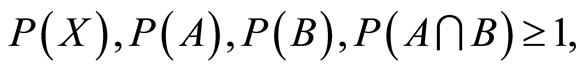 (6)
(6)
where  and
and 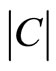 represents the cardinality of the subset
represents the cardinality of the subset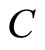 . The function N describes nonspecificity in evidence theory and is considered a generalized measure of uncertainty. In general, for arbitrary element
. The function N describes nonspecificity in evidence theory and is considered a generalized measure of uncertainty. In general, for arbitrary element 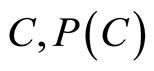 indicates the degree of evidence focusing on
indicates the degree of evidence focusing on , while
, while 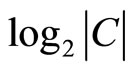 indicates the lack of specificity of this evidential claim. The larger the value of
indicates the lack of specificity of this evidential claim. The larger the value of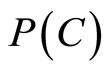 , the stronger the evidence; the larger the set
, the stronger the evidence; the larger the set 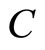 (and
(and ), the less specific the evidence. The total beliefs
), the less specific the evidence. The total beliefs 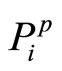 and
and 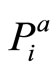 assess not only
assess not only  and
and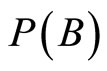 , but
, but  as well. This corresponds to the premise that both the principal and the agent forecast not only their own
as well. This corresponds to the premise that both the principal and the agent forecast not only their own , but also the degree to which their claim coincides with the claim of the opponent player, i.e.
, but also the degree to which their claim coincides with the claim of the opponent player, i.e.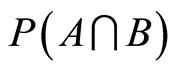 . The constraints are represented with three linear algebraic equations of four unknowns and by the requirement that the unknowns be nonnegative and real. The first two equations represent the evidence relative to the principal and to the agent respectively; the third inequality represents a general constraint in evidence theory. After selecting
. The constraints are represented with three linear algebraic equations of four unknowns and by the requirement that the unknowns be nonnegative and real. The first two equations represent the evidence relative to the principal and to the agent respectively; the third inequality represents a general constraint in evidence theory. After selecting  as an independent variable, the following is obtained
as an independent variable, the following is obtained
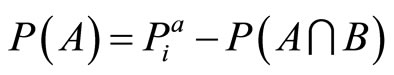 (7)
(7)
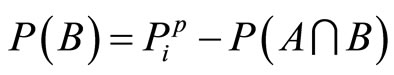 (8)
(8)
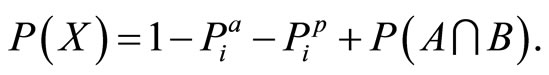 (9)
(9)
Since all unknowns must be nonnegative, from the first two equations one can evaluate the upper bound for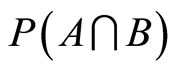 . Further, from
. Further, from
 (10)
(10)
 (11)
(11)
it follows that
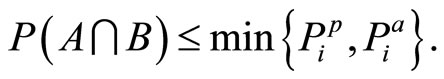 (12)
(12)
The third equation with respect to  specifies the lower bound of
specifies the lower bound of . Indeed, for
. Indeed, for  it follows that:
it follows that:
 (13)
(13)
 (14)
(14)
If 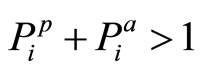 then
then
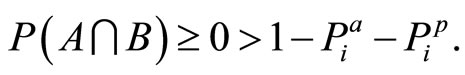 (15)
(15)
But  should be nonnegative, hence for the lower bound it follows that
should be nonnegative, hence for the lower bound it follows that
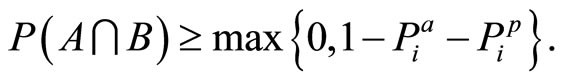 (16)
(16)
The bounds, thus, are
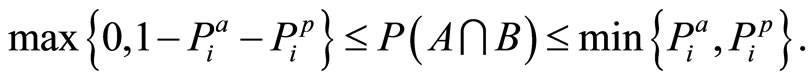 (17)
(17)
Using Equations (7)-(9), the objective function N now can be expressed in terms of . After some rearrangements and simplification the result is
. After some rearrangements and simplification the result is
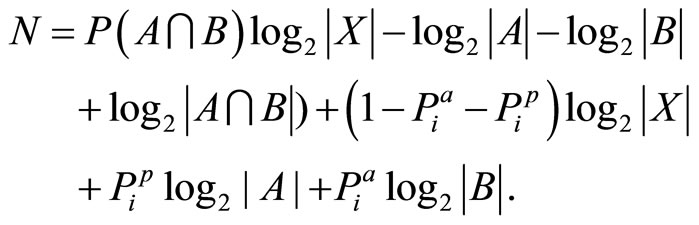 (18)
(18)
It is clear that only the first term in this expression can influence the value of the objective function, so it can be rewritten as
 (19)
(19)
where
 (20)
(20)
and
 (21)
(21)
are constants. The solution of the optimization problem depends only on the value of K1. The assumption is made that A, B, and 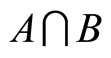 are non-empty subsets in X and thus
are non-empty subsets in X and thus . If
. If 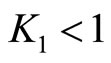 then
then  and the maximum of N is attained after minimization of
and the maximum of N is attained after minimization of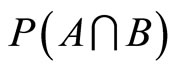 , i.e.
, i.e. , and
, and 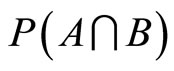 attains a minimum equal to its lower bound. If
attains a minimum equal to its lower bound. If 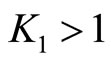 then
then 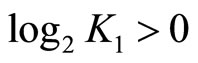 and must maximize
and must maximize  , i.e.
, i.e. . When
. When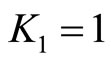 ,
,  , and thus N is independent of
, and thus N is independent of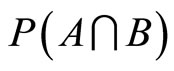 . This implies that every value in the interval
. This implies that every value in the interval  is a solution of the optimization problem. The complete solution for
is a solution of the optimization problem. The complete solution for 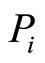 relative to y∗ can thus be expressed by the following equations:
relative to y∗ can thus be expressed by the following equations:
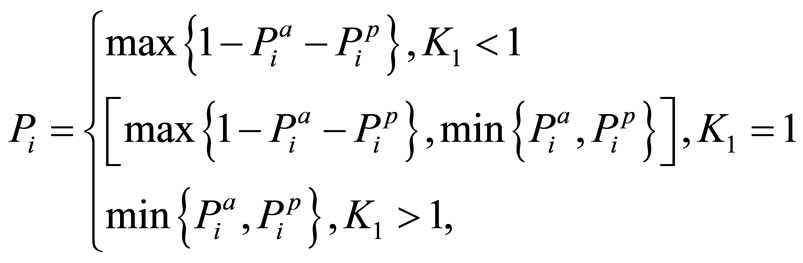 (22)
(22)
where 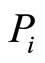 is the associated degree of belief.
is the associated degree of belief.
4. Model Problem
The following model refers to the principal
 (23)
(23)
What happens to the agent? The agent needs to have his participation and incentive compatibility constraints satisfied. This results in known A and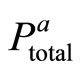 , but uncertain
, but uncertain 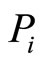 and λ. Where
and λ. Where 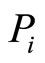 is defined in the sense of Equation (22). Hence, the agent behaves with respect to the following model:
is defined in the sense of Equation (22). Hence, the agent behaves with respect to the following model:
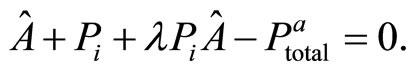 (24)
(24)
In general, we can use the following system to describe the principal-agent relationship:
 (25)
(25)
 (26)
(26)
In this system the unknown are 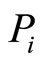 and λ. Solving the system gives us:
and λ. Solving the system gives us:
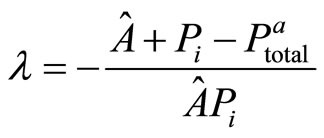 (27)
(27)
and
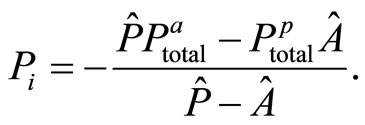 (28)
(28)
Let us investigate how  is affected by the extrinsic rewards vector. This means to investigate the first derivative of
is affected by the extrinsic rewards vector. This means to investigate the first derivative of 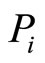 with respect to P. The latter is
with respect to P. The latter is
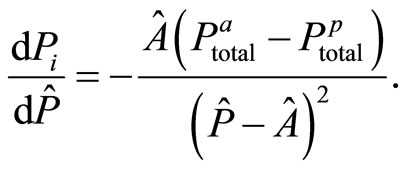 (29)
(29)
Clearly A is positive and hence the sign of 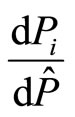 depends on the sign of
depends on the sign of . The following two cases can be considered:
. The following two cases can be considered:
1)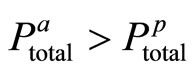 , with a possible interpretation that the extrinsic reward policy employs controlling effect, and this is a signal for the agent which decreases his intrinsic motivation, i.e.
, with a possible interpretation that the extrinsic reward policy employs controlling effect, and this is a signal for the agent which decreases his intrinsic motivation, i.e.
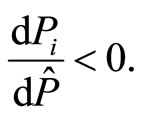 (30)
(30)
2)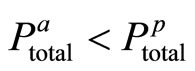 , with a possible interpretation that the extrinsic reward policy plays an informational role, which increases the agent’s intrinsic motivation, i.e.
, with a possible interpretation that the extrinsic reward policy plays an informational role, which increases the agent’s intrinsic motivation, i.e.
 (31)
(31)
5. Conclusion
This paper proposes a novel approach to model the effect of economic incentives on motivation by employing subjective probability concept. While economic models represent the utilities from monetary incentives and private benefits in an additive form, studies in psychology show that extrinsic and intrinsic motivation are non-additive and that there exists a continuum between the two. The proposal of this paper is to extend the formal set-up by employing a non-additive probability model, which allows capturing the effects from interaction. The model produces results consistent with the evidence in social psychology studies.
REFERENCES
- B. Frey and R. Jegen, “Motivation Crowding Theory,” Journal of Economic Surveys, Vol. 15, No. 5, 2001, pp. 589-611. doi:10.1111/1467-6419.00150
- A. Festré, “Incentives and Social Norms: A Motivation-Based Economic Analysis of Social Norms,” Journal of Economic Surveys, Vol. 24, No. 3, 2009, pp. 511-538. doi:10.1111/j.1467-6419.2009.00594.x
- E. Deci, “Effects of Externally Mediated Rewards on Intrinsic Motivation,” Journal of Personality and Social Psychology, Vol. 18, No. 1, 1971, pp. 105-115. doi:10.1037/h0030644
- E. Deci and R. Ryan, “Intrinsic Motivation and Self-Determination in Human Behavior,” Plenum, New York, 1985.
- E. Deci, R. Koestner and R. Ryan, “A Meta-Analytic Review of Experiments Examining the Effects of Extrinsic Rewards on Intrinsic Motivation,” Psychological Bulletin, Vol. 125, No. 6, 1999, pp. 627-668. doi:10.1037/0033-2909.125.6.627
- E. Fehr and A. Falk, “Psychological Foundations of Incentives,” European Economic Review, Vol. 46, No. 4-5, 2002, pp. 687-724. doi:10.1016/S0014-2921(01)00208-2
- D. Bem, “Self-Perception: The Dependent Variable of Human Performance,” Organizational Behavior and Human Performance, Vol. 2, No. 2, 1967, pp. 105-121. doi:10.1016/0030-5073(67)90025-6
- D. Bem, “Self-Perception Theory,” In: L. Berkowitz, Ed., Advances in Experimental Social Psychology, Academic Press, New-York, Vol. 6, 1972.
- R. Benabou and J. Tirol, “Self-Confidence and Personal Motivation,” Quarterly Journal of Economics, Vol. 117, No. 3, 2002, pp. 871-916. doi:10.1162/003355302760193913
- M. Gagne and E. Deci, “Self-Determination Theory and Work Motivation,” Journal of Organizational Behavior, Vol. 26, No. 4, 2005, pp. 331-362. doi:10.1002/job.322
- D. Dubois and A. Prade, “A Note on Measures of Specificity for Fuzzy Sets,” International Journal of General Systems, Vol. 10, No. 4, 1985, pp. 279-283. doi:10.1080/03081078508934893
- G. Klir, “Principles of Uncertainty: What Are They? Why We Need Them?” Fuzzy Sets and Systems, Vol. 74, No. 1, 1995, pp. 15-31. doi:10.1016/0165-0114(95)00032-G
- D. Dubois and A. Prade, “The Principle of Minimum Specificity as a Basis for Evidential Reasoning,” In: B. Bouchon-Minier and R. Yager, Eds., Uncertainty in Knowledge-Based Systems, Springer, New-York, 1987.
NOTES
1The main feature of subjective probability is that it recovers the intuitive concept of probability as a degree of belief. In contrast to the standard theory, these beliefs can be represented by non-additive probabilities.
2x is defined in the sense of standard incentive schemes, while y can be interpreted as the subjective intrinsic reward from performing a particular task. Due to its nature, Pi(y) cannot be formally measured. However, a proxy can be constructed to give us an approximation of the degree of an agent’s intrinsic motivation.

