Optics and Photonics Journal
Vol.3 No.1(2013), Article ID:29262,7 pages DOI:10.4236/opj.2013.31021
Steady-State Behavior of Semiconductor Laser Diodes Subject to Arbitrary Levels of External Optical Feedback
Institut Mines-Telecom, Telecom SudParis, Département Electronique et Physique, UMR 5157 CNRS, Evry, France
and CEA Saclay Nano-Innov, Gif sur Yvette, France
Email: qin.zou@telecom-sudparis.eu
Received November 21, 2012; revised December 12, 2012; accepted December 30, 2012
Keywords: Semiconductor Lasers; External Optical Feedback; Iterative Traveling-Wave Model; Compound Cavity Modes; Lang-Kobayashi Model; External Cavity Modes; Feedback Lasers
ABSTRACT
This paper investigates the steady-state behavior of a semiconductor laser subject to arbitrary levels of external optical feedback by means of an iterative travelling-wave (ITW) model. Analytical expressions are developed based on an iterative equation. We show that, as in good agreement with previous work, in the weak-feedback regime of operation except for a phase shift the ITW model will be simplified to the Lang-Kobayashi (LK) model, and that in the case where this phase shift is equal to zero the ITW model is identical to the LK model. The present work is of use in particular for distinguishing the coherence-collapse regime from the strong-feedback regime where low-intensity-noise and narrow-linewidth laser operation would be possible at high feedback levels with re-stabilization of the compound laser system.
1. Introduction
Continuous efforts have been made since the last three decades on the dynamics of semiconductor lasers with external optical feedback, because of a large variety of interesting properties they exhibit. A laser with delayed feedback builds an ideal system for analyzing and exploring typical phenomena encountered in a nonlinear time-delayed system, such as bifurcations, thresholds of instability (or stability) and routes to deterministic chaos. On the other hand, external optical feedback can severely affect the spectral behavior of a laser. It can also produce undesirable effects whose effective control is therefore essential for many applications such as optical-fiberbased transmission and sensor systems, since both of them are highly dependent on the spectral quality (temporal coherence and frequency stability) of the used light sources.
In parallel with numerous experimental investigations, theoretical approaches have also been developed aimed at a better understanding of the nonlinear dynamics of a compound laser system (see for example, Tromborg et al. [1], Schunk and Petermann [2], and Binder and Cormack [3]). Most of these approaches have been developed on the basis of the rate equations proposed by Lang and Kobayashi (LK) [4]. For the weak-feedback regime of operation (feedback power ratio less than −30 dB), these approaches have been found to describe adequately various phenomena so far observed experimentally, such as the threshold of coherence collapse (CC), the low-frequency fluctuations (LFFs), and the period-doubling route to chaos [5]. The LK rate equations have also been used to explain the physical mechanisms of the steady-state [6] and transient [7] LFFs, as well as of the chaotic itinerancy for the case of relatively strong feedback [6].
It has been shown that the LK rate equations can be solved analytically by use of asymptotic methods (A detailed description can be found in [8]). In this approach, a laser with weak optical feedback is regarded as a weaklyperturbed nonlinear dynamic system and the threshold of instability corresponds to the first Hopf bifurcation of the LK rate equations. An attempt has been made at interpreting experimental findings of InAs/InP quantum-dash Fabry-Perot lasers by using this approach, such as the onset of CC and the transition from the regime of LFFs to the regime of so-termed fully-developed coherence collapse (FDCC) [9].
Originally, the LK rate equations were proposed to model a single-mode laser with weak feedback and large delays. When the reflectivity of the external reflecting surface is comparable with or greater than the laser facet reflectivity, strong feedback should be taken into account. In this case, the use of the LK model would no longer be justified. Thus, in order to describe the behavior of a feedback laser with arbitrary feedback levels, an iterative traveling-wave (ITW) model was developed [10,11]. By using this model, dynamic and noise properties of a laser subject to strong optical feedback were numerically investigated [12]. The ITW model predicts in particular a significant decrease of the intensity noise in the strongfeedback regime.
More recently, Radziunas et al. used the travelingwave (TW) approach proposed in [13,14] to model a feedback laser, where the system is described by partial differential equations for the electrical fields which counter-propagate along the longitudinal axis of the laser and are coupled through the usual carrier rate equation. A comparison has been made between the LK and TW models, with emphasis on the stability analysis of cavity modes in their continuous-wave states [15].
This paper investigates the steady-state behavior of a feedback laser with arbitrary feedback levels by means of the ITW model. It may be considered as an extension of the works of Langley et al. [12] and Spencer et al. [16]. We provide additional information about the physical insight into a compound laser system and discuss the similarities and the differences between the ITW and LK models. In Section 2, steady-state solutions will be derived for the external cavity modes and compared with previous work. In Sections 3 and 4, a detailed quantitative comparison between the ITW and LK models will be made and the rigorous condition will be given, under which the ITW model will be simplified to the LK model. Finally, Section 5 will summarize our conclusions.
2. Iterative Traveling-Wave Model
Consider the configuration of Figure 1. A single-longitudinal-mode laser diode is in resonance with an external Fabry-Perot cavity. We assume that r1, r2 and r3 are all real and dispersionless. For this three-mirror system, the dominant resonator is defined by the mirrors with reflection coefficients r1 and r3, and multiple round trips inside the external cavity should be in general taken into account for an arbitrary feedback level.

Figure 1. Schematic drawing of a laser diode with external optical feedback. ω0: emission (angular) frequency of the laser without feedback; τin: internal round-trip time; r1: reflection coefficient of the rear facet of the laser; r2: reflection coefficient of the front facet of the laser; r3: reflection coefficient of the external mirror; Ẽ(t): right-moving electric field passing through the laser front facet; L: length of external cavity assumed empty.
2.1. Steady-State Solutions
The right-moving electrical field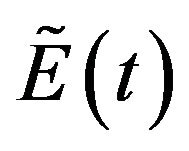 , calculated at steps of the internal round-trip time τin (in seconds) satisfies the following iterative equation [12,16]
, calculated at steps of the internal round-trip time τin (in seconds) satisfies the following iterative equation [12,16]
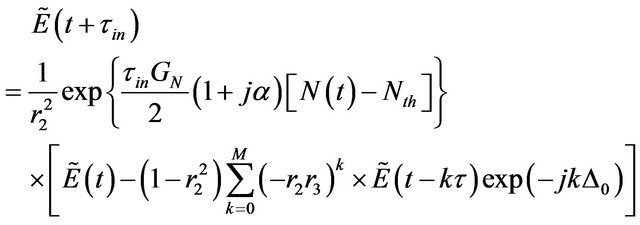 (1)
(1)
In this equation, GN (in s−1∙m3) is the differential gain; α is the linewidth enhancement factor (LEF);  (in m−3) is the carrier density and
(in m−3) is the carrier density and 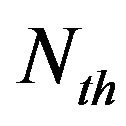 its threshold; τ (in seconds) is the external round-trip time and
its threshold; τ (in seconds) is the external round-trip time and  (in rad,
(in rad, ) is the initial feedback phase associated with the emission frequency of the solitary laser operating near threshold.
) is the initial feedback phase associated with the emission frequency of the solitary laser operating near threshold.
By inserting 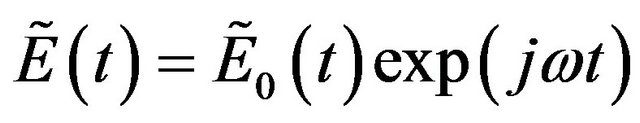 into Equation (1) and considering steady-state solutions, we obtain the following expressions for the excess gain
into Equation (1) and considering steady-state solutions, we obtain the following expressions for the excess gain 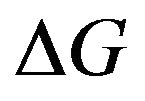 (in s−1) and the feedback phase Δ (in rad,
(in s−1) and the feedback phase Δ (in rad,  with ω: possible emission frequency) due to the compound structure
with ω: possible emission frequency) due to the compound structure
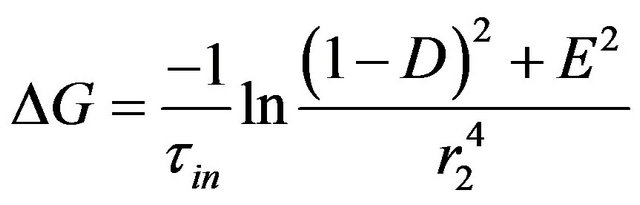 (2)
(2)
and
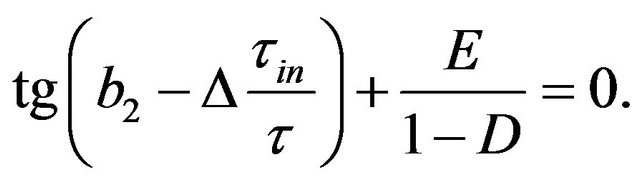 (3)
(3)
In the above two equations, D (dimensionless), E (dimensionless) and b2 (in rad) are written respectively as
 (4)
(4)
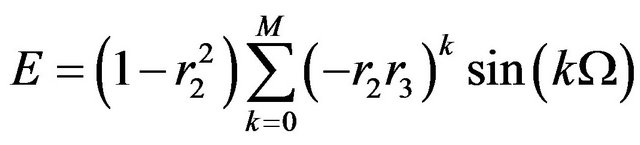 (5)
(5)
and
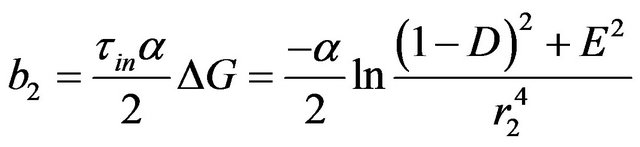 (6)
(6)
where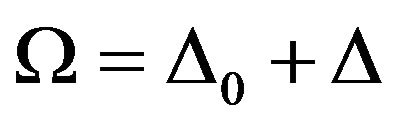 .
.
The steady-state behavior of a possible mode (with phase Δ and excess gain ) produced by a feedback laser under multiple-reflection configuration is described by Equations (2)-(6). We will show in Section 3 that in the case of low feedback levels
) produced by a feedback laser under multiple-reflection configuration is described by Equations (2)-(6). We will show in Section 3 that in the case of low feedback levels , except for a phase shift, these equations will reduce to the well-employed forms obtained from the LK rate equations. In the following, a cavity mode referred to the LK model will be called an external cavity mode (ECM) and if this mode is referred to the ITW model, it will be called a compound cavity mode (CCM), as suggested in [15].
, except for a phase shift, these equations will reduce to the well-employed forms obtained from the LK rate equations. In the following, a cavity mode referred to the LK model will be called an external cavity mode (ECM) and if this mode is referred to the ITW model, it will be called a compound cavity mode (CCM), as suggested in [15].
2.2. Initial Feedback Phase
Let us first examine the initial feedback phase . With a given system, the phase (or normalized emission frequency) Δ of a possible mode, being in dependence on
. With a given system, the phase (or normalized emission frequency) Δ of a possible mode, being in dependence on , is determined through the so-called phase equation. Under the consideration of low feedback levels, the phase equation has a simpler form and two particular situations have been introduced and widely studied, where Δ is predefined and
, is determined through the so-called phase equation. Under the consideration of low feedback levels, the phase equation has a simpler form and two particular situations have been introduced and widely studied, where Δ is predefined and  is then determined from Δ. The first situation corresponds to the “maximum gain mode” defined by the condition
is then determined from Δ. The first situation corresponds to the “maximum gain mode” defined by the condition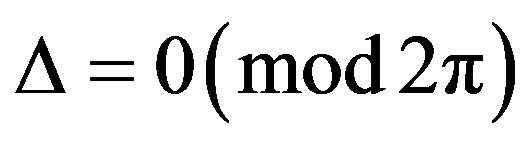 . This gives rise to
. This gives rise to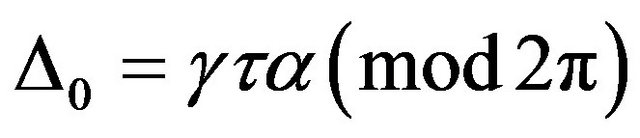 , where γ (in s−1) is the feedback rate defined as usual by [1,2]
, where γ (in s−1) is the feedback rate defined as usual by [1,2]
 (7)
(7)
In the second situation, the initial frequency remains unchanged  and the related mode is called the “minimum linewidth mode”. We have thus
and the related mode is called the “minimum linewidth mode”. We have thus 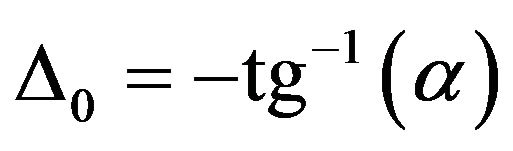 .
.
We introduce here another category of modes, where 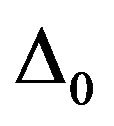 is determined directly from Equation (3). So by putting r3 = 0 and M = 0 in Equations (4) and (5), we obtain
is determined directly from Equation (3). So by putting r3 = 0 and M = 0 in Equations (4) and (5), we obtain , E = 0 and, from Equation (6), b2 = 0. Equation (3) becomes then
, E = 0 and, from Equation (6), b2 = 0. Equation (3) becomes then
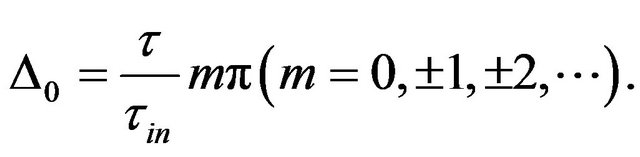 (8)
(8)
It follows that the change of  values is parameterized by the ratio
values is parameterized by the ratio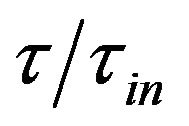 . We note that for both the “maximum gain mode” and the “minimum linewidth mode” there exists the solution
. We note that for both the “maximum gain mode” and the “minimum linewidth mode” there exists the solution  (when
(when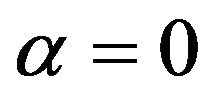 ), and that this corresponds to the zero-order solution (m = 0) of Equation (8). For simplicity and principle demonstration, we will use in the following
), and that this corresponds to the zero-order solution (m = 0) of Equation (8). For simplicity and principle demonstration, we will use in the following  as the value of the initial feedback phase. We will show that in the weak-feedback regime
as the value of the initial feedback phase. We will show that in the weak-feedback regime  quantitative agreement between the ITW and LK models can be obtained only with this initial phase value.
quantitative agreement between the ITW and LK models can be obtained only with this initial phase value.
2.3. Excess Gain
A possible CCM has its gain written as
 (9)
(9)
where τp (in seconds) is the photon lifetime and 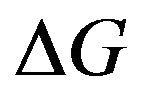 is the excess gain due to feedback whose expression is given by Equation (2). A contour plot of the evolution of
is the excess gain due to feedback whose expression is given by Equation (2). A contour plot of the evolution of 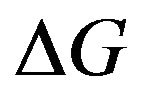 as functions of Δ and r3 is shown in Figure 2. As can be seen from this figure,
as functions of Δ and r3 is shown in Figure 2. As can be seen from this figure, 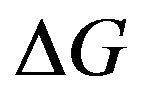 peaks at the critical
peaks at the critical
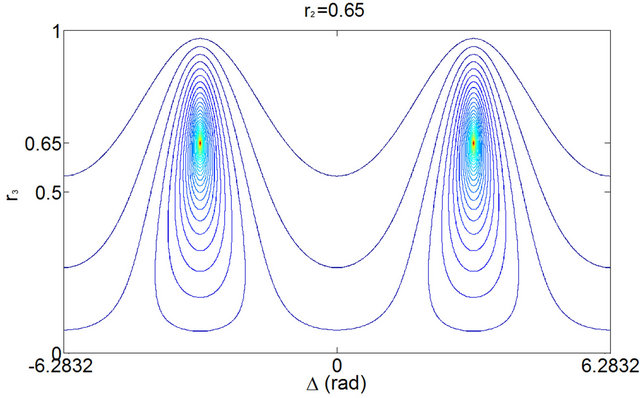
Figure 2. Contour plot of the excess gain ΔG in the vicinity of the initial feedback phase Δ0 (Δ0 = 0), as functions of the CCM feedback phase Δ and the reflection coefficient r3, for r2 = 0.65, α = 5, τin = 9 ps, τ = 0.9 ns, and M = 100.
point r3 = r2, which corresponds to a symmetrical (FabryPerot) external cavity.
2.4. Modal Density of Photons
From the standard rate equation for the carrier density N [1,4] and by assuming a linear relation between the gain G and N, we can derive the expression for the density of photons (or photon number) I (in m−3) of a CCM. Here I is calculated directly from , we have thus in steady state
, we have thus in steady state
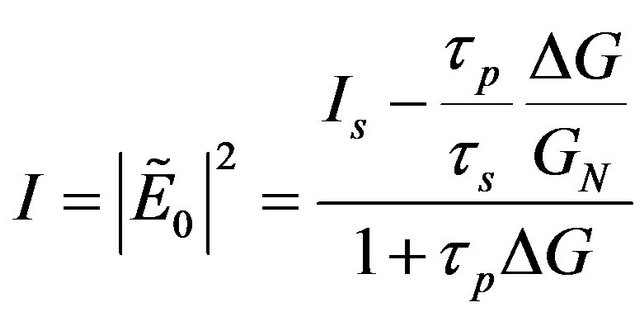 (10)
(10)
where Is is the density of photons for the solitary laser. It is written as
 (11)
(11)
where J (in s−1∙m−3) is the pumping current and τs (in seconds) is the carrier life time. An example of the typical evolution of I as functions of Δ and r3 is shown in Figure 3.
A typical phenomenon can be observed from this figure: high values of the reflection coefficient r3 do have an effect on enhancement of the density of photons. In this example, I is much higher in the strong-feedback regime than in the moderate-feedback regime (~5 × 1020 m−3 against ~3 × 1020 m−3, which is the threshold value Is for the solitary laser). As a consequence, the average intensity noise would be decreased in the strong-feedback regime because of higher I values. This result agrees quite well with the work of Langley et al. [12]. They used the ITW model to characterize the transition from the CC regime to the strong-feedback regime for a given r2 value through the relative intensity noise (RIN) (Fig-
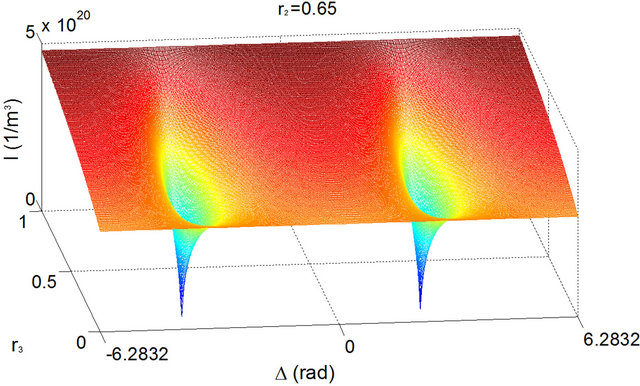
Figure 3. Plot of the density of photons I in the vicinity of the initial feedback phase Δ0 (Δ0 = 0) as functions of the CCM feedback phase Δ ranging from −2π to 2π and the reflection coefficient r3, for r2 = 0.65. The values of the other parameters are α = 5, τin = 9 ps, τ = 0.9 ns, τs = 2 ns, τp = 2 ps, GN = 1.1 × 10−12 s−1∙m3, Is = 3 × 1020 m−3, and M = 100.
ure 2(a), in [12]). We see from this figure that with increasing of r3, there are three well distinguished regimes for the RIN: the weak-feedback regime (r3 < 0.005), the noisy CC regime, and the strong-feedback regime (r3 > 0.1). The RIN increases in the CC regime as expected but decreases significantly (more than 10 dB/Hz) in the strong-feedback regime compared to its values in the weak-feedback regime. This result implies that a stable laser operation with low intensity-noise levels would be possible under the condition of strong feedback. In fact, stable and narrow-linewidth operation has been already observed with systems in configuration of strong optical feedback [17].
Another phenomenon is related to the FDCC regime [7]. This regime has been identified for a large pumping current, corresponding therefore to higher output power. In a recent investigation, InAs/InP quantum-dash FabryPerot lasers emitting at 1.57 μm were assessed for their tolerance to external optical feedback by using a freespace setup with a “short” (L = 0.5 m) external cavity [18]. In these experiments, the regime of FDCC was attained for a pumping current of about 30 mA at a rather high feedback level (−1.2 dB in terms of power ratio) with a 600-μm-long laser. As can be seen from the measured RF (radio frequency) spectra reported in this reference ([18], Figure 5(b)), the FDCC regime is characterized by a significant increase of the RF peak power around the relaxation oscillation frequency of the solitary laser, and hence by a high output power in steady state at high levels of feedback. We note that such a behavior manifested by a coherence-collapsed laser can be quite well understood using the formalism developed from the ITW model as can be seen from the RIN spectra simulations ([12], Figure 2(b)), and that the FDCC regime cor responds roughly to the beginning of the strong-feedback regime, as can be seen from the plot of photon density,
 (a)
(a)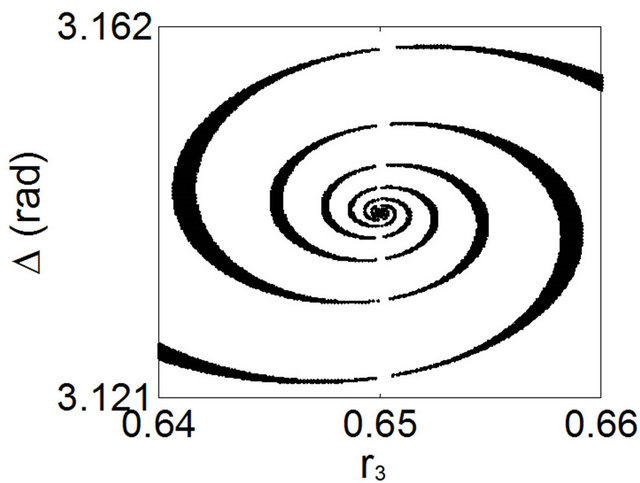 (b)
(b)
Figure 4. Zoom on two particular regions in Figure 5. (a) Region corresponding to small values of r3 (moderatefeedback regime, where the use of the LK model may still be justified); (b) Whirl-shape region near the critical point r3 = r2, at which the maximum number of CCMs is found.
i.e. Figure 3, in the present text.
2.5. Phase Condition
For a given compound-cavity structure, the phase condition determines the emission frequency of a possible CCM. The phase Δ associated with this mode should satisfy the transcendental Equation (3). In general only numerical solutions are possible.
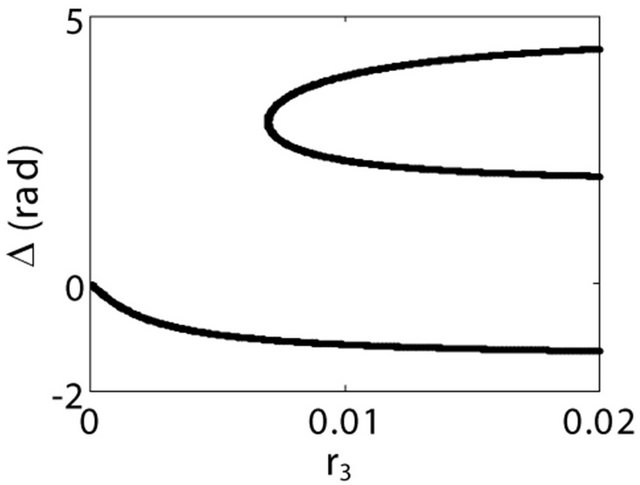
An example of bifurcation diagrams of the CCMs is shown in Figure 5. The value of each point was obtained by a numerical solution of Equation (3). For greater  values, it will suffice to repeat the “pattern”. We present in Figure 4 two particular regions in Figure 5, where is found in (a) the shape predicted by the LK model as expected. We see from Figure 5 that, when r3 < r2, same as a classical bifurcation pattern, all the modes (except the first mode
values, it will suffice to repeat the “pattern”. We present in Figure 4 two particular regions in Figure 5, where is found in (a) the shape predicted by the LK model as expected. We see from Figure 5 that, when r3 < r2, same as a classical bifurcation pattern, all the modes (except the first mode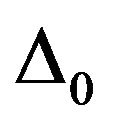 ) emerge by pairs and their number progressively increases with r3. The maximum number of modes is attained at the point r3 = r2, corresponding to a symmetrical external cavity. For r3 > r2, the modes will disappear also by pairs. Finally, the number of modes will become minimal in the strong-feedback regime. We think that Figure 5 is equivalent to the bifurcation diagram for the normalized carrier density illustrated in [12] (Figure 4), showing clearly that high feedback levels can prevent a feedback laser from noisy output.
) emerge by pairs and their number progressively increases with r3. The maximum number of modes is attained at the point r3 = r2, corresponding to a symmetrical external cavity. For r3 > r2, the modes will disappear also by pairs. Finally, the number of modes will become minimal in the strong-feedback regime. We think that Figure 5 is equivalent to the bifurcation diagram for the normalized carrier density illustrated in [12] (Figure 4), showing clearly that high feedback levels can prevent a feedback laser from noisy output.
3. Convergence to the Model of Lang and Kobayashi
In this section, we will show that in the weak-feedback

Figure 5. Bifurcation diagram of the CCMs. The values of the parameters are α = 5, τin = 9 ps, τ = 0.9 ns, Δ0 = 0, r2 = 0.65, and M = 100.
regime , except for a phase term, the ITW model will reduce to the LK model.
, except for a phase term, the ITW model will reduce to the LK model.
Thus, in the case of low feedback levels, there will be only one reflection (M = 1). Equations (4) and (5) are simplified as
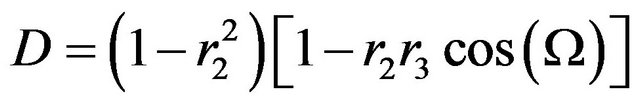 (12)
(12)
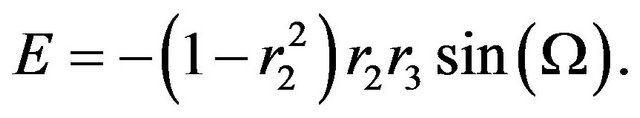 (13)
(13)
Inserting the above two equations into Equation (2) and using the approximations  and
and  for small x values, we obtain the expression for the steady-state excess gain
for small x values, we obtain the expression for the steady-state excess gain
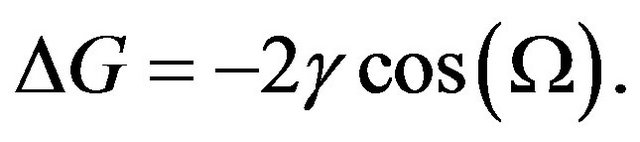 (14)
(14)
In the same way, for the phase Equation (3), we have
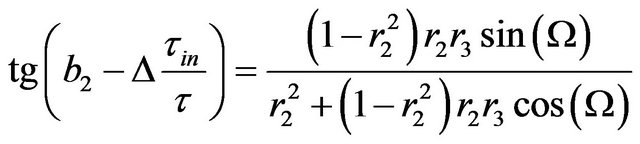 (15)
(15)
where
 (16)
(16)
By making some approximations and using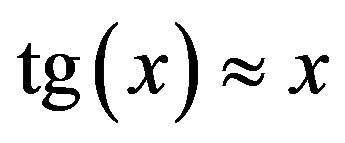 , we obtain the phase condition
, we obtain the phase condition
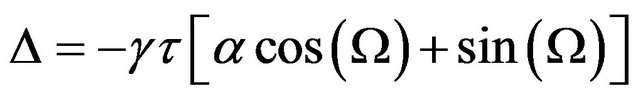 (17)
(17)
It follows that except for a phase shift , Equations (14) and (17) have the same forms as those derived from the LK rate equations. This result confirms the work of Radziunas et al. [15]. They showed a good qualitative agreement between the ECM and CCM solutions at moderate feedback levels. They also found a quantitative agreement for low feedback levels.
, Equations (14) and (17) have the same forms as those derived from the LK rate equations. This result confirms the work of Radziunas et al. [15]. They showed a good qualitative agreement between the ECM and CCM solutions at moderate feedback levels. They also found a quantitative agreement for low feedback levels.
4. Diagram of the Photon Density versus the Mode Phase
It is known that for a laser operating in the weak-even moderate-feedback regime a common way to represent the possible steady states of the ECMs at a fixed feedback level is through an ellipse showing the density of photons I versus the feedback phase Δ, and that only a finite number of ECM points are possible which are all located on the ellipse [8,19].
For the case of an arbitrary feedback level, the  diagram with a given pumping current J can be established first by expressing Δ as a function of
diagram with a given pumping current J can be established first by expressing Δ as a function of  and then by combining the result with Equation (10). We have respectively from Equations (2) and (3)
and then by combining the result with Equation (10). We have respectively from Equations (2) and (3)
 (18)
(18)
and from Equations (14) and (17) for the case of 
 (19)
(19)
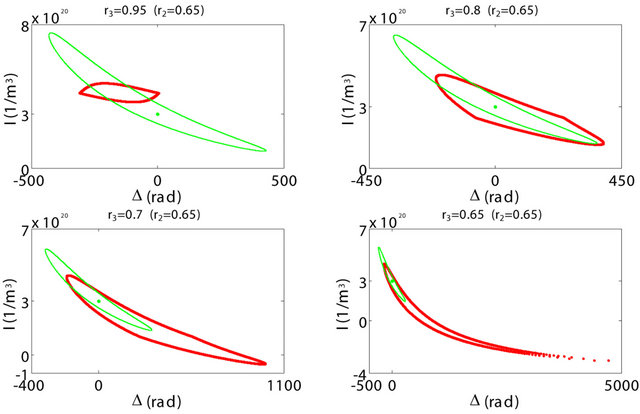
Figure 6 shows the plots of the 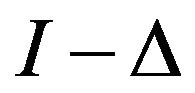 diagram for various values of r3, using respectively Equations (18) and (19). Two typical phenomena inside the CC regime are clearly shown in this figure: a “banana”-like shape and a shift, to positive phase values, of the CCM fixed points due to the inclusion of multiple reflections in the ITW model, as also observed by Spencer et al. when they used the ITW model to establish the possible steady states in the I versus
diagram for various values of r3, using respectively Equations (18) and (19). Two typical phenomena inside the CC regime are clearly shown in this figure: a “banana”-like shape and a shift, to positive phase values, of the CCM fixed points due to the inclusion of multiple reflections in the ITW model, as also observed by Spencer et al. when they used the ITW model to establish the possible steady states in the I versus 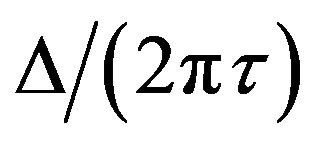 plane ([16], Figure 1). We also observe, in Figure 6, a perfect overlap of the two ellipses for r3 = 0.003. This is because we have taken (for simplicity and principle demonstration)
plane ([16], Figure 1). We also observe, in Figure 6, a perfect overlap of the two ellipses for r3 = 0.003. This is because we have taken (for simplicity and principle demonstration)  as the initial phase value.
as the initial phase value.
Finally, let us make a direct comparison between the iteration equation for the ITW model and the rate equation for the LK model. It can easily be shown that at low feedback levels, any stationary solution to Equation (1) will lead to the following equation
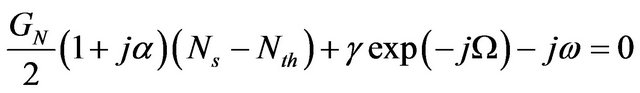 (20)
(20)
where 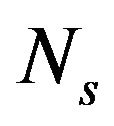 is the steady-state carrier density. Under the same condition, the LK rate equation will reduce to
is the steady-state carrier density. Under the same condition, the LK rate equation will reduce to
 (21)
(21)
These two equations show, together with Equations (14) and (17), that the two models are strictly identical if and only if  [see also Figure 6(b) for r3 = 0.003].
[see also Figure 6(b) for r3 = 0.003].
5. Conclusions
This paper provides additional information about the physical insight into a compound laser system with arbitrary feedback levels. Analytical expressions have been
 (a)
(a) (b)
(b)
Figure 6. Evolution of the I − Δ diagram as a function of r3. The diagrams are determined respectively from Equation (18) (red curves, M = 100) and Equation (19) (green curves). The green dots refer to the solitary-laser solution. (a) r3 = 0.95, 0.8, 0.7 and 0.65; (b) r3 = 0.6, 0.4, 0.1 and 0.003. The values of the other parameters are r2 = 0.65, Δ0 = 0, α = 5, τin = 9 ps, τ = 0.9 ns, τs = 2 ns, τp = 2 ps, GN = 1.1 × 10−12 s−1∙m3, and Is = 3 × 1020 m−3.
developed based on an iterative travelling-wave model, which enable a characterization in a rigorous way of a cavity mode in its steady state. We show that with decreasing of the reflection coefficient of the external mirror three regimes emerge successively which can clearly be distinguished from bifurcation diagram and gain plot: they are strong-feedback, coherence-collapse, and moderate-feedback regimes. This latter covers the weakfeedback regime where the use of the model of Lang and Kobayashi is entirely justified.
We find that maximum number of modes is obtained when the external cavity becomes symmetrical. This state may cause a noisiest laser output. In the strong-feedback regime, a feedback laser is characterized by a minimum mode number and a high density of photons. This behavior confirms previous experimental observations, indicating that beyond the coherence-collapse regime, the system could be re-stabilized and that as a result stable laser operation with low intensity-noise level could be expected with external-mirror reflectivity close to 1. A novel class of modes has been proposed, which is parameterized by the ratio between the external and internal round-trip times. We have also examined the similarities and the differences between the iterative travelling-wave and Lang-Kobayashi models. We find that in the weakfeedback regime these two models are identical only if the initial feedback phase is equal to zero.
The present work is above all useful for determination of the external feedback levels required for stable and noiseless laser output, especially those corresponding to the entrance and the exit of the coherence-collapse regime.
Future investigations will include a detailed analysis of the coherence-collapse regime by means of these two models.
REFERENCES
- B. Tromborg, J. H. Osmundsen and H. Olesen, “Stability Analysis for a Semiconductor Laser in an External Cavity,” IEEE Journal of Quantum Electronics, Vol. 20, No. 9, 1984, pp. 1023-1032. doi:10.1109/JQE.1984.1072508
- N. Schunk and K. Petermann, “Numerical Analysis of the Feedback Regimes for a Single-Mode Semiconductor Laser with External Feedback,” IEEE Journal of Quantum Electronics, Vol. 24, No. 7, 1988, pp. 1242-1247. doi:10.1109/3.960
- J. O. Binder and G. D. Cormack, “Mode Selection and Stability of a Semiconductor Laser with Weak Optical Feedback,” IEEE Journal of Quantum Electronics, Vol. 25, No. 11, 1989, pp. 2255-2259. doi:10.1109/3.42053
- R. Lang and K. Kobayashi, “External Optical Feedback Effects on Semiconductor Injection Laser Properties,” IEEE Journal of Quantum Electronics, Vol. 16, No. 3, 1980, pp. 347-355. doi:10.1109/JQE.1980.1070479
- J. Ye, H. Li, and J. G. McInerney, “Period-Doubling Route to Chaos in a Semiconductor Laser with Weak Optical Feedback,” Physical Review A, Vol. 47, No. 3, 1993, pp. 2249-2252. doi:10.1103/PhysRevA.47.2249
- T. Sano, “Antimode Dynamics and Chaotic Itinerancy in the Coherence Collapse of Semiconductor Lasers with Optical Feedback,” Physical Review A, Vol. 50, No. 3, 1994, pp. 2719-2726. doi:10.1103/PhysRevA.50.2719
- J. Zamora-Munt, C. Masoller and J. García-Ojalvo, “Transient Low-Frequency Fluctuations in Semiconductor Lasers with Optical Feedback,” Physical Review A, Vol. 81, No. 3, 2010, Article ID: 033820. doi:10.1103/PhysRevA.81.033820
- T. Erneux and P. Glorieux, “Laser Dynamics,” Cambridge University Press, New York, 2010.
- Q. Zou and S. Azouigui, “Analysis of Coherence-Collapse Regime of Semiconductor Lasers under External Optical Feedback by Perturbation Method,” Chapter 5, Semiconductor Laser Diode Technology and Applications, Edition InTech, 2012, pp. 71-86.
- J. Mørk, “Rep. S48,” Danish Center for Applied Mathematics and Mechanics, 1989.
- F. Sporleder, “Travelling Wave Line Model for Laser Diodes with External Optical Feedback,” Proceedings of the URSI International Symposium on Electromagnetic Theory, International Union of Radio Science, Brussels, 1983, pp. 585-588.
- L. N. Langley, K. A. Shore and J. Mørk, “Dynamical and Noise Properties of Laser Diodes Subject to Strong Optical Feedback,” Optics Letters, Vol. 19, No. 24, 1994, pp. 2137-2139. doi:10.1364/OL.19.002137
- J. E. Carroll, J. Whiteaway and R. Plumb, “Distributed Feedback Semiconductor Lasers,” Institution of Electrical Engineers, London and SPIE Optical Engineering Press, 1998.
- U. Bandelow, M. Radziunas, J. Sieber and M. Wolfrum, “Impact of Gain Dispersion on the Spatio-Temporal Dynamics of Multisection Lasers,” IEEE Journal of Quantum Electronics, Vol. 37, No. 2, 2001, pp. 183-188. doi:10.1109/3.903067
- M. Radziunas, H. J. Wünsche, B. Krauskopf and M. Wolfrum, “External Cavity Modes in Lang-Kobayashi and Traveling Wave Models,” Proceedings of SPIE, Vol. 6184, 2006. doi:10.1117/12.663546
- P. S. Spencer, C. R. Mirasso and K. A. Shore, “Effect of Strong Optical Feedback on Vertical-Cavity SurfaceEmitting Lasers,” IEEE Photonics Technology Letters, Vol. 10, No. 2, 1998, pp. 191-193. doi:10.1109/68.655354
- C. E. Weiman and L. Holberg, “Using Diode Lasers for Atomic Physics,” Review of Scientific Instruments, Vol. 62, No. 1, 1991.
- S. Azouigui, B. Kelleher, S. P. Hegarty, G. Huyet, B. Dagens, F. Lelarge, A. Accard, D. Make, O. Le Gouezigou, K. Merghem, A. Martinez, Q. Zou and A. Ramdane, “Coherence Collapse and Low-Frequency Fluctuations in Quantum-Dash Based Lasers Emitting at 1.57 μm,” Optics Express, Vol. 15, No. 21, 2007, pp. 14155- 14162. doi:10.1364/OE.15.014155
- C. H. Henry and R. F. Kazarinov, “Instability of Semiconductor Lasers Due to Optical Feedback from Distant Reflectors,” IEEE Journal of Quantum Electronics, Vol. 22, No. 2, 1986, pp. 294-301. doi:10.1109/JQE.1986.1072959

