Journal of Minerals & Materials Characterization & Engineering, Vol. 10, No.13, pp.1263-1275, 2011
jmmce.org Printed in the USA. All rights reserved
1263
Experimental Methods of Determining Fracture Toughness of Fiber
Reinforced P olymer Composites under Various Loading Conditions
M.S. Sham Prasad*1, C.S. Venkatesha2, T. Jayaraju3
1 Dept. of Industrial & Production Engineering, National Institute of Engineering, Mysore, India
2 Dept. of Mechanical Engineering, U BDT college of Engineering, Davangere, India
3 Dept. of Mechanical Engineering, National Institute of Engineering, Mysore, India
*Corresponding Author:*[e-mail]
ABSTRACT
Polymer composites is a typical material consisting of a matrix reinforced with fiber/filler and
the general nature of construction of the material itself provides innumerable sites for the
initiation of a defect or for the growth of delamination. The life expectancy of composite
structure requires a clear understanding of the material’s response to the growth of interlaminar
delamination under Mode I, Mode II, Mode III and Mixed Modes. Fracture testing of fiber
reinforced polymer-matrix composites is an active area of research. Even though substantial
progress in the area of fracture testing has been achieved, there are still several problems
awaiting solution. The new aspects in the experimental studies of interla minar and intralaminar
fracture toughness of polymer matrix composites were emphasized in this review paper. The
different modes to evaluate the fracture energy were listed and their suitability was mentioned.
Keywords: Interlaminar, Delamination, Intralaminar, Fracture toughness
1. INTRODUCTIO N
Composites belong to a new class of materials developed that are strong, have low densities, and
not easily corroded. Polymer matrix composites can be processed to get higher mechanical
strength and other desired properties. Composite materials are heterogeneous in compositi on and
an-isotropic in mechanical behavior. Polymer composites have emerged as important structural
engineering materials in automotive, marine, aerospace, transportation, infrastructure
applications and as well as in civil engineering applications, because of their high strength to
weight ratio. Compared t o met als, fractur e toughness charact erizati on of co mposit e materials are
still in the process of development. The aim of the review paper is to present and discuss
problems from the development of the test methods arising mainly from the specific properties of
Polymer Matrix Composites.

1264 M.S. Sham Prasad, C.S. Venkatesha, T. Jayaraju Vol.10, No.13
2. FRACTURE MECHANICS
Tensil e test result s apply to m aterial that d oes not contain crack s or stress co n cen trato rs , such as
brittle inclusions. When crack like defects are present either as surface cracks or internal ones,
failure may begin at much lower applied stresses. The applied stress is greatly magnified at the
crack tip due to zero area (theoretically). For a ductile material, it can deform locally when the
stress is high, blunting the crack tip reducing the intensity of stress [1]. For brittle material, the
crack will propagate through the stressed region with little deformation. The small scale plastic
region around the crack will continue to propagate across the specimen. Fracture may be defined
as the mechanical separation of a solid owing to the application of stress. Fractures of
engineeri ng materi al are cate goriz ed as ducti le or britt le fractures. Duct ile fractur es absorb more
energy, while brittle fractures absorb little energy, and are generally characterized by fracture
with flat surfaces. Fracture toughness is related to the amount of energy required to create
fracture surfaces. In brittle materials such as glass the energy required for fracture is simply the
intrinsic surface energy of the material, as demonstrated by Griffith. For structural alloys at room
temperature considerably energy is required for fracture because plastic deformation
accompanies the fracture process. The application of fracture mechanics concepts has identified
and quantified the primary parameters that affect structural integrity. These parameters include
the magnitude and range of the applied stresses, th e size, s hape, orient atio n of cracks / cr ack li ke
defects, rate of propagation of the existing cracks and the fracture toughness of the material. Two
categories of fracture mechanics are Linear Elastic Fracture Mechanics (LEFM) and Elastic-
Plast i c Fractur e Me chan i cs (EP FM) . Th e Linear E l ast i c Fractu r e Mechanic s ( LEFM) appr o ach t o
fracture analysis assumes that the material behaves elastically at regions away from the crack,
except for a small region of inelastic deformation at the crack tip. The fracture resistance is
determined in terms of the stress- int ensificati on factor, K and str ain energ y rele ase rate G. The
energy released during rapid crack propagation is a basic m aterial property and is not influenced
by part size. According to ASTM the stress intensity factor K can be written as
)(gfaKI πσ = (1)
Where ‘a’ i s t he i ni ti al cr ack len gth, ‘f (g)’ is the dimensionless factor for the s peci m en geom et ry
and loading condition and the KI, the Mode I critical stress intensity factor. The specimen size
must be chosen such that there is small scale plasticity around the crack tip. If a large plastic
zone develops ahead of the crack tip then the condition of “small scale yielding” for LEFM
applicability are not met [2]. One of the underlying principles of fracture mechanics is that the
unstable fracture occurs when the stress intensity factor at the crack tip reaches a critical value,
KC. The greater the value of fracture toughness, the higher the intensity of stress required to
produce crack propagation and the greater the resistance of the material to brittle fracture. The
critical stress intensity factor is determined using relatively simple laboratory specimen, the
limiting value being K IC / K IIC / K IIIC. The Elastic-Plastic fracture mechanics is used when there
is large scale crack tip plasticity (blunting).
2.1 Modes of Fracture
Figure 1 defines the three modes of loading, Mode I, opening or tensile mode, Mode II, sliding
or shear mode, and Mode III, tearing mode. Fracture mechanics concepts are essentially the same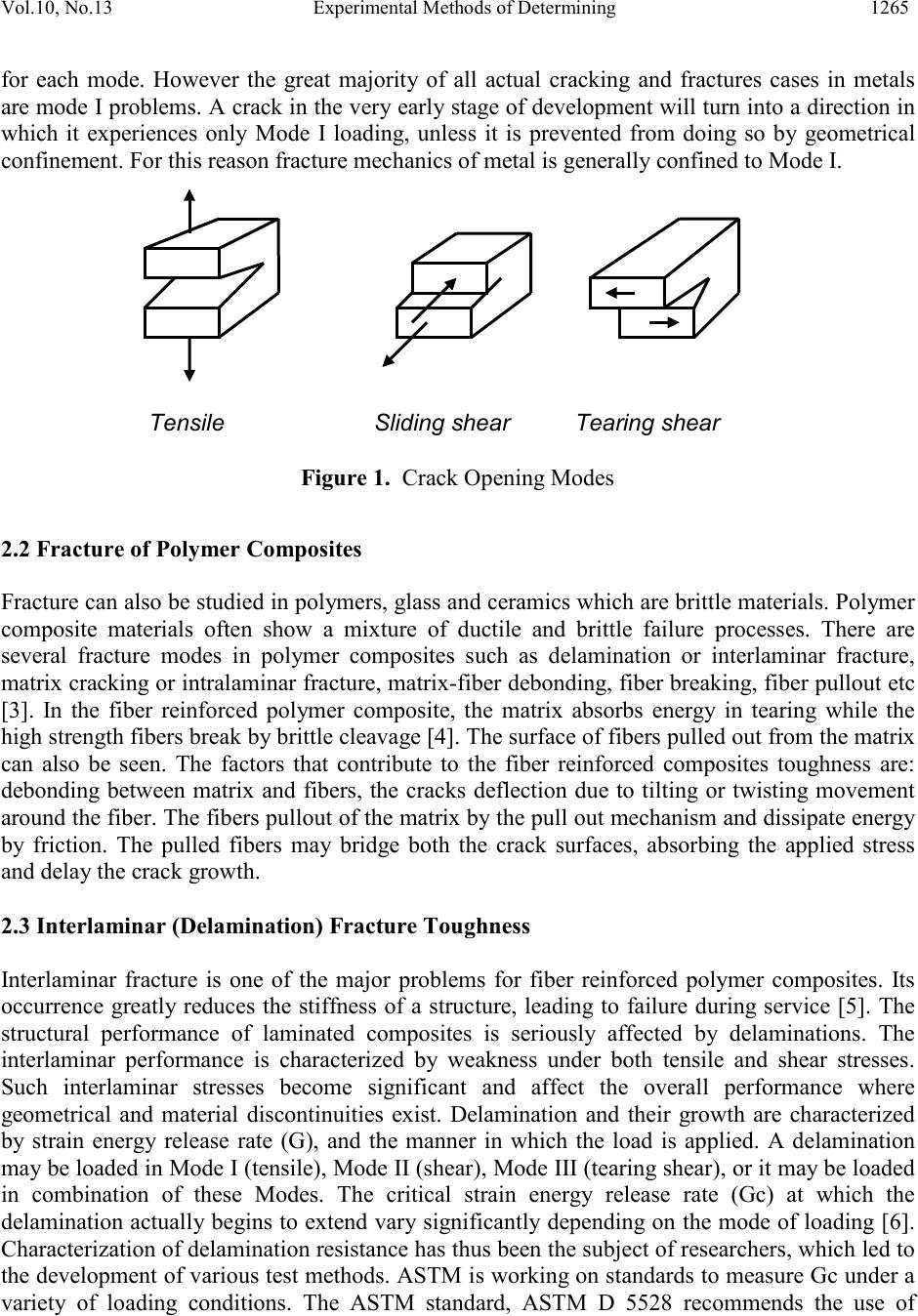

Vol.10, No.13 Experimental Methods of Determini ng 1265
for each mode. However the great majority of all actual cracking and fractures cases in metals
are mode I problems. A crack in the very early stage of development will turn into a direction in
which it experiences only Mode I loading, unless it is prevented from doing so by geometrical
confinement. For this reason fracture mechanics of metal is generally confined to Mode I.
2.2 Fracture of Polymer Composites
Fracture c an als o be st udied in pol ymers, glas s and ceramics which ar e brit tle m aterial s. Polymer
composite materials often show a mixture of ductile and brittle failure processes. There are
several fracture modes in polymer composites such as delamination or interlaminar fracture,
matrix cracking or i ntralam inar fract ure, matrix-fiber debonding, fiber breaking, fiber pullout etc
[3]. In the fiber reinforced polymer composite, the matrix absorbs energy in tearing while the
high strength fibers break by brittle cleavage [4]. The surface of fibers pulled out from the matrix
can also be seen. The factors that contribute to the fiber reinforced composites toughness are:
debonding between matrix and fibers, the cracks deflection due to tilting or twisting movement
around the fiber. The fibers pullout of the matrix by the pull out mechanism and dissipate energy
by friction. The pulled fibers may bridge both the crack surfaces, absorbing the applied stress
and delay the crack growth.
2.3 Interlaminar (Delamination) Fracture Toughness
Interlaminar fracture is one of the major problems for fiber reinforced polymer composites. Its
occurrence greatly reduces the stiffness of a structure, leading to failure during service [5]. The
structural performance of laminated composites is seriously affected by delaminations. The
interlaminar performance is characterized by weakness under both tensile and shear stresses.
Such interlaminar stresses become significant and affect the overall performance where
geometrical and material discontinuities exist. Delamination and their growth are characterized
by strain energy release rate (G), and the manner in which the load is applied. A delamination
may be loaded in Mode I (tensile), Mode II (shear), Mode III (tearing shea r), or it ma y be loaded
in combination of these Modes. The critical strain energy release rate (Gc) at which the
delamination actually begins to extend var y significantly depending on the mode of loading [6].
Characterization of delamination resistance has t hus been the subje ct of resear ch ers, which led to
the development of various test methods. AS TM is working on standards to measure Gc under a
variety of loading conditions. The ASTM standard, ASTM D 5528 recommends the use of
Tensile Sliding shear Tearing shear
Figure 1. Crack Opening Modes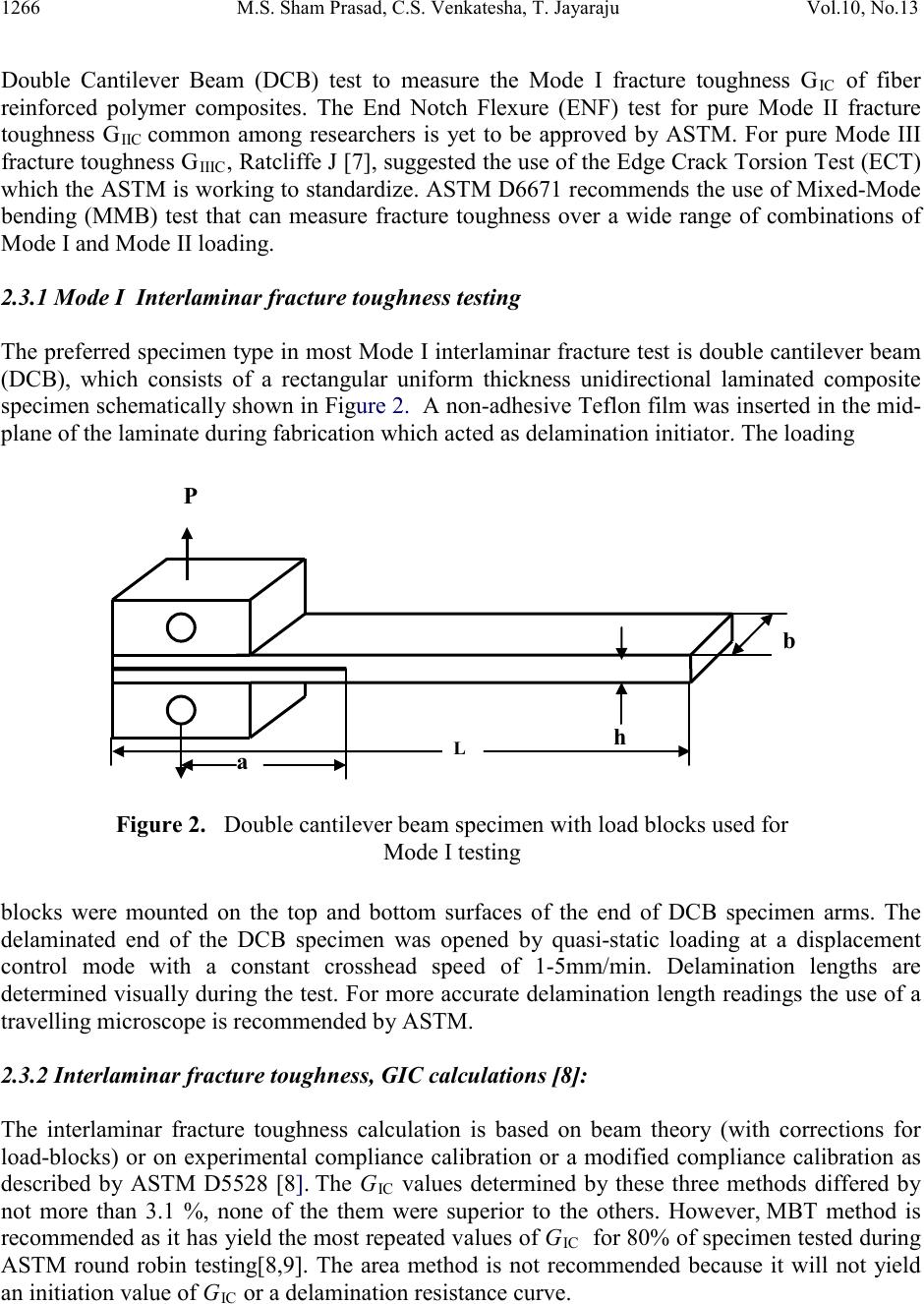

1266 M.S. Sham Prasad, C.S. Venkatesha, T. Jayaraju Vol.10, No.13
Double Cantilever Beam (DCB) test to measure the Mode I fracture toughness GIC of fiber
reinforced polymer composites. The End Notch Flexure (ENF) test for pure Mode II fracture
toughness GIIC common among researchers is yet to be approved by ASTM. For pure Mode III
fractur e toughn ess GIIIC, Ratcliffe J [7], su ggested t he use of the Edge Crack Torsion Test (ECT)
which the AS TM is working to standardize. ASTM D6671 recommends the use of Mixed-Mode
bending (MMB) test that can measure fracture toughness over a wide range of combinations of
Mode I and Mode II loading.
2.3.1 Mode I Interlaminar fracture toughness testing
The pref erred specimen type in m ost Mode I interlaminar fracture test is double cantilever beam
(DCB), which consists of a rectangular uniform thickness unidirectional laminated composite
specimen schematically shown in Figure 2. A non-adhesive Teflon film was inserted in the mid-
plane of the laminate during fabrication which acted as delamination initiator. The loading
blocks were mounted on the top and bottom surfaces of the end of DCB specimen arms. The
delaminated end of the DCB specimen was opened by quasi-static loading at a displacement
control mode with a constant crosshead speed of 1-5mm/min. Delamination lengths are
determined visually during the test. For more accurate delamination length readings the use of a
travelling microscope is recommended by ASTM.
2.3.2 Interlaminar fracture toughness, GIC calculations [8]:
The interlaminar fracture toughness calculation is based on beam theory (with corrections for
load-blocks) or on experimental compliance calibration or a modified compliance calibration as
described by ASTM D5528 [8]. The GIC values determined by these three methods differed by
not more than 3.1 %, none of the them were superior to the others. However, MBT method is
recommended as it has yield the most repeated values of GIC for 80% of s pecimen tested during
ASTM round robin testing[8,9]. The area method is not recommended because it will not yield
an initiation value of GIC or a delamination resistance curve.
a
h
b
L
P
Figure 2. Double cantilever beam specimen with load blocks used for
Mode I testing

Vol.10, No.13 Experimental Methods of Determini ng 1267
2.3.2.1 Modified beam theory (MBT) method:
The strain energy release rate is calculated as follows:
(2)
Where P = load, δ = load point displacement, b = specimen width and a = delamination length
In practice, equation (2) will overestimate GI because the beam is not perfectly built-in (i.e.,
rotation may occur at the delamination front). The modified equation (3) corrects for this rotation
by treating the DCB as if it contained a slightly longer delamination, a + Δ where Δ may be
determined experimentally by generating a least squares plot of the cube r oot of compliance, C1/3
as a function of delamination length.
(3)
2.3.2.2 Compliance calibration (CC) method:
In this method a least squares gr aph of log (δi/Pi) versus log (a) is generated using the visually
observed delamination onset values and all the propagation values. A straight line is drawn
through the data that results in the best least-squares fit. The exponent n from the slope of this
line is calculated according to
yxn ∆∆=
where Δy & Δx are increment value of y & x
respectively. The Mode I interlaminar fracture toughness is determined as follows:
(4)
2.3.2.3 Modified compliance calibration (MCC) method:
In this method a least squares graph of the delamination length normalized by specimen
thickness, a/h, as a function of the cube root of compliance, C1/3 is plotted using the visually
observed delamination onset values and all the propagation values. The slope of this line is S1.
The Mode I interlaminar fracture toughness is calculated as follows:
(5)
Morais et al. [10-11] and Choi et al. [12] assessed the applicability of DCB test for
multidirectional laminates. Multidirectional laminates frequentl y pose problems because of crack
branching or deviations of the delamination from the central plane. Both effects invalidate the
analysis according to the ASTM standard D5528. Delamination resistance on multidirectional
laminates can probably be quantified for initiation only. No significant dependence on the
delaminating interface (fiber orientation) was observed. For cross-ply composites (alternating
00 and 900 orientations stacked on top of each other), extensive testing yielded about 50% of
ab
P
G
I
2
3
δ
=
)(2
3
∆+
=ab
P
GI
δ
ab
nP
G
I
2
δ
=
hbS
CP
G
I1
3/22
2
3
=

1268 M.S. Sham Prasad, C.S. Venkatesha, T. Jayaraju Vol.10, No.13
invalid tests due to deviation from the mid-plane[13,14]. These laminates yielded initiation
values similar to those observed in the corresponding unidirectional laminate.
2.3.3 Mode II interlaminar fracture toughness testing
Most high performance composites are designed [15] to have superior in-plane strength and
stiffness . Interlaminar performance is characterized by pronounced weakness under both shear
and tensile stresses. In many lamin ates, the strength reduction has been observed due to
delamination between plies. Delamination induced failure is normally a result of a combination
of compressive and bending stresses caused by the delaminated plies as they buckle out of plane.
Fiber breakage and matrix cracking also have an effect on the strength. Interlaminar shear,
tension and the matrix cracking largely cause internal delamination which in turn gives rise to
residual stresses that further reduces the strength [16].
The End-notched flexure (ENF) test [17] is one of the methods designed to measure the
interlaminar fracture toughness under in-plane shear deformation mode, commonly known as
Mode II. Early round robin work on mode II ENF had been conducted jointly by JIS, ASTM and
ESIS but has not resulted in international consensus [13] . Several factors contributed to that, first
the ENF-test is essentially unstable and thus allows only determination of initiation values but
not of resistance curves. Second, the question of friction contributions was raised and this
resulted in the question whether Mode II data were to be regarded as apparent values with no
significance as materials data [18]. The measured G IIC is believed to represent the critical strain
energ y release rat e for crack gro wth from the ins ertion film. In this test, the load was introduced
by flex u ral f orc es to produce a cr ack f ro m t he i ns e rt . Th e c rack t hen ex t end ed as a res ul t of s h ear
forces at the crack tip as shown in Figure 3.
Mode II interlaminar fracture toughness is calculated from the initial crack length and the load-
deflection curve using the highest load and deflection level [19] as
(6)
Where F is the load (N), δ the displacement (mm), B the specimen width (mm) and a is the
delamination length (mm).
2t
L
a
F
Figure 3. ENF specimen under load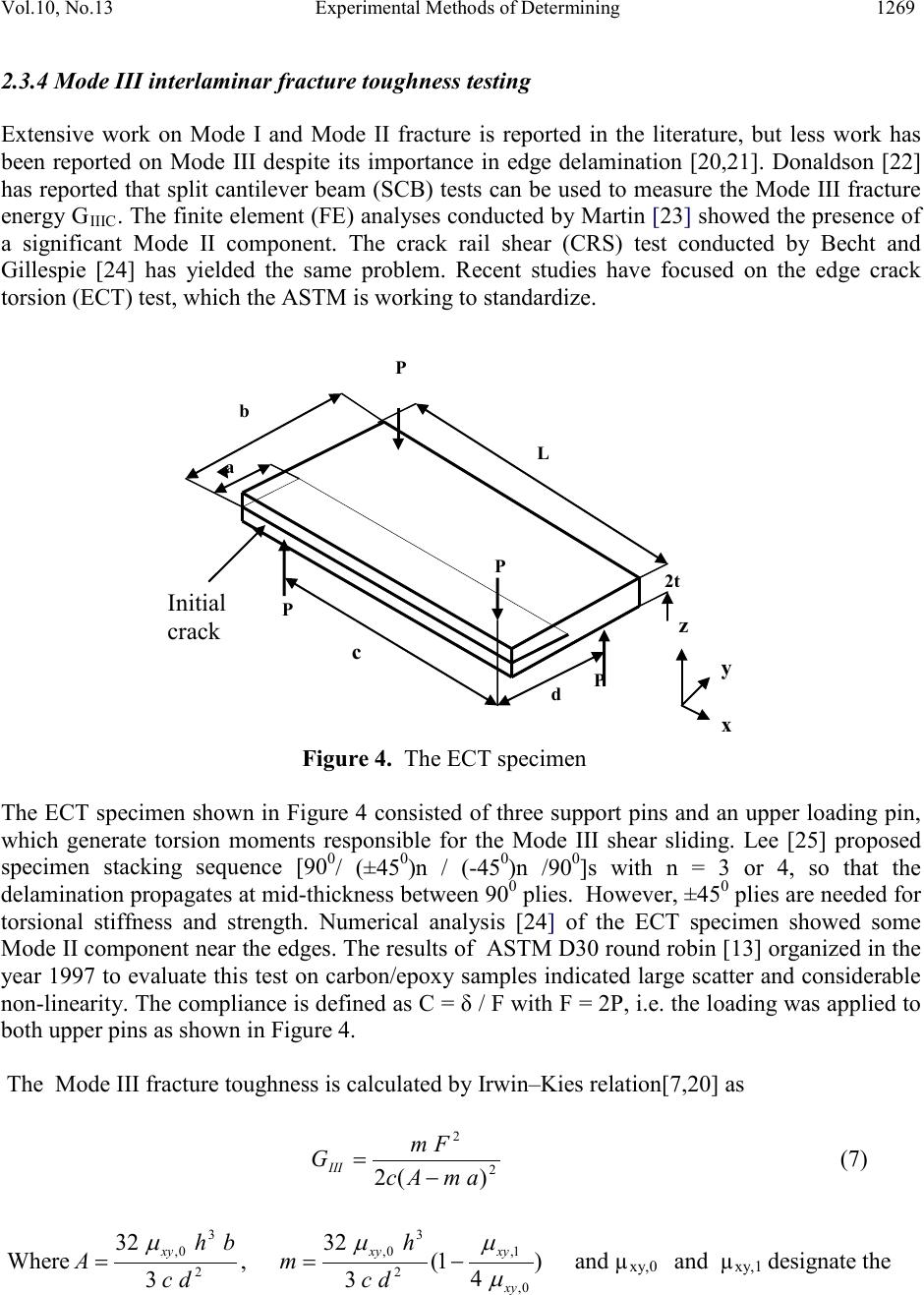
)34/1(2
9
33
2
aLB
aF
GII + =
δ

Vol.10, No.13 Experimental Methods of Determini ng 1269
Initial
crack
x
y
z
P
P
P
2t
L
d
c
a
b
P
Figure 4. The ECT specimen
2.3.4 Mode III interlaminar fracture toughness testing
Extensive work on Mode I and Mode II fracture is reported in the literature, but less work has
been reported on Mode III despite its importance in edge delamination [20,21]. Donaldson [22]
has reported that split cantilever beam (SCB) tests can be used to measure the Mode III fracture
energ y GIIIC. The fin ite elem ent (FE) an alyses conduct ed b y Mart in [23] showed the pres ence of
a significant Mode II component. The crack rail shear (CRS) test conducted by Becht and
Gillespie [24] has yielded the same problem. Recent studies have focused on the edge crack
torsion (ECT) test, which the ASTM is working to standardize.
The ECT specimen shown in Figure 4 consisted of three support pins and an upper loading pin,
which generate torsion moments responsible for the Mode III shear sliding. Lee [25] proposed
specimen stacking sequence [900/ (±450)n / (-450)n /900]s with n = 3 or 4, so that the
delamination propagates at mid-thickness between 900 plies. However, ±450 plies are ne eded fo r
torsional stiffness and strength. Numerical analysis [24] of the ECT specimen showed some
Mode II component near the edges. The results of ASTM D30 round robin [13] organized in the
year 1997 to evaluate this test on carbon/epoxy samples indicated large scatter and considerable
non-linearity. The compliance is defined as C = δ / F with F = 2P, i.e. the loading was applied to
both upper pins as shown in Figure 4.
The Mode III fracture toughness is calculated by Irwin–Kies relation[7,20] as
2
2
)(2 amAc
Fm
GIII − =
(7)
Where
2
3
0,
3
32
dc
bh
Axy
µ
=
,
)
4
1(
3
32
0,
1,
2
3
0,
xy
xyxy
dc
h
m
µ
µµ
−=
and µxy,0 and µxy,1 designate the

1270 M.S. Sham Prasad, C.S. Venkatesha, T. Jayaraju Vol.10, No.13
CLT torsional shear moduli of the uncracked and cracked parts of the specimen, respectively,
derived by Lee [25].
2.3.5 Mixed mode I+II interlaminar fracture toughness testing
The problem of delamination in composite materials has made significant developments in
interlaminar fracture testing with different modes. Early studi es w ere co ncen trated on pure Mode
I and pure Mode II fracture of unidirectional laminates, but in recent years the attention has
diverted on realistic Mixed Mode I + II loadings [26]. However, a few literatures are available
on Mixed Mode fracture of multidirectional and woven laminates [26-29,]. The mixed mode
bending (MMB) test is considered the best method for evaluating the fracture toughness over a
wide range of Mode combinations as recommended by ASTM D 6671[30].
The MMB test shown in Figure 5 can be viewed as the superposition of the double cantilever
beam and end notched flexure tests. Force equilibrium of the loading lever enables determination
of the pure mode loads as suggested by ASTM D6671/ D6671M.
2
232
22
)(
16
)3(12ha
ELhb
LcF
G
If
I
χ +
−
=
(8)
2
232
22 )42.0
(
16
)(9 ha
ELhb
LcF
G
If
II
χ +
+
=
(9)
IIIT
GGG +=
(10)
2.4 Intralaminar Fracture Toughness
The matrix cracking or a crack apparently running parallel to fibers ( Intralaminar) through the
thickness is also one of the problems encountered in fiber reinforced polymer composite.
Extensive research work carried on interlaminar fracture has led to the development and
standardization of interlaminar fracture toughness testing on various Modes. In recent years
a
2L
c
P
Figure 5. Mixed Mode Bending specimen

Vol.10, No.13 Experimental Methods of Determini ng 1271
attention has been diverted to evaluation of intralaminar fracture. Since a standard test method
has not been evolved, the plane strain fracture toughness test methods based on ASTM D 5045
(meant for plastics /particulate polymer composite) is used by researchers.
Garg [31] studied the influence of width, thickness and specimen type on intralaminar
(transv erse) fracture of graphite/ epoxy laminates using compact- tension and three- point bend
specim en s . His result shows that that KIC is independent of geometry and thickness of the
specimen. Parhizgar et.al. [32] showed that intralaminar fracture toughness depends on fiber
orientation, the value of KIC being twice for 900 oriented fibers then 00 oriented fibers, even
though the failure is due to matrix cracking. Jose et. al. [33] investigated intralaminar fracture
toughness on carbon / epoxy with 00, 900 fiber oriented and cross-ply (00 /900) lamin at es. They
observed that the mode of failure is by self similar crack breaking the fiber for cross ply
laminate. For 00 and 900 fiber oriented laminates the mode of failure was similar to results of
Parhizgar. Pinho et. al [34,35] have found that the Mode I intralaminar critical energy release
rate for through the thickness crack growth was very similar to the interlaminar toughness in
unidirectional laminates, so interlaminar cri tical ener g y rele ase rat e can be a good app rox imat ion
for intral ami nar en er g y releas e rate.
2.4.1 Intralaminar fracture toughness testing
These test methods based on ASTM D 5045 involve loading a notched specimen that has been
precracked, in either tension (compact tension) or three-point bending [36]. The significance of
test methods and many conditions of testing are identical to ASTM E 399. The specimens for
fracture toughness testing is either Compact Tension or Three Point Bend was machined from
the laminates in accordance with the dimension given ay ASTM D 5045 as shown in Figure 6
and Figure 7 respectively.
The initial portion a V notch has to be machined with a milling cutter or with a diamond saw and
a starter crack has to be introduced at the root of the notch by tapping or sawing a fine razor
blade [36]. The ratio of crack length to width (a / W) is to be maintained between 0.45 and 0.55.
The pre-cracked fract ure speci men i s loaded with suitable loading devices. For Compact tension
specimen a loading clevis is required and for loading three point bend specimens a bending rig
0.25W dia
2 hol es
B
0.6W
0.6W
0.275W
W
a
Figure 6. Compact Tension specimen
configuration

1272 M.S. Sham Prasad, C.S. Venkatesha, T. Jayaraju Vol.10, No.13
with either moving or stationary rollers of sufficiently large diameter is required. The test is
performed under displacement control mode with displacement rates of 0.5 mm/min or 1 mm/
min [34] and the load versus displacement curve is obtained. It is recommended [36] that at least
three test specimens need to be tested for each material. The KIC value is calculated from this
load by equations that have been established on the basis of LEFM.
2.4.1.1 Calculation of critical stress intensity factor, KIC [ 3 6]:
In order to establish that a valid KIC has been determined, calculate a conditional result, KQ.
Load the specimen and obtain Load -displacement curve. Draw a best straight line to determine
the initial compliance, C. C is given by the reciprocal of the slope of line(C = tan θ). Draw a
second line with compliance 5 % greater than that of initial line. If the maximum load that the
specim en was able to sustain, Pmax, falls within the two lines, use Pmax to calculate KQ. If Pmax
falls outside the lines then use the intersection of second line and the load curve as PQ.
Furthermore, if Pmax / PQ<1.1, then use PQ in the calculation of KQ. However, if Pmax / PQ > 1.1,
the test is invalid. Check the validity of KQ via the siz e criteria. Calculate
2
)/(5.2 yQ K σ
, where
σy is the yield stress of the material. If this value is less than the specimen thickness, B, the cr ack
length, a, and the ligament (W − a), then KQ is equal to KIC. Otherwise the test is not a valid KIC
test.
2.4.1.2 For compact tension specimen:
The fracture loads P Q, o btained from the tests ar e used to det ermine K IC values ( M Pa.m1/2) as a
measure of fracture toughness by using the following data reduction scheme.
=
IC
K
( ) xf
BW
P
Q








2/1
(11)
Where B = specimen thickness, cm, W = specimen width, cm, a = crack length, cm and
Where
( )
( ) ( )
2/3
432
1
64.572.1432.1364.4866.02
x
xxxxx
xf
−
−+−++
=
2.4.1.3 Three point bend specimen (SENB):
The fracture loads PQ, obtained from the tests are similarly used to determine KIC values
(MPa.m 1/2) as a measure of fracture toughness by using the following data reduction scheme
W
4W
a
B
Figure 7. Three Point Bend (SENB)
specimen configuration

Vol.10, No.13 Experimental Methods of Determini ng 1273
=
IC
K
( ) xf
BW
P
Q








2/1
(12)
Where ( )
( ) ( )()
( ) ( )
2/3
2
2/1
121
7.293.315.2199.1
6xx
xxxx
xxf −+
+−−−
=
3. CONCLUSIO N
The development of interlaminar fracture tests of polymer-matrix composites has been rather
slow. Even for Mode I loading, standardization of test methods took about a decade.
Multidirectional lay-ups frequently pose problems with Mode I loading because of crack
branching and/or deviations of the delamination from the central plane. Both effects invalidate
the analysis according to the ASTM standard. Tests for other loading Modes and rates are still
under development. Early round robin work on Mode II ENF conducted jointly by JIS, ASTM
and ESIS has not yet resulted in international consensus. Compared to Mode I and Mode II
fracture, much less work has been reported on Mode III, despite its importance in edge
delamination. Application of standardized test methods to new types of reinforcements has been
tried in research laboratories, but has lead to questions about the validity of the data.
Intralaminar fracture toughness testing has recent ly gained its importan ce by resea rchers but still
a standard test method has not yet evolved.
REFERENCES
1. John M Barsom, Stanley, T Rolfe. (1987). Fracture and Fatigue control in structures:
Application of Fracture Mechanics. Second Edition. Prentice Hall. Inc. USA.
2. Todd M Mower, Victor C Li. (1987). Fracture characterization of random short fiber
reinforced thermoset resin composites. Engineering fracture Mechanics. 26(4): 593-603.
3. C K H Dharan. (1978). Fracture mechanics of composite materials. Journal of engineering
materials and technology. 100: 223-247.
4. R V Silva, D Spinelli, W W Bose Filho, S Claro Neto, G O Chierice, J R Tarpani. (2006).
Fracture toughness of natural fibers/castor oil polyurethane composites. Composite Science
and Technology. 66: 1328-1335.
5. Mehdi Barikani, Hossein Saidpour, and Mutlu Sezen. (2002). Mode-I Interlami nar Fr act ure
Toughness in Unidirectional Carbon-fiber/Epoxy Composites. Iranian Polymer
Journal.11(6): 413-423.
6. Reeder J R. (1993). A Bilinear Failure Criterion for Mixed-Mode Delamination. composite
Materials: Testing and Design, ASTM STP 1206, E.T.Camponeschi, Jr., Ed.ASTM Int., W.
Conshohocken, PA. 11: 303-322.
7. Ratcliffe J. (2004)."Characterization of the Edge Crack Torsion (ECT) Test for Mode III
Fracture Toughness Measurement of Laminated Composites", in proceeding of the 19th
ASC/ASTM Technical Conference. Atlanta.
8. ASTM D5528. (1994). Standard test method for Mode I interlaminar fracture toughness of
unidirectional fiber reinforced polymer matrix composites.

1274 M.S. Sham Prasad, C.S. Venkatesha, T. Jayaraju Vol.10, No.13
9. O’Brien T K , and Martin R H. (1993). Results of ASTM Round Robin Testing for Mode
I Interlaminar Fracture Toughness of Composite Materials. Journal of Composites
Technology and Research. 15(4): 269 – 281.
10. A B de Morais. (2003). Double cantilever beam testing of multidirectional laminates.
Composite Part A: Applied S ci en ce. A34(12): 1135–1142.
11. Pereira A B, de Morais A B. (2004). Mode I interlaminar fracture of carbon/epoxy
multidirectional laminates. Composite Science and Technology. 64: 2261–2270.
12. Choi N S, Kinloch A J, Willams J G. (1999). Delamination fracture of multidirectional
carbon-fib er / epoxy composites under mode I, mode II and mixed mode I/II loading.
Journal of Composite Material. 33(1): 73–100.
13. A J Brunner, B R K Blackman an d P Davies. (2008). A status report on delamination
resistance testing of polymer–matrix composites. Engineering Fracture Mechanics.75:
2779–2794.
14. Brunner A J, Flueler P . (2005). Prospects in fracture of engineering laminates. Engineering
Fracture Mechanics. 72(6): 899–908.
15. Hossein Saidpour, Mehdi Barikani, and Mutlu Sezen. (2003). Mode-II Interlaminar Fracture
Toughness of Carbon/Epoxy Laminates. Iranian Polymer Journal.12 (5): 389-400.
16. Jones R, Broughton W, Mousley R F, and Potter R T. (1985). Compression failure of
damaged gr aph it e epoxy laminat es. C omposite Structures. 3: 167-186.
17. Davies P. (1993). ESIS protocols for interlaminar fracture testing of composites. France,
IFREMER brochure.
18. O’Brien T K. (1998). Interlaminar fracture toughness: the long and winding road to
standardization. Composites- Part B: Engineerin g. 29B(1): 57–62.
19. Gibson R F. (1994). Principles of Composite Material Mechanics. McGraw Hill, USA: 395-
397.
20. A B de Morais, A B Pereira, M F S F de Moura, A G Magalhães. (2009). Mo de III
interlaminar fracture of carbon/epoxy laminates using the edge crack torsion (ECT) test.
Composites Science and Technology. 69: 670–676.
21. Wang S S. (1983). Fracture mechanics for delamination problems in composite materials.
Journal of Composite Materials. 17: 210–233.
22. Donaldson S L. (1988). Mode III interlaminar fracture characterization of composite
materials. Composite Science and Technology. 32: 225–249.
23. Martin R H. (1991). Evaluation of the split cantilever beam for Mode III interlaminar
delamination testing. In: O’Brien TK, editor. ASTM STP 1110. Composite materials: fatigue
and fracture, Philadelphia (PA): ASTM. 3: 243–266.
24. Becht G, Gillespie J W. (1988). Design and analysis of the Cracked Rail Shear specimen for
Mode III interlaminar fracture. Composite Science and Technology. 31: 143–157.
25. Lee S M. (1993). An Edge Crack Torsion Method for Mode III Delamination Fracture
Testing. Journal of Composite Technology and Research. 15(3): 193-201.
26. Choi N S, Kinloch A J, Williams J G. (1999). Delamination fracture of multidirectional
carbon-fiber /epoxy composites under Mode I, Mode II and Mixed-Mode I/II loading.
Journal of Composite Material. 33: 73–100.
27. Andersons J, Konig M. (2004). Dependence of fracture toughness of composite laminates on
interface ply orientations and delamination growth direction. Composite Science and
Technology. 64: 2139–2152.

Vol.10, No.13 Experimental Methods of Determini ng 1275
28. A B de Morais, A.B. Pereira. (2006). Mixed mode I + II inte rl ami nar fr actu r e of glass/ epo xy
multidirectional laminates – Part 1: Analysis. Composites Science and Technology. 66:
1889–1895.
29. F Dharmawan, G Simpson, I Herszberg, S John. (2006). Mixed Mode fracture toughness of
GFRP composites. Composite Structures. 75: 328-338.
30. ASTM D6671/ D6671M. (2006). Standard test method for Mixed ModeI - Mode II
interlaminar fracture toughness of unidirectional fiber-reinforced polymer–matrix
composites.
31. Amar C Garg. (1986). Intralaminar and interlaminar fracture in Graphite /Epoxy laminates.
Engineering Fracture Mechanics. 23 (4): 719-733.
32. Parhizgar S, Zachary L W, Sun C T. (1982). Application of the principle of linear elastic
mechanics to composite materials. International Journal of Fracture. 20: 3-15.
33. S Jose, R Ramesh Kumar, M K Jana, G. Venkateshwara Rao. (2001). Intralaminar fracture
toughness of a cross –ply laminate and its constituent sub-laminates. Composite Science and
Technology. 61: 1115-1122.
34. Pinho, Robinson P, Lannucci L. (2006). Fracture toughness of the tensile and compressive
fiber failure modes in laminated composites. Composite Science and Technology. 66: l2069-
2079
35. Pinho, Robinson P, Lannucci L. (2009). Developing a four point bend specimen to measure
the mode I intralaminar fracture toughness of unidirectional laminated composites.
Composite Science and Technology. 69:1303-1309.
36. ASTM D5045. (1996). Standard test method for plane strain fracture and strain energy
release rate of plastic materials.