 Journal of Minerals & Materials Characterization & Engineering, Vol. 10, No.13, pp.1233-1241, 2011 jmmce.org Printed in the USA. All rights reserved 1233 Model for Per iodic Analysis of the Quantity of Water Evaporated during Thermo-processing of Clay Designated for Pr od uc ti on of Oven R ef ractory C. I. Nwoye1*, B. C. Chukwudi2, P. C. Agu3 and C. C. Ugwuegbu3 1*Department of Met allurgic al and Materials Engineering, Nnamdi Azikiwe University, Awka, Nigeria 2Department of Mechanical Engineering, Imo State University, Owerri, Nigeria. 3Department of Materials and Metallurgical Engineering, Federal University of Technology, Owerri, Nigeria. *Corresponding Author: chikeyn@yahoo.com Abstract A model has been derived for periodic analysis of the quantity of water evaporated during thermo -processing of clay designated for production of oven refractory. The model; γ = exp lnt 1.3 2.9206 shows that the quantity of evaporated water during the drying process is dependent on the drying time, with the evaporating surface being constant . It was found that the validity of the model is rooted on the expression lnγ = (lnt/Logβ)N where both sides of the equation are correspondingly almost equal. The maximum deviation of the model-predicted quantity of evaporated water from the corresponding experimental value is less than 19% which is quite within the acceptable deviation range of experimental results. Water evaporation rate as obtained from experiment and derived model were evaluated to be 0.0536 and 0.0337g mins-1 respectively. Keywords: Model, Water Evaporation, Thermo -processing, Clay, Oven Refractory. 1. INTRODUCTION It is commonly believed that clay deposits exist in several locations all over the world. However, the few products of clay used today have shown that clays are under utilized. Clays are composed basically of minerals such as kaolinite, montmorillonite, and illite in addition to varying amounts of quartz sand, micas, feldspars, gypsum, iron compounds and organic materials [1].  1234 C. I. Nwoye, B. C. Chukwudi Vol.10, No.13 It has b een shown [2] that clays of alumino-silicat e minerals have ex celle nt high t emperatur e volume stability, mechanical strength, thermal shock resistance and creep resistance. Refractories and kiln linings made from these alumino-silicate materials have found application in industrial fields, such as metallurgical and building materials industries [2]. Report [1] has indicated that clay minerals are activated when subjected to high temperature as result of physical and chemical changes which alter their properties. A study [3] on the drying of wet clay indicates three stages of drying: increasing rate, constant and decreasing rate and also revealed that at constant rate, the evaporation rate and evaporation surface are constant. A model [4] has been derived for predicting the quantity of water evaporated during the primary-stage processing of a bioceramic material sourced from kaolin. The model; E = Exp[0.3424(LogT)2.439] (1) shows that the quantity of evaporated water during the drying process is dependent on the drying temperature, the evaporating surface being constant. It was found that the validity of the model is rooted on the expression (Logβ x lnE)N = LogT where both sides of the expression are correspondingly approximately equal to 2. The respective deviation of the model-predicted quantity of evaporated water from the corresponding experimental value was found to be less than 19% which is quite within the acceptable deviation range of experimental results, hence depicting the usefulness of the model. Model for calculating the quantity of water lost by evaporation during ove n drying of clay at 900C has been derived [5]. The model; γ = exp[(lnt)1.0638 - 2.9206] (2) indicated that the quantity of evaporated water, γ during the drying process is dependent on the drying time t, the evaporating surface being constant. The validity of the model was found to be rooted in the expression (Logβ + lnγ)N = lnt. Derivation of a model [6] for predicting the quantity of water evaporated during drying of clay at a temperature range 80-1100C has been carried out. The model; E= exp[0.3424(LogT)2.3529] (3) indicates that the quantity of evaporated water during the drying process is dependent on the drying temperature, the evaporating surface being constant. The validity of the model is rooted in the expression (lnE x Log β)N = Log T since both sides of the expression are correspondingly approximately equal to 2. The respective deviation of the model-predicted quantity of evaporated water from the corresponding experimental value is less than 20% which is quite within the acceptable deviation range of experimental results, hence depicting the usefulness of the model. Water evaporation per unit rise in the drying temperature evaluated from experimental and model-predicted results are 0.078 and 0.0502g/0C respectively, indicating proximate agreement. A model has been derived by Nwoye et al [7] for quantifying the extent and magnitude of water evaporated during time dependent drying of clay. The model;  Vol.10, No.13 Model for Perio dic Analysis of t he Quantit y 1235 γ = exp((lnt/2.9206)1.4) (4) indicates that the quantity of evaporated water γ during the drying process (at 900C) is dependent on the drying time, t, with the evaporating surface being constant. It was found that the validity of the m odel is rooted in the expression lnγ = (lnt/Logβ)N where both sides of the expre ssi on a re correspondingly almost equal. Nwoye et al. [8] derived a model for predictive analysis of the quantity of water evaporated during the primary- stage processing of a bioceramic material sourced from kaolin. The model; α = e(lnt/2.199 2) (5) shows that the quantity of water α, evaporated at 1100C, during the drying process is also dependent on the drying time t, where the evaporating surface is constant. It was found that the validity of the model is rooted on the expression (lnt/lnα)N = Logβ where both sides of the expression are correspondingly approximately equal to 3. The respective deviation of the model-predicted quantity of evaporated water from the corresponding experimental value was found to be less than 22% which is quite within the acceptable deviation range of experimental results. The present work is to derive a model for periodic analysis of the quantity of water evaporated during thermo-processi ng of clay (from Olokoro (Nigeria)) designated for production of oven refractory. 2. MATERIALS AND METHODS The clay sample was crushed to particle size of 425µm and homogenized separately; mixing thoroughly with 10g bentonite (binder) and 6% water (of total weight). It was, moulded and dried at a temperature of 900C in an electric oven to enhance loss of water by evaporation through a drying time range; 50-130mins. A mould of surface area 833mm2 was used to make a rectan gular sh ape of th e clay product. The initi al and fi nal masses of the cla y sampl es were obtained before and after drying respectively to evaluate the mass of water removed from the material. 2. 1 Model Formulation Experimental data (Table 1) obtained from the research work carried out were used for the model formulation. Computational analysis of the experimental data shown in Table 1, gave rise to Table 2 which indicate that; lnγ = lnt N (approximately) (6) Log β γ = exp lnt N (7) Log β  1236 C. I. Nwoye, B. C. Chukwudi Vol.10, No.13 Introducing the values of β and N into equation (7) γ = exp lnt 1.3 (8) 2.9206 Where (γ) = Weight of water lost by evaporation during the drying process (g) (β) = Area of evaporating surface (mm2) N = 1.3; (Collapsibility coefficient of binder-clay particle boundary at the drying temperature of 900C) calculated using a soft ware: C-NIKBRAN [9] t = Drying time (mins.). γM = γ values predicted by model. Table 1: Variation of quantity of evaporated water with drying time 3. BOUNDARY AND INITIAL CONDITIONS Consider a rectangular shaped clay product of evaporating surface area:833mm2, exposed to dryi ng in the oven while it was in wet condition. Initially, atmospheric levels of oxygen are assumed. Atmospheric pressure was assumed to be acting on the clay samples during the drying process (since the furnace is not air-tight). The grain size of clay particles used is 425µm, weight of clay and binder (bentonite) used (for each rectangular product); 100g and 10g respectively, quantity of water used for mixing; 6% (of total weight), dr ying temperature used; 900C, and range of drying time used; (50-130 mins.). The boundary conditions are: Atmospheric levels of oxygen at the top and bottom of the clay samples since they are dried under the atmospheric condition. No external force due to compression or tension was applied to the drying clays. The sides of the particles and the rectangular shaped clay products are taken to be symmetries. 4. MODEL VALIDATION The model was validated by comparison of the model-predicted γ values and those from the experiment for equality. Comparison between these γ values reveals deviations of model- predicted γ from those of the experimental values. This is believed to be due to the fact that the surface properties of the clay and the physiochemical interactions between the clay and binder, which were found to have played vital role during the evaporation process were not 60 70 90 95 110 130 833 833 833 833 833 833 5.02 5.60 6.60 6.91 7.70 8.60 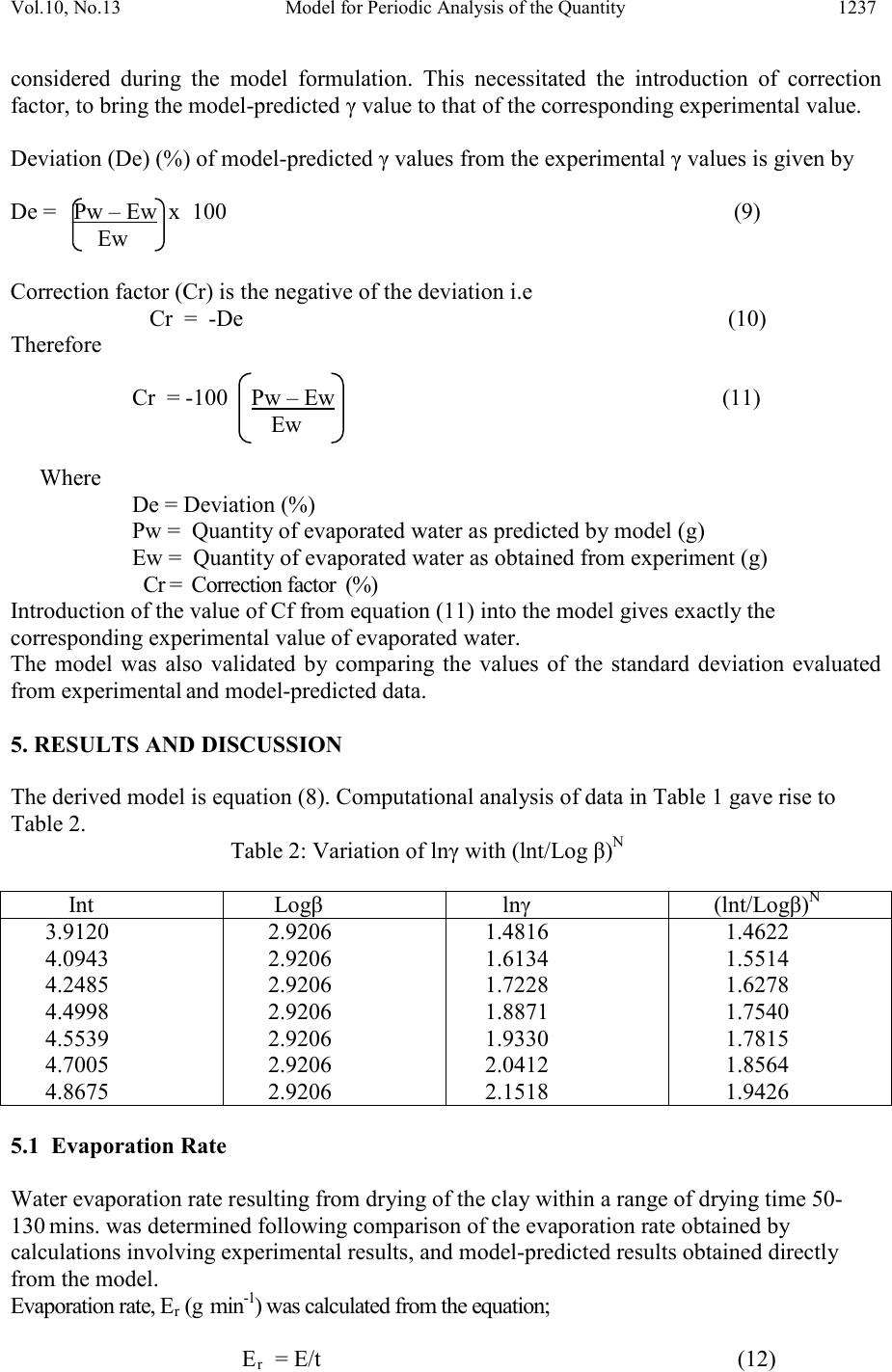 Vol.10, No.13 Model for Perio dic Analysis of t he Quantit y 1237 considered during the model formulation. This necessitated the introduction of correction factor, to bring the model-predicted γ value to that of the corresponding experimental value. Deviation (De) (%) of model-predicted γ values from the experimental γ values is given by De = Pw – Ew x 100 (9) Ew Correction factor (Cr) is the negative of the deviation i.e Cr = -De (10) Therefore Cr = -100 Pw – Ew (11) Ew Where De = Deviation (%) Pw = Quantity of evaporated water as predicted by model (g) Ew = Quantity of evaporated water as obtained from experiment (g) Cr = Correction factor (%) Introduction of the value of Cf from equation (11) into the model gives exactly the corresponding experimental value of evaporated water. The model was also validated by comparing the values of the standard deviation evaluated from experimental and model-predicted data. 5. RESULTS AND DISCUSSION The derived model is equation (8). Computational analysis of data in Table 1 gave rise to Table 2. Table 2: Variation of lnγ with (lnt/Log β)N 4.0943 4.2485 4.4998 4.5539 4.7005 2.9206 2.9206 2.9206 2.9206 2.9206 1.6134 1.7228 1.8871 1.9330 2.0412 1.5514 1.6278 1.7540 1.7815 1.8564 5.1 Evaporation Rate Water evaporation rate resulting from drying of the clay within a range of drying time 50- 130 mins. was determined following comparison of the evaporation rate obtained by calculations involving experimental results, and model-predicted results obtained directly from the model. Evaporation rate, Er (g min-1) was calculated from the equation; Er = E/t (12) 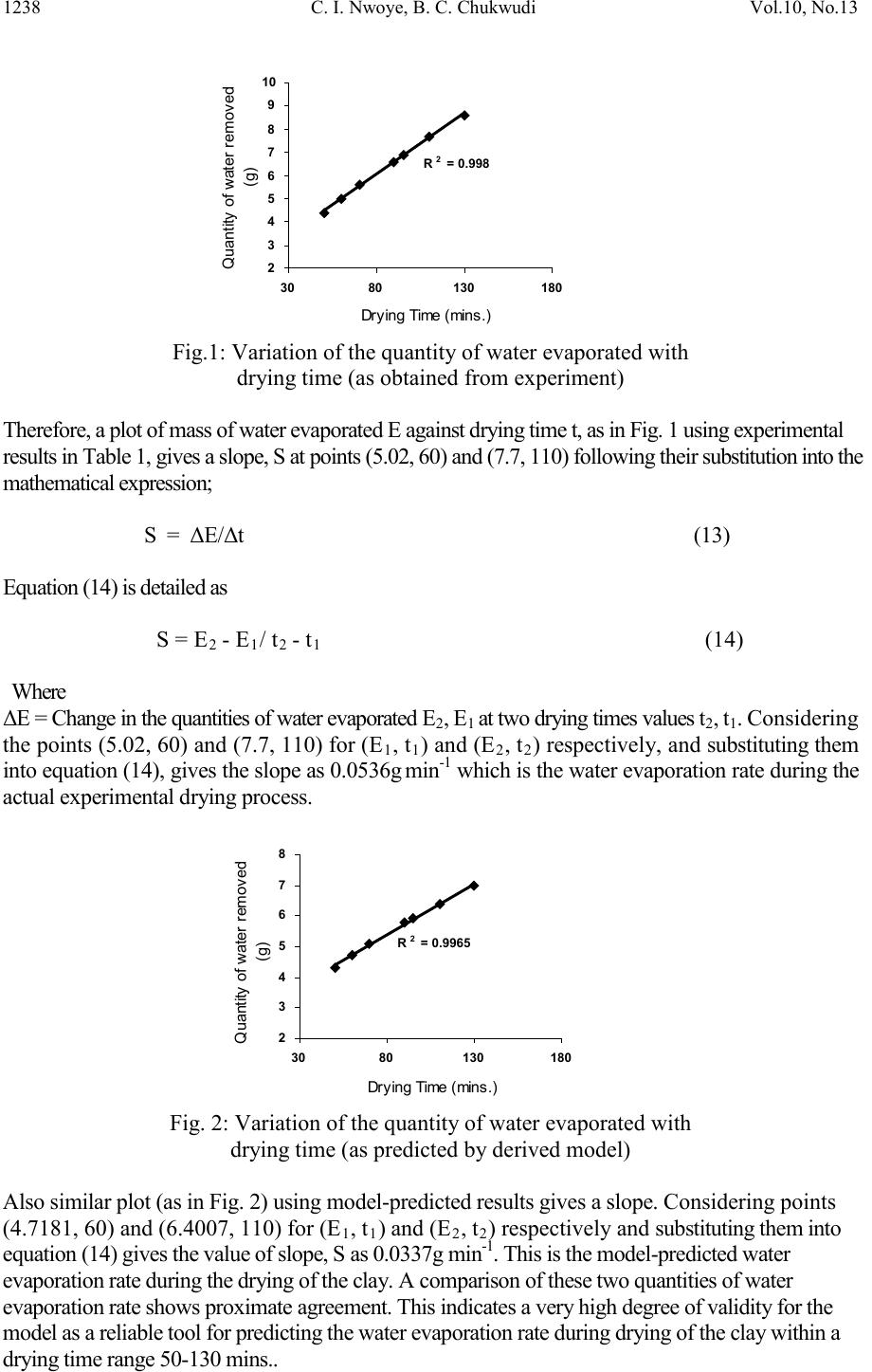 1238 C. I. Nwoye, B. C. Chukwudi Vol.10, No.13 Quantity of water removed (g) Fig.1: Variation of the quantity of water evaporated with drying time (as obtained from experi ment) Therefore, a plot of mass of water evaporated E against dry ing t ime t , as in F ig. 1 using e xperimenta l resu lts in Ta ble 1 , gives a slope , S a t points (5.02, 60) and (7.7, 110) f ollowing their substitution into the mathematical expression; S = ΔE/Δt (13) Equation (14) is detailed as S = E2 - E1/ t2 - t1 (14) Where ΔE = Change in the quantities of water evaporated E2, E1 at two dryin g t ime s values t2, t1. Considering the points (5.02, 60) and (7.7, 110) for (E1, t 1) an d (E2, t2) respectively, and su bstituting th em into equatio n (14), gives the slope as 0.0536g min-1 which is the water evaporation rate during the actual experimental drying process. Quantity of water removed (g) Fig. 2: Variation of the quantity of water evaporated with drying time (as predicted by derived model) Also sim i la r plot ( a s in F ig . 2) using model-predicted results gives a slope. Considering points (4.7181, 60) and (6.4007, 110) for (E1, t1) and (E2, t2) respectively and substituting them into equation (14) gives the va lue of s lope , S as 0. 0337g min -1. This is the model-predicted water evapo ra tion ra te du r ing the dry ing of the c l ay . A co mpar ison of the se two quan titi e s of wate r evapo ra tion ra te s hows p roxi mat e agr eeme nt. Th is i ndica te s a ve ry high degre e o f va l idity for the model as a reliable tool for predicting the water evaporation rate during drying of the clay within a drying time range 50-130 mins.. 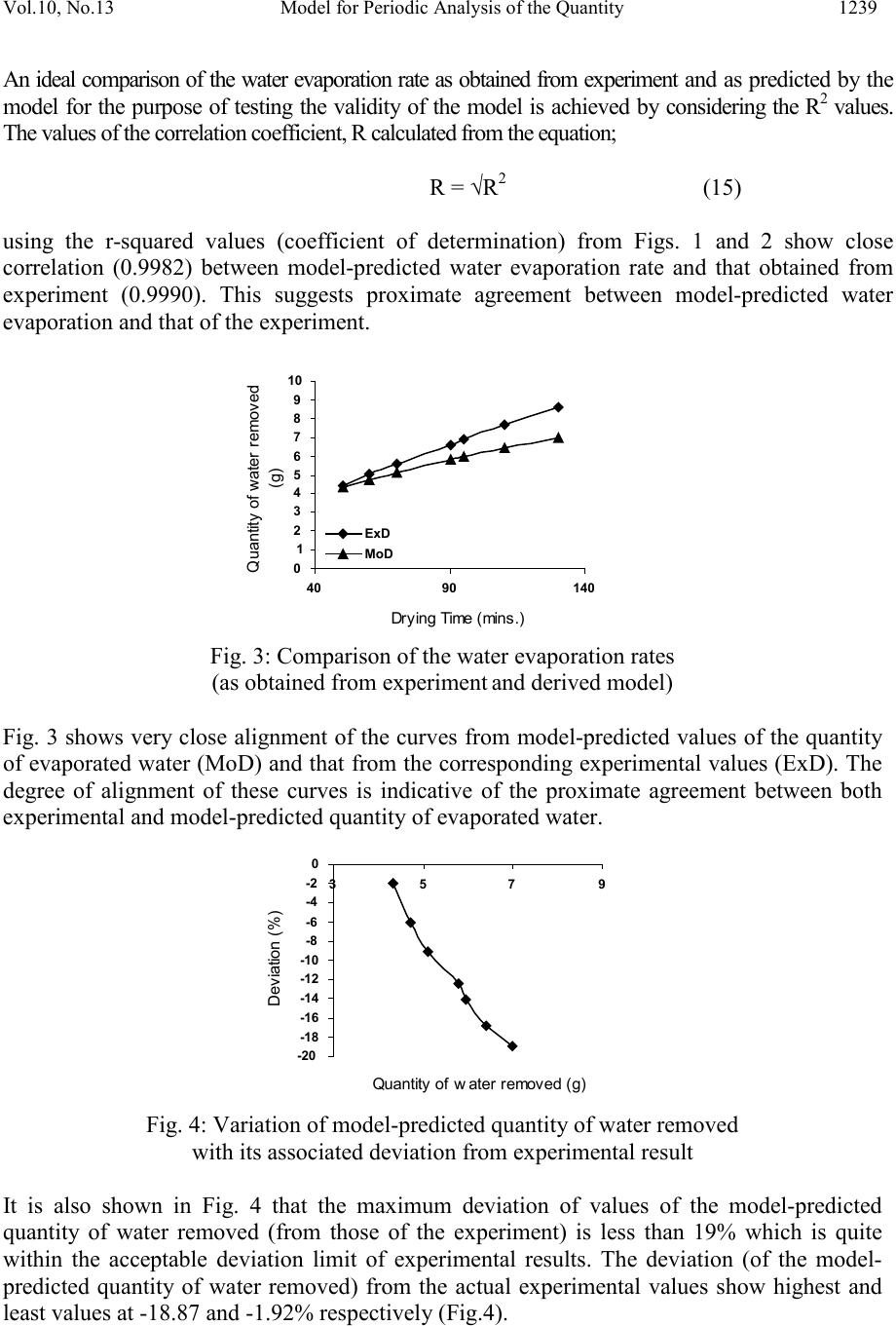 Vol.10, No.13 Model for Perio dic Analysis of t he Quantit y 1239 An ideal compari son of the water evapo ration r ate as obtai ned from experim ent and as predicted by the model for the purpose of testing the validity of the model is achieved by considerin g the R2 values. The values of the correlation coefficient, R calculated from the equation; R = √R2 (15) using the r-squared values (coefficient of determination) from Figs. 1 and 2 show close correlation (0.9982) between model-predicted water evaporation rate and that obtained from experiment (0.9990). This suggests proximate agreement between model-predicted water evaporation and that of the experiment. Quantity of water removed (g) Fig. 3: Comparison of the water evaporation rates (as obtained from experiment and derived model) Fig. 3 shows very close alignment of the curves from model-predicted values of the quantity of evaporated water (MoD) and that from the corresponding experimental values (ExD). The degree of alignment of these curves is indicative of the proximate agreement between both experimental and model-predicted quantity of evaporated water. -20 -18 -16 -14 -12 -10 -8 -6 -4 -2 0 3 57 9 Quantity of water removed (g) Fig. 4: Variation of model-predicted quantity of water removed with its associated deviation from experimental result It is also shown in Fig. 4 that the maximum deviation of values of the model-predicted quantity of water removed (from those of the experiment) is less than 19% which is quite within the acceptable deviation limit of experimental results. The deviation (of the model- predicted quantity of water removed) from the actual experimental values show highest and least values at -18.87 and -1.92% respectively (Fig.4). 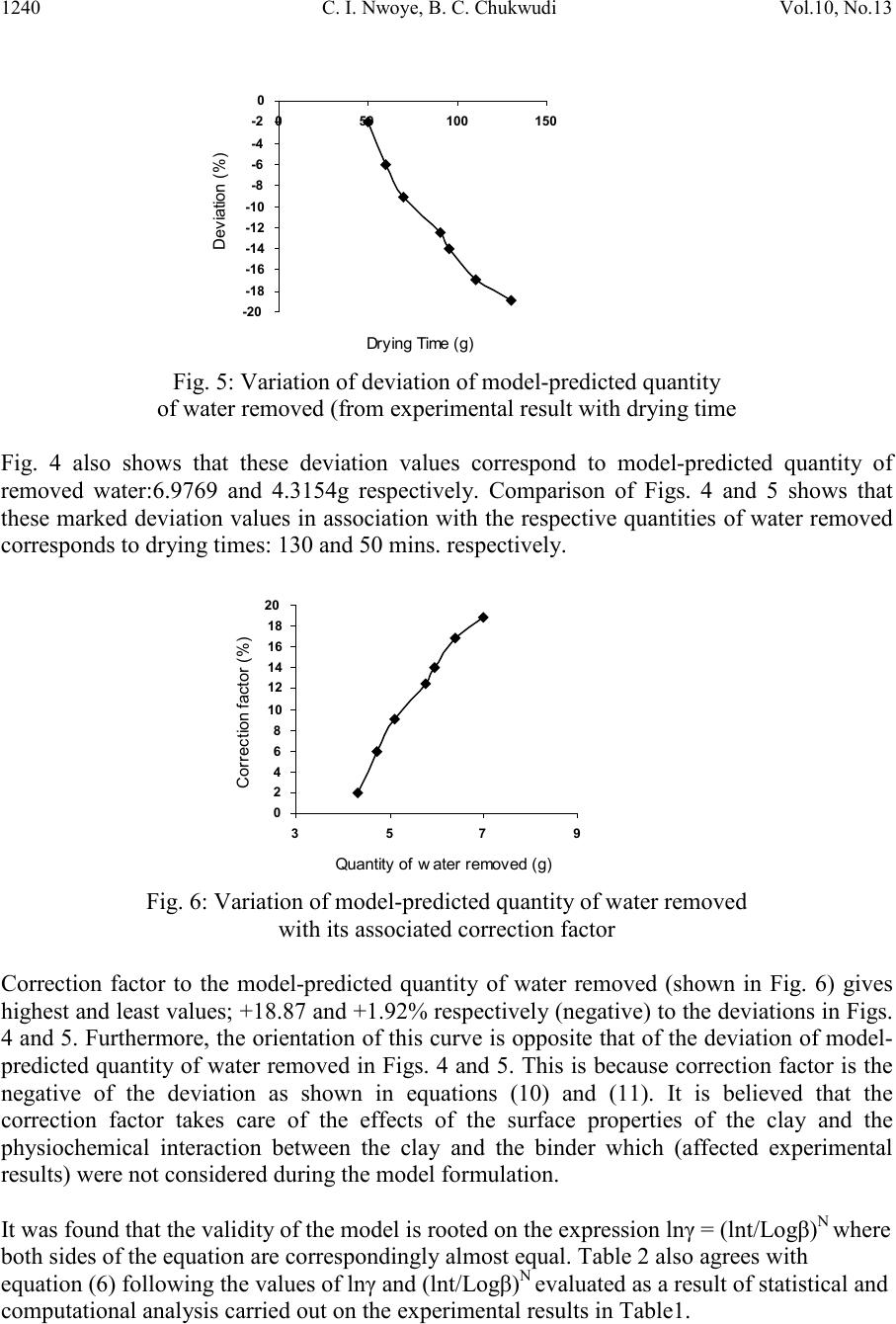 1240 C. I. Nwoye, B. C. Chukwudi Vol.10, No.13 -20 -18 -16 -14 -12 -10 -8 -6 -4 -2 0 050100 150 Fig. 5: Variation of deviation of model-predicted quantity of water removed (from experimental result with drying time Fig. 4 also shows that these deviation values correspond to model-predicted quantity of removed water:6.9769 and 4.3154g respectively. Comparison of Figs. 4 and 5 shows that these marked deviation values in association with the respective quantities of water removed corresponds to drying times: 130 and 50 mins. respectively. Quantity of water removed (g) Fig. 6: Variation of model-predicted quantity of water removed with its associated correction factor Correction factor to the model-predicted quantity of water removed (shown in Fig. 6) gives highest and least values; +18.87 and +1.92% respectively (negative) to the deviations in Figs. 4 and 5. Furthermore, the orientation of this curve is opposite that of the deviation of model- predicted quantity of water removed in Figs. 4 and 5. This is because correction factor is the negative of the deviation as shown in equations (10) and (11). It is believed that the correction factor takes care of the effects of the surface properties of the clay and the physiochemical interaction between the clay and the binder which (affected experimental results) were not considered during the model formulation. It was found that the validity of the model is rooted on the expression lnγ = (lnt/Logβ)N where both sides of the equation are correspondingly almost equal. Table 2 also agrees wi t h equation (6) following the values of lnγ and (lnt/Logβ)N evaluated as a result of statistical and computational analysis carried out on the experimental results in Table1.  Vol.10, No.13 Model for Perio dic Analysis of t he Quantit y 1241 6. CONCLUSION The model gives a periodic analysis of the quantity of water evaporated during thermo- processing of Olokoro clay (designated for production of refractory) at 900C within a drying time range of 50-130 mins.. It was found that the validity of the model is rooted in expression lnγ = (lnt/Logβ)N where both sides of the expression are correspondingly almost equal. The maximum deviation of the model-predicted water evaporation rate from the corresponding experimental value is less than 19% which is quite within the acceptable deviation range of experi mental resul ts. Water evaporation rate as obtained from experiment and derived model were evaluated to be 0.0536 and 0.0337g min-1 respectively. Further works should incorporate more process parameters into the model with the aim of reducing the deviations of the model-predicted γ values from those of the experimental. REFERENCES [1] Shoaib, M. M., Amer, A. A., El-didamony, H., and A. A. H. El-sheikh. (2000).Effect of Calcination Temperature on the Clay-Limestone Mixes. Sil. Ind., 65(9-10): 95-100. [2] Liao, G., He, K., Li, L., and Jiang, M. (2004). Study on Application of Alumina In High- Purity Andalusite Based Refractory. J. Min., Mat., Charact. & Eng.. 3(2):81-89 [3] Reed, J. (1988). Principles of Ceramic Processing, Wiley Interscience Publication, 470- 482, Canada. [4] Nwoye, C. I., Okeke , K., Obi , M. C., Nwanyanwu U., Obasi , G. C. and Onyemaobi , O. O. (2010). Model for Predictive Analysis of the Quantity of Water Evaporated during the Primary-Stage Processing of Bioceramic Material Sourced from Kaolin, J. Min., Mat., Charact. & Eng. 9(2):147-155. [5] Nwoye, C. I. (2009). Model for Calculating the Quantity of Water Lost by Evaporation during Oven Drying of Clay. Researcher Journal, 1(3): 8-13. [6] Nwoye, C. I. (2009). Model for Predicting the Quantity of Water Evaporated during Initial Stage Drying of Wet Clay Designated for Production of Bricks. J. Min., Mat. Ch aract . & Eng. 8(8): 647-658. [7] Nwoye, C. I., Nwakwuo, C. C., Obi, M. C., Obasi, G. C., Onyemaobi, O. O., (2009). Model for Quantifying the Extent and Magnitude of Water Evaporated during Time Dependent Drying of Clay. New York J. Sc . 2(3) : 55-58. [8] Nwoye, C. I., Okeke, K., Obi, M., Nwanyanwu, U., Ofoegbu, S. (2009). Model for Predictive Analysis of the Quantity of Water Evaporated during the Primary-Stage Processing of Bioceramic Material Sourced from Kaolin. J. Nat. Sc., 7(4): 79-84. [9] Nwoye, C. I. (2008). C-NIKBRAN. ‘‘Data Analytical Memory’’- Softw are
|