 Sociology Mind 2012. Vol.2, No.3, 282-288 Published Online July 2012 in SciRes (http://www.SciRP.org/journal/sm) http://dx.doi.org/10.4236/sm.2012.23037 Copyright © 2012 SciRes. 282 The Body Mass Index (BMI) and TV Viewing in a Co-Integration Framework Anastasia Victoria Lazaridi Department of Nutrition and Dietetics, Technological Education Institute (T.E.I.) of Larissa, Larissa, Greece Email: vicolazaridi@hotmail.com Received February 2nd, 2012; revised March 3rd, 2012; accepted April 2nd, 2012 Many techniques are met in the literature, trying to investigate the effect of TV watching hours on BMI. However, we haven’t traced any empirical study with co-integration analysis, as it is applied here. With this in mind, we present in this paper the proper methodology, based on the co-integration analysis for a detailed justification of the effect of TV viewing hours together with some minor changes in life style of participants on BMI. Apart from finding and testing an acceptable co-integration relation, we further for- mulated an error correction model to determine the coefficient of adjustment. All findings, which are fully justified, are presented in details in the relevant sections. It should be pointed out, that we haven’t met this type of analysis in the relevant literature. Keywords: BMI; Integration; Co-Integration; Error Correction Model; Coefficient of Adjustment; Spurious Regression Introduction It is worthy to mention that BMI has received particular at- tention in many research works (see for instance Ahn et al., 2011; Bridger et al., 2011; Browning et al., 2011; Eek et al., 2009; Farkas et al., 2005; Harbin et al., 2006; Komlos et al., 2006; Lee et al., 2008; Manios et al., 2004; Stea et al., 2008; Stenhammmar et al., 2010, among others). In most cases the effect of various factors on BMI was the main object. Besides, in many papers (see for instance Danner et al., 2008; Davison et al., 2006; Henderson, 2007; Lazarou et al., 2009, among others) an effort is made to investigate the effect of TV viewing hours on the BMI. Almost in all cases, cross-sectional data are used and the standard statistical methods are applied. Apart from simply presenting the results obtained from commercial com- puter packages (usually SPSS), no attempt is made to analyze the mathematics involved even for a plain justification of the results obtained. It seems that the computer output plays the role of the “follow me” car in the airports, driving the authors through a specific direction, without any explanation that this direction is the right one and why. Instead, a lot of redundant descriptive details are sited; no any specific and well-formu- lated model is presented, although the term “model” is exten- sively used. Regardless of the robustness of these methods, we haven’t seen in the relevant literature an empirical study with co-integration analysis, as it is applied here. With this in mind, we made an attempt to jump to the other side of the fence, con- sidering time series data and applying co-integration analysis in order to analytically investigate the effect of TV watching hours on BMI. This analysis requires that the series used must be integrated, of the same order, so that we can finally obtain a stationary linear combination (that can be a static regression) which constitutes the necessary and sufficient condition to con- clude that the series used are co-integrated and we don’t face the case of spurious regression. Further, we formulated an error correction model to determine the coefficient of adjustment. It is worthy to mention, that we haven’t met this type of analysis in the relevant literature. Data Used Initially, 50 volunteers from the greater region of Thessalo- niki, Greece, agreed to report regularly (twice per month) via an e-mail, their weight and height, together with some major re- marks, if necessary. Finally we obtained a continuous stream of such data from only 32 individuals (40% males and 60% fe- males), for almost 3 years, which means 72 reports (2 per month), by each participant1. At the very beginning, the age of participants vary between 17 and 21 years. As mentioned above, we received individual reports every 15th day (i.e. two reports per month). Each time we calculated the BMI of each partici- pant and finally2 we computed the mean BMI, regarding the 32 cases. The same calculations hold for the mean hours of TV viewing during the period of 15 days. These 72 mean values refer to series {BMIi}, {TVHi} (i = 1, 2, 3, ···, 72), which are presented in appendix. It should be noted however, that the majority of the participants stated that from the 62nd observa- tion (i.e. from middle of the 31st month) and onwards, they increase there seating hours, for various reasons (decreasing physical exercise, working from home, etc.). To capture this structural change in participants lifestyle, we introduced a dummy (binary) variable (i), which takes the value 1 for the last 11 observations (from 62 up to 72), and the value of zero elsewhere. d It is noted that we denote by Y the natural logs of BMI [i.e. Yi = ln(BMIi)] and by X the natural logs of TV hours [i.e. Xi = ln(TVHi), i = 1, 2, 3, ···,72]. Since the latter variables (i.e. Y 1Last report received beginning of 2012. 2It is recalled that the formula used to compute BMI is: 2 Weightin kg BMI Height inm 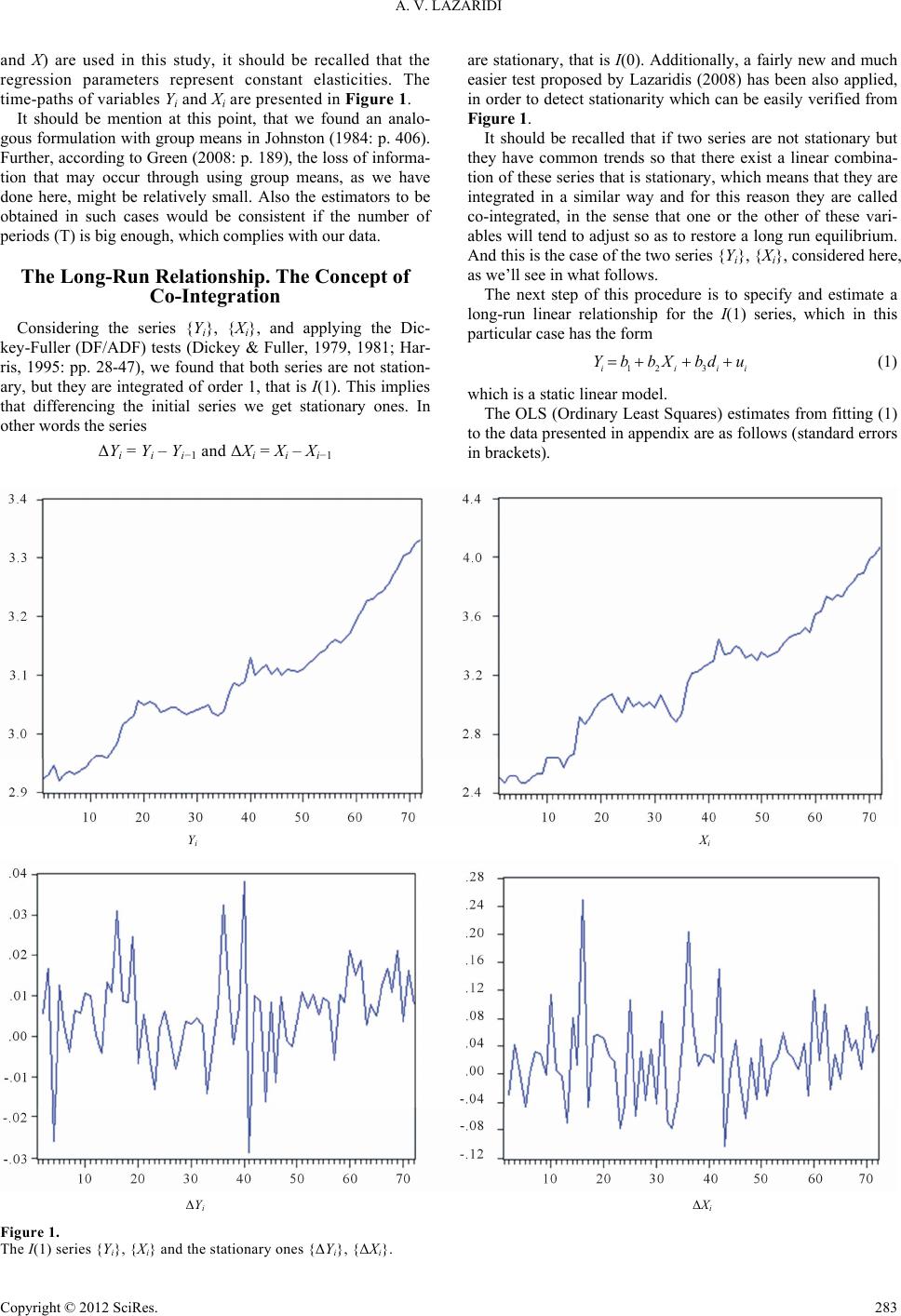 A. V. LAZARIDI and X) are used in this study, it should be recalled that the regression parameters represent constant elasticities. The time-paths of variables Yi and Xi are presented in Figure 1. It should be mention at this point, that we found an analo- gous formulation with group means in Johnston (1984: p. 406). Further, according to Green (2008: p. 189), the loss of informa- tion that may occur through using group means, as we have done here, might be relatively small. Also the estimators to be obtained in such cases would be consistent if the number of periods (T) is big enough, which complies with our data. The Long-Run Relationship. The Concept of Co-Integration Considering the series {Yi}, {Xi}, and applying the Dic- key-Fuller (DF/ADF) tests (Dickey & Fuller, 1979, 1981; Har- ris, 1995: pp. 28-47), we found that both series are not station- ary, but they are integrated of order 1, that is I(1). This implies that differencing the initial series we get stationary ones. In other words the series ΔYi = Yi – Yi−1 and ΔΧi = Xi – Xi−1 are stationary, that is I(0). Additionally, a fairly new and much easier test proposed by Lazaridis (2008) has been also applied, in order to detect stationarity which can be easily verified from Figure 1. It should be recalled that if two series are not stationary but they have common trends so that there exist a linear combina- tion of these series that is stationary, which means that they are integrated in a similar way and for this reason they are called co-integrated, in the sense that one or the other of these vari- ables will tend to adjust so as to restore a long run equilibrium. And this is the case of the two series {Yi}, {Xi}, considered here, as we’ll see in what follows. The next step of this procedure is to specify and estimate a long-run linear relationship for the I(1) series, which in this particular case has the form 12 3iii YbbXbd u i (1) which is a static linear model. The OLS (Ordinary Least Squares) estimates from fitting (1) to the data presented in appendix are as follows (standard errors in brackets). Yi Xi ΔYi ΔXi Figure 1. he I(1) series {Yi}, {Χi} and the stationary ones {ΔΥi}, {ΔΧi}. T Copyright © 2012 SciRes. 283  A. V. LAZARIDI 0.013644 0.0044550.00533 ˆ2.3751910.2226990.04106 174.08 49.993 7.708 val. 0.0 0.0 0.0 Hansen 0.21 iii YXd t p 2 2, 69 0.24 0.13 0.987, 0.012, 1.4, 2853.8, Condition number21.17 RsDWdF CN (1a) It is recalled that Hansen (1992) statistics, reveal that the model coefficients, individually considered, are stable for all conventional levels of significance (α = 0.01, 0.05, 0.10). The low value of the condition number (CN) indicates that no mul- ticollinearity problems exist (Lazaridis, 2007). Finally from the p-values we conclude that all coefficients are significant. This implies that hours of TV viewing are (positively) associated with BMI. This is in line with the findings of Danner (2008: p. 1101). Obviously, the same applies for the change of lifestyle of participants from 62nd observation and onwards. Also, the joined effect of both variables (X and d) is significant, accord- ing to the large value (2853.8) of F statistic. It may be worthy to mention at this point, that Danner (2008) using pooled data estimates a model where the only explanatory variable is a categorical one [time and (time)2, p. 1103], taking arbitrary values, so that one may argue that the correct specification of the model is questionable. Besides no model testing results are presented and no explanation is provided about the subscript i (i.e. where this subscript refers to). Next (same page), the au- thor presents the estimated results of two models (fixed effects and random effects) without even a vague explanation of what a random effects model is, what estimation process is applied in this case and how the random effects are computed, if they are needed. Mainly, there is a lack of any proper testing (see Hausman, 1978), in order to justify as to whether the fixed effects or the random effects model is more suitable for the data used. In other cases (see for instant Lazarou et al., 2009), one reads the term “regression models” (page 71), but no such a model is explicitly presented in the typical form, as the one seeing in (1a). Henderson (2007), speaks about “modeling la- tent growth curves” (p. 547), without any sufficient and ana- lytical explanation of what it is and whether any conventional model tests have been applied. In other cases, misleading statis- tical measures are presented as in Browning et al. (2011: p. 1383), where the plain arithmetic mean (30.6 Kg), of a sample where weight varies from 2.5 to 117.8 Kg is reported. In similar cases with such a large range, a sort of weighted mean, where the weights will be related somehow to the age, or at least the median (even if classification of the data is necessary), may be more representative measures of central tendency. Finally, from the small value (0.012) of the standard error of estimate (s) seeing in (1a), we may conclude that uncertainty is rather limited when forecasting the values of the dependent variable. Note that in such a case, a measure of uncertainty is the width of the relevant confidence interval. According to Granger and Newbold (1974), high t-values, high 2 (i.e. the adjusted coefficient of determination 2 ), together with low values of the DW d statistic, when a static regression of two independent random walks is estimated [as in (1a)], then we are facing the case of spurious regression, with undesired properties. However, a static regression between non-stationary variables will not be a spurious regression, if the variables have common trends, for instance if they are inte- grated of first order and the OLS residuals are stationary. Then the series [here {Yi} and {Xi}] are integrated in a similar way and for this reason they are called co-integrated. This implies that although the series under consideration are non-stationary, there exists a stationary linear combination of these variables. To show that {Yi} and {Xi} are co-integrated, we compute the OLS residuals {} from: ˆi u ˆ ˆii uYY i (2) ˆ0.2226990.04106 2.375191 iii i uYX d (2a) Then we run the following regression without constant term, since for the OLS residuals 0 ˆ. i u 11 1 1 ˆˆ ˆ q ii jij j ububui (3) The value of q is set such that, after excluding the terms with insignificant coefficients, the noises εi to be white, as it will be explained in details later on. With q = 0, the estimation results are as follows: 1 0.004455 ˆˆ 0.727716 6.35 val. 0.0 ii uu t p (3a) DW d = 2, AIC (Akaike’s Information Criterion)3 = −6.105. With q = 1 and 2, we get the following estimation results. 11 0.14473 0.11991 ˆˆ ˆ 5.9505 0.173559 4.111 1.447 val. 0.0 0.152 DW d = 2, AIC =6.0955 ii uu t p i u (3b) 11 0.146112 0.1549430.12268 ˆˆ ˆ 0.582877 0.1935220.008113 3.552 1.249 0.0661 val. 0.0 0.216 0.947 DW d = 1.9 ii i uu u t p 2 ˆ i u , AIC = 6.065 (3c) (It is recalled that when the value of DW d statistic is close to 2, then we may conclude that no problem of first order auto- correlation exists). Although in all cases there is no any problem of autocorrela- tion and heteroscedasticity, we considered model (3a), since in the other two models- and for higher values of q the additional explanatory variables are insignificant, as it is verified from the corresponding p-values. Hence the value of t-statistic (−6.35), which refers to the estimated coefficient of , will be taken into consideration next. 1 ˆi u Since the series ˆi u is the result of specific calculations and in the simplest case are the OLS residuals, it is not advis- able (Harris, 1995: pp. 54-55) to apply the Dickey-Fuller (DF/ ADF) test, as we do with any variable in the initial data set. We have to compute the tu statistic from McKinnon (1991: pp. 267-276) critical values (see also Harris, 1995: Table A6, p. 158). This statistic (tu = Φ∞ + Φ1/Τ + Φ2/Τ2, where T denotes the sample size) for the static relationship seen in (1a) is: 3It is noted that in usual applications, when competing models are consid- ered, the one with the smallest value of AIC is preferred. Copyright © 2012 SciRes. 284  A. V. LAZARIDI α0.01 α0.05 α0.10 3.52 2.9 2.59 uuu ttt Since t = −6.35 < tu, the series ˆi u ˆ u is stationary for α = (0.01, 0.05, 0.10). Recall that the null [i ~ I(1)] is rejected in favor of H1 [~ I(0)], if t < tu. Hence (1) concerns a co-inte- grating relationship and can be considered as a longrun equilib- rium relationship. The estimation results seeing in (1a) are quite satisfactory. ˆi u A comparatively simple way (Lazaridis, 2008) to test that for the noises ei in (3), with q = 0, we don’t have any problem of autocorrelation of higher order, is to compute the residuals from (3a) and to consider the corresponding Ljung-Box Q sta- tistics and particularly their p-values, which should be greater than 0.1 to say that no autocorrelation is present. For this par- ticular case, the corresponding Q statistics (column 4) together with p-values are presented in Table 1. From this table, we see that for all k (column 1) the corresponding p-values (column 5) are greater than 0.1, so we can conclude that there is no need to increase the value of q, to get Equations (3b) and (3c) in order to face autocorrelation problems. As far as heteroscedasticity is concerned, a practical way to trace it, is to find the explanatory variable which yields the smallest p-value for the corresponding Spearman’s correlation coefficient ( ˆi e r), or the larger Z* statistic (absolute value). Since in (3a) there is only one explanatory variable, we found: rs = 0.075, p = 0.48 and Z*= 0.63. From the p-value we conclude that we have to accept the null of homo- scedastic disturbances. When larger samples are considered, then Z* statistic is used, which is computed from: *1 1 1 s s r Zr T T We accept the null, if |Z*| < Zα/2. From the table of standard normal distribution we find: α2α2α2 α0.01 α0.05 α0.10 2.5758 1.96 1.6449ZZZ Hence we accept the null for all conventional levels of sig- nificance. It may be useful to mention that we reach to the same results when model (3b) and (3c) are considered. We pointed out however, why these models have been dropped. Having in mind some confusing remarks on this point, we underline once more that (1), which is a static regression, is a co-integrating relation, iff4 the residuals , computed from (1a), (2a) are stationary. Apart from the proper test shown above, the stationarity of ˆi u ˆi u may be detected from Figure 2 presented above. From the estimated co-integration regression (1a), we can tell that the dummy di, used as a proxy to capture the change in lifestyle of the participants, had a significant effect on BMI. We see also that the elasticity of the TV viewing hours is 0.222699. It is worthy to mention here, that taking into account that the quotient of sample standard deviations of Yi and Xi is 0.107777/0.433222 = 0.248, the estimated long-run response of 0.222699 in (1a) is reasonable close, which is another verifica- tion that this co-integration analysis has resulted to an accept- able model for investigating the relations between BMI and Table 1. Residuals : Autocorrelations, PAC, Q statistics and p-values. ˆi e Values of k AC PAC Q_Stat (L-B) p value Q_Stat (B-P) p value 1 −0.041 −0.0410.127 0.720 0.1220.726 2 0.1700.169 2.320 0.313 2.1940.333 3 −0.0070.005 2.324 0.507 2.1980.532 4 0.1620.138 4.378 0.357 4.0830.394 5 −0.090 −0.0835.014 0.414 4.6590.458 6 0.0570.004 5.275 0.508 4.8910.557 7 −0.133 −0.1146.729 0.457 6.1660.520 8 0.0430.008 6.884 0.549 6.3000.613 9 −0.132 −0.0778.353 0.498 7.5470.580 10 −0.100 −0.1319.209 0.512 8.2630.603 11 −0.103 −0.04710.12 0.518 9.0180.620 12 −0.055 −0.05510.40 0.580 9.2390.682 13 −0.0270.036 10.46 0.655 9.2920.750 14 −0.060 −0.04410.80 0.701 9.5510.794 15 −0.033 −0.02110.90 0.759 9.6310.842 16 0.0830.092 11.56 0.773 10.120.859 17 0.0790.078 12.17 0.789 10.570.877 18 0.0390.031 12.32 0.829 10.690.907 19 0.0670.017 12.78 0.849 11.010.923 20 0.0590.009 13.13 0.871 11.260.939 21 0.2300.197 18.63 0.608 15.020.821 22 −0.132 −0.17120.49 0.552 16.270.801 23 −0.079 −0.18121.17 0.570 16.720.822 24 −0.094 −0.11422.15 0.570 17.350.833 25 −0.061 −0.10522.58 0.602 17.620.857 26 0.0020.143 22.58 0.656 17.620.889 27 −0.115 −0.08024.14 0.621 18.560.885 Figure 2. The stationary series ˆi u, computed from (2a). 4If and only if. Copyright © 2012 SciRes. 285  A. V. LAZARIDI TV viewing hours. Thus we may conclude that an increase by 10% of TV viewing hours, may result to an increase of about 2.2% of BMI. The Short Run Relationship The lagged values of the residuals computed from the static long-run equation (i.e. 1), serve as an error correction me- chanism in a short-run dynamic relationship, where the addi- tional explanatory variables may appear in first differences and lagged first differences. All variables in this equation, known also as error correction model (ECM), are stationary so that, from the statistical point of view it is a standard single equation model, where all the classical tests are applicable. It should be noted, that the lag structure should be so selected in order to eliminate autocorrelation and to obtain at the same time a sig- nificant adjustment coefficient, which refers to 1. With this in mind the short-run ECM corresponding to (1a) may have the form: ˆi u ˆi u 1 1 0.00131 0.02160.020.116 ˆˆ 0.001986 0.12430.0430.2858 val. 0.13 0.0 0.025 0.016 Hansen 0.23 0.14 0.398 0.23 RESET F0 i iii YXX p u 2 3, 66 .879 (val.0.46) 0.33,0.009, DW d2.25,12.5, Condition number2.03 p Rs F (4) According to Hansen statistics, all coefficients-individually considered seem to be stable for α = (0.01, 0.05). The condition number reveals that there is no any multicollinearity problem. That no autocorrelation of higher order exists can be detected from the table which is analogous to Table 1 and refers to the residuals of Equation (4), where all the p-values corresponding to the Ljung-Box Q statistics are greater than 0.1. In models like the one seeing in (4), the term 1 usually produces the smallest p-value, regarding the t-statistic of the corresponding Spearman’s correlation coefficient ˆi u r, or the larger Z* statis- tic (absolute value). In this particular case we have: rs = 0.16, t = 1.336, p = 0.156 and Z* = 1.329, which means that no hetero- scedasticity problems exist. Finally the RESET test (Ramsey, 1969), shows that there is no any specification error. Before interpreting the estimation results, a further comment should be made about the sign of the coefficient of adjustment (−.2858). It is recalled that the residuals have been com- puted from (2), that is . However, if we compute these residuals from ˆi u ˆ ˆii uYY i i 1i u ˆ ˆii uYY (5) Then Equation (4) will take the form: 1 0.00131 0.02160.020.116 ˆˆ 0.001986 0.12430.0430.2858 iii YXX (6) In other words, the sign of the coefficient of adjustment de- pends upon the relation (2 or 5) used to compute the residuals entered in the ECM with one period lag. In any case, this coef- ficient is significant at α = 0.05. From Equations (4) and (6) we see that the adjustment coefficient (0.2858) gives a satisfactory percentage, regarding the BMI convergence towards a long run equilibrium. Besides, the significance of the coefficient of dis- equilibrium error (i.e. the coefficient of adjustment), in- dicates that in the long run there is a causality effect from TV viewing hours to BMI. Also, the coefficient of ΔXi is significant, so that we may conclude that changes in TV viewing hours influence BMI. In the short-run, a change of the hours viewing TV by 1%, results to an increase of BMI by about 124% from one period to the next. 1 ˆi u Another point which deserves further attention refers to the condition number reported here, although we don’t see it in other studies (see for instance Nguyen, 1987; Ouyang et al., 2000, among others). In many applications, particularly when the variables are in logs, then in the corresponding statistical models the value of CN is extremely high revealing in most cases a severe multicollinearity problem. And it seems that this is the main reason, for not reporting this statistic in relevant applications. However, Lazaridis (2008) has shown that in such cases, usually we have spurious multicollinearity. Conclusion We applied detailed co-integration analysis to investigate the effect of TV viewing hours on BMI. For this particular case, we found that the elasticity of TV viewing hours will not exceed 0.223, which implies that if these hours increase by 10%, than the expected increase of BMI will be about 2.2%. It has been verified that TV viewing hours influence BMI together with the lifestyle change of the participants, captured by the dummy variable di. It is also verified that changes of the TV viewing hours influence BMI and a 1% change of the hours watching TV, may results to a change of BMI by about 0.124% from one period to the next. These findings do not mean that TV viewing hours might be inefficient in the long run, since from co-integration analysis we found that the adjustment coefficient is significant and it will be expected to fluctuate around 0.28, giving thus a satisfactory percentage, regarding the BMI con- vergence towards a long run equilibrium. Ceteris paribus, BMI is expected to undergo significant effects in the long run, from TV viewing hours. It should be emphasized however, that this analysis is based upon self-reported data. Also the sample size (32 cases), to compute relevant means may be considered insufficient. This gives rise to further research by increasing the number of par- ticipants and mainly to have available authorized data. Addi- tionally, if the number of participants may be considerably increased, separately estimation results could be obtained for mails and females, to better trace possible similarities and dif- ferences. Also, an effort should be made to capture the change in life-style of participants, by more official indices instead of a plain binary variable used here. Finally, if the number of peri- ods (T) can be further increased, then we may reach to more detailed and robust results, regarding the effect of TV viewing hours and changes of life-style on BMI, separately for males and females. In fact, in this research work we didn’t pay par- ticular attention regarding data collection, since the main aim of the study was to analytically present a new approach to face similar tasks, which has not met in the relevant literature. REFERENCES Ahn, S., Zhao, H., Smith, M. L., Ory, M. G., & Phillips, C. D. (2011). BMI and lifestyle changes as correlates to changes in self-reported diagnosis of hypertension among older Chinese adults. Journal of the American Society of Hypertension, 5, 21-30. Copyright © 2012 SciRes. 286  A. V. LAZARIDI Copyright © 2012 SciRes. 287 doi:10.1016/j.jash.2010.12.001 Bridger, S. R., & Bennett I. A. (2011). Age and BMI interact to deter- mine work ability in seafarers. Occupational Medicine, 61, 157-162. doi:10.1093/occmed/kqr003 Browning, B., Thormann, K., Donaldson, A., Halverson, T., Shinkle, M., & Kletzel, M. (2011). Busulfan dosing in children with BMIs ≥ 85% undergoing HSCT: A new optimal strategy. Biology of Blood and Marrow Transplantation, 17, 1383-1388. doi:10.1016/j.bbmt.2011.01.013 Danner, M. F. (2008). A national longitudinal study of the association between hours of TV viewing and the trajectory of BMI growth among US children. Journal of Pediatric Psychology, 33, 1100-1107. doi:10.1093/jpepsy/jsn034 Davison, K. K., Marshall, S. J., & Birch, L. L. (2006). Cross-sectional and longitudinal associations between TV viewing and girls body mass index, overweight, and percentage of body fat. Journal of Pe- diatrics, 149, 32-37. doi:10.1016/j.jpeds.2006.02.003 Dickey, D. A., & Fuller, W. A. (1979). Distribution of the estimators for autoregressive time series with a unit root. Journal of the Ameri- can Statistical Association, 74, 427-431. Dickey, D. A., & Fuller, W. A. (1981). Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica, 49, 1057- 1072. doi:10.2307/1912517 Dickey, D. A., Jansen, D. W., & Thornton, D. L. (1994). A Primer on cointegration with an application to money and income. In B. B. Rao (Ed.), Cointegration for the applied economist. London: St. Martin’s Press. Eek, F., & Östergren, O. P. (2009). Factors associated with BMI change over five years in Swedish adult population. Results from the Scania Public Health Cohort Study. Scandinavian Journal of Public Health, 37, 532-544. doi:10.1177/1403494809104359 Farkas, T. D., Vemulapalli, P., Haider, A., Lopes, M. J., Gibbs, E. K., & Teixeira, A. J. (2005). Laparoscopic Roux-en-Y gastric bypass is safe and effective in patients with BMI ≥ 60. Obsesity Surgery, 15, 486-493. doi:10.1381/0960892053723466 Freedman, S. D., Katzmarzyk, T. P., Dietz, H. W., Srinivasan, R. S., & Berenson, S. G. (2010). The relation of BMI and skinfold thicknesses to risk factors among young middle-aged adults: The Bogalusa Heart Study. Annals of Human Biology, 37, 726-737. doi:10.3109/03014461003641849 Granger, C. W. J., & Newbold, B. (1974). Spurious regressions in eco- nometric model specification. Journal of Econometrics, 2, 111-120. doi:10.1016/0304-4076(74)90034-7 Green, H. W. (2008). Econometric analysis (6th ed). Pearson, NJ: Pren- tice Hall. Hansen, B. E. (1992). Testing for parameter instability in linear models. Journal of Policy Modelling, 14, 517-533. doi:10.1016/0161-8938(92)90019-9 Harbin, G., Shenoy, C., & Olson, J. (2006). Ten-year comparison of bmi, body fat, and fitness in the workplace. American Journal of In- dustrial Medicine, 49, 223-230. doi:10.1002/ajim.20279 Harris, R. (1995). Using cointegration analysis in econometric model- ling. London: Prentice Hall. Hausman, J. A. (1978). Specification tests in econometrics. Econo- metrica, 46, 1251-1271. doi:10.2307/1913827 Henderson, V. R. (2007). Longitudinal association between television viewing and body mass index among white and black girls. Journal of Adolescent Health, 41, 544-550. doi:10.1016/j.jadohealth.2007.04.018 Johnston, J. (1984). Econometric methods (3rd ed.). New York: McGraw-Hill Book Company. Komlos, J. (2006). The height increments and BMI values of elite Cen- tral European children and youth in the second half of the 19th cen- tury. Annals of Human Biology, 33, 309-318. doi:10.1080/03014460600619203 Lazaridis, A. (2007). A note regarding the condition number: The case of spurious and latent multicollinearity. Quality & Quantity, 41, 123- 135. doi:10.1007/s11135-005-6225-5 Lazaridis, A. (2008). Singular value decomposition in cointegration analysis. A note regarding the difference stationary series. Quality & Quantity, 42, 699-710. doi:10.1007/s11135-007-9120-4 Lazarou, C., & Soteriades, E. (2009). Children’s physical activity, TV watching and obesity in Cyprus: The CYKIDS study. European Journal of Public Health, 20, 70-77. doi:10.1093/eurpub/ckp093 Lee, J. W., Wang, W., Lee, Y. C., Hang, M. T., Ser, K. H., & Chen, J. C. (2008). Effects of laparoscopic mini-gastric bypass for type 2 diabetes mellitus: Comparison of BMI > 35 and < 35 kg/m2. Journal of Gastrointestinal Surgery, 12, 945-952. doi:10.1007/s11605-007-0319-4 MacKinnon, J. (1991). Critical values for co-integration tests. In R. F. Engle, & C. W. J. Granger (Eds.), Long-run economic relationships (pp. 267-276), Oxford: Oxford University Press. Manios, Y., Yiannakouris, N., Papoutsakis, C., Moschonis, G., Magkos, F., Skenderi, K., & Zampelas, A. (2004). Behavioral and physiologi- cal indices related to BMI an a cohort of primary schoolchildren in Greece. American Journal of Human Biology, 16, 639-647. doi:10.1002/ajhb.20075 Nguyen, D. (1987). Advertising, random sales response, and brand competition: Some theoretical and econometric implications. Journal of Business, 60, 259-279. doi:10.1086/296395 Ouyang, M., Zhou, D., & Zhou, N. (2002). Estimating marketing per- sistence on sales of consumer durables in China. Journal of Business Research, 55, 337-342. doi:10.1016/S0148-2963(00)00156-9 Ramsey, J. B. (1969). Tests for Specification error in classical linear least squares regression analysis. Journal of the Royal Statistical So- ciety, Series B, 31, 350-371. Stea, H. T., Wandel, M., Mansoor, A. M., Uglem, S., & Frolich, W. (2008). BMI, lipid profile, physical fitness and smoking habits of young male adults and the association with parental education. European Journal of Public Health, 19, 46-51. doi:10.1093/eurpub/ckn122 Stenhammar, C., Olson, G. M., Hulting, A.-L., Wettergren, B., Edlund, B., & Montgomery, S. M. (2010). Family stress and BMI in young children. Acta Paediatrica, 99, 1205-1212. doi:10.1111/j.1651-2227.2010.01776.x 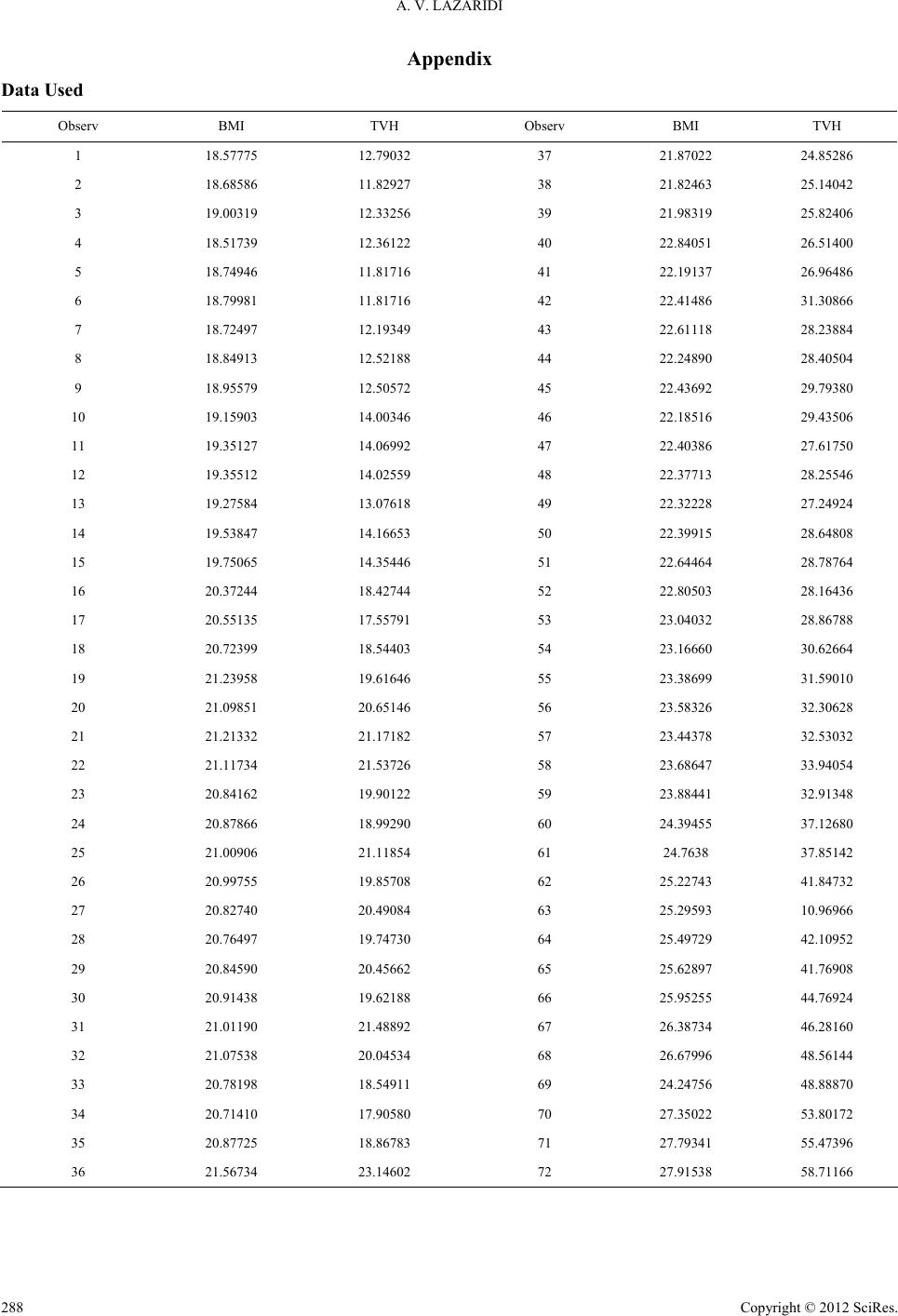 A. V. LAZARIDI Appendix Data Used Observ BMI TVH Observ BMI TVH 1 18.57775 12.79032 37 21.87022 24.85286 2 18.68586 11.82927 38 21.82463 25.14042 3 19.00319 12.33256 39 21.98319 25.82406 4 18.51739 12.36122 40 22.84051 26.51400 5 18.74946 11.81716 41 22.19137 26.96486 6 18.79981 11.81716 42 22.41486 31.30866 7 18.72497 12.19349 43 22.61118 28.23884 8 18.84913 12.52188 44 22.24890 28.40504 9 18.95579 12.50572 45 22.43692 29.79380 10 19.15903 14.00346 46 22.18516 29.43506 11 19.35127 14.06992 47 22.40386 27.61750 12 19.35512 14.02559 48 22.37713 28.25546 13 19.27584 13.07618 49 22.32228 27.24924 14 19.53847 14.16653 50 22.39915 28.64808 15 19.75065 14.35446 51 22.64464 28.78764 16 20.37244 18.42744 52 22.80503 28.16436 17 20.55135 17.55791 53 23.04032 28.86788 18 20.72399 18.54403 54 23.16660 30.62664 19 21.23958 19.61646 55 23.38699 31.59010 20 21.09851 20.65146 56 23.58326 32.30628 21 21.21332 21.17182 57 23.44378 32.53032 22 21.11734 21.53726 58 23.68647 33.94054 23 20.84162 19.90122 59 23.88441 32.91348 24 20.87866 18.99290 60 24.39455 37.12680 25 21.00906 21.11854 61 24.7638 37.85142 26 20.99755 19.85708 62 25.22743 41.84732 27 20.82740 20.49084 63 25.29593 10.96966 28 20.76497 19.74730 64 25.49729 42.10952 29 20.84590 20.45662 65 25.62897 41.76908 30 20.91438 19.62188 66 25.95255 44.76924 31 21.01190 21.48892 67 26.38734 46.28160 32 21.07538 20.04534 68 26.67996 48.56144 33 20.78198 18.54911 69 24.24756 48.88870 34 20.71410 17.90580 70 27.35022 53.80172 35 20.87725 18.86783 71 27.79341 55.47396 36 21.56734 23.14602 72 27.91538 58.71166 Copyright © 2012 SciRes. 288
|