Journal of Minerals & Materials Characterization & Engineering, Vol. 10, No.9, pp.865-874, 2011
jmmce.org Printed in the USA. All rights reserved
865
A Model for FeSiMg Alloy Production by Reduction Technique
Saeed Nabil Saeed Ghali
Steel Technology Department, Central Metallurgical Reseach & Development Institute
(CMRDI), P.O Box 87 Helwan, 11722, Egypt.
ABSTRACT
Ferrosilicon magnesium is basic foundry alloys used for the production of ductile cast iron.
Magnesium content plays an important role in the produced alloy grades from dolomite ore.
The focus of the present work is to simulate mathematical model to predict magnesium
content in the ferrosilicon magnesium, which produced by silicothermic reduction of calcined
dolomite. The basic assumptions of this model are: constant low viscosity of molten charge,
the reaction is irreversible of second order and the reaction is isothermal. The reaction is
based on the following equation:
22
22 SiOSiMgSiMgO
+
→
+
The results of previous work was found to be in a good coincidence with the predicted values
by the model
][])[(
]1][)[(
][
]][)[(
]][)[(
o
SiMgOKt
o
SiMgOKt
oo
SieMgO
eSiMgO
Mg
oo
oo
−
−
=−
−
where [Mg] is the concentration of magnesium metal in ferrosilicon magnesium alloy in
mol/L. [Sio] and (MgOo) are the initial concentration of silicon and magnesium oxide in
charge in mol/L, while t is time in second, K is the reaction rate constant ( 3.26588x10-7 L
Sec-1 mol-1). The predicted values are greater than the experimental values; this may be
attributed to the use of concentration instead of the activity. The predicted values of
magnesium content in ferrosilicon magnesium alloy are in a good agreement with the
experimental results obtained in previous work at low viscosity.
Keywords: activity , model, ferrosilicon, magnesium, reduction, viscosity
1. INTRODUCTION
Ferrosilicon magnesium is the one alloy of magnesium that is used to produce all types of
ductile iron casting under all types of foundry conditions. Dolomite represents a source of
both magnesium and calcium as it consists mainly of double carbonate of Ca and Mg.
Calcinated dolomite seems to be a suitable cheap raw material for the production of

866 Saeed Nabil Saeed Ghali Vol.10, No.9
ferrosilicon magnesium alloy in EAF or in induction furnace [1-7]. The production of
ferrosilicon magnesium from dolomite could be carried out either by metallothermic process
using silicon and / or Al or by carbothermic process [8-13].
Magnesium content plays an important role in the produced alloy grades from dolomite ore.
The silicothermic process of magnesium oxide is controlled by factors. The most important
factors are physical properties of slag, the concentrations of reactants, reaction rate constant,
reaction time and reaction temperature. At constant temperature, time and low viscosity the
reaction rate mainly depends on the concentrations of reactants. In this paper, a mathematical
model will be designed to predict magnesium content in ferrosilicon magnesium alloy which
is produced by silicothermic reaction of calcinated dolomite at low viscosity of slag.
2. MATHEMATICAL MODEL
The focus of the present work is to create a mathematical model to predict magnesium
content in ferrosilicon magnesium alloy, which is produced by silicothermic reduction of
calcinated dolomite. The basic assumption of this model is the low and almost unchangeable
viscosity of slag during the reaction. Ferrosilicon magnesium alloy is produced by reduction
of calcinated dolomite ore with ferrosilicon containing silicon 75 mass content in %. The
reaction is based on the equation:
)(][][2)(2
22
SiOSiMgSiMgO
K
+→+ (1)
This system is controlled by chemical and kinetic roles. The limitations of this model are the
following:
• The reaction takes place at low slag viscosity and nearly unchanged
• The above reaction is isothermal and irreversible
• The reaction is second order
• Concentration of reducing agent (in molar) is greater than the magnesium oxide ( [Si]
> (MgO))
• There is a mass balance in the above reaction
The rate of change of magnesium content in ferrosilicon magnesium alloy is directly
proportional to the concentration of magnesium oxide and silicon metal. There is a mass
balance in this system.
)(
2
1
][
2
1
][)(
22
SiOSiMgSiMgO
K
+→+ (2)
[Mg
2
Si] go to molten metal and (SiO
2
) go to slag. Every one mole from [Mg
2
Si] has two
moles from Mg, i.e. the rate of change of Mg with time depends on the initial concentrations
of the reactants.

Vol.10, No.9 A Model for FeSiMg Alloy Production 867
The reaction in equation (2) means that one mole from magnesium oxide reduced by one
mole of silicon metal to give one mole of magnesium. This can be writing as:
][][)( MgSiMgO
K
→+ (3)
The above reaction can be rewrite as:
XBA
K
→+ (4)
XXBXA
K oo
→−+− )()( (5)
Where at zero time:
(MgO) = initial concentration of magnesium oxide = (MgO
o
) = A
o
(6)
[Si] = initial concentration of silicon metal = [Si
o
] = B
o
(7)
[Mg] = initial concentration of magnesium metal = X = Zero (8)
At any time:
(MgO) = A = A
o
– X (9)
[Si] = B = B
o
– X (10)
[Mg] = X (11)
From equation (3), the rate of change in magnesium content is directly proportional with the
concentrations of reactants.
])[(
][ SiMgOK
dt
Mgd= (12)
From equations 9, 10, 11 & 12, we obtain
))(( XBXAK
dt
dx
oo
−−= (13)
Rearrange and integration of two sides of equation (13)
∫ ∫
=
−− dtK XBXA
dx
oo
))(( (14)
∫
+=
−− tconsKt XBXA
dx
oo
tan
))(( (15)
The left side of equation (15)
)()())((
121
XB
C
XA
C
XBXA oooo −
+
−
=
−−
(16)
))((
)()(
))((
1
21
XBXA
XACXBC
XBXA
oo
oo
oo
−−
−+−
=
−− (17)

868 Saeed Nabil Saeed Ghali Vol.10, No.9
From the parameters of X
21
0CC
−
−
=
(18)
From the parameters of X
0
o
ACBC
2
0
1
1+= (19)
From equations (18) and (19)
oo
A
B
C
−
=1
1
(20)
oo
A
B
C
−
=1
2
(21)
From equations (15), (16), (20) and (21), the left side of equation (15)
∫∫ ∫
−−
+
−−
=
−− )(
1
)(
1
))((X
o
B
dx
o
B
o
AX
o
A
dx
o
A
o
BX
o
BX
o
A
dx
(22)
Take
y = A
0
– x (23) and hence dy = -dx (24)
z =B
0
– x (25) and hence dz= -dx (26)
From equations (22-26)
∫∫ ∫
+−
−
=
−− ][
1
))((z
dz
y
dy
ABXBXA
dx
oooo
(27)
∫∫ ∫
−
−
=
−− ][
1
))((z
dz
y
dy
BAXBXA
dx
oooo
(28)
∫
−
−
=
−− ]ln[ln
1
))((zy BAXBXA
dx
oooo
(29)
∫
−
=
−− ][ln
1
))(( z
y
BAXBXA
dx
oooo
(30)
From equations (23), (25) and (30)
∫
−
−
−
=
−− ] )(
)(
[ln
1
))((XB
XA
BAXBXA
dx
o
o
oooo
(31)
From equations (15) and (31)
.]
)(
)(
[ln
1constKt
XB
XA
BA
o
o
oo
+=
−
−
− (32)
From boundary conditions, at zero time, from equation (8), X = 0
.][ln
1const
B
A
B
A
o
o
oo
=
− (33)
From equations (32) and (33)
][ln
1
]
)(
)(
[ln
1
o
o
ooo
o
oo
B
A
BA
Kt
XB
XA
BA −
+=
−
−
− (34)
Kt
B
A
BAXB
XA
BA
o
o
ooo
o
oo
=
−
−
−
−
−][ln
1
]
)(
)(
[ln
1 (35)

Vol.10, No.9 A Model for FeSiMg Alloy Production 869
Kt
XBA
XAB
BA
oo
oo
oo
=
−
−
−] )(
)(
[ln
1 (36)
)(]
)(
)(
[ln
oo
oo
oo
BAKt
XBA
XAB −=
−
− (37)
)(
)(
)(
oo
BAKt
oo
oo
e
XBA
XAB
−
=
−
− (38)
)(
)()(
oo
BAKto
o
o
o
eXB
B
A
XA
−
−=− (39)
)(
)()(
oo
BAKt
o
o
oo
eX
B
A
AXA
−
−=− (40)
oBAKtoBAKt
o
o
AeAXeX
B
A
oooo
−=−
−− )()(
)*( (41)
]1[]1[
)()(
−=−
−−
oooo
BAKtoBAKt
o
o
eAe
B
A
X (42)
]1[
]1[
)(
)(
−
−
=
−
−
oo
oo
BAKt
o
o
BAKto
e
B
A
eA
X (43)
][
]1[
)(
)(
oBAKto
BAKtoo
BeA
eBA
X
oo
oo
−
−
=
−
−
(44)
][])[(
]1][)[(
][
]][)[(
]][)[(
o
SiMgOKt
o
SiMgOKt
oo
SieMgO
eSiMgO
Mg
oo
oo
−
−
=
−
−
(45)
At initial time, t = 0
1
][])[(
]1][)[(
][
0
0
=
−
−
=
oo
oo
SieMgO
eSiMgO
Mg (46)
This means that the model verifies the boundary conditions
In case of K is very large, and [Si] > (MgO),
From equation (45)
][])[(
]1][)[(
][
]][)[(*
]][)[(*
o
SiMgOt
o
SiMgOt
oo
SieMgO
eSiMgO
Mg
oo
oo
−
−
=
−∞
−∞
(47)
][])[(
]1][)[(
][
oo
oo
SieMgO
eSiMgO
Mg −
−
=
∞−
−∞
(48)
)(
][
])[(
][
o
o
oo
MgO
Si
SiMgO
Mg =
−
−
= (49)
This means that all magnesium oxide will be reduced by silicon
In case of at infinity time and [Si]> (MgO)
)(
][])[(
]1][)[(
][
]][)[(**
]][)[(**
o
o
SiMgOK
o
SiMgOK
oo
MgO
SieMgO
eSiMgO
Mg
oo
oo
=
−
−
=
−∞
−∞
(50)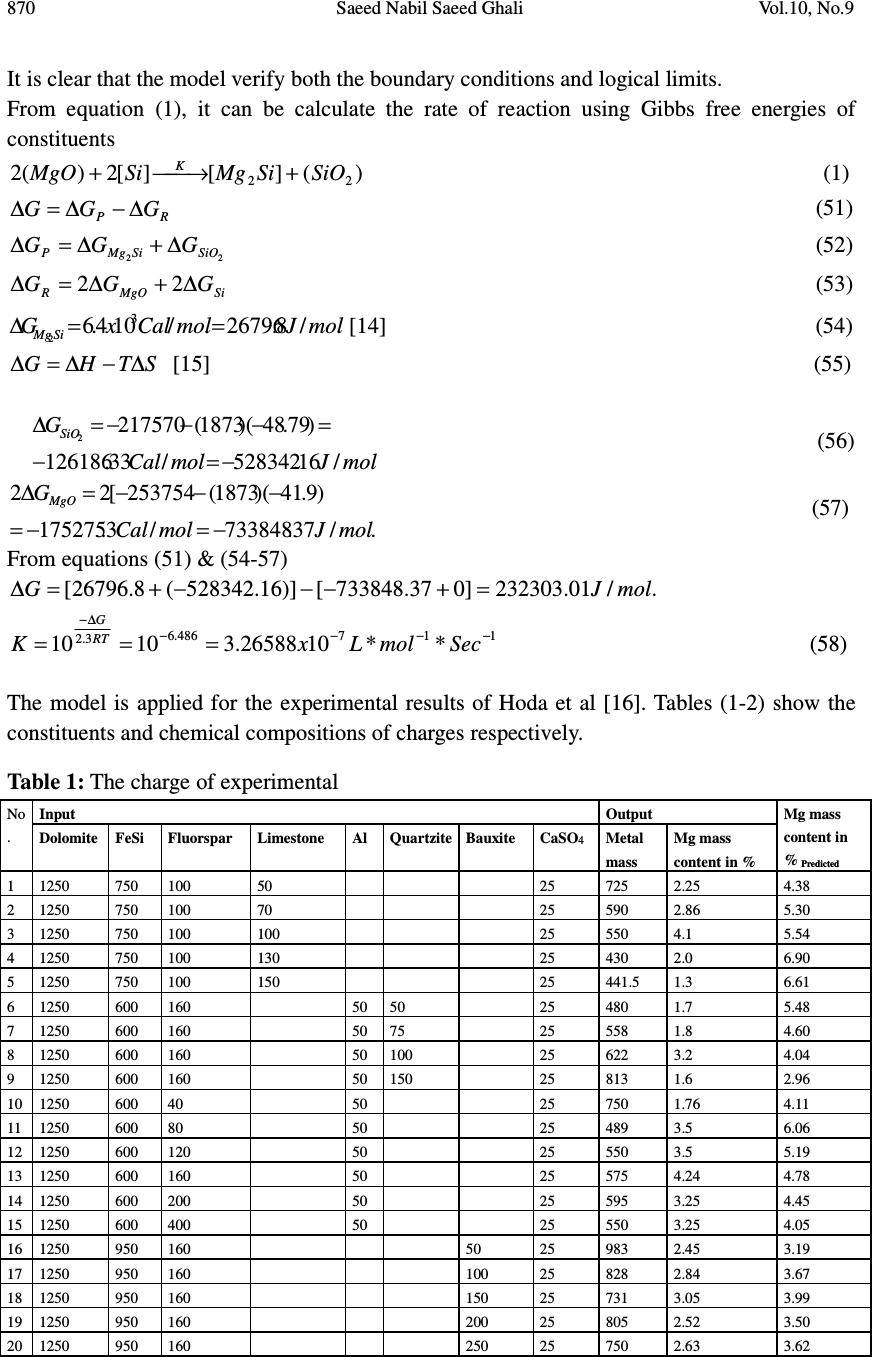

870 Saeed Nabil Saeed Ghali Vol.10, No.9
It is clear that the model verify both the boundary conditions and logical limits.
From equation (1), it can be calculate the rate of reaction using Gibbs free energies of
constituents
)(][][2)(2
22
SiOSiMgSiMgO
K
+→+ (1)
RP
GGG
∆
−
∆
=
∆
(51)
22
SiOSiMgP
GGG ∆+∆=∆ (52)
SiMgOR
GGG
∆
+
∆
=
∆
22 (53)
./8.26796./104.6
3
2
mol
JmolCalxG
SiMg
==∆ [14] (54)
STHG
∆
−
∆
=
∆
[15] (55)
mol
J
mol
Cal
G
SiO
/
16
.
528342
/
33
.
126186
)79.48)(1873(217570
2
−=−
=
−
−
−
=
∆
(56)
.
/
37
.
733848
/
3
.
175275
)9.41)(1873(253754[22
mol
J
mol
Cal
G
MgO
−=−=
−
−
−
=
∆
(57)
From equations (51) & (54-57)
./01.232303]037.733848[)]16.528342(8.26796[ molJG
=
+
−
−
−
+
=
∆
117486.6
3.2
**1026588.31010
−−−−
∆−
===SecmolLxK
RT
G
(58)
The model is applied for the experimental results of Hoda et al [16]. Tables (1-2) show the
constituents and chemical compositions of charges respectively.
Table 1: The charge of experimental
Input Output
No
. Dolomite FeSi Fluorspar Limestone Al Quartzite
Bauxite CaSO
4
Metal
mass
Mg mass
content in %
Mg mass
content in
%
Predicted
1 1250 750 100 50 25 725 2.25 4.38
2 1250 750 100 70 25 590 2.86 5.30
3 1250 750 100 100 25 550 4.1 5.54
4 1250 750 100 130 25 430 2.0 6.90
5 1250 750 100 150 25 441.5 1.3 6.61
6 1250 600 160 50 50 25 480 1.7 5.48
7 1250 600 160 50 75 25 558 1.8 4.60
8 1250 600 160 50 100 25 622 3.2 4.04
9 1250 600 160 50 150 25 813 1.6 2.96
10 1250 600 40 50 25 750 1.76 4.11
11 1250 600 80 50 25 489 3.5 6.06
12 1250 600 120 50 25 550 3.5 5.19
13 1250 600 160 50 25 575 4.24 4.78
14 1250 600 200 50 25 595 3.25 4.45
15 1250 600 400 50 25 550 3.25 4.05
16 1250 950 160 50 25 983 2.45 3.19
17 1250 950 160 100 25 828 2.84 3.67
18 1250 950 160 150 25 731 3.05 3.99
19 1250 950 160 200 25 805 2.52 3.50
20 1250 950 160 250 25 750 2.63 3.62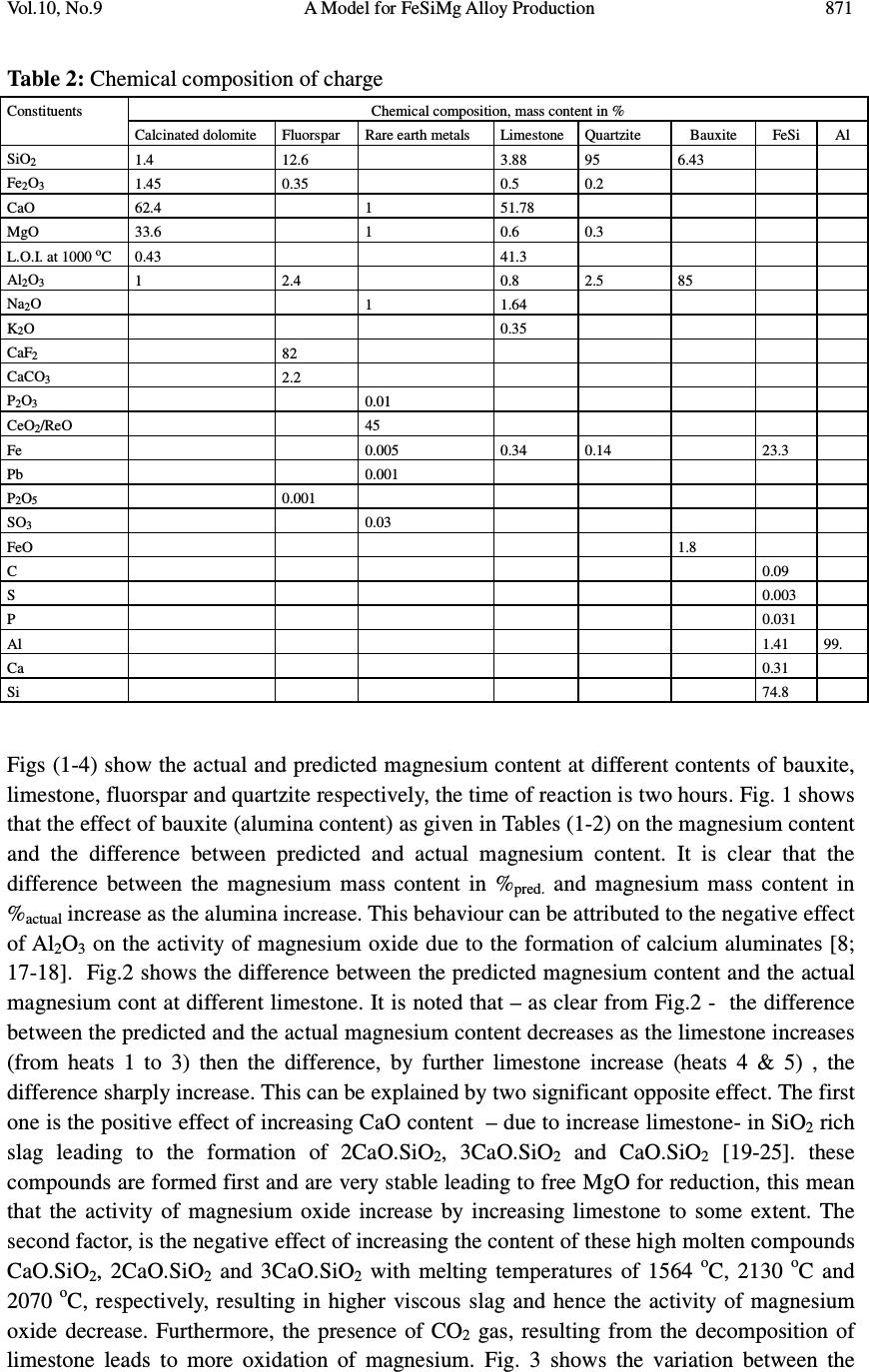

Vol.10, No.9 A Model for FeSiMg Alloy Production 871
Table 2: Chemical composition of charge
Chemical composition, mass content in % Constituents
Calcinated dolomite Fluorspar Rare earth metals Limestone Quartzite Bauxite FeSi Al
SiO
2
1.4 12.6 3.88 95 6.43
Fe
2
O
3
1.45 0.35 0.5 0.2
CaO 62.4 1 51.78
MgO 33.6 1 0.6 0.3
L.O.I. at 1000
o
C 0.43 41.3
Al
2
O
3
1 2.4 0.8 2.5 85
Na
2
O 1 1.64
K
2
O 0.35
CaF
2
82
CaCO
3
2.2
P
2
O
3
0.01
CeO
2
/ReO 45
Fe 0.005 0.34 0.14 23.3
Pb 0.001
P
2
O
5
0.001
SO
3
0.03
FeO 1.8
C 0.09
S 0.003
P 0.031
Al 1.41 99.
Ca 0.31
Si 74.8
Figs (1-4) show the actual and predicted magnesium content at different contents of bauxite,
limestone, fluorspar and quartzite respectively, the time of reaction is two hours. Fig. 1 shows
that the effect of bauxite (alumina content) as given in Tables (1-2) on the magnesium content
and the difference between predicted and actual magnesium content. It is clear that the
difference between the magnesium mass content in %
pred.
and magnesium mass content in
%
actual
increase as the alumina increase. This behaviour can be attributed to the negative effect
of Al
2
O
3
on the activity of magnesium oxide due to the formation of calcium aluminates [8;
17-18]. Fig.2 shows the difference between the predicted magnesium content and the actual
magnesium cont at different limestone. It is noted that – as clear from Fig.2 - the difference
between the predicted and the actual magnesium content decreases as the limestone increases
(from heats 1 to 3) then the difference, by further limestone increase (heats 4 & 5) , the
difference sharply increase. This can be explained by two significant opposite effect. The first
one is the positive effect of increasing CaO content – due to increase limestone- in SiO
2
rich
slag leading to the formation of 2CaO.SiO
2
, 3CaO.SiO
2
and CaO.SiO
2
[19-25]. these
compounds are formed first and are very stable leading to free MgO for reduction, this mean
that the activity of magnesium oxide increase by increasing limestone to some extent. The
second factor, is the negative effect of increasing the content of these high molten compounds
CaO.SiO
2
, 2CaO.SiO
2
and 3CaO.SiO
2
with melting temperatures of 1564
o
C, 2130
o
C and
2070
o
C, respectively, resulting in higher viscous slag and hence the activity of magnesium
oxide decrease. Furthermore, the presence of CO
2
gas, resulting from the decomposition of
limestone leads to more oxidation of magnesium. Fig. 3 shows the variation between the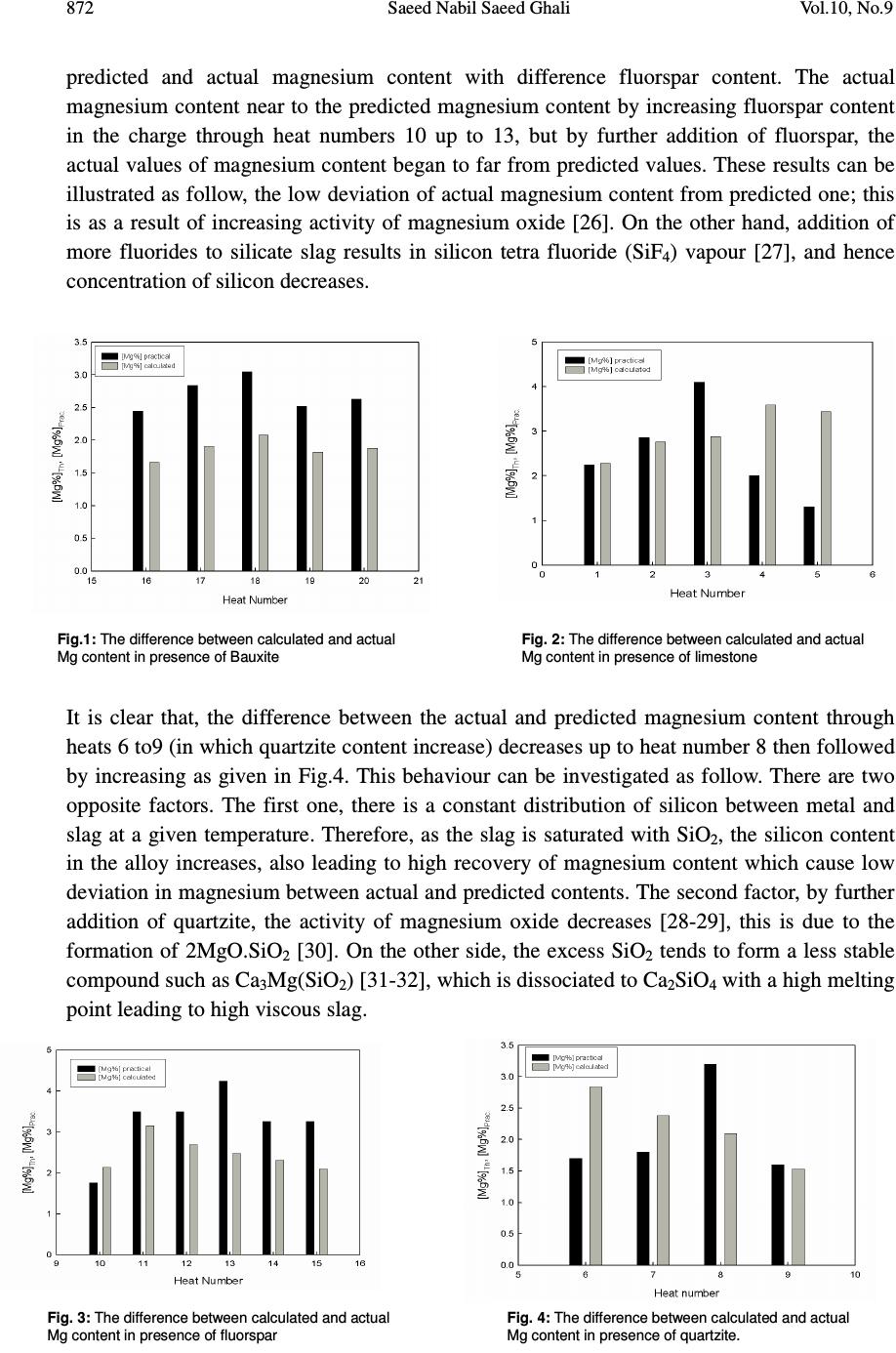

872 Saeed Nabil Saeed Ghali Vol.10, No.9
predicted and actual magnesium content with difference fluorspar content. The actual
magnesium content near to the predicted magnesium content by increasing fluorspar content
in the charge through heat numbers 10 up to 13, but by further addition of fluorspar, the
actual values of magnesium content began to far from predicted values. These results can be
illustrated as follow, the low deviation of actual magnesium content from predicted one; this
is as a result of increasing activity of magnesium oxide [26]. On the other hand, addition of
more fluorides to silicate slag results in silicon tetra fluoride (SiF
4
) vapour [27], and hence
concentration of silicon decreases.
It is clear that, the difference between the actual and predicted magnesium content through
heats 6 to9 (in which quartzite content increase) decreases up to heat number 8 then followed
by increasing as given in Fig.4. This behaviour can be investigated as follow. There are two
opposite factors. The first one, there is a constant distribution of silicon between metal and
slag at a given temperature. Therefore, as the slag is saturated with SiO
2
, the silicon content
in the alloy increases, also leading to high recovery of magnesium content which cause low
deviation in magnesium between actual and predicted contents. The second factor, by further
addition of quartzite, the activity of magnesium oxide decreases [28-29], this is due to the
formation of 2MgO.SiO
2
[30]. On the other side, the excess SiO
2
tends to form a less stable
compound such as Ca
3
Mg(SiO
2
) [31-32], which is dissociated to Ca
2
SiO
4
with a high melting
point leading to high viscous slag.
Fi
g.1:
The difference between calculated and actual
Mg content in presence of Bauxite
Fig.
2:
The difference between calculated and actual
Mg content in presence of limestone
Fig.
3:
The difference between calculated and actual
Mg content in presence of fluorspar
Fig.
4:
The difference between calculated and actual
Mg content in presence of quartzite.

Vol.10, No.9 A Model for FeSiMg Alloy Production 873
3. CONCLUSIONS
The predicted magnesium contents are greater than the experimental values. The most
important reason is attributed to the use of concentrations instead of activities.
• Based on the assumptions, low viscosity, and the reduction of magnesium oxide by
silicon metal, the reaction is controlled by rate of reaction and concentration of
reactants (MgO) and [Si].
• The equation have been derived is function in initial concentration of reactants, time,
reaction rate constant as shown, ][])[(
]1][)[(
][
]][)[(
]][)[(
o
SiMgOKt
o
SiMgOKt
oo
SieMgO
eSiMgO
Mg
oo
oo
−
−
=
−
−
• The reaction rate constant of the reaction :
)(][][2)(2
22
SiOSiMgSiMgO
K
+→+ is
117
**1026588.3
−−−
=SecmolLxK
• Volatilization of magnesium metal during the reduction of magnesium oxide process
has a great negative significant effect on the gab between the predicted and actual
values of magnesium content.
• Finally the difference between the actual and predicted mainly depends on effect of
additions on the activities of magnesium oxide and reducing agent, and viscosity of
the reaction medium.
REFERENCES
1. 461964 (U.S.S.R.), 8(1975), M. A. Kekelidze et al., Auth. Cert., Bynll. Izobr.,
2. M. A. Ryss et al.: Stal, April, (1973), p. 303.
3. D. I. Saginadze et al.: Stal, 2 (1977), p.140.
4. D. I. Saginadze et al.: Steel in the USSR, 16 (1986), p. 533
5. F. N. Tavadze et al.: Nauka Proizvodstva, C51, (1983), p. 243.
6. 727704 (U.S.S.R.), 14(1980), F. N. Tavadze et al., Auth. Cert., Bynll. Izobr.
7. V. Varbanov et al.: Works of the Iron and Steel Inst., VIII (1977).
8. D. J. G. Ives: Principles of the extraction of metals, London, (1969).
9. H. J. T. Ellingham: I. Soc. Chem. Ind., Lond., 1944 & C.W. Dannatt and H.J.T.
Ellingham: Disc Faraday Soc., 4 (1948), p. 126
10. N. P. Lyakiskev et al.: Alyuminotermiya "Aluminothermy", Moscow, (1978), p. 424
11. M. A. Merritt and E. V. Marcossi: Electric Furnace Conf. Proc., New York, 29 (1972), p.
184.
12. V. Ryachikov, V. G.. Mizin., and A. S. Dubrovin: Steel In U.S.S.R., 12 (1982), p. 264.
13. P. Sokolov and N. L. Ponomarov: Introduction to Metallothermic, Moscow, (1990), p.
134.
14. W. Klemm and H. Wwstlinning: Z.anorg. Chem., 245, (1941), p. 365.
15. R.G. Ward, M.A., Ph. D: An introduction to the physical chemistry of iron & steel
making, Edward Arnold (Publishers) LTD, (1962), p. 212/213.
16. H. El-Faramawy et al.: Ferrosilicon Magnesium Production, Scandinavian Journal of
Metallurgy, 32 (2003) p. 37/46.
17. M. Alper, et al: J. Am. Ceram. Soc., 45 (1962) No. 6, p. 263/8

874 Saeed Nabil Saeed Ghali Vol.10, No.9
18. R. A. Howald & N. B. Roy: CALPHAD 15(1991) No. 2, p. 159/72
19. B. Ellingstaeter & T. Rosenquist: Journal of Metals, 6 (1956), p. 111.
20. L M. Pidgeon: Trans Met Soc AIME, 226 (1963) p. 821
21. L. M. Pidgeon & J. K. King: Trans Faraday Soc, 40 (1948) p. 197.
22. V. Ryabchikov & A. S. Mikulinskii: Chemical Abstract, 35 (1962) p. 62.
23. J. M. Taguri & L M. Pidgeon: Can J Chem, 39 (1961) p. 540
24. K. Tomasek, I. Imsis & O. Sesveiec: Light Metals, Proc. Conf., Montreal, Quebec, 25-
29 August (1996) p. 213
25. J. R. Wynnyckj, L. M. Pidgeon: Met Trans 2 (1971) p. 979
26. C. Chen & W. Zhao: Acta Met. Sinica, 19 (1983) No. 1 , A1/A8
27. K. C. Mills & B. J. Keene: Int Metal Review, 1 (1981) p. 21/69
28. J. F. Elliott, M. Gleiser & V. Ramakrishna: Thermochemistry for Steelmaking. Vol. II,
Reading. Palo Alto/London (1963).
29. H. R. Rein, J. Chipman: Trans. Metallurg. Soc. AIME, 233 (1965), p. 415/425
30. S. Kambayashi, E. Katao: J. Chem. Thermodyn. 15 (1983) No. 8, p. 701/707
31. W. T. Hughes, C. E. Ransky & E. F. Emle: Advan Extr Met Proc Symp, London (1968)
429
32. R. B.Winkler: Vacuum metallurgy, Elsevier, London, (1971)193