Journal of Minerals & Materials Characterization & Engineering, Vol. 10, No.9, pp.777-803, 2011
jmmce.org Printed in the USA. All rights reserved
777
Studies on Cold Workability Limits of Brass Using Machine Vision System
and its Finite Element Analysis
J. Appa Rao
1
, J. Babu Rao
1*
, Syed Kamaluddin
2
and NRMR Bhargava
1
1
Dept of Metallurgical Engineering, Andhra University, Visakhapatnam – 530 003, India
2
Dept of Mechanical Engineering, GITAM University, Visakhapatnam – 530 045, India
*Corresponding Author: [e-mail]
ABSTRACT
Cold Workability limits of Brass were studied as a function of friction, aspect ratio and
specimen geometry. Five standard shapes of the axis symmetric specimens of cylindrical
with aspect ratios 1.0 and 1.5, ring, tapered and flanged were selected for the present
investigation. Specimens were deformed in compression between two flat platens to predict
the metal flow at room temperature. The longitudinal and oblique cracks were obtained as
the two major modes of surface fractures. Cylindrical and ring specimen shows the oblique
surface crack while the tapered and flanged shows the longitudinal crack. Machine Vision
system using PC based video recording with a CCD camera was used to analyze the
deformation of 4 X 4 mm square grid marked at mid plane of the specimen. The strain paths
obtained from different specimens exhibited nonlinearity from the beginning to the end of the
strain path. The circumferential stress component
θ
σ
increasingly becomes tensile with
continued deformation. On the other hand the axial stress
z
σ
, increased in the very initial
stages of deformation but started becoming less compressive immediately as barreling
develops. The nature of hydrostatic stress on the rim of the flanged specimen was found to be
tensile. Finite element software ANSYS has been applied for the analysis of the upset forming
process. When the stress values obtained from finite element analysis were compared to the
measurements of grids using Machine Vision system it was found that they were in close
proximity.
KEY WORDS: Friction, Upsetting, Vision System, Finite Element Analysis
NOMENCLATURE
D
b
= Bulge diameter
D
e
= End diameter

778 J Appa Rao, J Babu Rao, Syed Kamaluddin and NRMR Bhargava Vol.10, No.9
D
0
= Initial diameter of the cylindrical sample
H
0
= Initial height of the cylindrical sample
H
0
/ D
0
= Aspect ratio
K = Strength coefficient
n = Strain- hardening exponent
w
0
= Original width of the square grid
w
i
= Current width of the square grid
α = Strain ratio (slope of the strain path)
ε
z
= Axial strain
ε
θ
= Circumferential strain
ε
= Effective strain
σ
= Effective stress
σ
H
= Hydrostatic stress [(σ
r
+ σ
θ
+ σ
z
)/3]
σ
r
= Radial stress component
σ
z
= Axial stress component
σ
θ
= Circumferential stress component
1. INTRODUCTION
Metal forming refers to a group of manufacturing methods by which the given shape of a
work piece is converted to another shape without change in the mass or composition of the
material. Forming process has become increasingly important in almost all manufacturing
industries such as aerospace, steel plants and automobiles applications. The upsetting of
solid cylinders is an important metal forming process and an important stage in the forging
sequence of many products. Cold forming process minimizes material wastage, improves
mechanical properties such as yield strength and hardness and provides very good surface
finish. The tools used are also subjected less thermal fatigue [1-4]. Metal flow is influenced
mainly by various parameters like specimen geometry, friction conditions, characteristics of
the stock material, thermal conditions existing in the deformation zone, and strain rate. Metal
flow influence the quality and the properties of the formed product; the force and energy
requirements of the process. A large segment of industry depends primarily on the
predominant applications of this process which includes coining, heading and closed die
forming. The various parts produced by this process are screws, rivets, nuts and bolts etc [5].
The surface roughness of platens determines the friction coefficient and it plays a dominant
role in any metal forming operation. It affects the detailed material flow and the deformation
characteristics of the work piece, the wear and fatigue failure of the tool, and the mechanical
properties of the formed parts. In the cold working of high strength materials a good
lubrication or low frictional constraint is always the key to a viable process. Minimizing
friction is profitable since it reduces the force and energy required for the prior amount of
deformation. A good lubricant or low coefficient of friction at the tool –material interface
always minimizes the stresses induced in the forming tool and prevent direct tool and work

Vol.10, No.9 Studies on Cold Workability Limits of Brass and its FEA 779
piece contact, which contributes to longer tool life and better quality control. Of the many
laboratory tests utilized for friction studies the ring test technique originated by Kunogi [6]
and further developed by Male and Cockcroft [7] has the greatest capability for quantitatively
measuring friction under normal processing conditions.
When ever a new component is produced there is usually a trial and error stage to tune the
progress, this helps in obtaining a component without defects, using required quantity of raw
material. Previous experience of designers and manufacturers gives an important aid in
reducing these trails. Use of new materials associated with new shapes and designs create the
possibility of new behaviour. For better understanding of this behaviour and better
knowledge of metal flow free deformation is to be studied. A systematic and detailed study of
free deformation can be used to predict the metal flow under various working conditions and
with various tool and work piece geometries. This information can then be used to design
better forgings, to make improved intermediate dies, and to avoid the defects and failure of
materials during plastic working. The finite element simulation helps in analyzing the
process and predicting the defects that may occur at the design stage itself. Therefore,
modifications can be made easily, before tool manufacturing and part production, reducing
the trail and error stage and its associated costs [8-14].
Copper and its alloys constitute one of the major groups of commercial metals. Copper and
its alloy forgings offer a number of advantages over parts produced by other processes,
including high strength as a result of their fibrous texture, fine grain size, and structure. They
can be made to closer tolerances and with finer surface finish than sand castings, and, while
forgings are somewhat more expensive than sand castings, their cost can be justified in light
of their soundness and generally better properties. Brass and bronze are two basic types of
copper alloys. Brass is a metal composed primarily of copper and zinc. Brass is stronger and
harder than copper. It is easy to form into various shapes, a good conductor of heat, and
generally resistant to corrosion from salt water. Because of these properties, brass forgings
are commonly used in valves, screws, fittings, radiators, refrigeration components, and other
low- and high- pressure gas and liquid handling products. Industrial and decorative hardware
products are also frequently forged [15].
Thus a thorough understanding of the deformation process (forming behavior) and the factors
limiting the forming of sound parts is important not only from a scientific or engineering
view point but also from an economic view point. Present investigation makes an attempt to
study the deformation behavior of Brass by upsetting at room temperature using Machine
Vision System. Aspect ratio, specimen geometry and friction at contact surfaces were studied
as process parameters. Machine Vision System has been adopted to study and analyze the
flow behavior of materials during upsetting, which minimizes experimentation process. The
non-contact and non-destructive methods can represent a real advance for displacement,
stress and strain measurements. Control of these parameters may thus be exercised to produce
conditions favorable for enhanced deformation to fracture.

780 J Appa Rao, J Babu Rao, Syed Kamaluddin and NRMR Bhargava Vol.10, No.9
2. MATERIALS AND METHODS
The workability experiments were carried out on Brass. The material was procured from
local market of 2000 mm length X 25 mm diameter (Ф) size of hot rolled rods. The chemical
composition of the brass was given in Table 1.
Table 1 Chemical composition of the Brass used in workability tests.
Material % Copper % Zinc % Tin Other element.
Commercial Brass 59.3 39.4 0.14 ------
Standard specimens of cylindrical with aspect (H
0
/D
0
) ratios of 1.0, 1.5, flanged, tapered and
ring of standard dimensions were prepared from the procured rods of 25 mm diameter using
a conventional machining operations of turning, facing, drilling and boring. The machined
out specimens were shown in Figure 1. Geometries and specifications of specimens for
workability tests were given in Table 2. The average surface roughness at the flat and curved
surfaces of the specimens was measured as 4 microns and 3 microns respectively. Surf tester
was used for the measurement. The upset tests were performed on all the specimens by
placing them between the smooth finished flat platens having a 4 microns surface roughness.
Extreme care was taken to place the specimens concentric with the axis of the platens. The
tests were carried out at a constant cross head speed of 0.5 mm/min using a computer
controlled servo hydraulic 100 T universal testing machine (Fuels and Industrial Engineers
(FIE), India– UTE model) to obtain different strain paths. The experimental set up of PC
based on line video recording system for grid measurement during upsetting was shown in
Figure 2.
Ring compression tests were conducted to determine the friction factor ‘m’ for a given set of
flat platens. Standard ring compression samples of Outside Diameter (OD): Inside Diameter
(ID): Height (H) = 6: 3: 2 (24:12:8 mm) were prepared from the procured rods of 25 mm
diameter and were deformed slowly at a ram speed of 0.25 mm/sec on FIE make
Compression Testing Machine (CTM- Model-1M 30-0113, 200 T capacity).
Figure 1: Photograph showing the cylindrical samples for upsetting, with different
geometries of H
0
/D
0
= 1.0, 1.5 and Ring, Tapered and Flanged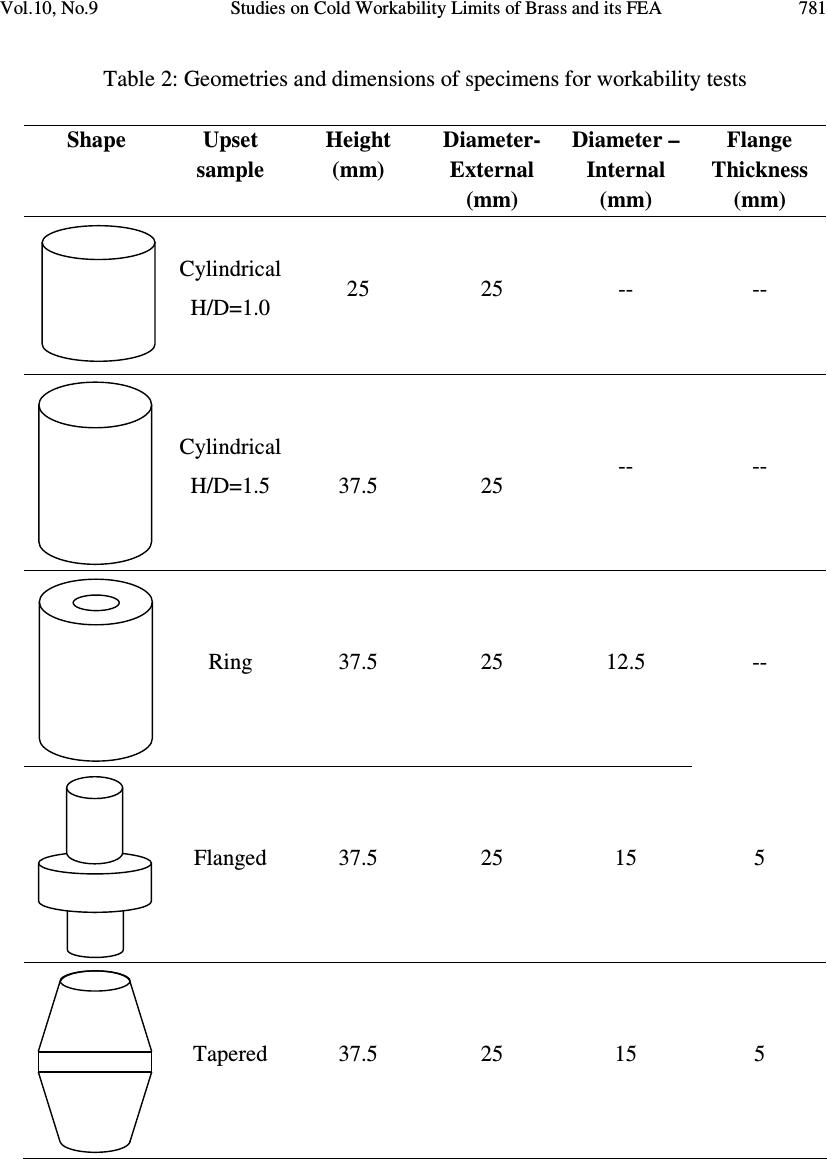

Vol.10, No.9 Studies on Cold Workability Limits of Brass and its FEA 781
Table 2: Geometries and dimensions of specimens for workability tests
Shape Upset
sample
Height
(mm)
Diameter-
External
(mm)
Diameter –
Internal
(mm)
Flange
Thickness
(mm)
Cylindrical
H/D=1.0 25 25 -- --
Cylindrical
H/D=1.5 37.5 25 -- --
Ring 37.5 25 12.5 --
Flanged 37.5 25 15 5
Tapered 37.5 25 15 5

782 J Appa Rao, J Babu Rao, Syed Kamaluddin and NRMR Bhargava Vol.10, No.9
Figure 2: Experimental set up of PC based on line video recording system for grid
measurement during upsetting on 100T computer controlled servo hydraulic UTM
A PC based system consisting of a video camera with an integrated digitizing capacity, 640 X
480 pixels resolution, 256 colour full depth, 20 pictures per second shutter speed, mounted
with a magnifying lens was used to record the images of the upsetting process. A 4 X 4 mm
square grid was marked at mid height of the standard specimen as shown in figure 3a. Online
video images of grid were recorded during the deformation process till the crack initiation
site was observed. The distortions of grid from recorded images were analyzed offline. The
images were selected at deformation steps of 5% using the software animation shop 3.0 and
were transported to paint shop pro 7.0 for further processing to get the enhanced noiseless
images of high clarity.
The axial and the circumferential strains were calculated for each element from the
measurements obtained according to:
z
ε
= ln










0
h
hi
and
θ
ε
= ln








0
w
w
i
Where h
0
and w
0
are the initial height and width of an element (Figure 3a) respectively, and h
i
and w
i
are the current height and width of the element, respectively (Figure 3b).

Vol.10, No.9 Studies on Cold Workability Limits of Brass and its FEA 783
Figure 3: Schematic diagram of upset tests showing grids for strain measurements
(a) Before deformation (b) after deformation
3. RESULTS AND DISCUSSION
3.1 Friction Factor
The decrease in internal diameter of the ring compression test was plotted against the
deformation on Male and Cockcroft [7] calibration curves in increments of 10% deformation.
When these ring compression values were fit into calibration curves for the given set of dies,
it was found that the friction factor ‘m’ with high finish dies was nearly equal to 0.30, as
shown in Figure 4 .The same set of dies was used for upset tests also. Figure 5 shows the
ring compression samples before and after deformation.
-60
-40
-20
0
20
40
60
80
100
010 20 30 40 50 60 70 80 90
% Deformation
%Decrease in Internal Dia
m=1.0 m=0.8
m=0.6
m=0.4
m=0.2
m=0.12
m=0.08
m=0.04
m=0.02
m=0
Figure 4: Ring test calibration curves. Changes of the minimum internal diameter as a
function of the reduction in height.

784 J Appa Rao, J Babu Rao, Syed Kamaluddin and NRMR Bhargava Vol.10, No.9
(a) (b)
Figure 5: Ring compression specimen (OD: ID: H = 6:3:2)
(a) Undeformed (b) 30% deformation
3.2 Finite Element Analysis of Ring Compression Test
Finite element analysis of ring compression test was carried out for given frictional condition.
Rigid-flexible contact analysis was performed for this process. For such analysis, rigid tools
need not be meshed. The ring specimen was meshed with 10-node tetrahedral elements
(solid 92 in ANSYS Library). Element size was selected on the basis of convergence criteria
and computational time. The program will continue to perform equilibrium iterations until the
convergence criteria are satisfied.
The results of the FE analysis for ring compression shows that decrease in the average inside
diameter against deformation has a variation of about 10% compared to experimental results.
The variation might be due to non uniform friction in the later stages of deformation. Figure
6 shows the undeformed and deformed mesh after 30% deformation of the FEA models of
ring compression test (OD: ID: H = 6:3:2) with friction factor (m) = 0.30.
(a) (b)
Figure 6: Quarter FEA model of ring specimen (a) Undeformed (b) 30% Deformed

Vol.10, No.9 Studies on Cold Workability Limits of Brass and its FEA 785
3.3 Load - Displacement Curves
Figure 7 shows the load - displacement curve for brass under friction factor ‘m’ = 0.3 for all
the geometry of the specimens. The load requirement increased with increase in the axial
displacement of the specimen, it was true for all the specimens. Further an increase in aspect
ratio from 1.0 to 1.5; the load required gets reduced for the same amount of deformation. For
a fixed diameter, a shorter specimen will require a greater axial force to produce the same
percentage of reduction in height, because of the relatively larger undeformed region [16].
Present experimental results were in significance with the above discussion. As per the
geometry of the specimen is concerned, to deform the component, tapered specimen required
more load than ring and flanged specimens. The experimental loads reveal that geometry of
the object also effect the load required for the deformation process.
0.00
100.00
200.00
300.00
400.00
500.00
600.00
0.002.004.006.008.0010.00 12.00 14.00
Displacement,mm
Load, KN
H/D=1.0
H/D=1.5
Ring
Tapered
Flanged
Figure 7: Load – displacement curves for Brass in different specimen geometries with friction
factor ‘m’=0.30
Figure 8 shows the representative plot of σ vs ε generated from the upsetting test data
carried out at slow speed with H
0
/D
0
= 1.0 using mirror finished dies. This data was treated
to be material property [17] and used as input for finite element analysis. This curve was fit
into Holloman power law [18-24],
n
K)( εσ ∗=
results the flow curve equation as σ = 832
* ( ε )
0.285
for brass.

786 J Appa Rao, J Babu Rao, Syed Kamaluddin and NRMR Bhargava Vol.10, No.9
0.00
100.00
200.00
300.00
400.00
500.00
600.00
700.00
0.00 0.050.10 0.15 0.20 0.250.30 0.35 0.400.45 0.50
True Plastic Strain
True Stress,Mpa
Figure 8: True stress vs true plastic strain
The specimens of various geometries which were subjected plastic deformation by upsetting
up to the fracture initiation were shown in Figure 9. The longitudinal crack and oblique crack
were obtained as the two major modes of surface fractures. The mode of fracture depends
mainly on the state of stress and the state of strain, both of which in turn depend on the
degree of deformation and the slope of the strain path. The longitudinal crack is usually
obtained when the axial surface stress is tensile, while the oblique crack is obtained when the
axial surface stress is compressive. Cylindrical and ring specimen shows the oblique surface
crack while the tapered and flanged shows the longitudinal crack.
H
0
/D
0
=1.0 H
0
/D
0
=1.5
(a)
Ring Tapered Flanged
(b)
Figure 9: Modes of surface cracking for different specimen geometries.
a) Short (H
0
/D
0
=1.0) and long (H
0
/D
0
=1.5) cylindrical specimens
(b) Ring, Tapered and Flanged specimens.

Vol.10, No.9 Studies on Cold Workability Limits of Brass and its FEA 787
3.4 Experimental Strain and Stress analysis using Machine Vision System
Surface strains, circumferential strain (
θ
ε
) and axial strain (
z
ε
) were evaluated for the
geometric mid-sectional grid of the specimens and the results were plotted in Figure 10.
Homogeneous deformation corresponds to ideal condition, that is, deformation without
friction or barreling with a constant slope (α) of
θ
ε
/
z
ε
= -0.5. The line with a slope
θ
ε
/
z
ε
= -0.5 on
θ
ε
vs
z
ε
plot and which intersects the ordinates at
θ
ε
≈ 0.3 is an estimate
of a fracture line for upsetting test performed on circular cylinders [25]. Though the intercept
0.3 on the ordinate may be approximately correct for steels, it may differ for material to
material. Brownrigg et al [26] and H.A. Kuhn et al [27] reported these values of intercepts as
0.29, 0.32, and 0.18 for the 1045 steel, 1020 steel and 303 stainless steel respectively. In the
present work this intercept value was observed to be 0.07.
The deviation of slope of the experimentally determined relationship between axial strain
(
z
ε
) and circumferential strain (
θ
ε
), from that corresponding to homogeneous deformation
represents barreling. This deviation was less when the specimen - die interface friction was
low. In such cases ‘
α
’ was found to be independent of
z
ε
throughout deformation and
significant deviation was not observed from the ideal relationship for homogeneous
deformation. The strain paths obtained from cylindrical specimens with aspect ratios 1.0 and
1.5 deviated from the line with slope – 0.5, which represents homogeneous deformation. The
deviation increased as barreling developed. Flanged and tapered specimen geometries may
be regarded as specimens artificially prebulged by machining [28]. Flanged specimen
exhibited a strain path similar to that found in axial tension. This is because very little axial
compression was applied to the rim during the circumferential expansion caused by
compressive deformation of the specimen. Tapered specimen gave strain path with slope
somewhere between tension and compression tests [17]. For ring specimen the flow of the
material was dominant on the outer periphery compared to the inside periphery of the mid
section, the deviation from homogeneous line was observed to be more than the solid
cylinder of aspect ratio 1.5.
It is interesting to note that all strain paths obtained from different specimens exhibited
nonlinearity from the beginning to the end of the strain path. It is also observed that the slope
at a point on the strain path increases as that point moves toward the end of the strain path or
the fracture point. This means that at the fracture point, the incremental axial strain
component (d
z
ε
) is almost zero, while the incremental circumferential strain component
(d
θ
ε
) is very high. This change in the slope of the strain path has a great effect on the stress
state at the surface of the specimen. The curve fitting technique was used (because of the
scatter in the experimental data for axial and circumferential strains) to obtain a smooth
relationship between the axial strain (
z
ε
) and circumferential strain (
θ
ε
). This relationship
represents the equations of the strain paths. Some of these equations for five strain paths
obtained from different specimens are given in Appendix A. The ends of the strain paths
represent the fracture points. Joining all the fracture points on all strain paths gives the
workability limit for the alloy considered.

788 J Appa Rao, J Babu Rao, Syed Kamaluddin and NRMR Bhargava Vol.10, No.9
0.00
0.05
0.10
0.15
0.20
0.25
-0.40 -0.35 -0.30 -0.25-0.20 -0.15 -0.10-0.050.00
Axial strain
Circumferential strain
H/D=1.0
H/D=1.5
Ring
Flanged
Tapered
Homogeneous Deformation
Fracture line
Figure 10: Circumferential strain
θ
ε
as a function of axial strain
z
ε
at the equatorial
free surface for Brass (with friction factor ‘m’= 0.30)
Knowledge of the experimental plastic strain history allows experimental evaluation of stress
components during deformation (Appendix B). Effective stress ( σ ), and stress components,
circumferential stress (
θ
σ
) , axial stress (
z
σ
) and hydrostatic stress (
H
σ
) as a function of
effective strain ( ε ) calculated from grid measurements of images obtained from Machine
Vision technique for brass of cylindrical samples aspect ratios of 1.0 and 1.5, and also for
ring, tapered and flanged were represented in Figure11. In an idealized situation of uniaxial
compression, the circumferential stress
θ
σ
, is zero and the axial stress
z
σ
is equal to the yield
stress,
0
σ
. Under this condition the hydrostatic component of the stress,
H
σ
would be equal
to
Z
σ
/3 and would always be compressive; a state of instability will never occur in
homogeneous deformation. Hence according to an instability theory of fracture ductile
fracture will never occur in homogenous deformation. On the other hand if the friction
between the specimen and platens is more, the deformation departed from the homogeneous
case, which results barrel develops in the specimen. The tensile circumferential surface stress
component
θ
σ
is non zero and the hydrostatic component of stress
H
σ
become less
compressive and in some cases tensile.
The present results referring to Figure 11, the circumferential stress component
θ
σ
increasingly becomes tensile with continued deformation. On the other hand the axial
stress
z
σ
, increased in the very initial stages of deformation but started becoming less
compressive immediately as barreling develops. For unfractured specimens the axial
stress
z
σ
will always be compressive. However for the specimens where surface fracture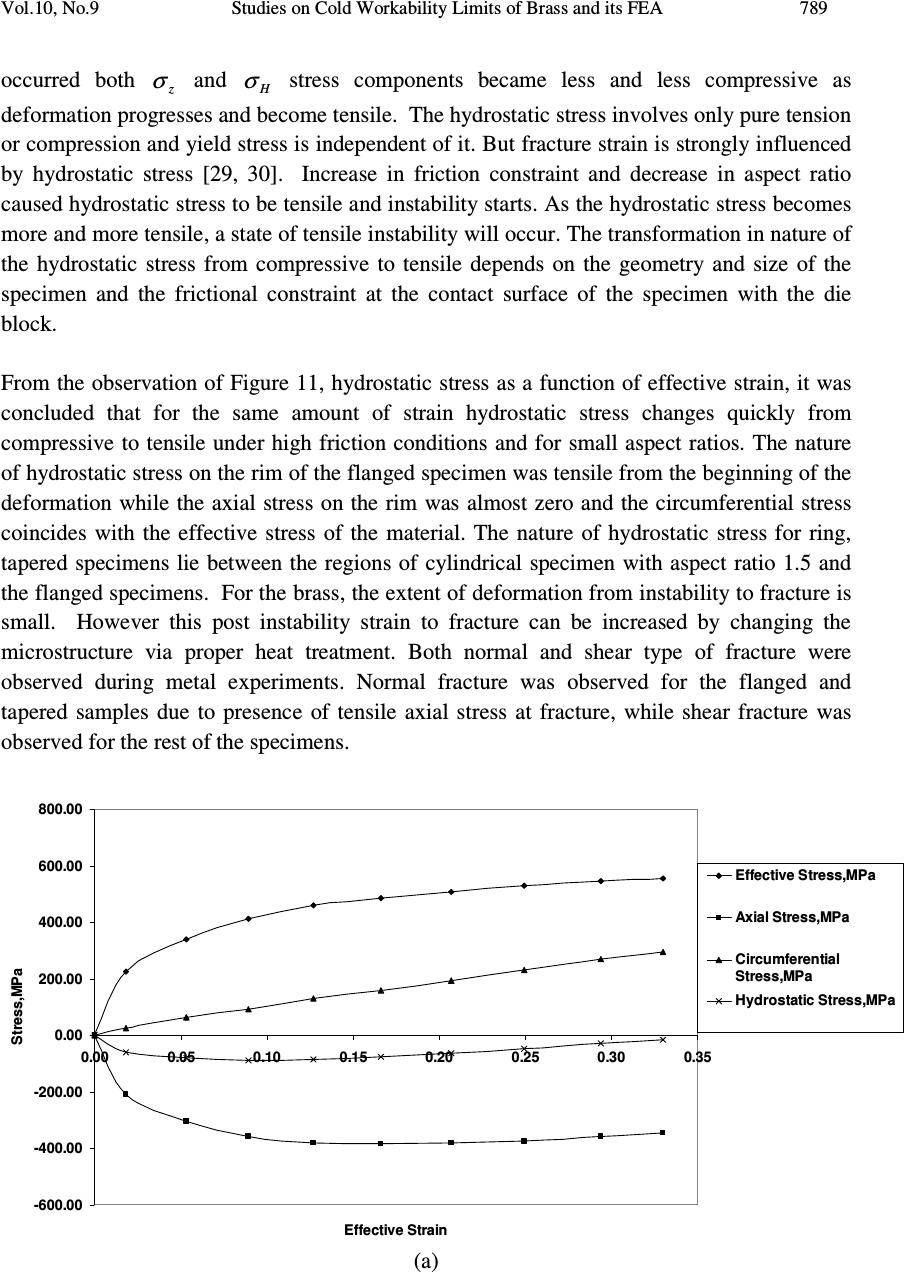

Vol.10, No.9 Studies on Cold Workability Limits of Brass and its FEA 789
occurred both
z
σ
and
H
σ
stress components became less and less compressive as
deformation progresses and become tensile. The hydrostatic stress involves only pure tension
or compression and yield stress is independent of it. But fracture strain is strongly influenced
by hydrostatic stress [29, 30]. Increase in friction constraint and decrease in aspect ratio
caused hydrostatic stress to be tensile and instability starts. As the hydrostatic stress becomes
more and more tensile, a state of tensile instability will occur. The transformation in nature of
the hydrostatic stress from compressive to tensile depends on the geometry and size of the
specimen and the frictional constraint at the contact surface of the specimen with the die
block.
From the observation of Figure 11, hydrostatic stress as a function of effective strain, it was
concluded that for the same amount of strain hydrostatic stress changes quickly from
compressive to tensile under high friction conditions and for small aspect ratios. The nature
of hydrostatic stress on the rim of the flanged specimen was tensile from the beginning of the
deformation while the axial stress on the rim was almost zero and the circumferential stress
coincides with the effective stress of the material. The nature of hydrostatic stress for ring,
tapered specimens lie between the regions of cylindrical specimen with aspect ratio 1.5 and
the flanged specimens. For the brass, the extent of deformation from instability to fracture is
small. However this post instability strain to fracture can be increased by changing the
microstructure via proper heat treatment. Both normal and shear type of fracture were
observed during metal experiments. Normal fracture was observed for the flanged and
tapered samples due to presence of tensile axial stress at fracture, while shear fracture was
observed for the rest of the specimens.
-600.00
-400.00
-200.00
0.00
200.00
400.00
600.00
800.00
0.000.05 0.10 0.15 0.20 0.25 0.300.35
Effective Strain
Stress,MPa
Effective Stress,MPa
Axial Stress,MPa
Circumferential
Stress,MPa
Hydrostatic Stress,MPa
(a)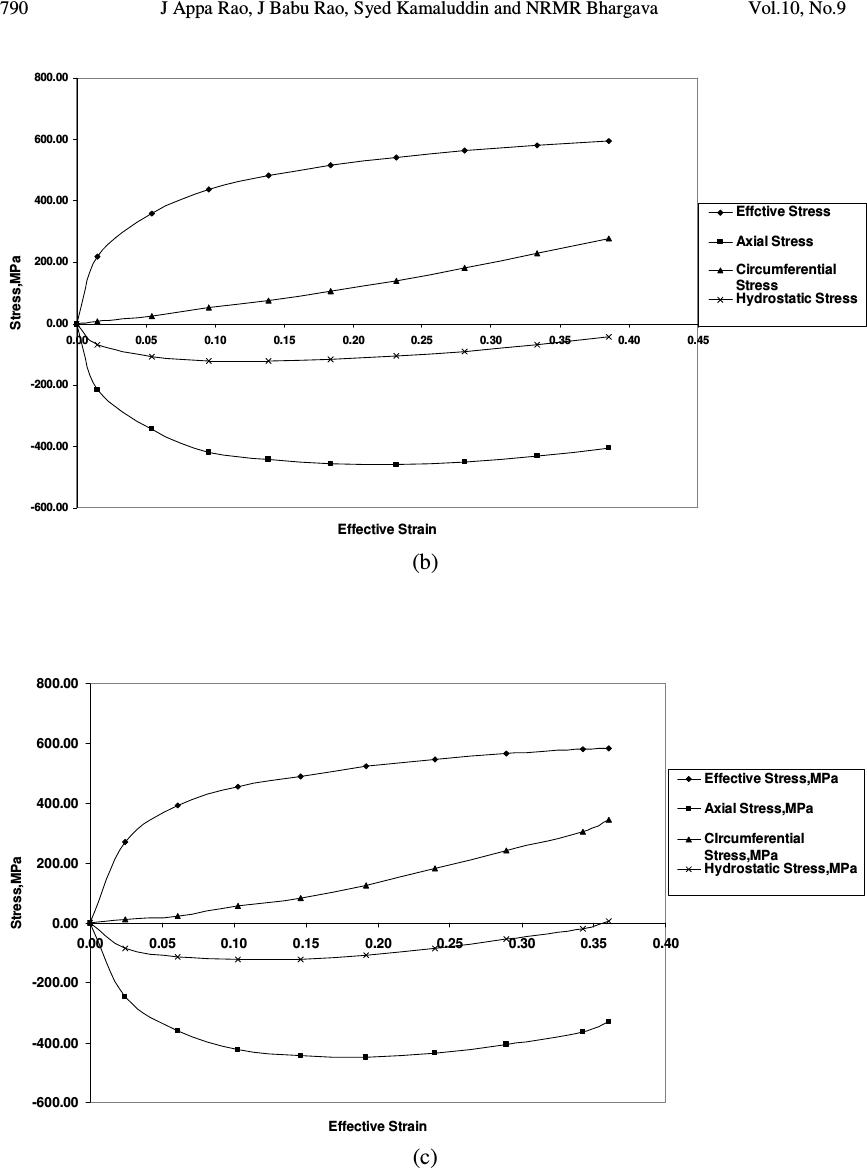

790 J Appa Rao, J Babu Rao, Syed Kamaluddin and NRMR Bhargava Vol.10, No.9
-600.00
-400.00
-200.00
0.00
200.00
400.00
600.00
800.00
0.00 0.05 0.10 0.15 0.200.25 0.30 0.35 0.40 0.45
Effective Strain
Stress,MPa
Effctive Stress
Axial Stress
Circumferential
Stress
Hydrostatic Stress
(b)
-600.00
-400.00
-200.00
0.00
200.00
400.00
600.00
800.00
0.00 0.050.10 0.15 0.200.25 0.300.35 0.40
Effective Strain
Stress,MPa
Effective Stress,MPa
Axial Stress,MPa
CIrcumferential
Stress,MPa
Hydrostatic Stress,MPa
(c)

Vol.10, No.9 Studies on Cold Workability Limits of Brass and its FEA 791
-50.00
0.00
50.00
100.00
150.00
200.00
250.00
300.00
350.00
400.00
0.00 0.050.10 0.15 0.200.25 0.30
Effective Strain
Stress,MPa
Effective Stress,MPa
Axial Stress,MPa
Circumferential Stress,MPa
Hydrostatic Stress,MPa
(d)
-300.00
-200.00
-100.00
0.00
100.00
200.00
300.00
400.00
500.00
600.00
0.00 0.05 0.10 0.15 0.20 0.250.30 0.35
Effective Strain
Stress,MPa
Effective Stress,MPa
Axial Stress,MPa
Circumferential
Stress,MPa
Hydrostatic Stress,MPa
(e)
Figure 11: Effective stress ( σ ), stress components
θ
σ
,
z
σ
and
H
σ
as a function of
Effective strain ( ε ) for copper under low friction condition (Friction factor ‘m’=0.30) (a)
H
0
/D
0
= 1.0, (b) H
0
/D
0
= 1.5, (c) Ring, (d) Flanged, (e) Tapered.

792 J Appa Rao, J Babu Rao, Syed Kamaluddin and NRMR Bhargava Vol.10, No.9
4. FINITE ELEMENT MODELING
Finite element analysis of deformation behavior of cold upsetting process was carried out for
cylindrical specimens with aspect ratios of 1.0 and 1.5 and also for ring, tapered and flanged
specimens. Since computers with high computational speed are now available in the market
at relatively cheaper cost, the time of computation is not a major constraint for solving the
problems of small sized 3-D models. Further, the tetrahedral elements can easily be
accommodated in any shape [31]. This reduces the number of iterations and steps to be
solved. Owing to these facts the present problem was solved using 3-D model. The analysis
can also be extended to non axisymmetric problems using a full 3-D model. In the present
analysis, quarter portion of 3-D model was considered with symmetric boundary conditions.
Rigid-flexible contact analysis was performed for the forming process. For such analysis,
rigid tools need not be meshed. The billet geometry was meshed with 10-node tetrahedral
elements (solid 92 in ANSYS Library). Element size was selected on the basis of
convergence criteria and computational time. Too coarse a mesh may never converge and
too fine a mesh requires long computational time without much improvement in accuracy.
The program will continue to perform equilibrium iterations until the convergence criteria are
satisfied. It will check for force convergence by comparing the square root of sum of the
squares (SRSS) of the force imbalances against the product of the SRSS of the applied loads
with a tolerance set to 0.005. Since the tolerance value in the program is set to 0.5%, the
solution will converge, only if the out of balance force is very small leading to more accurate
results.
Material models were selected based on the properties of the tooling and billet materials.
Due to high structural rigidity of the tooling, only the following elastic properties of tooling
(H13 steel) were assigned assuming the material to be isotropic [32]. Young’s Modulus E =
210 GPa and Poisson’s ratio υ = 0.30. For billet material model selected is isotropic Mises
plasticity with E = 110 GPa, υ = 0.375 and plastic properties obtained from Hollomon power
law equation. As the nature of loading is non-cyclic, Bauschinger effect could be neglected
and the non-linear data was approximated to piecewise multi linear with 10 data points. Care
is taken that the ratio of stress to strain for first point equals to Young’s modulus of copper.
The material was assumed to follow the Isotropic hardening flow rule. Suitable elastic
properties were also assigned for the material chosen for analysis. As the experiments were
conducted at room temperature, the material behavior was assumed to be insensitive to rate of
deformation [33- 35].
A 3-D, 8-noded, higher-order quadrilateral element CONTA 174 (of ANSYS library) that can
be located on the 3-D solid or shell elements with mid side nodes is used. It can be
degenerated to 3-7 node quadrilateral/triangular shapes. Contact surface was meshed with
CONTA 174. TARGE 170 (of ANSYS library) is used to represent various 3-D target
surfaces for the associated contact elements. The contact elements themselves overlay the
solid elements describing the boundary of a deformable body that is potentially in contact
with the rigid target surface, defined by TARGE 170 [36]. Hence a target is simply a

Vol.10, No.9 Studies on Cold Workability Limits of Brass and its FEA 793
geometric entity in space that senses and responds when one or more contact elements move
into a target segment element.
5. VALIDATION OF FEA RESULTS
Figure 12 shows the specimen before deformation. There was zero friction at metal-die
contact and no apparent bulging; the deformation can be treated as homogeneous, figure 13.
The variation in the values of radial diameter at 50% deformation obtained from finite
element analysis and calculated values from volume constancy condition is 0.7% [37]. This
small variation may be neglected in non linear finite element analysis such as in large
deformation / metal forming applications.
The profiles of radial displacement and total strain distribution for all the specimens were
shown in figures from 14 to 17. The hydrostatic stress (
H
σ
) profiles for Cylindrical
specimens of 1.0 and 1.5, ring, tapered and flanged were shown in figures from 18 to 22 at
the point of fracture initiation. The comparison of various stress values obtained after first
crack appearance from finite element analysis and measurement of grids using vision system
were tabulated in Table 3. All these results were in close agreement to experimental values
with a maximum error of less than 15%.

794 J Appa Rao, J Babu Rao, Syed Kamaluddin and NRMR Bhargava Vol.10, No.9
(a) (b)
(c) (d)
(e)
Figure 12: FEA modeled Undeformed specimens (a) Cylindrical specimen, H
o
/D
o
=1.0
(b) Cylindrical specimen, H
o
/D
o
=1.5 (c) Ring (d) Tapered and (e) Flanged

Vol.10, No.9 Studies on Cold Workability Limits of Brass and its FEA 795
(a) (b)
Figure 13: Cylindrical specimen (H
o
/D
o
=1.0) at 50% deformation under zero friction
(a) Radial Displacement (b) Total Strain Distribution
(a) (b)
Figure 14: Cylindrical specimen (H
o
/D
o
=1.5) at the point of fracture initiation (32%
deformation) under friction factor ‘m’=0.3
(a) Radial Displacement (b) Total Strain Distribution

796 J Appa Rao, J Babu Rao, Syed Kamaluddin and NRMR Bhargava Vol.10, No.9
(a) (b)
Figure 15: Ring specimen at the point of fracture initiation (30% deformation) under
friction factor ‘m’=0.3 (a) Radial Displacement (b) Total Strain Distribution
(a) (b)
Figure 16: Tapered specimen at the point of fracture initiation (27% deformation) under
friction factor ‘m’=0.3 (a) Radial Displacement (b) Total Strain Distribution

Vol.10, No.9 Studies on Cold Workability Limits of Brass and its FEA 797
(a) (b)
Figure 17: Flanged specimen at the point of fracture initiation (24% deformation) under
friction factor ‘m’=0.3 (a) Radial Displacement (b) Total Strain Distribution
Figure 18: Hydrostatic stress at the point of fracture initiation (27% deformation) of
Cylindrical specimen (H
o
/D
o
=1.0).
Figure 19: Hydrostatic stress at the point of fracture initiation (32% deformation) of
Cylindrical specimen (H
o
/D
o
=1.5).

798 J Appa Rao, J Babu Rao, Syed Kamaluddin and NRMR Bhargava Vol.10, No.9
Figure 20: Hydrostatic stress at fracture initiation (30% deformation) of Ring specimen
Figure 21: Hydrostatic stress at fracture initiation (27% deformation) of Tapered specimen.
Figure 22: Hydrostatic stress at fracture initiation (24% deformation) of Flanged specimen.

Vol.10, No.9 Studies on Cold Workability Limits of Brass and its FEA 799
Table 3: Comparison of experimental and FEA results for Brass
Stress, MPa
Specimen
geometry
θ
σ
(circumferential
z
σ
(axial)
H
σ
(hydrostatic)
H/D=1.0 301 (296) -341 (-347) -15 (-17)
H/D=1.5 280 (278) -403 (-405) -42 (-42)
Ring 376 (353) -303 (-327) 16 (09)
Flanged 384 (380) 07 (09) 131 (131)
Tapered 376 (379) -130 (-175) 67 (68)
Note: Numbers inside the parenthesis indicates the experimental values
6. CONCLUSIONS
1. Friction factor ‘m’ was determined experimentally for given set of dies.
2. Inverse FEA modeling and analysis was successfully performed from the
experimentally obtained friction factor values.
3. Vision system was successfully employed in the measurement of grid distortion at
equatorial surface for the analysis of stress components. Implementation of Vision
system reduced the extent of experimentation.
4. The workability limit for brass has been determined experimentally. The workability
limit is a useful tool in the design and manufacturing stages of any product.
5. At the beginning of deformation axial compressive stress increased in magnitude but as
the deformation progress the magnitude reduced. Hydrostatic stress also reduced in
magnitude as the deformation increased. Increase in friction constraint and decrease in
aspect ratio caused hydrostatic stress to be tensile.
6. The nature of hydrostatic stress on the rim of the flanged specimen is found to be
tensile.
7. The nature of hydrostatic stress for ring, tapered specimens lie between the regions of
cylindrical with aspect ratio 1.5 and the flanged specimens.
8. The time history data is useful in designing the intermediate dies for new materials with
quite a small number of deformation experimental trials reducing the lead-time of design
cycle.
9. Results obtained by finite element analysis closely matched with the experimental
values and hence the model is validated.

800 J Appa Rao, J Babu Rao, Syed Kamaluddin and NRMR Bhargava Vol.10, No.9
ACKNOWLEDGEMENTS
The authors thank the AICTE, New Delhi for their financial support under AICTE – CAYT
scheme (File No:1-51/FD/CA/(19) 2006-2007) and also the Departments of Metallurgical
and Civil Engineering, AU College of Engineering, Andhra University Visakhapatnam for
providing necessary support in conducting the experiments.
Appendix A: Experimental Strain Path equations
Equations obtained by the best fit technique for the experimental strain components of
different strain paths were tested by compression.
S No Condition Strain path equation
1. H
0
/D
0
=1.0, m=0.30 ε
θ
= 0.3701 ε
z 3
+ 0.9116 ε
z 2
– 0.5606 ε
z
2. H
0
/D
0
=1.5, m=0.30 ε
θ
= -0.6628 ε
z 3
+ 0.1807 ε
z 2
– 0.5284 ε
z
3. Ring, m=0.30 ε
θ
= -1.8429 ε
z 3
– 0.075 ε
z 2
– 0.5367 ε
z
4. Tapered, m=0.30 ε
θ
= -8.1524 ε
z 3
+ 0.105 ε
z 2
– 0.763 ε
z
5. Flanged, m=0.30 ε
θ
= -247.96 ε
z 3
– 10.863 ε
z 2
– 2.1981 ε
z
Appendix B: Stress Components as a function of the slope of the strain path (α)
The Levy-von Mises yield criterion can be written in terms of principal stresses as
σ =
2
3J = [
2
θ
σ +
2
z
σ -
z
σ
σ
θ
]
2/1
------------ (1)
Because the transverse stress component
r
σ
is zero on the free surface. Here J
2
is the
second invariant of the stress deviator.
The plastic strain increment at any instant of loading is proportional to the instantaneous
stress deviator, according to the Levy-Von Mises stress strain relationship: i.e.
d
ij
ε
=
ij
σ
' d
λ
----------------- (2)
where d
λ
is non negative constant which may vary throughout the loading history.
For
r
σ
= 0, equation (2) yields
θ
θθ
σσ
σσ
ε
ε
−
−
=
z
z
z
d
d
2
2
or
2
21
+
+
=
α
α
σ
σ
θ
z
------------ (3)
where
z
d
d
ε
ε
α
θ
=
is a parameter which can be determined by experimental measurements of
the ratio of the principal strain components in the
θ
and z directions on the free surface of the

Vol.10, No.9 Studies on Cold Workability Limits of Brass and its FEA 801
specimen, figure 9. Substituting equations (3) and (1) gives the following expression for
θ
σ
and
z
σ
.
2/1
2
2
21
2
21
1
−















+
+
+






+
+
−=
α
α
α
α
σσ
z
---------------(4)
And






+
+
=
α
α
σσ
θ
2
21
z
----------------------(5)
By convention, compressive stresses are negative, thus the lower sign in equation (4) is used
in evaluating
z
σ
. σ denotes the effective flow stress for an isotropic material for the
appropriate effective strain ε at the free surface.
In terms of the principal strain increments
(
)
2/1
22
3
2
z
z ddddd εεεεε
θ
θ ++= ------------------(6)
where, the incompressibility condition 0
=
+
+
zr
ddd
ε
ε
ε
θ
has been used.
The effective strain at the free surface from equation (6) is given by
ε =
∫
z
d
ε
ε
0
=
3
2
(
)
z
d
z
εαα
ε
2/1
0
2
1
∫
++ -----------------(7)
where the integration can be performed along the strain path provided the principal axes of
the strain increment do not rotate relative to element.
The equations (4),(5) and (7), will enable us to calculate the stresses and effective strains on
the geometric centre of the bulge surface (shown in figure 5) and are identical to the
equations derived by Kudo and Aoi and David et al [38, 39]. Theoretically,
α
may take any
value between -
∞
and +
∞
but there is no real value of
α
for which
θ
σ
or
z
σ
would increase
with out bounds. In the present experimental situation the range of
α
is limited to -2 to -1/2.
As
α
increases, the tensile stress
θ
σ
increases but the hydrostatic stress
H
σ
=
(
)
z
σ
σ
θ
+
/3,
becomes more and tensile which leads to a higher probability of fracture.

802 J Appa Rao, J Babu Rao, Syed Kamaluddin and NRMR Bhargava Vol.10, No.9
REFERENCES
1. Jolgaf, M., Hamouda, A.M.S., Sulaiman, S., Hamdan, M.M, 2003, Development of a
CAD/CAM system for the closed–die forging process, J of Material Processing
Technology, 138: 436-442.
2. Rajiv Shivpuri, 2004, Advances in Numerical Modeling of Manufacturing process,
Application to steel, Aerospace and Automotive Industries. Trans. Indian. Inst. Metals,
57: 345-366
3. Taylan Altan., Hannan, D A N, 2002, Forging: Prediction and Elimination of Defects in
cold forging using process simulation, The Engineering Research Center for Met shape
manufacturing. http.www.ercnsm.org. 2002.
4. Victor Vazquez., Taylan Altan., 2000, New Concepts in die design–physical and
Computer Modeling applications. J of Materials Processing Technology, 98: 212 – 223.
5. www.forging.org
6. Kunogi, 1954, Reports of the scientific Research Institute, Tokyo.30: 63.
7. Male, A. T., and Cockcroft, M.G, 1964-65, A Method for the Determination of the
Coefficient of Friction of Metals under Conditions of Bulk Plastic Deformation. J. Inst. of
Metals. 93: 38.
8. Altan T Male, and Vincent Depierre, 1970, Transactions of the ASME J of Lubrication
Technology, July 1970: 389 – 397.
9. Samantha S.K, 1975, Effect of friction and specimen geometry on the ductile fracture in
upset. Institute of Engineering Materials and Technology. Transactions of ASME, Jan
1975: 14-20.
10. Santos, Duarte, D. J.F., Anareis, Rur Neto, Ricardo Paiva, Rocha, A.D, 2001, The use of
finite element simulation for optimization of Metal forming and tool design. J of Material
Processing Technology. 119: 152 -157.
11. Kobayashi, S., Oh, S.I. and Altan T, 1989, Metal forming and Finite Element Method,
Oxford University Press, New York.
12. Lee, C.H., and Kobyashi, S, 1973, New solutions to rigid plastic deformation problems
using a matrix method. J of Engineering for Industry Trans. of ASME. 95: 865.
13. Jackson, J.E, J.r., and Ramesh, MS, 1992, The rigid plastic finite element method for
simulation of deformation processing, Numerical Modeling of Material deformation
Processes. Springer-Verlag, London, pp 48 – 177.
14. Bathe K.J, 1996, Finite Element Procedures- Prentice – Hall, pp 622.
15. ASM Hand Book, 1996, Forming and Forging, ASM International.
16. George E. Dieter, 1928, Mechanical Metallurgy- McGraw-Hill Book Company, London
17. Gouveia, B.P.P.A, Rodrigues, J.M.C. and Martins, P.A.F, 1996, Fracture Predicting In
Bulk Metal Forming. Int. J. Mech. Sci.38: 361-372
18. Ungair, T., Gubicza, J.,Ribairik, G. and Borbeily, A., 2001, J. of Applied
Crystallography. 34: 298
19. Iwahashi, Y., Horita, Z., Nemota, M. and Langdon, T.G., 1998, Metall Mater Trans A
29: 2503
20. Komlira. S,.Horita, Z., M. Nemoto and T.G.Longdon., 1999, J. of. Mater. Res. 14: 4044

Vol.10, No.9 Studies on Cold Workability Limits of Brass and its FEA 803
21. Erik Parteder and Rolf Bunten., 1998, Determination of flow curves by means of a
compressive test under sticking friction conditions using on iterative finite-element
procedure, J. of materials processing Technology. 74:227-233
22. Hollomon, J. H., 1945, Transactions, AIME. 162: 268
23. Wei Tong., 1998, Strain Characterization of propagative deformation bands. J of the
mechanics and physics of solids. 46 (10):2087 – 2102
24. Johs A. Bailey., 1969, The plane strain forging of Aluminum and An Aluminum alloy at
low strain rates and elevated temperatures. Int J of Mechanical Science. 11: 491 – 507.
25. Samantha, S.K., 1975, Effect of friction and specimen geometry on the ductile fracture in
upset. Institute of Engg Materials and Techn., Transactions of ASME. 14:20
26. Brownrigg, A., Duncan, J.L. and Embury, J.D., 1979, Free Surface Ductility of Steels in
Cold Forging, Internal Report, McMaster University, Hamilton, Ontario, Canada.
27. Kuhn, H.A., Lee, P.W. and Erturk, T., 1973, A Fracture Criterion for Cold Forming, J of
Engg Materials and Techn, Transactions of the ASME: 213 – 218
28. Erman, E., Kuhn, H.A., and Fitzsimons, G., 1983, Novel test specimens for workability
testing, in compression testing of Homogeneous Materials and Composites. ASTM STP,
808: 279
29. George E Dieter., 1988, Mechanical Metallurgy, McGraw-Hill Book Company-London,
pp.45-46
30. B. Rozzo, P., Deluca, B. and Rendina, R., 1972, A new method for the prediction of
formability limits in metal sheets, Sheet Metal Forming and Formability: Proceedings of
the 7
th
biennial Conference of the International Deep Drawing Research group
31. Wu, W.T., Jinn, J.T. and Fischer, C.E.: Scientific Forming Technologies Corporation,
Chapter15.
http://www.asminternational.org/Template.cfm?Section=BrowsebyFormat&template=Ec
ommerce/FileDisplay.cfm&file=06701G_ch.pdf
32. http://www.matweb.com
33. Kobayashi S., 1970, Deformation Characteristics and Ductile Fracture of 1040 Steel in
Simple Upsetting of Solid Cylinders and Rings, J of Engineering for Industry, Trans
ASME, Series B, May 92 (2): 391 -399
34. Lee, C.H. and Kobayashi, S., 1973, New Solutions to Rigid-Plastic Deformation
Problems Using a Matrix Method. Journal Eng. Ind. (Trans. ASME), 95: 865
35. Zeinkiewiez, O.C., 1984, Flow Formulation for Numerical Solution of Forming Processes
in J.F.T. Pittman et al. (Eds), Numerical Analysis of Forming Processes, Wiley. New
York, pp.1- 44
36. Ansys 8.0 Reference Manual.
37. Syed Kamaluddin, J Babu Rao, MMM Sarcar and NRMR Bhargava, 2007, Studies on
Flow Behavior of Aluminum Using Vision System during Cold Upsetting. Met and
Mater. Trans. B, 38 B: 681-688.
38. Kudo, H, and Aoi, K., 1967, Effect of Compression Test Condition Upon Fracturing of a
Medium Carbon Steel – Study on Cold – Forgeability Test; Part II, Journal of the Japan
Society of Technical Plasticity, 8:17-27
39. David, W, Manthey, Dr. Daeyong Lee, Rebecca M. Pearce, 2005, The Need for Surface
Strain Measurement. Metal Forming Magazine.