Paper Menu >>
Journal Menu >>
 Journal of Minerals & Materials Characterization & Engineering, Vol. 10, No.7, pp.661-669, 2011 jmmce.org Printed in the USA. All rights reserved 661 Application of Automated Ball Indentation for Property Measurement of Degraded Zr2.5Nb Kamal Sharma*, P.K. Singh, Vivek Bhasin and K.K. Vaze RSD, BARC, Trombay, Mumbai, 400085 India *Corrsponding Author: hello_kamal@yahoo.com ABSTRACT In this work, Automated Ball Indentation (ABI) technique is based on load controlled multiple indentations (at a single penetration location) of a polished surface by a spherical indenter (0.7 to 1.46 mm) and indentation depth is progressively increased to a maximum user specified limit with intermediate partial unloading. This technique permits measurement of yield strength, stress-strain curve, strength coefficient and strain hardening exponent. ABI Testing was carried out on samples of Zr-Nb2.5 (Pressure Tube Material) with different heat treatment conditions in which temperature was varying (550 degree to 900 degree and retention time was varying 0.5 to 6 hour and furnace cooled. For all these test material and conditions, the ABI derived results were in very good agreement with those from conventional standard test methods. Keywords: Automated Ball Indentation, Irradiated Nuclear Material, Miniature Specimen Testing, Zr-2.5 Nb 1. INTRODUCTION The integrity of safety-related components in a nuclear reactor (such as the pressure retaining components viz. reactor pressure vessels (RPVs), pressure tubes) is crucial for continued safe operation of the reactor. Material property measurement is an element in this safety assessment. The mechanical property changes for materials susceptible to neutron radiation embrittlement, which in turn limits service life. Conventional testing (Charpy impact, tensile test, and fracture toughness) of surveillance specimens (if available) poses the problem of exposure to significant amount of radiation.  662 Kamal Sharma, P.K. Singh, Vivek Bhasin and K.K. Vaze Vol.10, No.7 So determination of mechanical properties of materials by using non-conventional techniques has been an active area of research for a long time. Among some nondestructive methods for determining mechanical properties of materials, a semi-destructive type of testing, called Automated Ball Indentation (ABI) has been developed. The Automated Ball Indentation technique is capable of extracting degraded mechanical behavior and properties of thermally aged or irradiated materials from very small specimens. The significance of this technology is obvious to the nuclear industry where neutron irradiation space is limited and irradiation cost scales up with specimen volume. For this evaluation the specimen undergoes multiple indentations by a spherical ball indenter. Furthermore, this method can be used to characterize weldments and associated Heat Affected Zone (HAZ), it also avoids the need to fabricate test specimen, and it is relatively rapid. 2. REVIEW OF EARLIER WORK A few research groups have published a series of investigations on ball indentation technique to evaluate mechanical properties. It was Mayer [1] who first developed a relationship between the mean pressure and indentation diameter to evaluate the yield strength of materials. T abor [2] gave an empirical relationship to find the representative strain of materials while indentation is done through a hard spherical ball. However, Tabor’s relation holds very close to the test observation when the indentation process becomes fully plastic. Haggag et.al. [3] did extensive work and developed an automated ball indentation test set up for determining flow properties directly from the test around a small volume of material. The location dependence of the mechanical properties was successfully measured by Murthy et.al. [4]. Gradients in mechanical and fracture properties of SA 533B steel welds were studied using ball indentation technique. The local stress-strain behaviors of different microstructure zones of the weld were observed at different temperatures. Haggag and Nansted [5] also described a simple technique for estimating the fracture toughness by coupling the measured flow properties with a modified but empirically correlated critical fracture strain model. Mathew et.al. [6] studied the effects of low temperature aging (673K) up to 18 months on the mechanical and fracture properties of cast CF-8 stainless steel in the range of 173-423K. A theoretical model is proposed to estimate fracture toughness of ferritic steel in the transition region from ball indentation test data by Byun, Kin, Hang [7]. The key concept of the model is that the indentation energy to a critical load is related to fracture energy of material. Using this set-up many research groups [8-11] studied flow properties of different materials through the thickness variation/gradient in mechanical and fracture properties and found good agreement with the conventional test results. Non-linear finite element and artificial neural network was used by Sharma et al. [12]. 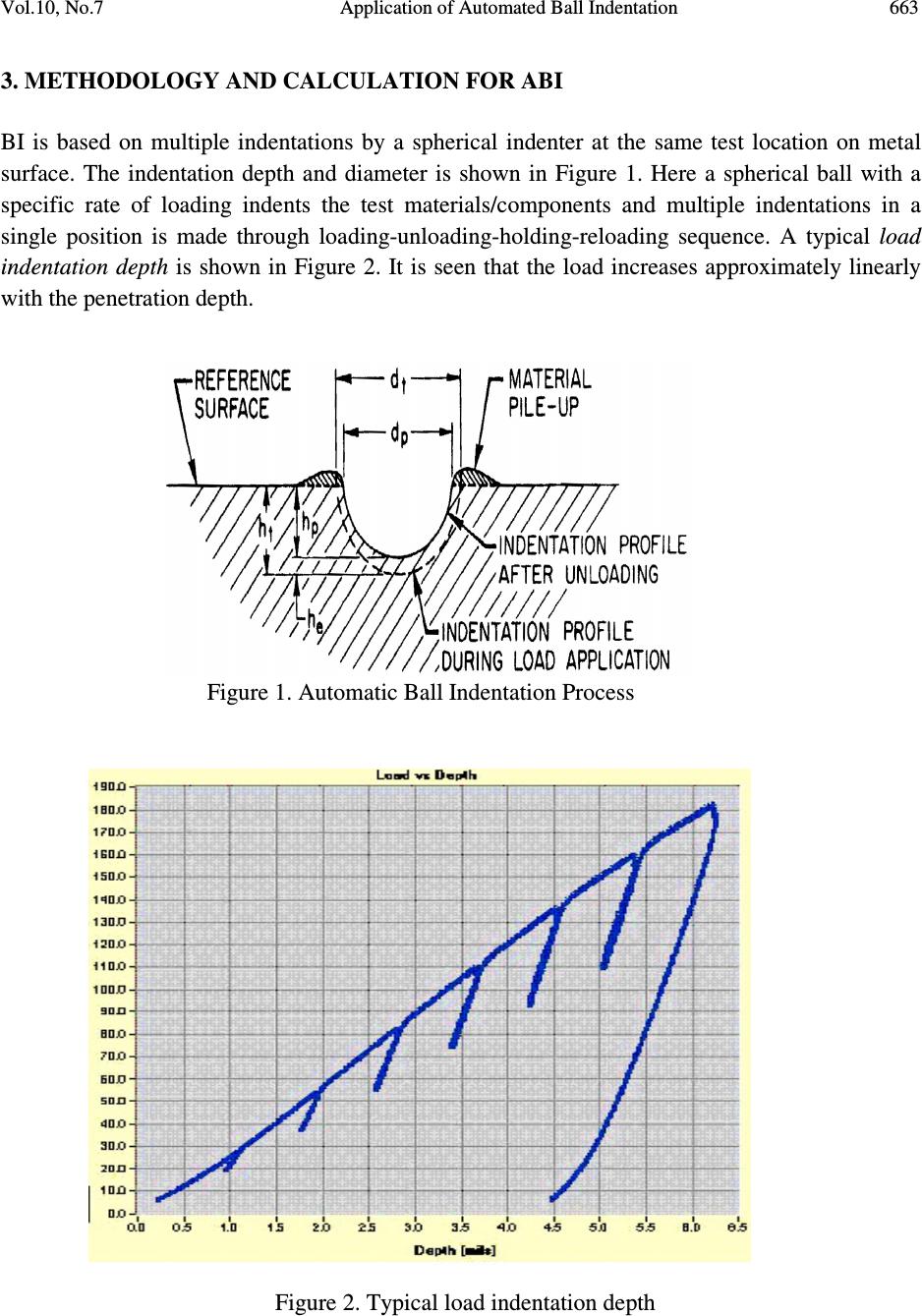 Vol.10, No.7 Application of Automated Ball Indentation 663 3. METHODOLOGY AND CALCULATION FOR ABI BI is based on multiple indentations by a spherical indenter at the same test location on metal surface. The indentation depth and diameter is shown in Figure 1. Here a spherical ball with a specific rate of loading indents the test materials/components and multiple indentations in a single position is made through loading-unloading-holding-reloading sequence. A typical load indentation depth is shown in Figure 2. It is seen that the load increases approximately linearly with the penetration depth. F ig ure 1 . Automatic Ball Indentation Process Figure 2. Typical load indentation depth  664 Kamal Sharma, P.K. Singh, Vivek Bhasin and K.K. Vaze Vol.10, No.7 Here two non-linear but opposing processes occur simultaneously, i.e. the non-linear decrease in the applied load with indentation depth due to the spherical geometry of the indenter and non- linear increase of load with indentation depth due to the work hardening of the test pieces. During each subsequent loading the amount of materials experiencing plastic deformation increases, so continuous yielding and strain hardening occurs simultaneously. In-contrast, for the case of a uni-axial tensile test the plastic deformation is confined only to the limited volume of test sample of gauge section. 3.1 True Strain In Figure 2 a schematic ball indentation profile in the loaded and unloaded condition is shown. Here h p , h t are the plastic and total indentation depth and d p , d t are the plastic and total indentation diameter. Beneath the indenter a complex deformation zone exists. The plastic zone and the indentation impression will expand as the indentation load increases. As the indenter is spherical in shape (having non-linear geometry) multiple stress-strain data points can be obtained. The strain field produced beneath the indenter is regarded as ‘representative’ strain as the total true strain (ε f ) by Tabor. ε f can be expressed as a function of d and D. ε f = f (d/D) (1) Where, D = indenter diameter and d = indentation diameter. After analyzing empirical data he found that ε f varies linearly with the ratio of d/D and found the linearity coefficient is equivalent to 0.2. Later on Haggag and his group calculated the true plastic strain (ε p ) as ε p = 0.2 (d p / D) (2) Where, d p = plastic indentation diameter. 3.2. True Stress An advancing spherical indenter generates multi-axial compressive stresses just beneath the indenter and due to these stresses an increasing volume of test material is forced to flow. The region of contact is a hemisphere of radius ‘a’. The mean pressure (p m ) over the region of contact is proportional to P 1/3 (applied load). Beside normal pressure, a shear stress also acts and the maximum shear stress acts along the axis of the indenter. Using the maximum shear stress theory as yielding criterion the uni-axial flow stress (σ) can be expressed by σ = p m / δ (3) Where δ is a constraint factor, which increases as the plastic zone increases and reaches a maximum until whole of the material around the indentation is in a state of full plasticity.  Vol.10, No.7 Application of Automated Ball Indentation 665 3.3 Evaluation of Tensile Strength (s uts ) The following expression was used for evaluating the engineering value of suts: suts = K (n/e)n (4) Where, suts = The engineering vale of UTS K = strength coefficient and n = strain hardening exponent The K and n values can be determined through the regression analysis of the following power law equation for different values of s and ep from equations (2) and (3). The flow curve may be expressed as: s = K. epn (5) Where, s = true stress ep=true plastic strain and these values can be obtained by fitting various data points of load (P) and indentation plastic diameter (dp ) in the following expressions. ep = K1 (dp / D) (6) s = 4.P / p.dp2. d (7) Where, P = applied load dp= plastic indented diameter and d=constrained factor depending on applied load and materials tested. The plastic diameter of the indentation can be calculated through the regression analysis of the following Hertzian equation: Where, E 1 and E 2 are the Young’s Modulus of the indenter and the specimen tested, h p is plastic depth of the indentation. 322 22 21 } 25.0 25.0 {) 11 (735.2 dhdh dh D EE Pd ppp pp p −+ + += (8)  666 Kamal Sharma, P.K. Singh, Vivek Bhasin and K.K. Vaze Vol.10, No.7 d can be expressed as d = 1.12 + t ln f (9) Where, f is a function of a parameter t, and its value is dependent on the flow stress and plastic strain of the test piece. An iteration method has been utilized to determine d values by using BI software developed by us. Again, t is a function of a m that is dependent on strain rate sensitivity and work hardening characteristic of the test materials. 3.4 Evaluation of Yield Strength (YS) Here the total penetration depth (h t ) is measured while the load is applied and the depth is converted to a total indentation diameter (d t ) using following equation: dt=2(ht.D-ht2)0.5 (10) Where, dt = total indentation diameter D = diameter of the indenting ball and ht = total penetration depth The data points from all loading cycles are fit by linear regression analysis to the following relationship of Meyer relation: P/dt2=A (dt / D )m-2 (11) Where, m = Meyer’s coefficient P = applied load and A = material parameter sy= bm. A (12) Where bm = Material constant and can be calculated with a known value of sy. Then this bm will be same for a specific class of materials irrespective of heat-treatment and mechanical working. The value of bm is determined for each class or type of materials from the various known YS values by using BI analysis software. 4. CONDITION OF MATERIAL The heat treatment condition of the test is shown in Table 1. 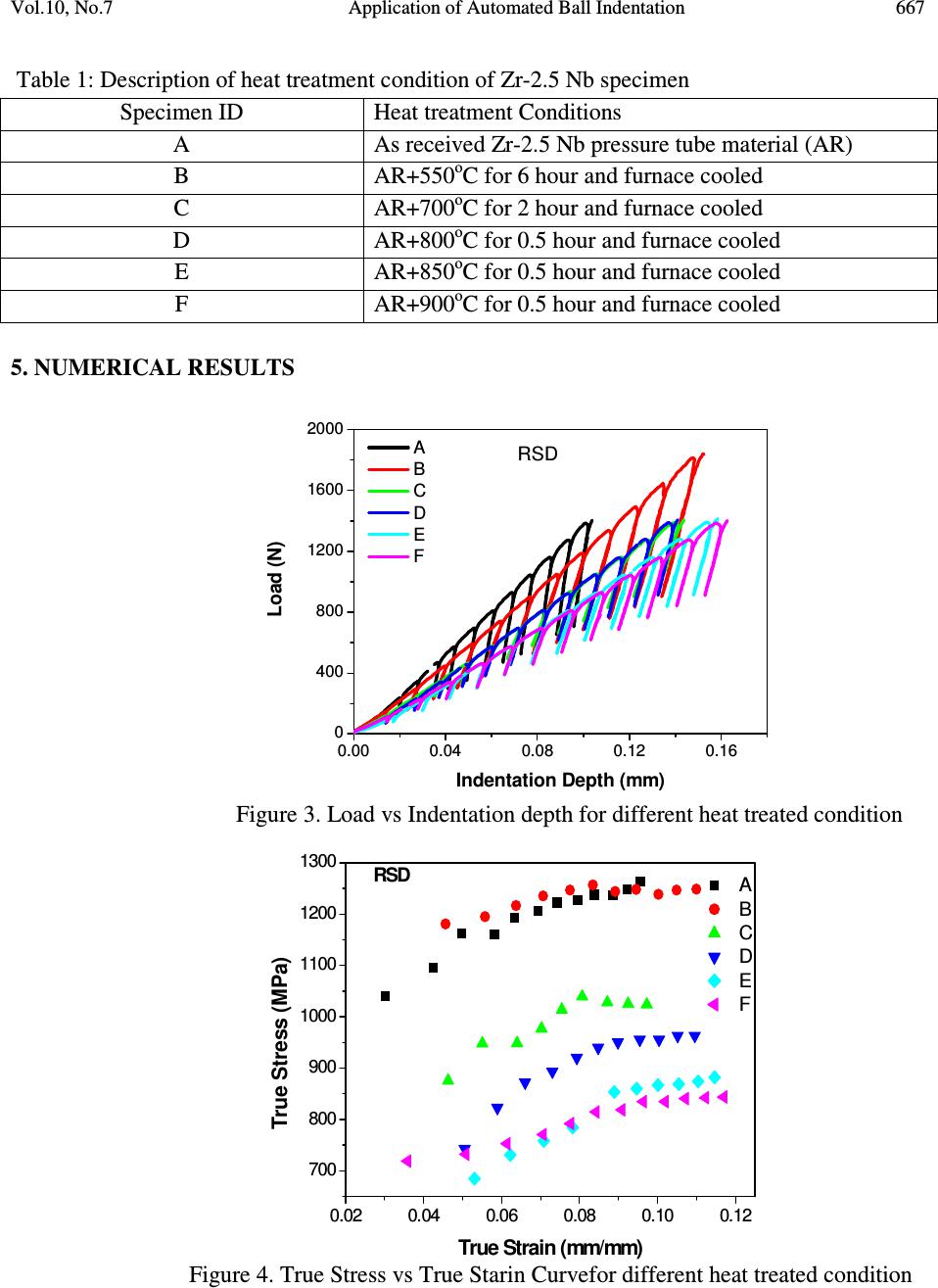 Vol.10, No.7 Application of Automated Ball Indentation 667 Table 1: Description of heat treatment condition of Zr-2.5 Nb specimen Specimen ID Heat treatment Conditions A As received Zr-2.5 Nb pressure tube material (AR) B AR+550 o C for 6 hour and furnace cooled C AR+700 o C for 2 hour and furnace cooled D AR+800 o C for 0.5 hour and furnace cooled E AR+850 o C for 0.5 hour and furnace cooled F AR+900 o C for 0.5 hour and furnace cooled 5. NUMERICAL RESULTS 0.00 0.04 0.08 0.12 0.16 0 400 800 1200 1600 2000 RSD Load (N) Indentation Depth (mm) A B C D E F Figure 3. Load vs Indentation depth for different heat treated condition 0.020.040.060.08 0.10 0.12 700 800 900 1000 1100 1200 1300 RSD True Stress (MPa) True Strain (mm/mm) A B C D E F Figure 4. True Stress vs True Starin Curvefor different heat treated condition  668 Kamal Sharma, P.K. Singh, Vivek Bhasin and K.K. Vaze Vol.10, No.7 Table 2: Comparsion of ABI Testing and Conventional Testing Results Sample No ABI Results (MPa) Conventional (MPa) % Error YS UTS YS UTS YS UTS A 658 862 606 811 8.58 6.29 B 580 830 551 780 5.26 6.41 C 518 656 492 642 5.28 2.18 D 486 604 456 594 6.58 1.68 E 445 561 420 540 5.95 3.89 F 402 523 386 501 4.15 4.39 6. CONCLUSIONS 1. Plot of the load and indentation depth for different heat treatment conditions shows that ABI technique is sensitive to the change in tensile properties due to the heat treatment conditions. 2. Yield strength and UTS of the material decreases with increase in heat treatment temperature corresponding reduction in hold time. This observation is consistent with that of conventional test results. 3. Change in YS and UTS of the heat-treated material with respect to as received condition of the material are also consistent with that of conventional tests. 4. True stress strain curve also reflects the effect heat treatment on the tensile properties of the material, thereby indicating that ABI technique is sensitive to detection of variation in mechanical properties. 5. Although conventional tests show that there is increase in percentage elongation of 100 % with respect to the as received condition of the material. Holman’s equation used for evaluation of strain hardening exponent may not be suitable for this material. 6. Finally it can be inferred that ABI can be used in-situ for evaluation of change in mechanical properties of the ageing component, which will help in residual life estimation and extension of the components if mechanical properties for virgin material is known. REFERENCES 1.) E. Meyer and Z. Ver, Dtsch. Ing. 52 (1908). 2.) D. Tabor The Hardness of Metals; 1951 3.) F. M. Haggag, American Society for Testing and Materials, Philadelphia, pp 27-44, 1993. 4.) K. L. Murthy, P.Q. Mirgania, and M. D. Mathew, International journal of Pressure Vessel and Piping, 76 (1999) 361. 5.) F M Haggag and R K Nanstad, PVP, 170 (1989).  Vol.10, No.7 Application of Automated Ball Indentation 669 6.) M D Mathew, K L Murthy, L M Lietzan and V N Shah, A269 (1999) 186. 7.) T. S. Byan, J. W. Kim, J. H. Hong, Journal of Nuclear Materials, 252 (1998) 187. 8.) Y H Lee, W J Ji and D Kwon, Experimental Mechanics, 44 (2004). 9.) Ghosh Sabita et. al. Mater. Lett, 62 (2008) 2619. 10.) Hyungyil Lee et.al., J Mech. Phy of Solids, 53 (2005) 2037. 11.) G. Das et.al. J. Mat. Res. Adv. Tech., Metallkunde, 95 (2004) 1120. 12.) K. Sharma, V. Bhasin & A K Ghosh, JJMIE, 4 (2010). |

