Materials Sciences and Applicatio ns, 2010, 1, 46-52
doi:10.4236/msa.2010.12009 Published Online June 2010 (http://www.SciRP.org/journal/msa)
Impact of Sulphate Counter Ion in the Migration
of Sodium Ion through Soils
Puvvadi Venkata Sivapullaiah1, Maya Nayak2, Pon napureddy Hari Prasad Reddy3, Jangam Sumalatha4
1Indian Institute of Science, Bangalore, India; 2B. M. Sreenivasaish College of Engineering, Bangalore, India; 3National Institute of
Technology, Warangal, India; 4M. S. Ramaiah Institute of Technology, Bangalore, India.
Received February 22nd, 2010; revised April 30th, 2010; accepted May 3rd, 2010.
ABSTRACT
Laboratory advection-diffusion tests are performed on two regional soils-Brown Earth and Red Earth -in order to assess
their capacity to control contaminant migration with synthetic contaminant solution of sodium sulphate with sodium
concentr ation of 1000 mg/L. The test was de signed to study the tr ansport/attenuatio n behaviour of sodium in t he presence
of sulphate. Effective diffusion coefficient (De) that takes into consideration of attenuation processes is used. Cation
exchange capacity is an important factor for the attenuation of cationic species. Monovalent sodium ion cannot usually
replace other cations and the retention of sodium ion is very little. This is particularly true when chloride is anion is
solution. However, sulphate is likely to play a role in the attenuation of sodium. Cation exchange capacity and type of
exchangeable ions of soils are likely to play an important role. The effect of sulphate ions on the effective diffusion
coefficient of sodium, in two different types of soils, of different cation exchange capacity ha s been studied. The effective
diffusion coefficients of sodium ion for both the soils were calculated using Ogata Bank’s equation. It was shown that
effective diffusion coefficient of sodium in the presence of su lphate is lower for Brown Ea rth than for Red Earth due to
exchange of sodium with calcium ions from the exchangeable complex of clay. The soil with the higher cation exchange
retained more sodi um. Consequentl y, the breakthr ough times and the number of pore volumes of sodium i on increase with
the cation exchange capacity of soil.
Keywords: Cation Exchange Capacity, Clays, Effective Diffusion Coefficient, Hydraulic Conductivity, Porous Media,
Sodium, Sulphate
1. Introduction
Natural clay deposits and compacted clay liners can act as
barriers for contaminant migration and limit contamination
of ground water resources. Available mathematical mod-
els can be used to estimate the potential rates of migration
of ions in soils, based on which the thickness of liners is
designed considering the type of contaminants, local hy-
drology and nature of barrier material. This study de-
scribes results of laboratory column tests performed on
two local soils to understand the processes controlling the
migration of sodium ion and to assess their potential for
liner application. Sodium ion is relatively least retarded of
all cations. The retardation of other cations will be more
and hence is possible to design thickness of liners based
on studies conducted on sodium ions. Generally the re-
tardation of sodium is least in presence of chloride ions.
The effect of other ions suc h as sulphate on the retardation
of sodi um i s not est ablishe d. Base d on the out com e of t he
results it may be possible to economically design the
thickness of liner to contain leachates where similar con-
ditions exist. Transport of ions in porous media is con-
trolled by a variety of physical, chemical and biological
processes [1,2]. The physical processes include diffusion,
adve ction and dis persion. T he chemical processes include
sorption, dissolution/precipitation, complexation, hydroly-
sis/substitutio n and oxidation.
When dealing with transport through aquifers the key
transport mechanisms are usually advection and disper-
sion. The factors primarily affecting transport of species
through porous media are hydraulic conductivity, k, dis-
persion coefficient D, and the retardation factor, R. The
hydraulic conductivity affects the seepage velocity (vs),
which caus es advection flow dr iven by hydrauli c gradient.
Dispersion is the mixing process that causes the concen-
tration front of species to spread out. Dispersion has two
components: mechanical dispersion due to seepage ve-
locity and di ffusion due to con centration gradient. Fo r low
permeable s oils such as clay s, the advect ion com ponent of
dispersion, also called mechanical dispersion, is negligi-

Impact of Sulphate Counter Ion in the Migration of Sodium Ion Through Soils 47
ble [3]. Theref ore, for all prac tical purposes, dispe rsion, D,
is equal to Dm [4]. Thus diffusion is of major significance
in the solute transport in porous fine-grained soils. Same
is the case in any soils in which the velocity of fluid is low.
Advection-dispersion flow occurs when seepage velocity
is small and diffusion coefficient becomes an important
factor.
The molecular diffusion coefficient is a fundamental
property of the solute and the solvent (water). Molecular
diffusion coefficients are tabulated for many chemicals in
water. The rate of diffusion is sensitive to a number of
parameters. Maximum rates of migration by diffusion
occur in bulk or free water at extreme dilution. Free solu-
tion diffusion coefficient (D0) would normally represent
these maximum values. The rate of chem ical movement or
mass flux through a soil may be slower than by diffusion
in pure water. Diffusion through a network of clay parti-
cles involves the diffusive movement of the species of
interest in the pore water between clay particles. The
tortuosity factor accounts for the increased distance of
transport and the more tortuous pathways experienced by
solutes diffusing through porous media, the lower is the
tortuosity factor. Porous media diffusion coefficient (Dp)
takes into consideration of tortuosity factor [5,6]. The
porous system diffusion coefficient Dp can be calculated
from Fick’s law by
Dp  D0WT  De
where WT is complex tortuosity factor, D0 is free solution
diffusion coefficient;  is volumetric water content;.
WT  ffe(L/Le)2 D0  D0
  ffe(L/Le)2
where ff is the decreased fluidity factor related to ad-
sorbed double layer factor; e is the electrostatic interac-
tion factor; (L/L e)2 is the ge ometric tortuosity factor and 
is the tortuosity factor for the clay. In saturated soils, the
diffusion coefficient is even less than porous media dif-
fusion coefficient, Dp, due to attenuation processes. The
diffusion c oeffi cient, whi ch takes i nto acc ount the variou s
attenuation processes, is called effective diffu sion coeffi-
cient, De.
1.1 Effect of Attenuation Processes on Diffusion
Coefficients
The transport of ions through the soils may be retarded
through the processes of sorption, precipitation, biodeg-
radation, and filtration. The attenuation processes in-
cluded are: cation removal, anion removal, and biodeg-
radation. The important process for sorption of cations is
by ion exchange at exchange sites and in the inter-layers
of clays.
Other attenuation processes influence the effective
diffusion coefficient (De). However, the difference be-
tween porous media diffusion coefficient and effective
diffusion coefficient is very little for conservative ions
like chloride. Determination of diffusion coefficients of
some common ions is important in estimating the total
breakthrough times. Colum n tests are usually employed [7]
to determine the diffusion coefficients. Diffusion coeffi-
cients are determined fro m the breakthrough curves plot-
ted using column test data.
Generally sodium ion is retarded very little because
normally sodium cannot replace other exchangeable ions
of soil and adsorbed on to the clay surface. Barone et al. [8]
have shown that the adsorption of sodium and potassium
is affected by other exchangeable ions in the leachate.
Anion plays an important role in this adsorption. It is
proposed to study the retention of sodium in the presence
of sulphate in soils of different cation exchange capacity.
It is important to determine the effective diffusion coef-
ficient (De) of sodium in soils to model its migration
through them using advection-dispersion equation. It is
proposed to determine the diffusion coefficient of sodium
for soils in the presence of sulphate ions.
2. Materials
2.1 Brown Earth
Brown earth obtain ed from a construction site on Airport
road in Bangalore was used in this study. The sample was
collected b y open excavat ion from a de pth of 1 me ter from
natural ground. Th e soil was dried and passed through IS
425-micron sieve. The soil belongs to CH as per unified
soil classification.
2.2 Red Earth
Red earth used in this study was obtained from Indian
Institute of Science Campus, Bangalore. The soil was
collected b y open excavat ion from a de pth of 1 me ter from
natural ground. Th e soil was dried and passed through IS
425-micron sieve. The properties of both the soils used are
determ i ned as A STM st an dar ds a n d pre se nt e d in Table 1.
3. Experimental Procedures for Soil Column
Test
The apparatus used in this study was designed such that
both diffusion and advective-diffusion tests could be per-
formed (Figure 1).
The experimental set up consists of following four
major components namely: Influent Reservoir, Pressure
System, Column Assembly and Effluent Collector.
3.1 Preparation of Sodium Sulphate Solution
About 3.086 grams of Na2SO4 was weighed accurately
and dissolved in water and made upto one litre in volu-
metric flask. T he solution prepared for t he study contained
about 1000 ppm of sodium and 2088 ppm of sulphate.

48 Impact of Sulphate Counter Ion in the Migration of Sodium Ion Through Soils
Table 1. Index and physico chemical prope r t ies of soils use d
Property Brown
Earth Red Earth
Specific gravity 2.63 2.64
Liquid Limi t % 67.5 38.0
Plastic Limit % 23.2 21.0
Shrinkage Limit % 13.4 18.0
Max Dry Density, g/cm3 1.63 1.68
Optimum Moisture Content % 27.5 19.2
Cation Exchange capacity,
(meq/100g) 33 18
Unified soil Classification SymbolCH CI
Figure 1. Experimental set up for soil column test
3.2 Sample Preparation and Placement in the
Column
The oven dried soils of Red Earth and Brown Earth of
required quantity was mixed with necessary amount of
water separately as to prepare sample of required density.
The soils were mixed thoroughly and kept in polythene
bag in a humid desiccator overnight to achieve uniform
moisture content. The soil was then compacted to the
required density by dividing the soil into 3 equal parts by
weight and then, each part is compacted into the (speci-
men) Plexiglas s cylinder, one by one using a screw jack to
ensure uniform compaction for the entire specimen in the
column of Plexiglas cylin der of 32 cm long, 9.2 cm inner
diameter and 0.5 cm thick. The dry density of soil was
0.85 times of Proctor’s maximum dry density at water
content 2% lower than optimum water content.
3.3 Influent Reservoir
The Influent Reservoir consists of a tank made of glass or
polyethylene with two opening. One is at the top for
transferring the synthetic source solution of interest into it
and the other is at the bottom to allow it to migrate through
the soil specimen. The solution is placed in the reservoir
and stirred at frequent intervals so as to maintain constant
initial concentration. The solution is then passed through
the soil compacted in the column at high constant hy-
draulic gradient to reduce the testing duration to reason-
able period. Pressure gauge is connected to the influent
reservoir and to the column assembly. A uniform pressu re
of 15 kPa is maintained throughout the ex-perimental pe-
riod by controlling the flow rate from the influent reser-
voir.
3.4 Relative Concentration of Sodium Ion in the
Effluent
The Effluent is collected in the effluent collector con-
sisting o f a m easur i ng ja r co ve red at t he top so as t o a v oi d
evaporation of collected leachate. The volume of the ef-
fluent that comes out of the colu mn with time was moni-
tored at regular intervals and the concentration of sodium
ion is measured. Know ing the initial and concen tration of
sodium after different intervals, relative concentration
(C/C0) of sodium is calculated and the breakthrough cur-
ves are plotted.
4. Determination of Effective Diffusion
Coeffiecients
Simple solutions to Ogata Bank’s equation allowed de-
termination of the diffusion coefficient using experimen-
tal results. In order to obtain the values of effective dif-
fusion coefficients, a plot of relative concentration versus
time or number of pore volumes are plotted. From the
plot the time (t0.16) corresponding to C/C0 = 0.16 and
time (t0.84) corresponding to C/C0 = 0.84 are obtained.
e
0
C1 1U
erfc
C2 2UD/vL






 



Using these values and knowing the thickness of liner
(L) and k nowin g the v a lue o f velocity, effective diffusion
coefficient is calculated using the following Ogata Bank’s
equation:
U = vnAt/ALn = vt/L
J0.84 = [(U – 1)/U1/2], when C/C0 = 0.84
J0.16 = [(U – 1)/U1/2], when C/C0 = 0.16
From which De = vL/8 [J0.84 – J0.16]2
In addition to the above modified Ogata Bank’s equa-
tion another expression for calculating the effective dif-
fusion co-efficient of ionic s pecies of interest are given [9]
as follows:
2
0.16 0.84
e
0.16 0.84
xvt xvt 1
D8tt











Impact of Sulphate Counter Ion in the Migration of Sodium Ion Through Soils 49
where t0.16 = time at C/C0 = 0.16;
t0.84 = time at C/C0 = 0.84
It was observed that the values of effective diffusion
co-efficient obtained using both Ogata Bank’s equation
and Fried and Cambarnous equation were same.
5. Results and Discussion
The various aspects examined for Brown Earth and Red
Earth are
1) Rate of flow of salt solution through the compacted
soil column;
2) Variation of concentration of individual ions in the
effluent with time;
3) Calculation of diffusion coefficient of ions;
4) Prediction of the breakthrough curves.
5.1 Brown Earth
Rate of flow of sodium sulphate solution through soil
column:
Brown earth is compacted into the column assembly
and initially saturated with distilled water. Then the so-
dium sulphate solution containing 1000 ppm of sodium is
passed through the soil column under a pressure of 15 kPa.
The rate of flow of the leachate through the soil colum n is
monitored.
While carrying out column experiments it is necessary
to monitor the rate of flow of influent fluid through soil
column. For this the volume of leachate (or effluent) col-
lected for different periods is measured. Using this data
variation of rate of flow with time is plotted as shown in
Figure 2. From the graph it can be observed that the
variation of rate of fl ow is almost constant with an average
rate of flow being 3.78 × 10-4 cm3/s. This amounts to an
average permeability of about 1.1 × 10-6 cm/s.
It can be seen from Figure 3 that the cumulative vol-
ume increases linearly upto about 480 hours with the
cumulative rate of leachate flow being about 8.26 × 10-4
cm3/s. With further increase in time leachate flow rate
reduces with an average cumulative flow rate being 4.35 ×
0.0002
0.00025
0.0003
0.00035
0.0004
0.00045
0.0005
0.00055
0.0006
0.00065
0 1000200030004000500
Cumulative time (Hours)
Flow rate (cm3/sec)
0
Sodium Sulphate
Brown Earth
Figure 2. Variation of flow rate of sodium sulphate solution
with time in Brown Earth
10-4 cm3/s and hence velocity also reduces. This decrease
in velocity may be due to precipitation of salts formed by
reaction between leachate and the soil. Proba bly Ca2+ ions
present on the surface of clay particles as exchangeable
ions reacts with sulphate to form Ca2SO4.
Ca2+Clay + Na2SO4  Ca2SO4 + Na+Clay
Normally Na+ ions cannot replace exchangeable Ca2+
from clay exchangeable ion complex. But because of
precipitation of Ca2SO4, Calcium ions are removed from
ion complex and Na+ ions get into exchangeable ion
complex. With increase in time all the exchangeable Ca2+
are precipitated as Ca2SO4. No more precipitation occurs
after the complete removal of available calcium and the
rate of flow through th e soil remains constant. Then the
seepage velocity remains fairly constant for long time.
This constant velocity is about 5.46 × 10-6 cm/s.
Variation of concentration of sodium ion with cumu-
lative time.
The effective diffusion coefficients of ions in both the
soils were determined from the curve of variation of
concentration with time using the Ogata Bank’s equation.
The detailed calculations are shown in Table 2.
Figure 4 shows the variation of relative concentration
of sodium ion with cumulative time, which represents the
breakthrough curve of sodium. From the graph it can be
seen that, the curve is S-Shaped and the relative concen-
tration increasing gradually with time. 50% of the initial
concentration (i.e., C/C0 = 0.5) of Na+ is reached at 2210
hours and 100% of initial concentration (i.e., C/C0 = 1)
after 4854 hours.
From the curve the value of t0.16 (time corresponding to
C/C0 = 0.16) and t0.84 (time corresponding to C/C0 = 0.84)
are obtained which are used in calculating the diffusion
co-efficient of Na+ ion. The diffusion co- efficient of Na+-
ion as calculated is 2.771 × 10-6. Also the total time taken
for the leachate to reach C/C0 = 1 is obtained which is
useful in designing the thickness of liner.
5.2 Red Earth
Rate of flow of sodium sulphate solution through Red
Earth soil column.
0
1000
2000
3000
4000
5000
6000
7000
8000
01000 2000 3000 4000 5000 6000
Cumulative Time (Hours)
Cumulative V olu me (cm3)
Sodium Sul phate
Brown Ea rth
Figure 3. Variation of cumulative volume with time for
Brown Earth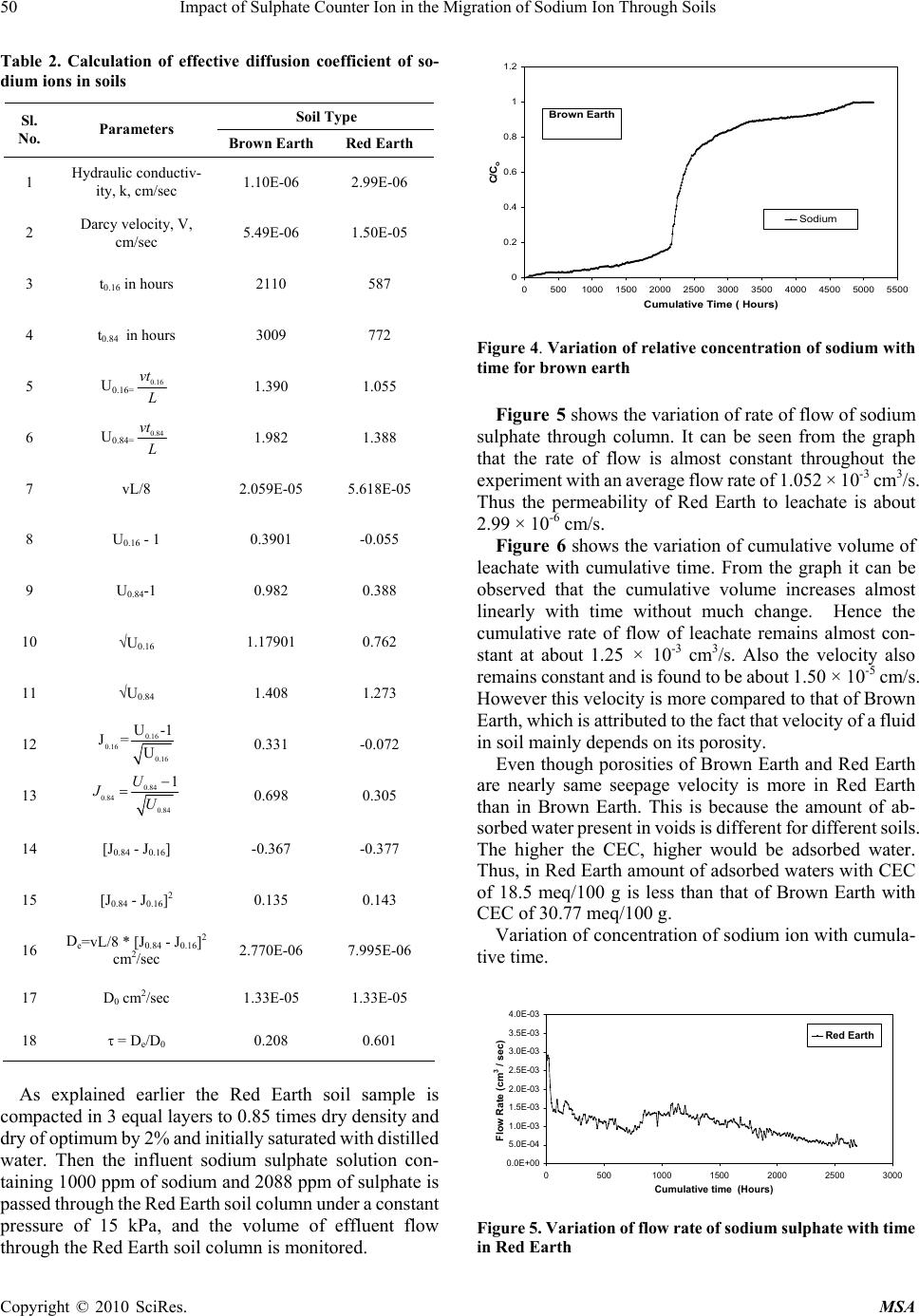

50 Impact of Sulphate Counter Ion in the Migration of Sodium Ion Through Soils
Table 2. Calculation of effective diffusion coefficient of so-
dium ions in soils
Soil Type
Sl.
No. Parameters B rown Earth Red Earth
1 Hydraulic conductiv-
ity, k, cm/sec 1.10E-06 2.99E-06
2 Darcy velocity, V,
cm/sec 5.49E-06 1.50E-05
3 t0.16 in hours 2110 587
4 t0.84 in hours 3009 772
5 U0.16= 0.16
vt
L
1.390 1.055
6 U0.84= 0.84
vt
L
1.982 1.388
7 vL/8 2.059E-05 5.618E-05
8 U0.16 - 1 0.3901 -0.055
9 U0.84-1 0.982 0.388
10 U0.16 1.17901 0.762
11 U0.84 1.408 1.273
12 0.16
0.16
0.16
U-1
J=U 0.331 -0.072
13 0.84
0.84
0.84
1U
JU

 0.698 0.305
14 [J0.84 - J0.16] -0.367 -0.377
15 [J0.84 - J0.16]2 0.135 0.143
16 De=vL/8 * [J0.84 - J0.16]2
cm2/sec 2.770E-06 7.995E-06
17 D0 cm2/sec 1.33E-05 1.33E-05
18  = De/D0 0.208 0.601
As explained earlier the Red Earth soil sample is
compacted in 3 equal layers to 0.85 times dry density and
dry of optimum by 2% and i nitially saturated with distilled
water. Then the influent sodium sulphate solution con-
taining 1000 ppm of sodium and 2088 ppm of sulphate is
passed throu gh the Red Earth soil col umn under a constant
pressure of 15 kPa, and the volume of effluent flow
through the Red Earth soil column is monitored.
0
0.2
0.4
0.6
0.8
1
1.2
05001000 1500 2000 2500 3000 3500 4000 4500 5000 5500
Cumulative Time ( Hours)
C/C
o
Sodium
Brown Earth
Figure 4. Variation of relative concentration of sodium with
time for brown earth
Figure 5 shows the variation of rate of flow of sodium
sulphate through column. It can be seen from the graph
that the rate of flow is almost constant throughout the
experiment wit h an average flow rate of 1. 052 × 10-3 cm3/s.
Thus the permeability of Red Earth to leachate is about
2.99 × 10-6 cm/s.
Figure 6 shows the variation of cumulative volume of
leachate with cumulative time. From the graph it can be
observed that the cumulative volume increases almost
linearly with time without much change. Hence the
cumulative rate of flow of leachate remains almost con-
stant at about 1.25 × 10-3 cm3/s. Also the velocity also
remains constant and is found to be about 1.50 × 10-5 cm/s.
However this velocity is more compared to that of Brown
Earth, which is attributed to the fact that velocity of a flui d
in soil mainly depends on its porosity.
Even though porosities of Brown Earth and Red Earth
are nearly same seepage velocity is more in Red Earth
than in Brown Earth. This is because the amount of ab-
sorbed water present in voids is different for differe nt soils.
The higher the CEC, higher would be adsorbed water.
Thus, in Red Earth amount of adsorbed waters with CEC
of 18.5 meq/100 g is less than that of Brown Earth with
CEC of 30.77 meq/100 g.
Variation of concentration of sodium ion with cumula-
tive time.
0.0E+00
5.0E-04
1.0E-03
1.5E-03
2.0E-03
2.5E-03
3.0E-03
3.5E-03
4.0E-03
05001000 1500 20002500 3000
Cumulative time (Hours)
Flow Rate (cm
3
/ sec)
Red Earth
Figure 5. Variation of flo w rate of sodium sulphate with time
in Red Earth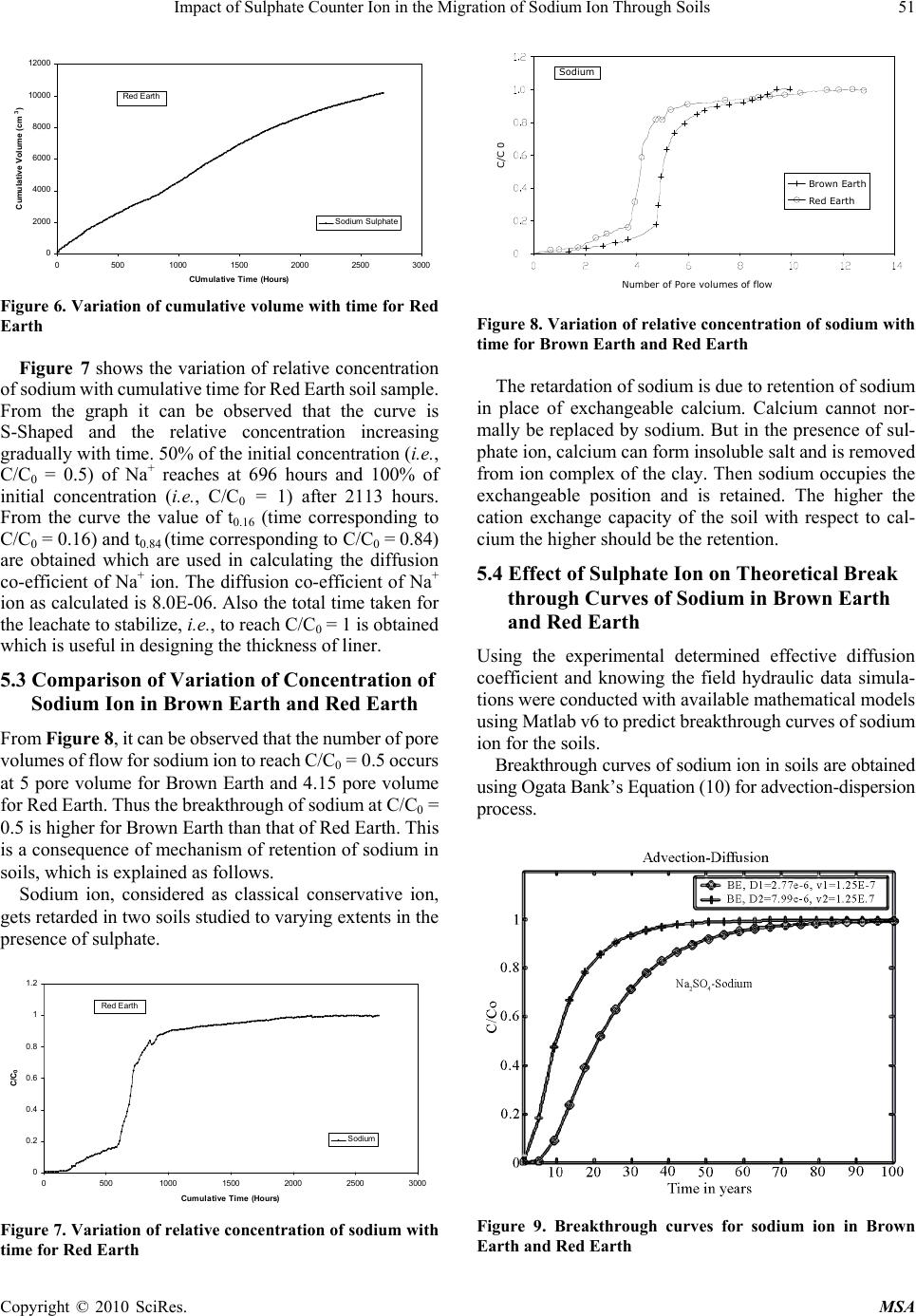

Impact of Sulphate Counter Ion in the Migration of Sodium Ion Through Soils 51
0
2000
4000
6000
8000
10000
12000
05001000 1500 2000 2500 3000
CUm u lativ e Tim e
(
Hou r s
)
Cumulative Volume (cm3)
Sodi um S ul phat e
Red Eart h
Figure 6. Variation of cumulative volume with time for Red
Earth
Figure 7 shows the variation of relative concentration
of sodium with cum ulative time for Red Earth soil sample.
From the graph it can be observed that the curve is
S-Shaped and the relative concentration increasing
gradually with time. 50% of the initial concentration (i.e. ,
C/C0 = 0.5) of Na+ reaches at 696 hours and 100% of
initial concentration (i.e., C/C0 = 1) after 2113 hours.
From the curve the value of t0.16 (time corresponding to
C/C0 = 0.16) and t0.84 (time corresponding to C/C0 = 0.84)
are obtained which are used in calculating the diffusion
co-efficient of Na+ ion. The diffusion co-efficient of Na+
ion as calculated is 8.0E-06. Also the total time taken for
the leachate to stabilize, i.e., to reach C/C0 = 1 is obtained
which is useful in designing the thickness of liner.
5.3 Comparison of Variation of Concentration of
Sodium Ion in Brown Earth and Red Earth
From Figure 8, it can be observed that the number of pore
volumes of fl ow for sodium ion to reach C/C0 = 0.5 occurs
at 5 pore volume for Brown Earth and 4.15 pore volume
for Red Eart h. Thus the breakthrou gh of sodi um at C/C0 =
0.5 is h i gher fo r Brown Ear th than t h a t of Red E a r th. This
is a consequence of mechanism of retention of sodium in
soils, which is explained as follows.
Sodium ion, considered as classical conservative ion,
gets retarded in two soils studied to varying extents in the
presence of sulphate.
0
0.2
0.4
0.6
0.8
1
1.2
05001000 1500 2000 2500 3000
Cumulative Time (Hours)
C/C0
So di um
Red E arth
Figure 7. Variation of relative concentration of sodium with
time for Red Earth
C/C 0
Number of Pore volumes of flow
Brown Earth
Red Ea rt h
Sodium
Figure 8. Variation of relative concentration of sodium with
time for Brow n Earth and Red Earth
The retardation of so dium is due to retention of s odium
in place of exchangeable calcium. Calcium cannot nor-
mally be replaced by sodium. But in the presence of sul-
phate ion, calcium can form insoluble salt and is removed
from ion complex of the clay. Then sodium occupies the
exchangeable position and is retained. The higher the
cation exchange capacity of the soil with respect to cal-
cium the higher should be the retention.
5.4 Effect of Sulphate Ion on Theoretical Break
through Curves of Sodium in Brown Earth
and Red Earth
Using the experimental determined effective diffusion
coefficient and knowing the field hydraulic data simula-
tions were conducted with available m athematical models
using Matlab v 6 to predict bre akthroug h curves of sodium
ion for the soils.
Breakthrough curves of sodium ion in soils are obtained
using Ogata Bank’s Equation (10) for advection-dispersion
process.
Figure 9. Breakthrough curves for sodium ion in Brown
Earth and Red Earth

52 Impact of Sulphate Counter Ion in the Migration of Sodium Ion Through Soils
ss
0e
e
C1 ZvtvZZvt
erfcexp erfc
C2 D
2(Dt) 2(Dt)

 



  

 
 
 

s
e





where, C/C0 = ratio of effluent concentration to influent
concentration
De = Effective diffusion coefficient of contaminating
species
Z = Thickness of the liner
t = Time
vs =Seepage velocity of pore fluid
Two types of compacted soils were considered in the
simulation. The thickness of the clay layer used in the
liner system was 1 m. For obtaining vs, the usual perme-
ability of most in-situ soils of about 1.25 × 10-7 cm/s and
porosity of about 0.4 is assumed. The hydraulic gradient
of 1 is taken. The theoretical breakthrough curves of so-
dium obtained are presented in Figure 9. It can be ob-
serv ed th at us ing th e exp eri mentally determined effective
diffusion coefficient and assuming the same field condi-
tions breakthrough of so dium ion in Brow n Earth is about
24 years where as for Red Earth is about 11 years. Thus it
can be concluded that sodium ion is taking considerably
more time for breakthrough in Brown Earth than in Red
Earth. Thus the effect of small variation in the effective
diffusion coefficients is significant on breakthrough
times.
6. Conclusions
1) The number of pore volumes required for break-
through for sodium is higher for Brown Earth than Red
Earth. Consequently the effective diffusi on co-efficient of
sodium is much lower for Brown Earth than Red Earth.
Because of higher cation exchange capacity of Brown
Earth sodium is retarded more in B rown Eart h than in Red
Earth.
2) The reason for the retardation of sodium by these
soils is the exchange of sodium with calcium ions from the
exchangeable complex of clay. The exchange is possible
because of removal of calcium from the exchangeable
complex to form calcium sulphate, sodium ions occupy
exchangeable sites and are retarded.
3) At same field conditions small variation in the ef-
fective diffusion coefficient causes large variations in the
breakthrough times for different type of soils.
REFERENCES
[1] R. A. Freeze and J. A. Cherry, “Groundwater,” Prentice-
Hall, Inc., EngleWood Cliffs, 1979.
[2] D. E. Daniel and C. D. Shackel ford, “Diffu sion in Sat urated
Soil. I: Background,” Geotechnical Engineering, Vol. 117,
No. 3, 1991, pp. 467-484.
[3] R. W. Gillham and J. A. Cherry, “Contaminant Transport by
Ground Wate r in Non Indurated Deposits, in Rec ent Trends
in Hydrogeology,” In: T. N. Narisimhan, Ed., Geological
Society of America, 1982, pp. 31-62.
[4] Y. Acar and L. Haider, “Transport of Low-Concentration
Contaminant in Saturated Earthen Barriers,” Geotechnical
Engineering, Vol. 116, No. 7, 1990, pp. 1031-1052.
[5] R. K. Rowe, R. M. Quigley and R. J. Booker, “Clayey
Barrier Systems for Waste Disposal Facilities,” E & FN
Spon Press, London, 1995.
[6] H. D. Sharma and S. P. Lewis, “Waste Containment
Systems, Waste Stabilization and Landfills: Design and
Evaluation,” John Wiley & Sons Inc., New York, 1994.
[7] C. D. Shackelford, “Labora tory Diffusion Testi ng for Waste
Disposal: A Review,” Journal of Contaminant Hydrology,
Vol. 7, No. 3, 1991, pp. 177-217.
[8] F. S. Barone, E. K. Yanful, R. M. Quigley and R. K. Rowe,
“Effect of Multiple Contaminant Migration on Diffusion
and Adsorption of Some Domestic Waste Contaminants in a
Natural Clayey Soil,” Canadian Geotechnical Journal,Vol.
26, 1988, pp . 189-1 98.
[9] J. J. Fried and M. A. Combarnous, “Dispersion in Porous
Media,” In: Show, V. T. Ed., Advances in Hydroscience,
Academic Press, New York, Vol. 7, 1971, pp. 169-282.
[10] A. Ogata and R. B. Banks, “A Solution of the Differential
Equation of Longitudinal Dispersion in Porous Media,” US
Geological S urvey , No. 411-A, 1961, p. 7.