Journal of Minerals & Materials Characterization & Engineering, Vol. 9, No.7, pp.635-642, 2010
jmmce.org Printed in the USA. All rights reserved
635
Determination of Bond index of Birnin- Gwari Iron Ore in Nigeria
K.J. Olatunji* and A.G. Durojaiye
Mineral Resources Engineering Department, Kwara State Polytechnic, Ilorin, Nigeria
*Corresponding Author:
ABSTRACT
Bond index is useful in designing of grinding system in mineral processing. In this study, the
Bond work index of Birnin- Gwari iron ore in northern Nigeria is determined using modified
Bond’s method using ‘reference ore’. Samples of iron ore were sourced using random method,
reference minerals; marble and granite of known weight and iron ore of known weight were
ground using the laboratory ball mill grinding machine. 80% passing size for the iron ore
marble and granite samples were obtained at 100μm sieve size for the feeds and products. The
work index of reference minerals; marble and granite were used to calculate the work index of
iron ore. The value of 28.66 Kwh/short ton and 24.92 Kwh/short ton were obtained. The value of
20.39 Kwh/short ton was selected as it is within the range indicated by previous research work
on iron ore in Nigeria.
Keywords: Bond index, Birnin-Gwari iron ore, modified, reference minerals, mineral processing.
1. INTRODUCTION
Iron ore deposits are usually present as iron oxides (magnetite, Fe3O4; haematite, Fe2O3),
hydroxides (geotite, FeO(OH)), limonite, 2Fe2O3.H2O and carbonates (siderite, FeCO3). Nigeria
has a lot of iron ore deposits in different locations around the country with their respective
proven and unproven reserves. (Geological Survey of Nigeria, 1980; Battey, 1981).
Communition in mineral processing plant or mill takes place as a sequence of crushing and
grinding processes. Crushing reduces the particle size of run-off-mine ore to such a level that
grinding can be carried out until the mineral and gauges are substantially produced as separated
particles (Wills, 2006).

636 K.J. Olatunji and A.G. Durojaiye Vol.9, No.7
The most widely used parameter to measure ore grindability is the Bond work index, Wi
(Magdalimovic,1989). Numerically the work index is the energy required in Kwh/short ton to
reduce a given material from theoretically infinite size to 80% passing size of 100 microns
(Onemine, 2009).
The determination of work index using modified Bond’s method can be compared to method of
determining it by Berry and Bruce (1966). This method requires the use of a reference ore of
known grindability.
The objective of this study is to determine the grindability of Birnin-Gwari iron ore in Northern
Nigeria using the modified Bond’s method.
2. MATERIALS AND METHODS
Samples of iron ore were obtained from Birnin-Gwari iron ore deposit hill, marble from Igbetti
and granite from Ilorin using random sampling method. The samples were collected at various
spot, 5m apart. 20kg of each mineral was obtained for the study.
The samples were broken manually with a sledge hammer to provide the required size acceptable
to laboratory jaw crusher. The samples were crushed and pulverized, part of pulverized samples
were weighed for sieve analysis. The modified Bond’s method of determining the net work index
of ore involves use of reference ore of which grindability is known. The procedure is as follows.
1. 100g each of samples of the ore under test and the reference ore are crushed and
pulverized in the laboratory mill machine for an hour,
2. The samples of test and reference ores were taken and sized by sieving into a number of
size fraction using the automatic sieve shaker for 15 minutes.
3. Each size fraction of the test and the reference ores were weighed and the value noted
“feed”.
4. The “feed “ test and reference ores were each gathered together and introduced into the
laboratory mill machine and ground for 15 minutes.
5. The test and the reference ores from the laboratory ball mill machine were sized and each
sieve fractions was weighed and the value noted as the product or discharge.
6. Sieve analysis.
The ground samples were sieved into the following sieve size fractions; + 365 μm, -355
μm, +250 μm, -250 μm, +180 μm, -180 μm, +125 μm, -125 μm, +90 μm, -90 μm, +63
μm, -63 μm using automatic sieve shaker for 15 minutes.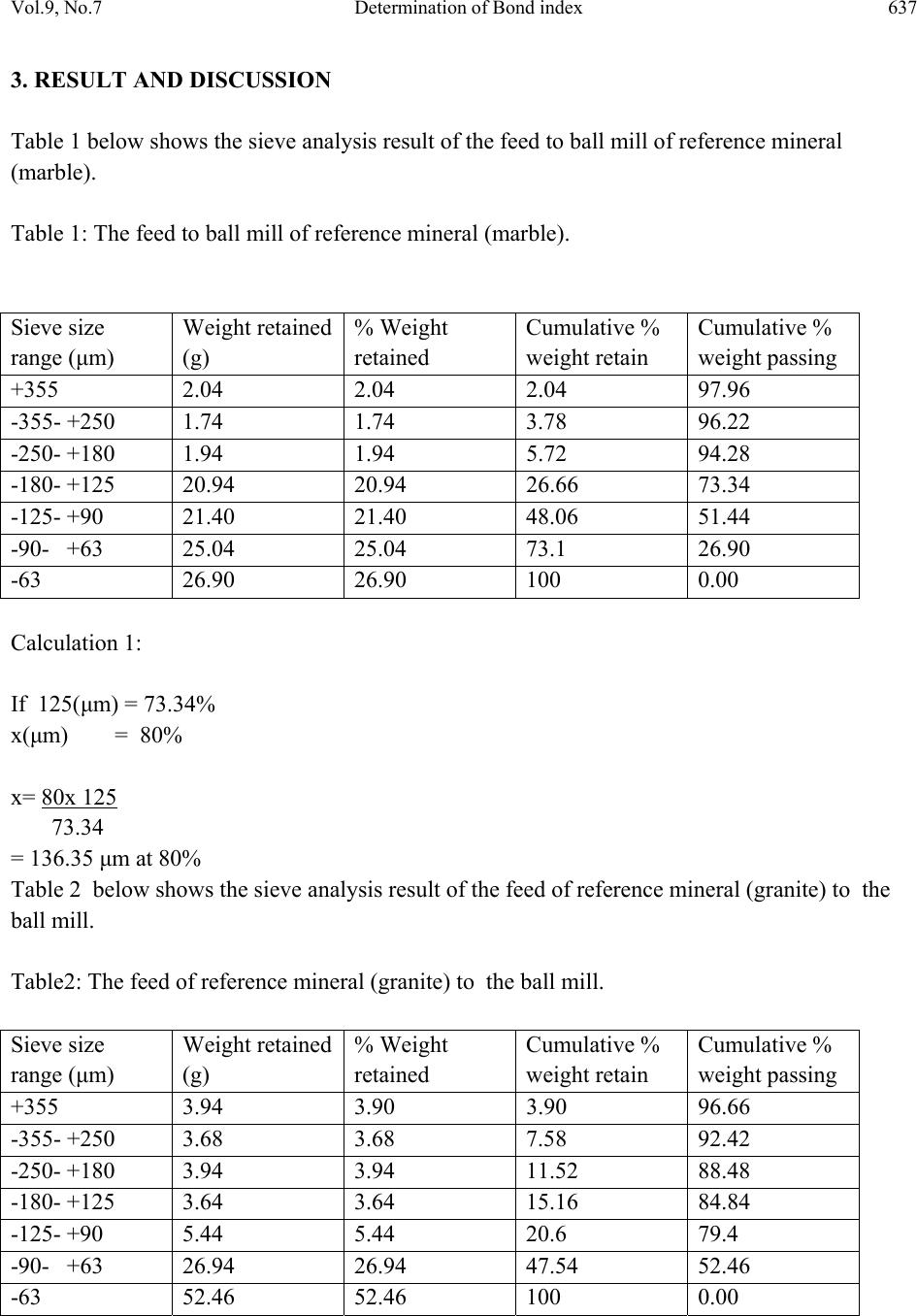

Vol.9, No.7 Determination of Bond index 637
3. RESULT AND DISCUSSION
Table 1 below shows the sieve analysis result of the feed to ball mill of reference mineral
(marble).
Table 1: The feed to ball mill of reference mineral (marble).
Sieve size
range (μm)
Weight retained
(g)
% Weight
retained
Cumulative %
weight retain
Cumulative %
weight passing
+355 2.04 2.04 2.04 97.96
-355- +250 1.74 1.74 3.78 96.22
-250- +180 1.94 1.94 5.72 94.28
-180- +125 20.94 20.94 26.66 73.34
-125- +90 21.40 21.40 48.06 51.44
-90- +63 25.04 25.04 73.1 26.90
-63 26.90 26.90 100 0.00
Calculation 1:
If 125(μm) = 73.34%
x(μm) = 80%
x= 80x 125
73.34
= 136.35 μm at 80%
Table 2 below shows the sieve analysis result of the feed of reference mineral (granite) to the
ball mill.
Table2: The feed of reference mineral (granite) to the ball mill.
Sieve size
range (μm)
Weight retained
(g)
% Weight
retained
Cumulative %
weight retain
Cumulative %
weight passing
+355 3.94 3.90 3.90 96.66
-355- +250 3.68 3.68 7.58 92.42
-250- +180 3.94 3.94 11.52 88.48
-180- +125 3.64 3.64 15.16 84.84
-125- +90 5.44 5.44 20.6 79.4
-90- +63 26.94 26.94 47.54 52.46
-63 52.46 52.46 100 0.00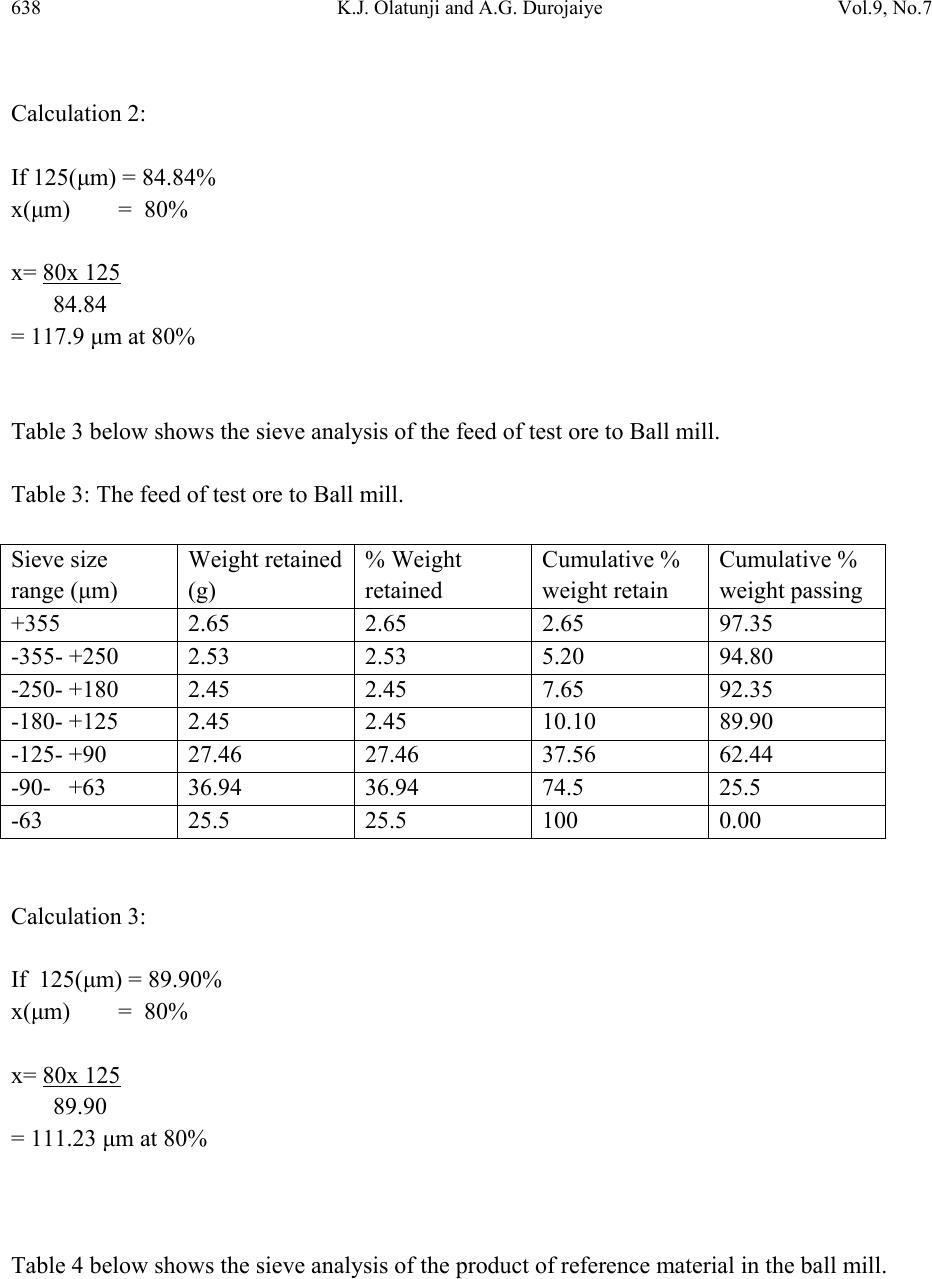

638 K.J. Olatunji and A.G. Durojaiye Vol.9, No.7
Calculation 2:
If 125(μm) = 84.84%
x(μm) = 80%
x= 80x 125
84.84
= 117.9 μm at 80%
Table 3 below shows the sieve analysis of the feed of test ore to Ball mill.
Table 3: The feed of test ore to Ball mill.
Sieve size
range (μm)
Weight retained
(g)
% Weight
retained
Cumulative %
weight retain
Cumulative %
weight passing
+355 2.65 2.65 2.65 97.35
-355- +250 2.53 2.53 5.20 94.80
-250- +180 2.45 2.45 7.65 92.35
-180- +125 2.45 2.45 10.10 89.90
-125- +90 27.46 27.46 37.56 62.44
-90- +63 36.94 36.94 74.5 25.5
-63 25.5 25.5 100 0.00
Calculation 3:
If 125(μm) = 89.90%
x(μm) = 80%
x= 80x 125
89.90
= 111.23 μm at 80%
Table 4 below shows the sieve analysis of the product of reference material in the ball mill.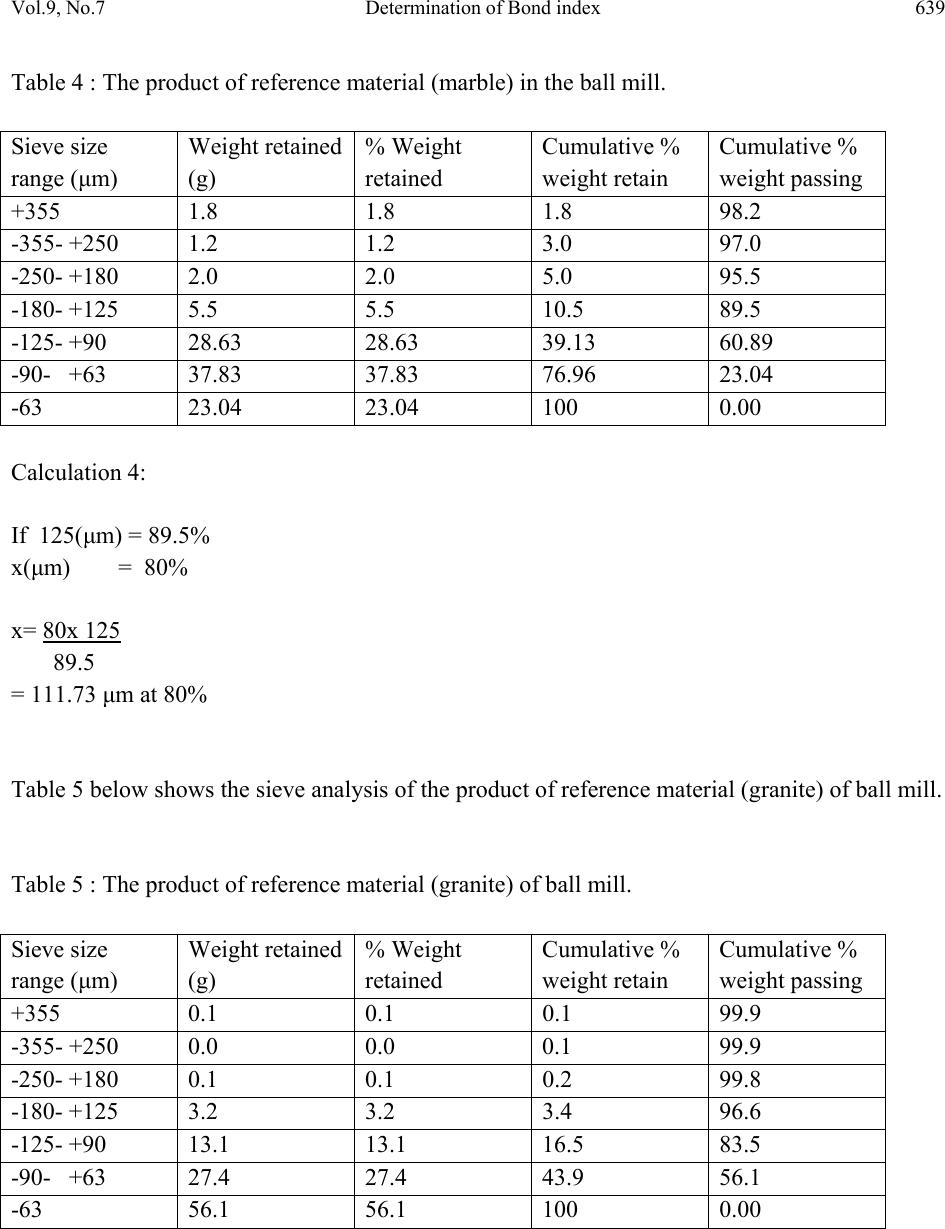

Vol.9, No.7 Determination of Bond index 639
Table 4 : The product of reference material (marble) in the ball mill.
Sieve size
range (μm)
Weight retained
(g)
% Weight
retained
Cumulative %
weight retain
Cumulative %
weight passing
+355 1.8 1.8 1.8 98.2
-355- +250 1.2 1.2 3.0 97.0
-250- +180 2.0 2.0 5.0 95.5
-180- +125 5.5 5.5 10.5 89.5
-125- +90 28.63 28.63 39.13 60.89
-90- +63 37.83 37.83 76.96 23.04
-63 23.04 23.04 100 0.00
Calculation 4:
If 125(μm) = 89.5%
x(μm) = 80%
x= 80x 125
89.5
= 111.73 μm at 80%
Table 5 below shows the sieve analysis of the product of reference material (granite) of ball mill.
Table 5 : The product of reference material (granite) of ball mill.
Sieve size
range (μm)
Weight retained
(g)
% Weight
retained
Cumulative %
weight retain
Cumulative %
weight passing
+355 0.1 0.1 0.1 99.9
-355- +250 0.0 0.0 0.1 99.9
-250- +180 0.1 0.1 0.2 99.8
-180- +125 3.2 3.2 3.4 96.6
-125- +90 13.1 13.1 16.5 83.5
-90- +63 27.4 27.4 43.9 56.1
-63 56.1 56.1 100 0.00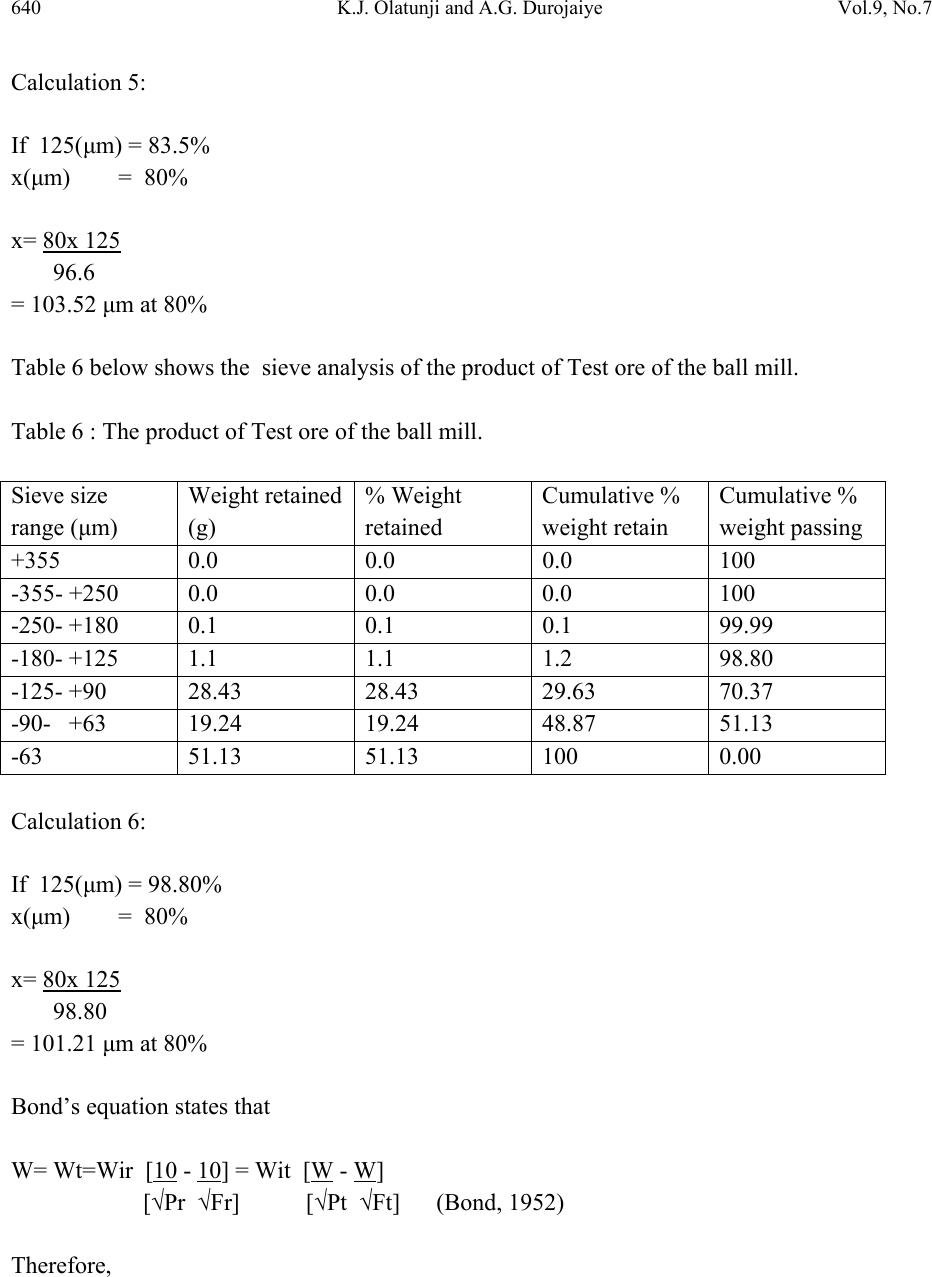

640 K.J. Olatunji and A.G. Durojaiye Vol.9, No.7
Calculation 5:
If 125(μm) = 83.5%
x(μm) = 80%
x= 80x 125
96.6
= 103.52 μm at 80%
Table 6 below shows the sieve analysis of the product of Test ore of the ball mill.
Table 6 : The product of Test ore of the ball mill.
Sieve size
range (μm)
Weight retained
(g)
% Weight
retained
Cumulative %
weight retain
Cumulative %
weight passing
+355 0.0 0.0 0.0 100
-355- +250 0.0 0.0 0.0 100
-250- +180 0.1 0.1 0.1 99.99
-180- +125 1.1 1.1 1.2 98.80
-125- +90 28.43 28.43 29.63 70.37
-90- +63 19.24 19.24 48.87 51.13
-63 51.13 51.13 100 0.00
Calculation 6:
If 125(μm) = 98.80%
x(μm) = 80%
x= 80x 125
98.80
= 101.21 μm at 80%
Bond’s equation states that
W= Wt=Wir [10 - 10] = Wit [W - W]
[√Pr √Fr] [√Pt √Ft] (Bond, 1952)
Therefore,

Vol.9, No.7 Determination of Bond index 641
Wit = Wir [10 - 10]
[√Pr √Fr]
[W - W]
[√Pt √Ft]
where , Wir= work index of the reference ore
Wit= work index of test ore
Pr= The diameter of the reference ore product, 80% of which passes through 100 μm aperture.
Pt = The diameter of the test ore product, 80% of which passes through 100 μm aperture.
Fr = The diameter of the reference ore feed, 80% of which passes through 100 μm aperture.
Ft = The diameter of the test ore feed, 80% of which passes through 100 μm aperture.
Wr = work input in kilowatt hour/ short ton for reference ore and
Wt = work input in kilowatt hour /short ton for test ore
Considering marble as reference mineral,
Ft = 111.23 μm
Fr = 136.35 μm
Pt = 101.21 μm
Pr = 111.73 μm
Wit = Wir ( 10/ √Pr – 10/√Fr)
Wit (10/ √Pt – 10/√Fr)
= 12,74 ( 10/ 111.73 – 10/√136.35)
(10/ √101.21 – 10/√111.23)
=24.92 Kwh/s ton
Considering granite as reference mineral,
Pt = 101.21 μm
Ft = 111.23 μm
Fr = 117.9 μm
Pr = 103.52 μm
Wit = Wir ( 10/ √Pr – 10/√Fr)
Wit (10/ √Pr – 10/√Fr)
= 15,13 ( 10/ 103.52 – 10/√117.9)
(10/ √101.21 – 10/√111.23)
=20.39 Kwh/s ton

642 K.J. Olatunji and A.G. Durojaiye Vol.9, No.7
The work index of 20.39 Kwh/s ton value obtained when granite was a reference ore is within
the limit of work index of some iron ores in Nigeria (Weiss, 1965 and Thomas, 2007).
4. CONCLUSION AND RECOMMENDATIONS
The study shows that work index of Birnin –Gwari iron ore can be taken as 28.66 Kwh/ston i.e.
20.39 Kwh of energy is required to reduce one ton of Birnin- Gwari iron ore from 80% passing.
It is hereby recommended that the value of work index obtained in this study should serve as a
guide for designing grinding plant for Birnin- Gwari iron ore in northern Nigeria.
REFERENCES
Battey M.H (1981): Mineralogy for Students, Longman Inc., New York, pp 91, 159-263.
Berry T.F and Bruce R.W (1966): A simple method of determining the grindability of ores,
Canadian Mining Journal (July).
Bond F.C (1952), The third law of communition, Trans AIME 193.
Geological Survey of Nigeria (1980): The Geology of Part of South Western Nigeria Bulletin
No 31 Vol 26. pp.1-47.
Magdalimovic N.M (1989): Calculation of energy required for grinding in a ball mill, Journal of
Mineral Processing 25, (Jan) 41.
One mine (2010): Summary and Determination of the Bond Work index using an ordinary
Laboratory Batch Ball mill,http;//www.onemine.org/search/summary.cmf
Thomas D.G (2002): Beneficiation of the Totomuro Iron Ore Deposit, M.Sc Thesis, Department
of Metallurgical Engineering, A.B.U, Zaria (unpublished).
Weiss N.L (1985): Mineral Processing handbook by American Institute of Mining, Metalurgical
and Petroleum Enginering Incorporated, Kingsport Press,New York.