Journal of Minerals & Materials Characterization & Engineering, Vol. 9, No.5, pp.483-493, 2010
jmmce.org Printed in the USA. All rights reserved
483
Model for Assessment and Computational Analysis of the Concentration of
Zinc Dissolved during Leaching of Sphalerite in Butanoic Acid Solution
C. I. Nwoye1*, and I. E. Mbuka2
1Department of Metallurgical and Materials Engineering, Nnamdi Azikiwe University, Awka,
Anambra State, Nigeria.
2Department of Metallurgical and Materials Engineering, Federal University of
Technology Owerri, Nigeria.
*Corresponding Author:
ABSTRACT
A model for assessment and computational analysis of the concentration of zinc dissolved during
leaching of sphalerite in butanoic acid solution has been derived. The model
Zn = Antilog [(exp(γ/α))0.6173]
is dependent on the initial and final pH of the leaching solution. The validity of the model was
found to be rooted in the expression (Log Zn)1.62 = exp(γ/α) where both sides of the expression
are approximately equal to 3. The maximum deviation of the model-predicted concentrations of
dissolved zinc from that of the corresponding experimental values is less than 14% which is quite
within the acceptable deviation limit of experimental results.
Keywords: Model, Dissolved Zinc, Sphalerite, Butanoic Acid Solution, Leaching.
1. INTRODUCTION
Sphalerite (ZnS) is the most important zinc sulphide mineral and is the main source from which
zinc is produced commercially. It exists naturally in association with other metal sulphide
minerals, such as chalcopyrite (CuFeS2), galena (PbS), and Pyrite (FeS2). In mineral processing
engineering, the concentrates of these sulphide minerals are collected separately using selective
conventional froth flotation.

484 C. I. Nwoye, and I. E. Mbuka Vol.9, No.5
The conventional process of zinc recovery from sphalerite involves roasting to zinc oxide or
sulphate, leaching the resultant calcine with dilute sulphuric acid and electrodepositing the zinc
from the purified leach solution [1]. The roasting step produces SO2 gas, however environmental
restriction imposed on sulphide smelters have resulted to the development of alternative methods
including hydrometallurgical routes which eliminates production of SO2.
Various leaching studies have been carried out [2-7] using ammonia solution, nitric acid [8],
hydrochloric acid [9-11], sulphuric acid [12, 13] and oxidizing agents such as ferric ions [14-20].
Adebayo et al., [21] investigated the leaching of sphalerite with hydrogen peroxide and nitric
acid solutions. The result of the investigation shows that leaching of sphalerite is dependent on
temperature and stirring speed and inversely proportional to the ore size. The activation energy
was found to be 28kJmol-1 suggesting that the reaction is chemically controlled at the surface of
the particle.
Olubambi et al. [22] carried out investigation on the effectiveness of hydrogen peroxide as an
oxidant for the sulphuric acid leaching of zinc and copper from a complex sulphide ore. The
result of the investigation indicates that the concentrations of zinc and copper decreased while
silica, sulphur, iron and lead contents increased. Dissolution results [22] show that leaching rate
of copper was lower than that of zinc. The highest recoveries of zinc and copper were obtained at
a leaching time of 180 minutes, stirring speed of 160 rpm, ore particle size of 75μm and a
concentration of 1M H2SO4/ 1M H2O2. It was observed that the leaching rate of zinc and copper
increased with increasing hydrogen peroxide concentration while increased stirring speed had a
negative leaching effect as it promotes hydrogen peroxide decomposition [22].
Nwoye [23] derived a model for predicting the initial solution pH at pre-assumed final pH and
concentration of dissolved zinc, during leaching of galena in butanoic acid solution. The model
α = 1.4γ (1)
ln[(Zn)1/3]
shows that the initial pH of the leaching is dependent on the values of the pre-assumed final
solution pH and concentration of dissolved zinc. The validity of the model was rooted in the
expression eN(γ/α) = 3√Zn where both sides of the expression were approximately equal to 4. The
respective deviation of the model-predicted initial solution pH value from that of the
corresponding experimental value was less than 2% which is quite within the acceptable
deviation limit of experimental results.

Vol.9, No.5 Model for Assessment and Computational Analysis 485
2. MODEL
During the leaching process, the ore was assumed to be stationary in the reaction vessel and
contains the un-leached lead and zinc as part of reaction remnants. The ore was attacked by
hydrogen ions from butanoic acid within the liquid phase, and in the presence of oxygen.
2.1 Model Formulation
Results from experimental work [24] carried out at SynchroWell Research Laboratory, Enugu
were used for the model derivation. These results are as presented in Table 1.
Computational analysis of these experimental results [24] shown in Table 1, resulted to Table 2
which indicate that;
(Log Zn)N = exp(γ/α) (approximately) (2)
Introducing the value of Z into equation (2)
(Log Zn)1.62 = exp(γ/α) (3)
Multiplying the indices of both sides of equation (3) by 1/1.62 reduces it to;
Log Zn = (exp(γ/α))1/1.62 (4)
Log Zn = [(exp(γ/α))0.6173] (5)
Zn = Antilog [(exp(γ/α))0.6173] (6)
N = 1.62 (Dissolution coefficient of zinc in butanoic acid) determined in the experiment [24].
α = Initial pH of the butanoic acid leaching solution just before the leaching process started.
γ = Final pH of the butanoic acid leaching solution at time t.
Zn = Concentration of dissolved Zn during the leaching process (mg/kg)
Equation (6) is the derived model.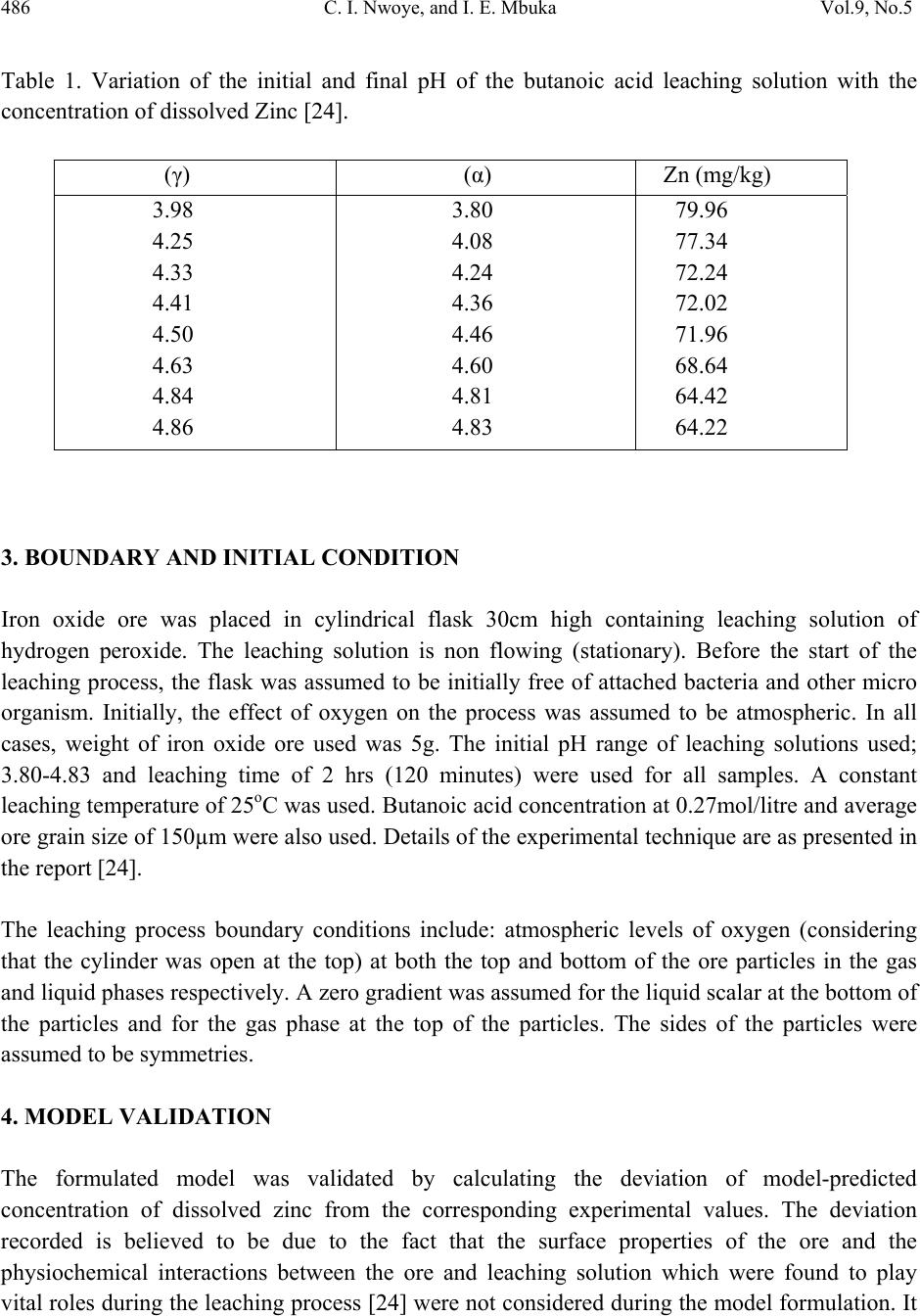

486 C. I. Nwoye, and I. E. Mbuka Vol.9, No.5
Table 1. Variation of the initial and final pH of the butanoic acid leaching solution with the
concentration of dissolved Zinc [24].
(γ) (α) Zn (mg/kg)
3.98
4.25
4.33
4.41
4.50
4.63
4.84
4.86
3.80
4.08
4.24
4.36
4.46
4.60
4.81
4.83
79.96
77.34
72.24
72.02
71.96
68.64
64.42
64.22
3. BOUNDARY AND INITIAL CONDITION
Iron oxide ore was placed in cylindrical flask 30cm high containing leaching solution of
hydrogen peroxide. The leaching solution is non flowing (stationary). Before the start of the
leaching process, the flask was assumed to be initially free of attached bacteria and other micro
organism. Initially, the effect of oxygen on the process was assumed to be atmospheric. In all
cases, weight of iron oxide ore used was 5g. The initial pH range of leaching solutions used;
3.80-4.83 and leaching time of 2 hrs (120 minutes) were used for all samples. A constant
leaching temperature of 25oC was used. Butanoic acid concentration at 0.27mol/litre and average
ore grain size of 150µm were also used. Details of the experimental technique are as presented in
the report [24].
The leaching process boundary conditions include: atmospheric levels of oxygen (considering
that the cylinder was open at the top) at both the top and bottom of the ore particles in the gas
and liquid phases respectively. A zero gradient was assumed for the liquid scalar at the bottom of
the particles and for the gas phase at the top of the particles. The sides of the particles were
assumed to be symmetries.
4. MODEL VALIDATION
The formulated model was validated by calculating the deviation of model-predicted
concentration of dissolved zinc from the corresponding experimental values. The deviation
recorded is believed to be due to the fact that the surface properties of the ore and the
physiochemical interactions between the ore and leaching solution which were found to play
vital roles during the leaching process [24] were not considered during the model formulation. It

Vol.9, No.5 Model for Assessment and Computational Analysis 487
is expected that introduction of correction factor to the predicted concentration of dissolved zinc,
gives exactly the corresponding experimental values.
Deviation (De) (%) of model-predicted initial pH values from those of the experiment is given
by
De = mI – eI x 100 (7)
eI
Where mI = Model-predicted initial pH values
eI = Experimental initial pH values
Since correction factor (Cr) is the negative of the deviation,
Cr = - De (8)
Substituting equation (7) into equation (8) for De,
Cr = -100 mI - eI
eI (9)
It was observed that addition of the corresponding values of Cr from equation (9) to the model-
predicted initial pH gave exactly the corresponding experimental initial pH values [24].
5. RESULTS AND DISCUSSION
Computational analysis of these experimental results [24] shown in Table 1, resulted to Table 2 .
Table 2. Variation of exp(γ/α) with (Log Zn)1.62
(γ/α) exp(γ/α) Log Zn (Log Zn)1.62
1.0474
1.0417
1.0212
1.0115
1.0090
1.0065
1.0062
1.0062
2.8502
2.8340
2.7765
2.7497
2.7429
2.7360
2.7352
2.7352
1.9029
1.8884
1.8588
1.8575
1.8571
1.8366
1.8090
1.8077
2.8357
2.8007
2.7300
2.7269
2.7259
2.6773
2.6125
2.6094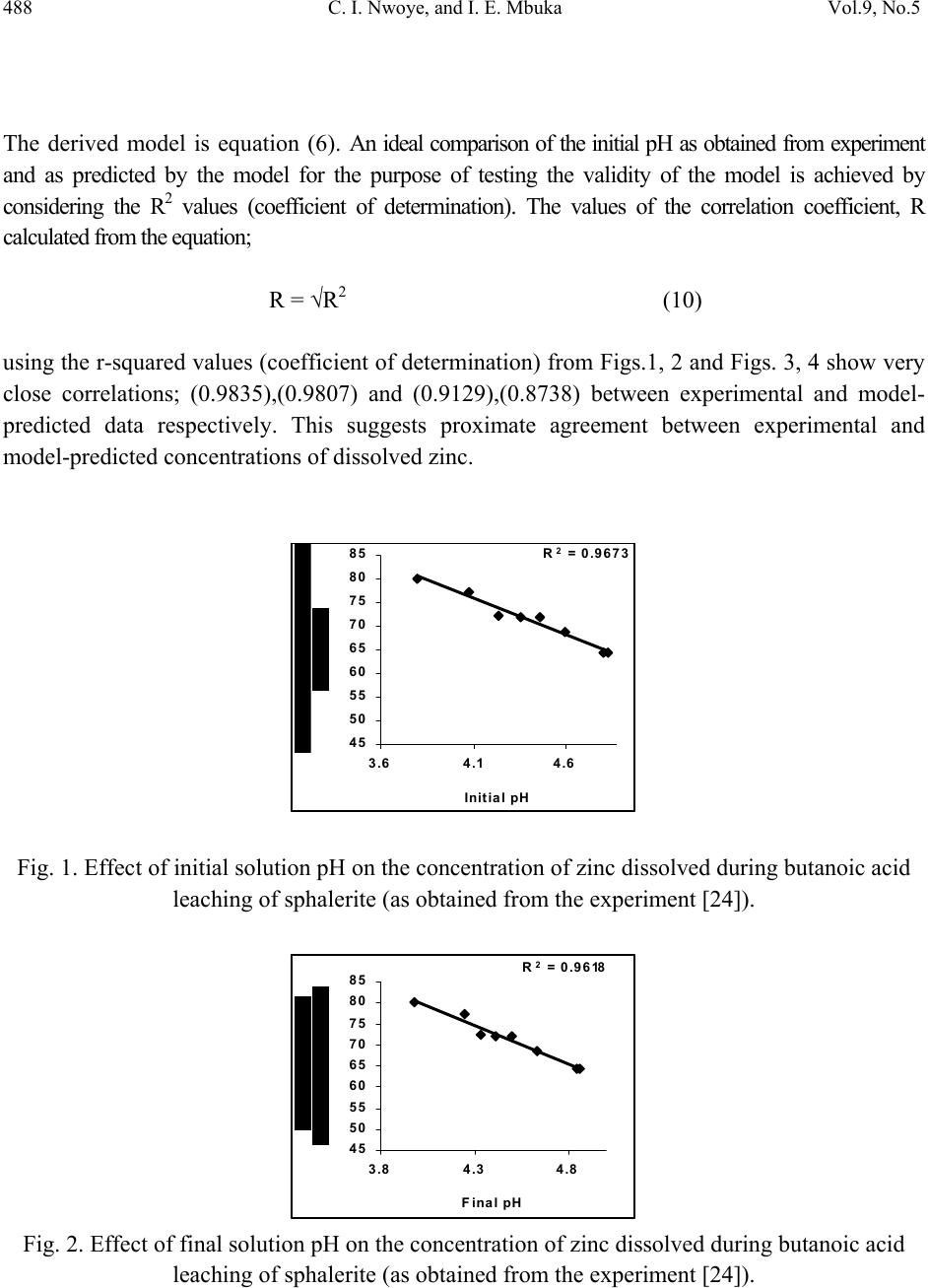

488 C. I. Nwoye, and I. E. Mbuka Vol.9, No.5
The derived model is equation (6). An ideal comparison of the initial pH as obtained from experiment
and as predicted by the model for the purpose of testing the validity of the model is achieved by
considering the R2 values (coefficient of determination). The values of the correlation coefficient, R
calculated from the equation;
R = √R2
(10)
using the r-squared values (coefficient of determination) from Figs.1, 2 and Figs. 3, 4 show very
close correlations; (0.9835),(0.9807) and (0.9129),(0.8738) between experimental and model-
predicted data respectively. This suggests proximate agreement between experimental and
model-predicted concentrations of dissolved zinc.
R
2
= 0.9673
45
50
55
60
65
70
75
80
85
3.64.1 4.6
Initial pH
Fig. 1. Effect of initial solution pH on the concentration of zinc dissolved during butanoic acid
leaching of sphalerite (as obtained from the experiment [24]).
R
2
= 0.9618
45
50
55
60
65
70
75
80
85
3.84.3 4.8
F inal pH
Fig. 2. Effect of final solution pH on the concentration of zinc dissolved during butanoic acid
leaching of sphalerite (as obtained from the experiment [24]).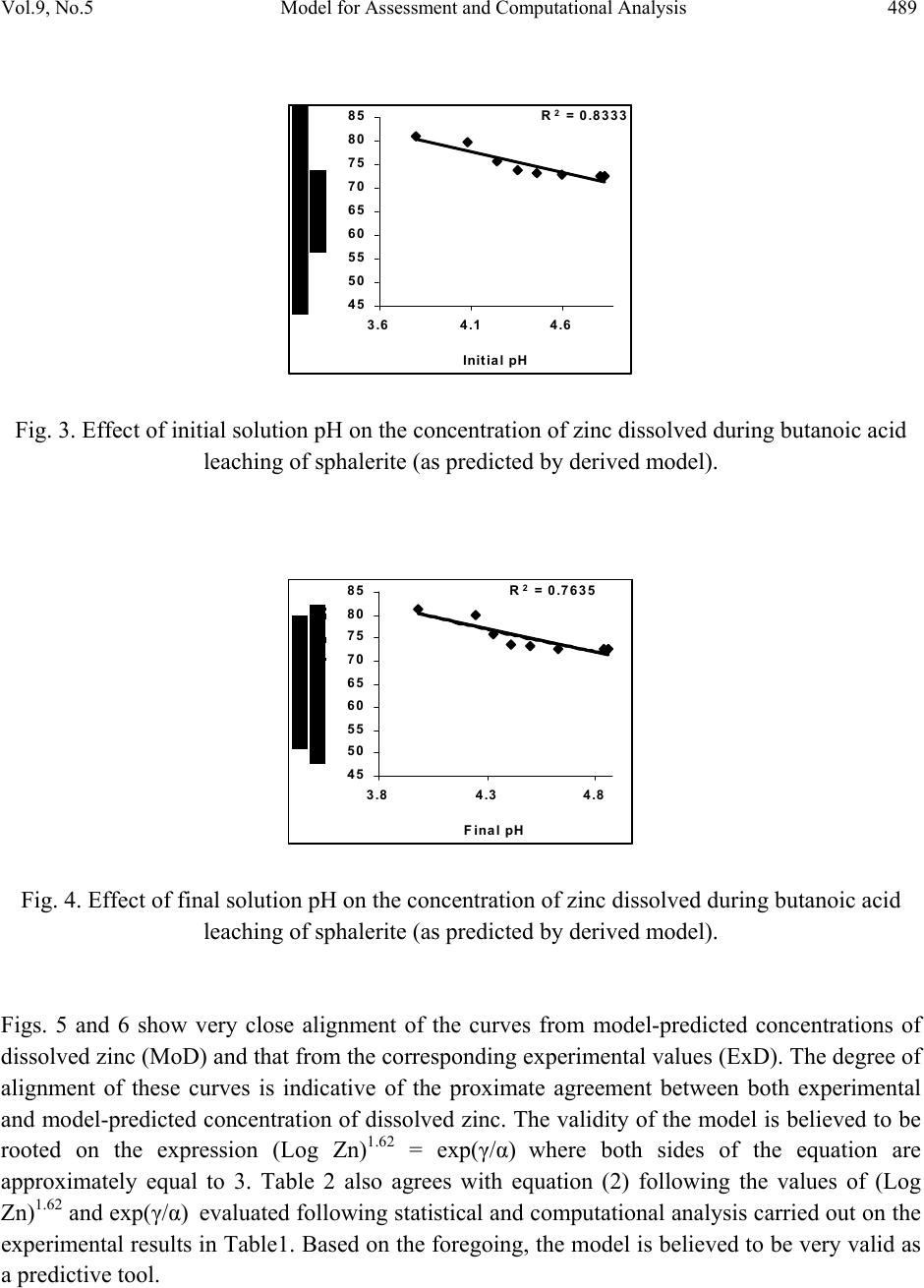

Vol.9, No.5 Model for Assessment and Computational Analysis 489
R
2
= 0.8333
45
50
55
60
65
70
75
80
85
3.64.1 4.6
Initial pH
Fig. 3. Effect of initial solution pH on the concentration of zinc dissolved during butanoic acid
leaching of sphalerite (as predicted by derived model).
R
2
= 0.7635
45
50
55
60
65
70
75
80
85
3.84.3 4.8
F inal pH
Fig. 4. Effect of final solution pH on the concentration of zinc dissolved during butanoic acid
leaching of sphalerite (as predicted by derived model).
Figs. 5 and 6 show very close alignment of the curves from model-predicted concentrations of
dissolved zinc (MoD) and that from the corresponding experimental values (ExD). The degree of
alignment of these curves is indicative of the proximate agreement between both experimental
and model-predicted concentration of dissolved zinc. The validity of the model is believed to be
rooted on the expression (Log Zn)1.62 = exp(γ/α) where both sides of the equation are
approximately equal to 3. Table 2 also agrees with equation (2) following the values of (Log
Zn)1.62 and exp(γ/α) evaluated following statistical and computational analysis carried out on the
experimental results in Table1. Based on the foregoing, the model is believed to be very valid as
a predictive tool.

490 C. I. Nwoye, and I. E. Mbuka Vol.9, No.5
45
50
55
60
65
70
75
80
85
3.64.1 4.6
Initial pH
Ex
MoD
Fig. 5. Comparison of the concentrations of dissolved zinc relative to the initial solution pH as
obtained from experiment [24] and derived model.
45
50
55
60
65
70
75
80
85
3.8 4.3 4.8
F inal pH
Ex
MoD
Fig. 6. Comparison of the concentrations of dissolved zinc relative to the final solution pH as
obtained from experiment [24] and derived model.
Table 3 shows insignificant positive and negative deviations of the model-predicted
concentration of dissolved zinc from the corresponding experimental values, which were less
than 14%, hence quite within the acceptable deviation limit of experimental results. The least and
highest magnitude of deviation of the model-predicted concentration of dissolved zinc (from the
corresponding experimental values) are +1.41% and +13.08%.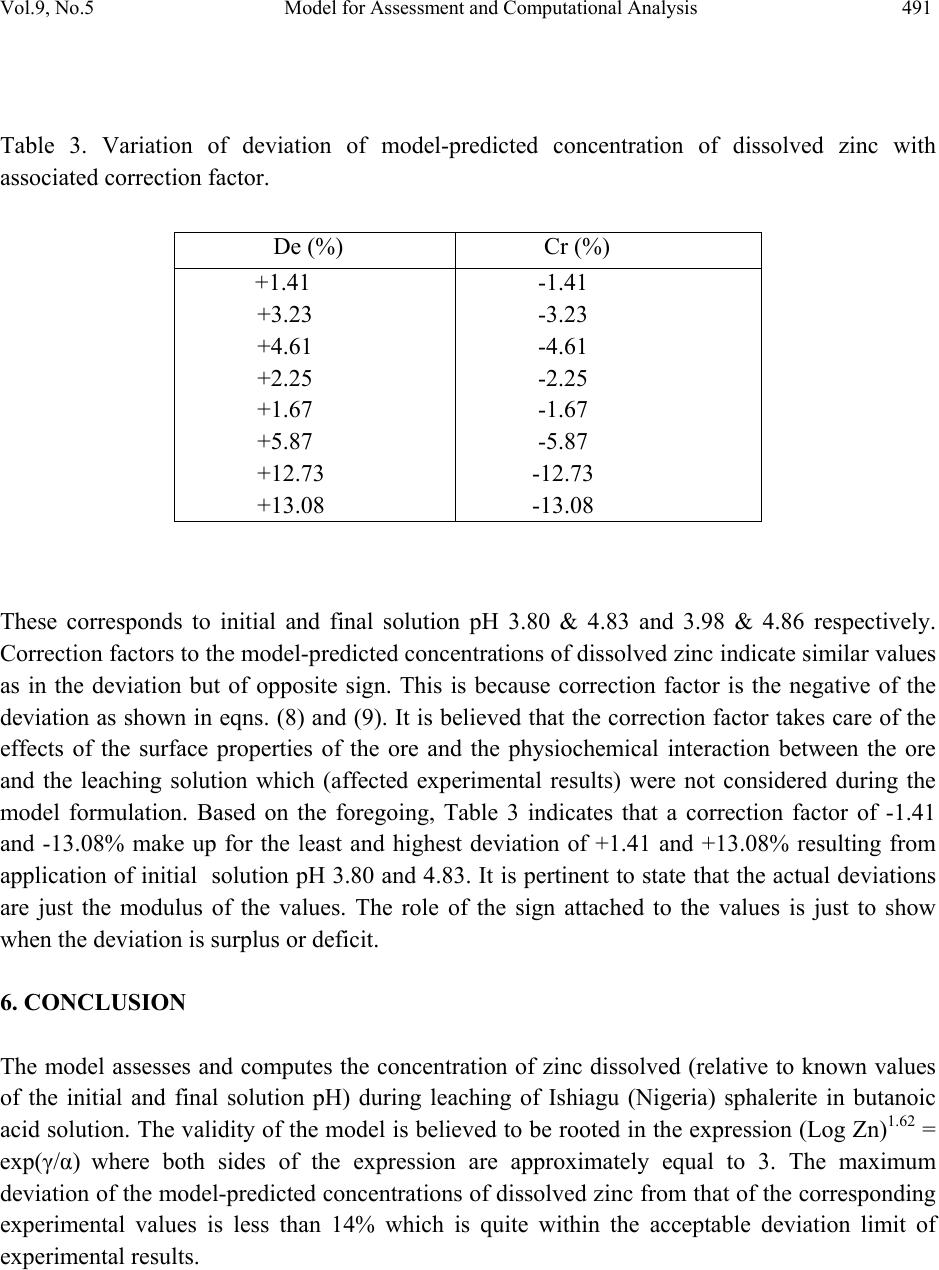

Vol.9, No.5 Model for Assessment and Computational Analysis 491
Table 3. Variation of deviation of model-predicted concentration of dissolved zinc with
associated correction factor.
These corresponds to initial and final solution pH 3.80 & 4.83 and 3.98 & 4.86 respectively.
Correction factors to the model-predicted concentrations of dissolved zinc indicate similar values
as in the deviation but of opposite sign. This is because correction factor is the negative of the
deviation as shown in eqns. (8) and (9). It is believed that the correction factor takes care of the
effects of the surface properties of the ore and the physiochemical interaction between the ore
and the leaching solution which (affected experimental results) were not considered during the
model formulation. Based on the foregoing, Table 3 indicates that a correction factor of -1.41
and -13.08% make up for the least and highest deviation of +1.41 and +13.08% resulting from
application of initial solution pH 3.80 and 4.83. It is pertinent to state that the actual deviations
are just the modulus of the values. The role of the sign attached to the values is just to show
when the deviation is surplus or deficit.
6. CONCLUSION
The model assesses and computes the concentration of zinc dissolved (relative to known values
of the initial and final solution pH) during leaching of Ishiagu (Nigeria) sphalerite in butanoic
acid solution. The validity of the model is believed to be rooted in the expression (Log Zn)1.62 =
exp(γ/α) where both sides of the expression are approximately equal to 3. The maximum
deviation of the model-predicted concentrations of dissolved zinc from that of the corresponding
experimental values is less than 14% which is quite within the acceptable deviation limit of
experimental results.
De (%) Cr (%)
+1.41
+3.23
+4.61
+2.25
+1.67
+5.87
+12.73
+13.08
-1.41
-3.23
-4.61
-2.25
-1.67
-5.87
-12.73
-13.08

492 C. I. Nwoye, and I. E. Mbuka Vol.9, No.5
ACKNOWLEDGEMENT
The author thanks Dr. Ekeme Udoh and Pearl Bassey, modelling experts at Linkwell Modelling
Centre Calabar for his technical inputs. The management of SynchroWell Nig. Ltd. Enugu is also
appreciated for permitting and providing the experimental data used in this work.
REFERENCES
[1] Bogue, R.G., Reynolds, R.R. (1951) Report on the Lead-Zinc Deposits of the Abakiliki
District Ogoja Province, Nigeria (unpublished manuscripts).
[2] Udum, J.T., (1998) Beneficiation Studies of Ishiagu Pb – Zn ore Trans SME/AIME 24(1):
500
[3] Okoro, C.C. (2004) Hydrometallurgical Extraction of Lead from Ishiagu Galena, B. Eng.
Project Materials and Metallurgical Engineering Dept., Federal University of Technology
Owerri.
[4] Onyemaobi, O. O.(1990) Evaluation of Flotation Performance of Nigeria’s Sphalente (ZnS)
Without Activation by copper. Ife Journal of Tech. 2(2):21-25.
[5] Onyemaobi, O.O. Anyakwo, C.N. (1996) Factors Affecting the Performance of Nigeria’s
Lead and Zinc Ores for Industrial Usage JSET, 3(1): 46.
[6] Onyemaobi, O.O. (1990) Flotability of Ishiagu Galena as Raw Materials for Smelters.
Nigeria Journal of Applied Science 8 (1): 93-101.
[7] Agha, U.H. (1990) Role of PH on Flotation of Sphalerite from Ishiagu Lead-Zinc Ore,
Nigeran Journal of Applied Science 2 (2):4-6.
[8] Olubambi, P.A, Ndlovu, S., Potgieter, H., Borode, J.O. (2007) Effects of Ore Mineralogy on
the Microbial Leaching of Low Grade Complex Sulphide Ore. Hydrometallurgy 86: 96-104.
[9] Olubami, P.A., Borode, J.O., Ndlovu, S. (2006) Sulphuric Acid Leaching of Zinc and Copper
from Nigerian Complex Sulphide Ore in the Presence of Hydrogen Peroxide. Journal of the
Southern African Inst. Of Mining and Metallurgy 106: 765-769.
[10] Nwoye, C. I. (2008) Ph.D Thesis, Metallurgical and Materials Engineering Department,
Federal University of Technology, Owerri,178.
[11] Haver, F.P., Wong, M. M. (1971) Recovering Elemental Sulfur from Non-Ferrous Minerals.
Rep.Invest. U.S Bur. Mines 7474,20 in Orlowska L and Golab B; Microbial Leaching
of Blende Flotation Concentrate using Acidithiobacillus Ferrooxidans and Acidithiobacillus
Thiooxidans Physicochemical Problems of Mineral processing 37,1990,58.
[12] Sklodowska, R. (1990) Microbial Leaching of Blende Flotation Concentrate using
Acidithiobacillus Ferrooxidans and Acidithiobacillus Thiooxidans; Physico Chemical
Problems of Mineral Processing 37:58.
[13] Cwalina, W. (1994) Microbial Leaching of Blende Flotation Concentrate using

Vol.9, No.5 Model for Assessment and Computational Analysis 493
Acidithiobacillus Ferrooxidans and Acidthiobacillus Thiooxidans Physicochemical
Problems of Mineral Processing 37:58.
[14] Makita, M., Esperon, M., Pereyra, B., Lopez, A., Orrantia, E. (2004) Reduction of Arsenic
Content in a Complex Galena Concentrate by Acidithiobacillus Ferrooxidans; BioMed
Central Biotechnology, 4:22 doi: 10.1186/1472-6750-6750-4-22 (published on line)
[15] Williamson, S., Rimstidt, M., Smith, T., Schumate, H. (2005) Rates of Leaching in Single
and Two Phase System. Min. mag., 3
[16] Prosper, I. (2005) Acid leaching of lead sulphide, J. Med. Central. 3(4):13-16.
[17] Rawlings, D.E. (2005) Characteristics and Adaptability of Iron and Sulphur Oxidizing
Microorganisms Used for the Recovery of Metals from Minerals and Their Concentrates,
Bio Med Central, 4:13 doi 10:1186/1475-2859-4-13 (published on line)
[18] Dutrizac, J.E. (1986) The Dissolution of Galena in Ferric Chloride Media, Metallurgical
Transactions B, 17B: 77.
[19] Seon-Hyo, K. K., Henein, H., Warren, G.W (1986) An Investigation of the
Thermodynamics and Kinetics of the Ferric Chloride Brine Leaching of Galena
Concentrate. Metallurgical Transaction B, 17B:26.
[20] Dix, R.B., Hendrix, J. L. (1986) Kinetics of Cl2-O2 Leaching of Lead–Zinc Flotation
Concentrates. University of Nevada Reno, 89557
[21] Pinches, A. (1975) Bacterial Leaching of an Arsenic Bearing Sulphide Concentrate. The
Institute of Mining and Metallurgy, England, 34.
[22] Nwoye, C. I. (2008) SynchroWell Research Work Report, DFM Unit, No 2008600, 15-28.
[23] Nwoye, C. I. (2009) Model for Predicting the Initial Solution pH at Pre-Assumed Final pH
and Concentration of Dissolved Zinc during Leaching of Galena in Butanoic Acid Solution.
Journal of Minerals, Material Characterization & Engineering,8(8):621-633.
[24] Nwoye, C. I. (2006) SynchroWell Research Work Report, DFM Unit, No 20061103, 56-64.