Paper Menu >>
Journal Menu >>
 Journal of Minerals & Materials Characterization & Engineering, Vol. 9, No.5, pp.411-426, 2010 jmmce.org Printed in the USA. All rights reserved 411 Solubility of Supercritical CO2 in Polystyrene during Foam Formation via Statistical Associated Fluid Theory (SAFT) Equation of State Brian A. Ott and G. Caneba* Department of Chemical Engineering, Michigan Technological University *Corresponding Author: caneba@mtu.edu ABSTRACT The use of supercritical fluids, such as CO2, for polymer foam formation has become popular in the last decade. These physical blowing agents are environmentally responsible, and are able to provide certain processing advantages during foam formation. In order to be able to understand foam formation under relatively high pressures and temperatures, thermodynamic phase equilibrium analysis is required coupled with a good equation of state. The Statistical Associated Fluid Theory (SAFT) equation of state (EOS) is studied in detail for the carbon dioxide/polystyrene system, under supercritical CO2 conditions. The SAFT EOS is found to perform better than the Soave-Redlich-Kwong (SRK) EOS, especially when considering liquid phase compositions and densities. Experimental data from the literature is used to validate model parameters cited in the literature for polystyrene-CO2 binary systems under supercritical conditions. The analysis is done with the assumption that the vapor phase is pure CO2 and in equilibrium with the liquid CO2-polystyrene condensed phase. Keywords: Carbon dioxide, polystyrene, SAFT, polymer foams, supercritical fluid 1. INTRODUCTION In the last decade, there has been a n i nter est developed in the use of supercritical fluids, such as CO2, for the formation of polymer foams. Unlike chemical blowing agents (CBAs) added conveniently into the polymer formulation and subsequently produces a gas during polymer processing, the use of supercritical fluid has become very attractive. Technically, these  412 Brian A. Ott and G. Caneba Vol.9, No.5 supercritical fluids used for foam formation fall under physical blowing agents, which includes pentane and Freons® fo r polystyrene and other th ermoplastic polymers. Many physical blowing agents (PBAs) in polymer foams tend to be environmentally undesirable and highly volatile, and the y a re implicated in various health and environment concerns. An example are the group of chlorofluorocarbons (CFCs) used in the production of a large range of foam products, including the heat shielding foam on the Space Shuttle’s External fuel tank. CFCs were banned in the 1990’s from use due to their proven destruction of the Earth’s ozone layer. Foams produced using chemical blowing agents tend to have a relatively long set-up time, i.e., it takes awhile for the foam to firm up. The chemical reaction proceeds more slowly as more solid polymer is produced; initially producing a foam e d product that is tacky to the touch until the reactants have reacted more fully, which can take over an hour in the case of household insulators. Investigation into non-toxic PBAs has focused on common gases such as Nitrogen (N2) and carbon dioxide (CO2) [1]. These molecules are smaller than conventional PBAs, are non-toxic, and carry a much lower environmental impact. Although some caution is taken with respect to carbon dioxide and its status as a greenhouse gas, it is noted that the polyurethane foam discussed above also produces carbon dioxide and the un-reacted parts of polyurethane are more toxic and cause an irritating odor upon application. Instead of dissolving the polymer in a solvent, such as polystyrene dissolved in aceto ne , the gases (N2 or CO2) could be dissolved into the polymer under supercritical conditions for the gas. Elevated pressures are required to condense the gas into liquid form and the temperature may be adjusted above or below the critical temperature. Although polyst y r e n e can completely dissolve in acetone at room temperature and atmospheric pressure, the amount of CO2 readily dissolving into polystyrene at these conditions is negligible. In general, an increase in pressure and a decrease in temperature will increase the solubility of the gas in the polymer. Once the polymer has been adequately saturated with the supercritical fluid PBA, the pressure can be released and the drop in pressure will cause the gas to evaporate and phase separate, foaming the polymer. Higher concentrations of dissolved gas will result in a foam with a higher expansion ratio. The temperature at which the pressure is released also has an impact on the product foam. If the foaming temperature is below the effective glass transition temperature of the mixture, the polymer will be too glassy to foam significantly. However, if the polymer- supercritical fluid is above its effective glass transition tem p era ture, then the rubbery nature of the foam will allow it to expand under the pressure of the escaping gas. Experimental methods can be costly and time consuming due to the high pressure equipment involved in saturation exper iments and the time it can take for a gas to diffuse into the polymer. Mathematical modeling can aide in understanding the effects pressure and temperature has on  Vol.9, No.5 Solubility of Supercritical CO2 in Polystyrene 413 these three areas. Although n ot expected to be a replacement for experimentation, modeling results are used as a starting point for experimentation, resulting in the reduction of the number of experiments nee ded to be carried out, and thus reducing the operationa l costs and time. The saturation of a polymer with a gas is a thermodynamic phase equilibrium problem. Many equation of state (EOS) models of varying complexity have been tested [2]. These models take advantage of either adjustable parameters to best fit exper i mental data or models based on first principles that can use properties of substances, such as critical pressure, Pc, and critical temperature, Tc, to model thermodynamic behavior. Simpler models tend to be applicable to noninteracting or symmetrically interacting systems, such as Henry’s law used for dilute simple solutes in solvents; while more complex models tend to be applicable to more complicated and macromolecular systems. Polymer systems tend to be among the most complex systems to model due to the large size and distribution of the molecular weight of the polymer, interactions between side groups of the polymer, and their inability to exist in a vapor state since they will thermally decompose before the temperature becomes hot enough for them to vaporize. An EOS that has shown promise for modeling polymer/gas systems with minimum adjustable parameters is the Statistical Associated Fluid Theory (SAFT) [3-12]. This publication revolves around the implementation of the SAFT EOS for fluid phase equilibrium calculations, or as in the polymer/gas system the saturation limit of the gas in th e p oly mer. The foregoing results of the use of the SAFT EOS for CO2-polystyrene system show good agreement with experimental data, without having to use any adjustable parameter. 2. PHASE EQUILIBRIUM For a system to be considered in thermodynamic equilibrium, the temperature and pressure of each phase as well as the component fugacity of each phase must be equal [2]. This set of equalities is expressed in Equations 1-3. (1) (2) (3) Here, P is the pressure (bar), T is the tempe rat ur e (K ), a nd f is the fugacity (bar). Superscripts, and , denote the pha s e s, w hile the su bscript, , denotes the components. The fugacity of each component is expressed in Equations 4 and 5 for the liquid and vapor phases, respectively. The fugacity represents the ch emical potential of a system in terms of partial pressure. (4) (5)  414 Brian A. Ott and G. Caneba Vol.9, No.5 where represents the fugacity coefficient, t he superscripts, L and V, denote the liquid and vapor phases, respectively, and liquid and vapor mole fractions are expressed by and , respectively. The fugacity accounts for deviations from a pure component system of an ideal gas. In a single component system containing an ideal gas, the mole fraction, , and fugacity coefficient, , would be equal to 1. The chemical potential between two states can be expressed by partial derivatives of the Gibbs energy and Helmholtz energy as shown in Equation 6. ,, ,, (6) An appropriate equation of state must be chosen to apply to the evaluation of the expressions for the chemical potential as shown in Equation 6. The SAFT EOS has been developed as an expression for the residual Helmholtz energy. 3. SAFT EOS The residual Helmholtz energy as defined by the SAFT EOS uses up to 5 adjustable parameters: , /, and ∞ for all molecules and and for self-associating molecules. The total residual Helmholtz energy is expressed in Equation 7. The equations presented are for multiple component systems, while pure component derivations are available in literature[11]. (7) where, ares - total residual Helmholt z e ne r g y . ahs - hard sphere contribution to the residual Helmholtz energy. achain - chain contribution to the residual Helmholtz energy. aassoc - association contribution to the res idual Helmholtz e nergy. adisp - dispersion force contribution to the residual Helmholtz energy. The development of the SAFT equations used in this paper is based on prior works in the field [3-16]. Two separate mixing rule conventions are used: van der Waal’s one-fluid (vdW1) mixing rules used for low pressure systems, and volume fraction (vf) mixing rules for use in high pressure systems near the critical point. Also, the paramerization of Huang and Radosz [13] is used with the above-mentioned mixing rules. 3.1. Expression for Compressibility Factor, Z SAFT, a pressure explicit EOS, is used in the derivation of important thermodynamic properties. A pressure explicit EOS is capable of determining multiple densities at a single pressure for a  Vol.9, No.5 Solubility of Supercritical CO2 in Polystyrene 415 specific composition and temperature, as opposed to a volume specific EOS which can solve for only one density for a given pressure. This is important for phase equilibrium problems since in the 2-phase L+V region, there are two dis t i n ct densities, and , for a specified pressure. In other words, when system pressure and temperature are specified, an appropriate EOS must be able to determine phase compositions, and , as well as both phase densities, and . A pressure explicit EOS is w r i t t e n i n t he form of Equation 8. ,, (8) The over bar on the composition, , denotes a vector of all the components’ mole fractions. In this form, density, temperature, and mole fraction are the independent variables. The SAFT EOS calculates the reduced residual Helmholtz energy, , with the same independent variables. ,, (9) where N is the total number of moles and R is the ideal gas constant. The compressibility factor, Z, is defined in Equation 10 and related to by Equation 10. ,, ,, (10) ,, 1 , (11) In Equation 11 the partial of with respect is taken at constant temperature and composition. 3.2. Expression for Fugacity Coefficient, An expression for the fugacity coefficient, , is needed for each component and each phase of the system in order to so lve phas e equilibrium problems through Equations 1-5. An expression for the fugacity coefficient has been developed by Prausnitz [2] as a function of the reduced residual Helmholtz energy, , and is expressed in Equation (12). ,, 1 (12) The partial derivative with respect to is taken at constant density, temperature, and holding all other components constant. For a single component system, Equation 12 reduces to the form in Equation 13. 1 (13)  416 Brian A. Ott and G. Caneba Vol.9, No.5 Rowlinson and Swinton [16] developed a method to express partial derivatives with respect to the number of moles of a component, /, in terms of partial derivatives with respect to mole fraction, /, that includes both the independent mole fractions, and the dependant mole frac t i o n , . In most texts, a capital D is used to express this Rowlinson- Swinton (RS) partial differential operator, but a script-D, , will be used here as to not to confuse it with the parameter D used in the Huang-Radosz parameterization scheme. For a system of m components, there are m-1 independent mole fractions and one mole fraction dependent on the values of all others through Equation 14. For convenience, the dependent mole fraction will be component 1. 1 (14) The only restraint on the other mole fraction is that their value exist between 0 and 1, or 0 1. An in depth derivation of the RS partial differential is given in literature, but the important result of the relationship betwee n and is shown in Equation 15. ,, ,, ,, (15) The variable q represents any intensive property on a per mole basis for which q=Q/N is true, where N is the total number of moles of the system and Q is the intensive property, such as volume. Before applying the RS partial differential operator, the first term on the right hand side of Equation 12 is partially evaluated in Equation 16. ,, ,, (16) The righthandside partial differential operator is now applied to the second term on the righthandside of Equations 16 and 17. ,, – (17) The subscript denotes summation over all parameters A through H and the subscript , is for all components 1 through m. The result is the final expression for the fugacity coefficient, , as shown in Equation 18.  Vol.9, No.5 Solubility of Supercritical CO2 in Polystyrene 417 – 1 (18) or short-hand form as 1 (19). For a two-component or binary system 1 (20) 1 (21) Upon inspection, all parameters are functions of mole fraction, so Equations 20 and 21 do not simplify any further. However, one can reduce the number of calculation steps by observing that you can rewrite part of these equations in the form provided in Equation 22. (22) Equations 20 and 21 es tablish the fugacity coe fficient, , as a function of density, temperature, and composition. With the SAFT EOS which is a complicated function of composition, this is done by assuming values of x1 in order to determine ρ, P, and finally i and fi [17]. 3.3. Equilibrium Composition Solver The equilibrium composition solver program uses data from the fugacity vs. mole fraction. The solution of the equilibrium compositions occurs when the ratio of mole fractions, , is equal to the ratio of fugacity coefficients, for all components as shown in Equation 23. 0 (23) An exact solution to Equation 23 for both components would t a k e a n in f i n i t e nu mber of iterations to determine; therefore a value greater than zero is a c c e p t a ble as long as the equilibrium mole fractions are accurate to an acceptable number of significant digits. For a binary system, the function expressed in Equation 24 is used to accurately determine the equilibrium compositions.  418 Brian A. Ott and G. Caneba Vol.9, No.5 (24) In Equation 24, the fu nction, , is the sum of the absolute value of Equation 23 for both components. Instead of equating them to 0, however their su mmation is calculated and if the value is less than a pre-determined acceptable tolerance, , the solution has been found. The smallest possible value of is set at 10 since MatLab is limited to the d ouble-precision accuracy of 16 significant digits. 4. RESULTS Results of all SAFT EOS predictions involving CO2 are shown here. For single-component systems, saturation pressure and phase densities calculated from the SAFT EOS are compared to experimental data. For the binary systems, phase densities and mole fractions calculated from the SAFT EOS are compared to experimental data. Also, for binary systems, SAFT EOS results are compared to the Soave-Redlich-Kwang (SRK) EOS. 4.1. Pure Component CO2 System Since carbon dioxide will be used in the carbon dioxide/polystyrene system, an investigation into SAFT’s capabilities for modeling CO2 as a pure component is warranted. The SAFT EOS program calculates saturation pressures, , and phase densities, and , over a range of temperatures up to the critical temperature for carbon dioxide, = 30.1 oC. The single component system calculates the fugacity coefficient for each phase, and for a specific temperature and over a r ang e of pressures using de ns it i es t ha t are interpolated from th e curve. Figure 1 shows the liquid and vapor phase fugacity coefficients as a function of pressure at a temperature of -13 oC. The pressure at which the two fugacity curves intersect is the saturation pressure, at the specified temperat ure . Figure 2 shows a plot of the saturation pressure as a function of temperature for both the SAFT EOS model and experimental data taken from literature. Notice that as the temperature approaches the critical temperature for carbon dioxide, the SAFT EOS model diverges from the experimental data, underpredicting th e s a turation pressure. Th e divergence of the model from the experimental data is c ommon for all EOS as the temperature approaches the critical temperature. Th e experimental data was taken from Vargaftik [18] and the SAFT parameters were taken from Huang and Radosz [11]. The density of each phase is also plotted as a function of temperature for both the SAFT EOS model and the experimental data in Figure 3. Notice that at the critical temperature, the vapor 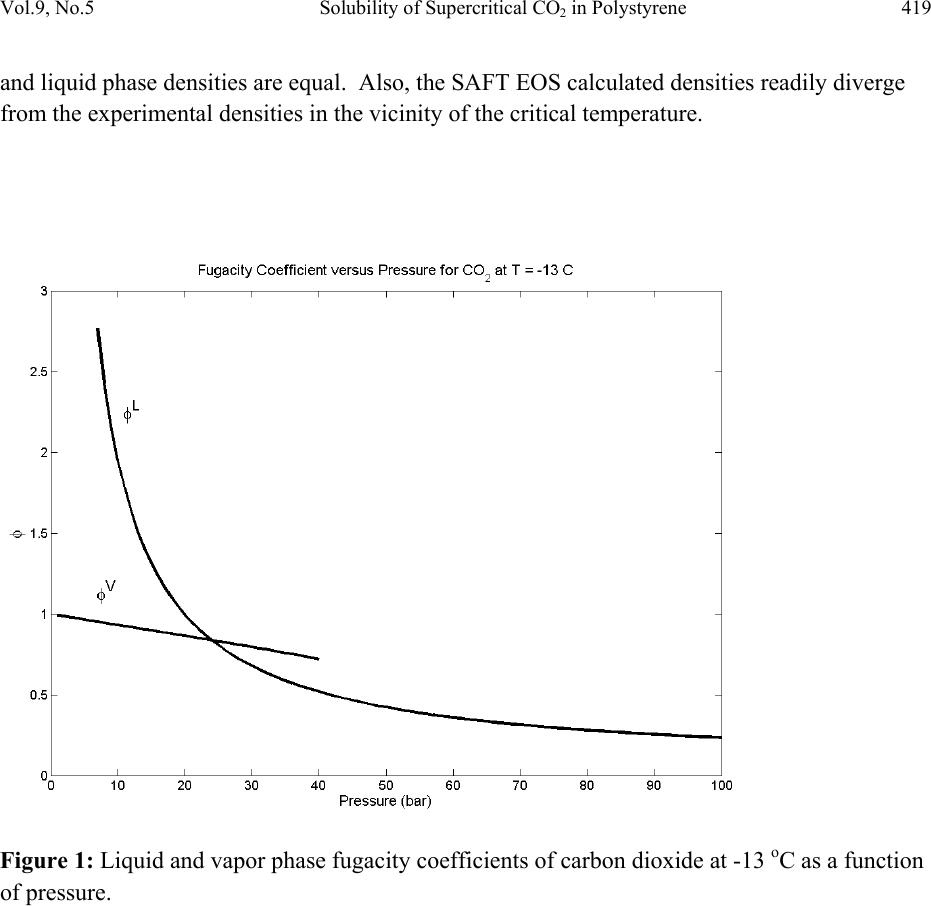 Vol.9, No.5 Solubility of Supercritical CO2 in Polystyrene 419 and liquid phase densities are equal. Also, the SAFT EOS calculated densities readily diverge from the experimental densities in the vicinity of the critical temperature. Figure 1: Liquid and vapor phase fugacity coefficients of carbon dioxide at -13 oC as a function of pressure. 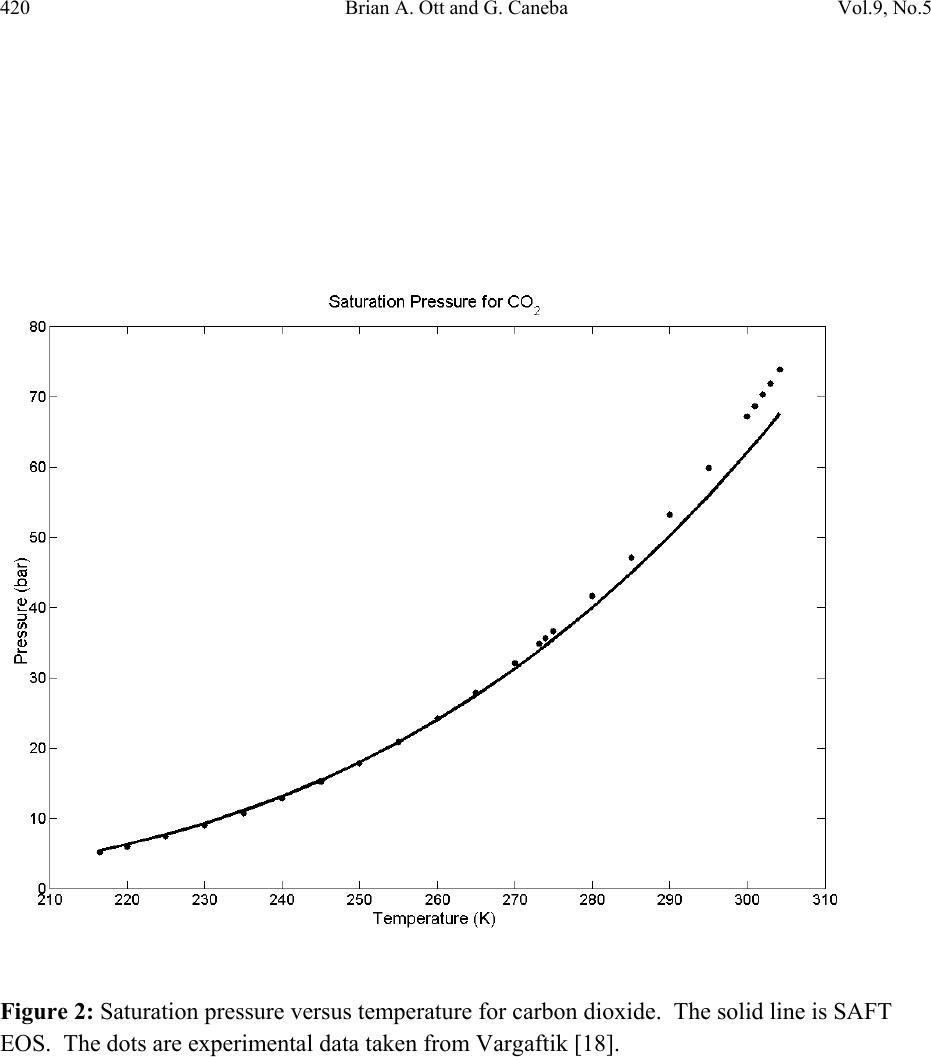 420 Brian A. Ott and G. Caneba Vol.9, No.5 Figure 2: Saturati on p re s s ur e v e r su s te mperature for carbon dioxide. The solid line is SAFT EOS. The dots are experimental data taken from Vargaftik [18].  Vol.9, No.5 Solubility of Supercritical CO2 in Polystyrene 421 Figure 3: Equilibrium liquid and vapor densities versus temperature for carbon dioxide. The solid line is from SAFT EOS. The dots are liqui d and vapor equilibrium densities taken from Vargaftik [18]. The star is the experimental critical density. 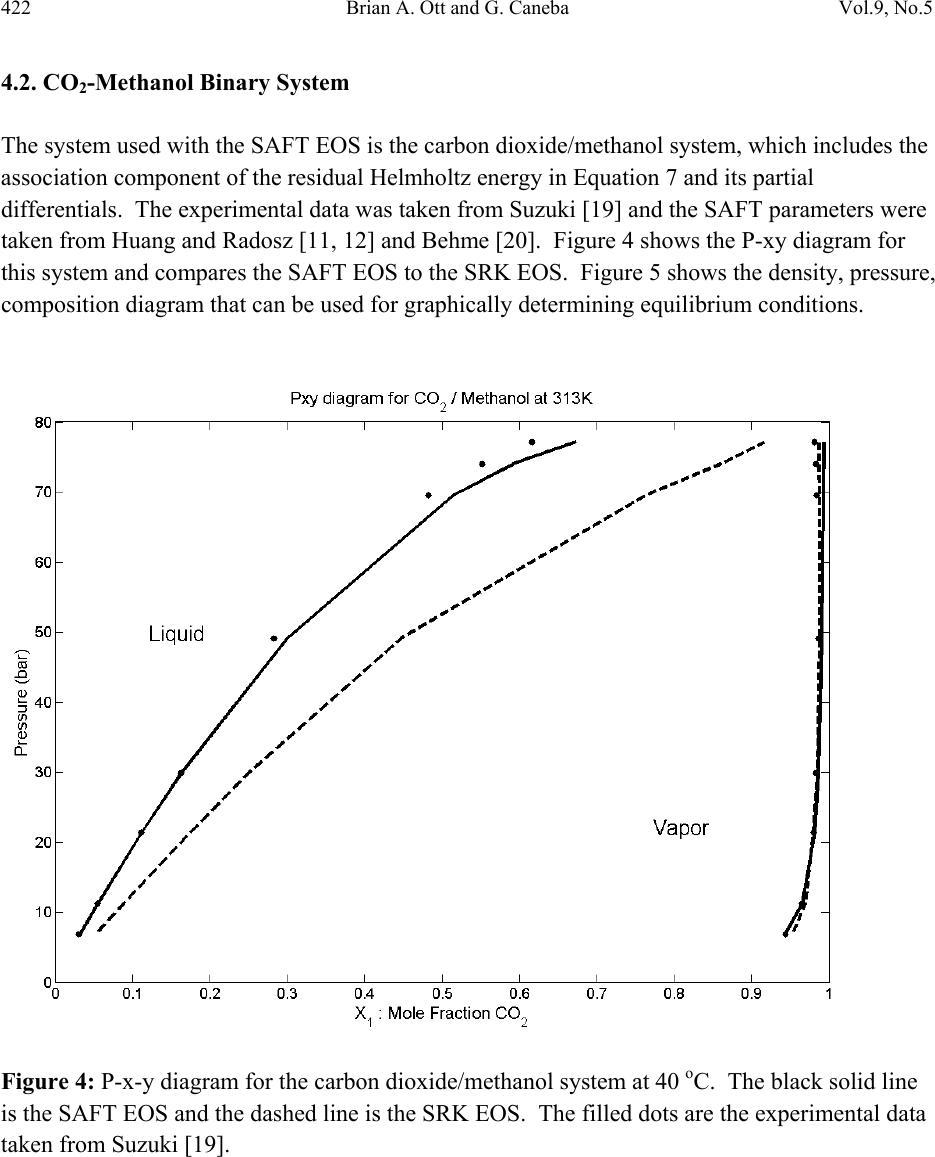 422 Brian A. Ott and G. Caneba Vol.9, No.5 4.2. CO2-Methanol Binary System The system used with the SAFT EOS is the carbon dioxide/methanol system, which includes the association componen t of the re sid ua l H el mholtz energy in Equation 7 and its partial differentials. The experimental data was taken from Suzuki [19] and the SAFT parameters were taken from Huang and Radosz [11, 12] and Behme [20]. Figure 4 shows the P-xy diagram for this system and compares the SAFT EOS to the SRK EOS. Figure 5 shows the density, pressure, composition diagram that can be used for graphically determining equilibrium conditions. Figure 4: P-x-y diagram for the carbon dioxide/methanol system at 40 oC. The black solid line is the SAFT EOS and the dashed line is the SRK EOS. The filled dots are the experimental data taken from Suzuki [19]. 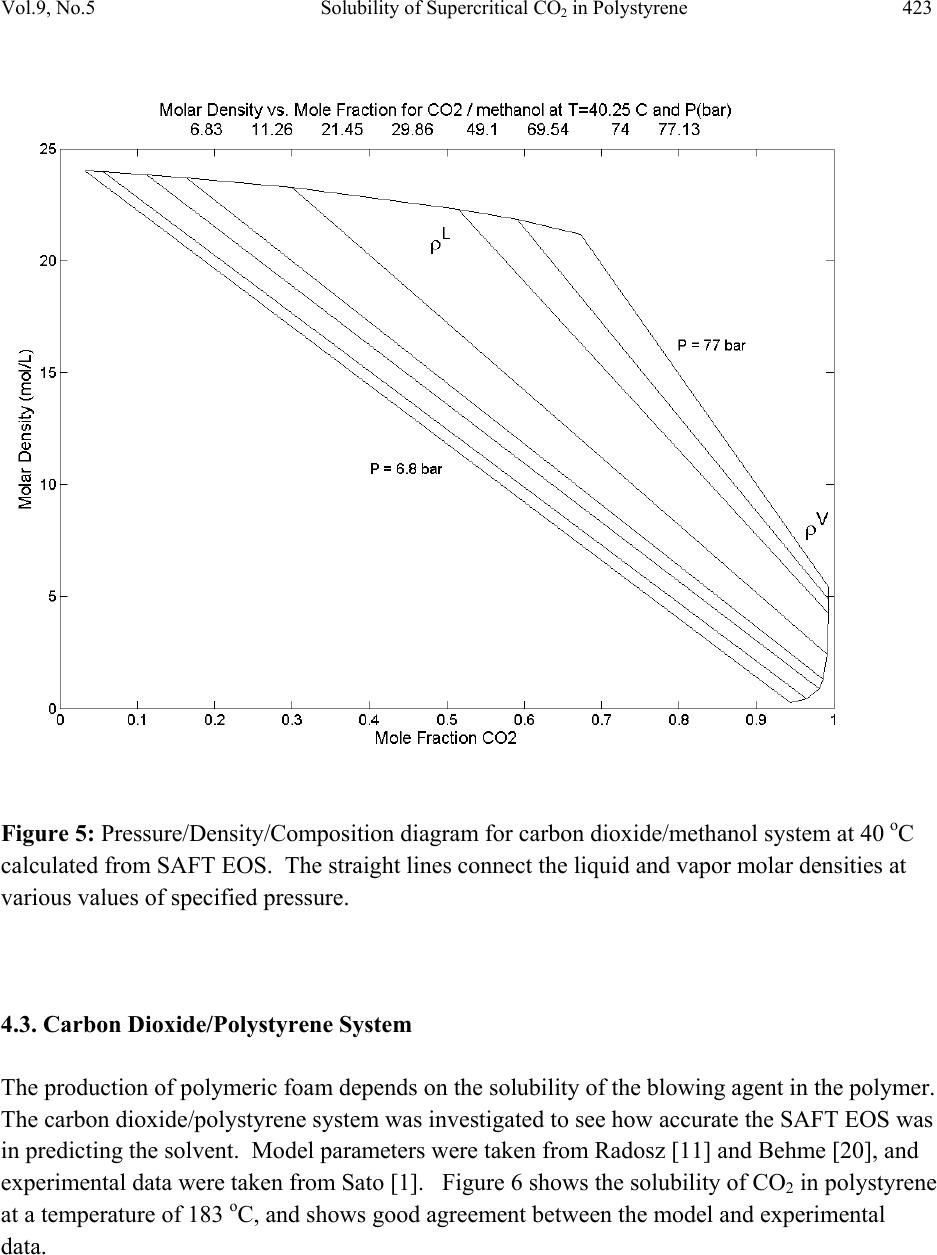 Vol.9, No.5 Solubility of Supercritical CO2 in Polystyrene 423 Figure 5: Pressure/Density/Composition diagram for carbon dioxide/methanol system at 40 oC calculated from SAFT EOS. The straight lines connect the liquid and vapor molar densities at various values of specified pressure. 4.3. Carbon Dioxide/Polystyrene System The production of polymeric foam depends on the solubility of the blowing agent in the polymer. The carbon dioxide/polystyre ne s yst em was investigated to see how accurate the SAFT EOS was in predicting the solvent. Model parameters were taken from Radosz [11] and Behme [20], and experimental data were taken from Sato [1]. Figure 6 shows the solubility of CO2 in polystyrene at a temperature of 183 oC, and shows good agreement between the model and experimental data.  424 Brian A. Ott and G. Caneba Vol.9, No.5 Figure 6: Solubility of carbon dioxide in polystyrene at 453K. The line is SAFT EOS model. The dots are experimental data taken from Sato [1]. The model parameters published in literature were determined by assuming that the vapor phase is pure carbon dioxide. The fugacity of carbon dioxide was determined at 1 and the corresponding composition with the same fugacity was determined for the polystyrene rich phase. The SAFT EOS programs developed models the phase equilibrium of a variety of system with good accuracy for a variety of systems. For the pure component systems, the saturation pressures are calculated with good accuracy up to the vicinity of the critical pressure (Figures 1 and 2), where divergence from experimental data is observed. The equilibrium densities are accurate, but divergence from the experimental data is observed in the vicinity of the critical density (Figure 3). Model divergence in the critical region is common among all equations of state. This can lead to inaccuracies in phase eq ui l ib ri u m composition calculations for binary systems when one or both components are near their critical points. The binary systems display good consistency to experimental data. The liquid phase e quilibrium mole fractions are modeled less accurately than their respective vapor phase mole fractions and  Vol.9, No.5 Solubility of Supercritical CO2 in Polystyrene 425 the SAFT EOS tends to over-predict the peak of the equilibrium curve on the P-x-y diagram (Figure 4). The calculated equilibrium phase densities tend to diverge from the experimental towards the peak pressure as well (Figure 4). The SAFT EOS and the SRK EOS are compared to the experimental data for the CO2-Methanol binary system. Both EOSs correlate the vapor phase compositions, but at as the p re ssure approaches the critical point, the SAFT EOS is more consistent with the experimental data (Figure 4). The SAFT EOS better represents the experim en tal da ta whe n c ons ide rin g t he equilibrium phase densities, especially the liquid phase densities (Figure 4). No experimental data on the equilibrium phase densities for the carbon dioxide/methanol system were available; thus, no comparison was made between the two EOSs for the equilibrium phase densities. Overall, the SAFT E O S performed better than the SRK EOS. Finally, the SAFT EOS has been shown to accurately predict the solubility of carbon dioxide in polystyrene (Figure 6), even at supercritical fluid conditions for the CO2. A caveat is worth mentioning; that the use o f t he SAFT EOS was based on forcing one of the phases to be pure CO2 vapor. This may be true with high molecular weight polystyrene and CO2, but should not be assumed to be generally the case for binary systems. Also, experimental data indicates that this is so [1]. If experiments show the possibility of the existence of two liquid phases as well a vapor phase, then a three-phase analysis would have to be required. This could be done by extending Equations 1-5 to three phases in equili brium, although i t i s n o t c le a r h ow the SAFT EOS will predict the composi t i o ns of the two liquid phases. 5. CONCLUSION The SAFT EOS model has been developed that can accurately predict phase equilibrium compositions and densities for a various CO2-based pure component and binary systems, culminating in the CO 2-polystyrene system. This model can be used to determine the SAFT EOS parameters for pure substances. Additionally, the model can be used to predict phase equilibrium properties for systems at relatively high pressures and temperatures at which no equilibrium data is available, using a minimum of fitting parameters. REFERENCES 1. Sato, Y., et al., Solubilities of carbon dioxide and nitrogen in polystyrene under high temperature and pressure. Fluid Phase Equilibria, 125, (1996), 129. 2. Prausnitz, J.M., R.N. Lichtenthaler, and E.G. de Azevedo, Molecular Thermodynamics of Fluid-Phase Equilibria. 3rd ed. 1999, Prentice Hall, Upper Saddle River, NJ. 3. Dolezalek, F., Zur Theorie der binaren Gemische und konzentrierten Losungen. Z. Phys. Chem., 64, (1908), 727.  426 Brian A. Ott and G. Caneba Vol.9, No.5 4. Carnahan, N.F. and K.E. Starling, Equation of State for Nonattracting Rigid Spheres. The Journal of Chemical Physics,. 51(2), (1969), 635. 5. Beret, S. and J.M. Prausnitz, Perturbed Hard-Chain Theory: An Equation of State for Fluids Containing Small or Large Molecules. AIChE Journal, 21(6), (1975) 1123. 6. Wertheim, M.S., Fluids with Highly Directional Attractive Forces. I. Statistical Thermodynamics. Journal of Statistical P hy s ic s, . 35(1), (1984) 19. 7. Wertheim, M.S., Fluids with Highly Directional Attractive Forces. II. Thermodynamic Perturbation Theory and Integral Equations. Journal of Statistical Physics, 35(1), (1984), 35. 8. Wertheim, M.S., Fluids with Highly Directional Attractive Forces. III. Multiple Attraction Sites. Journal of Statistical Physics,. 42(3), (1986) 459. 9. Wertheim, M.S., Fluids with Highly Directional Attractive Forces. IV. Equilibrium Polymerization. Journal of Statistical Physics, 42(3), (1986), 477. 10. Chapman, W.G., et al., SAFT: Equation-of-State Solution Model for Associating Fluids. Fluid Phase Equilibria,. 52 , (1989), 31. 11. Huang, S.H. and M. Radosz, Equation of State for Small, Large, Polydisperse, and Associating Molecules. Ind. Eng. Chem. Res.,. 29, (1990), 2284. 12. Huang, S.H. and M. Radosz, Equation of State for Small, Large, Polydisperse, and Associating Molecules: Extension to Fluid Mixtures. Ind. Eng. Chem. Res.,. 30(8), (1991), 1994. 13. Chen, S.S. and A. Kreglewski, Applications of the Augmented van der Waals Theory of Fluids. I. Pure Fluids. Berichte der Bunsen-Gesellschalt,. 81(10), (1977), 1048. 14. Topliss, R., Techniques to Facilitate the Use of Equations of State for Complex Fluid- Phase Equilibria. 1985, University of California, Berkeley. 15. Huang, S.H. and M. Radosz, Additions and Corrections. Industrial and Engineering Chemistry, 32, (1993), 178. 16. Rowlinson, J., Swinton, F, Liquids and Liquid Mixtures. 3rd ed. 1982, London: Butterworth Scientific. 17. Ott, B., “Fluid Phase Equilibrium as modeled by the Statistical Associated Fluid Theory (SAFT) Equation of State”, Ph.D. Dissertation, Michigan T echnological University, 2009. 18. Vargaftik, N.B., Tables on the Thermophysical Properties of Liquids and Gases. 1975, Washington, D.C.: Hemisphere Publishing Co. 19. Suzuki, K., et al., Isothermal Vapor-Liquid Equilibrium Data for Binary Systems at High Pressures. Journal of Chemical and Engineering Data, 35, (1990), 63. 20. Behme, S., G. Sadowski, and W. Arlt, Modeling of the separation of polydisperse polymer systems by compressed gasses. Fluid Phase Equilibria, 158-160, (1999), 869. |

