Journal of Minerals & Materials Characterization & Engineering, Vol. 9, No.4, pp.275-319, 2010
jmmce.org Printed in the USA. All rights reserved
275
Characterizing and Modeling Mechanical Properties of Nanocomposites-
Review and Evaluation
Hurang Hua*, Landon Onyebuekea, Ayo Abatanb
aDepartment of Mechanical and Manufacturing Engineering, Tennessee State University,
Nashville, TN 37209, USA
bDepartment of Engineering Technology, Miami University, Hamilton, OH 45011, USA
*Corresponding Author: [e-mail]
ABSTRACT
This paper presents a critical review of the current work of experiment, theory of micro-nano-
mechanics, and numerical analysis on characterizing mechanical properties of nanocomposites.
First, the classifications of nanomaterials are presented. Then nanoindentation testing and the
corresponding finite element modeling are discussed, followed by analytical modeling stiffness of
nanocomposites. The analytical models discussed include Voigt and Reuss bounds, Hashin and
Shtrikman bounds, Halpin–Tsai model, Cox model, and various Mori and Tanaka models. These
micromechanics models predict stiffness of nanocomposites with both aligned and randomly
oriented fibers. The emphasis is on numerical modeling includes molecular dynamics modeling
and finite element modeling. Three different approaches are discussed in finite element
modeling, i.e. multiscale representative volume element (RVE) modeling, unit cell modeling, and
object-oriented modeling. Finally, the mechanism of nanocomposite mechanical property
enhancement and the ways to improve stiffness and fracture toughness for nanocomposites are
discussed.
Key words: Nanocomposites; Mechanical properties; Multiscale modeling; Finite element
analysis (FEA); Object-oriented modeling.
1. INTRODUCTION
Nanoscience and nanotechnology refer to the understanding and control of matter at the
atomic, molecular or macromolecular levels, at the length scale of approximately 1 to 100

276 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
nanometers, where unique phenomena enable novel applications. Nanotechnologies are the
design, characterization, production and application of structures, devices and systems by
controlling shape and size at nanometer scale. According to Braun et al. [1], from 1980s, the
growth of research papers dealing with the prefix called ‘nano’ is exponential. Among all the
work, characterizing and modeling mechanical properties of nanocomposites is one of the most
important subjects.
Nanocomposites are composite materials in which the matrix material is reinforced by one or
more separate nanomaterials in order to improve performance properties. The most common
materials used as matrix in nanocomposites are polymers (e.g. epoxy, nylon, polyepoxide,
polyetherimide), ceramics (e.g. alumina, glass, porcelain), and metals (e.g. iron, titanium,
magnesium).
Nanomaterials are generally considered as the materials that have a characteristic dimension (e.g.
grain size, diameter of cylindrical cross-section, layer thickness) smaller than 100 nm.
Nanomaterials can be metallic, polymeric, ceramic, electronic, or composite. Nanomaterials are
classified into three categories depending on their geometry, as shown in Fig. 1 [2,3]:
1. Nanoparticles: When the three dimensions of particulates are in the order of nanometers,
they are referred as equi-axed (isodimensional) nanoparticles or nanogranules or nanocrystals.
2. Nanotubes: When two dimensions are in the nanometer scale and the third is larger,
forming an elongated structure, they are generally referred as ‘nanotubes’ or
nanofibers/whiskers/nanorods.
3. Nanolayers: The particulates which are characterized by only one dimension in nanometer
scale are nanolayers/nanoclays/nanosheets/nanoplatelets. These particulate is present in the form
of sheets of one to a few nanometer thick to hundreds to thousands nanometers long.
The nanomaterials can also be distinguished in three types as natural, incidental, and engineered
nanomaterials depending on their pathway [4]. Natural nanomaterials, which are formed through
natural processes, occur in the environment (e.g. volcanic dust, lunar dust, magneto-tactic
bacteria, minerals, etc.). Incidental nanomaterials occur as the result of man made industrial
processes (e.g. coal combustion, welding fumes, etc.). Engineered nanomaterials are produced
either by lithographically etching of a large sample to obtained nanoparticles, or by assembling
smaller subunits through crystal growth or chemical synthesis to grow nanomaterials of the
desired size and configuration. Engineered nanomaterials most often have regular shapes, such as
tubes, spheres, rings, etc. U.S. Environmental Protection Agency divides engineered
nanomaterials into four types. They are carbon-based materials (nanotubes, fullerenes), metal-
based materials (including both metal oxides and quantum dots), dendrimers (nanosized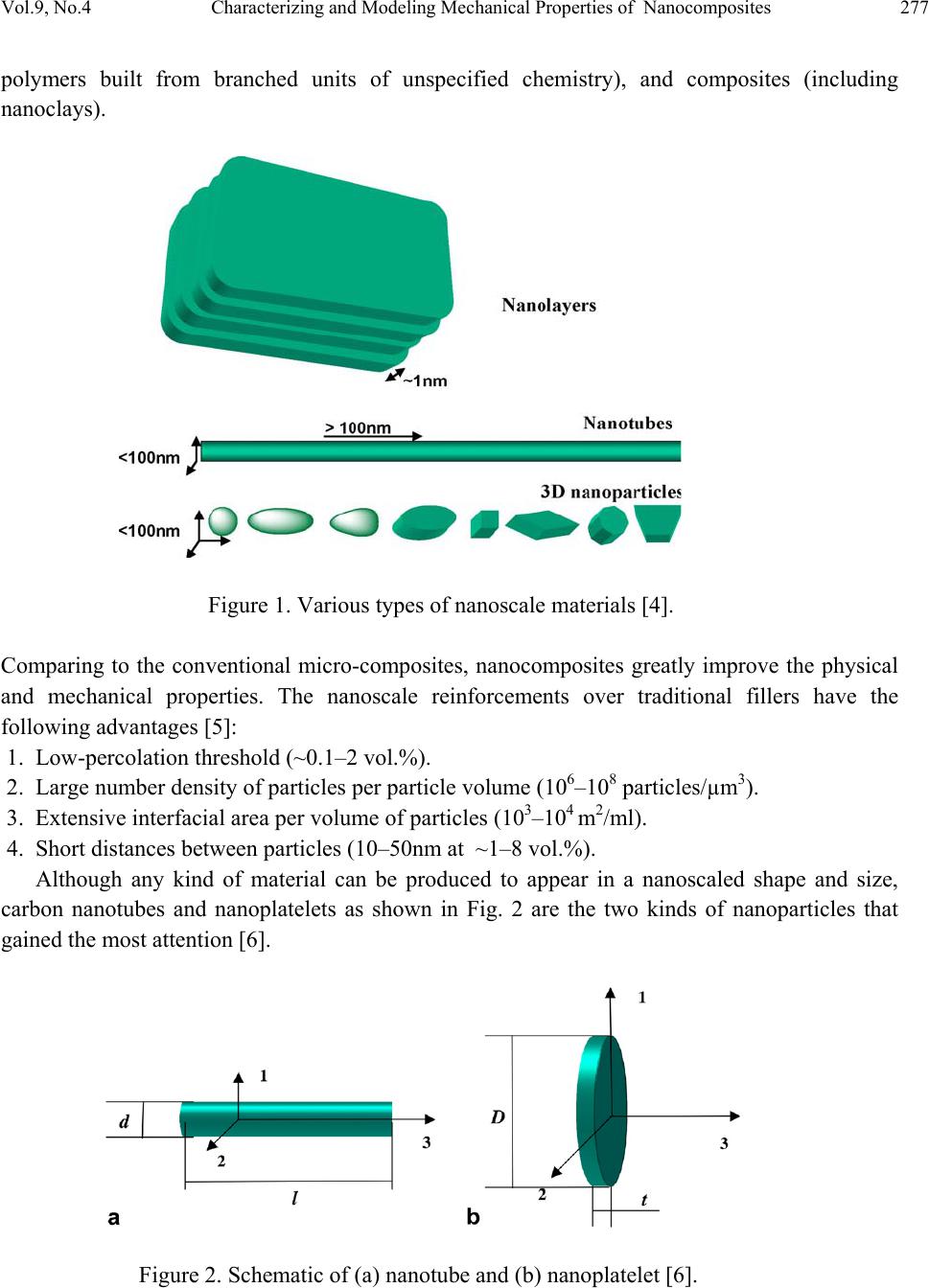

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 277
polymers built from branched units of unspecified chemistry), and composites (including
nanoclays).
Figure 1. Various types of nanoscale materials [4].
Comparing to the conventional micro-composites, nanocomposites greatly improve the physical
and mechanical properties. The nanoscale reinforcements over traditional fillers have the
following advantages [5]:
1. Low-percolation threshold (~0.1–2 vol.%).
2. Large number density of particles per particle volume (106–108 particles/µm3).
3. Extensive interfacial area per volume of particles (103–104 m2/ml).
4. Short distances between particles (10–50nm at ~1–8 vol.%).
Although any kind of material can be produced to appear in a nanoscaled shape and size,
carbon nanotubes and nanoplatelets as shown in Fig. 2 are the two kinds of nanoparticles that
gained the most attention [6].
Figure 2. Schematic of (a) nanotube and (b) nanoplatelet [6].

278 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
This paper presents a thorough review of characterizing and modeling mechanical properties of
nanocomposites. The critical review covers the current work on the experiment, theory, and
numerical analysis in this area. Nanoindentation testing and the finite element modeling are
discussed, followed by analytical modeling stiffness of nanocomposites. The numerical modeling
includes molecular dynamics modeling and finite element modeling. Three different approaches
are discussed in finite element modeling, i.e. multiscale representative volume element (RVE)
modeling, unit cell modeling, and object-oriented modeling. Finally, the mechanism of
nanocomposites mechanical property enhancement is explored, and the ways to improve their
stiffness and fracture toughness are discussed.
2. CHARACTERIZING AND MODELING OF NANOCOMPOSITES
2.1 Nanoindentation Tests and Computing Simulations
There are different ways to experimentally characterize nanocomposites. For example, tensile
and flexural tests (mostly conducted on Instron machines), impact tests (conducted on pendulum
impact testing machine) [7-11], and micro-compression tests [12,13]. Nanoindentation test is
one of the most effective and widely used methods to measure the mechanical properties of
materials. This technique uses the same principle as microindentation, but with much smaller
probe and loads, so as to produce indentations from less than a hundred nanometers to a few
micrometers in size. During the past dozen years or so, it has been widely used in measuring the
mechanical properties of various nanocomposites [14-25] and human enamel and dentin [26-38].
Hardness (H) and elastic modulus (E) are calculated from the load-displacement curve obtained
from a nanoindentation test. A typical load-displacement curve is shown in Fig. 3. As the
indenter penetrates into the specimen, the loading curve climbs up. At some point, the maximum
load Pmax is reached, and then followed by the unloading. If the material is perfectly elastic and
has no hysteresis, the loading curve and the unloading curve will be identical. hmax gives a
measure of the total maximum deformation, while hf represents the maximum permanent
(plastic) deformation (final penetration depth).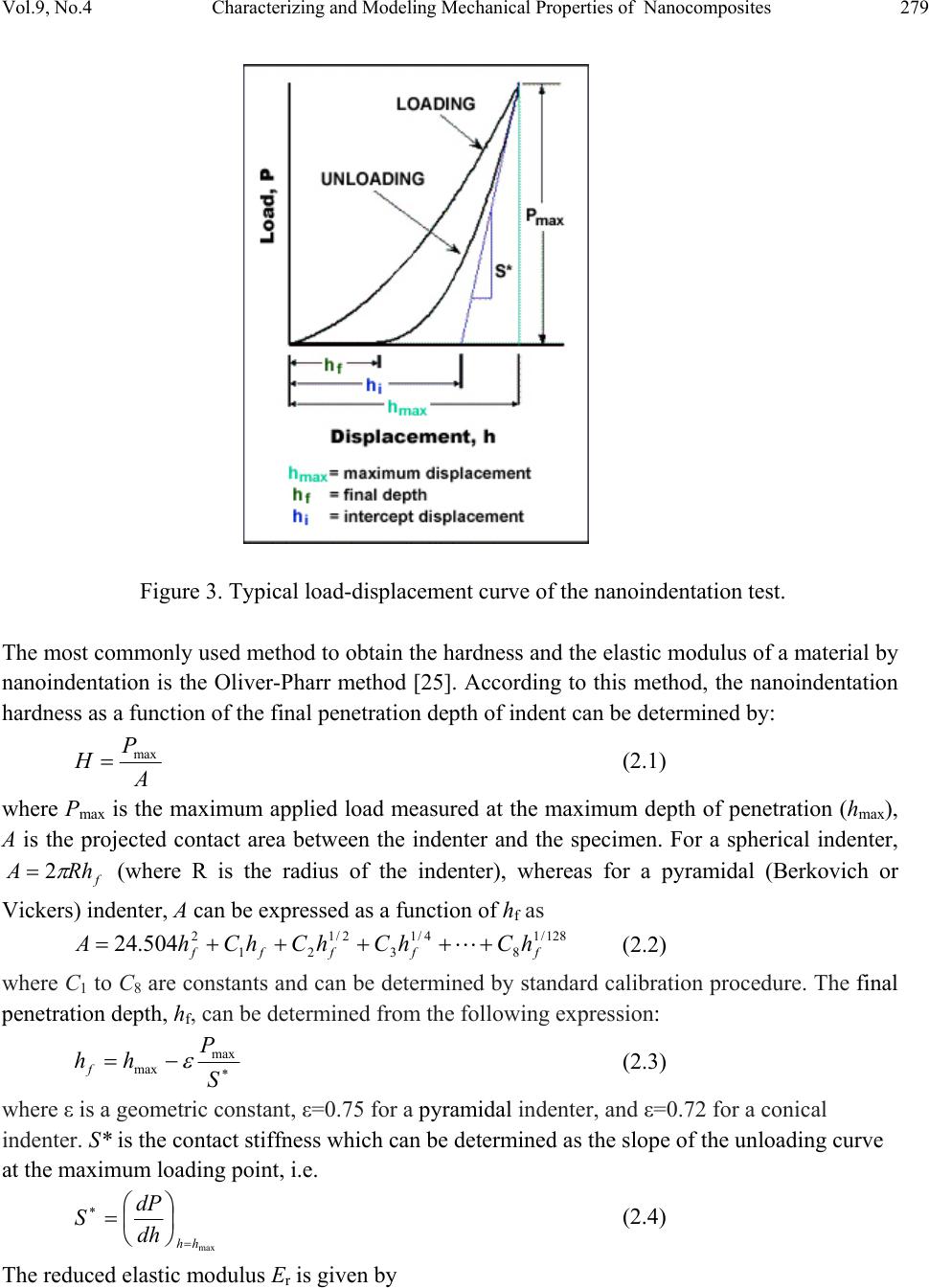

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 279
Figure 3. Typical load-displacement curve of the nanoindentation test.
The most commonly used method to obtain the hardness and the elastic modulus of a material by
nanoindentation is the Oliver-Pharr method [25]. According to this method, the nanoindentation
hardness as a function of the final penetration depth of indent can be determined by:
A
P
Hmax = (2.1)
where Pmax is the maximum applied load measured at the maximum depth of penetration (hmax),
A is the projected contact area between the indenter and the specimen. For a spherical indenter,
f
RhA
π
2= (where R is the radius of the indenter), whereas for a pyramidal (Berkovich or
Vickers) indenter, A can be expressed as a function of hf as
128/1
8
4/1
3
2/1
21
2
504.24 fffff hChChChChA +++++= L (2.2)
where C1 to C8 are constants and can be determined by standard calibration procedure. The final
penetration depth, hf, can be determined from the following expression:
∗
−=
S
P
hhfmax
max
ε (2.3)
where ε is a geometric constant, ε=0.75 for a pyramidal indenter, and ε=0.72 for a conical
indenter. S* is the contact stiffness which can be determined as the slope of the unloading curve
at the maximum loading point, i.e.
max
hh
dh
dP
S
=
∗⎟
⎠
⎞
⎜
⎝
⎛
= (2.4)
The reduced elastic modulus Er is given by

280 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
A
S
Er
π
β 2
∗
= (2.5)
where
β
is a constant that depends on the geometry of the indenter. For both a Berkovich and a
Vicker’s indenter,
β
=1.034, whereas for both a conical and a spherical indenter,
β
=1. The
specimen elastic modulus (Es) can then be calculated as:
i
i
s
s
rEEE
22 11
1
υυ −
+
−
= (2.6)
Where si E, and si,
υ
are the elastic modulus and Poisson’s ratio, respectively, for the indenter
and the specimen. For a diamond indenter, Ei is 1140 GPa and i
υ
is 0.07. The contact stiffness,
S*, can be derived from the unloading curve which simply obeys the following power law
n
f
hhBP )( −= (2.7)
where B and n are empirical constants that can be determined by fitting the experimentally
measured pairs of data (P, h) during unloading. Thus the contact stiffness can be expressed as
1
max )(
max
−
=
∗−=
⎟
⎠
⎞
⎜
⎝
⎛
=n
f
hh
hhBn
dh
dP
S (2.8)
Therefore, the specimen’s hardness H and elastic modulus s E will be obtained from this set of
equations.
Indentation is a highly nonlinear problem. It involves large plastic deformation, material
nonlinearity, and contact. In order to better understand and characterize the mechanical
properties and to provide guidelines for proper design of experiments, finite element method is
often used to simulate the nanoindentation tests [14, 15, 18, 38-51]. It is also noted that the
primary mechanical properties extracted from a nanoindentation test are the hardness and the
elastic modulus. Finite element simulation could be employed to get other properties, such as
yield stress and hardening [38, 52-58]. Fig. 4(a) shows the geometry of indentation of a
cylindrical specimen with a conical indenter, and 4(b) shows the Mises stress contour from the
finite element analysis [15]. Note that the finite element meshes are the two-dimensional (axi-
symmetric) elements. Fig. 5 shows a three- dimensional nanoindentation finite element mesh
system [18]. Note that because of symmetry, only half of the specimen volume was modeled.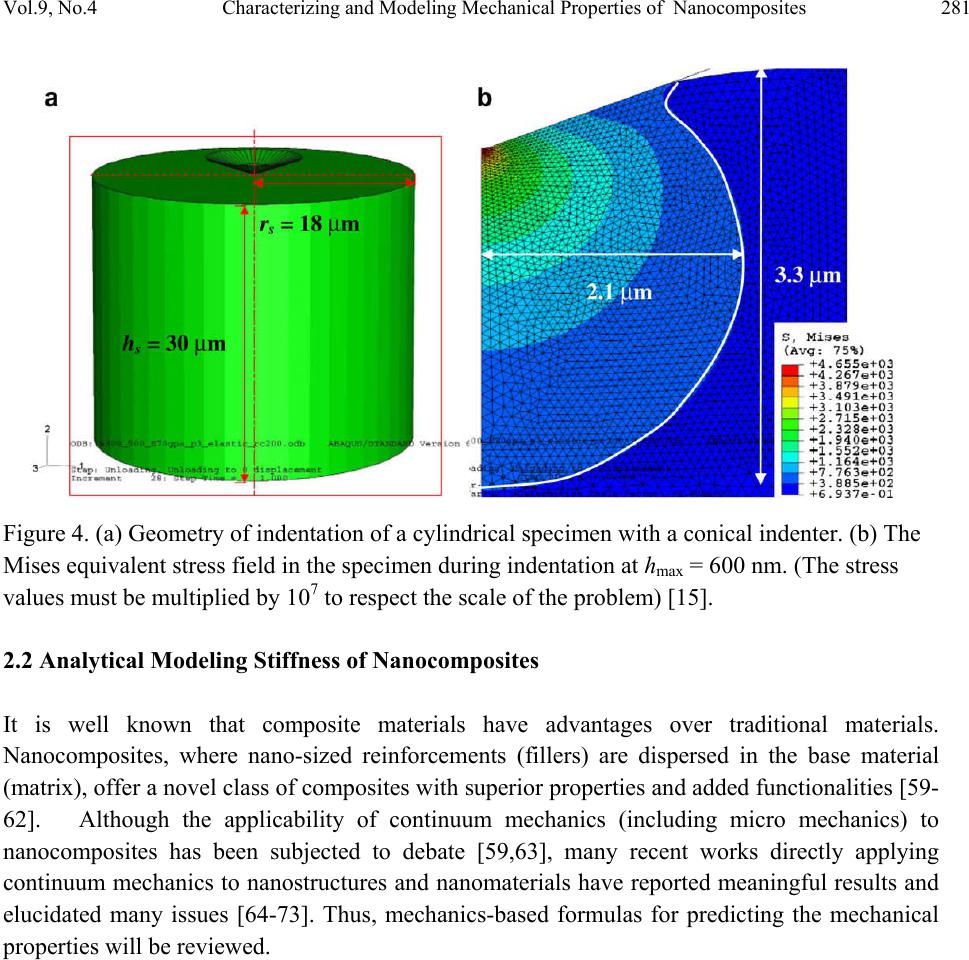

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 281
Figure 4. (a) Geometry of indentation of a cylindrical specimen with a conical indenter. (b) The
Mises equivalent stress field in the specimen during indentation at hmax = 600 nm. (The stress
values must be multiplied by 107 to respect the scale of the problem) [15].
2.2 Analytical Modeling Stiffness of Nanocomposites
It is well known that composite materials have advantages over traditional materials.
Nanocomposites, where nano-sized reinforcements (fillers) are dispersed in the base material
(matrix), offer a novel class of composites with superior properties and added functionalities [59-
62]. Although the applicability of continuum mechanics (including micro mechanics) to
nanocomposites has been subjected to debate [59,63], many recent works directly applying
continuum mechanics to nanostructures and nanomaterials have reported meaningful results and
elucidated many issues [64-73]. Thus, mechanics-based formulas for predicting the mechanical
properties will be reviewed.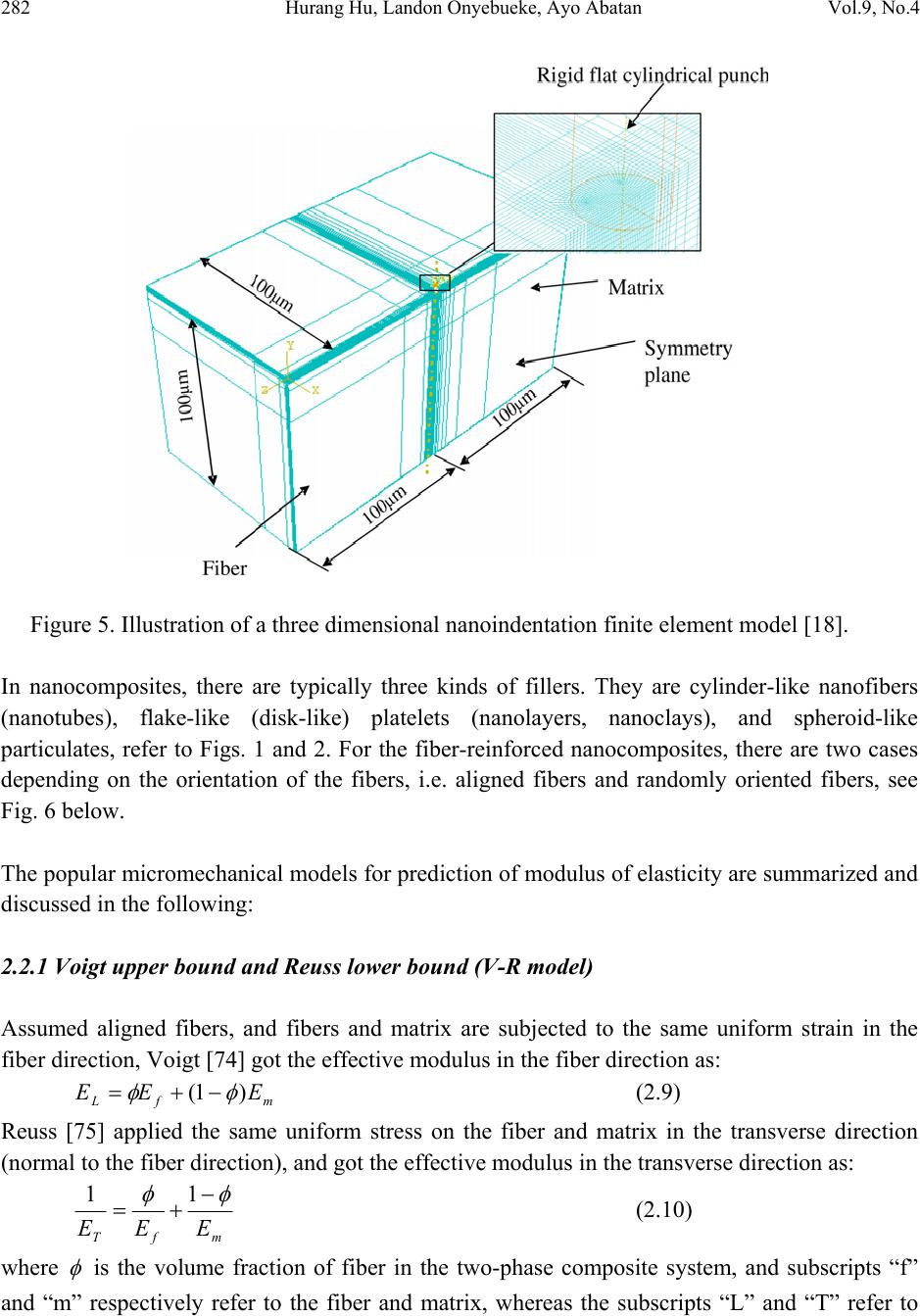

282 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
Figure 5. Illustration of a three dimensional nanoindentation finite element model [18].
In nanocomposites, there are typically three kinds of fillers. They are cylinder-like nanofibers
(nanotubes), flake-like (disk-like) platelets (nanolayers, nanoclays), and spheroid-like
particulates, refer to Figs. 1 and 2. For the fiber-reinforced nanocomposites, there are two cases
depending on the orientation of the fibers, i.e. aligned fibers and randomly oriented fibers, see
Fig. 6 below.
The popular micromechanical models for prediction of modulus of elasticity are summarized and
discussed in the following:
2.2.1 Voigt upper bound and Reuss lower bound (V-R model)
Assumed aligned fibers, and fibers and matrix are subjected to the same uniform strain in the
fiber direction, Voigt [74] got the effective modulus in the fiber direction as:
mfL EEE )1(
φ
φ
−+= (2.9)
Reuss [75] applied the same uniform stress on the fiber and matrix in the transverse direction
(normal to the fiber direction), and got the effective modulus in the transverse direction as:
mfT EEE
φ
φ
−
+= 11 (2.10)
where
φ
is the volume fraction of fiber in the two-phase composite system, and subscripts “f”
and “m” respectively refer to the fiber and matrix, whereas the subscripts “L” and “T” refer to

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 283
the longitudinal and transverse directions, respectively. Equation (2.9) is the parallel coupling
formula, and it is also called the “rule of mixtures”, whereas (2.10) is the series coupling
formula, and it is also called the “inverse rule of mixtures”.
a. Aligned fibers b. Randomly oriented fibers
c. Aligned platelets d. particulates
Figure 6. Schematics of nanocomposites: (a) with aligned fibers; (b) with randomly
oriented fibers; (c) with aligned platelets; and (d) with randomly oriented particulates [6].
Equations (2.9) and (2.10) can be extended to any two-phase composites regardless the shape of
the filler, and L
E and T E represent the upper and lower bounds of the modulus of the composite,
respectively. Note that in these formulas, only three parameters are involved, i.e. modulus of the
fiber and the matrix, and the fiber volume fraction.
2.2.2 Hashin and Shtrikman upper and lower bounds (H-S model)
Hashin and Shtrikman [76,77] assumed macroscopical isotropy and quasi-homogeneity of the
composite where the shape of the filler is not a limiting factor, and estimated the upper and lower
bounds of the composite based on variational principles of elasticity. Depending on whether the
stiffness of the matrix is more or less than that of the filler, the upper and lower bounds of the

284 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
bulk moduli, upper K and lower K, and shear moduli, upper G and lower G, of the composite are given
as:
1
43
31
)1(
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
+
−
−+=
fffm
fupper GKKK
KK
φ
φ
(2.11)
1
43
)1(31
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
−
+
−
+=
mmmf
mlower GKKK
KK
φ
φ
(2.12)
1
)43(5
)2(6
1
)1(
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
+
+
−
−+=
fff
ff
fm
fupperGKG
GK
GG
GG
φ
φ
(2.13)
1
)43(5
)2)(1(6 1
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
+−
+
−
+=
mmm
mm
mf
mlower GKG
GK
GG
GG
φ
φ
(2.14)
where the subscripts “f” and “m” refer to the filler (fiber) and matrix, respectively. The upper
and lower bounds of the elastic modulus can then be calculated using the following relation:
GK
K
E/31
9
+
= (2.15)
Similar to Voigt and Reuss models, H-S model only involves three parameters.
2.2.3 Halpin-Tsai model (H-T model)
For aligned fiber-reinforced composite materials, Halpin and Tsai [78-81] developed the
equations for prediction of elastic constants based on the work of Hermans [82] and Hill [83].
The H-T model is a semi-empirical model, and the longitudinal and transverse moduli are given
by:
m
L
L
LE
dl
E
φη
φη
−
+
=1
)/(21 (2.16)
m
T
T
TEE
φη
φη
−
+
=1
21 (2.17)
where l and d are the length and diameter of the fiber, and L
η
and T
η
take the following
expressions:
mf
mf
LEdlE
EE
)/(2+
−
=
η
(2.18)
mf
mf
TEE
EE
2+
−
=
η
(2.19)
For aligned nanoplatelets as shown in Fig. 6 (c), equations (2.16) to (2.19) may still be used by
replacing (l/d) with (D/t), where D and t are respectively the diameter and thickness of the
platelet (refer to Fig. 2).

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 285
H-T model takes the consideration of the fiber geometry, and has five independent parameters.
2.2.4 Hui-Shia model (H-S model)
Mori and Tanaka [84] developed analytical expressions for elastic constants based on the
equivalent inclusion model of Eshelby [85]. Taya and Mura [86] and Taya and Chou [87] used
Mori-Tanaka approach to predict the longitudinal modulus of fiber-reinforced composites, Weng
[88] and Tandon and Weng [89] further developed equations for the complete set of elastic
constants of composite materials with aligned spheroidal isotropic inclusions. Based upon the
results of Tandon and Weng [89], Hui and Shia [90] and Shia et al. [91] derived simplified
formulas for predicting the overall moduli of composites with aligned reinforcements with
emphases on fiber-like and flake-like reinforcements, and found that their theoretical predictions
agree well with experimental results. The H-S model presents the Young’s modulus as follows:
1
1
−
⎥
⎦
⎤
⎢
⎣
⎡−=
ξ
φ
mL EE (2.20)
1
31
(
4
1
−
⎥
⎦
⎤
⎢
⎣
⎡
Λ+
+−=
ξξ
φ
mTEE (2.21)
where
⎥
⎦
⎤
⎢
⎣
⎡
−
−−
−+
−
+=1
2/)1(
)1(3 2
2
α
α
φφξ
gg
EE
E
mf
m (2.22)
⎥
⎦
⎤
⎢
⎣
⎡
−
−+
−=Λ 1
2)25.0(3
)1( 2
22
α
αα
φ
g (2.23)
⎪
⎪
⎩
⎪
⎪
⎨
⎧
≤+−−
−
≥−−
−
=
−
−
1 ]cos1[
)1(
1 ]cosh1[
)1(
12
2/32
12
2/32
αααα
α
α
αααα
α
α
g (2.24)
and
α
is the aspect ratio of the filler, defined as the ratio of the filler’s longitudinal (with
Young’s modulus L
E) length to its transverse (with Young’s modulus T E) length. For example,
refer to Fig. 2, dl /=
α
for nanotube, Dt /
=
α
for nanoplatelet, and L
E will be along axis 3,
and T E will be along axis 1 (or 2).
2.2.5 Wang-Pyrz model (W-P model)
For a composite material composed of an isotropic matrix and randomly oriented transversely
isotropic spheroids, Qiu and Weng [92] and Chen et al. [93] gave the formulas for the overall
bulk and shear moduli using the Mori-Tanaka method. These formulas are expressed in terms of

286 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
the Eshelby tensor [85], thus are not final. Wang and Pyrz [94] further gave the closed and
concise formulas for the overall bulk modulus and shear modulus as follows:
)1(1 αφ
φϕ
−−
+= mm KKK (2.25)
)1(1 βφ
φ
ψ
μμμ
−−
+= mm (2.26)
The expressions for
ϕ
,
ψ
,
α
and
β
are given in the Appendix.
Note that W-P model is based on the Mori-Tanaka approach, and deals with the composite
materials reinforced with randomly oriented and transversely isotropic spheroids. By varying the
aspect ratio, the oblate spheroids can be approximate to platelets, and the prolate spheroids can
be approximate to fibers.
2.2.6 Cox model (Shear lag model)
Shear lag model was the first micro-mechanics model for fiber-reinforced composites. Cox [95]
analyzed a single fiber of length l and radius f r, which is encased in a concentric cylindrical
shell of matrix having radius R. He derived the longitudinal modulus as
mfLL EEE )1(
φ
φ
η
−+= (2.27)
where L
η
is a length-dependent efficiency factor,
2/
)2/tanh(
1l
l
L
β
β
η −= (2.28)
with
)/ln(
4
2
2
φ
μ
β
Rff
m
KEr
= (2.29)
R
K is a constant that depends on the fiber packing arrangements. For some typical fiber packing
arrangements, the values of R
K are given in Table 1 [96].
Table 1. Values for R
K in Eq. (2.29)
FIBER PACKING R
K
Cox 3/2
π =3.628
Composite cylinders 1.000
Hexagonal 32/
π =0.907
Square 4/
π
=0.785
It is well known that the orientation of the dispersed phase has a dramatic effect on the
composite modulus. It is apparent from their geometry that flake-like platelets can provide equal

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 287
reinforcement in two directions, if appropriately oriented, while fibers provide primary
reinforcement in one direction. If the longitudinal modulus L
E and the transverse modulus T E
are known, then the effective modulus of the composite with randomly oriented fibers and
platelets in all three orthogonal directions are given by [97]:
TL
fiber
DEEE 816.0184.0 3+= (2.30)
TL
platelet
DEEE 51.049.0 3+= (2.31)
2.3 Molecular Dynamics Simulation
In modeling mechanical properties of nanocomposites, there are two main approaches: one is
molecular dynamics simulation using direct methods, and the other is finite element simulation
using “continuum” methods. Molecular dynamics simulation is a technique that allows one to
determining the physical and mechanical properties of materials in nanoscale through solving
Newton’s equations of motion with the atoms interacting through assumed interatomistic
potentials [98, 99]. It generates information such as atomic positions, velocities and forces from
which some macroscopic properties can be derived by means of statistical mechanics. Molecular
dynamics simulation usually consists of three constituents: (1) a set of initial conditions (e.g.,
initial positions and velocities of all particles in the system); (2) the interaction potentials to
represent the forces among all the particles; (3) the evolution of the system in time by
numerically solving a set of classical Newtonian equations of motion for all particles in the
system [100]. In 1997, Cornwell et al. used molecular dynamics to predict the elastic properties
of single-walled carbon nanotubes [101]. In recent years, molecular dynamics simulation has
been extensively used in predicting mechanical properties of carbon nanotubes and nanotubes
reinforced composites [102-109], graphite/epoxy nanocomposites [110-112], and other
nanocomposites [113-119].
Molecular dynamics simulation involves the proper selection of interaction potentials, numerical
integration, periodic boundary conditions, and the controls of pressure and temperature to mimic
physically meaningful thermodynamic ensembles. The interaction potentials together with their
parameters form a force field which describes in detail how the particles in a system interact with
each other. Such a force field may be obtained by quantum method, empirical method or
quantum-empirical method. The criteria for selecting a force field include the accuracy,
transferability and computational speed. The total potential energy U may consist of a number of
bonded and non-bonded interaction terms:
∑∑∑
∑
∑
−
++++= bondednoninversiontorsionanglebond UUUUUU (2.32)
The first four terms represent bonded interactions, i.e., bond-stretching between two bonded
atoms, angle-bending by three neighboring atoms, angle variation between two planes formed by
four neighboring atoms, and angle variation of two planes formed by four atoms where one atom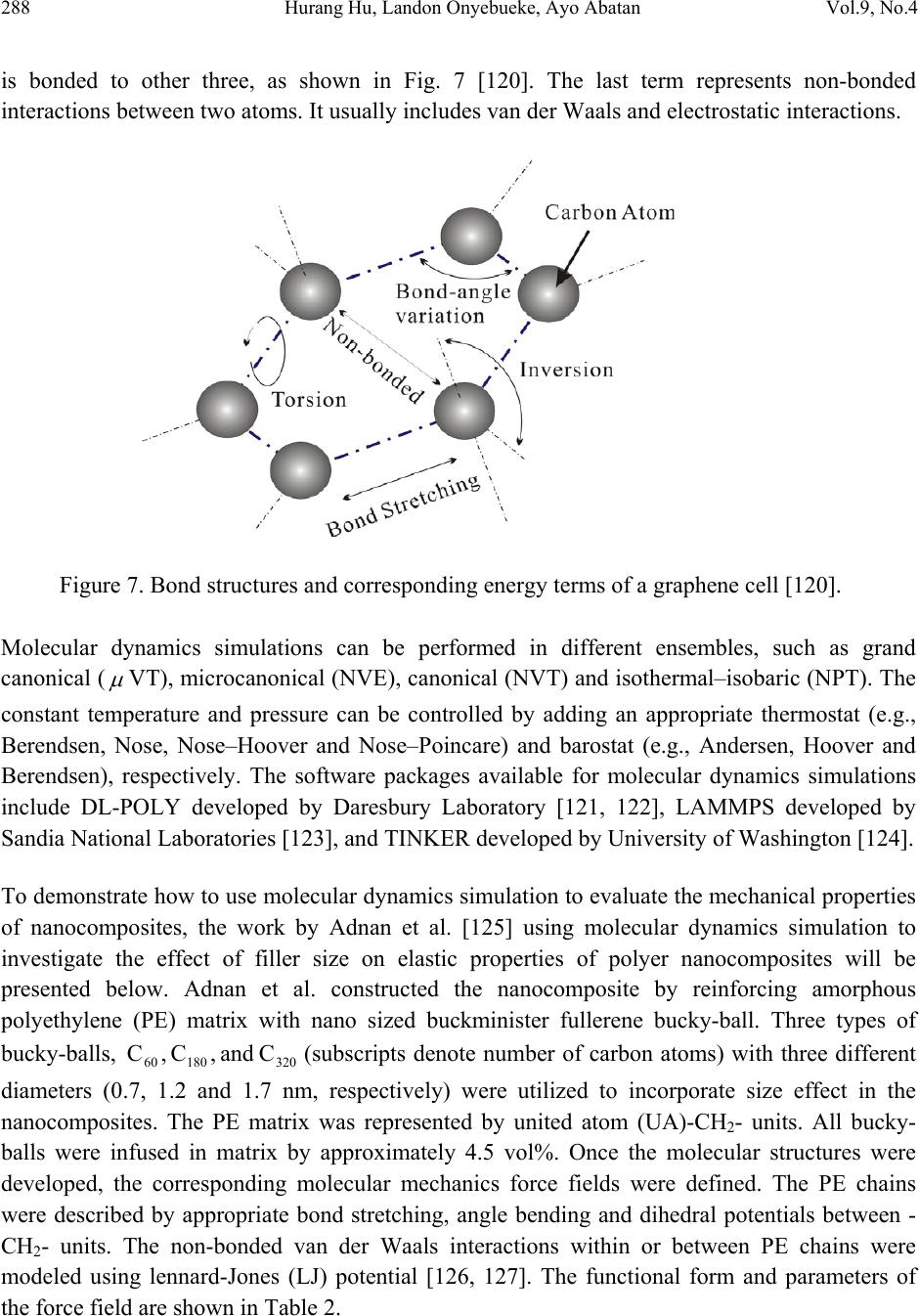

288 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
is bonded to other three, as shown in Fig. 7 [120]. The last term represents non-bonded
interactions between two atoms. It usually includes van der Waals and electrostatic interactions.
Figure 7. Bond structures and corresponding energy terms of a graphene cell [120].
Molecular dynamics simulations can be performed in different ensembles, such as grand
canonical (
μ
VT), microcanonical (NVE), canonical (NVT) and isothermal–isobaric (NPT). The
constant temperature and pressure can be controlled by adding an appropriate thermostat (e.g.,
Berendsen, Nose, Nose–Hoover and Nose–Poincare) and barostat (e.g., Andersen, Hoover and
Berendsen), respectively. The software packages available for molecular dynamics simulations
include DL-POLY developed by Daresbury Laboratory [121, 122], LAMMPS developed by
Sandia National Laboratories [123], and TINKER developed by University of Washington [124].
To demonstrate how to use molecular dynamics simulation to evaluate the mechanical properties
of nanocomposites, the work by Adnan et al. [125] using molecular dynamics simulation to
investigate the effect of filler size on elastic properties of polyer nanocomposites will be
presented below. Adnan et al. constructed the nanocomposite by reinforcing amorphous
polyethylene (PE) matrix with nano sized buckminister fullerene bucky-ball. Three types of
bucky-balls, 32018060C and ,C ,C(subscripts denote number of carbon atoms) with three different
diameters (0.7, 1.2 and 1.7 nm, respectively) were utilized to incorporate size effect in the
nanocomposites. The PE matrix was represented by united atom (UA)-CH2- units. All bucky-
balls were infused in matrix by approximately 4.5 vol%. Once the molecular structures were
developed, the corresponding molecular mechanics force fields were defined. The PE chains
were described by appropriate bond stretching, angle bending and dihedral potentials between -
CH2- units. The non-bonded van der Waals interactions within or between PE chains were
modeled using lennard-Jones (LJ) potential [126, 127]. The functional form and parameters of
the force field are shown in Table 2.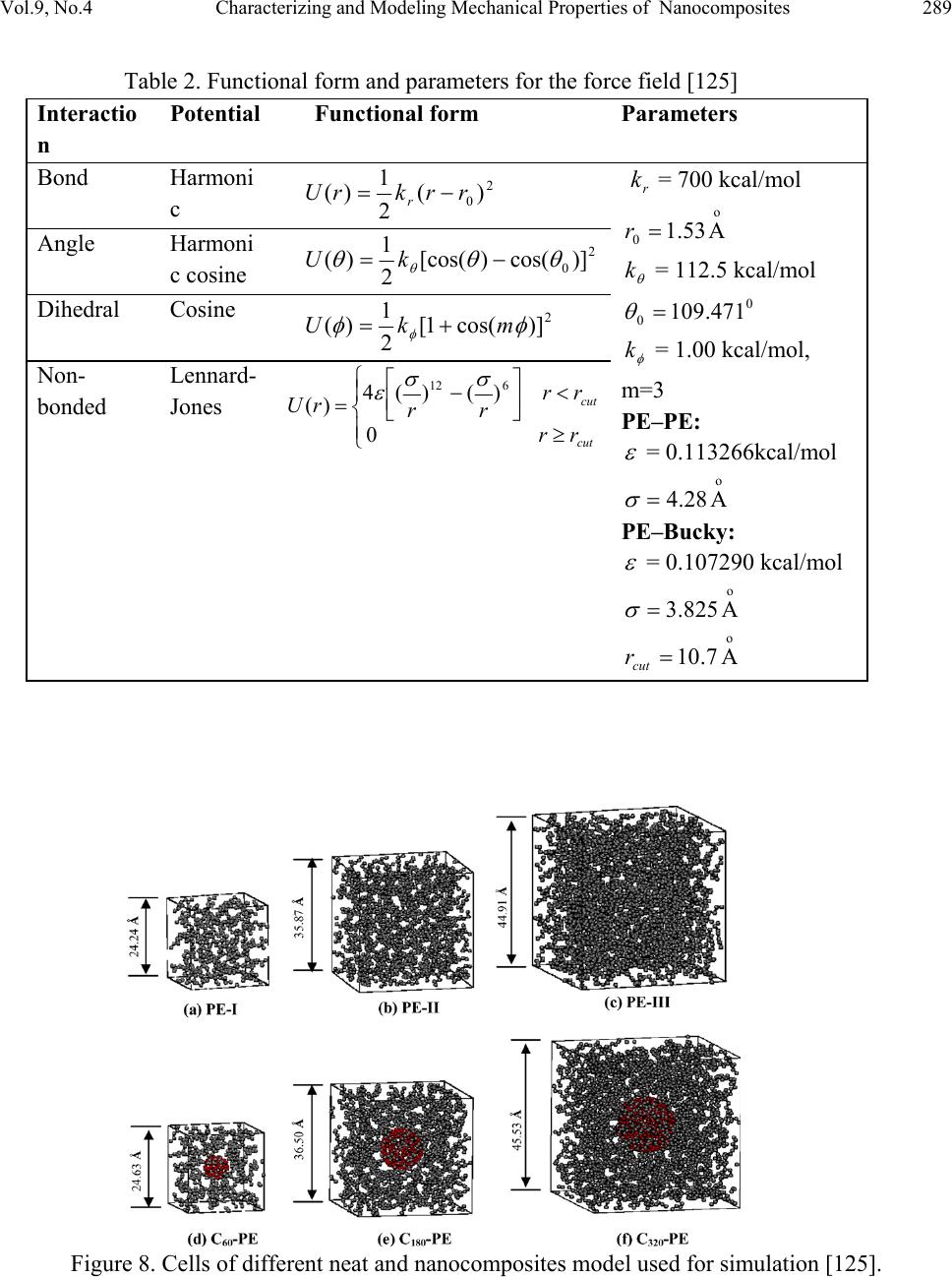

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 289
Table 2. Functional form and parameters for the force field [125]
Interactio
n Potential Functional form Parameters
Bond Harmoni
c
2
0)(
2
1
)(rrkrU r−= r
k = 700 kcal/mol
o
0A53.1=r
θ
k = 112.5 kcal/mol
0
0471.109=
θ
φ
k = 1.00 kcal/mol,
m=3
PE–PE:
ε
= 0.113266kcal/mol
o
A28.4= σ
PE–Bucky:
ε
= 0.107290 kcal/mol
o
A825.3= σ
o
A7.10=
cut
r
Angle Harmoni
c cosine
2
0)]cos()[cos(
2
1
)( θθθ
θ
−= kU
Dihedral Cosine
2
)]cos(1[
2
1
)( φφ
φ
mkU +=
Non-
bonded
Lennard-
Jones ⎪
⎩
⎪
⎨
⎧
≥
<
⎥
⎦
⎤
⎢
⎣
⎡−
=
cut
cut
rr
rr
rr
rU
0
)()(4
)(
612
σσ
ε
Figure 8. Cells of different neat and nanocomposites model used for simulation [125].

290 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
Fig. 8 shows the cells of different neat and nanocomposites model used for simulation. Periodic
boundary conditions were employed to replicate the unit cells in three dimensions. Software
package DL_PLOY (version 2.14) was used in the simulation. All the calculations were carried
out at a temperature of 3000K with 0.5 fs time steps. Two major steps of simulation for both neat
polymer and nanocomposites were performed. In the first step, the equilibrium state of the
molecular model was obtained, and then the model was subjected to different strain fields and re-
equilibrated. Adnan et al. applied a uniform strain field (0.5%) to the periodic cells of both neat
polymer and nanocomposites. For the cases of hydrostatic tension and hydrostatic compression,
they evaluated the bulk modulus K, and their results were shown in Table 3.
Table 3. Evaluation of bulk modulus K for various nanocomposites [125]
System Type Hydrostatic Compression Hydrostatic Tension
K(GPa) % Gain/loss K(GPa) % Gain/loss
PE-C60 3.529 17.39 3.478 22.29
PE-C180 3.454 14.90 3.272 15.04
It is evident from Table 3 that elastic properties of nanocomposites are improved appreciably
with the infusion of bucky-balls in PE matrix, and they are also significantly affected by the size
of reinforcing bucky-balls.
2.4 Finite E lement Modeling
As a very general and powerful numerical analysis tool, finite element method was used to
predict mechanical properties of composite materials started in early 1970s [128-129]. Since
then, various finite element models have been developed to characterize all kinds of composite
materials [e.g. 130-136]. In 1991, Sumio Iijima, a Japanese scientist, discovered carbon
nanotubes (CNTs) which possess exceptionally high stiffness and strength, as well as superior
electrical and thermal properties [137-139]. Soon after that CNTs were used as reinforcement in
developing nanocomposite materials. In the past decade or so, there have been explosively
experimental work [e.g. 7, 8, 140-155] and analytical work [e.g. 156-169], as well as finite
element modeling work [e.g. 170-198] on developing, analyzing and characterizing CNT
reinforced nanocomposites and other nanocomposites. In the following, three finite element
modeling approaches will be discussed. They are multiscale representative volume element
(RVE) modeling, unit cell modeling, and object-oriented modeling.
2.4.1 Multiscale RVE modeling
Liu and Chen [180] extended the RVE concept used by Hyer [199] and Nemat-Nasser and Hori
[200] for conventional fiber-reinforced composites at the microscale to nanoscale, and evaluated
the effective mechanical properties of CNT-based composites by using a three-dimensional

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 291
nanoscale RVE based on elasticity theory and solved by the finite element method. An RVE is
composed of a single (or multiple) nanofiller(s) with surrounding matrix material, plus proper
boundary conditions to account for the effects of the surrounding materials. It is used as a
building block to assemble the composite. Zhang et al. [201] linked continuum analysis with
atomistic simulation by incorporating interatomic potential and atomic structures of CNTs
directly into the constitutive law. Shi et al. [185] presented a hybrid atomistic/continuum
mechanics method to study the deformation and fracture behavior of CNTs embedded in
composites. The method is based on a representative unit cell divided into three distinct regions
analyzed using an atomistic potential, a continuum method based on the Cachy–Born rule and a
micromechanics method, respectively. Li and Chou [180] proposed a multi-scale modeling
approach to study the compressive behavior of CNT/polymer composites. They modeled the
nanotube at the atomistic scale and analyzed the matrix deformation using the continuum finite
element method. The van der Waals interactions between carbon atoms and the finite element
nodes of the matrix were simulated using truss rods.
The multiscale RVE integrates nanomechanics and continuum mechanics, thus bridging the
length scales from the nano- through the mesoscale. The procedure of multiscale RVE modeling
is exhibited by the work of Tserpes et al. [172] in the following. Tserpes et al. proposed a
multiscale RVE to investigate the tensile behavior of CNT/polymer composites. The RVE is a
rectangular solid whose entire volume is taken up by the matrix, and the nanotube is modeled as
a three-dimensional (3D) elastic beam. The 3D solid elements and beam elements are used to
model the matrix and nanotube, respectively. The RVE is synthesized in two steps. First, the
behavior of the isolated nanotube is simulated using the progressive fracture model [202]. The
concept of the model is based on the assumption that carbon nanotubes, when loaded, behave
like space-frame structures. The bonds between carbon atoms are considered as load-carrying
members while carbon atoms as joints of the members. The non-linear behavior of the C-C
bonds is modeled by the modified Morse interatomic potential [203], and the nanotube structure
is modeled by finite element method. Second, the nanotube is inserted into the matrix to form the
RVE. The matrix is modeled by solid elements, and the nanotube is represented by 3D elastic
beam elements created by binding the nodes of the matrix. The synthesis of the RVE is shown in
Fig. 9.
2.4.2 Unit cell modeling
The conventional unit cell concept is the same as the RVE [132, 204]. Here we define a unit cell
as a special RVE that it has a relatively big size (usually in micrometers) and contains a
significant number of fillers (usually in tens to hundreds or more). Such defined unit cell is still
the building block of the composite, but as it gets more complicated, analytical models are
difficult to establish or too complicated to solve, and numerical modeling and simulation become
a necessity.

292 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
Figure 9. Synthesis of the RVE [172].
The most common method used to characterize the mechanical properties of nanocomposites
with unit cell is the finite element method. Hbaieb et al. [177] examined the Young’s modulus of
nanoclay/polymer nanocomposites with both 2D and 3D unit cells using the finite element
method. Four unit cells were created. They are, respectively, 2D and 3D aligned and randomly
oriented nanoclay particles models, as shown in Fig. 10. Two kinds of boundary conditions are
considered. They are periodic boundary conditions and symmetrical boundary conditions. For
the 2D models (both aligned and random cases) the periodic boundary conditions are:
u(RE)=u(LE)+ 1
δ
v(RE)=v(LE)
u(TE)=u(BE)
v(TE)=v(BE)+ 2
δ
where RE, LE, TE, BE and 1
δ
and 2
δ
are the right, left, top, bottom edges and the axial and
transverse displacements, respectively. The symmetrical boundary conditions for the 2D models
are:
u(LE)=0
v(BE)=0
u(RE)=
δ

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 293
where
δ
is the given normal displacement in the x direction. In addition, all edges are free of
shear traction and the top edge is free of normal traction as well.
For the 3D models (both aligned and random cases) only symmetrical boundary conditions are
applied, and they are given as:
u(LF)=0
v(BF)=0
w(BKF)=0
u(RF)=
δ
where LF, BF, BKF and RF stand for left face, bottom face, back face and right face. All other
faces are free of any displacement or traction constraints. The numerical results indicated that 2D
models do not predict the elastic modulus of clay/polymer nanocomposites accurately. The Mori-
Tanaka model [89] gives reasonably accurate predictions of the stiffness of the nanocomposites
whose volume fraction is less than 5% for aligned particles but underestimates the stiffness at
higher volume fractions. For randomly oriented particles the W-P model [94] overestimates the
stiffness of the nanocomposites.
Figure 10. Mesh details of the model for (a) 2D aligned particle distribution, (b) 2D
randomly oriented-particle distribution, (c) 3D aligned particle distribution, and (d) 3D
randomly oriented-particle distribution. Particle volume fraction is 5%, the particle aspect
ratio is 50, Ep/Em=100,
ν
m=0.35,
ν
p=0.2. Subscripts p and m represent particle and
matrix, respectively [177].
Recently, Lee et al. [170] used a 3D unit cell model to analyze the deformation behavior of
randomly distributed Al18B4O33 whisker-reinforced AS52 magnesium alloy matrix composite.
The Al18B4O33 whiskers are m
μ
3010 − long and m
μ
0.15.0
−
in diameter. The dimensions of

294 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
the unit cell are 3
202010 m
μ
×× which contains (fully or partially) 260 whiskers. The volume
fraction of the whiskers is 15%. Fig. 11 shows a typical unit cell (with the meshes of the
whiskers) and an optical micrograph of the composite. For the Young’s modulus and overall
elastic-plastic response of the composite, the finite element modeling results are in excellent
agreement with the experimental results.
Figure 11. (a) 3D random whisker-reinforced composite model, and (b) an optical micrograph of
squeeze-infiltrated Al18B4O33/Mg random whisker composite [170].
2.4.3 Object-oriented modeling
In both multiscale RVE modeling and unit cell modeling, two basic assumptions are made. First,
nanofillers can be idealized to simple geometries such as spheres, ellipsoids, cylinders, or cubes.
And second, nanocomposites can be reproduced by assembling a large number of such RVEs (or
unit cells). This can be a serious limitation when dealing with complex and highly heterogeneous
nanocomposites. For example, for highly variable and irregular angular structure of fillers, using
approximation of simple geometrical particles could not capture the complex morphology, size,
and spatial distribution of the reinforcement. Therefore, the object-oriented modeling which is
able to capture the actual microstructure morphology of the nanocomposites becomes necessary
in order to accurately predict the overall properties.
The object-oriented modeling is a relatively new approach. It incorporates the microstructure
images such as scanning electron microscopy (SEM) micrographs into finite element grids. Thus
the mesh reproduces exactly the original microstructure, namely the inclusions size, morphology,
spatial distribution, and the respective volume fraction of the different constituents. A object-
oriented finite element code, OOF [205, 206], developed by National Institute of Standards and
Technology (NIST), has been extensively used in analyzing fracture mechanisms and material
properties of heterogeneous materials [207-216] and mechanical properties of nanocomposites

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 295
[8, 178, 179, 217]. In the following, a 2D object-oriented finite element modeling will be
discussed, followed by a 3D modeling.
Figure 12. Typical example of creating OOF model of PP/organoclay nanocomposites (5
wt% in clay content): (a) original SEM image, (b) captured SEM image portion, (c) image
segmentation using pixel selection, and (d) finite element mesh (highlighted regions contain
organoclay particles and the rest are PP matrices) [8].
Dong et al. [8] studied the mechanical properties of polypropylene (PP)/organoclay
nanocomposites with different clay contents ranging from 1 to 10 wt%. Their work started with
the specimen fabrication through experimental characterization to theoretical predictions and
numerical modeling using OOF. SEM micrographs from longitudinal loading direction of the
specimen were captured and mapped onto the finite element model, as shown in Fig. 12. The
actual nano/microstructures (their size, shape, and distribution etc.) of the PP and the organoclay
were used in the computational model, and each phase was attributed the corresponding material
properties. The OOF modeling results for the tensile modulus show a good agreement with the
experimental data and theoretical predictions.
Chawala et al. [178] used 3D object-oriented finite element modeling to evaluate the mechanical
behavior of SiC particle-reinforced Al composites. For a volume of 3 20100100 m
μ
×× cell,
there are about 100 SiC particles which produce 20% volume fraction. They compared the

296 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
results of the Young’s modulus and the stress-strain relations from the object-oriented
(microstructure-based) model with the results of the experiment and the numerical results from
simplified models (which include rectangular prism, multiparticle-ellipsoids, and multiparticle-
spheres, etc.). Some of the results were shown in Fig. 13. Their results indicate that 3D
microstructure-based model can accurately predict the properties of particle-reinforced
composites, while the simple analytical models can not as they do not account for the
microstructural factors that influence the mechanical behavior of the material.
Figure 13. Comparison between 3D finite element models incorporating actual
microstructure and approximation to spherical particles: (a) FEM models, (b) von Mises
stress distribution in particles, and (c) plastic strain in matrix [178].
3. MECHANICAL PROPERTY ENHANCEMENT
Fillers added to matrix can change the mechanical properties of the matrix material. Comparing
to traditional composite materials, nanocomposites have the following characterizations:
1. Nanoparticles can substantially improve the mechanical properties of the host matrix
materials [140,142,218-220]. Even at very low filler volume content such as 1-5%, a
considerable improvement of the mechanical properties can be achieved [143, 221-223].
2. It is observed that for some nanocomposites, with the same filler volume fraction, the
stiffness and strength increases as the particle size decreases [125,182, 224-227].

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 297
3. In general, the stiffness of nanocomposites tends to increase as the filler volume fraction
increases. This function may be nonlinear. There may exist a critical volume fraction
beyond which the stiffness starts decrease [228].
For conventional composite materials, micromechanics theories consider that the overall
mechanical properties of composites are functions of constituent properties, constituent volume
fraction, inclusion shapes and orientations, and state of dispersion. It does not consider the
interactions between filler and matrix at their interface. For nanocomposites, the mechanical
property enhancement not only depends on the above factors, but also depends on the interaction
between the filler and the matrix.
3.1 Mechanisms of stiffness and strength enhancement
It is widely accepted that there is an interphase exist between the nanofillers and the matrix
material in nanocomposites. This interphase is a transition region, which extends nanometers to
micrometers over which the mechanical and physical properties change from the properties of
filler to the properties of the matrix. Among many researchers who studied the nanocomposites
interphase behavior, Boutaleb et al. [156] investigated the influence of interphase on the overall
behavior of silica spherical nanoparticle/polymer composites by means of analytical and finite
element methods. Fig. 14 shows a schematic of a composite material containing randomly
located spherical nanoparticles (left) and a spherical nanoparticle coated with a graded interphase
(right). The interphase is represented as a third phase around the nanoparticles. A model of
axisymmetric RVE with periodical boundary conditions was examined. The analysis results
show that the interphase is a dominant parameter controlling the overall nanocomposite
behavior.
To estimate the elastic modulus of the interphase in polymer nanocomposites, Saber-Samandari
and Khatibi [229] developed a 3D unit cell model to represent the three constituent phases
including particle, interphase and matrix. The elastic modulus of the interphase at any point, r, is
described by a power law as:
2/
)/(/)(
n
fi
i
fimfimi rr
rr
rrEErrErE ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
−+= (3.1)
where Em and Ef are matrix and nanoparticle elastic moduli, respectively, rf and ri are the filler
and interphase radii, and n is the intragallery enhancement factor which depends on the
chemistry and surface treatment of the particles considered.

298 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
Figure 14. Schematic of a composite material containing randomly located spherical
nanoparticles (left) and a spherical nanoparticle coated with an interphase (right) [156].
How exactly the interphase affects the nanocomposites properties is still a research topic. Some
intend to think the interphase refined the grain size of matrix leads to smaller critical flaw size
and higher strength. Some researchers believe that nanoparticles yield dislocations around them,
and these dislocations release residual stresses in the matrix. Thus the defect size along the grain
boundaries is reduced. There are also some researchers who think nanofillers impart additional
strength of their own to the matrix through the interphase. Nevertheless to say, the strengthening
mechanism of nanocomposites is not fully understood. Several mechanical properties of
nanocomposites are also improved for the same reason, such as hardness, wear resistance, and
thermal shock resistance.
The interaction between nanofillers and matrix is the key to the nanocomposites properties
enhancement. There are many factors affecting that interaction, such as the filler volume
(weight) fraction, degree of dispersion, the filler geometry and orientation, etc. We assume the
same volume fraction and identical degree of dispersion, only the filler geometry (aspect ratio)
and orientation will be considered. We define a reactive surface area per unit volume of filler,
γ
,
as
V
A
= γ (3.2)
where A and V are surface area and volume of the filler, respectively. Table 4 shows the major
axis and the
γ
value for some typical geometry of the nanofillers.
Consider three most common geometries, i.e., sphere (nanoparticles), disk (nanoplatelets,
nanolayers), and cylinder (nanotubes, nanofibers). For the cuboid, if a=b=c, it becomes a cube,
close to sphere; if a=b>>c, it becomes a platelet; if a>>b
≈
c, it becomes a rod, close to cylinder.
Assume that the diameter of the sphere, the diameter of the cylinder cross-section, and the

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 299
thickness of the disk are the same. According to the values in Table 4, the reinforcement
efficiency of the three geometries in the major axis direction, from good to poor, is sphere-
cylinder-disk. But nanoplatelets are thought to possess better reinforcement effects than those of
spherical and fiber-like particles [230].
Table 4.
γ
value and the major axis for typical filler geometries
Name Shape
γ
Parameters
Cylinder tat
4
)
12
(2 ≈+ as a
t
<
<
t-diameter of cross
section area, a-
length
t-thickness, a-radius
t-thickness, a and b-
length and width
t-diameter
a, b and c-lengths
of the three sides
t-base diameter
h-height
Disk-like
platelet
tat
2
)
11
(2 ≈+ as a
t
<
<
Rectangula
r platelet
tbat
2
)
111
(2 ≈++ as
ba
t
,<<
Sphere
t
6
Cuboid )
111
(2 cba ++
Cone
)
411
(3 22 thh++
As the filler orientation is very important in reinforcement, equation (3.2) has to be modified to
account for the effect of orientation of the filler surfaces. Now we define an effective surface
area per unit volume of filler,
γ
, as
V
A
=
γ
(3.3)
where
A
is the effective filler surface area, and it represents the portion of surfaces which is
normal to the direction of major axis (see Table 4). The value of
γ
for sphere, disk, and cylinder
in the major axis is 3/2t, 2/t, and 4/t, respectively. Therefore, in the major direction shown, the
order of reinforcement efficiency, from good to poor, is cylinder-disk-sphere.
If the nanofillers are randomly oriented, the reinforcement efficiency of nanospheres is probably
better than that of nanolayers, and the reinforcement efficiency of nanolayers is probably better

300 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
than that of nanocylinders. This is because sphere is isotropic, and disk is transversely isotropic,
and cylinder is anisotropic.
For all the geometries of the filler, as the characteristic dimension (the smallest dimension)
decreases, the value of
γ
will increase. That is, the smaller the filler, the better enhancement it
will provide. This is similar to the Hall-Petch effect on the strength of metals. Hall-Petch relates
the yield stress of a metal to its average grain diameter d as
2/1
0
−
+= kd
y
σ
σ
(3.4)
where 0
σ
and
k
are the constants related to the material of interest. The yield stress increases as
the grain size decreases. It is also interesting to note that just as Hall-Petch equation does not
apply to extremely fine grain sizes, fine size filler enhancement on nanocomposites may also
have a limit. Schiotz and Jacobsen [231] investigated nanocrystalline copper, and pointed out
that there may be a maximum in the strengthening that can be obtained by decreasing the grain
size, so that below a certain critical grain size the strength begins to decrease again as the grain
size decreases.
3.2 Fracture Toughness
Nanocomposites can not only improve stiffness and strength, but also fracture toughness [232-
242]. In general, the fracture toughness of nanocomposites increases as the volume fraction
increases, and increases as the nanofiller size decreases. For silica/epoxy nanocomposites,
Ragosta et al. [235] found the fracture toughness improved as the volume fraction of 15-nm
silica particles increases. Similar results were obtained by Zhang et al. [234] with 25-nm silica
particles, and by Chen et al. [232] with 12-nm silica particles. Through experiments and an
analytical model, Adachi et al. [233] studied the mode I fracture toughness of silica/epoxy
nanocomposites, and found that the toughness increased drastically as the silica volume fraction
increased and the particle diameters decreased. In nanocomposites with a low volume fraction of
particles, the volume fraction affected the fracture toughness more; and with high volume
fractions, the particle size affected the fracture toughness more.
Just as for stiffness and strength, the toughening mechanism of nanocomposites is also mainly
from the interaction between the fillers and the matrix. Awaji et al. [243] observed silicon
carbide/alumina nanocomposites by transmission electron microscopy (TEM), and found that
silicon carbide nanoparticles were dispersed both inside the alumina grains and on the grain
boundaries. The fracture toughness is improved by the change of fracture mode from
intergranular fracture of monolithic alumina to transgranular fracture of nanocomposites. Fig. 15
shows a schematic illustration of the toughening mechanism [244]. Nanoparticles are dispersed
within the matrix grains. Then sub-grain boundaries or dislocation networks are generated
around the nanoparticles (Fig. 15A). When the tip of a propagating large crack reaches this area,
these dislocations in the matrix will operate as nano-crack nuclei in the vicinity of the

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 301
propagating crack tip (Fig. 15B). The highly stressed frontal process zone (FPZ) ahead of the
crack tip is then released by nano-crack nucleation, and the nano-cracks expand the FPZ size,
enhancing the fracture toughness of the materials [236].
Figure 15. Schematic description of the toughening mechanism in nanocomposites.
(A) Intra-type nano-structure, (B) FPZ creation [244].
4. CONCLUDING REMARKS
Characterizing and modeling mechanical properties of nanocomposites is reviewed and
evaluated. Nanocomposites are made by dispersing nanofillers (e.g., silicate and ceramic
nanoparticles, CNTs, etc.) into matrix (e.g., some polymers, ceramics, metals, etc.). Comparing
with conventional composite materials, nanocomposites have numerous advantages such as high
mechanical and physical properties, and high reinforcement efficiency. The high enhancement of
mechanical properties of nanocomposites is mainly attributed to the interaction between the
nanofillers and the matrix material through the interphase which is a transition region from the
nanofillers to the matrix, and the high value of the reactive surface area per unit volume of
nanofillers.
Comprehensive understand of the mechanisms of mechanical property enhancement is crucial in
order to achieve the longstanding goal of predicting nanoparticles–nanocomposites–property
relationships in material design and optimization. Experimental characterizing and
nanomechanics-based computer modeling and simulation of mechanical properties of
nanocomposites are the two wings in understanding the mechanisms. Many traditional
simulation techniques have been employed, and some novel simulation techniques have been

302 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
developed to study nanocomposites. These techniques represent approaches at various time and
length scales from molecular scale to microscale, and then to macroscale, and have shown
success to various degrees in addressing many aspects of nanocomposites. The simulation
techniques developed thus far have different strengths and weaknesses, depending on the need of
research. Despite substantial progress made in the past decade, there are a number of challenges
in computer modeling and simulation. New concepts, theories and computational tools should be
developed. In general, there are two fronts that should be pointed out. First, there is a need to
develop new and improved simulation techniques at individual time and length scales. Secondly,
it is important to integrate the developed methods at wider range of time and length scales,
spanning from quantum domain to molecular domain, to mesoscopic domain, and finally to
macroscopic domain, to form a useful tool for exploring the structural and mechanical properties,
as well as optimizing design of nanocomposites [100]. Specific challenges and the solution
strategies are discussed in the following:
1. In either developing new or characterizing the current exist nanocomposites, a
comprehensive approach should be adopted that integrates the experimental techniques
with nanomechanics-based analytical explorations and computer modeling and
simulation.
2. New computational tools are specially needed in the area of multiscale RVE modeling.
The multiscale RVE modeling is in nature a “local-global” approach. In order to catch the
local nano/micro characteristics, quantum mechanics or molecular dynamics needs to be
explored. But the prediction of global macro-mechanical properties requires the
continuum mechanics-based finite element method. How to transit from local to global
becomes a research issue. Ogata et al. [198] proposed a way of combing quantum
mechanics, molecular dynamics, and finite elements. In regions where the atoms obey the
laws of continuum mechanics, the finite element method is used. However, in critical
areas such as the extremity of a fracture, molecular dynamics and even quantum
mechanics are required to obtain a more detailed study of the fracture process. The
transition from the global to local levels involves a change of scale. Xiao and Belytschko
[245] proposed a way of improving the numerical compatibility between regions modeled
by molecular dynamics and those modeled using the finite element method. The
suggested method is introducing a broad transition region by superposing the finite
element mesh of the continuum region on the atomistic structure of the molecular
dynamics region. Clearly, there is still a lot of work needs to be done in connecting the
local parameters to the global parameters.
3. In object-oriented finite element modeling, 2D modeling has been extensively used in
nanocomposites [e.g. 8, 179, 217], and there are also some works on 3D modeling [e.g.
178]. There are still issues to be resolved in 3D modeling, especially advanced object-
oriented 3D finite element codes.

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 303
ACKNOWLEDGEMENTS
This work was supported by the funding from the Air Force Office of Scientific Research and the
Department of Defense Research & Engineering Office with grant number FA9550-08-1-0230.
The first two authors would also like to acknowledge the significant interaction and support from
Drs. Jennifer Stewart-Wright and Evelyn Maria Thompson from Tennessee State University.
APPENDIX
Formulas Related to the Overall Moduli:
2
1
3
1
F
F
Tiijj ==
α
)
22
(
5
1
)
3
1
(
5
1
2
15
43 F
FF
FF
TT iijjijij
−
++=−= β
)362(
3
1
27271616
2
BFAFBFAF
F+++=
ϕ
5
)(
5
2
)2(
5
1
3
4
4
3
27162918
2
ϕ
ψ
−+++++=F
A
F
A
BFBFAFAF
F
where
))(23)(43(
3
1
)]2()32)(1[(
3
1
)]1(2)493)(1(
2
1
[
3
1
1
21
211
BBR
ARfRARfRF
−−−+
−++−+−+−+−+=
θ
θθθ
)2)](2()[43(
2
1
])1()[43()]1()1)(1[()3)(1(
2
1
1
212121
2
21212
ABBAAAfRfR
BBRARfRAfRF
+++−−+−+
−+−+−++−++−+=
θθθ
θθθθ
43 )]()
2
3
(1[1 AfRfF θθ +++−+=
34 )]()3[25.01 AfRfF −+++=
θ
θ
])1()[43()]1()1)(1[()3)(1(
2
1
221215 BBRARfRAfRF θθθθ −+−+−++−++−+=
226 )32)(43(
2
1
)]2()32)(1[(
2
1
1BRARfRF θθ −−+−++−+=
117 )23)(43()]1(4)493)(1[(
2
1
1BRARfRF −−+−+−+−+= θθθ
228 )1)(43()]1()1)(1[(1 BRARfRF
θ
θ
−
−
+
−++−+=

304 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
119 )43()3)(1(
2
1
1BRAfRF −++−+= θθ
The constants R, i
A(i =1, 2, 3, 4) and i B (i =1, 2) are non-dimensional ones related to the elastic
constants of the isotropic matrix and the transversely isotropic inhomogeneity.
mm
m
K
R
μ
μ
43
3
+
=
1
1−
−
=
m
ff lk
A
μ
,
m
ff ln
A
μ 2
2
−
=, 1
3−=
m
f
m
A
μ
, 1
4−=
m
f
p
A
μ
m
ff
m
ff lk
K
lk
B
μ 6
22
9
2
1
−
−
+
=,
m
ff
m
ff ln
K
ln
B
μ 69
2
2
−
−
+
=
where k, n, m, p, and l are the notations adopted by Hill. They can be expressed in general by
stiffness tensor components as
)(
2
1
22332222 CCk += , 1111
Cn =, )(
2
1
22332222 CCm −= , 1212
Cp
=
, 1122
Cl
=
For an isotropic material, the above constants degenerate into
μ
3
1
+= Kk, μ
3
4
+= Kn ,
μ
=
=pm , μ
3
2
−= Kl
f and
θ
are related to the geometry of the spheroidal inhomogeneity, which are
spheroid, prolatefor 1/),32(
1
spheroid, oblatefor 1/),23(
1
321
2
2
132
2
2
⎪
⎪
⎩
⎪
⎪
⎨
⎧
==<=>=−
−
=>==<=−
−
=
caaaaac
caaaaac
f
χθ
χ
χ
χθ
χ
χ
spheroid prolatefor }cosh)1({
)1(
spheroid oblatefor })1({cos
)1(
12/12
2/32
2/121
2/32
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−−
−
−−
−
=
−
−
χχχ
χ
χ
χχχ
χ
χ
θ
REFERENCES
[1] Braun T, Schubert A, Zsindely S. Nanoscience and nanotechnology on the balance.
Scientometrics 1997;38:321–325.
[2] Alexandre M, Dubois P. Polymer-layered silicate nanocomposites: preparation, properties
and uses of a new class of materials. Mater Sci Eng 2000;28:1–63.
[3] Herron N, Thorn DL. Nanoparticles: uses and relationships to molecular clusters. Adv
Mater 1998;10:1173–84.

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 305
[4] Kumar AP, Depan D, Tomer NS, Singh RP. Nanoscale particles for polymer degradation
and stabilization-Trends and future perspectives. Progress in Polymer Science, 2009; 34:
479-515.
[5] Vaia RA,Wagner HD. Framework for nanocomposites. Mater Today 2004;7:32–7.
[6] Liu H, Brinson LC. Reinforcing efficiency of nanoparticles: A simple comparison for
polymer nanocomposites. Compos Sci Technol 2008; 68: 1502-1512.
[7] Thilly L, Petegem SV, Renault PO, Lecouturier F, Vidal V, Schmitt B, Swygenhoven V. A
new criterion for elastio-plastic transition in nanomaterials: Application to size and
composite effects on Cu-Nb nanocomposite wires. Acta Materialia 2009; 57: 3157-3169.
[8] Dong Y, Bhattacharyya D, Hunter, PJ. Experiental Characterisation and object-oriented
finite element modeling of polypropylene/organoclay nanocomposites. Comp Sci Technol
2008; 68: 2864-2875.
[9] Chen Q, Chasiotis I, Chen C, Roy A. Nanoscale and effective mechanical behavior and
fracture of silica nanocomposites. Comp Sci Technol. 2008; 68: 3137-3144.
[10] Chen WH, Cheng HC, Hsu YC, Uang RH, Hsu JS. Mechanical material characterization of
Co nanowires and their nanocomposite. Comp Sci Technol 2008; 68: 3388-3395.
[11] Song SY, Youn JR. Modelling of effective elastic properties of polymer based carbon
nanotube composites. Polymer 2006; 47, 1741-1748.
[12] Schuster, BE, Wei Q, Ervin MH, Hruszkewycz SO, Miller MK, Hufnagel TC, Ramesh KT.
Bulk and microscale compressive properties of a pd-based metallic glass. Scripta
Materialia 2007; 57 (6), 517-520.
[13] Zhang H, Schuster BE, Wei Q, Ramesh KT. The design of accurate micro-compression
experiments. Scripta Materialia 2006, 54(2), 181-186.
[14] Chang NK, Lin YS, Chen CY, Chang SH. Size effect of indenter on determining modulus
of nanowires using nanoindentation technique. Thin Solid Films 2009; 517: 3695-3697.
[15] Poon B, Rittel D, Ravichandran D. An analysis of nanoindentation in linearly elastic solids.
Int. J. Solids Struct. 2008; 45: 6018-6033.
[16] Han CF, Lin JF. Modeling to evaluate the contact areas of hard materials during the nano-
indentation tests. Sensors Actuators A 2008; 147(1): 229-241.
[17] Ling Z, Hou J. A nanoindentation analysis of the effects of microstructures on elastic
properties of Al2O3/SiC composites. Comp. Sci. Technol. 2007; 67: 3121-3129.
[18] Lee SH, Wang S, Pharr GM, Xu H. Evaluation of interphase properties in a cellulose fiber-
reinforced polypropylene composite by nanoindentation and finite element analysis.
Composites: Part A 2007; 38: 1517-1524.
[19] Qi HJ, Teo KBK, Lau KKS, Boyce MC, Milne WI, Robertson J, Gleason KK.
Determination of mechanical properties of carbon nanotubes and vertically aligned carbon
nanotube forests using nanoindentation. J. Mech. Phy. Solids. 2003; 51: 2213-2237.
[20] Li X, Bhushan B. A review of nanoindentation continuous stiffness measurement technique
and its applications. Mater Charact. 2002; 48:11–36.

306 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
[21] Gao SL, Mader E. Characterisation of interphase nanoscale property variations in glass
fiber reinforced polypropylene and epoxy resin composites. Composites: Part A 2002;
33:559–576.
[22] Hodzic A, Stachurskia ZH, Kim JK. Nano-indentation of polymer–glass interfaces part I
experimental and mechanical analysis. Polymer 2000;41:6895–905.
[23] Downing TD, Kumar R, Cross WM, Kjerengtroen L, Kellar JJ. Determining the interphase
thickness and properties in polymer matrix composites using phase imaging atomic force
microscopy and nanoindentation. J Adhes Sci Technol 2000;14:1801–12.
[24] Munz M, Sturm H, Schulz E, Hinrichsen G. The scanning force microscope as a tool for
the detection of local mechanical properties within the interphase of fiber reinforced
polymers. Composites: Part A 1998; 29A:1251–9.
[25] Oliver WC, Pharr GM. An improved technique for determining hardness and elastic
modulus using load and displacement sensing indentation experiments. J Mater Res 1992;
7(6):1564–83.
[26] Fong H, Sarıkaya M, White SN, Snead ML. Nanomechanical properties profiles across
dentin—enamel junction of human incisor teeth, Mater. Sci. Eng. 2000; C7: 119—128.
[27] Zysset PK, Guo XE, Hoffler CE, Moore KE, Goldstein SA. Elastic modulus and hardness
of cortical and trabecular bone lamellae measured by nanoindentation in the human femur,
J. Biomech. 1999; 32: 1005—1012.
[28] Habelitz S, Marshall GW, Balooch M, Marshall SJ. Nanoindentation and storage of teeth,
J. Biomech. 2002; 35: 995—998.
[29] Cuy JL, Mann AB, Livi KJ, Teaford MF, Weihs TP. Nanoindentation mapping of the
mechanical properties of human molar tooth enamel. Arch. Oral Biol. 2002; 47: 281—291.
[30] Marshall GW, Balooch M, Gallagher RR, Gansky SA, Marshall SJ. Mechanical properties
of the dentinoenamel junction: AFM studies of nanohardness, elastic modulus, and
fracture. J. Biomedic. Res. 2001; 54: 87—95.
[31] Poolthong S, Mori T, Swain MV. Determination of elastic modulus of dentin by small
spherical diamond indenters. J. Dent. Mater. 2001; 20: 227—236.
[32] Habelitz S, Marshall SJ, Marshall GW, Balooch M. Mechanical properties of human dental
enamel on the nanometer scale. Arch. Oral Biol. 2001; 46: 173—183.
[33] Xu HHK, Smith DT, Jahanmir S, Romberg E, Kelly JR, Thompson VP, Rekow ED.
Indentation damage and mechanical properties of human enamel and dentin. J. Dent. Res.
1998; 77: 472—480.
[34] Kinney JH, Balooch M, Marshall SJ, Marshall GW, Wehs TP. Atomic force microscope
measurements of the hardness and elasticity of peritubular and intertubular human dentin.
J. Biomech. Eng. 1996; 118: 133—135.
[35] Meredith N, Sherriff M, Setchell DJ, Sivanson SAV. Measurements of the microhardness
and Young modulus of human enamel and dentin using an indentation technique. Arch.
Oral Biol. 1996; 41: 539—545.

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 307
[36] Kinney JH, Balooch M, Marshall SJ, Marshall GW, Weihs TP. Hardness and Young’s
modulus of peritubular and intertubular dentine. Arch. Oral Biol. 1996; 41: 9-13.
[37] van Meerbeek B, Willems G, Celis JP, Roos JR, Braem M, Lambrechts P, Vanherle G.
Assessment by nanoindentation of the hardness and elasticity of the resin—dentin bonding
area. J. Dent. Res. 1993; 72: 1434—1442.
[38] Toparli M, Koksal NS. Hardness and yield strength of dentin from simulated nano-
indentation tests. Comp Meth Progr Biomedi 2005; 77, 253-257.
[39] Shin C, Jin HH, Kim MW. Evaluation of the depth-dependent yield strength of a
nanoindented ion-irradiated Fe–Cr model alloy by using a finite element modeling. J. Nucl.
Mater. 2009; 392(3): 476-481.
[40] Li B, Gu YD, English R, Rothwell G, Ren XJ. Characterisation of nonlinear material
parameters of foams based on indentation tests. Mater. Design 2009; 30(7): 2708-2714.
[41] Wang, T.H., Fang, T.H., Lin, Y.C. A numerical study of factors affecting the
characterization of nanoindentation on silicon. Mater. Sci. Eng. 2006; 447: 244–253.
[42] Pelletier H, Krier J, Mille P. Characterization of mechanical properties of thin films using
nanoindentation test. Mech. Mater. 2006; 38: 1182-1198.
[43] Yu, N., Polycarpou, A.A., Conry, T.F. Tip-radius effect in finite element modeling of sub-
50 Nm shallow nanoindentation. Thin Solid Films 2004; 450, 295–303.
[44] Dao M, Chollacoop N, Vliet KJV, Venkatesh TA, Suresh S. Computational modeling of
the forward and reverse problems in instrumented sharp indentation. Acta Mater. 2001; 49,
3899–3918.
[45] Zhang W, Subhash G. Finite element analysis of interacting Vickers indentations on brittle
materials. Acta Mater. 2001; 49 (15): 2961-2974.
[46] Zhang W, Subhash G. An elastic–plastic-cracking model for finite element analysis of
indentation cracking in brittle materials. Int. J. Solids Struct. 2001; 38(34/35): 5893-5913.
[47] Lichinchi, M., Lenardi, C., Haupta, J., Vitalib, R. Simulation of Berkovich nanoindentation
experiments on thin films using finite element method. Thin Solid Films 1998; 312: 240–
248.
[48] Gan L, Ben-Nissan B. The effects of mechanical properties of thin films on nano-
indentation data: Finite element analysis. Comp. Mater. Sci. 1997; 8: 273-281.
[49] Zeng K, Giannakopoulos AE, Rowcliffe DJ. Vickers indentations in glass—II. Comparison
of finite element analysis and experiments. Acta Metallur. Mater. 1995; 43: 1945-1954.
[50] Kral ER, Komvopoulos K, Bogy DB. Elastic–plastic finite element analysis of repeated
indentation of a half-space by a rigid sphere. J. Appl. Mech. 1993; 75: 829–841.
[51] Wang HF, Yang X, Bangert H, Torzicky P, Wen L. Two-dimensional finite element
method simulation of Vickers indentation of hardness measurements on TiN-coated steel.
Thin Solid Films 1992; 214: 68-73.
[52] Maritza GJ. Veprek-Heijman, Ratko G. Veprek, Ali S. Argon, David M. Parks and Stan
Veprek. Non-linear finite element constitutive modeling of indentation into super- and
ultrahard materials: The plastic deformation of the diamond tip and the ratio of hardness to

308 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
tensile yield strength of super- and ultrahard nanocomposites. Surf. Coat. Technol. 2009;
203: 3385-3391.
[53] Jiang W, Batra RC. Identification of elastic constants of FCC metals from 2D load-
indentation curves. Comp. Mater. Sci. 2009; 45(2): 511-515.
[54] Harsono E, Swaddiwudhipong S, Liu ZS. Material characterization based on simulated
spherical-Berkovich indentation tests. Scrip. Mater. 2009; 60(11): 972-975.
[55] Geng K, Yang F, Grulke EA. Nanoindentation of submicron polymeric coating systems.
Mater. Sci. Eng. A. 2008; 479(1/2): 157-163.
[56] Farrissey LM, McHugh PE. Determination of elastic and plastic material properties using
indentation: Development of method and application to a thin surface coating. Mater. Sci.
Eng A 2005; 399: 254-266.
[57] Zeng K, Soderlund E, Giannakopoulos AE, Rowcliffe DJ. Controlled indentations: a
general approach to determine mechanical properties of brittle materials. Acta Mater. 1996;
44: 1127-1141.
[58] Yoshino M, Aoki T, Chandrasekaran N, Shirakashi T, Komanduri R. Finite element
simulation of plane strain plastic–elastic indentation on single-crystal silicon. Int. J. Mech.
Sci. 2001; 43 (2): 313-333.
[59] Fisher FT, Brinson LC. Nanomechanics of nanoreinforced polymers. In: Rieth M,
Schommers W, editors. Handbook of theoretical and computational nanoscience. American
Scientific Publishers; 2006. 253–360.
[60] Moniruzzaman M, Winey KI. Polymer nanocomposites containing carbon nanotubes.
Macromolecules 2006;39(16):5194–5205.
[61] Thostenson ET, Li CY, Chou TW. Nanocomposites in context. Compos Sci Technol
2005;65: 491–516.
[62] Ajayan PM, Schadler LS, Braun PV. Nanocomposite science and technology. Weinheim:
WILEY-VCH Verlag GmbH & Co. KGaA; 2003.
[63] Srivastava D, Wei CY, Cho K. Nanomechanics of carbon nanotubes and composites. Appl
Mech Rev 2003; 56: 215–30.
[64] Leamy MJ. Bulk dynamic response modeling of carbon nanotubes using an intrinsic finite
element formulation incorporating interatomic potentials. Int J Solids Struct 2007; 44: 874–
94.
[65] Odegard GM, Gates TS. Modeling and testing of the viscoelastic properties of a graphite
nanoplatelet/epoxy composite. J Intell Mater Syst Struct 2006;17: 239–46.
[66] Sears A, Batra RC. Buckling of multiwalled carbon nanotubes under axial compression.
Phys Rev B 2006; 73:085410-1–085410-11.
[67] Arroyo M, Belytschko T. Continuum mechanics modeling and simulation of carbon
nanotubes. Meccanica 2005;40(4–6):455–69.
[68] Odegard GM, Clancy TC, Gates TS. Modeling of the mechanical properties of
nanoparticle/polymer composites. Polymer 2005; 46: 553–62.

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 309
[69] Arroyo M, Belytschko T. Finite element methods for the non-linear mechanics of crystalline
sheets and nanotubes. Int J Numer Methods Eng 2004;59(3):419–56.
[70] Zhu LJ, Narh KA. Numerical simulation of the tensile modulus of nanoclay-filled polymer
composites. J Polym Sci 2004; 42: 2391–406.
[71] Wu YP, Jia QX, Yu DS, Zhang LQ. Modeling Young’s modulus of rubber–clay using
composite theories. Polym Testing 2004; 23: 903–9.
[72] Luo J-J, Daniel IM. Characterization and modeling of mechanical behaviour of
polymer/clay nanocomposites. Compos Sci Technol 2003;63:1607–16.
[73] Fornes TD, Paul DR. Modeling properties of nylon 6/clay nanocomposites using composite
theories. Polymer 2003;44:4993–5013.
[74] Voigt W. Uber die beziehung zwischen den beiden elasticitatsconstanten isotroper korper.
Ann Phys 1889; 38:573–87.
[75] Reuss A. Berechnung der fliebgrenze von mischkristalen auf grund der
plastizitatsbedingung fur einkristalle. ZAMM 1929; 9:49–58.
[76] Hashin Z, Shtrikman, S. A variational approach to the theory of the elastic behavior of
multiphase materials. J Mech Phys Solids 1963; 11: 127-40.
[77] Hashin Z, Analysis of composite materials-a survey. J. Appl. Mech. 1983; 50: 481-505.
[78] Halpin JC. Primer on composite materials: analysis. Lancaster: Technomic Publishing
Company; 1984.
[79] Halpin JC, Kardos JL. The Halpin-Tsai equations: a review. Polym Eng Sci 1976; 16: 344-
52.
[80] Halpin JC. Stiffness and expansion estimates for oriented short fiber composites. J Compos
Mater 1969; 3:742-4.
[81] Halpin JC, Tsai SW. Effect of environmental factors on composite materials; Air Force
Technical Report AFML-TR 67-423. Dayton, OH: Wright Aeronautical Laboratories;
1967.
[82] Hermans JJ. The elastic properties of fiber oriented materials when the fibers are aligned.
Proc Kon Ned Akad v Wetensch B 1967; 65: 1-9.
[83] Hill R. Theory of mechanical properties of fibre-strengthened materials: I elastic behaviour.
J Mech Phys Solids 1964; 12: 199-212.
[84] Mori T, Tanaka K. Average stress in matrix and average elastic energy of materials with
misfitting inclusions. Acta Metall 1973; 21:571–4.
[85] Eshelby JD. The determination of the elastic field of an ellipsoidal inclusion and related
problems. Proc R Soc London A 1957; 241:376–96.
[86] Taya M, Mura T. On stiffness and strength of an aligned short-fiber reinforced composite
containing fiber-end cracks inder uniaxial applied stress. J Appl Mech 1981; 48: 361-7.
[87] Taya M, Chou T-W. On two kinds of ellipsoidal inhomogeneities in an infinite elastic
body: an application to a hybrid composite. Int J Solids Struct 1981; 17: 553-63.
[88] Weng GJ. Some elastic properties of reinforced solids, with special reference to isotropic
ones containing spherical inclusions. Int J Engng Sci 1984; 22 :845-56.

310 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
[89] Tandon GP, Weng GJ. The effect of aspect ratio of inclusions on the elastic properties of
unidirectionally aligned composites. Polym Compos 1984;5:327–33.
[90] Hui CY, Shia D. Simple formulae for the effective moduli of unidirectional aligned
composites. Polym Eng Sci 1998;38:774–82.
[91] Shia D, Hui CY, Burnside SD, Giannelis EP. An interface model for the prediction of
Young’s modulus of layered silicate-elastomer nanocomposites. Polym Compos
1998;19:608–17.
[92] Qiu YP, Weng GJ. On the application of Mori-Tanaka’s theory involving transversely
isotropic spheroidal inclusions. Int J Eng Sci 1990; 28: 1121-37.
[93] Chen T, Dvorak GJ, Benveniste Y. Mori-Tanaka estimate of the overall elastic moduli of
certain composite materials. J Appl Mech 1992; 59: 539-46.
[94] Wang J, Pyrz R. Prediction of the overall moduli of layered silicate-reinforced
nanocomposites-part I: basic theory and formulas. Compos Sci Tech 2004;64:925-934.
[95] Cox HL. The elasticity and strength of paper and other fibrous materials. Brit J Appl Phys
1952; 3: 72-9.
[96] Tucker III CL, Liang E. Stiffness prediction for unidirectional short-fiber composites:
Review and evaluation. Compos Sci Tech 1999; 59: 655-671.
[97] Van Es M, Xiqiao F, Van Turnhout, Van der Giessen E. Comparing polymer-clay
nanocomposites with conventional composites using composite modeling. In: Al-Malaika
S, Golovoy AW, editors. Specially polymer additives: principles and applications. CA
Malden, MA: Blackwell Science; 2001. Chapter 21.
[98] Rapaport DC. The Art and Science of Molecular Dynamics Simulation. Cambridge:
Cambridge University Press; 2004.
[99] Frenkel D, Smit B. Understanding molecular simulation: from algorithms to applications.
2nd ed. San Diego: Academic Press; 2002.
[100] Zeng QH, Yu AB, Lu GQ. Multiscale modeling and simulation of polymer
nanocomposites. Prog. Polym. Sci. 2008; 33: 191–269
[101] Cornwell CF, Wille LT. Elastic properties of single-walled carbon nanotubes in
compression. Solid State Commun 1997;101:555–8.
[102] Zhu R, Pan E, Roy AK. Molecular dynamics study of the stress-strain behavior of carbon-
nanotube reinforced Epon 862 composites. Mater Sci Eng A 2007; 447: 51-57.
[103] Mokashi VV, Qian D, Liu YJ. A study on the tensile response and fracture in carbon
nanotube-based composites using molecular mechanics. Compos Sci Technol
2007;67:530–40.
[104] Zheng QB, Xue QZ, Yan KO, Hao LZ, Li Q, Gao XL. Investigation of molecular
interactions between SWNT and polyethylene/polypropylene/polystyrene/ polyaniline
molecules. J Phys Chem C 2007;111:4628–35.
[105] Sun X, Zhao W. Prediction of stiffness and strength of single-walled carbon nanotubes by
molecular-mechanics based finite element approach. Mater Sci Eng 2005; 390: 366-71.

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 311
[106] Xiao JR, Gama BA, Gillespie Jr JW. An analytical molecular structural mechanics model
for the mechanical properties of carbon nanotubes. Int J Solids Struct 2005; 42: 3075-92.
[107] Bao WX, Zhu CC, Cui WZ. Simulation of Young’s modulus of single-walled carbon
nanotubes by molecular dynamics. Physica B. 2004; 352: 156-63.
[108] Saether E, Frankland SJV, Pipes RB. Transverse mechanical properties of single-walled
carbon nanotube crystals. Part I: determination of elastic moduli. Compos Sci Tech
2003;63:1543-50.
[109] Odegard GM, Gates TS, Wise KE, Park C, Siochi EJ. Constitutive modeling of nanotube–
reinforced polymer composites. Compos Sci Tech 2003; 63: 1671-87.
[110] Scarpa F, Adhikari S, Phani AS. Effective elastic mechanical properties of single layer
grapheme sheets. Nanotechnology 2009; 20: 065709.
[111] Hemmasizadeh A, Mahzoon M, Hadi E, Khandan R. A method for developing the
equivalent continuum model of single layer grapheme sheet. Thin Solid Films 2008; 516:
7636-40.
[112] Cho J, Luo JJ, Danial IM. Mechanical characterization of graphite/epoxy nanocomposites
by multi-scale analysis. Compos Sci Tech 2007; 67: 2399-407.
[113] Prathab B, Subramanian V, Aminabhavi TM. Molecular dynamics simulations to
investigate polymer–polymer and polymer–metal oxide interactions. Polymer 2007;48:
409–16.
[114] Suter JL, Coveney PV, Greenwell HC, Thyveetil MA. Large-scale molecular dynamics
study of montmorillonite clay: emergence of undulatory fluctuations and determination of
material properties. J Phys Chem C 2007;111: 8248–59.
[115] Ward DK, Curtin WA, Qi Y. Mechanical behavior of aluminum-silicon nanocomposites:
A molecular dynamics study. Acta Materialia 2006; 54: 4441-51.
[116] Patel RR, Mohanraj R, Pittman CU. Properties of polystyrene and polymethyl
methacrylate copolymers of polyhedral oligomeric silsesquioxanes: a molecular dynamics
study. J Polym Sci Part B: Polym Phys 2006;44: 234–48.
[117] Bizet S, Galy J, Gerard JF. Molecular dynamics simulation of organic–inorganic
copolymers based on methacryl–POSS and methyl methacrylate. Polymer 2006;47:8219–
27.
[118] Minisini B, Tsobnang F. Molecular dynamics study of specific interactions in grafted
polypropylene organomodified clay nanocomposite. Compos Part A: Appl Sci Manuf
2005;36:539–44.
[119] Sen TZ, Sharaf MA, Mark JE, Kloczkowski A. Modeling the elastomeric properties of
stereoregular polypropylenes in nanocomposites with spherical fillers. Polymer
2005;46:7301–8.
[120] Lau K, Gu C, Hui D. A critical review on nanotube and nanotube/nanoclay related polymer
composite materials. Composites: Part B 2006; 37: 425–436.
[121] Smith W, Forester TR. DLPOLY-2.14 manual; 2004. Internet Source:
http://www.cse.clrc.ac.uk/msi/software/DL_POLY/MANUALS/USRMAN2.pdf.

312 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
[122] Smith W, Forester TR. DL_POLY_2.0: A general-purpose parallel molecular dynamics
simulation package. J Mol Graph 1996; 14: 136-41.
[123] Plimpton SJ. LAMMPS Documentation. Internet Source:
http://www.cs.sandia.gov/~sjplimp/lammps/doc/Manual.html.
[124] Ponder JW. TINKER: Software tools for molecular design, Version 3.8. Washington
University School of Medicine; 1998.
[125] Adnan A, Sun CT, Mahfuz H. A molecular dynamics simulation study to investigate the
effect of filler size on elastic properties of polymer nanocomposites. Compos Sci Technol
2007;67:348–56.
[126] Mayo SL, Olafson BD, Goddard III WA. DREIDING: A generic force field for molecular
simulations. J Phys Chem 1990; 94: 8897–909.
[127] Binder K. Monte carlo and molecular dynamics simulations in polymer science. New
York: Oxford University Press; 1995.
[128] Broutman LJ, Panizza G. Micromechanics studies of rubber-reinforced glassy polymers.
Int J Polymeric Mat 1971; 1: 95-109.
[129] Agarwal BD, Broutman LJ. Three-dimensional finite element analysis of spherical particle
composites. Fibre Sci Tech 1974; 7: 63-77.
[130] Needleman A. A continuum model for void nucleation by inclusion debonding. J Appl
Mech 1987; 54: 525-531.
[131] Christman T, Needleman A, Suresh S. An experimental and numerical study of
deformation of metal-ceramic composites. Acta Metall Mater 1989; 37: 3029-50.
[132] Llorca J, Needleman A, Suresh S. An analysis of the effects of matrix void growth on
deformation and ductility in metal-ceramic composites. Acta Metall Mater 1991; 39: 2317-
35.
[133] Tvergaard V. Analysis of tensile properties for a whisker-reinforced metal-matrix
composite. Acta Metall Mater1990; 38: 185-94.
[134] Lee BJ, Mear ME. Effect of inclusion shape on stiffness of isotropic and transversely
isotropic two-phase composites. Int J Solids Struct 1991; 28: 975-1001.
[135] Lee BJ, Mear ME. Effect of inclusion shape on stiffness of nonlinear two-phase
composites. J Mech Phys Solids 1991; 39: 627-49.
[136] Banks-Sills L, Leiderman V, Fang D. On the effect of particle shape and orientation on
elastic properties of metal matrix composites. Composites: Part B 1997; 28B:465-81.
[137] Iijima S. Helical microtubles of graphitic carbon. Nature 1991; 354: 56-8.
[138] Treacy MMJ, Ebbesen TW, Gibson TM. Exceptionally high Young’s modulus observed
for individual carbon nanotubes. Nature 1996; 381: 680-7.
[139] Popov VN, Van Doren EV, Balkanski M. Elastic properties of single-walled carbon
nanotubes. Phys Rev B 2000; 61: 3078-84.
[140] Uddin MF, Sun CT. Strength of unidirectional glass/epoxy composite with silica
nanoparticle-enhanced matrix. Compos Sci Technol 2008; 68: 1637-43.

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 313
[141] Zhang J, Wu T, Wang L, Jiang W, Chen L. Microstructure and properties of Ti3SiC2/SiC
nanocomposites fabricated by spark plasma sintering. Compos Sci Technol 2008; 68: 499-
505.
[142] Tsai JL, Wu MD. Organoclay effect on mechanical responses of glass/epoxy
nanocomposites. J Compos Mater 2007; 41: 2513.
[143] Cho J, Chen JY, Daniel IM. Mechanical enhancement of carbon fiber/epoxy composites by
graphite nanoplatelet reinforcement. Scripta Mater 2007; 56: 685.
[144] Kanagaraj S, Varanda FR, Zhiltsova TV, Oliveira MSA, Simoes JAO. Mechanical
properties of high density polyethylene/carbon nanotube composites. Compos Sci Technol
2007; 67: 3071-7.
[145] Katti KS, Sikdar D, Katti DR, Ghosh P, Verma D. Molecular interactions in intercalated
organically modified clay and clay-polycaprolactam nanocomposites: experiments and
modeling. Polymer 2006; 47: 403-14.
[146] Wang ZD, Lu JJ, Li Y, Fu SY, Jiang SQ, Zhao XX. Studies on thermal and mechanical
properties of PI/SiO2 nanocomposite films at low temperature. Composite A 2006; 37: 74-
9.
[147] Buryachenko VA, Roy A, Lafdi K, Anderson KL, Chellapilla S. Multi-scale mechanics of
nanocomposites including interface: experimental and numerical investigation. Compos Sci
Technol 2005; 65: 2435-65.
[148] Dalton BA, Collins S, Munoz E, Razal MJ, Von Howaed E, Ferraris PJ, et al. Super-tough
carbon-nanotube fibers. Nature 2003; 423: 703-5.
[149] Zhu HW, Xu CL, Wu DH, Wei BQ, Vajtai R, Ajayan PM. Direct synthesis of long single-
walled carbon nanotube strands. Science 2002; 296: 884-6.
[150] Yu MF, Lourie O, Dyer MJ, Moloni K, Kelly TF, Ruoff RS. Strength and breaking
mechanics of multiwalled carbon nanotubes under tensile load. Science 2000; 287: 637-40.
[151] Li F, Cheng HM, Bai S, Su G, Dresselhaus MS. Tensile strength of single-walled carbon
nanotubes directly measured from their macroscopic ropes. Appl Phys Lett 2000; 77: 3161-
3.
[152] Bower C, Rosen R, Jin L, Han J, et al. Deformation of carbon nanotubes in nanotube-
polymer composites. Appl Phys Lett 1999; 74: 3317-19.
[153] Schadler LS,Giannaris SC, Ajayan PM. Load transfer in carbon nanotube epoxy
composites. Appl Phys Lett 1998; 73: 3842-44.
[154] Wagner HD, Lourie O, Feldman Y, Tenne R. Stress-induced fragmentation of multiwall
carbon nanotubes in a polymer matrix. Appl Phys Lett 1998; 72: 188-90.
[155] Wong EW, Sheehan PE, Lieber CM. Nanobeam mechanics: elasticity, strength, and
toughness of nanorods and nanotubes. Science 1997; 277: 1971-5.
[156] Boutaleb S, Zairi F, Mesbah A, Nait-Abdelaziz M, Gloaguen JM, Boukharouba T,
Lefebvre JM. Micromechanics-based modeling of stiffness and yield stress for
silica/polymer nanocomposites. Int J Solids Struct 2009; 46: 1716-26.

314 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
[157] Ashrafi B, Hubert P. Modeling the elastic properties of carbon nanotube array/polymer
composites. Compos Sci Technol 2006; 66: 387-96.
[158] Berhan L, Yi YB, Sastry AM, Munoz E, Selvidge M, Baughman RJ. Mechanical
properties of nanotube sheets: Alterations in joint morphology and achievable moduli in
manufacturable materials. Appl Phys 2004; 95: 4335-45.
[159] Odegard GM, Pipes RB, Hubert P. Comparison of two models of SWCN polymer
composites. Comp Sci Technol 2004; 64: 1011-20.
[160] Thostenson ET, Chou TW. On the elastic properties of carbon nanotube-based composites:
modeling and characterization. J Appl Phys D 2003; 36: 573-82.
[161] Pipes RB, Hubert P. Scale effects in carbon nanostructures: self-similar analysis. Nano Lett
2003; 3: 239-43.
[162] Pipes RB, Hubert P. Helical carbon nanotube arrays: mechanical properties. Comps Sci
Technol 2002; 62: 419-28.
[163] Tu ZC, Ou-yang ZC. Single-walled and multiwalled carbon nanotubes viewed as elastic
tubes with the effective Young’s moduli dependent on layer number. Phys Rev B 2002; 65:
233-407.
[164] Zhou G, Duan WH, Gu BL. First-principles study on morphology and mechanical
properties of single-walled carbon nanotube. Chem Phys Lett 2001; 333: 344-9.
[165] Qian D, Liu WK, Ruoff RS. Mechanics of C60 in nanotubes. J Phys Chem B 2001; 105:
10753-8.
[166] Govindjee S, Sackman JL. On the use of continuum mechanics to estimate the properties
of nanotubes. Solid State Comm 1999; 110: 227-30.
[167] Gao GH, Cagin T, Goddard WA. Energetics, structure, mechanical and vibrational
properties of single-walled carbon nanotubes. Nanotech 1998; 9: 184-91.
[168] Krishnan A, Dujardin E, Ebbesen TW, Yianilos PN, Treacy MMJ. Young’s modulus of
single-walled nanotubes. Phys Rev B 1998; 58: 14013-9.
[169] Cornwell CF, Wille LT. Elastic properties of single-walled carbon nanotubes in
compression. Solid State Comm 1997; 101: 555-8.
[170] Lee WJ, Son JH, Kang NH, Park IM, Park YH. Finite-element analysis of deformation
behaviors in random-whisker-reinforced composite. Scripta Mater 2009; 61: 580-3.
[171] Qiao R, Brinson C. Simulation of interphase percolation and gradients in polymer
nanocomposites. Compos Sci Technol 2009; 69: 491-9.
[172] Tserpes KI, Papanikos P, Labeas G, Pantelakis SpG. Multi-scale modeling of tensile
behavior of carbon nanotube-reinforced composites. Theoret Appl Fract Mech 2008; 49:
51-60.
[173] Gonzalez C, Llorca J. Mechanical behavior of unidirectional fiber-reinforced polymers
under transverse compression: microscopic mechanisms and modeling. Compos Sci
Technol 2007; 67: 2795-806.
[174] Saber-Samandari S, Afaghi-Khatibi A. Evaluation of elastic modulus of polymer matrix
nanocomposites. Polym Compos 2007; 28: 405-11.

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 315
[175] Scocchi G, Posocco P, Fermeglia M, Pricl S. Polymer–clay nanocomposites: a multiscale
molecular modeling approach. J Phys Chem B 2007;111:2143–51.
[176] Fermeglia M, Pricl S. Multiscale modeling for polymer systems of industrial interest. Prog
Org Coat 2007;58:187–99.
[177] Hbaieb K, Wang QX, Chia YHJ, Cotterell B. Modeling stiffness of polymer/clay
nanocomposites. Polymer 2007; 48: 901-9.
[178] Chawla N, Sidhu RS, Ganesh VV. Three-dimansional visualization and microstructure-
based modeling of deformation in particle-reinforced composits. Acta Mater 2006; 54:
1541-8.
[179] Cannillo V, Bondioli F, Lusvarghi L, Montorsi M, Avella M, Errico ME, Malinconico M.
Modeling of ceramic particles filled polymer-matrix nanocomposites. Compos Sci Technol
2006; 66: 1031-7.
[180] Li C, Chou TW. Multiscale modeling of compressive behavior of carbon
nanotube/polymer composites. Compos Sci Technol 2006; 66: 2409-14.
[181] Ji B, Gao H. Elastic properties of nanocomposite structure of bone. Compos Sci Technol
2006; 66: 1212-8.
[182] Bondioli F, Cannillo V, Fabbri E, Messori M. Epoxy-silica nanocomposites: preparation,
experimental characterization, and modeling. J Appl Polym Sci 2005; 97: 2382-2386.
[183] Borodin O, Bedrov D, Smith GD, Nairn J, Bardenhagen S. Multiscale modeling of
viscoelastic properties of polymer nanocomposites. J Polym Sci Part B: Polym Phys 2005;
43:1005–13.
[184] Buryachenko VA. Effective elastic moduli of triply periodic particulate matrix composites
with imperfect unit cells. Int J Solids Struct 2005;42:4811–32.
[185] Shi D, Feng X, Jiang H, Huang YY, Hwang K. Multiscale analysis of fracture of carbon
nanotubes embedded in composites. Int J Fract 2005; 134: 369–86.
[186] Buryachenko VA, Tandon GP. Estimation of effective elastic properties of random
structure composites for arbitrary inclusion shape and anisotropy of components using
finite element analysis. Int J Multiscale Comput Engng 2004;2:29–45.
[187] Avella M, Bondioli F, Cannillo V, Errico ME, Ferrari AM, Focher B. Preparation,
characterisation and computational study of poly (epsilon-caprolactone) based
nanocomposites. Mater Sci Technol 2004;20:1340–4.
[188] Chen XL, Liu YJ. Square representative volume elements for evaluating the effective
material properties of carbon nanotube-based composites. Comput Mater Sci 2004; 29: 1-
11.
[189] Sheng N, Boyce MC, Parks DM, Rutledge GC, Abes JI, Cohen RE. Multiscale
micromechanical modeling of polymer nanocomposites and the effective clay particle.
Polymer 2004; 45:487–506.
[190] Porter D. Pragmatic multiscale modelling of bone as a natural hybrid nanocomposite.
Mater Sci Eng A 2004; 365:38–45.

316 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
[191] Fisher FT, Bradshaw RD, Brinson LC. Fiber waviness in nanotube-reinforced polymer
composites-1: modulus predictions using effective nanotube properties. Compos Sci
Technol 2003;63:1689–703.
[192] Bradshaw RD, Fisher FT, Brinson LC. Fiber waviness in nanotube-reinforced polymer
composites-II: modeling via numerical approximation of the dilute strain concentration
tensor. Compos Sci Technol 2003;63:1705–22.
[193] Li C, Chou TW. A structural mechanics approach for the analysis of carbon nanotubes. Int
J Solids Struct 2003;40:2487–99.
[194] Liu YJ, Chen XL. Evaluations of the materials properties of carbon nanotube-based
composites using a nanoscale representative volume element. Mech Mater 2003; 35: 69-81.
[195] Odegard GM, Gates TS, Nicholson LM, Wise KE. Equivalent continuum modeling of
nano-structured materials. Compos Sci Technol 2002;62:1869–80.
[196] Starr FW, Glotzer SC. Simulations of filled polymers on multiple length scales. In:
Nakatani AI, Hjelm RP, Gerspacher M, Krishnamoorti R, editors. Filled and
Nanocomposite Polymer Materials, Materials Research Symposium Proceedings.
Warrendale: Materials Research Society, 2001. pp. KK4.1.1–KK4.1.13.
[197] Glotzer SC, Starr FW. Towards multiscale simulations of filled and nanofilled polymers.
In: Cummings PT, Westmoreland PR, Carnahan B, editors. Foundations of Molecular
Modeling and Simulation: Proceedings of the 1st international conference on molecular
modeling and simulation. Keystone: American Institute of Chemical Engineers, 2001. pp.
44–53.
[198] Ogata S, Lidorikis E, Shimojo F, Nakano A, Vashishta P, Kalia RK. Hybrid finite-
element/molecular-dynamics/electronic-density-functional approach to materials
simulations on parallel computers. Comp Phys Comm 2001; 138: 143-54.
[199] Hyer MW. Stress analysis of fiber-reinforced composite materials. McGraw-Hill, Boston,
1998.
[200] Nemat-Nasser S, Hori M. Micromechanics: Overall properties of heterogeneous materials.
Elsevier, Amsterdam, 1999.
[201] Zhang P, Huang Y, Geubelle PH, Klein PA, Hwang KC. The elastic modulus of single-
wall carbon nanotubes: a continuum analysis incorporating interatomic potential. Int J
Solids Struct 2002;39: 3893–906.
[202] Tserpes KI, Papanikos P. A progressive fracture model for carbon nanotubes. Compos Part
B 2006; 37: 662-9.
[203] Belytschko T, Xiao S, Schatz G, Ruoff R. Atomistic simulations of nanotube fracture.
Phys Rev B 2002; 65: 235430.
[204] Steglich D, Siegmund T, Brocks W. Micromechanical modeling of damage due to particle
cracking in reinforced metals. Comput Mater Sci 1999; 16: 404-13.
[205] Langer SA, Fuller ER, Carter WC. OOF: an image-based finite element analysis of
material microstructures. Comput Sci Eng 2001;3:15–23.

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 317
[206] Langer SA, Reid ACE, Haan SI, Garcia RE. The OOF2 manual: Revision 3.2 for OOF2
Version 2.0 beta 8, NIST, USA. Online:
http://www.ctcms.nist.gov/~langer/oof2man/index.html.
[207] Ganesh VV, Chawla N. Effect of particle orientation anisotropy on the tensile behavior of
metal matrix composites: experiments and microstructure-based simulation. Mater Sci Eng
A 2005; 391: 342-53.
[208] Cannillo V, Manfredini T, Montorsi M, Boccaccini AR. Use of numerical approaches to
predict mechanical properties of brittle bodies containing controlled porosity. J Mater Sci
2004;39:4335–7.
[209] Cannillo V, Manfredini T, Montorsi M, Boccaccini AR. Investigation of the mechanical
properties of Mo-reinforced glassmatrix composites. J Non-Crystal Solids 2004;344:88–93.
[210] Chawla N, Patel BV, Kopman M, Chawla KK, Saha R, Patterson BR, Fuller ER, Langer
SA. Microstructure-based simulation of thermomechanical behavior of composite materials
by object-oriented finite element analysis. Mater Characteriz 2003; 49: 395–407.
[211] Cannillo V, Pellacani GC, Leonelli C, Boccaccini AR. Numerical modeling of the fracture
behavior of a glass matrix composite reinforced with alumina platelets. Composites Part A
2003;34:43–51.
[212] Cannillo V, Leonelli C, Manfredini T, Montorsi M, Boccaccini AR. Computational
simulations for the assessment of the mechanical properties of glass with controlled
porosity. J Porous Mater 2003;10:189–200.
[213] Wang Z, Kulkarni A, Deshpande S, Nakamura T, Herman H. Effects of pores and
interfaces on effective properties of plasma sprayed zirconia coatings. Acta Mater 2003;
51: 5319-34.
[214] Zimmermann MH, Baskin DM, Faber KT, Fuller Jr ER, Allen AJ, Keane DT. Fracture of a
textured anisotropic ceramic. Acta Mater 2001;49:3231–42.
[215] Zimmermann A, Carter WC, Fuller ER. Damage evolution during microcracking of brittle
solids. Acta Mater 2001;49:127–37.
[216] Saigal A, Fuller Jr ER, Langer SA, Carter WC, Zimmermann MH, Faber KT. Effect of
interface properties on microcracking of iron titanate. Scripta Mater 1998;38:1449–53.
[217] Avella M, Bondioli F, Cannillo V, Errico ME, Ferrari AM, Focher B, Malinconico M,
Manfredini T, Montorsi M. Preparation, characterization and computational study of poly
(
ε
-caprolactone) based nanocomposites. Mater Sci Technol 2004;20:1340–4.
[218] Iwahori Y, Ishiwata S, Sumizawa T, Ishikawa T. Mechanical properties improvements in
two-phase and three-phase composites using carbon nanofiber dispersed resin. Compos
Part A 2005; 36: 1430.
[219] Wang H, Bai Y, Liu S, Wu J, Wong CP. Combined effects of silica filler and its interface
in epoxy resin. Acta Mater 2002; 50: 4369-77.
[220] Lan T, Pinnavaia TJ. Clay-reinforced nanocomposites. Chem Mater 1994; 6: 2216-9.
[221] Subramaniyan AK, Sun CT. Enhancing compressive strength of unidirectional polymeric
composites using nanoclay. Compos Part A 2006; 37: 2257.

318 Hurang Hu, Landon Onyebueke, Ayo Abatan Vol.9, No.4
[222] Wetzel B, Haupert F, Zhang MQ. Epoxy nanocomposites with high mechanical and
tribological performance. Comps Sci Technol 2003; 63: 2055-67.
[223] Ou Y, Yang F, Yu ZZ. A new conception on the toughness of nylon 6/silica
nanocomposite prepared via in situ polymerization. J Polym Sci B 1998; 36: 789-95.
[224] Cho J, Joshi MS, Sun CT. Effect of inclusion size on mechanical properties of polymeric
composites with micro and nanoparticles. Compos Sci Technol 2006; 66: 1941-52.
[225] Chisolm N, Mahfuz H, Rangari VK, Adnan A, Jeelani S. Fabrication and mechanical
characterization of carbon/SiC-epoxy nanocomposites. Compos Struct 2005; 67: 115-24.
[226] Voros G, Pukanszky B. Prediction of the yield stress of composites containing particles
with an interlayer of changing properties. Composites A 2002; 33: 1317-22.
[227] Reynaud E, Jouen T, Gauthier C, Vigier G, Varlet J. Nanofillers in polymeric matrix: a
study on silica reinforced PA6. Polymer 2001; 42: 8759-68.
[228] Kontou E, Anthoulis G. The effect of silica nanoparticles on the thermomechanical
properties of polystyrene. J Appl Polym Sci 2007; 105: 1723-31.
[229] Saber-Samandari S, Khatibi AA. The effect of interphase on the elastic modulus of
polymer based nanocomposites. In: Liu HY, Hu XZ, Hoffman M, editors. Fracture of
materials: moving forwards. Switzerland: Tans Tech Publications; 2006. pp. 199–204.
[230] Carrado KA, Xu L. In situ synthesis of polymer-clay nanocomposites from silicate gels.
Chem Mater 1998; 10: 1440-5.
[231] Schiotz J, Jacobsen KW. A maximum in the strength of nanocrystalline copper. Science
2003; 301: 1357-59.
[232] Chen Q, Chasiotis I, Chen C, Roy A. Nanoscale and effective mechanical behavior and
fracture of silica nanocomposites. Compos Sci Technol 2008; 68: 3137-44.
[233] Adachi T, Osaki M, Araki W, Kwon S. Fracture toughness of nano- and micro-spherical
silica-particle-filled epoxy composites. Acta Mater 2008; 56: 2101-9.
[234] Zhang H, Zhang Z, Friedrich K, Eger C. Property improvements of in situ epoxy
nanocomposites with reduced interparticle distance at high nanosilica content. Acta Mater
2006: 54: 1833.
[235] Ragosta G, Abbate M, Musto P, Scarinzi G, Mascia L. Epoxy-silica particulate
nanocomposites: chemical interactions, reinforcement and fracture toughness. Polymer
2005; 46: 10506.
[236] Choi S, Awaji H. Nanocomposites-a new material design concept. Sci Technol Adv Mater
2005; 6: 2-10.
[237] Lee J, Yee AF. Fracture of glass bead/epoxy composites: on micro-mechanical
deformations. Polymer 2000; 41: 8363.
[238] Gao L, Wang HZ, Hong JS, Miyamoto H, Miyamoto K, Nishikawa Y, de la Torre D.
Mechanical properties and microstructures of nano-SiC-Ai2O3 composites densified by
spark plasma sintering. J Eur Ceram Soc 1999; 19: 609-13.

Vol.9, No.4 Characterizing and Modeling Mechanical Properties of Nanocomposites 319
[239] Davidge RW, Brook RJ, Cambier F, Poorteman M, Leriche A, O’sullivan D, Hampshire S,
Kennedy T. Fabrication, properties, and modeling of engineering ceramics reinforced with
nanoparticles of silicon carbide. Br Ceram Trans 1997; 96: 121-7.
[240] Carroll L, Sternitzke M, Derby B. Silicon Carbide particle size effects in alumina-based
nanocomposites. Acta Mater 1996; 44: 4543-52.
[241] Zhao J, Steans LC, Harmer MP, Chan HM, Miller GA, Cook RF. Mechanical behavior of
alumina-silicon carbide nanocomposites. J Am Ceram Soc 1993; 76: 503-10.
[242] Niihara K. New design concept of structural ceramics-ceramic nanocomposites. J Ceram
Soc Japan 1991; 99: 974-82.
[243] Awaji H, Choi SM. Review: ceramic-based nanocomposites. In: SG Pandalai (Ed.), Recent
Research Developments in Materials Science & Engineering 2002; 1: 585-597.
[244] Awaji H, Choi SM, Yagi E. Mechanisms of toughening and strengthening in ceramic-
based nanocomposites. Mech Mater 2002; 34: 411-22.
[245] Xiao SP, Belytschko T. A bridge domain method for coupling continua with molecular
dynamics. Comput Methods Appl Mech Eng 2004; 193: 1645-69.